Universidad de Chile Facultad de Ciencias F´ısicas y - U

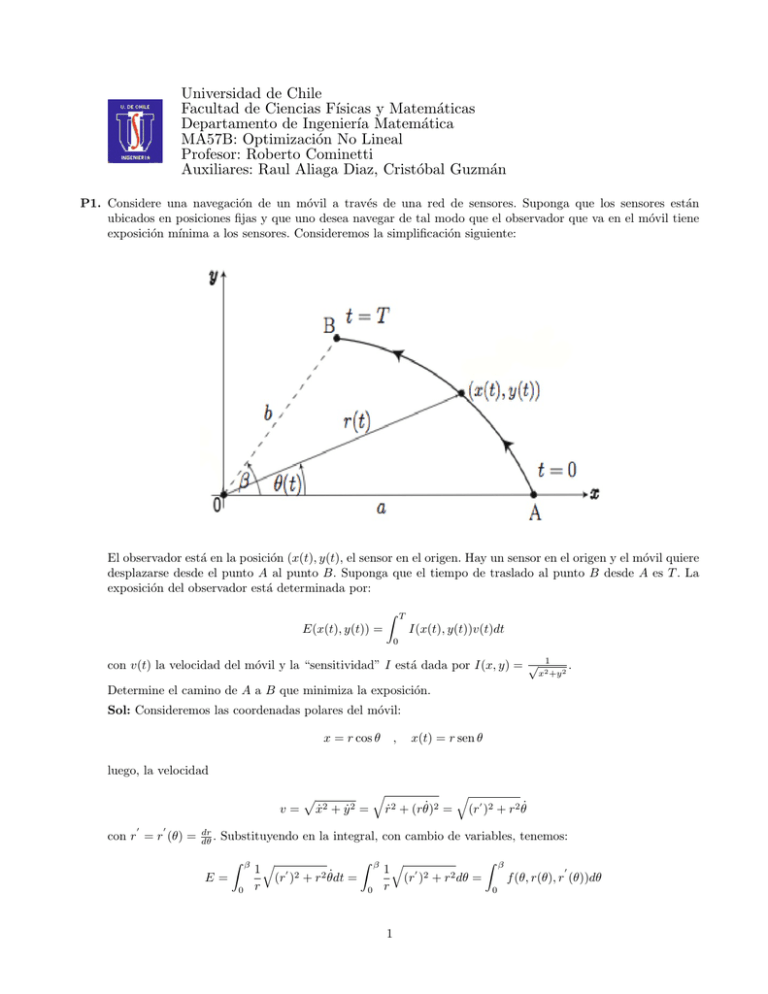
Universidad de Chile
Facultad de Ciencias Fı́sicas y Matemáticas
Departamento de Ingenierı́a Matemática
MA57B: Optimización No Lineal
Profesor: Roberto Cominetti
Auxiliares: Raul Aliaga Diaz, Cristóbal Guzmán
P1. Considere una navegación de un móvil a través de una red de sensores. Suponga que los sensores están
ubicados en posiciones fijas y que uno desea navegar de tal modo que el observador que va en el móvil tiene
exposición mı́nima a los sensores. Consideremos la simplificación siguiente:
El observador está en la posición (x(t), y(t), el sensor en el origen. Hay un sensor en el origen y el móvil quiere
desplazarse desde el punto A al punto B. Suponga que el tiempo de traslado al punto B desde A es T . La
exposición del observador está determinada por:
Z
T
E(x(t), y(t)) =
I(x(t), y(t))v(t)dt
0
con v(t) la velocidad del móvil y la “sensitividad” I está dada por I(x, y) = √
1
.
x2 +y 2
Determine el camino de A a B que minimiza la exposición.
Sol: Consideremos las coordenadas polares del móvil:
x = r cos θ
,
x(t) = r sen θ
luego, la velocidad
v=
0
0
con r = r (θ) =
dr
dθ .
p
ẋ2
+
ẏ 2
q
=
ṙ2 + (rθ̇)2 =
q
(r0 )2 + r2 θ̇
Substituyendo en la integral, con cambio de variables, tenemos:
Z
E=
0
β
1
r
q
(r0 )2 + r2 θ̇dt =
Z
0
β
1
r
q
1
(r0 )2 + r2 dθ =
Z
β
0
f (θ, r(θ), r (θ))dθ
0
Como f no depende de theta, podemos tomar la ecuación de Euler Lagrange:
d ∂f
∂f
( 0)−( )=0
dθ ∂r
∂r
e integrarla una vez para obtener
f −r
0
∂f
= constante
∂r0
substituyendo por lo términos adecuados, tenemos:
r
p
0
(r )2 + r2
= constante
o bien rr0 = constante, lo cual tras integración lleva a r = c1 exp(c2 θ), constantes que podemos determinar
usando las condiciones de borde, lo cual brinda como resultado:
r(θ) = a exp(θ
2
ln(b/a)
)
β