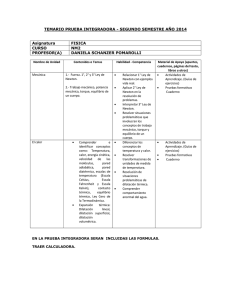
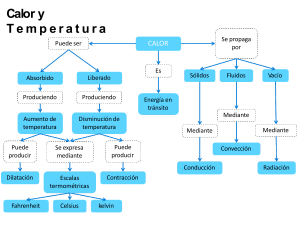
GUIA DE LABORATORIO Nº XX

GUÍA Nº 2
DILATACIÓN LONGITUDINAL DE LOS CUERPOS SÓLIDOS
1.- Introducción
Se aplica la ley cero de la Termodinámica, transferencia de calor y las propiedades
vibracionales de las partículas que conforman las redes atómicas de los materiales
2.- Aprendizajes Esperados
a) De acuerdo al programa de estudios
2.1.- Criterios de Evaluación
a) Determinar cambio de longitud de un alambre por efecto del cambio de
temperatura.
3.-Materiales
a)
b)
c)
d)
e)
f)
g)
h)
1 alambre de cobre de 0.5 m de largo y 0.2 mm. de diámetro
1 cronometro
1 multitester con un cable punta – caimán y otro punta - punta
1 Regla metálica
2 bases de soporte
Una fuente de poder y un cable punta - caimán
1 regla metálica pequeña y cinta adhesiva
1 masa de 20 grs.
4.- Actividades
4.1.- Procedimiento
Construya el sistema que propone la Figura N°1.
Se construye, el dispositivo de la figura para medir la dilatación térmica de un
filamento de material conductor de calor especifico 0.092 cal / gr º C y masa 0.2 gr:
Asignatura: Física Termodinámica
Área Ciencias Básicas
Responsables: Patricio Pacheco H./Jacqueline
Alea P.
Fecha actualización: Otoño 2009
Regla metálica pequeña
Regla
18 cm
3 cm
0.2 cm
Cronometro
Amperímetro
2.198
seg
0.8 A
4 Volt
220 volts
Fuente de Poder
Figura N°1
a) Calcule el valor del coeficiente de dilatación y compare con el de tabla
18.4 *10-6 (1 / ºC) a través del error porcentual. Discuta las fuentes de error
b) Preparación experimental de la experiencia: Prenda la fuente de poder y ajuste
el experimento a los valores sugeridos
4.2.- Cálculo y Resultados
Desarrollo de la experiencia para obtener los valores de interés
a) Calcule el valor del coeficiente de dilatación y compare con el de tablas 18.4
*10-6 (1 / ºC) a través del error porcentual. Discuta las fuentes de error
b) Si es posible solicite otros tipos de alambre y complete el Cuadro N°1.
Material
Aluminio
Cobre
Acero
Deformación ∆l
Porcentaje respecto l0
Cuadro N°1
Asignatura: Física Termodinámica
Área Ciencias Básicas
Responsables: Patricio Pacheco H./Jacqueline
Alea P.
Fecha actualización: Otoño 2009
c) ¿Qué metal se dilata mas fuertemente, cual menos fuertemente? Ordene.
Dilatación fuerte→________________________________________________
Dilatación mediana→______________________________________________
Dilatación Pequeña→______________________________________________
d) La tabla siguiente da el coeficiente de dilatación térmica para diferentes materiales:
Plexiglas 0,000070 K
Aluminio 0,000024 K
−1
−1
Hormigón 0,000012 K
Hierro
0,000012 K
−1
−1
Porcelana 0,000003 K
Cobre
0,000019 K
−1
−1
e) ¿Por qué se utiliza hierro (acero) en combinación con el hormigón y ningún otro
material?
_______________________________________________________________
f) ¿Por qué motivo se dejan pequeños espacios libres entre los rieles de los
ferrocarriles?
_______________________________________________________________
4.3.- Investigación Previa al Experimento:
a) ANEXO MATEMATICO
1. En la relación serial para la dilatación:
L ( t ) = L (T ) +
0
(T − T )
0
1!
 dL (T ) 


 dT  T =T0
+
(T − T )
0
 d L (T ) 
 2 
 dT  T =T0
2
2
2!
+
(T − T )
0
3!
3
 d L (T ) 
+ ....
 3 
dT
 T =T0

3
es posible aplicar restricciones. Tal como su nombre lo indica, si la dilatación es lineal
en la temperatura los términos:
2
O
=
(T − T )
0
2!
2
 d L (T ) 
 2 
 dT  T =T0
2
+
(T − T )
0
3!
3
 d L (T ) 
+ ....
 3 
 dT  T =T0
3
Se denominan términos de orden superior a uno en la variable de temperatura por lo
que su contribución es no lineal. Es un hecho físico probado que las sustancias
muestran comportamiento de dilatación lineal pero en un rango de temperatura que es
propio a la naturaleza de cada sustancia, luego al forzarlas mas allá de esos rangos
significa que los términos cuadráticos, cúbicos, etc en la temperatura se hacen
importantes. Mas todavía la sustancia empleada puede dejar su estado natural y entrar
en ebullición e incluso evaporación.
Los termómetros de Mercurio empleados en clase tienen un rango de tolerancia
aproximado hasta 150 °C y con mucho 250 °C. Es por esto que el fabricante indica en
la graduación del instrumento hasta donde se hace responsable (del orden de 120 °C
en los termómetros de Laboratorio).
Asignatura: Física Termodinámica
Área Ciencias Básicas
Responsables: Patricio Pacheco H./Jacqueline
Alea P.
Fecha actualización: Otoño 2009
2. Procedimiento de Calculo con ejemplo numérico de la figura Nº1
Q = V I ∆t =
4 * 0.8 * 2.198
cal = 1.68 cal
4.186
l 0 = (0.18 m) 2 + (0.03 m) 2 = 0.1825 m, l = (0.18 m) 2 + (0.032 m) 2 = 0.1828 m
∆l = l − l 0 = 0.0003 m
1.68 cal
= 91.3 º C
cal
0.092
0.2 gr
gr º C
∆l = α l 0 ∆T
∆T =
α=
Q
=
cm
0.0003 m
∆l
1
=
= 18.0 * 10 − 6
l 0 ∆T 0.1825 m 91.3 º C
ºC
ε% =
1
1
− 18.4 * 10 − 6
º C 100 = 2.2%
ºC
1
18.4 * 10 − 6
ºC
18.0 * 10 − 6
5.- Bibliografía
1. R. Serway, Vol. I, Física, Editorial Mc Graw – Hill, 2005
2. Termodinámica, Tomo I, Yunus A. Cengel - Michael A. Boles, Editorial McGraw
- Hill, 1999
3. Termodinámica Técnica Fundamental, M.W. Zemansky - H.C. Van Ness,
Editorial Aguilar S.A. , España, 1980
Asignatura: Física Termodinámica
Área Ciencias Básicas
Responsables: Patricio Pacheco H./Jacqueline
Alea P.
Fecha actualización: Otoño 2009