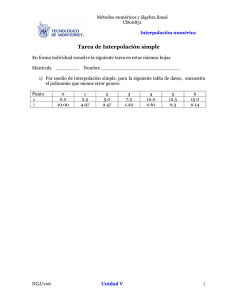
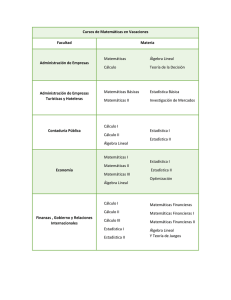
Apuntes de Métodos Numéricos 2o E.T.S.I. Telecomunicación

Apuntes de Métodos Numéricos
2o E.T.S.I. Telecomunicación
Universidad de Málaga
Carlos García Argos ([email protected])
http://pagina.de/telecos-malaga
Realizado con KLYX, un front-end para LATEX
Curso 1999/2000
Índice General
1 Errores
3
1.1
Introducción a los métodos numéricos computacionales . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
1.2
Generación y propagación de errores . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
1.3
Inestabilidad de problemas y métodos numéricos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9
2 Álgebra lineal numérica I
11
2.1
Métodos directos para sistemas lineales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
2.2
Sistemas sobredeterminados y pseudoinversas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
2.3
Estimaciones de error . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
2.4
Métodos iterativos para sistemas lineales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
3 Álgebra lineal numérica II
44
3.1
Cálculo de autovalores y autovectores . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44
3.2
Métodos de reducción a matriz tridiagonal y a matriz Hessenberg . . . . . . . . . . . . . . . . . . . . . . 46
3.3
Métodos iterativos de las potencias, de Jacobi y QR . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49
4 Interpolación y aproximación
56
4.1
Interpolación polinomial, de Hermite y trigonométrica . . . . . . . . . . . . . . . . . . . . . . . . . . . . 56
4.2
Teoría de la aproximación en espacios vectoriales normados . . . . . . . . . . . . . . . . . . . . . . . . . 65
4.3
Aproximación por mínimos cuadrados polinomial y trigonométrica,
discreta y continua . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67
4.4
La transformada discreta de Fourier y el algoritmo FFT . . . . . . . . . . . . . . . . . . . . . . . . . . . . 70
5 Derivación e integración numéricas
72
5.1
Métodos de derivación numérica . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72
5.2
Métodos de integración numérica de Newton-Côtes y de Gauss . . . . . . . . . . . . . . . . . . . . . . . 74
5.3
Método de extrapolación de Richardson y métodos adaptativos . . . . . . . . . . . . . . . . . . . . . . . 79
6 Métodos numéricos para ecuaciones diferenciales ordinarias
80
6.1
Problema de valor inicial . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 80
6.2
Métodos unipaso de Taylor y de Runge-Kutta . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 80
6.3
Métodos multipaso y predictores-correctores . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 80
6.4
Convergencia y estabilidad de los métodos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 80
6.5
Problema de contorno . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 80
6.6
Métodos del disparo, de diferencias finitas y de elementos finitos . . . . . . . . . . . . . . . . . . . . . . 80
1
ÍNDICE GENERAL
7 Resolución de ecuaciones no lineales
2
81
7.1
Métodos de iteración de punto fijo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 81
7.2
Teoremas de convergencia . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 81
7.3
Métodos para ecuaciones algebraicas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 81
7.4
Sistema de ecuaciones no lineales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 81
7.5
Iteración de punto fijo, métodos de Newton y cuasi-Newton . . . . . . . . . . . . . . . . . . . . . . . . . 81
8 Métodos numéricos de optimización
82
8.1
Optimización no restringida . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 82
8.2
Métodos iterativos de descenso, del gradiente, del gradiente cojungado, de Newton y cuasi-Newton . . 82
8.3
Problema de mínimos cuadrados no lineal: método de Levenberg-Marquardt . . . . . . . . . . . . . . . 82
8.4
Programación no lineal . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 82
8.5
Métodos de penalización, de conjunto activo y de programación cuatrática secuencial . . . . . . . . . . 82
Capítulo 1
Errores
1.1 Introducción a los métodos numéricos computacionales
El objetivo de los Métodos Numéricos es el de obtener soluciones aproximadas. Se trabaja con números reales. Los
Métodos Numéricos comprenden el desarrollo y la implementación y uso de algoritmos numéricos y de software
para la resolución de un problema físico, a partir de un modelo matemático del sistema físico en cuestión.
Al trabajar con ordenadores, existen indeterminaciones en los resultados, ocasionados por el uso de la numeración
en punto flotante, las consecuentes discretizaciones de intervalos continuos y la necesariedad de que las series sean
finitas (dado que hay que parar).
1.2 Generación y propagación de errores
Hay varios tipos de errores que pueden aparecer en la resolución de problemas:
Errores experimentales o de medición: son errores anteriores al cálculo y por tanto no aplicables a los Métodos
Numéricos.
Errores en el cálculo numérico:
- Al operar en punto flotante (ordenadores). Son errores de redondeo.
- De discretización o truncamiento: son errores propios de los métodos numéricos (no se hace el límite infinito, la
integral con todos los valores del intervalo, etc.).
Implementación del método: errores de programación.
A continuación únicamente vamos a considerar los errores de cálculo numérico.
Veamos la representación de números:
Representación de un número real x en el sistema decimal:
x
= c1c2c3 cn:cn+1 n+2
= c1 10n 1 + c2 10n 1 + + cn + cn10+1 + c100
+ cj 2 f0; 1; : : : 9g
Representación de un número real x en base :
3
CAPÍTULO 1. ERRORES
4
= d1d2 dk :dk+1 (
dk+1 dk+2
n
1
n
2
= d1 + d2 + + dk + + 2 + dj 2 f0; 1 : : : 1g
En los sistemas computacionales suele ser = 2; 8; 16.
x
Representación normalizada:
x
Donde:
= :d1d2 dk dk+1 e
d1 6= 0; e 2 Z y d1 d2 dk dk+1 es la mantisa normalizada.
El almacenamiento en una máquina se realiza de la siguiente forma:
signo
exponente(e)
mantisa normalizada
Tabla 1.1: Almacenamiento de un número normalizado
La mantisa normalizada consta de t dígitos y es l
e L.
Los números que existen para la máquina son los que se pueden representar mediante todas las combinaciones de
esta forma de representación, los demás no son representables para ella.
Para almacenar números en una máquina (ordenador) tenemos la numeración en punto flotante: t dígitos en base y
exponente e entre l y L.
F (; t; l; L)
= +:000 0 0 [
f:d1d2d3 dt c; 0 < d1 < ; 0 di < ; i = 2 : t; l e Lg
Al representar los números de esta forma, se pierden infinitos valores de la recta real.
x
= (:d1d2 dt e) + :dt+1 e t
= u c + v e t ; 1 juj < 1; 0 jvj < 1
El primer paréntesis (u) es la parte del número que podemos representar con este tipo de almacenamiento, mientras
que el segundo paréntesis (v) no nos cabe. Tenemos dos opciones:
Nos quitamos v sin más: truncamos el número.
fl (x) = xC = u e
Redondeamos el número. Es lo más habitual en los ordenadores de hoy día.
fl (x) = xR =
8
<
:
u e
jvj <
u e + c t u > 0 ; jv j u e c t u < 0 ; jv j 1
21
21
2
CAPÍTULO 1. ERRORES
5
Una vez aplicado el redondeo, si es necesario, se vuelve a normalizar el número.
Ejemplo:
0:999974 104 y vamos a redondearlo a 4 cifras:
0:9999 104 + 0:0001 104 = 1:0000 104 número no normalizado:
1:0000 104 = 0:1000 105 ya está normalizado
Tenemos el número
|
Ahora vamos a ver los errores en la representación de números en punto flotante, si x es un valor aproximado de x: el
error que resulta de sustituir x por su forma en punto flotante, x , se llama error de redondeo (tanto si se usa redondeo
como truncado).
E = x x
Error absoluto de x : jE j = jx
Error de x :
Error relativo de x :
=
x x
x
xj
Las cotas de error en la representación de números en punto flotante truncada (si x
EC = v e t
jEC j = jvj e t < e t
jC j = jfl(jxx)j xj < jexj t eet = 1
1
6= 0) son:
t
= 0):
Y las cotas para la representación de números en punto flotante redondeada (x 6
8
<
ER = :
v e t
jvj < 12
e
t
(1 v) e t u > 0; jvj 121
( 1 v) u < 0; jvj 2
jERj e2 t
jR j 2 t
1
Ejemplo:
Consideremos los errores absolutos y relativos:
= 0:3000 101 y p = 0:3100 101 el error absoluto es 0:1 y el relativo 0:333 ^3 10 1.
Si p = 0:3000 10 3 y p = 0:3100 10 3 el absoluto es 0:1 10 4 y el relativo 0:333 ^
3 10 1 .
Si p = 0:3000 104 y p = 0:3100 104 el error absoluto es 0:1 10 3 y el relativo 0:333 ^
3 10 1.
Si p
Se observa que el error relativo es el mismo aún cambiando en varios órdenes de magnitud el número. El error
relativo es ma ś significativo que el absoluto.
|
Veamos algunas definiciones:
= 21 1 t .
Epsilon de máquina es el menor número > 0 tal que fl (1 + ) 6= 1, el número que hay que sumarle a otro para
que se obtenga el número siguiente en la numeración de la máquina.
Ejemplo: en Matlab, el epsilon de máquina eps es una constante que vale 2 52 .
Se llama unidad de redondeo en base al número CAPÍTULO 1. ERRORES
6
Un valor x aproximado a x tiene k dígitos fraccionarios exactos o correctos en base si cumple:
jx xj < 12 k
(1.1)
Un valor x aproximado a x tiene k dígitos significativos en base si cumple:
x
x
x <
1 1
2
k
(1.2)
Las dos últimas definiciones son especialmente importantes.
Ahora consideremos la aritmética de punto flotante.
Errores generados en la aritmética de punto flotante:
+; ; ; =g.
Definimos una operación con el símbolo Æ, de forma que Æ 2 f
En una unidad aritmético-lógica se utilizan registros como unidades de almacenamiento de los datos que se van a
operar. Estos tienen t posiciones para almacenar la mantisa, aunque en ocasiones se dispone de s posiciones adicionales, que nos pueden servir para almacenar los datos significativos de los datos en caso de que tengamos que
desplazar los bits de la mantisa de alguno de ellos.
Si tenemos dos números en punto flotante:
fl (x) = xi (mx ; ex )
fl (y ) = yi (my ; ey )
Donde mx ; my son las mantisas de x e y y ex ; ey los exponentes de x e y respectivamente, al hacer la suma, si tenemos
que desplazar la mantisa (cuando ex 6 ey por ejemplo), se pueden perder dígitos si no se dispone de posiciones
adicionales para almacenarlos. Al multiplicar, las mantisas son de t dígitos, así que el resultado será de t dígitos,
con lo cual podemos perder una cantidad considerable de precisión en el cálculo.
=
2
= t, pero esto implica un coste bastante elevado, por lo que se suele alcanzar un
= 1, aunque soluciones radicalmente económicas no tienen dígitos adicionales.
El caso más deseable es que s
compromiso. A veces se usa s
El error relativo al hacer una operación Æ es:
fl
Siendo = 12 1
t y x
(x Æ y ) (x Æ y ) r
x Æ y (1.3)
= fl (x) ; y = fl (y).
El valor de r depende del de s:
es redondeado
) r = 1 2sisielelnunmero
u
mero
es truncado
2
si el nu
mero es redondeado
s=1 ) r=
4 si el nu mero es truncado
s = 0 ) r puede ser muy grande para sumas y restas
s=t
(1.4)
En el último caso, r depende de los operandos, y no tiene demasiada influencia para multiplicaciones y divisiones.
Por tanto: si hay posiciones adicionales, el error cometido no es realmente problemático, sin embargo, cuando no hay
ninguna posición adicional, podemos tener un error muy grande. Esto ocurre, por ejemplo, al trabajar con números
reales de doble precisión, que ocupan al almacenarlos todas las posiciones del registro, incluidas las adicionales, con
lo que se comporta como si s
.
=0
Conclusión: una máquina finita comete errores, tanto al almacenar datos como al operar con ellos.
CAPÍTULO 1. ERRORES
7
Propagación de errores:
Dadas dos aproximaciones de x e y , x e y respectivamente, el error total en el resultado de una operación aritmética
Æ es la suma del error generado y el propagado:
fl (x Æ y ) x Æ y = fl (x Æ y ) x Æ y + x Æ y x Æ y
(1.5)
Donde:
fl (x Æ y ) x Æ y x Æ y x Æ y
()
es el error generado
es el error propagado
(x ) y jy
Si sólo hay cotas Æ para los errores absolutos en los operandos, jx xj Æ
en el supuesto de jx j Æ x y jy j Æ y , para el error absoluto se verifica:
( )
( )
Suma
Resta
Multiplicacion
Division
Æ (x + y ) = Æ (x ) + Æ (y )
Æ (x y ) = Æ (x ) + Æ (y )
Æ (x y ) = jy j Æ(x ) + jx j Æ (y )
jx jÆ(y ) , y; y 6= 0
Æ xy = jy jÆ(x j)+
y j2
y j Æ (y ), es claro que,
(1.6)
Veamos la demostración para el caso de la multiplicación:
Si , son los errores relativos de x e y respectivamente:
x
y
x y xy
= x (1 + )
= y (1 + )
= x (1 + ) y (1 + )
= xy + xy + xy
= y (x x) + x (y
xy
y ) + (x
x) (y y)
Y tomando valores absolutos se obtiene la expresión antes vista. Los dos primeros paréntesis van multiplicados por
y y x respectivamente, los cuales hay que sustituir por y y x respectivamente ya que el número que se conoce es la
aproximación, el número almacenado en la máquina.
Volviendo sobre el grupo de ecuaciones (1.6), se puede observar que la división puede tener una cota de error grande,
ya que y puede ser muy pequeño, con lo que su cuadrado lo es más y el cociente se hace muy grande.
Veamos ahora las cotas de error relativo:
Si y son los errores relativos de x e y respectivamente,
j(x +y ) (x+y)j Æ(x )+Æ(y )
jx+yj
jx+yj
j(x y ) (x y)j Æ(x )+Æ(y )
Resta
jx yj
jx y j
n j(xyjx) y(jxy)j Multiplicacio
j
j + j j
x ) ( x )j
j
(
y
y
n
Divisio
j x j = 1+ jj + j j
Suma
(1.7)
y
Desde el punto de vista del error relativo, las operaciones peligrosas son las sumas y las restas, ya que se divide y si
los números son pequeños, la cota de error puede ser muy grande.
CAPÍTULO 1. ERRORES
8
Aparecen las diferencias cancelativas, operaciones de resta que pueden anular o casi anular términos que realmente no
se anulan, introduciendo un error más grande todavía. Se dan en sumas con operandos de signo contrario y casi del
mismo módulo, y en diferencias de números con el mismo signo y módulos también aproximados.
Ejemplo:
p
1 + x p1
0
x si x nos va a salir un resultado erróneo al operar directamente. Para obtener un resultado
mejor, factorizamos la suma:
1 + x p1
p
x=
p11++xx +(1p1 x)x = p1 + x 2+x p1 x
Este resultado es preferible, ya que es un número muy pequeño multiplicado por 2 dividido entre un número que es
aproximadamente 2. De la otra forma, al hacer la raíz de
x siendo x un número muy pequeño queda prácticamente
la raíz de 1, con lo que el resultado es mucho menos preciso.
1+
|
Veamos lo que ocurre con funciones (sucesión de operaciones, una forma de generalizar el error para n operaciones):
= ()
= ( )
f x donde y es el resultado y x el dato, y y f x siendo x e y las aproximaciones de
Tenemos y
respectivamente. Si f es derivable, podemos desarrollar la función en series de Taylor:
0
f (x) = f (x ) + f (x ) (x x ) +
Si f
0
00
f (x )
(x ) 6= 0:
2! (x
xey
x ) 2 + : : :
jy yj = f 0 (x ) jx xj
0
(x ) = 0 hay que considerar la siguiente derivada.
Si ahora tenemos más de un dato: y = f (x1 ; x2 ; : : : xn ); y = f (x1 ; x2 ; : : : ; xn )
Si f
Haciendo de nuevo el desarrollo de Taylor y cojiendo la primera derivada de cada término:
jy
n X
@f jxi x j krf (x )k kx x k
yj =
(
x
;
x
;
:
:
:
;
x
)
1 2
n i
2
2
@x
i
i=1
(1.8)
Donde la desigualdad viene de la desigualdad de Cauchy-Schwartz y el subíndice 2 indica que es la “norma 2”, es
decir, la norma de un vector tal y como se la conoce (raíz cuadrada de las componentes al cuadrado).
rf (x ) =
@f
@x
1
.
..
@f
@xn
~y = f~ (~x) ) k~y
Donde Jf
x=
.. . xn x1
~y k kJf (~x )k k~x ~x k
(~x ) es el jacobiano de f.
La norma de una matriz A, kAk se calcula haciendo la raíz cuadrada del radio espectral de la matriz por su traspuesta,
que es el módulo mayor de los autovalores de la matriz:
1 ; 2 ; : : : ; n autovalores de la matriz A:
= (A) = i =8i; j i > j ; i 6= j es el radio espectral de A.
p
kAk = (At A)
(1.9)
CAPÍTULO 1. ERRORES
9
1.3 Inestabilidad de problemas y métodos numéricos
Vamos a empezar con algunos ejemplos:
Ejemplo 1:
= R01 xx+6 dx usando la fórmula recurrente I k = k1 6Ik
1 teniendo I0 = ln 67 .
Si usamos una calculadora científica normal, obtenemos (tras mucho teclear) el valor I 20 = 22875:75. Sin embargo,
Calcular la integral I 20
20
hemos de notar que estamos evaluando una integral positiva en todo el intervalo de integración, con lo que el resultado debería ser positivo. Por otro lado, aunque no se vea a simple vista, este resultado en módulo es demasiado
grande. El mismo cálculo, realizado con Matlab, usando 16 dígitos de precisión, devuelve I 20
:
:::
Este resultado puede parecer exacto, pero aún así, sigue sin serlo, ya que acotando la integral, por la de una función
mayor:
= 0 1690451452
I20 <
Z
0
1 x20
6
dx =
1
1
21 6 = 126 = 0:0079365
un valor menor que el obtenido, y si tiene que ser mayor que el valor real de la integral, está claro que ninguno de
los dos resultados obtenidos es válido.
Este ejemplo refleja la incertidumbre en el resultado cuando manejamos números reales que al almacenarlos podemos hacer que se pierdan dígitos significativos.
|
Ejemplo 2:
Resolver el polinomio de segundo grado x 2
+ 1000x + 6:2521308 = 0 usando 8 dígitos de resolución.
p
Podemos emplear la fórmula que siempre hemos usado para la ocasión: x = b 2ba 4ac , y obtenemos los resulta2
dos siguientes con una calculadora:
x1 =
0:00625500
x2 =
999:99375
Teóricamente, al operar con las raíces se obtiene:
x1 + x2
x1 x2
x1 + x2 =
=
=
c
a
b
a
1000:000005
x1 x2 = 6:2549609
CAPÍTULO 1. ERRORES
10
En los cálculos realizados con Matlab (función roots):
x1
x2
=
=
0:00625216989
999:99374783
|
Ejemplo 3:
Se tienen los siguientes sistemas de ecuaciones:
0:9999 1 x1 = 0:002 2 2
y1
0:006
0:99995 1 x2 = 0:002 2 2
y2
0:006
y
Se obtienen las siguientes soluciones:
x1 = 10 y1 =
x2 = 20 y2 =
9:997
19:997
Se observa que a pesar de variar muy poco un dato las soluciones cambian enormemente (en comparación con el
cambio del dato).
|
A partir de los ejemplos podemos ver que hay diferentes comportamientos para diferentes tipos de problemas, ya
sea por el método de resolución empleado o por otras causas.
Se dice que un método es inestable si para la mayoría de los casos da buenos resultados, pero en algunos casos, ya sea
por la forma de los datos o por la forma de operarlos, se obtienen grandes diferencias (ejemplos 1 y 2).
Decimos que tenemos un problema mal condicionado si para pequeñas variaciones de los datos del problema, se obtienen grandes diferencias en los resultados independientemente del método o métodos empleados (ejemplo 3).
Si cuando resolvemos por un método un problema obtenemos un resultado diferente que la solución exacta, cabe
plantearse si la diferencia viene de un método inestable o de un problema mal condicionado. Para ello, se realiza un
análisis, que puede ser de cuatro tipos:
1. Análisis progresivo de error: partiendo de los errores en los datos, analizar, avanzando según los cálculos, los
errores acumulados.
2. Análisis regresivo de error: una vez obtenido el resultado, ver de qué problema es solución exacta (en el ejemplo
1, cuando hacemos x1 x2 y x1 x2 lo que hacemos es ver qué coeficientes son los de la ecuación que realmente
se ha resuelto). Es la forma más exacta de verificar la estabilidad de un método.
+
3. Análisis estadístico de error: se trata a los errores como variables aleatorias, con lo que se obtiene una función de
distribución, a partir de la cual se haya la varianza, la media, etc.
4. Análisis intervalar de error o por aritmética de intervalos: como no se conoce el dato preciso, se trabaja con un
intervalo en el que sabemos que está ese dato, y operamos con los extremos izquierdo y derecho del mismo, de
forma que sabemos que el resultado está dentro de un intervalo que es el que obtenemos como resultado. Este
método es reciente y se está desarrollando.
Capítulo 2
Álgebra lineal numérica I
Introducción
En la mayoría de los problemas hay que resolver sistemas de ecuaciones lineales, aquí vamos a ver algunos métodos
para resolverlas.
Empecemos por ver algunos conceptos básicos:
Representación matricial de sistemas de ecuaciones:
a11 x1 + : : : + a1n xn
..
.
an1 x1 + : : : + ann xn
=
..
.
=
b1
..
.
bn
(2.1)
Dado este sistema, hay que encontrar los valores de xi para los que se cumplen las relaciones.
0
A=B
@
1
0
.. C
. A
ann
x=B
@
a11 : : : a1n
..
.
an1
..
.
:::
1
0
.. C
. A
xn
b=B
@
x1
b1
1
.. C
. A
bn
(2.2)
Donde A se llama matriz del sistema, x vector de incógnitas y b vector de términos independientes.
En notación matricial, el sistema se escribe:
A x = b.
A la matriz Ajb se la llama matriz ampliada, y resulta de añadir el vector de términos independientes como la última
columna de la matriz del sistema:
0
B
@
a11 : : : a1n b1
..
.
an1
..
..
.
ann
.
:::
1
.. C
. A
bn
(2.3)
Teorema de Rouché-Frobenius para la existencia de soluciones de un sistema de ecuaciones lineales:
r (A) 6= r ([Ajb])
r (A) = r ([Ajb]) = n
r (A) = r ([Ajb]) < n
Donde r
(
)
Incompatible no existe solucion
Compatible determinado una unica solucion
Compatible indeterminado infinitas soluciones
(
(
)
(A) representa el rango de la matriz A.
Como introducción a un método de resolución que no se recomienda su uso, veamos la:
11
)
CAPÍTULO 2. ÁLGEBRA LINEAL NUMÉRICA I
12
Regla de Cramer:
Dado un sistema representado por su matriz del sistema A y por el vector de términos independientes b, las componentes de su vector de incógnitas x se obtienen de la siguiente forma:
det Aj
xj =
det (A)
(2.4)
Donde Aj es la matriz resultante de sustituir la columna j de la matriz A por el vector de términos independientes, y
det A representa el determinante de la matriz A.
( )
Este método es muy ineficiente, tiene un orden de O
n2 n!
operaciones para resolver el sistema.
Definición: Dadas dos sucesiones fxn g y fyn g diremos que yn es del orden de xn , yn
si existen dos constantes C y N tales que:
= O (xn ) (’O’ de Landau)
jynj C jxn j n > N
2.1 Métodos directos para sistemas lineales
Fundamentos de Álgebra matricial en los apuntes de Álgebra de 1o de Luis Gimilio Barboza.
2.1.1 Introducción: métodos directos e indirectos
Se dice que un método para resolver un problema es directo si tras un número finito de operaciones con los datos del
problema se obtiene una solución al problema, que, en general, será aproximada.
En los métodos iterativos se calcula una sucesión de vectores que son aproximaciones a la solución: x(s) , y en el
límite, tiende a la solución del problema: x.
(s)
x = slim
!1 x
Cuando se usa un ordenador para resolver un problema por un método de este tipo, no queda más remedio que
truncar la solución, es decir, realizar un número finito de iteraciones para obtener una solución aproximada.
Normalmente los métodos iterativos se emplean sólo con problemas de gran tamaño, en los que las matrices están
esparcidas o dispersas (tienen la mayoría de elementos iguales a cero).
Un ejemplo en telecomunicaciones sería el flujo de una red de ordenadores a nivel internacional (Internet).
2.1.2 Métodos directos
El fundamento básico de estos métodos es que existen sistemas fáciles de resolver, así que trataremos de transformar
el problema que tenemos a uno fácil de resolver.
Tenemos un sistema Ax
= b siendo A una matriz cuadrada. Tenemos varios casos:
A es diagonal. En este caso, las soluciones son:
b
xi = i i = 1 : : : n
aii
(2.5)
CAPÍTULO 2. ÁLGEBRA LINEAL NUMÉRICA I
A es ortogonal (A
13
1 = At ):
x = A 1 b = At b
A es triangular superior (todos los elementos por debajo de la diagonal principal son cero):
n
xi = b1ii bi
xn = abnn
(2.6)
Pn
j =i+1 aij xj
i=n
1 : 1 : 1 (Sustitucion regresiva)
(2.7)
A es triangular inferior:
1 aij xj i = 2 : n (Sustitucion progresiva)
j =1
x1 = ab111 xi = a1ii bi
Pi
(2.8)
2.1.3 Teorema de equivalencia de sistemas
Sea M una matriz invertible (no singular). Entonces los sistemas
decir, tienen el mismo conjunto de soluciones.
Así pues, vamos a basar los métodos en pasar de A x
de resolver (alguno de la sección anterior).
A x = b y M A x = M b son equivalentes, es
= b a A^ x = ^b equivalentes donde el último sistema sea fácil
A^ = M A; ^b = M b
En los métodos que vamos a emplear no vamos a llegar a calcular una matriz M, simplemente vamos a transformar
A en A mediante operaciones elementales.
^
Esto se puede ver de otra forma:
Si existe tal matriz M, entonces
forma que:
A = M 1 A^.
N A^ x = b :
De este modo, podemos plantearnos una factorización
N y = b
A^ x = y
es la solucion intermedia
es la solucion final
2.1.4 Método de eliminación de Gauss
Trabajamos con la matriz ampliada del sistema y hacemos la transformación:
h
i
[Ajb] A^j^b
de forma que la última sea triangular o diagonal.
0
In = B
@
1
:::
0
.
..
.
..
:::
01
.. C
. A
1
=
e1 e2 : : : en
A = N A^ de
CAPÍTULO 2. ÁLGEBRA LINEAL NUMÉRICA I
14
In es lo que se conoce como matriz unidad, y ei son los vectores unitarios de la base canónica (dispuestos como filas).
Definimos una operación elemental como:
0
Eji () = I + ej eti = j
B
B
B
B
B
B
@
1
:::
.
i
:::
01
0
::: :::
0C
C
0
:::
..
.
..
..
.
0
..
.
..
.
..
0
.. C
. C
C
(2.9)
.. C
. A
.
1
:::
det (Eij ()) = Entonces, al hacer Eji
a la original):
() A = A + ej eti A nos quedaría la matriz de sistema siguiente (que además es equivalente
0
@
aj 1 + ai1
1
Igual que A
ajn + ain
:::
Igual que A
A
+ ai1, tiene que ser =
aj1 .
ai1
Se define una permutación de una matriz, Pij como el intercambio de la fila i con la fila j :
De forma que, si queremos anular el elemento aj 1
Pij = e1 e2 : : : ej ei+1 : : : ej 1 ei ej +1 : : : en
det (Pij ) =
1
El determinante de la matriz resultante es el mismo que la original pero cambiado de signo.
0
Pij A =
i B
B aj 1
B
B
j @
:::
ai1 : : :
Igual
:::
Igual
:::
Igual
1
: : : ajn
:::
C
C
C
C
ain A
Triangularización:
Primer paso:
Pj1 1
j1 1
(1)
j1
En1 (n1 ) E21 (21 ) Pj1 1 j 1 = aa(1)
11
Eji (ji ) representa una operación de suma de la fila i multiplicada por ji con la fila j .
La matriz resultante de esta operación:
CAPÍTULO 2. ÁLGEBRA LINEAL NUMÉRICA I
0
B
B
B
@
Donde los superíndices
1
0
C
C
.. C
. A
B
B
B
B
@
a11 : : : a1n b1
a21 : : : a2n b2
..
.
an1
..
..
.
ann
.
:::
15
bn
(1) : : : a(1) b(1)
a(1)
11 a12
1(1)n 1(1)
0 a(1)
22 : : : a2n b2
..
.
0
..
.
..
.
..
.
(1) (1)
a(1)
n2 : : : ann bn
1
C
C
C
C
A
(1) indican que son los resultados de una operación elemental con la primera fila de la matriz.
El siguiente paso sería:
Pj2 2
j2 2 (para no deshacer la operacion anterior)
(2)
j2
En2 (n2 ) E32 (32 ) Pj2 2
j 2 = aa(2)
22
La matriz que nos queda:
0
B
B
B
B
B
@
(1) : : : b(1)
a(1)
11 a12
1(2)
0 a(2)
:
:
:
b
22
2
..
(2)
.
0 a33 b(2)
3
..
.
..
.
..
.
..
.
1
C
C
C
C
C
A
El paso k-ésimo del método:
Pjk k
! Enk (nk ) Ek+1;k (k+1;k) Pjk k jk k
Y al terminar se obtiene la siguiente matriz:
0
B
B
B
B
B
B
B
@
(1) : : : a(1) b(1)
a(1)
11 a12
1(2)n 1(2)
0 a(2)
22 : : : a2n b2
..
.
..
.
0
El superíndice de la última fila es realmente n
y lo dejamos como n.
0
..
0
:::
..
.
.
0
..
.
..
.
(
n
ann)
..
.
..
.
(
bnn)
1
C
C
C
C
C
C
C
A
1, así que hacemos una operación adicional que no sirve para nada
A lo largo de todo el proceso hemos multiplicado la matriz ampliada por matrices invertibles, por lo que el sistema
que hemos obtenido al final tiene la misma solución que el original. La solución se obtiene por sustitución regresiva,
como hemos visto antes.
(i)
Llamamos pivotes a los elementos que se quedan en la diagonal principal, aii .
El orden de este algoritmo es de O
2n
3
3
operaciones.
Estrategias de pivotaje o formas de escojer los pivotes:
Se usan para elegir los elementos que irán en la diagonal principal de forma que los errores de redondeo influyan lo
menos posible en el error del resultado.
Se busca la estabilidad numérica del resultado.
Hay dos formas: pivotaje parcial y pivotaje total.
CAPÍTULO 2. ÁLGEBRA LINEAL NUMÉRICA I
16
1. Pivotaje parcial:
En el paso k: se coje de la misma columna el elemento cuyo módulo sea mayor de los que hay a partir de la fila k.
(k
max
a
j k jk
1) = ja j
jk k
Se intercambian entonces las filas j y jk .
Este método no es numéricamente estable, ya que hay matrices para las cuales el crecimiento del error invalida
el resultado. Son casos muy raros en la práctica, pero teóricamente es inestable.
2. Pivotaje total:
En lugar de escojer el elemento mayor de la misma columna se escoje el mayor de la matriz que queda por
triangulizar.
max a(k
ni;j k ij
1) = a(k 1) rs
Se intercambian las filas r y j y las columnas s y k .
Al intercambiar columnas se intercambian también las incógnitas, por lo que hay que mantener un vector de
índices que controle el orden de las incógnitas.
Este método es el más estable, numéricamente.
Ejemplo:
Vamos a ver el desarrollo por Gauss de un sistema:
0
h
A(1) jb(1)
i
B
=B
@
6 2
12 8
3 13
6 4
2 4 12 1
6 10 34 C
C
9 3 27 A
1 18 38
Haciendo pivotaje parcial y operando con la primera fila (que ahora es la que era antes la segunda):
0
h
A(2) jb(2)
i
12:0000 8:0000 6:0000 10:0000 34:0000 1
B 0:0000
2:0000 1:0000 1:0000 5:0000 C
=B
@ 0:0000
A
11:0000 7:5000 0:5000 18:5000 C
0:0000 0:0000 4:0000 13:0000 21:0000
Pivotando de nuevo la segunda por la tercera fila:
0
6:0000 10:0000 34:0000 1
7:5000 0:5000 18:5000 C
A
0:3636 0:9091 1:6364 C
4:0000 13:0000 21:0000
0
6:0000 10:0000 34:0000 1
7:5000 0:5000 18:5000 C
A
4:0000 13:0000 21:0000 C
0:0000 0:2727 0:2727
12:0000 8:0000
h
i B
0:0000 11:0000
(3)
(3)
A jb = B
@ 0:0000
0:0000
0:0000 0:0000
12:0000 8:0000
i B
h
0:0000 11:0000
A(4) jb(4) = B
@ 0:0000
0:0000
0:0000 0::0000
CAPÍTULO 2. ÁLGEBRA LINEAL NUMÉRICA I
17
Y ya tenemos la matriz del sistema triangulada.
Si se hubiese hecho pivotaje total, en el primer paso, el 18 habría pasado a ser el primer elemento, y habría que
llevar el orden de las incógnitas.
|
Diagonalización:
Ahora la matriz del sistema junto con el vector de términos independientes se transforma en una matriz diagonal,
para ello, se hacen ceros por encima del pivote.
Y
i6=k
Las matrices quedan:
0
B
B
B
@
1
0
C
C
.. C
. A
B
B
B
B
@
a11 a12 : : : a1n b1
a21 a22 : : : a2n b2
..
.
an1
..
.
an2 : : : ann bn
Eik (ik ) Pjk k
(1) : : : a(1) b(1)
a(1)
11 a12
1(1)n 1(1)
0 a(1)
22 : : : a2n b2
..
.
0
..
.
..
.
(1)
: : : a(1)
nn bn
0
1
0
C
C
C
C
A
B
B
B
B
@
::: a(11n)
0
..
.
0
0
:::
(
n)
a22 : : :
..
.
0
0
n)
: : : a(nn
0
b(1n)
b(2n)
..
.
(
bnn)
1
C
C
C
C
A
Esta vez sí que son n pasos para conseguir la matriz diagonal.
A priori no hay ninguna ventaja con respecto a la triangulización, ya que hay que realizar el doble de operaciones.
Se usa cuando se quiere calcular la inversa de la matriz A:
A x = I ; A x(1) x(2) : : : x(n)
=
e1 e2 : : : en
A x(i) = ei i = 1 : n (n sistemas)
[AjI ] Gauss!Jordan
h
i
DjI (n) Dividiendopor
! pivotes I jA 1
Estrategias de escalado:
Para evitar trabajar con números muy pequeños, se puede hacer un escalado de las ecuaciones o de las incógnitas:
D1 1 A D2 y = D1 1 b
x = D2 1 y
Siendo D1 y D2 matrices diagonales.
Estrategia de equilibrado: que los elementos de la matriz D1 1 A D2 estén en un mismo rango de valores.
CAPÍTULO 2. ÁLGEBRA LINEAL NUMÉRICA I
18
2.1.5 Métodos de Crout y Doolittle
Se basan en la factorización LU de la matriz del sistema, de forma que quede el producto de una matriz triangular
superior (U) y una triangular inferior (L):
0
B
A =LU =B
B
l11 0 : : :
l21 l22 : : :
.
@ ..
ln1
..
.
ln2 : : :
0
0
10
CB
CB
.. C B
. A@
lnn
u11 u12 : : : u1n
0 u22 : : : u2n
..
.
0
0
..
.
:::
1
C
C
.. C
. A
unn
(2.10)
En principio, al operarlas saldrían n2 ecuaciones con n2
incógnitas, lo cual no es nada práctico. Para evitarlo, se
igualan los elementos de la diagonal principal de una de las dos matrices triangulares a uno (lii
o uii
).
+1
=1
=1
El método de Crout es el que iguala la diagonal principal de la matriz U a 1, mientras que el método de Doolittle es el
que iguala la diagonal principal de la matriz L a 1.
Primero veamos algunos conceptos:
Definición: dada una matriz A n n, se denominan submatrices principales sucesivas a las submatrices:
0
Ai = B
@
a11 : : : a1i
..
.
ai1
..
.
:::
1
.. C
. A
aii
; i=1:n
(Ai ) para i = 1 : n.
Teorema 2.1. Dada una matriz cuadrada A, si det (Ai ) 6= 0 8i = 1 : n 1, entonces la matriz admite factorización
LU (L matriz triangular inferior y U triangular superior) con lii = 1 o uii = 1. Es condición suficiente de matriz
factorizable, no necesaria. Si la matriz es invertible y existe su factorización LU, los menores principales sucesivos de
la matriz hasta el de orden n 1 son no nulos y la factorización es única. Es condición necesaria y suficiente.
y menores principales sucesivos a los determinantes det
Definición: una matriz P cuadrada de orden n es una matriz de permutación si se puede expresar como producto
de matrices elementales Pij .
Teorema 2.2. Sea A matriz cuadrada invertible, entonces existe una matriz de permutación P tal que la matriz P
admite factorización LU:
A
P A=LU
Ahora veamos los dos métodos antes mencionados:
Método de Crout:
l
j=2:n
= ai1 i = P
1 : n u11 = 1 u1i = al i i = 2 : n
j 1l u
lij = aij
k=1 ik kj i = j :Pnj
ujj = 1; Si j < n : uji = aji kljj ljk uki i = j + 1 : n
(2.11)
= a1i i = P
1 : n l11 = 1 l1i = uai i = 2 : n
j 1l u
uji = aji
j:n
k=1 jk ki i = P
aij jk lik ukj
i=j+1:n
ljj = 1; Si j < n : lij =
ujj
(2.12)
1
11
1
=1
Método de Doolittle:
j =2:n
(i1
u
( 1i
El orden de estos métodos es de O
1
11
1
=1
2n
3
3
operaciones.
CAPÍTULO 2. ÁLGEBRA LINEAL NUMÉRICA I
19
2.1.6 Método de Cholesky
Se utiliza cuando la matriz del sistema es simétrica:
A = At .
A = L Lt
0
l11 : : :
A=B
@
l
j=2:n
811
<
:
..
.
ln1
..
.
:::
0
10
l11 : : : ln1
.. C B ..
. A@ .
lnn
..
0
.
:::
1
.. C
. A
lnn
= paq
11 li1 = al i i = 2 : n
Pj 1 2
ljj = ajj
k=1 lP
jk
aij jk lik ljk
i=j+1:n
Si j < n; lij =
ljj
1
11
1
=1
3
El orden del método de Cholesky es de O n3
(2.13)
operaciones, la mitad que los anteriores.
Teorema 2.3. Una matriz A admite factorización Cholesky si y sólo si es definida positiva.
0 8x 6= 0. O bien, es definida positiva si, y
( ) 0 = 1 : n.
Definición: una matriz A simétrica es definida positiva si xt A x >
sólo si, sus menores principales sucesivos son positivos: det Ai > i
Teorema 2.4. Una matriz A semidefinida positiva admite factorización Cholesky para L triangular inferior con todos
sus elementos lij 2 R.
Si la matriz A es simétrica e indefinida, se puede usar una factorización L D Lt :
A = L D Lt
A = L U = L D U^ A==A U^ t DLt
t
^
) U^ = Lt
^ = 1.
Con D diagonal y U tal que uii
El algoritmo es:
d(11 = a11
vi = aji
j=2:n
djj = ajj
1 vk lik lji = vi ; i = 1 : j
dii
k=1 vk ljk
Pi
Pkj =11
1
(2.14)
Siendo v un vector auxiliar.
No toda matriz simétrica indefinida puede factorizarse de esta forma, por ejemplo:
A=
0 1
1 0
Sin embargo, para toda matriz simétrica indefinida existe una matriz de permutación P tal que:
P A P t = L B Lt
Para B simétrica y diagonal por bloques
vamos a desarrollarlos, sólo citarlos.
1 1 o 2 2. Se hace por los métodos de Aasen y Bunch-Kaufman, pero no
CAPÍTULO 2. ÁLGEBRA LINEAL NUMÉRICA I
20
2.1.7 Ejercicio de examen, convocatoria de diciembre, 1999.
Dada la matriz
0
B
A=B
@
2 6 41
2 1 2C
A
0 1 2C
0 0 1 determinar 2 R para que A admita factorización LU.
Solución:
det (Ai ) 6= 0 i = 1 : 3
det (A1 ) = det (A2 ) = 2 4
det (A3 ) = 3 5 + 12
Igualando a cero los resultados, nos quedan los siguientes valores para los que se anulan los menores:
=0
= 2
= 3
Vemos que A es factorizable LU 8 2 R
f0; 2; 2; 3g
Ahora cabe preguntarse si es factorizable para alguno de esos valores. Para ello, utilizamos la segunda parte del
teorema 1:
det (A) = 3
7 + 14
Y vemos que, para los valores encontrados:
=0
=2
= 2
= 3
)
)
)
)
det (A) = 0
det (A) 6= 0
det (A) 6= 0
det (A) 6= 0
Sin embargo, para los tres últimos valores no es factorizable, ya que sus menores son nulos.
4
Ejemplo:
Dada la matriz
4 4 0 1
B 3 1 C
A=B
A
@ 4 5 1C
0 1 1 3
0
hacer factorización Cholesky en función de y concretar los valores de para los que es posible la factorización en
aritmética real.
CAPÍTULO 2. ÁLGEBRA LINEAL NUMÉRICA I
21
Se ve que la matriz es simétrica, así que podemos expresarla:
0
B
A=B
@
l11 0 0 0
l21 l22 0 0
l31 l32 l33 0
l41 l42 l43 l44
1
C t
CL
A
Aplicando el algoritmo de la factorización, llegamos a los siguientes valores:
l11 = 2
p
l21 = 2 l22 = 122 2
l31 = 2
l32 = 0
l33 = 1
q
2
l41 = 0 l42 = p12 2 l43 = 1 l44 = 2012 222
Para que sea factorizable tiene que ser definida positiva, los determinantes son fáciles de calcular, teniendo en
cuenta:
2 l22
2 lii2
det (Ai ) = (det (Li ))2 = l11
Por tanto,
det (A1 ) = 4 > 0
det (A2 ) = 12 2
det (A3 ) = det (A2 )
Y el determinante de la matriz del sistema:
22
det (A) = 20
Para que sea factorizable:
20 222 > 0
12 > 0
p
10
p
10
p
12
p
12
Que tiene
<<
y
<<
por lo que cojemos la más restrictiva. Además, si
p dos soluciones,
también es factorizable porque los menores sucesivos son no nulos.
=
10
Así pues, la matriz es factorizable por Cholesky si y sólo si:
p
p
10 10
|
Ejemplo:
CAPÍTULO 2. ÁLGEBRA LINEAL NUMÉRICA I
22
Determinar los valores de para los que A es factorizable LU y resolver el sistema A
A y b:
0
B
A () = B
@
2 11
2 1C
A
2 1C
1 3
1 2
0 1
0 0
0
B
b=B
@
() x = b para = 2, siendo
1 1
3 C
A
5 C
1
Empecemos por calcular los menores sucesivos de A:
det (A1 ) = det (A2 ) = 2
det (A3 ) = 2
3
4
0; 32 ; 2.
Con lo que se obtiene que es factorizable (en condición suficiente) para 2 R
Veamos si para alguno de esos valores es factorizable.
det (A) = (2
1) ( 2)
Así, para cada uno de los valores de :
=0
= 32
=2
)
)
)
Invertible; no existe factorizacion
Invertible y tampoco es factorizable
No es invertible
En el último caso, como la matriz no es invertible, el teorema no nos asegura nada, por lo que tenemos que intentar
factorizar:
0
2
B 1
A (2) = B
@ 0
0
3
2
1
0
2
2
2
1
0
11
l11
B l21
1C
Crout
B
A = @ l31
1C
2
l41
10
l22
l32 l33
l42 l43 l44
Y ahora hallamos los valores de los elementos:
Para la primera columna de L:
l11 = 2
l21 = 1
l31 = 0
l41 = 0
La primera fila de U:
l11 u12 = 3; u12 = 32
l11 u13 = 2; u13 = 1
l11 u14 = 1; u14 = 12
CB
CB
A@
1
u12 u13 u14
1 u23 u24
1 u34
1
1
C
C
A
CAPÍTULO 2. ÁLGEBRA LINEAL NUMÉRICA I
23
Segunda columna de L:
l21 u12 + l22 = 2; l22 = 12
l31 u12 + l32 = 1; l32 = 1
l41 u12 + l42 = 0; l42 = 0
Segunda fila de U:
l21 u13 + l22 u23 = 2; u23 = 2
l21 u14 + l22 u24 = 1; u24 = 1
Tercera columna de L:
l31 u13 + l32 u23 + l33 = 2; l33 = 0
l41 u13 + l42 u23 + l43 = 1; l43 = 1
Tercera fila de U:
l31 u14 + l32 u24 + l33 u34 = 1;
0 u34 = 0
El resultado de esta última ecuación es que u 34 puede valer lo que uno quiera, el problema vendría al intentar
resolverlo con un ordenador, ya que no soporta la división por cero y no trabaja con parámetros. Hacemos u 34 .
=
Por último, la última columna de L:
l41 u14 + l42 u24 + l43 + l44 = 2; l44 = 2 Con este resultado, lo que ocurre es que tenemos infinitas factorizaciones posibles, por lo que la matriz A es factorizable si, y sólo si:
2R
0; 32
Veamos ahora la segunda parte del problema: resolver el sistema para 0
2 0 0 0
B 1 1 0
0
2
A (2) = B
@ 0 1 0
0
0 0 1 2 10
= 2:
1 32 1 12
CB 0 1 2 1
CB
A@ 0 0 1 0 0 0 1
La solución se obtiene al resolver:
Ly =b
U x =y
1
C
C
A
CAPÍTULO 2. ÁLGEBRA LINEAL NUMÉRICA I
24
Habiendo operado, se obtiene:
x=
5 s t
9 3t 7 + 3t 1 2t
1
2
y=
t
s + (2 ) t =
1
|
2.1.8 Métodos de ortogonalización
Definición: Se dice que una matriz Q es ortogonal si Qt Q
= Q Qt = I .
kQ xk22 = xt Qt Q x = xt x = kxk22
La ventaja desde el punto de vista numérico de las transformaciones ortogonales es que son normas isométricas (se
mantiene dicha norma), por tanto, estas transformaciones son estables numéricamente.
Pregunta: ¿Y entonces porqué no hacemos todo con transformaciones ortogonales y nos olvidamos de Gauss, Cholesky
y los demás?
Respuesta: Porque las transformaciones ortogonales son menos eficientes que el resto de los métodos, si tenemos
una matriz A m n a ortogonalizar, el número de operaciones es O n2 m n3 , por lo que en el caso de matrices
cuadradas, hay que hacer 3 veces más operaciones que por el método de triangularización de Gauss.
3
Este método se suele usar cuando la estabilidad numérica es prioritaria.
Hay dos métodos que vamos a estudiar: el método de Givens y el método de Householder.
Método de Givens:
Se define una matriz de Givens:
0
Gpq =
B
B
B
B
B
B
B
B
B
B
B
@
= cos
1
:::
0
.
..
.
..
.
..
:::
0
:::
0
:::
..
.
= sen
0
:::
0
:::
01
cos :::
sen :::
0C
C
p
.
cos :::
0
q
0
:::
..
.
..
.
..
sen :::
0
:::
..
.
p
..
.
..
.
..
.
q
..
.
.. C
. C
C
.. C
. C
C
C
C
.. C
. A
1
En adelante, consideraremos c
ys
.
La premultiplicación por Gtpq equivale a una rotación de radianes en el plano de coordenadas
contrario al de las agujas del reloj. Únicamente se cambian las filas p y q.
Gtpq x = x1 : : : xp 1 c xp
Si queremos anular el q-ésimo elemento:
(2.15)
(p; q) en sentido
s xp xp+1 : : : xq 1 s xp + c xq : : : xn t
CAPÍTULO 2. ÁLGEBRA LINEAL NUMÉRICA I
25
s xp + c xq = 0
Entonces:
8
= xxpq ) < s = pxp +q xq
x
: c= p p
c2 + s2 = 1
xp +xq
s
c
x
2
2
2
2
(2.16)
El método de Givens consiste en sucesivas transformaciones de rotación usando matrices de Givens hasta reducir la
matriz A rectangular m n a una triangular. Si m n:
=
Gtn Gt1 A
R1
A 2 Rmn R1 2 Rnn
0
Siendo R1 triangular superior.
=
La matriz Q G1 Gn no se suele calcular y sólo se almacena un número por rotación en la posición anulada. Se
suele usar este método con matrices dispersas.
Método de Householder:
Matriz de Householder:
H =I
2
vv
vt v
t
(2.17)
Donde v es un vector no nulo, de forma que el producto v vt es una matriz cuadrada y v t v un número.
La matriz H es simétrica y ortogonal:
H Ht = H2 = I + 4
v vt v vt
(vt v)2
Fijado un vector x 2 Rn , la elección de v permite obtener H
v=
0
:::
0
4 vvt vv = I
t
x con varios elementos nulos:
xk + signo (xk ) xk+1 : : : xn t
(2.18)
Donde
=
v
uX
u n 2
t
x
j =k
0
1
H x=x
z }| {
2v vt x = x 2vt x v v =
vt v
vt v
B
B
B
B
B
B
B
B
B
B
@
(2.19)
j
x1
..
.
xk 1
xk
xk+1
..
.
xn
1
0
C
C
C
C
C
C
C
C
C
C
A
B
B
B
B
B
B
B
B
B
B
@
0
..
.
xk
0
signo (xk ) xk+1
..
.
xn
1
C
C
C
C
C
C
C
C
C
C
A
CAPÍTULO 2. ÁLGEBRA LINEAL NUMÉRICA I
26
t
Si demostramos que 2vvt vx
, podemos hacer ceros a partir de donde queramos.
El multiplicar por el signo de xk es para evitar diferencias cancelativas.
=1
El método de Householder consiste en la sucesiva realización de transformaciones (un total de n) de reflexión utilizando matrices de Householder hasta reducir A 2 Rmn a una matriz triangular. Si m n:
Hn H1 A =
t
Demostremos 2vvt vx
R1
R1 2 Rnn
0
triangular superior
= 1:
2vt x = 2
vt v
x2k + jxk j + x2k+1 + : : : + x2n
(xk + signo (xk ) )2 + x2k+1 + : : : + xn
2
= 2 22 ++ 2jxjkxjkj = 1
Expresión analítica del método:
0
0
H1 B
@
a11 : : : a1n
..
.
an1
..
.
:::
1
.. C
. A
ann
=
B
B
B
B
B
@
(1)
(1)
a(1)
11 a12 : : : a1n
0
..
.
..
.
..
.
..
.
..
.
(1)
0 qPa(1)
n2 : : : 1 ann
n a2
a11 + signo (a11 )
j =1 ji C
B
1
C
C
C
C
C
A
0
a21
B
v (1) = B
B
@
C
C
C
A
..
.
an1
v(1) v(1)t
v(1)t v(1)
H1 = I
2
Hi = I
::: 0
2 vv ii tvvi i
i)
1 vi(+1
También podemos escribir:
v (i) =
No se calcula explícitamente Q
de A eliminadas.
0
( )
( )t
( )
( )
(i)
: : : vm
t
(2.20)
= H1 Hn, pues con los v(i) basta almacenar los vj(i) j = i + 1 : m en las posiciones
El orden del método es de O n2 m n3 operaciones, por lo que es preferible a Givens si la matriz tiene pocos
ceros (es densa), pero si lo usamos para matrices dispersas, hacemos operaciones con ceros innecesarias.
2
Ejemplo:
Resolver el siguiente sistema usando el método de Householder:
0
63 41 88 1 1
60 51 10 C
B 42
[Ajb] = B
@ 0
A
28 56 5 C
126 82 71 2
63 + p632 + 422 + 1262 1 0 210 1
B
C B 42 C
42
C=B
C
v (1) = B
@
A @ 0 A
0
126
126
0
CAPÍTULO 2. ÁLGEBRA LINEAL NUMÉRICA I
27
0
0
2 + 282 + 5:62
B
30
:
8
+
30
:
8
v (2) = B
@
28
5:6
p
1
C
C
A
|
2.2 Sistemas sobredeterminados y pseudoinversas
2.2.1 Sistemas sobredeterminados
A x = b A 2 Rmn m > n
Usualmente este tipo de sistemas no tiene solución, ¿qué hacemos pues?
Tratamos de calcular x tal que
kA x bk22 = min
kA x bk22
x
Sea la solución básica de mínimos cuadrados.
Gtn Gt1 [Ajb] =
R11 R12
0
0
R1 c
0 d
y
z
=
c
d
R11 y + R12 z = c
z = 0 ) R11 y = c
A=Q
AP
=Q
R1
0
R11 R12
0
0
kA x bk22 = Qt (A x b)22
Siendo R1 x
R1 x c
d
2
2
= c la solución de mínimos cuadrados.
=
R1
0
x
c
d
2
2
CAPÍTULO 2. ÁLGEBRA LINEAL NUMÉRICA I
28
Teorema 2.5. El vector x es solución de mínimos cuadrados (o de
sistema de ecuaciones normales:
min kA x bk22) si, y sólo si, x es solución del
At A x = At b
Si el rango de A es n la solución es única:
x = (At A) 1 At b.
Método de las ecuaciones normales:
=
Consiste en aplicar Cholesky a At A x At b. sin embargo, este es un problema mal condicionado, así que se usa
el método basado en transformaciones ortogonales (Givens, Householder).
Método Gram-Schmidt clásico/modificado:
Trata de calcular directamente la factorización Q1 R1 de A:
A = Q1 R1 A 2 Rmn Q1 2 Rmn R1 2 Rnn
Q1 es normalizada (no es ortogonal porque no es cuadrada): Qt1 Q1 = 1:
Ax=b
Q1 R1 x = b
) R1 x = Qt1 b
Necesita que las columnas sean linealmente independientes.
Cómo hacer la factorización: Método de Gram-Schmidt
Notamos A y Q como matriz de columnas y R triangular:
0
a(1) a(2) : : : a(n)
=
q (1) q (2) : : : q (n)
B
@
r11 : : : r1n
..
.
0
:::
1
.. C
. A
rnn
q (1) q (1) = 1 a(1) = q (1) r11
t
Se trata de escoger r11 de forma que q (1) sea normalizado:
t
q (k) q (k) = 1
q (k) q (i) = 0; i = 1 : k 1
t
t
t
(
i
)
q q (k) = q (i) a(n) rin q (i) q (i)
t
Por tanto:
rik =
t
q (i) a(k)
q (i)t q (i)
(2.21)
CAPÍTULO 2. ÁLGEBRA LINEAL NUMÉRICA I
29
Nos queda la columna k :
a(k) = r1k q (1) + : : : + rkk q (k)
( k)
(1)
( k 1)
q (k) = a r1n q r:::kk r1;k 1 q
(2.22)
Este método calcula las columnas k-ésima de Q1 y R1 en el paso k .
Sin embargo, este método es numéricamente inestable porque los q(k) pierden ortogonalidad, así que se usa el Método
de Gram-Schmidt modificado, que reorganiza el cálculo:
( k)
rkk = a(k) 2 ;
q (k) = arkk
p
rki = q (k) a(i) ; a(i) = a(i) rki q (k) i = k + 1 : n
)
k=1:n
(2.23)
Esto modifica la matriz A, aunque se puede escoger almacenar Q1 en una matriz diferente. Se calcula la k-ésima fila
de R1 y la k-ésima columna de Q1 en el paso k-ésimo.
Los dos métodos de Gram-Schmidt requieren del orden de
2mn2 operaciones.
2.2.2 Pseudo-inversas
Dada una matriz rectangular A, la pseudo-inversa de Moore-Penrose,
1.
2.
A+ , cumple los siguientes axiomas:
A+ A A+ = A+
A A+ A = A
(A A+)t = A A+
t
4. (A+ A) = A+ A
3.
5. Al trabajar con matrices complejas:
A A+ = A A+
Siendo B
= B t con B la conjugación de los elementos de la matriz.
Si A es rectangular y At A invertible, A+
= (At A) 1 At .
Teorema 2.6. Cualquier vector x es solución mínimos cuadrados de un sistema A x
mínima norma, si y sólo si se cumple:
= b, y además x = A+ b tiene
A x = A A+ b
Demostración:
kA x bk22 = A x A A+ b + A A+ b b22
= A x A A+ b22 + A A+ b b22 + 2 A x A A+ bt A A+ b b
CAPÍTULO 2. ÁLGEBRA LINEAL NUMÉRICA I
30
Siendo:
2xt At A A+
I b = 2xt At At A At At b = 0
y:
2bt A A+t A A+
como A+ A A+
I b=
2bt A A+ A A+
A A+
= A+, lo de arriba vale cero, y queda:
kA x bk22 = A x A A+ b22 + A A+ b b22

Cómo calcular la pseudo-inversa:
Toda matriz rectangular se puede descomponer en el producto de una ortogonal, una diagonal rectangular y otra
ortogonal:
0
A=U Donde i
B
B
B
B
B
B
B
@
1
0
0
..
::: :::
.
..
.
..
.
r
0 0
..
.
::: :::
01
C
0C
C
..
.
..
.
0
C
C
C
C
A
Vt
0 se llaman valores singulares de la matriz y i2 son los autovalores de A At o At A.
AV
=U S
A V (i) = i U (i)
At = V S U t ; At U (i) = i V (i)
Multiplicando por la traspuesta:
At A V (i) = i2 V (i)
A At U (i) = i2 U (i)
(2.24)
CAPÍTULO 2. ÁLGEBRA LINEAL NUMÉRICA I
31
A+ = V S + U t
(2.25)
Donde
0
S+ =
1
1
B ..
B .
B
B
B
B
@
0
..
.
0
01
::: ::: :::
..
.
.. C
. C
C
1
r
..
0C
C
(2.26)
.. C
. A
.
0
::: ::: :::
Un ejemplo de aplicación de este método es la compresión de imágenes:
A =U SVt =
n
X
i=1
i U (i) V (i)
t
Esto sirve para reconstruir la matriz A, y si tenemos una matriz original
20 valores singulares, se queda en una mucho más pequeña ( ).
60 1000
A muy grande (digamos 1000 1000), con
La solución de mínimos cuadrados es:
X 1
t
V (i) U (i) b
xLS = A+ b =
i=1 i
r
2.3 Estimaciones de error
Ahora vamos a ver lo próximos que están dos vectores, en lugar de números.
Definición: Se definen las normas de un vector x 2 Rn de la siguiente forma:
kxk1 =qPnj=1 jxj j
kxk2 = Pnj=1 jxj j2
kxkp = Pnj=1 jxj jp p
kxk1 = maxj jxj j
(2.27)
1
Definición: Para una matriz A 2 Rnn , se define la norma matricial como una aplicación kk Rnn
:
1.
2.
3.
4.
! R tal que:
kAk 0, kAk = 0 , A = 0
k Ak = jj kAk
kA + Bk kAk + kBk
kA Bk kAk kBk
Definición: norma matricial natural o inducida:
kAk = sup kAkxkxk = kmax
kA xk
xk=1
x6=0
(2.28)
CAPÍTULO 2. ÁLGEBRA LINEAL NUMÉRICA I
32
Norma 1:
kAk1 = sup kAkxkxk1 = imax
=1:n
x6=0
1
n
X
j =1
jaji j
(2.29)
Norma 2:
kAk2 = sup kAkx kxk2 = (At A) = max
i i
p
x6=0
2
(2.30)
Norma infinita:
kAk1 = sup kAkxkxk1 = imax
=1:n
x6=0
1
n
X
j =1
jaij j
(2.31)
El ínfimo de todas las normas matriciales que pueden definirse de A es el radio espectral de la matriz:
(A) = inf kAk
kk
Definición: Si tenemos una matriz H invertible, se define la norma transformada por una matriz como:
kAkH = H 1 A H En el caso vectorial:
kxkH = H 1 x
Definición: Se dice que una norma matricial es consistente con una vectorial si cumple:
kA xk kAk kxk 8A; x
Definición: Una matriz consistente se dice subordinada si hay un sólo vector x que cumpla la igualdad, es decir:
9!x0 = 0= kA x0 k = kAk kx0 k
Si kk es norma subordinada a una vectorial, se cumple que kI k
= 1.
Un ejemplo de norma consistente no subordinada es la norma de Frobenius:
kAkF =
Ya que kI kF
= pn.
v
u n n
uX X
t
j =1 i=1
jaij j2
CAPÍTULO 2. ÁLGEBRA LINEAL NUMÉRICA I
Definición: Dada una sucesión de vectores
33
(s) x se define su límite de la siguiente forma:
lim x(s) = x si slim
s!1
!1 x
x(s) = 0
En el caso matricial (dada la sucesión fAs g):
lim
A
s!1 s
= A si slim
!1 kA
As k = 0
Todo esto sin distinción de normas, ya que todas son equivalentes.
Teorema 2.7. (para una matriz convergente):
lim Bs = 0 , (B) < 1
s!1
Teorema 2.8. Serie matricial geométrica:
I + B + : : : + Bs + : : : =
converge a
(I
1
X
s=0
Bs
B ) 1 si y sólo si (B ) < 1.
2.3.1 Condicionamiento de una matriz invertible
A 2 Rnn invertible, y si queremos resolver el sistema A x = b, podemos resolver
+ b donde representan pequeñas perturbaciones en A y en b. El error relativo en la
Teorema 2.9. Dada una matriz
el sistema A
A y b
solución es:
( + ) =
ky xk (A) kAk + kbk kxk
1 (A) kAk kbk
x la solución exacta y (A) = kAk A 1 (se lee “kappa de A”) cuantifica la sensibilidad
A x = b a las perturbaciones y se llama número de condición de A. Si A es singular, vale 1.
Siendo
I = A A 1;
Se dice que la matriz es perfectamente condicionada si
condicionada si es un número próximo a 1.
1 = kI k kAk A
1 (A) = 1, mal condicionada si (A) es un número grande y bien
1 = min kAk
(A) A+A singular kAk
Se perturba A hasta que A
del problema
+ A sea singular.
Condicionamiento de un problema de mínimos cuadrados:
CAPÍTULO 2. ÁLGEBRA LINEAL NUMÉRICA I
34
Para el problema de mínimos cuadrados se usa el número de condición en norma 2, dado por:
^
mn
2 (A) = 1 ; A 2 R ; m n; rango (A) = n
r
Teorema 2.10. Dados xLS y x soluciones respectivas de mínimos cuadrados de los sistemas:
min kA x bk2 min k(A + A) x (b + b)k2
con A; A 2 Rmn ; m n; rango ( A) = n y b; b 2 Rm . Si se cumple:
siendo = kA xLS
bk2 , entonces
o
n
= max kkAAkk22 ; kkbbkk22 < n1 ((AA)) kbk2
6= 1
0
1
kx^ xLS k2 @2 (A) q kbk2 + (A)2 q A + O 2
2
2
kxLS k2
kbk22 2
kbk22 2
2.3.2 El residual y el refinamiento iterativo
Se define el residual de x como:
r =b Ax
^
^=b
Si tenemos una solución calculada x, A x
r, mientras que para una solución exacta x, A x = b.
A (^x x) = r
Error absoluto de la solución calculada:
kx^ xk A 1 krk
Error relativo:
kx^ xk A 1 krk
kxk
kxk
El residuo no nos dice la diferencia entre la solución exacta y la calculada.
kAk kxk kbk ) kx^kxkxk (A) kkrbkk
Si resolvemos el sistema A (^
x x) = r (o A (x x^) = r):
Ay =r
Una vez que tengamos calculada la y , x
x^ = y ; x = x^ + y .
=
Esto es genial para obtener la solución exacta ¿no? Pues no, porque al resolver A y r volvemos a cometer error, y
sólo obtenemos una solución un poco más aproximada a la exacta. Esta es la base del refinamiento iterativo. Se suele
hacer 2 o 3 veces.
CAPÍTULO 2. ÁLGEBRA LINEAL NUMÉRICA I
35
2.4 Métodos iterativos para sistemas lineales
2.4.1 Definición
Dado un sistema
Ax=b
con A de gran tamaño y dispersa, un método apropiado para resolverlo es alguno iterativo, que básicamente consiste
en construir una sucesión x(s) de aproximaciones a la solución o soluciones del sistema.
Un método iterativo es consistente con un problema si existe el límite
s!1 x(s) x , donde x es la solución del
problema.
lim
=
2.4.2 Métodos de punto fijo
x(s+1) = B x(s) + c B 2 Rnn ; c 2 Rn ; s = 0; 1; : : :
(2.32)
Teorema de consistencia del método de punto fijo. El método de punto fijo (2.32) es consistente con un sistema de
I B A 1 b.
ecuaciones A x b para una matriz A no singular si y sólo si I B es no singular y c
=
=(
)
Lectura del teorema:
lim x(s) = x entonces lim x(s+1) = lim B x(s) + c, y por tanto x = B x + c.
Estamos resolviendo el sistema relativo al método. Como (I B ) x = c, dado que I B es invertible, existe una
única solución y es la misma que la de A x = b.
Si existe el límite

La consistencia no asegura la convergencia.
Teorema de convergencia del método de punto fijo. El método de punto fijo (2.32), siendo consistente con un sistema,
1 c, con cualquier vector inicial x(0) si y sólo si B < . Es condición necesaria y suficiente.
converge a I B
(
)
( ) 1
Expresado de otra forma, como condición suficiente:
=(
)
1
El método de punto fijo (2.32) converge a x
I B c con cualquier vector inicial
norma matricial subordinada, y además se satisfacen las siguientes cotas de error:
x
s k
(k+1)
( k)
x(s) kB k 1kxkB k x k para k = 0; 1; : : : ; s
x
1
x(0) si kB k < 1 para alguna
(2.33)
x(s) kB ks x x(0) (2.34)
Nota: es pregunta habitual de examen pedir el número de iteraciones mínimo para que el error cometido sea menor
que un determinado valor . Para ello, cojemos la segunda parte de la desigualdad:
kB ks k kx(k+1) x(k) k
1 kB k
Se toman entonces logaritmos y se despeja s. Esta cota se llama cota de error a priori. Existe una cota de error a
posteriori, que es da una mejor acotación pero hay que calcular la iteración en la que se acota:
x
s k
(s)
(s
x(s) kB k 1kxkB k x
1)
k

CAPÍTULO 2. ÁLGEBRA LINEAL NUMÉRICA I
36
2.4.3 Comparación de métodos
Definición: factor medio de reducción por iteración:
!
x(s) s
x(0) x
x
1
kBk
(2.35)
Definición: razón media por iteración:
(kBsk) s
1
(2.36)
Se dice que un método con matriz B1 es más rápido que otro con matriz B2 si el radio espectral de B1 es menor que
el de B2 .
2.4.4 Métodos de descomposición o partición regular
=
=
Si tenemos el sistema A x
b con A regular, y A M N con M regular, tenemos que
ecuación relativa al método de partición regular, dado un vector inicial x(0) . Es decir:
M x(s+1) = N x(s) + b
M x
= N x + b es la
) x(s+1) = M 1 N x(s) + M 1 b
Los métodos clásicos de este tipo están definidos para matrices A con elementos de la diagonal principal no nulos y
tienen la siguente partición:
A = D +L+R
Siendo:
0
B
D=B
B
@
a11
0
..
.
0
0
:::
a22 : : :
..
.
::: :::
0
0
..
.
ann
1
0
C
C
C
A
L=B
B
B
@
0
a21
..
.
an1
0
0
:::
:::
..
.
an2 : : :
01
0C
C
.. C
. A
0
0
0 a12
B 0
0
B
R=B
.
@ ..
0 0
: : : a1n
: : : a2n
..
.
:::
..
.
0
1
C
C
C
A
(2.37)
Según la forma de la matriz B que se use, hay tres métodos clásicos:
Método de Jacobi:
BJ = D 1 (L + R)
(2.38)
Invierte la matriz diagonal, D.
El cálculo de cada componente del vector x(s) se realiza del siguiente modo:
x(s+1) =
i
bi
iP1
j =1
aij x(js)
aii
n
P
j =i+1
aij x(js)
i=1:n
Es decir, que se opera con todas las componentes del vector anterior excepto con la que estamos calculando.
(2.39)
CAPÍTULO 2. ÁLGEBRA LINEAL NUMÉRICA I
37
Método de Gauss-Seidel:
Las componentes ya calculadas se usan para calcular las siguientes en la misma iteración. Acelera la convergencia,
sin embargo no se puede asegurar que en general sea mejor que Jacobi.
BGS =
(D + L) 1 R
(2.40)
Para el cálculo de cada componente se usa la fórmula:
x(s+1) =
i
bi
iP1
j =1
aij x(js+1)
aii
n
P
j =i+1
aij x(js)
i=1:n
(2.41)
Método SOR (Sobrerrelajación):
BSOR = (D + ! L) 1 (1 ! ) D ! R
0
(2.42)
1
1
Donde ! es el factor de relajación. Si < ! < el método se llama de subrelajación, mientras que si ! > es
de sobrerrelajación, los cuales se pueden usar para acelerar la convergencia de sistemas que son convergentes por el
método de Gauss-Seidel.
La fórmula es la siguiente:
x(i s+1) = (1 ! ) x(i s) +
! bi
iP1
j =1
n
P
aij x(js+1)
j =i+1
aii
aij x(s)
!
j
(2.43)
Como complemento a los métodos, veamos los de Richardson y el SOR simétrico:
Método de Richardson:
x(s+1) = x(s) + b A x(s)
(2.44)
Con arbitrario no nulo.
Método SOR simétrico (SSOR):
1
x(s+ 2 ) = (1 ! ) x(s) + ! D 1 L x(s+1=2) D 1 R x(s) + D 1 b x(s+1) = (1 ! ) x(s+1=2) + ! D 1 L x(s+1=2) D 1 R x(s+1) + D 1 b
En el SOR se hace el cálculo de
1 a n, en el SSOR de n a 1.
(2.45)
CAPÍTULO 2. ÁLGEBRA LINEAL NUMÉRICA I
2.4.4.1
38
Teoremas de convergencia
Definición: Matriz de diagonal dominante:
Se dice que una matriz A es de diagonal dominante estrictamente (por filas) si cumple:
jaii j >
n
X
j=1
jaij j 8i
(2.46)
j 6=i
Es decir, que el elemento de la diagonal principal en valor absoluto es mayor que la suma de los valores absolutos de
los elementos restantes de la fila.
=
Teorema 2.11. Dado un sistema A x
b siendo A de diagonal dominante estrictamente, los métodos de Jacobi y
Gauss-Seidel son convergentes a la solución del sistema.
Demostración: para el método de Jacobi.
BJ
Con bij
=
aij y b
ii
aii
= [bij ]
= 0. Entonces:
kBJ k1 = max
i
n
X
j =1
P
j 6=i
aij
jbij j = max
<1
i jaii j
Por tanto, Jacobi converge si es matriz de diagonal dominante
Teorema de Kahan. Dada una matriz
sólo si < ! < .
0
2
A de elementos aii

6= 0 para todo i, el método SOR para esa matriz converge
=
Teorema de Ostrowski-Reich (importante). Dado un sistema A x
b con A simétrica definida positiva, el método
SOR converge a la solución del sistema para < ! < . Es condición suficiente. Como SOR es lo mismo que
Gauss-Seidel cuando !
, todo lo que verifiquemos para SOR se cumple para Gauss-Seidel.
0
=1
2
=
Teorema de Stein-Rosenberg (convergencia de Jacobi y Gauss-Seidel). Si se tiene un sistema A x b con A tal que aii
para i
n y aij para i 6 j , entonces se cumple una y sólo una de las siguientes posibilidades:
=1:
0
=
>0
0 < (BGS ) < (BJ ) < 1, con lo que convergen ambos métodos.
2. 0 = (BGS ) = (BJ ), con lo que también convergen ambos.
3. 1 < (BJ ) < (BGS ), con lo que no converge ninguno.
4. 1 = (BGS ) = (BJ ), tampoco converge ninguno.
Teorema 2.12. Dada una matriz A tridiagonal con aii 6= 0 para i = 1 : n, si los autovalores de BJ son reales, tanto
Jacobi como SOR para 0 < ! < 2 convergen o divergen simultáneamente. Si ambos convergen, entonces:
1.
(
(BSOR (! )) = 1
Siendo q
! + 12 ! 2 2 + !
! 1
1
! + 41 ! 2 2
0 < ! !0
!0 ! < 2
= (BJ ) y !0 la elección óptima de !, hallándose de la forma siguiente:
(2.47)
CAPÍTULO 2. ÁLGEBRA LINEAL NUMÉRICA I
39
!0 =
Si además de tridiagonal,
Ostrowsky-Reich).
A
2
1+ 1
p
(2.48)
2
es simétrica y definida positiva, SOR y Jacobi convergen (en virtud del teorema de
Ejemplo:
Dada la matriz A y el vector b:
0
A=@
2 1 01
1 2 1A
0 1 2
0
21
b=@ 4 A
2
Estudiar si el método iterativo de Jacobi converge a la solución del sistema A x
= b para A y b.
En caso afirmativo, determinar el número de iteraciones a realizar para que el error en la iteración m-ésima sea
t
5 , con x(0)
.
menor que 5 10
= 1 0 1
Solución:
La matriz A no es de diagonal dominante, así que buscamos Como BJ
=
(B J ).
D 1 (L + R), para hallar los autovalores de B J :
D
D 1 (L + R) I = 0 Multiplicandopor
)
Como D tiene inversa, jL
j Dj jL + R + Dj = 0
+ R + Dj = 0:
8
1 =q0
>
>
2 1 0 3
<
1 2 1 = 8 4 = 0 ) > 2 = q12
>
0 1 2 1
: =
3
2
q
(BJ ) = + 12 < 1 ) Jacobi converge
Ahora hallamos el número de iteraciones:
(m)
x
kBJ km2 x(1) x(0)
2 1 + kB k
x J
2
Primero hallamos el vector x (1):
x(1)
1 =
x(1)
2 =
2 + x(0)
2
2 =1
4 + x(0)
1
2
x(0)
3
=2
CAPÍTULO 2. ÁLGEBRA LINEAL NUMÉRICA I
40
x(0)
2
2
x(1)
3 =
2
=1
Por tanto:
(1)
x
x(0) 0
@
=
2
0 1
2 A = 2
0 2
kBJ k2 = (BJt BJ ) = (BJ2 ) = (BJ ) = p1
q
q
2
Ya que:
0
BJ
1
Tomando logaritmo en base
=@
p12
01 21 01
2 0
2
0 21 0
m
p12
1
A
2 5 10 5
p
1= 2 y despejando m:
m 340 11
|
Ejemplo:
()
Dada la matriz A , determinar si existen valores de para los cuales es convergente el método de Jacobi pero no
el de Gauss-Seidel.
0
2 1 1
1A
A ( ) = @ 1 2
0 1 2
Solución:
Necesitamos verificar la condición necesaria y suficiente.
Jacobi:
jD + L + Rj = 0 = 83 + 4 + Gauss-Seidel: j(D + L) + Rj = 0 = 2 (8 + + 4) )
1 = 0 doble
2 = +4
8
CAPÍTULO 2. ÁLGEBRA LINEAL NUMÉRICA I
Gauss-Seidel converge si Si 41
(B GS ) = +4
8 < 1, es decir, si 12 < < 4.
= 0 convergen ambos métodos.
0
2
> , es decir, que p es monótono
Jacobi: tenemos un polinomio de orden 3, con su derivada p creciente, con p 1
1 y p 1 1, lo que significa que sólo tiene una raiz real, al ser monótono creciente.
Calcularemos las raices complejas en función de una real que suponemos 1 . Aplicando Ruffini, llegamos a:
(
)=
( )=
( ) = 24 + 4 0
()
82 + 81 + 821 + 4 = 0
2 3 =
821 + 4 = 2 + 1
1 2
8
Al ser 2 y 3 raíces complejas conjugadas, tienen el mismo módulo:
j2 j2 = j3 j2 = 818+ 4 > 0
El radio espectral de B J es:
r
1
(BJ ) = 21 +
2
Lo cual nos lleva a que 21
< 0:5.
Despejando del polinomio sustituyendo 1 :
=
Con 1
831 + 41
= p12 :
p
p
4 2< <4 2
Es la condición de convergencia del método de Jacobi.
Intersecando las dos condiciones, para que converja Jacobi y no lo haga Gauss-Seidel:
p
4<4 2
Ya que para = 4 Gauss-Seidel no converge.
|
CAPÍTULO 2. ÁLGEBRA LINEAL NUMÉRICA I
42
2.4.5 Métodos iterativos basados en la optimización de una función
Es la base de los métodos más actuales. Se basa en pasar el problema de resolver un sistema de ecuaciones A x
a un problema de optimización. Para ello se define una función a minimizar, la función objetivo:
1
2
(x) = xt A x bt x
=b
(2.49)
Siendo A matriz simétrica definida positiva.
Por tanto, se trata de hallar
min (x). La condición necesaria de mínimo es:
x es minimo
, r (x ) = 0
Por tanto:
r (x) = A x b
Que satisface:
A x = b
La función que hemos definido tiene un único mínimo, global, y es estrictamente convexa.
1
1
(x + v ) = (x ) + v t r (x ) + v t A v = (x ) + v t A v > (x )
2
Ahora se trata de construir la solución x(s) de forma que 2
x(s+1) < x(s) .
De esa forma:
x(s+1) = x(s) + s d(s)
Donde d(s) es la dirección de movimiento s es la longitud de paso, en la dirección d(s) . Se trata de un proceso de búsqueda
o movimiento hacia la solución, es decir, que sólo interesan las direcciones hacia las que decrece.
Fijada una dirección d(s) , y desarrollando en series de Taylor:
x(s) + d(s)
= ' () = x(s)
+ d(s) r
x(s)
+ 12 2 d(s)t r2
x(s)
d(s) : : :
Haciendo búsqueda en línea exacta:
0
' () = 0 = d(s)
t
r x(s) + d(s)t A d(s)
Donde hemos sustituido la Hessiana por A ya que es una forma cuadrática, por lo que es la propia matriz.
Despejando :
=
Donde r(s) es el residual.
d(s) r x(s)
d(s)t A d(s)
t
t
d(s) r(s)
= d(s)t A d(s)
(2.50)
CAPÍTULO 2. ÁLGEBRA LINEAL NUMÉRICA I
43
Método del gradiente:
La dirección es el residual, es decir, la de máximo decrecimiento, que cambiada de signo es la de máximo crecimiento,
ya que r
r x .
(
s
)
Mientras r 6
,
=
()
=0
x(s+1) = x(s) + s r(s)
Con
s =
t
r(s) r(s)
r(s)t A r(s)
(2.51)
Se puede demostrar que se cumple:
2 t
1
t
1 + b A2 b 22 ((AA)) + 11 x(s) + b A2 b
La convergencia es lineal, salvo si 2 (A) = 1, y es más lenta cuanto mayor sea 2 (A).
x(s+1)
Método del gradiente conjugado:
La dirección que se escoje es conjugada con las anteriores, es decir:
d(s) A d(j ) = 0 j = 1 : s
t
1
El algoritmo es el siguiente:
s=0
Mientras r(s)
6= 0
r(0) = b A x(0)
(0)
(0)
si s > 0; d(s) = r(s) + s d(s 1)
d =r
o
rs
x(s+1) = x(s) + s d(s)
s = k k
8
>
>
>
>
>
<
>
>
>
>
>
:
( )
kr s s k
r
s = d sk t Akd s
(
r(s+1) = r(s) s A d(s)
s = s+1
2
( )
( )
2
1)
2
2
2
(2.52)
2
( )
Con matrices vacías representa muy poco cálculo.
Teorema 2.13. Dado un sistema A x b siendo A simétrica definida positiva, si x(s) es la s-ésima iteración calculada
por el método del gradiente conjugado, se cumple:
=
x(s)
2s t
1 t
1
+ b A2 b 4 22 ((AA)) + 11 x(0) + b A2 b
En teoría es más rápido, ya que acaba a lo sumo en n iteraciones.
Si A es mal condicionada, se puede usar el método del gradiente conjugado precondicionado, en el que se elige una matriz
C simétrica definida positiva y se aplica el método del gradiente conjugado a:
A^ x^ = ^b
Siendo
A^ = C 1 A C 1 x^ = C x ^b = C 1 b
Capítulo 3
Álgebra lineal numérica II
3.1 Cálculo de autovalores y autovectores
3.1.1 Introducción
Vamos a tratar de encontrar los valores i
2C
= [i] x para x 6= 0 y A 2 C nn.
In ) = 0, y polinomio característico a p () = det (A
tales que A x
Se llama ecuación característica de la matriz A a det
(A
In ).
Se define el espectro de una matriz como el conjunto de autovalores de dicha matriz. El radio espectral es el máximo en
módulo de los autovalores.
El determinante de una matriz es el producto de todos sus autovalores.
traza ( A) = 1 + 2 + : : : + n =
n
P
aii .
i=1
Se dice que una matriz hermítica o simétrica es definida positiva si y sólo si sus autovalores son positivos, y además
los autovalores de toda matriz hermítica o simétrica son reales.
Se define la traza de una matriz como:
Los autovalores de la inversa de una matriz son los inversos de los autovalores de la matriz sin invertir.
Dos matrices semejantes tienen los mismos autovalores.
p (A) = 0.
Una matriz A es diagonalizable por semejanza unitaria si y sólo si es normal (A A = A A ).
Teorema de Cayley-Hamilton. Toda matriz satisface su ecuación característica:
Teorema 3.1.
Por tanto, toda matriz compleja hermítica es diagonalizable por una transformación de semejanza unitaria y toda
matriz real simétrica es diagonalizable por semejanza ortogonal.
Teorema de Rayleigh. Dada una matriz compleja y hermítica cuyos autovalores cumplen que n
n x A x
x x
n 1 : : : 1 :
n
1 x 2 C f0g
y cada cota se alcanza cuando x es el autovector del autovalor correspondiente.
Teorema de Jordan. Toda matriz es semejante a una matriz de Jordan:
0
J=
B
B
B
@
J1 (1 )
0
..
.
0
0 :::
J2 (2 ) : : :
0
..
.
0
0
..
.
: : : Jk (k )
0
1
C
C
C
A
44
con Ji
(i ) =
1 0
0 i 1
i
B
B
B .
B ..
B
@
..
.
0 0 0
0 0 0
:::
:::
0
0
1
C
C
.. C
. C
C
::: 1
: : : i
A
(3.1)
CAPÍTULO 3. ÁLGEBRA LINEAL NUMÉRICA II
45
Teorema de Schur. Dada una matriz A, existe otra matriz unitaria U de forma que se cumple:
U A U = T
Siendo T triangular superior.
3.1.2 Localización de los autovalores
Teorema de los círculos de Gerschgorin. Dada una matriz A real y cuadrada de orden n, y definiendo el dominio unión
de los círculos de Gershgorin:
D=
n
[
i=1
Ci ; Ci = fz 2 C = jz aii j i g ; i =
n
X
j=1
j 6=i
jaij j ; i = 1 : n
(3.2)
Si es un autovalor, entonces está dentro del dominio D.
Ejemplo:
Dada la matriz
0
A=@
1 2 41
3 1 2A
0 2 3
Se tiene que:
C1
C2
C3
Centro
-1
1
3
Radio
6
5
2
|
Si A es de diagonal dominante estrictamente, es invertible. Por otro lado,
dominante.
A
I
Teorema de Brauer. Dada la matriz A real y cuadrada de orden n, y un entero m tal que
no puede ser de diagonal
1mny
jamm aii j > m + i i = 1 : n; i 6= m
=
En ese caso, el círculo de Gershgorin Cm fz 2 C
y contiene un único autovalor de la matriz A.
= jz amm j m g es disjunto de los demás círculos de Gershgorin,
3.1.3 Métodos de cálculo del polinomio característico
Denotamos de forma general el polinomio característico de la matriz A:
p () = jA I j = (
¿Cuáles son los pi ?
1)n
n + p1 n 1 + : : : + pn
CAPÍTULO 3. ÁLGEBRA LINEAL NUMÉRICA II
46
Método de Le-Verrier:
Utiliza la relación entre las raices de una ecuación y sus coeficientes (relaciones de Newton):
a0 xn + a1 xn 1 + : : : + an
!
8
<
:
a0 s1 + a1 = 0
a0 sk + a1 sk 1 + : : : + ak 1 s1 + kak = 0
k =P2 : n
sk = ni=1 xki
Que, trasladado a nuestro polinomio característico:
p1 = s1
pk = k1 (sk + p1 sk 1 + : : : + pk 1 s1 )
k =P2 : n
sk = ni=1 ki
(3.3)
Los sk se obtienen como suma de los autovalores de potencias de la matriz A. El orden de este método es de O
operaciones.
Método de Faddeev-Souriau:
Es una modificación del método anterior que reorganiza el cálculo. Partiendo de B0
A1 = A B0
A2 = A B1
..
.
An = A Bn 1
= In:
p1 = traza ( A1 ) B1 = A1 + p1 In
p2 = traza2(A2 ) B2 = A2 + p2 In
pn =
..
.
traza(An )
n
..
.
(3.4)
Bn = An + pn In
Al final del proceso, en virtud del teorema de Cayley-Hamilton, Bn
n4
= 0.
Método de Danilevski:
Sólo como mención. Consiste en transformar la matriz A en una equivalente (por semejanza) cuyo polinomio característico sea fácil de determinar. Se transforma a una matriz de Frobenius:
0 :::
B
B
A!B1 0
0
B .
@ ..
0
..
.
:::
:::
:::
..
pn
..
.
..
.
.
1
p1
1
C
C
C
C
A
jF I j = p ()
3.2 Métodos de reducción a matriz tridiagonal y a matriz Hessenberg
3.2.1 Si A es tridiagonal
0
B
A=B
B
a1 c2 : : :
b2 a2 : : :
.
@ ..
0
..
:::
.
bn
0
0
1
C
C
.. C
. A
an
CAPÍTULO 3. ÁLGEBRA LINEAL NUMÉRICA II
jA I j =
a1
47
0
c2 : : :
..
b2
..
.
..
.
..
.
.
..
0
.
bn
:::
an bn =
a1
= (an
) jAn 1 I j
= (an
) pn 1 () bn cnpn 2 ()
..
.
..
.
bn 1
cn =
Entonces, queda, para los polinomios sucesivos:
p0 () = 1
p1 () = a1 pk () = (ak ) pk 1 () bk ck pk 2 () k = 2 : n
(3.5)
3.2.2 Si A es Hessenberg superior
0
B
A=B
B
@
Con todos los bi
a11 a12 : : : a1n
b2 a22 : : : a2n
..
.
..
0
.
:::
..
.
bn
1
C
C
.. C
. A
ann
6= 0 para i = 2 : n.
Se trata de anular los elementos de la última columna, multiplicando por s1
segunda, etc., siendo sn .
( )=1
() a la primera columna, por s2 () a la
Para ello, se utiliza la siguiente recurrencia, conocida como método de Hyman:
sn () = 1
k=n:
Si bk
1 : 2 ! sk 1 () =
(akk
) sk () +
bk
n
P
j =k+1
akj sj ()
(3.6)
6= 0.
De esta forma, se obtiene:
0
det (A In ) = (
Si se tiene bi
1)n+1 b2 bn @(a11
) s1 () +
n
X
j =2
1
a1j sj ()A
= 0 para algún i, se pueden hacer las recurrencias de las submatrices cuadradas principales.
CAPÍTULO 3. ÁLGEBRA LINEAL NUMÉRICA II
48
3.2.3 Reducción por semejanza de una matriz a tridiagonal o Hessenberg
La reducción por semejanza de una matriz a tridiagonal (si es simétrica) o Hessenberg superior (en otro caso) se suele
hacer por los métodos de Givens y Householder:
Gtp Gt1 A G1 Gp
Hn 1 H2 A H2 Hn 1
Para el caso de Givens, rotaciones de una matriz simétrica:
0
B
Gt1 B
B
@
a11 a21 : : : an1
a21 a22 : : : an2
..
.
an1
..
.
an2 : : :
(3 1)
0
1
..
.
ann
C
C
C
A
G1 =
B
B
B
B
B
B
@
a(1)
a(1)
0 : : : a(1)
11
21
n1
(1)
(1)
a21 a22 : : : : : : a(1)
n2
(1)
0 a(1)
:
:
:
:
:
:
a
32
n3
..
.
..
.
..
a(1)
n1 : : :
(1 3)
.
..
.
a(1)
nn
1
C
C
C
C
C
C
A
Tratamos de hacer un cero en ; y en ; . Al multiplicar por Gt1 , cambian las filas p y q , y al hacerlo por G1
las columnas p y q , por lo que hay que tener cuidado de que, al haber anulado ; , cuando anulemos ; , no
cambiemos ; , que es lo que ocurre si escogemos p
,q
. Entonces, escojemos la rotación sobre p; q de
forma que anulemos q; p
. Por ejemplo, en nuestro caso escogeríamos las filas ; para anular las filas ; ,
; para anular ; , etc.
(3 1)
(2 4)
(
(4 1)
(3 1)
(2 3)
=3 =1
1)
Si estamos haciendo transformación Householder, elegimos la simetría de
i
n de la columna i .
+1:
1
0
H2 B
@
H=I
..
.
:::
H de forma que se anulen los elementos
1
a11 : : : an1
..
.
an1
(1 3)
( )
(3 1)
.. C H
2
. A
ann
2 vvt vv
t
Con la elección adecuada de v , podemos hacer ceros a partir de la posición que queramos.
La primera transformación no tiene que tocar la primera columna, y de la misma forma, la
primera fila.
H2 = I
t
v (2) v (2)
2 v(2)t v(2)
Siendo
v (2) =
0
a21 + signo (a21 ) Los elementos que se quieren anular
z
Si la matriz A no es simétrica, llegamos a una matriz Hessenberg.
}|
a31 : : : an1
{
!
H2
no puede tocar la
CAPÍTULO 3. ÁLGEBRA LINEAL NUMÉRICA II
49
3.3 Métodos iterativos de las potencias, de Jacobi y QR
Estos son métodos que atacan directamente el cálculo de autovalores.
3.3.1 Método de las potencias, de la iteración inversa y deflación
3.3.1.1
Método de las potencias
Este método calcula el autovalor de máximo módulo de la matriz
ello, se realiza la siguiente iteración:
A, denotándose dicho autovalor como 1 .
y (k) = A y (k 1) = A(k) y (0) k = 1; 2; : : :
yp(k+1)
yp(k)
! 1
Estamos suponiendo que 1 domina a todos los demás autovalores (estrictamente mayor):
y (0) =
n
X
i=1
Para
(3.7)
j! j > j2j : : : jnj.
i x(i)
Donde x(i) son los autovectores asociados a los autovalores i de la matriz A.
En la aplicación práctica (sobre un ordenador) se requiere normalizar los vectores y(k) , usando, por ejemplo, la norma
infinito:
y (1) = A y (0) =
y (2) = A y (1) =
n
X
i=1
n
X
i=1
i i x(i)
i 2i x(i)
Es decir:
y (p+1) = A y (p) =
n
X
i=1
i (i p+1) x(i)
Sacando el dominante del sumatorio:
n
X
y (k) = k1 1 x(1) + i i
1
i=2
k
Ya que 1i
k
!
x(i) = ki i x(1)
! 0.
El problema con el que nos encontramos al utilizar este método con ordenadores, es que estamos elevando 1 a k , un
número que puede ser muy grande, y si 1 > , tenemos un overflow, mientras que si 1 < , underflow, y perdemos
la capacidad de cálculo.
Por tanto, normalizamos los y(k) con un p tal que:
1
1
CAPÍTULO 3. ÁLGEBRA LINEAL NUMÉRICA II
50
(k ) yp = y(k)1
Entonces, definimos el vector z(k) :
y (k )
z (k) = (k) y 1
De esta forma, nos queda:
y (k+1) = A z (k)
k = yp(k+1)
Y por tanto, k
! 1, con su signo.
yp(k+1)
yp(k)
Siendo v tal que v(k)
!0
(1) (k+1)
= 1 1xp (1)+ vp (k) ! 1 si 1 6= 0
1 xp + vp
El problema pues, es escoger un y (0) tal que 1 6
de redondeo pueden ocasionar a la larga que 1 6
= 0. Aunque se escoja un y(0) para
el que no se cumpla, los errores
= 0. Es prudente elegir varios y(0).
Por otro lado, si no se cumple que 1 es estrictamente dominante (que sea múltiple) o que 1 es complejo (por lo que
existe otro de módulo máximo, su conjugado), hay adaptaciones que no vamos a considerar.
Ahora la pregunta del millón: ¿va rápido o lento este método?
Pues eso depende de lo rápido que 1i tienda a cero, es decir, que cuanto más dominante sea 1 más rápido será el
método.
Hay una variante del método que consiste en desplazar el autovalor un cierto valor q , de forma que calculamos el
autovalor 1 q , aplicando el método de las potencias a A q I .
+
Con ello, el cociente 1i +qq tiende a 1, siendo más rápido.
3.3.1.2
Método de iteración inversa
Este método resuelve la problemática de hallar el autovalor de menor módulo, ya que invirtiendo los i el de menor
módulo se convierte en el de mayor módulo. Por tanto, las inversas de los autovalores son los autovalores de la
matriz inversa. No hay que invertir la matriz A, sólo hay que resolver el sistema de ecuaciones siguiente:
A y (k+1) = y (k)
Por algún método de factorización.
yp(k+1)
yp(k)
! 1
n
CAPÍTULO 3. ÁLGEBRA LINEAL NUMÉRICA II
51
Siendo n el autovalor de la matriz A de menor módulo.
Si se utiliza desplazamiento:
(A
q In ) y (k+1) = y (k)
yp(k+1)
yp(k)
! 1 q
n
Si A es simétrica, conviene usar el cociente de Rayleigh y la norma euclídea (en lugar de la norma infinito):
R (x) =
Interesa mucho factorizar la matriz A (o A
xt A x
xt x
q I ) para resolver rápidamente el sistema varias veces.
Todo lo visto anteriormente no sirve para una matriz ortogonal, ya que sus autovalores son todos de módulo la
unidad.
3.3.1.3
Método de deflación
Este método lo que hace es “desinflar” el problema. Se utiliza un autovalor 1 y un autovector x(1) para transformar
A y obtener otro autovalor como autovalor de una matriz de orden inferior.
Hay varias técnicas, alguna de las cuales vamos a comentar.
Teorema general de deflación.
t
B = A 1 x(1) v (1)
Con un v(1) tal que v (1)
t
x(1) = 1.
0; 2; : : : ; n g si A tiene de autovalores f1; 2 ; : : : ; n g.
Se puede demostrar entonces que B tiene de autovalores f
Deflación de Hotelling:
x(1)
x(1) 2
2
v (1) = Deflación de Wielandt:
A x(1) = 1 x(1)
(1)
ai x(1) = x(1)
i con xi 6= 0
Siendo ai la fila i de la matriz A.
CAPÍTULO 3. ÁLGEBRA LINEAL NUMÉRICA II
52
0
v (1) = B
@
ai1
1
1
.. C
. A
(1)
ain 1 xi
Como es un autovector, alguna componente es distinta de cero.
Ejemplo:
=6
el autovalor de módulo máximo, transformar A en
Dada la matriz A y 1
teniendo el autovector x (1) .
0
A=@
B mediante la deflación de Wielandt
4 1 1 1
1 3 2A
1 2 3
0
x(1) = @
1 1
1A
1
Hallamos el vector v (1) :
0
v (1) = @
Por tanto, aplicando B
=A
4 11
1A
1 6
1 x(1) v t :
0
B=@
0 0 0 1
3 2 1A
3 1 2
Y los valores de la submatriz
2 1
1 2
Son los restantes autovalores de A.
|
3.3.2 Método de Jacobi
Se aplica para matrices A simétricas. Se transforma en diagonal por semejanza mediante giros.
Ak+1 = Gtpk qk Ak Gpk qk
CAPÍTULO 3. ÁLGEBRA LINEAL NUMÉRICA II
53
Donde pk y qk dependen del paso en que nos encontremos. Sin considerar el subíndice k , la submatriz
tenemos que usar para la transformación es:
bpp
0
0
bqq
=
c
s
s
c
=
app apq
aqp aqq
=
c s
s c
2 2 que
Eligiendo s y c de forma que sc , por estabilidad numérica. Las filas p y q no tienen porqué estar juntas, sólo lo
marcamos así para ver cómo escojer s y c.
1
Se lleva el control de la suma de los cuadrados de los elementos no diagonales:
v
u
u
t
kAk2F
off (A) =
Como off
n
X
i=1
a2ii
(Ak+1)2 = off (Ak )2 2ap(kk)qk , off (Ak ) tiende a cero, y por tanto, Ak tiende a ser diagonal.
Para elegir pk y qk :
(k) 1. Criterio clásico: pk y qk tales que apk qk 2. Jacobi cíclico:
= maxi6=j a(ijk)
(pk ; qk ) siguen un orden.
(pk ; qk ) para los que ap(kk)qk no supere un cierto umbral.
3. Jacobi cíclico con filtro: se salta en el cíclico los pares
Ejemplo:
Reducir a tridiagonal la siguiente matriz:
0
5
B 1
A=B
@ 2
2
Aplicando H
1
1:5
2
1
2 2 1
2 1 C
C
9 5 A
5 1
= I 2 vvtvvt y calculando el vector v (1):
0
B
v (1) = B
@
0
1 + p12 + 22 + 22
2
2
0
B
H1 A H1 = B
@
0
B
v (2) = B
@
1
0
01
C B 4 C
C=B
C
A @ 2 A
2
5 3 0 0 1
3 9:5 4 3 C
A
0 4 1 1 C
0 3 1 1
1 0
0
C B
0
B
A=@
4 p16 + 9 C
3
0 1
0 C
A
9C
3
CAPÍTULO 3. ÁLGEBRA LINEAL NUMÉRICA II
54
0
B
H2 (H1 A H1 ) H2 = B
@
5 3
3 9:5
0 5
0 0
0
0 1
5
0 C
A
0:68 1:24 C
1:24 0:68
Por ser una matriz simétrica, sus autovalores son reales.
|
3.3.3 Método QR
Este método es esencial. Se consigue una matriz triangular o cuasitriangular realizando factorizaciones QR y multiplicando con el orden cambiado Q y R:
A1 = A
Ak = Qk Rk
Ak+1 = Rk Qk
(3.8)
Tendiendo Ak a triangular o cuasitriangular. Si es cuasitriangular, una parte de la matriz “se resiste” a ser triangular,
y lo que se hace es calcular los autovalores de esa parte por separado.
Qk Ak+1 = Qk Rk Qk = Ak Qk
Ak+1 = Qtk Ak Qk
Las matrices son semenjantes a A (multiplicamos por matrices invertibles), por tanto, los autovalores de Ak son los
de A. Es un método más lento, pero llega a la solución (en las iteraciones que sean, pero llega).
¿Qué matrices llegan a triangulares y cuáles a cuasitriangulares? La respuesta la tiene el siguiente teorema:
Teorema 3.2. El método QR sobre una matriz Hessenberg H irreducible de forma sucesiva, acaba siendo triangular
si y sólo si no existen dos autovalores distintos con el mismo módulo y multiplicidades de la misma paridad.
Por ejemplo, si una matriz Hessenberg tiene como autovalores 3 y -3, no acabará siendo triangular.
Se dice que una matriz H es irreducible si hi+1;i
6= 0 para i = 1 : n 1.
Los autovalores deben estar “en la misma caja”, es decir, que si al ir reduciendo por QR una matriz se obtiene una
cuasitriangular que va tendiendo a triangular, esto se aplica a las partes de la matriz diferentes que se “resisten” a ser
triangulares.
=
En la práctica, se reduce la matriz a Hessenberg o tridiagonal (si es simétrica) haciendo A1
Qt0 A Q0 ,
para anular los elementos de la primera subdiagonal por Givens, lo cual sólo requiere n-1 rotaciones, lo que
representa un coste muy pequeño.
Si Ak = Gk Rk , Qk es Hessenberg superior.
Ak+1 = Rk Qk es Hessenberg superior o tridiagonal simétrica.
CAPÍTULO 3. ÁLGEBRA LINEAL NUMÉRICA II
55
También se aplican desplazamientos para acelerar el proceso:
Hallar un k para que:
Hk
k In = Qk Rk
Hk+1 = Rk Qk + k In
eligiéndose cada k de forma que:
1.
2.
k) mientras h(k) 6= 0. Si es cero, se pasa a la fila anterior empezando por abajo.
k = h(nn
n;n 1
(k)
(k) !
h
h
(k)
n
1
;n
1
n 1;n
El autovalor de
es más próximo a hnn .
k)
(nn
k)
h(n;n
h
1
Con esta aceleración se puede llegar en unas 10 iteraciones, mientras que de la otra forma son necesarias alrededor
de 100.
Capítulo 4
Interpolación y aproximación
Introducción
Se tiene información de una función f para determinados valores de la/s variable/s independiente y dependiente.
Se trata de determinar un elemento p de una clase de funciones a elegir tal que p interpole a f (aproximación exacta)
en los puntos en los que se dispone de la información.
Por tanto, p es la que mejor aproxima f siguiendo algún criterio.
Esto nos puede servir para varias cosas:
1. Averiguar cuánto vale f
mación.
() si es difícil de evaluar. Vale p (), considerando el error de interpolación o aproxi-
(). Éste es p0 ().
Rb
Rb
3. Calcular a f (x) dx ! a p (x) dx.
4. Hallar un valor de tal que f () = y dado el valor de y .
2. Hallar el valor de f
0
4.1 Interpolación polinomial, de Hermite y trigonométrica
4.1.1 Interpolación polinomial
= ( )g i = 0 : n con xi distintos entre sí. Queremos determinar el
( ) = f (xi ) para i = 0 : n. Si no hay igualdad, no podemos llamarlo
Suponemos que tenemos los valores fxi ; yi f xi
polinomio p 2 Pn de grado máximo n tal que p xi
interpolación.
En primer lugar, veamos que la solución es única:
p 1 2 Pn y p2 2 Pn .
Entonces p1 (xi ) = f (xi ) 8i y p2 (xi ) = f (xi ) 8i.
Se cumple además que p 1 p2 2 Pn .
p1 (xi ) p2 (xi ) = 0 constituye un polinomio de grado n con n + 1 soluciones (ya que tenemos n + 1 valores), por
Suponemos que hay dos:
tanto:
p1 (x) = p2 (x)
Y la solución es única.
56
CAPÍTULO 4. INTERPOLACIÓN Y APROXIMACIÓN
4.1.1.1
57
Método de interpolación de Lagrange
Usamos una base fl0
(x) ; l1 (x) ; : : : ; ln (x)g para el espacio Pn, de forma que:
p (x) =
n
X
k=0
yk lk (x)
(4.1)
Esta es la fórmula de Lagrange, y se tiene, para cada valor que tenemos:
p (xi ) =
n
X
k=0
yk lk (xi ) = yi
La forma fácil de hacer esto es que sólo quede un sumando para cada xi :
yi li (xi ) = yi
Por tanto, se define a los li
(x) como funciones delta (delta de Kronecker):
lk (xi ) = Æik =
Por tanto, se pueden escribir los li
(x) = (x
0 i =6 k
1 i=k
(x) de la siguente forma:
(x
(xi
x 0 ) (x
li (x) =
Y si escribimos !n+1
x0 ) (x xi 1 ) (x xi+1 ) (x xn )
x0 ) (xi xi 1 ) (xi xi+1 ) (xi xn )
xn ), nos queda:
li (x) =
!n+1 (x)
(x xi ) !n0 +1 (xi )
Ejemplo:
Si se tiene la siguiente tabla de valores:
xi
yi
-1
0
4
1
4
2
3
-2
El polinomio de Lagrange nos queda:
p (x)
= 4 ( 1 x0)(x( 14) (x4) ( 1)1 1)
(x 4)(x 1)
+ 2 ((0x ++ 1)
1) (0 + 4)(0 1)
(x 0)(x 1)
+ 3 ((4x ++ 1)
1) (4 0)(4 1)
(
x + 1) (x 0)(x 4)
2 (1 + 1) (1 0)(1 4)
(4.2)
CAPÍTULO 4. INTERPOLACIÓN Y APROXIMACIÓN
58
|
El inconveniente de este método es que el polinomio cuesta más evaluarlo que con el algoritmo de Horner (Ruffini):
p (x) = a0 xn + a1 xn 1 + an
y = a0
y = yx + ai i = 1 : n
Además, si se añade otro dato, hay que volver a escribir el polinomio entero desde el principio.
4.1.1.2
Polinomio de interpolación de Newton
Se pretende con este método que al añadir un punto, sólo se añada un sumando al polinomio, sin alterar el resto.
Vamos a verlo paso a paso, empezando con un punto:
Se tiene
(x0 ; y0 ):
p0 (x) = y0
Si se añade un punto
(x1 ; y1 ):
p1 (x) = p0 (x) + a1 (x x0 ) !
p1 (x0 ) = p0 (x0 ) = y0
p1 (x1 ) = y1 = y0 + a1 (x1 x0 )
y y
a1 = 1 0
x1 x0
= f [x0 x1 ]
[x0 x1 ] se le llama diferencia dividida.
Añadimos un tercer punto (x2 ; y2 ):
Donde a f
p2 (x) = p1 (x) + a2 (x x0 )(x x1 ) !
y2 p1 (x2 )
a2 =
(x2 x0 ) (x2 x1 )
p2 (xi ) = p1 (xi ) i = 0 : 1
y2 = p2 (xi ) = p1 (xi ) + a2 (x2 x0 ) (x2 x1 )
= y2 ((yx02 + fx[0x)(0 xx21 ](xx21 ) x0 )) = f [x0 xx22]
f [x0 x1 ]
x1
Por inducción, llegamos a:
f [xi0 ; xi1 ; : : : xik ] =
(1)
}|
{
f [xi ; : : : ; xik ]
z
1
(2)
}|
f xi ; xi ; : : : ; xik
xik xi
z
0
0
1
{
1
(4.3)
CAPÍTULO 4. INTERPOLACIÓN Y APROXIMACIÓN
x
x0
x1
x2
x3
x4
x5
f (x)
f [x0 ]
f [x1 ]
f [x2 ]
f [x3 ]
f [x4 ]
f [x5 ]
59
Primeras diferencias
Segundas diferencias
f [x0 ; x1 ] = f [xx11]
f [x1 ; x2 ] = f [xx22]
f [x3 ; x2 ] = f [xx33]
f [x4 ; x3 ] = f [xx44]
f [x5 ; x4 ] = f [xx55]
f [x0 ; x1 ; x2 ] =
f [x1 ; x2 ; x3 ] =
f [x2 ; x3 ; x4 ] =
f [x3 ; x4 ; x5 ] =
f [x0 ]
x0
f [x1 ]
x1
f [x2 ]
x2
f [x3 ]
x3
f [x4 ]
x4
f [x1 ;x2]
x2
f [x2 ;x3]
x3
f [x3 ;x4]
x4
f [x4 ;x5]
x5
Terceras diferencias
f [x0 ;x1]
x0
f [x1 ;x2]
x1
f [x2 ;x3]
x2
f [x3 ;x4]
x3
f [x0 ; x1 x2 ; x3 ] = f [x1 ;x2 ;xx33] xf [0x0 ;x1 ;x2]
f [x1 ; x2 ; x3 ; x4 ] = f [x2 ;x3 ;xx44] fx[1x1 ;x2 ;x3 ]
f [x2 ; x3 ; x4 ; x5 ] = f [x3 ;x4 ;xx55] fx[2x2 ;x3 ;x4 ]
Tabla 4.1: Diferencias divididas para 6 puntos
El que está en (1) y no está en (2), tiene que estar en el denominador, lo mismo que está en (2) y no en (1).
Por tanto, nos queda el polinomio de interpolación siguiente:
Pn (x) = f [x0 ] + f [x0 ; x1 ] + : : : + f [x0 ; x1 ; : : : ; xn ](x x0 ) (x x1 ) (x xn 1 )
(4.4)
En la tabla (4.1) se puede ver un ejemplo de diferencias divididas sucesivas con 6 puntos.
Ejemplo:
Teniendo la siguiente tabla de valores, hallar el polinomio de interpolación de Newton:
xi
yi
-1
0
4
1
4
2
3
-2
Hallamos las diferencias divididas sucesivas:
a1 = 0 2( 41) = f [x0 ; x1 ] = 2
a2 = 4 3( 41) = f [x0 ; x2 ] = 51 !
2 4 = f [x0 ; x3 ] = 3 !
a3 = 1+1
( 2)
9
4 0 = f [x0 ; x1 ; x2 ] = 20
3 ( 2) = f [x0 ; x1 ; x3 ] = 1 !
1 0
1
5
1
1 4
9
20
= 2960
Tenemos, por tanto, el siguiente polinomio:
p ( x) = 4
2(x + 1) + 209 (x + 1)(x 0) + 29
60 (x + 1) x (x 4)
|
Fórmulas en diferencias finitas:
Esto es sólo como mención. Se usa para puntos equiespaciados, es decir, para xi
Se definen las siguientes diferencias:
f (x) = f (x + h) f (x); k = k 1
2. Regresiva: rf (x) = f (x) f (x h); rk = r rk 1
3. Central: Æf (x) = f (x + h=2) f (x h=2); Æk = Æ Æ k 1
1. Progresiva:
= xo + ih
CAPÍTULO 4. INTERPOLACIÓN Y APROXIMACIÓN
60
Son todos operadores lineales. La fórmula de Newton en diferencias finitas (progresiva)queda:
f [x0 ; : : : ; xk ] =
k f (x0 )
hk k !
Se puede hacer de forma similar para la diferencia regresiva, empezando por el último punto.
4.1.1.3
Error de interpolación
E (x) = f (x) Pn (x)
En los puntos xi , que son los datos de que se dispone, obviamente
distinto de cero.
(z ) = f (z ) Pn (z )
E (xi )
= 0.
En los demás, es normal que sea
f (x) Pn (x)
! (z )
!n+1 (x) n+1
= xi .
f es de clase n + 1 en el intervalo [min fxi ; xg ; max fxi ; xg]. también lo es, ya que se define a partir de operaciones
elementales de polinomios y no se cuentan los puntos en los que !n+1 (x) = 0, que son los xi .
(x) = 0 tiene n + 2 raices, siendo de grado n + 1. Aplicando el teorema de Rolle:
Para los x 6
9c 2 (min fxi ; xg ; max fxi ; xg) =0 = f (n+1) (c) 0 f (x!) P(xn)(x) (n + 1)!
n+1
Despejando:
f (n+1) (c)
f (x) Pn (x) =
(n + 1)! !n+1 (x) = E (x)
Donde c depende de x.
Esto es importante para acotar el error cometido al derivar o integrar con el polinomio de interpolación.
A continuación vemos otra expresión del error:
(
Teniendo el conjunto f xi ; f
(xi )) i = 0 : n; (x; f (x)) ; x 6= xi g
Pn+1 (z ) = Pn (z ) + f [x0 ; x1 ; : : : ; xn ; x] (z x0 ) (z xn )
Es el polinomio de interpolación de Newton añadiendo el punto x.
Pn+1 (x) = f (x) = Pn (x) + f [x0 ; : : : ; xn ; x] (x x0 ) (x xn )
Esto tiene poca utilidad con una tabla, pero si se conoce f , se puede acotar el error, derivando la función en un
intervalo a; b .
( )
max
axb f (n+1) (x)
jE (x)j j!n+1 (x)j
(n + 1)!
(4.5)
CAPÍTULO 4. INTERPOLACIÓN Y APROXIMACIÓN
61
Por tanto, si evaluamos en un punto que esté cerca de alguno de los puntos de interpolación obtenemos mayor
precisión por decrecer la función !n+1 x para dichos puntos.
()
No extrapolar salvo en puntos próximos a los extremos.
No usar muchos puntos de interpolación (derivadas de orden pequeño e interpolación de bajo grado).
Si se aumenta el número de puntos ¿el polinomio se parece más a f ?
No es lógico pensarlo, y en general no ocurre. Tampoco suele servir puntos concretos.
Teorema de Weierstrass. Una función continua y definida en un intervalo
quiera por un polinomio definido en ese intervalo.
[a; b] se puede aproximar tanto como se
4.1.2 Interpolación osculatorio y de Hermite
En problemas diferenciales se suele disponer de valores sobre la función y sobre su/s derivada/s:
0
x0 f (x0 ) f (x0 ) : : : f (k0 ) (x0 )
0
x1 f (x1 ) f (x1 ) : : : f (k1 ) (x1 )
..
.
xn
..
.
0
f (xn ) f (xn ) : : : f (kn ) (xn )
Se trata de determinar p 2 Pk0 +k1 +:::kn +n tal que:
p (xi ) = f (xi ) i = 0 : n
p(j ) (xi ) = f (j ) (xi ) j = 1 : ki
El conjunto de los polinomios osculantes Pk0 +k1 +:::kn +n es una generalización de los polinomios de Taylor y de Lagrange. La propiedad de estos polinomios es que dados n
números distintos x1 : : : xn y n
enteros no negativos m0 : : : mn , el polinomio osculante que aproxima a la función f 2 Cm a; b siendo m
fm0 : : : mng y
xi 2 a; b 8i
n, el el polinomio de menor grado que coincide con la función y todas sus derivadas de orden
menor o igual que mi en xi para i
n.
+1
[ ] =0:
[ ]
+1
= max
=0:
El grado de ese polinomio osculante será como mucho.
M
Los polinomios de Hermite se dan cuando mi
en cada punto. Este es un caso frecuente.
=
n
X
i=0
mi + n
= 1 i = 0 : n, es decir, cuando se conocen la función y la derivada primera
Al resolver estos polinomios
se dan diferencias divididas con puntos coincidentes, ya que se conoce más de un dato
por cada punto: f x k:+1
:: x
Teniendo la siguiente fórmula:
f [x0 : : : xn ; x] =
f (n+1) (c)
(n + 1)!
Al tomar límites cuando xi tiende a x para todo i, c tiende a x:
CAPÍTULO 4. INTERPOLACIÓN Y APROXIMACIÓN
lim f
xi !x
Por tanto, para k
62
n+2 puntos
x0 : : : xn ; x
+ 1 puntos coincidentes:
f [x; : : : ; x] =
(n+1) (x)
= f(n + 1)!
f (k) (x)
k!
(4.6)
Si hay puntos que coinciden y otros que no, y suponiendo que están ordenados:
(
f [x0 ; : : : ; xn ] =
4.1.2.1
f (n) (x0 )
n!
f [x1 :::xn ] f [x0 :::xn
xn x0
1
]
si x0
si x0
= xn
6= xn
(4.7)
Expresión de Newton para el polinomio de interpolación de Hermite
En la tabla (4.2) se pueden ver las diferencias divididas aplicables al caso de que haya puntos coincidentes.
zi
x0
x0
x1
x1
..
.
xn
xn
f [zi ]
f (x0 )
f (x0 )
f (x1 )
f (x1 )
..
.
f [zi 1 ; zi ]
0
f (x0 )
f [x0 ; x1 ]
0
f (x1 )
..
.
f (xn ) f [xn 1 ; xn ]
0
f (xn )
f (xn )
Tabla 4.2: Diferencias divididas indefinidas
El polinomio de interpolación sale, por tanto, de grado
P2n+1 (x)
4.1.2.2
=
+
+
+
+
2n + 1:
f [x0 ] + f [x0 ; x0 ] (x x0 )
f [x0 ; x0 ; x1 ](x x0 )2
f [x0 ; x0 ; x1 ; x1 ](x x0 )2 (x x1 )
:::
f [x0 ; x0 ; x1 ; x1 ; : : : ; xn ; xn ](x x0 )2 (x xn 1 )2 (x xn )
Forma de Lagrange
P2n+1 (x) =
^
n
X
i=0
f (xi ) Hi (x) +
n
X
0
i=0
f (xi ) H^ i (x)
(4.8)
Con Hi y Hi a determinar:
Hj (x) =
1 2(x
0
xj ) Ln;j (xj ) L2n;j (x)
(4.9)
y
H^ j (x) = (x xj ) L2n;j (x)
Donde Ln;j
(x) denota el j-ésimo coeficiente del polinomio de Lagrange de grado n.
(4.10)
CAPÍTULO 4. INTERPOLACIÓN Y APROXIMACIÓN
63
4.1.3 Métodos recurrentes
Vamos a ver el algoritmo de Neville para generar recursivamente aproximaciones polinómicas de Lagrange:
=
fxS g y T S
Dados S y T dos subconjuntos de fx0 ; x1 ; : : : ; xn g con S T
interpolación de grado k que utiliza los puntos de un conjunto C fx0 ; x1 ; : : :
los puntos xi todos distintos:
= fxT g, PC;k (x) es el polinomio de
; xn g siendo k + 1 el cardinal de C y
P
(x) (x xT ) PT;k 1 (x) (x xS )
PS [T ;k (x) = S;k 1
xS xT
(4.11)
0
Denotándose P0;:::n;k el polinomio en los puntos f ; : : : ng de grado k , se pueden ver en la tabla (4.3) las aproximaciones para polinomios de Lagrange usando el método de Neville.
xi
x0
x1
x2
..
.
xn
f (xi )
f (x0 )
f (x1 )
f (x2 )
1 punto
P0;0 ()
P1;0 ()
P2;0 ()
2 puntos
3 puntos
P0;1;1 ()
P1;2;1 ()
P0;1;2;2 ()
..
.
f (xn ) Pn;0 () Pn 1;n;1 () Pn 2;n 1;n;2 ()
Tabla 4.3: Aproximaciones para el método de Neville
4.1.4 Interpolación trigonométrica
[0 2 )
Pasa el problema de reales a complejos. Se toman puntos equiespaciados en ; , conociendo valores de la función
en esos puntos. Consiste entonces en expresar el polinomio de interpolación en función de senos y cosenos.
Si hay un número N par de puntos (N
= 2M ):
(x) = a20 +
y si es impar (N
M
X
(ak cos(kx) + bk sen(kx))
(4.12)
(ak cos(kx) + bk sen(kx)) + a2M cos(Mx)
(4.13)
k=1
= 2M + 1):
(x) = a20 +
M
X1
k=1
Recordamos las fórmulas de Moivre:
ix
cos x = e +e
2
ix
sen x = e 2ie
ix
ix
e = cos x + i sen x y e
Ya que ix
ix
= cos x
i sen x.
Usando esta fórmula de Moivre, el problema se queda como:
CAPÍTULO 4. INTERPOLACIÓN Y APROXIMACIÓN
64
M
ikx
X
(x) = a20 + ak e +e
2
k=1
=
0 +
M
X
ak
k=1
eikx e ikx
2i
k=1
M ak + ibk ikx
ibk ikx X
e
+
e
2
2
k=1
ikx
+
M
X
bk
Expresión compleja del polinomio trigonométrico:
ix
t (x) = 0 + 1 e +2
2eix + : : : + 1
N
(N 1)ix
e
(4.14)
Con los j complejos, que se pueden calcular de la siguiente forma:
j =
Siendo t
1 NX1 yk ! j = 1 NX1 yk ijk
N
e
k
N
N
2
k=0
(4.15)
k=0
(xk ) = yk para k = 0 : N 1.
Demostración:
Notamos !k
= eixk por comodidad, siendo x k = 2Nk .
1
B 1
B
B 1
B
0
B .
@ ..
1
1
1
:::
11
N
: : : !1
: : : !2N 1
!12
!22
!1
!2
..
.
!N2
!N 1 !N2 1 : : :
10
CB
CB
CB
CB
CB
A@
1
0
1
2
..
.
N
1
1
0
C
C
C
C
C
A
B
B
B
B
B
@
=
Que se denota:
F [i ] = [yi ] i = 0 : N
Moltiplicando por
1
(F )t (conjugada traspuesta):
(F )t F [i ] = (F )t [yi ] i = 0 : N 1
Queda entonces:
0
N
0
B
B
B .
@ ..
0
:::
N :::
0 0
..
.
0
0
1
C
C
.. C . A
[i] = (F )t [yi ]
::: N
Por tanto, la solución al sistema para hayar los j es inmediata:
1
y0
y1
y2
..
.
yN
1
C
C
C
C
C
A
CAPÍTULO 4. INTERPOLACIÓN Y APROXIMACIÓN
j =
1 NX1 yk !
65
k
N k=0
j
j=0:N
1
(4.16)
|
Para los coeficientes ah y bh :
0 = a20
j = aj 2ibj
N j = aj +2ibj
j =1:M
a0 = 20 aj = j + N j bj = i (j N j ) j = 1 : M
(4.17)
Para N impar y:
0 = a20
j = aj 2ibj
N j = aj +2ibj
j=1:M
a0 = 20 aj = j + N j bj = i (j N j ) j = 1 : M
Cuando los puntos xi no los tenemos para el intervalo
1
1
M = a2M
aM = 2M
(4.18)
[0; 2):
t ! x0 ; x0 + h; x0 + 2h; : : : ; x0 + (N
1) h
Definimos una nueva variable:
x!
t x0 2
h N
4.2 Teoría de la aproximación en espacios vectoriales normados
4.2.1 Introducción
Ahora tratamos de aproximar un elemento
siendo esta la mejor aproximación posible.
f
de un conjunto
E
mediante elementos de un subconjunto
V
de
E,
Hay que elegir un criterio de aproximación. Una vez fijado el criterio que seguimos tenemos que preguntarnos:
¿Bajo qué condiciones existe alguna mejor aproximación? ¿Es esta única?
¿Cómo se caracterizan las mejores aproximaciones?
¿Cómo se calculan?
Vamos a trabajar con espacios normados y subespacios de dimensión finita, y consideraremos aproximaciones mínimocuadráticas.
4.2.2 Teoremas y definiciones
Teorema 4.1. Dado un subespacio V del espacio normado E , de dimensión finita, para cada f 2 E existe alguna
mejor aproximación en V , y el conjunto de las mejores aproximaciones de f es un subconjunto convexo de V .
Definición:
Un subconjunto de un espacio V es convexo si cumple:
f + (1 ) g 2 V
2 V; 0 1
Si f; g
CAPÍTULO 4. INTERPOLACIÓN Y APROXIMACIÓN
66
Teorema 4.2. Si E es un espacio estrictamente convexo, para cada
subespacio V de dimensión finita.
2 E existe una y sólo una aproximación en un
f
Definición:
Un espacio es estrictamente convexo si:
8f; g= kf k = 6=kggk = 1 )
f
kf + (1 ) gk < 1
0<<1
Ejemplo:
El conjunto R2 con la norma infinito no es estrictamente convexo, ya que hay segmentos que unen puntos de norma
1 que a su vez son también de norma 1, en cambio, con la norma 2 sí es estrictamente convexo.
|
Definición:
Producto interior o escalar:
1.
2.
3.
hf; gi 0 y hf; f i = 0 , f = 0
hf; gi = hg; f i
hf + g; hi = hf; hi + hg; hi
p
E es normado con la norma kf k = hf; f i (un vector no tiene norma cero si no es el vector nulo).
E es estrictamente convexo.
Demostración:
kf + (1 ) gk2 + (1 ) kf gk2 = 2 hf; f i + (1 )2 hg; gi
+ 2 (1 ) hf; gi + (1 ) hf; f i
+ (1 ) hg; gi 2 (1 ) hf; gi
Como kf k
= kgk = 1, esto queda:
2 + (1 )2 + 2 (1 ) = 2 + 1 + 2
2 + 2 22 = 1
Y por tanto:
kf + (1 ) gk < 1
Si f
6= g y 0 < < 1, con lo cual es convexo.

Teorema 4.3. (Para caracterizar la mejor aproximación):
Un elemento v 2V
(subespacio con producto escalar) es la mejor aproximación de f
hf v; vi = 0 8v 2 V
2 E en V si y sólo si:
CAPÍTULO 4. INTERPOLACIÓN Y APROXIMACIÓN
67
4.2.3 Método de las ecuaciones normales
( ) =0:
Dada una base de V (n+1 dimensional), fi x ; i
ng, según la condición de ortogonalidad anterior, las coordenadas de la mejor aproximación v , ai en esa base son solución del siguiente sistema de ecuaciones normales:
n
X
i=0
hi (x) ; j (x)i ai = hf; j (x)i j = 0 : n
(4.19)
Con una base ortogonal el sistema de ecuaciones es sencillo de resolver.
Dada una base:
0
B
@
h0; 0i : : : h0; ni
..
.
..
.
hn; 0i : : : hn; ni
1
C
A
Que se conoce como Matriz de Gram, se dice que la base es ortogonal si cumple
hi; k i = 0
= k. Entonces, para el sistema anterior se tiene:
Para todo i 6
ak =
hk ; f i
hk ; k i
4.3 Aproximación por mínimos cuadrados polinomial y trigonométrica,
discreta y continua
4.3.1 Aproximación polinomial por mínimos cuadrados polinomial discreta
=1:
Dados m valores reales yi , para i
m, de una función f en los puntos xi , i
polinomio Pn de forma que minimice:
m
X
i=1
= 1 : m, el problema es determinar un
wi (yi Pn (xi ))2
Siendo wi pesos positivos.
La aplicación de esto es aproximar una información que se transmite y llega con ruido, dando mayor o menor peso
según resulte la forma de onda esperada.
Se puede utilizar la siguiente base:
0 (x) = 1; 1 (x) = 0; : : : ; n (x) = xn
hk ; j i = xk ; xj =
m
X
i=1
wi xki xji
CAPÍTULO 4. INTERPOLACIÓN Y APROXIMACIÓN
hk ; f i =
m
X
i=1
68
wi f (xi ) xki
El sistema de ecuaciones normales queda:
At W A a = At W y
Siendo las columnas de A los vectores:
v (k) = xk1 ; xk2 ; : : : ; xkm
t
k=0:n
W es diagonal con los pesos wi y el vector y = (y1 ; y2 ; : : : ym )t
Este sistema es mal condicionado, por lo que se soluciona el siguiente sistema (solución de mínimos cuadrados) por
alguno de los métodos de Householder, Givens o Gram-Schmidt:
M a=b
M
0
B
@
pw1 : : :
..
.
0
0
..
.
: : : pwn
10
1
CB .
A @ ..
1
=
x1
xm
p
p
W a; b = W y
1
0
.. C B .. C
. A@ . A
xnm
an
=B
@
x21 : : : xn1
x2m : : :
10
a0
f (x1 ) pw1
..
.
f (xn ) pwn
1
C
A
(4.20)
Usando una base de polinomios ortogonales en un conjunto de puntos xi , pk , se reduce el sistema de ecuaciones
normales a diagonal. Estos polinomios se pueden obtener aplicando la siguiente relación de recurrencia:
pj +1 (x) = j (x j ) pj (x) j pj 1 (x) ; p 1 (x) = 0; p0 (x) = A0 6= 0
donde los coeficientes son:
j hpj ;pj i
ji
j = AAj+1
j = hhppjj;xp
;pj i j = j 1 hpj 1 ;pj 1 i
j
Siendo Aj el coeficiente principal de pj .
4.3.2 Aproximación polinomial por mínimos cuadrados continua
Ahora consideramos tener información de la función en todos los puntos de un intervalo
Si tenemos un espacio de funciones continuas en un intervalo
hf; gi =
Z b
a
[a; b].
[a; b] con el producto escalar:
w (x) f (x) g (x) dx
CAPÍTULO 4. INTERPOLACIÓN Y APROXIMACIÓN
con w
exista
69
(x) 0 en [a; b], nula en un número finito de puntos, y de forma que para toda función continua en el intervalo
Z b
a
w (x) f (x) dx
tratamos de hallar el polinomio de grado a lo sumo n Pn que mejor aproxime a f . Esto implica minimizar
Z b
E=
Siendo Pn
Pn (x))2 dx
(f (x)
a
n
(x) = P ak xk :
k=0
E=
Z b
a
(f (x))2 dx
2
n
X
k=0
ak
Z b
a
xk f (x) dx +
Z b
n
X
a
k=0
ak xk
!2
dx
Por tanto, al minimizar para los aj :
@E
@aj
= 2
Z b
a
xj f (x) dx + 2
n
X
k=0
ak
Z b
a
xj +k dx = 0
Se obtiene el siguiente sistema de ecuaciones normales:
n
X
k=0
ak
Z b
a
xj +k dx =
[ ]
=
Z b
a
xj f (x) dx; j = 0 : n
(4.21)
El sistema tiene solución única dados f 2 C a; b y a 6 b. La resolución del sistema es inmediata si se usan polinomios
ortogonales sobre el intervalo con respecto a la función peso w x , generados con la recurrencia de la sección anterior.
En cambio, la evaluación de las integrales
Z b
a
()
w (x) f (x) pj (x) dx
normalmente requiere algún tipo de discretización si
tema siguiente).
f es muy complicada (integración numérica, que se verá en el
A continuación veremos algunas sucesiones de polinomios ortogonales:
Siendo P
Nombre
Intervalo
Peso
Legendre
[ 1; 1]
w (x) = 1
Chebyshev
[ 1; 1]
w (x) = p11 x2
Laguerre
[0; 1]
! (x) = e x
Hermite
[ 1; 1]
2
w ( x) = e x
Polinomio
hPj ; Pj i = 2j2+1
(j + 1) Pj+1 (x) = (2j+ 1) xPj (x) jPj 1 (x)
0
hTj ; Tj i = =2 jj =
>0
Tj +1 (x) = 2xTj (x) Tj 1 (x)
hLj ; Lj i = (j !)2
Lj +1 (x) = (2j + 1 x) Lj (xp) j 2 Lj 1 (x)
hHj ; Hj i = j !2j Hj +1 (x) = 2xHj (x) 2jHj 1 (x)
1 (x) = 0 y P0 (x) = 1, llevado a todos los polinomios, T; L y H .
CAPÍTULO 4. INTERPOLACIÓN Y APROXIMACIÓN
70
4.3.3 Aproximación trigonométrica por mínimos cuadrados discreta
2k equiespaciados, siendo k
Se tienen los puntos xk
N
de la función f en esos puntos yk ; k
N .
=
=0:
= 0 : N 1; N = 2M + 1, en el intervalo [0; 2] y los valores
1
Queremos obtener la función trigonométrica:
q
a X
(x) = 0 + (ak cos kx + bk sen kx) ; q M
2 k=1
(4.22)
de forma que minimice
NX1
k=0
(xk ))2
(yk
Como en el caso de interpolación trigonométrica, el problema se transforma en uno complejo en el que se determina
el polinomio
tn (x) = 0 + 1 ixe +2 2eix + : : : + n nix
e
Siendo j
2 C ; j = 0 : n y n = 2q N 1. Minimizando
NX1
k=0
( yk
En el espacio vectorial C N cuyo producto escalar es hx; y i
tn (xk ))2
= xt v y siendo
w(k) = 1; w1k ; w2k ; : : : ; wNk 1
t
2ik
ixk
N , los w(k) son ortogonales y de norma dos w(k) con k
n y wk
2
aproximación tn x es única y sus coeficientes se obtienen de la siguiente forma:
=0:
()
=e =e
j =
hy; w (j)i = 1
w(k) 2
2
= pN . En este caso, la mejor
NX1
y w j; j = 0 : n
N k=0 k k
La ortogonalidad de los w(k) permite asegurar que incrementando n, la nueva mejor aproximación se obtiene añadiendo términos a la anterior.
4.4 La transformada discreta de Fourier y el algoritmo FFT
La transformada discreta de Fourier de N valores yk ;
k=0:N
Yj =
NX1
k=0
1 son los N números siguientes:
yk wk j
(4.23)
CAPÍTULO 4. INTERPOLACIÓN Y APROXIMACIÓN
Para j
71
= 0 : N 1.
El algoritmo FFT o Transformada Rápida de Fourier permite evaluar los valores Yj con un coste de operaciones del
orden O N log2 N .
t:
Algoritmo de la FFT para N
( ))
(
= F F T (y; N )
N = 1, Y = y
función
si
Y
=2
en otro caso
m = N=2
w = e 2Ni
YT = F F T (y (1 : 2 : N ) ; m)
YB = F F T (y (2 : 2 : N) ; m)
d = 1; w; w2 ; : : : wm 1 t
z = d: YB Y = YYT + zz
T
fin
]
Capítulo 5
Derivación e integración numéricas
En este tema vamos a tratar de obtener la derivada o la integral de una función, de forma numérica, bien porque la
función sea muy compleja o porque tengamos una tabla de datos de esa función, con la que tengamos que trabajar
para obtener su derivada o integral.
5.1 Métodos de derivación numérica
5.1.1 Introducción
1
Dados k y , vamos a tratar de aproximar o calcular
fórmulas lineales del tipo:
n
X
i=0
=0:
f (k) (), de forma que tienda a un sólo número, a base de
Ai f (xi ) = f (k) ()
Donde xi ; i
n son los puntos donde se evalúa
derivación numérica.
f y Ai los coeficientes que nos encontraremos en la fórmula de
Tenemos varias opciones a la hora de elegir un método de resolver el problema:
1. Usar una función que interpole o aproxime a una tabla de datos:
Teniendo los valores xi ; f xi con i
n, si usamos la fórmula de interpolación, obtenemos
(
k
)
Pn , siendo:
()
(
( ))
=0:
f(k) ()
=
n
X
f (k) () = Pn(k) () + Dk E (x)x= = Ai f (xi ) + E (k) ()
i=0
Con Ai
= li(k) (), si usamos la interpolación de Lagrange.
2. Método de los coeficientes indeterminados: imponiendo que la fórmula sea exacta para xj con j
grado más alto posible. De esta forma, se obtiene el siguiente sistema:
Dk xj x= =
n
X
i=0
72
Ai xji ; j = 0; 1; 2; : : :
(5.1)
= 0 : k, siendo k el
CAPÍTULO 5. DERIVACIÓN E INTEGRACIÓN NUMÉRICAS
n
X
i=0
Ai xji
8
>
>
>
>
>
<
=>
73
0
j k 1
k!
j =k
(k+1)! j = k + 1
1!
(k+2)!
2
2! j = k + 2
>
>
>
>
: ..
(5.2)
..
.
.
El sistema es lineal en los Ai si los xi están fijados, no lineal en otro caso.
3. Desarrollo de Taylor:
f (k) () =
n
X
i=0
Ai f (xi )
=
=
n
X
i=0
m
X
j =0
0
m
X
Ai @
f (j ) ()
(xi
j =0 j !
n
1X
A (x
j ! i=0 i i
f (j ) ()
1
f (m+1) (c)
m+1 A
) +
(m + 1)! (xi + )
j
)
j
!
+
f (m+1) (c)
(xi )m+1
(
m
+
1)!
i=0
n
X
(5.3)
(5.4)
haciendo cero todos los coeficientes menos el de la derivada k-ésima:
n
1X
A (x
j ! i=0 i i
)
j
= 0k!
j = 0 : m; j 6= k
j=k
Con m hasta donde se pueda llegar, lo suficientemente grande.
Definición: grado de exactitud de una fórmula de derivación:
Una fórmula se dice de grado de exactitud q si q es el menor entero positivo para el que la fórmula es exacta para
todo polinomio de grado no mayor que q y no exacta para algún polinomio de grado q
.
n
P
Ai f xi se dice que es
Teorema 5.1. Si f es continuamente diferenciable hasta el orden necesario, una fórmula
i=0
interpolatoria si y sólo si su grado de exactitud es mayor o igual que n.
+1
Ejemplo:
Deducir una fórmula que estime la derivada segunda de una función como A 0 f
Usando la segunda opción, imponemos que sea exacta para 1; x; x 2 :
(
f (x) = 1 ! 0 = A0 + A1 + A2
f (x) = x ! 0 = A0 ( h) + A1 + A2 ( + h)
f (x) = x2 ! 2 = A0 ( h)2 + A1 2 + A2 ( + h)2
Montamos el sistema:
( )
h) + A1 f () + A2 f ( + h).
CAPÍTULO 5. DERIVACIÓN E INTEGRACIÓN NUMÉRICAS
0
@
1
1
h h)2 2
(
74
1
01
+h 0 A
( + h)2 2
Reduciendo por Gauss, queda:
0
1 1 1 01
@ 0 h 2h 0 A
0 0 2h2 2
Las soluciones, por tanto son:
A0 = h12 A1 = h2 A2 = h12
Y la fórmula queda:
00
f () =
f ( h)
2f () + f ( + h)
h2
|
5.1.2 Fórmulas de derivación numérica
En la tabla (5.1) vemos algunas de las fórmulas de derivación numérica más usuales, para las derivadas de orden
1, 2 y 3. El punto c es interior al intervalo de evaluación de la función en cada una de las fórmulas (por ejemplo,
; h en la fórmula progresiva de 3 puntos).
[
+2 ]
Estas fórmulas de derivación son inestables, debido a los errores de discretizacion (Ed ) y al evaluar f
f (xi ) = f^i + i !
n
X
i=0
(xi ) (i).
Ai i = Er
+
=
Siendo Er el error de redondeo. Para obtener un valor de h óptimo, hay que minimizar jEr j jEd j o jEr j
jEdj.
En general, lo segundo no da el mismo punto que lo primero, pero es más fácil de resolver, y la diferencia no es
demasiado grande.
Una problemática de la derivación numérica es que no existen fórmulas de derivación estables.
5.2 Métodos de integración numérica de Newton-Côtes y de Gauss
5.2.1 Introducción al método
n
Rb
P
Ahora tratamos de calcular o aproximar el valor de la integral a f x dx por
Ai f xi . Con w x (igual
i=0
a cero sólo en un número finito de puntos) una función peso, podemos calcular por la misma fórmula la integral
Rb
a w x f x dx.
()
( )
() ()
Si la primitiva es difícil de determinar o de evaluar, podemos usar alguno de estos métodos.
()
0
CAPÍTULO 5. DERIVACIÓN E INTEGRACIÓN NUMÉRICAS
0
f () = f (+hh) f ()
75
h f (2)
(c)
2
0
f () = 3f ()+4f (2+h h) f (+2h) + h3 f (3) (c)
0
f () = f ( 2h) 4f2(h h)+3f () + h3 f (3) (c)
0
f (+h) h f (3) (c)
f () = f ( h2)+
h
6
0
)+8f (+h) f (+2h) + h f (5) (c)
f () = f ( 2h) 8f ( h12
h
30
0
f () = 25f ()+48f (+h) 36f (12+2h h)+16f (+3h) 3f (+4h) + h5 f (5) (c)
00
f () = f ( h) 2fh()+f (+h) h12 f (4) (c)
00
f () = f () 2f (+hh)+f (+2h) hf (3) (c1 ) + h6 f (4) (c2 )
00
f ()+16f (+h) f (+2h) + h f (6) (c)
f () = f ( 2h)+16f ( h) 30
12h
90
000
f () = f ( 2h)+2f ( h2)h 2f (+h)+f (+2h) h4 f (5) (c)
2
3
3 puntos
Formula progresiva puntos
2
Formula regresiva
2
4
4
Formula centrada
5 puntos
5
Formula centrada de
Formula progresiva puntos
2
2
2
2
4
2
2
3
Tabla 5.1: Fórmulas de derivación numérica
1. Fórmulas interpolatorias: se usa el polinomio de interpolación para la función f con los puntos xi :
Z b
a
Con s
w (x) f (x) dx =
Z b
a
w (x) s (x) dx
(x) el polinomio interpolante o aproximatorio. Si f (x) = Pn (x) + E (x):
Z b
a
w (x) f (x) dx =
Z b
a
w (x) Pn (x) dx +
Z b
a
w (x) E (x) dx
Al usar la interpolaciń de Lagrange, tenemos que:
0
n Z b
X
i=0
con n+1
(x) = (x
B
@
1
w (x) li (x)
a |
{z
Ai
}
dxC
Af
(xi ) +
w (x) f (n+1) (c)
(n + 1)! n+1 (x)
a
Z b
(5.5)
x0 ) (x xn ).
2. Método de coeficientes indeterminados: de nuevo, se obtiene una fórmula exacta para un conjunto de funciones
básicas (polinomios de bajo grado, por ejemplo f x
xi ; i ; ; : : :, hasta el grado más alto posible. Queda
el sistema:
( )=
Z b
a
w (x) xi dx =
n
X
k=0
=0 1
Ak xik ; i = 0; 1; 2; : : :
(5.6)
CAPÍTULO 5. DERIVACIÓN E INTEGRACIÓN NUMÉRICAS
76
3. Desarrollo de Taylor:
Z
n
X f (j ) () X
f (j ) () b
w (x) (x )j dx Ai (xi )j
=
j
!
j
!
a
i=0
j =0
j =0
X
(5.7)
Definicion:
Se define el grado de exactitud de una fórmula de cuadratura de la misma forma que en el apartado anterior: Una fórmula
de cuadratura se dice de grado de exactitud q si dicho q es el menor entero positivo para el que la fórmula es exacta
para todo polinomio de grado no mayor que q y no exacta para algún polinomio de grado q
.
+1
Se puede ver también el mismo teorema que en el apartado de derivación numérica, sin ninguna variación.
5.2.2 Fórmulas de integración de Newton-Côtes
En la tabla (5.2) se pueden ver las fórmulas simples de Newton-Côtes cerradas, que son las que se usan cuando los
dos extremos del intervalo están contenidos en los puntos xi que se evalúan, y en la tabla (5.3) las fórmulas simples
de Newton-Côtes abiertas, que se usan para intervalos en los que ninguno de los extremos está en el conjunto de
los xi . Para aquellos intervalos en los que uno de los extremos está en el conjunto de puntos, la fórmula se llama
semiabierta, pero no vamos a verlas. En ambas tablas, c es un punto interior al intervalo de integración.
Para estas fórmulas de Newton-Côtes, no se distingue peso en el integrando, es decir:
puntos xi equiespaciados.
R x1
x0
R x2
x0
f (x) dx = h2 (f (x0 ) + f (x1 ))
h3 f (2)
12
f (x) dx = h3 (f (x0 ) + 4f (x1 ) + f (x2 ))
w (x) = 1, y se consideran los
(c)
h5 f (4)
90
Trapecios
( c)
R x3
Simpson
5
f (x) dx = 38h (f (x0 ) + 3f (x1 ) + 3f (x2 ) + f (x3 )) 380h f (4) (c)
R x4
2h
8h7 (6)
x0 f (x) dx = 45 (7f (x0 ) + 32f (x1 ) + 12f (x2 ) + 32f (x3 ) + 7f (x4 )) 954 f (c)
x0
Simpson
3=8
Boole
Tabla 5.2: Fórmulas de Newton-Côtes cerradas simples
R x1
x
R x2
x
R x3
x
R x4
x
1
1
1
f (x) dx = 2hf (x0 ) + h3 f (2) (c)
3
1
Punto medio
3
f (x) dx = 32h (f (x0 ) + f (x1 )) + 3h4 f (2) (c)
5
f (x) dx = 43h (2f (x0 ) f (x1 ) + 2f (x2 )) + 1445h f (4) (c)
h5 f (4) (c)
f (x) dx = 524h (11f (x0 ) + f (x1 ) + f (x2 ) + 11f (x3 )) + 95144
Tabla 5.3: Fórmulas de Newton-Côtes abiertas simples
5.2.3 Fórmulas compuestas
En este tipo de fórmulas lo único que se hace es romper el intervalo de integración en varios subintervalos, de forma
que se aplican las fórmulas simples que se deseen a cada subintervalo. Esto nos sirve para reducir el valor de h sin
tener que recurrir a usar más puntos, por contra, aumenta el cálculo a realizar.
CAPÍTULO 5. DERIVACIÓN E INTEGRACIÓN NUMÉRICAS
77
Por ejemplo, para aplicar el método de Simpson dividiendo en m subintervalos:
Z b
a
Siendo x0
f (x) dx =
Z x2
x0
f (x) dx +
Z x4
x2
f (x) dx + : : : +
Z x2m
x2m
2
f (x) dx
= a, x2m = b y h = b2ma .
Los errores de redondeo y discretización en la integración numérica van multiplicadas por h, con lo que tienden a
cero cuando h tiende a cero. Por tanto, las fórmulas de integración numérica son estables.
Ejemplo:
Determinar los coeficientes de la siguiente fórmula integral:
1
Z
1
Siendo fijo e incluido en el intervalo
¿es posible una mejor elección de ?
Usar la fórmula anterior para calcular
Empezamos por determinar los A i :
f (x) dx = A0 f (
1) + A1 f () + A2f (1)
[ 1; 1], de forma que la fórmula sea lo más exacta posible. Razonadamente,
R1
2
0 p5x+4 dx acotando el error cometido, y usando la mejor elección.
f (x) = 1
R1
f (x) = x
R1
1 dx = A0 + A1 + A2 = 2
1 xdx = A0 + A1 + A2 = 0
R
f (x) = x2 1 1 x2 dx = A0 + 2 A1 + A2 = 32
Montamos el sistema:
0
@
1 1 1 2 1
1 1 0 A
1 2 1 2=3
Y resolviendo el sistema, obtenemos los coeficientes siguientes:
1+3 A1 = 4 2 A2 = 1 3
A0 = 3(1+
)
3(1 )
3(1 )
2
El grado de exactitud de la fórmula es q , ya que es exacta para cualquier polinomio de grado menor o igual que
2 (como hemos exigido al crear el sistema de ecuaciones). Veamos si es exacta para x 3 :
Z
1
1
x3 dx = 0 = A0 + 3 A1 + A2
1 + 3 + 43 + 1 3
3(1 + ) 3(1 )2 3(1 )
= 34 =
= 0, el grado de exactitud es 2, y si es = 0, q 3.
Por tanto, si 6
CAPÍTULO 5. DERIVACIÓN E INTEGRACIÓN NUMÉRICAS
=0
Pero si , nos quedan como coeficientes A 0
es la de Simpson, cuyo grado de exactidud es 3.
78
= 1=3, A1 = 4=3 y A2 = 1=3, de forma que la fórmula que resulta
A continuación, pasamos a resolver la integral propuesta:
El intervalo de integracion es distinto al de la fórmula que tenemos que aplicar, con lo que necesitamos hacer un
cambio de variable para que los intervalos coincidan:
0
x
= 2x 1 ) x = 12 x0 + 1
Con el que la integral se transforma en:
Z
1
1
q
1 dx0
2
5 (x0 + 1) + 4 2
2
Aplicando la fórmula, nos queda:
Z
p
0 11 4 1
2
1
1
5
4
1
1
q
q +
p
+
=
+
dx =
3 2 3 132 3 3 3 6 13
1 25 (x0 + 1) + 4
1
!
|
5.2.4 Fórmulas de Gauss o de cuadratura superexactas
Se puede hacer una elección especial de los puntos xi y los coeficientes Ai de forma que el grado de exactitud de la
n
P
Ak f xk sea mayor que n.
fórmula
k=0
n
P
Teorema 5.2. Para que una fórmula
Ak f xk sea exacta para todo polinomio de grado a lo sumo n k con k k=0
(condición necesaria y suficiente), debe ser interpolatoria y además se cumple:
( )
+
( )
Z b
a
w (x) xj !n+1 (x) dx = 0; j = 0 : k
Como tiene que ser exacta para xj !n+1
mente, n k .
+
n
P
i=0
Ai f (xi ) exacta para todos los polinomios de grado 2n + 2.
Demostración:
Supongamos que una fórmula es de grado de exactitud
!n2 +1 es de grado 2n + 2.
Z b
Sin embargo, w
puede ser nula.
x0 ) (x xn )
(x), que es un polinomo de grado n + 1+ j , el grado de exactitud es, efectiva-
Teorema 5.3. No existe ninguna fórmula del tipo
a
1; !n+1 (x) = (x
1
w (x) ! 2
n+1
2n + 2:
(x) dx =
n
X
i=0
Ai !n2 +1 (xi ) = 0
(x) wn2 +1 (x) es un número positivo, sólo nulo en un número finito de puntos, por lo que la integral no
Se parte de un supuesto incorrecto, por tanto, no existe ninguna fórmula de grado de exactitud
2n + 2.

CAPÍTULO 5. DERIVACIÓN E INTEGRACIÓN NUMÉRICAS
5.3 Método de extrapolación de Richardson y métodos adaptativos
79
Capítulo 6
Métodos numéricos para ecuaciones
diferenciales ordinarias
6.1 Problema de valor inicial
6.2 Métodos unipaso de Taylor y de Runge-Kutta
6.3 Métodos multipaso y predictores-correctores
6.4 Convergencia y estabilidad de los métodos
6.5 Problema de contorno
6.6 Métodos del disparo, de diferencias finitas y de elementos finitos
80
Capítulo 7
Resolución de ecuaciones no lineales
7.1 Métodos de iteración de punto fijo
7.2 Teoremas de convergencia
7.3 Métodos para ecuaciones algebraicas
7.4 Sistema de ecuaciones no lineales
7.5 Iteración de punto fijo, métodos de Newton y cuasi-Newton
81
Capítulo 8
Métodos numéricos de optimización
8.1 Optimización no restringida
8.2 Métodos iterativos de descenso, del gradiente, del gradiente cojungado,
de Newton y cuasi-Newton
8.3 Problema de mínimos cuadrados no lineal: método de Levenberg-Marquardt
8.4 Programación no lineal
8.5 Métodos de penalización, de conjunto activo y de programación cuatrática
secuencial
82
Bibliografía
[1] Burden, R.L.; Faires, J.D. Análisis Numérico. Grupo Editorial Iberoamérica, 1985
83