CLASE 9 - MCC - 2016(...)

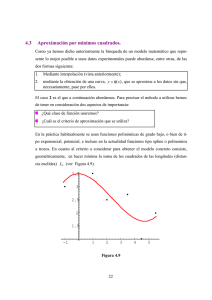
Interpolación por
Splines
Función Spline
•
•
•
•
Ajusta una curva suave a los puntos
Sigue la idea de la spline flexible de un dibujante
Consiste de polinomios definidos sobre subintervalos
Los polinomios se unen entre sí satisfaciendo ciertas
condiciones de continuidad
Aplicación: spline natural
Grados de una spline
Supongamos (n  1) puntos
(no necesariam ente igualmente espaciados)
(x i , y i )
i  0,1,...n
Deseamos ajustar un conjunto de polinomios de grado n
g i (x) desde x i hasta x i 1
Spline lineal
• Pendiente discontinua en los puntos
Polinomios de más alto grado
• F es chata (excepto entre -1 y 1)
• Se requieren ceros fuera de [-1,1]
• Así se crean las oscilaciones
• SOLUCIÓN? Ajustar distintos polinomios
Ajuste mixto
• Se ajustó una cuadrática en [-0.65, 0.65]
• P(x)=0 fuera de esa región
• Discontinuidad en las pendientes donde se unen los
polinomios
Definición
Una función spline de grado k con nodos
t 0  t1  t 2  ...  t n
es una función S tal que
a) en cada intervalo t i-1 , t i  S es un polinomio
de grado menor o igual que k
b) S tiene (k - 1) derivadas continuas en t 0 , t n 
Splines cúbicas
k 3
x  t0 , t1 
 S 0 ( x)
 S ( x)
 1
S ( x)  

S n 1 ( x)
x  t1 , t 2 

x  t n 1 , t n 
Si ( x)  ai x  bi x  ci x  d i
3
Incognitas
2
i  0, n  1
(coeficient es ) ? 4n
Se necesitan 4n ecuaciones
Balance de Ecuaciones
• Condiciones de interpolación
• Para los puntos interiores: 2(n-1) ecuaciones
• Para los extremos: 2 ecuaciones
• Condiciones de continuidad
• 2(n-1) ecuaciones
• Condiciones de extremo (terminales)
•
•
•
•
Spline cúbica natural ó
Spline enclavada ó
Spline periódica
2 ecuaciones
Condiciones de Interpolación
a) para los puntos interiores
Si 1 (ti )  yi  Si (ti )
b) para los extremos
S 0 (t0 )  y0
S n 1 (t n )  yn
1  i  n 1
Condiciones de Continuidad
Si1 (ti )  Si(ti )
Si1 (ti )  Si(ti )
1  i  n 1
1  i  n 1
Condiciones de Extremo:
Spline Cúbica Natural
S 0(t0 )  0
S n1 (t n )  0
• Derivada segunda igual a cero en los extremos=> derivada
primera constante
• => función lineal en los extremos
• La curva se “achata” cerca de los extremos
Condiciones de Extremo:
Spline Enclavada (clamped)
S 0 (t0 )  y0
S n 1 (t n )  yn
Aplicación: splines enclavadas
Condiciones de Extremo:
Spline Periódica
y0  y n
S 0 (t0 )  S n 1 (t n )
S 0(t0 )  S n1 (t n )
Ventaja: evita el fenómeno de Runge
Algoritmo de splines
cúbicas
Ecuaciones
Dados ( xi , yi ) ( xi 1 , yi 1 )
se tiene la ecuación :
g i ( x)  ai ( x  xi )3  bi ( x  xi ) 2  ci ( x  xi )  d i
Se desea una spline de la forma :
g ( x)  g i ( x)
para [ xi , xi 1 ]
i  0,1,...n  1
(1)
Condiciones
g i ( xi )  yi
i  0,1,..., n  1
(a)
g n 1 ( xn )  yn 1
g i ( xi 1 )  g i 1 ( xi 1 )
g i( xi 1 )  g i1 ( xi 1 )
i  0,1,..., n  2 (b)
g i( xi 1 )  g i1 ( xi 1 )
i  0,1,..., n  2 (d )
i  0,1,..., n  2 (c)
Solución
de (a) d i  yi
de (b)
i  0,1,..., n  1
(a )
yi 1  ai ( xi 1  xi ) 3  bi ( xi 1  xi ) 2  ci ( xi 1  xi )  yi
 ai hi  bi hi  ci hi  yi
3
2
i  0,1,..., n  1
hi  xi 1  xi
derivando :
g i( x)  3ai hi2  2bi hi  ci
g i( x)  6ai hi  2bi
i  0,1,..., n  1
(e)
Simplificación del desarrollo
zi  g i( xi )
zn  g n1 ( xn )
i  0,1,..., n  1
Coeficientes
de (e) zi  2bi
zi 1  6ai hi  2bi
Entonces
zi
bi 
2
zi 1  zi
ai 
6hi
(f)
(g)
Sustituyendo …
bi de ( f )
ai de ( g )
d i de (a)
en (1) y resolvemos para ci :
 zi 1  zi  3 zi 2
hi  hi  ci hi  yi
yi 1  
2
 6hi 
yi 1  yi 2hi zi  hi zi 1
ci 

hi
6
Invocando iguales pendientes
…
de (c) (igualdad de derivadas primeras en x  xi )
2

yi  3ai ( xi  xi )  2bi ( xi  xi )  ci  ci
en el intervalo anterior :
yi  3ai 1 ( xi  xi 1 ) 2  2bi 1 ( xi  xi 1 )  ci 1
yi  3ai 1hi 1  2bi 1hi 1  ci 1
igualando las yi y reemplazando los coeficient es :
2
Ecuación general
yi 
yi 1  yi 2hi zi  hi zi 1


hi
6
 zi  zi 1  2
zi 1
yi  yi 1 2hi 1 zi 1  hi 1 zi


 3
hi 1  2
hi 1 


2
hi 1
6
 6hi 1 
Ordenando :
 yi 1  yi yi  yi 1 

h i-1 zi 1  2hi 1  2hi zi  hi zi 1  6 

hi 1 
 hi
h i-1 zi 1  2hi 1  2hi zi  hi zi 1  6  f [ xi , xi 1 ]  f [ xi 1 , xi ]
En forma matricial:
h0
0

0


0


 z0 
2(h0  h1 )
h1
 
z1 


h1
2(h1  h2 )
h2
  z2 
 
0
h2
2(h2  h3 )
h3
  z3  




  


hn  2
2(hn  2  hn 1 ) hn 1   
  z n 1 
  
 zn 
 f [ x1 , x2 ]  f [ x0 , x1 ] 
 f [x , x ]  f [x , x ] 
2
3
1
2


 6  f [ x3 , x4 ]  f [ x2 , x3 ] 





 f [ xn 1 , xn ]  f [ xn  2 , xn 1 ]
n  1 ecuaciones n  1 incógnitas
Condiciones para Extremos
1. Spline natural
z0  0
zn  0
2. Spline enclavada
f ( x0 )  A
f ( xn )  B
a la izquierda : 2h0 z0  h1 z1  6( f [ x0 , x1 ]  A)
a la derecha : hn 1 z n 1  2hn z n  6( B  f [ xn 1 , xn ])
La matriz de coeficientes queda así:
Condición 1 (natural) :
z0  z n  0
h1
2( h0  h1 )



h1
2( h1  h2 )
h2


h2
2( h2  h3 ) h3








2( hn 2  hn 1 )
Condición 2 (clamped) :
f ( x0 )  A f ( xn )  B
2h0
h
 0




h1
2( h0  h1 )
h1
h1
2( h1  h2 )
h2

hn 2






2hn 1 
Condiciones para extremos
3. Parábolas en los extremos
z0  z1
zn 1  zn
4. Extrapolaciones lineales
z0 es extrapolación lineal de z1 y z2
a la izquierda :
z1  z0 z 2  z1

h0
h1
 z0 
(h0  h1 ) z1  h0 z 2
h1
(4.1)
zn es extrapolación lineal de z n 1 y zn -2
zn  zn 1 zn 1  z n  2
a la derecha :

hn 1
hn  2
(hn  2  hn 1 ) z n 1  hn 1 zn  2
 zn 
hn  2
(4.2)
La matriz de coeficientes queda así:
Condición 3 :
z0  z1
z n  z n 1
h1
(3h0  2h1 )



h
2
(
h

h
)
h
1
1
2
2




h2
2(h2  h3 ) h3






hn  2 (2hn  2  3hn 1 )
Condición 4 :
z0 y z n son extrapolaciones lineales
 usar (4.1) z0  g(z1,z 2 ) y (4.2) z n  g(zn-1,z n-2 )
 (h0  h1 )(h0  2h1 )

h1

h1







h12  h02
h1
2(h1  h2 )
h2
h2
2(h2  h3 )
h3

hn2 2  hn21
hn  2







(hn 1  hn  2 )(hn 1  2hn  2 ) 

hn  2

Observaciones
• Después de obtener los z, se pueden calcular los coeficientes
a, b, c para cada cúbica
• Matrices simétricas
• Datos igualmente espaciados, las matrices se reducen a
formas simples
Lectura obligatoria
• Gerald C.F., Wheatley P.O. Applied Numerical Analysis,
Addison Wesley, 7a Ed., 2004 - págs 168-179