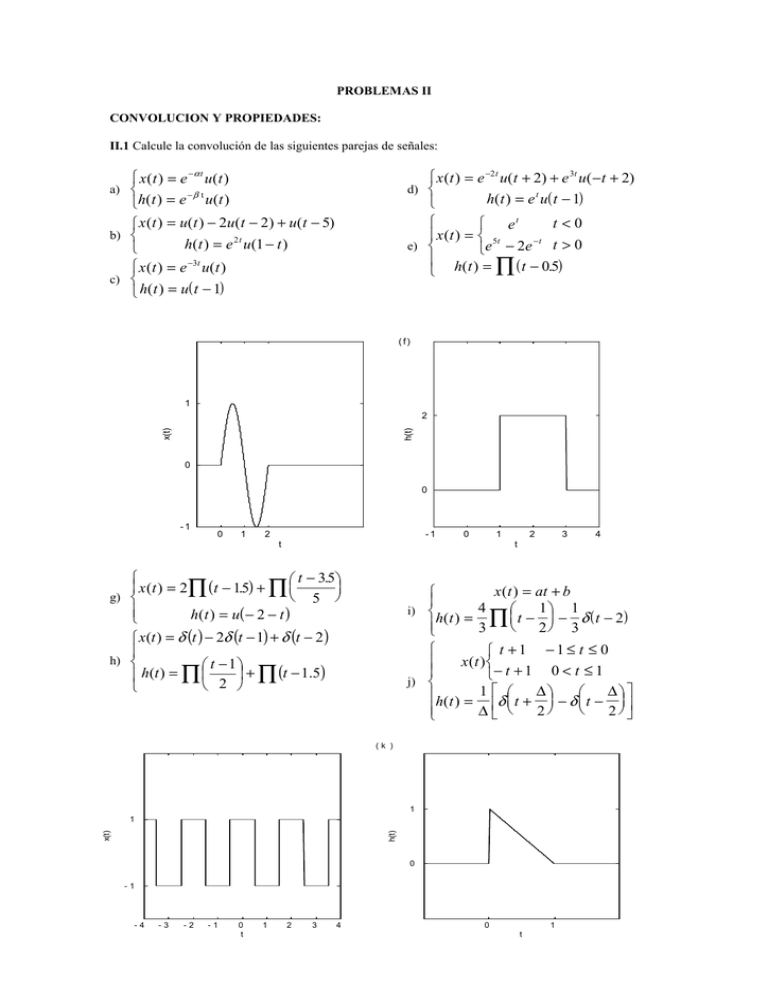
∏ ∏ ∏ ∏ ∏ ∏

PROBLEMAS II
CONVOLUCION Y PROPIEDADES:
II.1 Calcule la convolución de las siguientes parejas de señales:
 x (t ) = e −2 t u(t + 2) + e 3t u( − t + 2)
d) 
h(t ) = e t u( t − 1)


t<0
 et
 x ( t ) =  5t
−t
e) 
e − 2e t > 0
 h( t ) =
∏ ( t − 0.5)

 x ( t ) = e −α t u( t )
a) 
−β t
h(t ) = e u(t )
 x (t ) = u(t ) − 2u(t − 2) + u(t − 5)
b) 
h(t ) = e 2 t u(1 − t )

 x (t ) = e −3t u(t )
c) 
 h(t ) = u( t − 1)
( f)
1
x(t)
h(t)
2
0
0
-1
0
1
2
-1
0
1
t
2
3
. 

 t − 35
 x (t ) = 2∏ (t − 15
. ) + ∏

 5 
g) 

h(t ) = u( − 2 − t )
x (t ) = at + b


4
1 1

i) 
h( t ) = ∏  t −  − δ ( t − 2 )

 2 3
3

 t +1 −1≤ t ≤ 0
x (t ) 


− t + 1 0 < t ≤ 1
j) 
h(t ) = 1 δ  t + ∆  − δ  t − ∆  


∆  
2
2  
 x(t ) = δ (t ) − 2δ (t − 1) + δ (t − 2 )

h) 
 t − 1
 + ∏ (t − 1.5)
 h(t ) = ∏ 
 2 

(k )
1
x(t)
h(t)
1
0
-1
-4
-3
-2
-1
0
t
1
4
t
2
3
4
0
1
t
( l)
1
h(t)
x(t)
1
0
0
-1
-1
0
t
1
2
0
t
II.2 Dibuje y escriba las expresiones correspondientes a
a)
x ( t ) = 2e − t
;
A = 1 t 0 = 0.25
b)
x (t ) = 3 t
;
A = 1 t 0 = 14
3
[
[
]
c) x ( t ) = 3e − 3t cos 2π t − π 

4
][
2
y (t ) = x (t )∗ Aδ (t − t 0 ) donde:
d)
II.3 Demuestre que
1
]
x (t ) = t ( t − 0.1)
[ (
2
;
;
A = 1 t 0 = 0125
.
A = 1 t 0 = 0.2
)]
y (t ) = Bδ (t − t 1 ) ∗ Aδ ( t − t 0 ) es la función ABδ t − (t 0 + t 1 ) .
Aplicando esta propiedad, dibuje la señal:
y (t ) = 0.5δ ( t ) + 15
. δ ( t − 15
. ).
z (t ) = x (t )∗ y (t ) para x (t ) = 2δ ( t − 4.5) − 2δ ( t + 4.5) e
II.4 Sea h(t) el pulso triangular mostrado en la figura (a) y x(t) el tren de impulsos de la figura (b), es
decir: x ( t )
= ∑−∞ δ ( t − kT ) . Determine y dibuje y (t ) = x (t )∗ h(t ) para los valores de T
+∞
a): h(t)
siguientes: (a) T = 4, (b) T = 2, (c ) T = 3/2 (d) T = 1.
1
0
-1
0
1
t
b): x(t)
2
1
0
t
II.5 Si
x(t ) = 0
t > T1 y y (t ) = 0
t > T2 , entonces x(t ) ∗ y (t ) = 0
t > T3 .
Exprese T3 en términos de T1 y T2 . Compruebe esta propiedad convolucionando las funciones rectángulo:

t
 x (t ) = ∏  
 a=b=2
 a

cuando: 
t

a = 1 b = 3
 y (t ) = ∏  

b
∞
II.6 Definimos el área bajo una función continua v(t) como:
Av =
∫ v( t )dt . Demuestre que si
−∞
y (t ) = x (t )∗ h(t ) , entonces: Ay = Ax Ah .
RESPUESTA AL IMPULSO:
II.7 Determine justificadamente si los sistemas caracterizados por las siguientes funciones de respuesta al
impulso son causales y/o estables:
h(t ) = e −4 t u( t − 2)
−6 t
b) h( t ) = e u( 3 − t )
−2 t
c) h( t ) = e u( t + 50)
2t
d) h( t ) = e u( − 1 − t )
a)
e)
h(t ) = e −6 t
f)
h(t ) = te − t u(t )
g)
 t −100 



h(t ) =  2e − t − e  100   u(t )


II.8 Considere el SLI cuyas señales de entrada y salida vienen dadas por la siguiente
t
ecuación: y ( t )
=
∫e (
− t −τ )
x( τ − 2) dτ :
−∞
(a) ¿ Cual es la respuesta al impulso de este sistema ?
(b) Determine la respuesta del sistema cuando la entrada es: x ( t )
 t − 0.5
= ∏

 3 
II.9 Demuestre que si la respuesta de un SLI a x(t) es y(t), la respuesta del sistema a
x ' (t ) =
dx (t )
es
dt
y’(t):
(i) directamente a partir de las propiedades de linealidad e invariancia y la definición de derivada:
 x ( t ) − x ( t − h) 
x ' (t ) = Limh→0 

h


(ii) diferenciando la integral de convolución.
(iii) Examinando el siguiente sistema:
x(t)
Un SLI tiene como repuesta a la señal
u1(t)
h(t)
y’(t)
x (t ) = e −5t u(t ) , la señal y (t ) = sen(ω 0 t ) . Utilice el resultado
anterior para obtener la respuesta al impulso de este sistema.
(*) Nota: u1(t) es la respuesta al impulso del sistema derivador. No necesita saber su expresión analítica,
basta con saber que convolucionando u1(t) con una señal x(t), se obtendrá su derivada.
II.10 Considere el SLI con respuesta al impulso h0(t). La respuesta de dicho sistema cuando la entrada es
x0(t) es y0(t), que se muestra en la figura. Las siguientes funciones representan la señal de entrada y
respuesta al impulso para varios sistemas:
Entrada x(t)
(a) x ( t ) = 2 x 0 ( t )
(b)
(c)
(d)
(e)
(f)
x (t ) =
x (t ) =
x (t ) =
x (t ) =
x (t ) =
Respuesta al impulso h(t)
h(t ) = h0 (t )
h(t ) = h0 (t )
h(t ) = h0 (t + 1)
h(t ) = h0 (t )
h(t ) = h0 ( − t )
h( t ) = h ' 0 ( t )
x 0 ( t ) − x 0 ( t − 2)
x 0 ( t − 2)
x0 ( −t )
x0 ( −t )
x ' 0 (t )
y0(t)
2
0
-1
0
1
2
3
4
t
Obtenga la respuesta y(t) en los casos que sea posible.
II.11 Considere los dos sistemas en serie representados en la figura. El sistema A es lineal e invariante. El
sistema B es el inverso del sistema A. Si y1(t) es la respuesta a x1(t) e y2(t) a x2(t), conteste a las siguientes
cuestiones:
(a) ¿ Cual es la respuesta del sistema B a la entrada: ay1 ( t ) + by 2 (t ) donde a y b son constantes ?.
(b) ¿ Cual es la respuesta del sistema B a la entrada
x(t)
A
y1 ( t − τ ) ?
y(t)
B
x(t)
Acaba de demostrar que si A es LI y B es su inverso, también B es LI.
APLICACIONES:
II.12 Considere dos señales reales x(t) e y(t):
a) ¿ Cual es la relación entre Φxy y Φyx ?
b) ¿ Cual es la parte impar de Φxx ?
c) Suponga que la señal y ( t ) = x( t + T ) . Exprese Φxy y Φyy en función de Φxx.
d) Si x(t) es par, busque una relación entre su autoconvolución y su autocorrelación.
II.13 Obtenga la autocorrelación de las siguientes señales:
x1(t)
1
0
0
1
2
t
x2(t)
1
0
-1
0
1
2
3
4
5
6
7
t
II.14 Sea x(t) una señal real dada de duración finita, i.e.
t < 0
x ( t ) = 0
. Encuentre la respuesta al
t > T
impulso h(t) de un SLI tal que la respuesta a x(t) sea Φxx(t-T). Este SLI se denomina filtro sintonizado a la
señal x(t) .
En la mayoría de las aplicaciones, un mensaje codificado en una secuencia de dígitos binarios se
transmite bit a bit. Cada bit es transmitido enviando una señal dada al receptor (por ejemplo, x0(t) si el bit
es 0 y x1(t) si es 1). Así pues, el receptor debe ser capaz de reconocer si la señal es x0(t) o x1(t). Para ello,
el receptor está dotado de dos filtros sintonizados a cada una de dichas señales (“estar sintonizado”
significa que dicho filtro da una respuesta mayor cuando se recibe la señal a la que está sintonizado que
para cualquier otra).
Considere las señales representadas en la figura:
x0(t)
1
0
-1
0
1
2
3
4
3
4
t
x1(t)
1
0
-1
0
1
2
t
a) Dibuje el filtro sintonizado a cada una de ellas.
b) Si denominamos L0 el filtro sintonizado a x0(t) y L1 el sintonizado a x1(t), obtenga la respuesta
de L0 y L1 a x0(t) y x1(t).
II.15 Otra aplicación de los filtros sintonizados es en radar. El principio del radar es transmitir un pulso
electromagnético al objetivo de forma que se refleje en éste y retorne al punto emisor con un retardo
proporcional a la distancia a dicho objetivo. Idealmente, la señal recibida será simplemente una señal
retardada y con un cambio de amplitud respecto de la original.
Sea la señal real p(t) el pulso enviado. Demuestre que: Φ pp ( 0)
(
)
= max t Φ pp ( t ) . Utilice la
desigualdad de Schwartz:
b 2

u
(
t
)
v
(
t
)
dt
≤
 ∫ u (t )dt 
∫a
a

b
Utilizando el resultado anterior, demuestre que
retorna es:
1/ 2
b 2

 ∫ v (t )dt 
a

1/ 2
(
)
Φ xp (t 0 ) = max t Φ xp ( t ) si la señal que
x (t ) = α p( t − t 0 ) . De esta forma, el tiempo en el que la respuesta al filtro sintonizado a la
señal recibida alcanza el máximo permite calcular la distancia al objetivo.