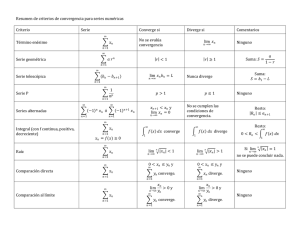
APUNTES SERIES CRITERIOS 1. Criterio del n#ésimo término para

UN I V E R S I D A D MA Y O R
F A C U L T A D D E IN G E N I E R Í A
SE G U N D O SE M E S T R E 2011
CÁLCULO INTEGRAL
APUNTES SERIES
CRITERIOS
Criterio del n-ésimo término para la divergencia
1.
Si la serie
1
P
an converge, entonces lim an = 0:
n=1
Si lim an 6= 0 o no existe, entonces
n!1
Criterio de la suma acotada
2.
Una serie
1
P
n!1
1
P
an diverge.
n=1
an de términos no negativos converge sí y solo sí sus
n=1
sumas parciales estan acotadas por arriba.
Criterio de la Integral
3.
Sea f una función continua, positiva no creciente en el intervalo
1
P
[1; 1[ y suponga que ak = f (k) para todo entero k: Entonces
an converge
n=1
R1
sí y solo sí 1 f (x) dx converge.
Criterio Serie p
4.
1
P
n=1
1
P
5.
p > 1 converge
p 1 diverge
1
np
rn converge si
1<r<1
n=1
Criterio de comparación ordinaria
6.
Suponga que 0
i)
Si
1
P
an
bn
,n
bn converge, también
n=1
ii)
Si
1
P
1
P
N
an converge.
n=1
an diverge, también
n=1
1
P
n=1
1
bn diverge.
Criterio de comparación al límite
7.
an
n!1 bn
Suponga que an
i)
0; bn > 0 y que lim
Si 0 < L < 1; entonces
Si L = 0 y
1
P
an y
n=1
juntas.
ii)
1
P
1
P
= L; entonces
bn convergen o divergen
n=1
bn converge, entonces
n=1
1
P
an converge
n=1
Criterio del cociente
8.
Sea
1
P
an una serie de términos positivos y supongase que
n=1
lim
n!1
an+1
an
=p
i)
Si p < 1 la serie converge.
ii)
Si p > 1 o lim
iii)
Si p = 1 el criterio no es concluyente.
n!1
an+1
an
= 1; la serie diverge.
Criterio de la raíz
9.
1
Si an > 0 y lim (an ) n = R; entonces
n!1
10.
i)
Si R < 1 la serie converge
ii)
Si R > 1 la serie diverge
Criterio de la serie alternante
Sea a1
a2 + a3
a4 :::::::::
Una serie alternante con an > an+1 > 0: Si lim an = 0; entonces la
n!1
serie converge.
11.
Criterio de la convergencia absoluta
Si
P
jun j converge, entonces
2
P
un converge.
Criterio del cociente absoluto
12.
Sea
P
un una serie de términos no nulos y suponga que
lim uun+1
=p
n
n!1
13.
i)
Si p < 1 la serie converge absolutamente.
ii)
Si p > 1 o lim
iii)
Si p = 1 el criterio no es concluyente.
n!1
an+1
an
= 1; la serie diverge.
Condicionalmente convergente
Si
cionalmente.
P
un converge y
P
jun j diverge, entonces la serie converge condi-
3
EJERCICIOS
1.
Indique si la serie converge o diverge. Si converge, determine su suma.
a)
1 h
P
2
k=0
b)
1
P
k=1
c)
1
P
k=1
d)
1
P
k=1
e)
1
P
k=2
f)
1
P
k=1
g)
1
P
k=6
1 k
4
1 k
5
+3
9 k
8
(R :
31
6 )
(R : Diverge)
k 5
k+2
(R : Diverge)
2
(k+2)k
3
(k+1)2
i
R:
3
2
3
k2
(R : 3)
4k+1
7k 1
R:
2
k 5
112
3
(R : Diverge)
2.
Escriba el decimal como una serie in…nita; luego determine la suma
de la serie y, por último, use el decimal para escribir el decimal como el cociente
de dos enteros.
a)
0; 22222:::::::
b)
0; 499999999::::::::
c)
0; 21212121:::::::
3.
Tres personas A, B y C dividen un premio como sigue. Primero lo dividen en cuartos, tomando cada uno una parte. Luego dividen el cuarto restante
en cuartos, tomando una parte cada uno y así sucesivamente. Demuestre que
cada uno recibe una tercera parte del premio.
4
4.
Analice la convergencia de la siguiente serie
1
X
1
n
ln
(n)
ln
(ln (n))
n=3
(R : Diverge)
5.
Use cualquiera de los criterios, para decidir acerca de la convergencia
o divergencia de la serie. Justi…que su conclusión indicando criterio.
a)
1
P
k2 +1
k2 +5
k=1
b)
1
P
k2
ek
k=1
c)
1
P
1
P
(R : Converge)
1000
k(ln(k))2
k=1
e)
(R : Converge)
p 2
k+2
k=1
d)
(R : Diverge)
1
P
(R : Converge)
k3
(R : Converge)
p1
n n+1
(R : Converge)
k2 e
k=1
f)
1
P
n=1
g)
1
P
8n
n!
n=1
h)
1
P
n
n=1
i)
1
P
k=1
j)
1
P
n=1
m)
(R : Converge)
(R : Converge)
ln(n)
2n
(R : Converge)
1
P
1
P
(R : Converge)
n+3
p
n2 n
n=1
l)
1 n
3
3k +k
k!
n=1
k)
(R : Converge)
4+cos(n)
n3
1
P
n=1
(R : Converge)
nn
(2n)!
(R : Converge)
5
1
P
n)
1 n
n
1
n=2
1
P
o)
ln
n=2
1
P
p)
1
2
n=1
1
P
q)
1
ln(n)
+
1
P
1
P
1
5n1:1
(R : Converge)
n+1
n
10n+1
(R : Diverge)
n+1
1
p
n(1+ n)
( 1)
( 1)
n=1
1
P
t)
n+1 n4
2n
1
P
n+1 n 1
1
( 1)
n=1
1
P
v)
1
P
w)
n=1
6.
(R : Diverge)
n sin(n)
p
n n
(R : Converge)
( 1)
n=1
( 3)n+1
n2
(R : Diverge)
¿ Para qué valores de p la siguiente serie converge?
1
X
1
p
n (ln (n))
n=2
7.
(R : Converge)
(R : converge)
( 1)
n=1
u)
(R : Converge)
n+1
( 1)
n=1
s)
(R : Diverge)
1 n
n
n=1
r)
(R : Diverge)
(R : p > 1)
Indique si la siguiente serie converge o diverge
2
3
4
1
+
+
+
::::::::
12 + 1 22 + 1 32 + 1 42 + 1
n!
n
n!1 n
8.
Demuestre que lim
9.
Analice la convergencia o devergencia de :
p
1
2 1
p
= 0; analizando la serie
1
1
+p
2+1
3 1
p
6
1
1
+p
3+1
4 1
P
n!
nn :
p
1
:::
4+1
10.
Calcule la suma de:
1
n
X
( 1)
72n
n=0
11.
49
50
Calcule la suma de :
1
X
n=1
12.
R:
3
1
+
n (n + 1) 2n
(R : 4)
Analice convergencia y divergencia de la serie según p 2 R
f0g :
1
X
pn n!
nn
n=1
13.
Si la serie
es divergente,
1
P
an es convergente. Demuestre que la serie
n=1
siendo bn =
1
P
n=1
an + 1:
7
(an + bn )
Series resueltas
1.
a)
Estudie la convergencia de las siguientes series
1
P
n=1
( 3)n
n2 9 n
Desarrollo
1
P
n=1
1
P
( 3)n
n2 9 n
n=1
3n
n2 9 n
Criterio de la Raíz
q
q
n
lim n n32 9n = lim n n12
n!1
n!1
3 n
9
Así
1
3
1
P
n=1
< 1 la
( 3)n
n2 9 n
converge.
Por lo tanto tanto
1
P
n=1
b)
1
P
n=1
p
3
p n
n3 +1
( 3)n
n2 9n Converge
p
3
p n
n!1 n3 +1
lim
1
P
n=1
c)
1
P
n=1
1
1
n!1 1+ pn3
= lim
p
3
p n
n3 +1
= 1 6= 0
Diverge.
sin2 (x)
1+n2
Desarrollo
1
P
n=1
1
P
sin2 (x)
1+n2
Como
1
P
n=1
n=1
1
n2
1
1+n2
1
P
n=1
1
n2
converge serie p > 1
8
q
n
1 1
n2 3 n
Absolutamente.
Desarrollo
Por lo tanto
n!1
1
1
p 2 = 3
n!1 3( n n)
1
P
3n
serie
n2 9n converge.
n=1
= lim
Como
= lim
1
P
Por lo tanto
n=1
d)
1
P
n=1
sin2 (x)
1+n2
Converge.
1
2n n
Desarrollo
Comparación al limite
Sea bn =
lim
n!1
1
2n
1
2n n
1
2n
2n
n n
n!1 2
= lim
1
P
Por lo tanto
n=1
e)
1
P
n=1
( convergente )
1
2n n
=1
Converge.
n!
1000n
Desarrollo
Criterio del cociente
(n+1)!
n+1
n!1 1000
(n)!
1000n
lim
=
1
P
Por lo tanto
n=1
f)
1
P
e
n!
1000n
(n+1)!
1000n
n+1
1000
(n)!
n!1
n+1
lim 1000
=1
n!1
= lim
Diverge
n 3
n
n=1
Desarrollo
Criterio de la raíz
lim
p
n
n!1
e
n n3
= lim e
=
Por lo tanto
1
P
e
n 3
n
n!1
1
lim
e n!1
n 3
n Converge.
n=1
9
1
nn
1
n
= lim
n!1
3
=
1
e
e
1
3
nn
g)
1
P
n=1
42n
n!
Desarrollo
Criterio del cociente
2(n+1)
lim 4
n!1 (n+1)!
Por lo tanto
1
P
n=1
h)
1
P
n=1
42n
n!
42n
n!
42(n+1)
n!1 (n+1)!
= lim
n!
42n
42
n!1 (n+1)
= lim
=0
Converge.
n
n2 +3n+4
Desarrollo
Criterio Comparación al limite
Sea bn =
lim
n!1
1
n
n
n2 +3n+4
1
n
Por lo tanto
1
P
n=1
i)
1
P
( divergente )
= lim
n!1
n
n2 +3n+4
n2
n2 +3n+4
1
n2
1
n2
1
4
3
n!1 1+ n + n2
= lim
=1
Diverge.
n n4
3n
( 1)
n=1
Desarrollo
Criterio convergencia absoluta
an+1
n!1 an
lim
=
Por lo tanto
1
P
n n4
3n
( 1)
n=1
j)
1
P
n sin
n=1
(n+1)4 3n
(n+1)4
1
4 = 3 lim
(n+1)
n
n4
3
n!1
n!1
4
1
n+1 4
1
lim
= 3 lim 1 + n1
3 n!1
n
n!1
= lim
Converge Absolutamente.
2
n
Desarrollo
lim n sin
n!1
2
n
= 2 lim
2
sin( n
)
n!1
10
2
n
=2
=
1
3
Por lo tanto
1
P
n sin
n=1
k)
1
P
n=1
2
n
Diverge.
n
n5 +1
Desarrollo
Criterio Comparación al limite
Sea bn =
1
n4
( Convergente )
n
5
n!1 n +1
1
n4
lim
Por lo tanto
1
P
n=1
1
P
l)
n=1
n
5
n!1 n +1
= lim
n4
1
n
n5 +1 Converge.
p
n
n+1
Desarrollo
Criterio de Comparación ordinaria
Se tiene que
Se analizará
p
n
n+1
1
n+1
1
P
n=1
1
n+1
Criterio comparación al limite
Sea bn =
1
n
lim 1
n!1 n+1
Así
1
P
n=1
Por lo tanto
m)
1
P
n=1
1
n+1
1
P
n=1
( Divergente )
1
n
n
n!1 n+1
= lim
Diverge
p
n
n+1
Diverge.
e2n
3e2n +n2
Desarrollo
11
=1
n5
5 +1
n
n!1
= lim
=1
= lim
Obs:
2
lim n2n
n!1 e
Por lo tanto
1
P
n=1
n)
1
P
n=1
e2n
2
n!1 e2n 3+ n2n
e
e2n
lim 2n
2
n!1 3e +n
e2n
3e2n +n2
= lim
n!1
1
2
3+ en2n
=
1
3
= 0 (L`H)
Diverge.
4n +n
n!
Desarrollo
Criterio del Cociente
lim
n!1
4n+1 +n+1
(n+1)!
4n +n
n!
= lim
n!1
= lim
4n+1 +n+1
n!
(n+1)!
4n +n
4n (4+ 4nn + 41n )
n
n!1 4n (n+1)(1+ 4n )
4+ 4nn + 41n
= lim
2
n
n!1 1+n+ n
4n + 4n
Obs:
Obs:
Por lo tanto
lim xx
n!1 4
2
lim nn
n!1 4
1
P
n=1
o)
1
P
n=1
n
3n+2
= 0(L`H)
= 0 (L`H)
4n +n
n!
Converge
n
Desarrollo
Criterio de la raíz.
r
n
n
lim n 3n+2
n!1
Por lo tanto
1
P
n=1
p)
1
P
n=1
n
3n+2
n
n!1 3n+2
= lim
=
n
Converge.
4+cos(n)
n3
Desarrollo
Criterio de Comparación Ordinario
12
1
3
=
=0
4n+1 +n+1
n
n!1 (n+1)(4 +n)
n
1
4+ 4n + 4n
lim
n
n!1 (n+1)(1+ 4n )
= lim
4+cos(n)
n3
Se tiene que 0 <
Luego
1
P
n=1
5
n3
1
P
p
n=2
1
n3 ;
n=1
4+cos(n)
n3
n=1
q)
1
P
=5
1
P
Por lo tanto
5
n3
Converge, serie p
Converge.
n
n ln3 (n)
Desarrollo
Criterio de la Integral
Sea f (x) =
f 0 (x) =
p
x
;x
x ln3 (x)
2:Así f (x) es positiva y continua.
1
3
2x 2 ln3 x
x 2 ln4 x
3
3
< 0 ( decreciente )
Así f satisface las condiciones del criterio de la integral.
Como
lim
x!1
R1
2
1
x dx
diverge
p
x
x ln3 (x)
1
x
= lim
p
x
ln3 (x)
x!1 p
x
x!1 48
= lim
Asi
R1
2
Por lo tanto
p
x
dx
x ln3 (x)
1
P
n=2
r)
1
P
n 1
( 1)
n=1
= lim
x!1
p
=1
Diverge
p
n
n ln3 (n)
Diverge.
2n+1
3n+1
Desarrollo
Criterio de la serie alternante
lim
n!1
2n+1
3n+1
Por lo tanto
1
P
n=1
=
2
3
6= 0
n 1
( 1)
2n+1
3n+1
13
x
6 ln2 (x)
Diverge.
p
x
24
ln(x)
x!1
= lim
2.
1
P
Analice la convergencia de la serie
1
P
n=1
an converge.
an +5
4an +10
se se sabe que la serie
n=1
Desarrollo
Como
1
P
an converge se tiene que lim an = 0
n!1
n=1
an +5
n!1 4an +10
Así lim
1
P
Por lo tanto
n=1
3.
1
2
=
an +5
4an +10
Diverge.
Si fan gn2N es convergente a 3 y fan+1
Demuestre que la serie
1
P
an g = bn + 2:
bn diverge.
n=1
Desarrollo
lim bn + 2 = lim an+1
n!1
n!1
lim bn =
n!1
Por lo tanto
1
P
an = 0 entonces
2
bn Diverge.
n=1
4.
Demuestre que para todo número real p, la serie
1
P
n=1
epn
n!
converge.
Desarrollo
Criterio del Cociente
epn
n!
p(n+1)
lim e
n!1 (n+1)!
Por lo tanto
1
P
n=1
5.
epn
n!
Demuestre que si
ep(n+1)
n!1 (n+1)!
= lim
n!
epn
ep
n!1 (n+1)
= lim
=0
Converge para todo número real p:
1
P
an diverge, también
n=1
1
P
n=1
Desarrollo
14
can diverge, c 6= 0:
Supongamos que
1
P
can converge.
n=1
1
P
Así
1
c
an =
n=1
1
P
can Converge.
n=1
1
P
Contradicción. Por lo tanto
can Diverge.
n=1
6.
1
P
¿Para qué valores de p la serie
n=2
1
n(ln(n))p
converge?
Desarrollo
Criterio de la Integral
Sea f (x) =
R1
2
1
x(ln(x))p ; x
2:Así f (x) es positiva y continua.
1
x(ln(x))p dx
Sea u = ln (x)
du = x1 dx
Entonces
R1
1
ln(2) up
Por lo tanto p > 1 para que
1
P
n=2
7.
Demuestre que
1
P
k=2
ln 1
1
k2
1
n(ln(n))p
=
la serie converga.
ln (2)
Desarrollo
1
P
k=2
ln 1
1
k2
n
P
= lim
n!1 k=2
n
P
= lim
n!1 k=2
n
P
ln k 2
= lim
ln (k
= lim
(ln (k
n!1 k=2
n
P
n!1 k=2
= lim ln
n!1
= ln (1)
15
= lim
n
P
n!1 k=2
1
k2 1
k2
ln k 2 = lim
n
P
n!1 k=2
1) + ln (k + 1)
1)
ln
ln (k)) +
ln (k)
n
P
ln (k
1) (k + 1)
ln (k)
(ln (k + 1)
ln (k))
k=2
= lim ((ln (1)
n!1
1
k2
ln 1
ln (n)) + (ln (n + 1)
n+1
n
ln (2) =
ln (2) = lim ln 1 +
n!1
ln (2)
ln (2)))
1
n
ln (2)
ln k 2
8.
Compruebe que la siguiente serie
1
P
k=2
de la integral.
k
k2 +3
diverge usando el criterio
Desarrollo
Sea f (x) =
x
x2 +3 ; x
x2 +3
(x2 +3)2
f 0 (x) =
2:Así f (x) es positiva y continua.
< 0 ( decreciente )
Así f satisface las condiciones del criterio de la integral.
R1
2
x
x2 +3 dx
k=2
9.
R1
2
x
x2 +3 dx
k
k2 +3
Diverge.
Como
n
P
=
Rb
x
dx = lim 12 ln
2
b!1 2 x +3
b!1
1
lim 12 ln b2 + 3
2 ln (7)
b!1
= lim
x2 + 3
b
2
=1
Diverge
Determine la suma de la siguiente serie
1
P
n=1
2n
(2n+1 1)(2n 1)
Desarrollo
2n
(2n+1 1)(2n 1)
A
B
= 2n+1
1 + 2n 1
)A= 1
)B=1
1
= 2n1 1 2n+1
1
2n
(2n+1 1)(2n 1)
Sn
lim
n!1
10.
=
1
21 1
1
22 1
=
1
2 1
1
2n+1 1
= 1
1
2n+1 1
+
1
22 1
1
23 1
1
2n 1
=1
Sume si es posible la siguiente serie
1
P
n=0
Desarrollo
16
1
2n
1
3n
1
2n+1 1
1
P
1
3n
1
2n
n=0
=
1
P
1
P
1 n
2
n=0
1 n
3
n=0
Ambas son series geométricas, luego:
1
P
n=
1
P
n=0
1 n
2
1 n
3
Por lo tanto
1
=
1
1
P
1
2
1
1
3
1
2n
n=0
11.
1
=
=2
=
1
3n
3
2
3
2
=2
1
2
=
Estudie el caracter de la siguiente serie:
1
P
n=1
3n +n2 +n
3n+1 n(n+1)
Desarrollo
1
P
n=1
3n +n2 +n
=
3n+1 n(n+1)
=
=
1
P
n=1
1
P
n=1
1
P
n=1
3n +n(n+1)
3n+1 n(n+1)
3n
3n+1 n(n+1)
1
3n(n+1)
+
1
P
+
1
P
n=1
n=1
n(n+1)
3n+1 n(n+1)
1
3n+1
La primera de estas series es telescópica, así
1
3
1
P
n=1
1
n+1
1
n
=
m
P
1
1
lim
3 m!1
n
n=1
1
n+1
=
1
lim 11
3 m!1
1
m+1
=
1
3
La segunda serie es geométrica, así
1
3
1
P
n=1
1 n
3
Por lo tanto
=
1
P
n=1
12.
1
P
n=1
1
3
1
3
1
1
3
1
6
=
=
1
3
=
3n +n2 +n
3n+1 n(n+1)
Sabiendo que an > 0 y
+
1
P
1
6
=
an es convergente, analizar la serie
n=1
(an )2
n+an
Desarrollo
Se tiene que 0
(an )2
n+an
a2n
an
17
1
2
= an
Como
1
P
an es convergente, entonces
n=1
13.
1
P
n=1
Determine el valor al cual converge la serie
(an )2
n+an
1
P
n=1
converge.
2
n(n+2)
Desarrollo
1
P
n=1
2
n(n+2)
m
P
2
m!1 n=1 n(n+2)
m
P
1
1
lim
n+2
m!1 n=1 n
m
P
1
1
lim
n
n+1
m!1 n=1
= lim
=
=
= lim
1
m!1
14.
Demuestre que la serie
1
2!
1
m+1
+
2
3
+ 3!
+ 4!
+
+
1
n+1
1
2
1
m+2
1
n+2
=
3
2
converge y calcule su calor.
Desarrollo
El término general de la serie es
k
(k+1)! ;
así la serie es
Criterio del cociente
lim n+1
n!1 (n+2)!
n
(n+1)!
(n+1)
n+1
n
n!1 (n+2)!
n+1
lim n(n+2)!
n!1
= lim
=
=0<1
Por lo tanto
1
P
k=1
k
(k+1)!
converge.
Para calcular su valor, calculemos la suma parcial
Sn
=
=
=
n
P
k=1
n
P
k=1
n
P
k=1
=1
k
(k+1)!
k+1 1
(k+1)!
1
k!
1
(k+1)!
1
(n+1)!
Así
lim Sn = 1
n!1
18
1
P
k=1
k
(k+1)!
Por lo tanto
1
P
k=1
k
(k+1)!
=1
15.
Se arroja una pelota desde una altura de 100 metros. Cada vez que
golpea el suelo, rebota hasta 23 de su altura anterior. Calcule la distancia total
que recorre hasta llegar al reposo.
Desarrollo
2
3
S = 100 + 2 100
2
3
= 100 + 2 100
= 100 + 200
1
P
k=1
= 100 + 200
2
3
1
+ 2 100
2 2
3
2 2
3
2 3
3
+
2 k
3
2
3
= 500
Por lo tanto recorre 500 metros.
19
+
+ 2 100
2 3
3
+