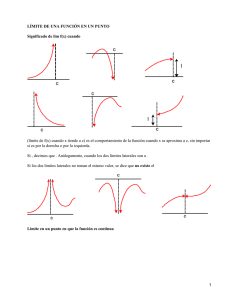
Límite de una función en un punto

UNIVERSIDAD NACIONAL DE TRES DE FEBRERO
UNTREF VIRTUAL
Análisis Matemático
Unidad 4 - Límite de una función en un punto
Límite de una función en un punto
El límite de una función para un valor de x es el valor al que la función tiende en los
alrededores de dicha x.
Ilustraremos este concepto con un ejemplo. En hombre camina dirigiéndose hacia una pared
con la siguiente particularidad: en cada etapa recorre la mitad de la distancia que lo separa de
su objetivo.
Por ejemplo, supongamos que se encuentra a 400 m. Primero recorre 200 m y se detiene. Luego recorre 100 m,
y luego 50 m y así sucesivamente.
¿El hombre llega a tocar la pared?
No, ya que siempre le faltará la mitad de la distancia. Sin embargo, está claro que el límite se su recorrido es la
pared.
Ese es el concepto de límite de una función en un punto: no importa lo que ocurre en ese punto, sino en los
alrededores del punto.
| Análisis Matemático
1/23
UNIVERSIDAD NACIONAL DE TRES DE FEBRERO
UNTREF VIRTUAL
Veamos un ejemplo más “matemático”
Tomemos la función
El dominio de esta función excluye al número uno, ya que dicho valor anula el denominador.
Vamos a hacer una tabla para que qué valores asume la función en un entorno de x=1
X
0,9
1,9
0,99
1,99
0,999
1,999
1
1,001
2,001
1,01
2,01
1,1
2,1
Si bien la función no existe para x=1, el límite de la función cuando x tiende a 1 es 2, ya que cuando más se
acerque x a 1, más se acercará y a 2.
Es decir, que lo que estamos estudiando es el comportamiento de la función en un “entorno
reducido de x”. (Valores muy cercanos a
, e xcluyendo
)
El límite de una función en un punto puede ser:
a) Definido
Es el caso en el que el valor del límite de la función en un punto coincide con el valor de la función en el dicho
punto.
| Análisis Matemático
2/23
UNIVERSIDAD NACIONAL DE TRES DE FEBRERO
UNTREF VIRTUAL
b) Inexistente
Decimos que no existe el límite de una función en un punto en dos casos.
b.1) Límites laterales diferentes
Por ejemplo:
En esta función, si nos acercamos a x = 3 desde los valores menores que tres (por la izquierda), la función
tiende a -1. Si nos acercamos por los valores mayores que 3 (por la derecha), la función tiende a 4.
Como los límites laterales son distintos decimos que no existe el límite de la función cuando x tiende a 3
| Análisis Matemático
3/23
UNIVERSIDAD NACIONAL DE TRES DE FEBRERO
UNTREF VIRTUAL
b.2) Resultado Infinito
La división por cero no está definida: pero si dividimos un número cualquiera por otro cada vez más pequeño, el
resultado obtenido tiende a un valor cada vez mayor.
c) Límites indeterminados
En este caso el resultado está “disfrazado”, nos da una expresión que no podemos resolver, por ejemplo:
En estos casos lo que debemos hacer es “salvar la indeterminación” mediante procedimientos matemáticos.
Para ilustrar estas definiciones vamos a analizar los límites en varios puntos de la siguiente función:
| Análisis Matemático
4/23
UNIVERSIDAD NACIONAL DE TRES DE FEBRERO
A medida que nos acercamos a
A medida que nos acercamos a
UNTREF VIRTUAL
Gesde su derecha, la función asume valores cada vez más negativos.
desde su izquierda, la función asume valores positivos cada vez más
altos.
Este es un límite definido: en un entorno reducido de x = 9, la función vale 0
Este también es un límite definido, no importa que la función no tenga imagen para x=2; lo que importa es que
en un entorno reducido de x=2 la función tiende a 5
Si nos acercamos a x = 6 desde la izquierda (es decir, desde los valores de x menores que 6), la función tiende
a4
Si nos acercamos a x = 6 desde la derecha (desde los valores mayores que x = 6), la función tiende a – 6
Como los límites laterales son diferentes, no existe el límite para x tendiendo a 6 en esta función
Si tomamos valores de x cada vez más negativos, los valores de la función se acercarán cada vez más
ay =2
| Análisis Matemático
5/23
UNIVERSIDAD NACIONAL DE TRES DE FEBRERO
UNTREF VIRTUAL
Si tomamos valores de x cada vez mayores, los valores de y también crecen indefinidamente
49) Calcular los límites indicados:
| Análisis Matemático
6/23
UNIVERSIDAD NACIONAL DE TRES DE FEBRERO
UNTREF VIRTUAL
Resolución de límites indeterminados
1º) Indeterminación
1.1) Cociente de dos Polinomios
Para resolver este tipo de indeterminaciones debemos factorear el numerador y el denominador con
cualquiera de los casos vistos.
Ej:
Primero reemplazamos la variable por el valor al que tiende el límite.
Para salvar la indeterminación factoreamos:
En el numerador aplicamos el Teorema de Gauss:
En el denominador podemos aplicar diferencia de cuadrados
Nuestro límite nos queda:
Una vez que simplificamos, volvemos a reemplazar, y obtenemos el valor del límite.
| Análisis Matemático
7/23
UNIVERSIDAD NACIONAL DE TRES DE FEBRERO
UNTREF VIRTUAL
1.2) Funciones irracionales
En estos casos vamos a tener raíces: y para salvar las indeterminaciones vamos a tener que racionalizar:
Ej 1
Multiplicamos y dividimos por el conjugado de
, que será
Si la expresión tiene raíces tanto en el numerador como en el denominador, hay que multiplicar y dividir
por ambos conjugados.
Ejemplo
Ordenamos
| Análisis Matemático
8/23
UNIVERSIDAD NACIONAL DE TRES DE FEBRERO
UNTREF VIRTUAL
Multiplicamos
Factoreamos y simplificamos
Reemplazamos
50) Calcular los siguientes límites:
| Análisis Matemático
9/23
UNIVERSIDAD NACIONAL DE TRES DE FEBRERO
UNTREF VIRTUAL
2º) Indeterminación
Para resolver indeterminación, sacamos como factor común la x de mayor grado, tanto en el numerador.
Por ejemplo:
Sacamos como factor común
en el numerador, y
en el denominador
Simplificamos
Debemos tener en cuenta que
Ya que si dividimos cualquier número por otro infinitamente grande el resultado tenderá a cero.
Entonces:
| Análisis Matemático
10/23
UNIVERSIDAD NACIONAL DE TRES DE FEBRERO
UNTREF VIRTUAL
Otra manera de resolver estos límites es dividir todos los términos por la x de mayor exponente.
Dividimos cada término por
Simplificamos
El numerador tiende a 6, y el denominador tiende a 0.
Ya que si dividimos cualquier número por otro cada vez más pequeño el resultado tiende a infinito.
3º) Indeterminación
Esta indeterminación se resuelve transformándola en
Sacamos común denominador
Ahora operamos igual que en el caso anterior, dividiendo todos los términos por
| Análisis Matemático
11/23
UNIVERSIDAD NACIONAL DE TRES DE FEBRERO
UNTREF VIRTUAL
Simplificamos
51) Calcular los siguientes límites:
| Análisis Matemático
12/23
UNIVERSIDAD NACIONAL DE TRES DE FEBRERO
UNTREF VIRTUAL
4º) Indeterminación
Para resolver esta indeterminación nos basaremos en estas dos fórmulas.
Ejemplo 1:
(la base tiende a 1 y el exponente tiende a infinito)
Para llegar a la expresión del número “e”, operamos del siguiente modo:
1º) Sumamos y restamos 1, en el siguiente orden:
2º) Sacamos común denominador entre el segundo y el tercer término de la base:
3º) Invertimos la fracción obtenida, de manera que su numerador sea 1:
Para llegar a la expresión del número “e”, el denominador de la fracción de la base debe figurar como
exponente. Para lograr esto, pero sin alterar la expresión, colocaremos como exponente a este
numerador, primero tal cual está, y a continuación, invertido. De esta manera estaremos elevando la
base a potencia 1, por lo cual no la modificamos pero le damos la forma que necesitamos para poder
| Análisis Matemático
13/23
UNIVERSIDAD NACIONAL DE TRES DE FEBRERO
UNTREF VIRTUAL
resolver nuestro límite.
Ya llegamos a la expresión del numero “e”
5º) Calculamos el límite del exponente:
Ejemplo 2:
Como en el ejemplo anterior, la base tiende a 1 y el exponente tiende a infinito. Pero como es un límite
para x tendiendo a cero, debemos usar la otra expresión del número e.
1º) Igual que antes, sumamos y restamos 1, y sacamos común denominador entre el segundo y el tercer
término:
2º) Colocamos la expresión algebraica resultante como exponente, primero invertida y luego tal cual
está:
| Análisis Matemático
14/23
UNIVERSIDAD NACIONAL DE TRES DE FEBRERO
UNTREF VIRTUAL
3º) Ya llegamos a la expresión del número “e”:
52) Calcular los siguientes límites
| Análisis Matemático
15/23
UNIVERSIDAD NACIONAL DE TRES DE FEBRERO
UNTREF VIRTUAL
Asíntotas
En la unidad de funciones ya vimos asíntotas verticales y horizontales, y aprendimos a calcularlas de una
manera “pragmática”.
Ahora vamos a aplicar el concepto de límite para comprender cómo se calcula una asíntota.
Asíntota vertical
Tiene una asíntota vertical en
si se cumple:
1º)
2º)
Ejemplo:
Primero calculamos el dominio:
Calculamos el límite de la función cuando
Por lo tanto
tiene una asíntota vertical en
Calculamos el límite de la función x tendiendo a 3
Salvamos la indeterminación
Por lo tanto la función no tiene asíntota vertical en x=3
La gráfica de esta función es:
| Análisis Matemático
16/23
UNIVERSIDAD NACIONAL DE TRES DE FEBRERO
UNTREF VIRTUAL
Si bien la función no tiene imagen en x=3, el límite en ese punto existe.
Asíntota Horizontal
Tiene asíntota horizontal en
Si:
Para la misma función
Por lo tanto la función tiene una asíntota horizontal en y = 0
| Análisis Matemático
17/23
UNIVERSIDAD NACIONAL DE TRES DE FEBRERO
UNTREF VIRTUAL
Asíntota oblicua
Las funciones racionales cuyo numerador es un grado mayor que el denominador tienen asíntotas
oblicuas.
La ecuación de la misma es la de una recta:
, y se calcula del siguiente modo:
Ejemplo:
La asíntota oblicua de esta función tiene como ecuación
Esta función tiene, además, dos asíntotas verticales:
Dominio:
| Análisis Matemático
18/23
UNIVERSIDAD NACIONAL DE TRES DE FEBRERO
Tiene asíntotas verticales en
UNTREF VIRTUAL
.
Entonces su gráfica tiene esta forma:
| Análisis Matemático
19/23
UNIVERSIDAD NACIONAL DE TRES DE FEBRERO
UNTREF VIRTUAL
53) Calcular las ecuaciones de las asíntotas de las siguientes funciones y realizar un
gráfico aproximado
| Análisis Matemático
20/23
UNIVERSIDAD NACIONAL DE TRES DE FEBRERO
UNTREF VIRTUAL
Continuidad de una función en un punto
Intuitivamente, decimos que una función es continua en un tramo cuando podemos
recorrerlo sin levantar el lápiz.
Por ejemplo:
En x= - 2, la función es continua.
En x=2; x=5; x=8, la función es discontinua.
En x=2 tienen un agujero, algo así como un bache en el camino. Este bache podría rellenarse, para que
el camino quede sin interrupciones. Entonces decimos que en x=2 la función tiene una “discontinuidad
| Análisis Matemático
21/23
UNIVERSIDAD NACIONAL DE TRES DE FEBRERO
UNTREF VIRTUAL
evitable”.
En x=8 la interrupción es más grave, es como un escalón que no puede salvarse. Este tipo de
discontinuidad se denomina “discontinuidad esencial de salto finito”.
En x=5 la discontinuidad también es esencial, pero como la función se va al infinito, se denomina
“discontinuidad esencial de salto infinito”.
Matemáticamente, definimos:
Una función es continua en
(
1º) Existe
Si:
pertenece al dominio)
2º) Existe
3º)
Si el límite existe pero no se cumplen la primera o la tercera condición, la función tendrá una
discontinuidad evitable en
.
Si el límite no existe, la discontinuidad es esencial.
Si los límites laterales son distintos pero finitos, es una discontinuidad esencial de salto finito.
Si los límites laterales tienen a infinito, es una discontinuidad esencial de salto finito.
| Análisis Matemático
22/23
UNIVERSIDAD NACIONAL DE TRES DE FEBRERO
UNTREF VIRTUAL
54) Para las siguientes funciones: hallar el dominio, determinar los puntos de
discontinuidad y clasificar las discontinuidades
55) Hallar, si es posible, el valor de
| Análisis Matemático
23/23
para que la función resulte continua