Sismología Aplicada y de Exploración

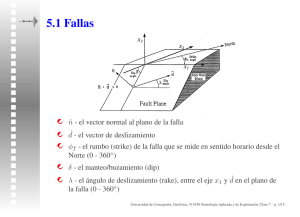
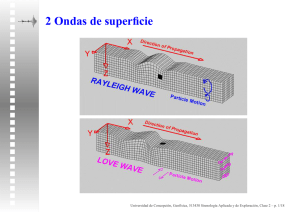
Sismología Aplicada y de Exploración
513430 - Sismología Aplicada y de Exploración
Apuntes adicionales
Matt Miller
http://mttmllr.com/sismologia.htm
Universidad de Concepción, Geofı́sica, 513430 Sismologı́a Aplicada y de Exploración, Clase 1 – p. 1/17
1 Ondas de cuerpo
Universidad de Concepción, Geofı́sica, 513430 Sismologı́a Aplicada y de Exploración, Clase 1 – p. 2/17
1.1 Deformación
En una dimensión:
x es una posición en el medio.
u es el desplazamiento de esta posición x desde su punto de equilibrio.
La deformación en esta situación, denominada ǫ11 , es:
ǫ11
δu
1
l2 − l1
u(x + δx) − u(x)
≃
≃
=
=
l1
δx
δx
2
∂u(x)
∂u(x)
+
∂x
∂x
(1.1)
Universidad de Concepción, Geofı́sica, 513430 Sismologı́a Aplicada y de Exploración, Clase 1 – p. 3/17
1.1 Deformación
En tres dimensiones:
u(x + δx) ≃ u(x) +

∂ux
∂x
 ∂u
 y
 ∂x
∂uz
∂x
∂ux
∂y
∂uy
∂y
∂uz
∂y

 
∂ux
dx
∂z

∂uy 
 dy 

∂z 
∂uz
dz
∂z
Universidad de Concepción, Geofı́sica, 513430 Sismologı́a Aplicada y de Exploración, Clase 1 – p. 4/17
1.1 Deformación
En otras palabras ...
u(x + δx) ≃ u(x) + J d
Podemos escribir J en componentes simétricos y asimétricos, J = ǫ + Ω:

∂ux
∂x
 ∂u

ǫ =  12 ∂xy +
 1 ∂uz
+
2
∂x

0
 ∂u

Ω =  12 ∂xy −
 1 ∂uz
−
2
∂x
∂ux
∂y ∂ux
∂z
∂ux
∂y ∂ux
∂z
∂ux
+
∂y
∂uy
∂y
1 ∂uz
+
2
∂y
1
2
1
2
1
2
∂ux
∂y
−
∂uy
∂x
∂uy
∂z
∂uy
∂x
∂uy
∂z
0
∂uz
∂y
−
1
2
1
2
1
2
1
2
∂ux
+
∂z
∂uy
+
∂z
∂uz
∂z
∂ux
∂z
∂uy
∂z
−
−
0
∂uz
∂x
∂uz
∂y






∂uz
∂x 
∂uz 
∂y 

Aquí, ǫ es el tensor de deformación y Ω es el tensor de rotación.
Universidad de Concepción, Geofı́sica, 513430 Sismologı́a Aplicada y de Exploración, Clase 1 – p. 5/17
1.1 Deformación
Un ejemplo en 2 dimensiones:
JA =
∂ux
∂x
∂uz
∂x
∂ux
∂z
∂uz
∂z
!
≃
0
θ
!
θ
0
;
JB ≃
!
0
−θ
θ
0
Una deformación del elemento de área tiene un tensor simétrico, y una
rotación tiene un tensor asimétrico. En sismología trabajamos en un marco de
referencia en que el medio no se esta girando, entonces podemos representar
la deformación del medio por el tensor de deformación:
ǫij
1
=
2
∂u(xj )
∂u(xi )
+
∂xj
∂xi
1
≡
2
∂uj
∂ui
+
∂xj
∂xi
(1.2)
Universidad de Concepción, Geofı́sica, 513430 Sismologı́a Aplicada y de Exploración, Clase 1 – p. 6/17
1.2 Esfuerzo
Consideremos un elemento de volumen en el medio:
Los tres vectores de tracción T1 , T2 y T3 representan las fuerzas por unidad
de área sobre las tres caras del cubo infinitesimal.
Para describir las fuerzas que actúan en un punto de un medio tres
dimensional, requerimos nueve elementos del tensor de esfuerzo σij . La
relación entre las tracciones y el esfuerzo es:
Ti = σij nj ≡ σji nj
(1.3)
Universidad de Concepción, Geofı́sica, 513430 Sismologı́a Aplicada y de Exploración, Clase 1 – p. 7/17
1.2 Esfuerzo
En el marco de referencia en que el medio no se esta girando, lo que aplica en
sismología:
Los esfuerzos no dan rotación.
Entonces, el tensor de esfuerzo es simétrico.
Por ejemplo, en el plano x − z, la balanza de los torques significa que
σ13 = σ31
Universidad de Concepción, Geofı́sica, 513430 Sismologı́a Aplicada y de Exploración, Clase 1 – p. 8/17
1.3 La ecuación de movimiento
La relación general entre el esfuerzo y la deformación es
σij = cijkl ǫkl
(1.4)
y para un medio homogéneo, isotrópico, continuo y elástico
cijkl = λδij δkl + µ(δik δjl + δil δjk )
(1.5)
λ y µ son los parámetros del Lamé, asociados con el medio:
µ es su rigidez (la resistencia contra las fuerzas de cizalle).
κ = λ + 23 µ es su módulo de incompresibilidad (la resistencia contra
las fuerzas de compresión).
La combinación de (1.4) y (1.5) da
σij = λδij ǫkk + 2µǫij
(1.6)
Note que ǫkk ≡ ∆ que representa la dilatación cubica.
Universidad de Concepción, Geofı́sica, 513430 Sismologı́a Aplicada y de Exploración, Clase 1 – p. 9/17
1.3 La ecuación de movimiento
La ecuación de movimiento para un cierto volumen V es
Z
V
∂ 2 ui
ρ 2 dV =
∂t
I
Ti dS +
Z
fi dV =
V
S
I
σij nj dS +
S
H
Z
fi dV
(1.7)
V
R
∂ai
dV , y
Usamos el teorema de divergencia de Gauss, S ai ni dS = V ∂x
i
ignoramos las fuerzas de cuerpo (valida para sismología de frecuencias
& 0.003 Hz), y entonces
Z
V
∂ 2 ui
ρ 2 dV =
∂t
Z
V
∂σij
dV
∂xj
(1.8)
Podemos usar la relación entre el esfuerzo y la deformación de antes, y la
simetría del tensor de deformación, para llegar al
∂ ∂uk
∂ 2 ui
ρ 2 = cijkl
∂t
∂xj ∂xl
(1.9)
Universidad de Concepción, Geofı́sica, 513430 Sismologı́a Aplicada y de Exploración, Clase 1 – p. 10/17
1.3 La ecuación de movimiento
Entonces para un medio simple, con λ y µ continuo (esta suposición requiere
mas justificación, porque claramente estos parámetros de Lamé varían dentro
de la Tierra, volveremos a este punto en una otra clase),
∂ 2 ui
ρ ∂t2
2
ρ ∂∂tu
2
∂uk
j ∂xl
∂uk
j ∂xl
∂
+ µδik δjl ∂x
=
∂
λδij δkl ∂x
=
∂
λ ∂x
=
∂
λ ∂x
=
λ∇(∇ · u) + µ∇2 u + µ∇(∇ · u)
∂uk
i ∂xk
∂
+ µ ∂x
∂uk
i ∂xk
∂
+ µ ∂x
∂uk
j ∂xl
∂
+ µδil δjk ∂x
∂uj
j ∂xi
∂ui
∂x
j
j
∂
+ µ ∂x
∂ui
j ∂xj
∂
+ µ ∂x
∂uj
i ∂xj
En la última línea hemos vuelto a la notación vectorial.
Universidad de Concepción, Geofı́sica, 513430 Sismologı́a Aplicada y de Exploración, Clase 1 – p. 11/17
1.3 La ecuación de movimiento
Entonces ...
ρü = (λ + µ)∇(∇ · u) + µ∇2 u
(1.10)
y usamos la identidad vectorial,
∇2 u = ∇(∇ · u) − (∇ × ∇ × u)
para llegar a la ecuación de movimiento usada en sismología:
ρü = (λ + 2µ)∇(∇ · u) − µ(∇ × ∇ × u)
{z
} |
{z
}
|
parte dilatacional
(1.11)
parte de cizalle
Universidad de Concepción, Geofı́sica, 513430 Sismologı́a Aplicada y de Exploración, Clase 1 – p. 12/17
1.4 Ondas-P
Como hemos visto en GTS, tomando la divergencia de la ecuación (1.11), y
recordando que
~ =0
∇ · (∇ × algo)
nos llega al
∂ 2 (∇ · u)
2
ρ
=
(λ
+
2µ)∇
(∇ · u)
∂t2
(1.12)
Esta ecuación muestra que cualquier distorsión que esta asociada con un
cambio en el volumen de los elementos del medio (∇ · u) se va a propagar en
la forma de una onda con una velocidad de
α=
s
λ + 2µ
=
ρ
s
κ + 34 µ
ρ
(1.13)
Eso es una onda-P!
Universidad de Concepción, Geofı́sica, 513430 Sismologı́a Aplicada y de Exploración, Clase 1 – p. 13/17
1.5 Ondas-S
Tomando el rotor de la ecuación (1.11), usando
~ =0
∇ × ∇algo
y una variación en la identidad vectorial usada antes
✿0
✘
✘
✘
✘× algo))
~ = ∇(∇ ✘
~
~
∇2 (∇ × algo)
· (∇
− (∇ × ∇ × (∇ × algo))
✘
✘
nos llega al
∂ 2 (∇ × u)
2
=
µ∇
(∇ × u)
ρ
∂t2
(1.14)
Esta ecuación muestra que cualquier distorsión que esta asociada con una
perturbación de cizalle de los elementos del medio (∇ × u) se va a propagar
en la forma de una onda con una velocidad de
β=
r
µ
ρ
(1.15)
Eso es una onda-S!
Universidad de Concepción, Geofı́sica, 513430 Sismologı́a Aplicada y de Exploración, Clase 1 – p. 14/17
1.6 La descomposición de Helmholtz
En el caso general, el desplazamiento en el medio u puede ser representado
por:
un potencial escalar Φ
y un potencial vectorial (sin divergencia) Ψ
u = ∇Φ + ∇ × Ψ
;
∇·Ψ=0
(1.16)
Entonces,
∇·u
=
∇2 Φ
∇×u
=
∇(∇
· Ψ) − ∇2 Ψ
∇ × ∇ × Ψ =✘
✘✘
✿0
✘
De las ecuaciones (1.12) y (1.14) entonces:
2 Φ) −
∇2 (∇
h
∇2 ∇2 Φ −
1 ∂2
2 Φ)
(∇
2
2
α ∂t i
1 ∂2Φ
α2 ∂t2
2
∂
2
−∇2 (∇2 Ψ) + β12 ∂t
2 (∇ Ψ)
h
i
1 ∂2Ψ
2
2
∇ ∇ Ψ − β 2 ∂t2
=
0
=
0
=
0
=
0
Universidad de Concepción, Geofı́sica, 513430 Sismologı́a Aplicada y de Exploración, Clase 1 – p. 15/17
1.6 La descomposición de Helmholtz
Del análisis anterior, se puede apreciar que con el desplazamiento u escrito en
esta manera:
Φ representa el desplazamiento asociado con la onda-P.
Ψ representa el desplazamiento asociado con la onda-S.
Para una onda plana que se propaga en el plano x − z (que significa que no
hay ningún variación en las propiedades de la onda (fase, amplitud) en la
∂
... = 0), el campo de desplazamiento
dirección ŷ; en términos matemáticos ∂y
es
u = uP + uS =
∂Ψy
∂Φ
−
∂x
∂z
x̂ +
∂Ψz
∂Ψx
−
∂z
∂x
ŷ +
∂Ψy
∂Φ
+
∂z
∂x
ẑ
(1.17)
El desplazamiento de esta onda esta en las direcciones x̂, ŷ y ẑ.
La onda P tiene movimiento particular en el plano x − z (Φ).
La onda S tiene dos componentes, la SH con movimiento particular en
la dirección ŷ (Ψx , Ψz ),
y la SV con movimiento particular en el plano x − z (Ψy ).
Universidad de Concepción, Geofı́sica, 513430 Sismologı́a Aplicada y de Exploración, Clase 1 – p. 16/17
1.7 Ondas Planas
Ondas planas, las soluciones a la ecuación de ondas, pueden estar
representadas por:
con
kα =
Φ = Aei(kα ·x−ωt)
(1.18)
Ψ = Bei(kβ ·x−ωt)
(1.19)
ω
k̂, y kβ =
k̂
α
β
ω
(1.20)
k̂ es en la dirección de propagación de la onda.
Universidad de Concepción, Geofı́sica, 513430 Sismologı́a Aplicada y de Exploración, Clase 1 – p. 17/17