2 Ondas de superficie

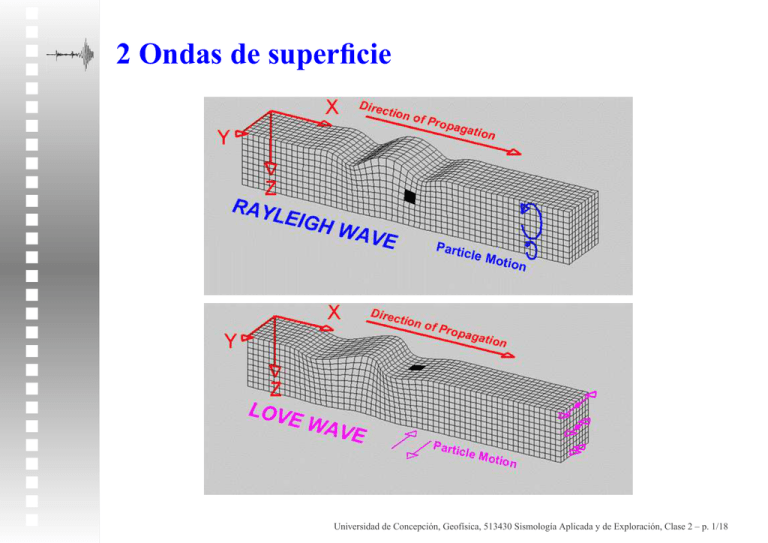
2 Ondas de superficie
Universidad de Concepción, Geofı́sica, 513430 Sismologı́a Aplicada y de Exploración, Clase 2 – p. 1/18
2.1 Semi espacio y superficie libre
Un semi espacio es un medio homogéneo que ocupa la mitad de un
volumen infinito.
La superficie libre es la única superficie que tiene un semi espacio.
A una distancia de +δ encima la superficie libre, en el vacío, los
elementos del tensor de esfuerzo están ceros σ31 = σ32 = σ33 = 0.
Hay continuidad de tracción a través de la superficie, entonces la
condición de borde en la superficie es que σ3j = 0.
(Note que la tracción es una medida de presión que una superficie se
aplica al elemento de volumen conectado).
Universidad de Concepción, Geofı́sica, 513430 Sismologı́a Aplicada y de Exploración, Clase 2 – p. 2/18
2.1.1 Ondas Rayleigh: formulación
Consideremos ondas P y S, viajando en el plano x1 − x3 que
interactúan con la superficie terrestre:
SI ellos generan una onda en la dirección x1 (horizontal), los
potenciales Φ y Ψ están:
Φ que en esta clase llamaremos φ
ψ2 que en esta clase llamaremos ψ
u2
=
=
=
f (x3 )ei(kx1 −ωt)
g(x3 )ei(kx1 −ωt)
h(x3 )ei(kx1 −ωt)
(2.2)
Note que podemos escribir u2 en la forma de ψ1 y ψ3 si
queremos, pero veremos que no vale la pena.
Universidad de Concepción, Geofı́sica, 513430 Sismologı́a Aplicada y de Exploración, Clase 2 – p. 3/18
2.1.2 La ecuación de ondas
Los potenciales tienen que satisfacer la ecuación de movimiento en el medio
(ver la sección 1.6)
∇2 φ −
∇2 ψ −
1
α2
1
β2
∂2φ
∂t2
∂2ψ
∂t2
=
0
=
0
Por ejemplo, para el caso φ,
0
∂2φ
∂x2
1
+
✒+
∂2φ
∂x2
2
∂2φ
∂x2
3
(ik)2 f (x3 ) +
f ′′ +
1 ∂2φ
α2 ∂t2
∂ 2 f (x3 )
∂x2
3
ω2
f
α2 ω2
2 f
2 −k
α
2
c
k2 α2 − 1 f
2
f ′′ − k
f+
f ′′ +
−
−
(iω)2
f (x3 )
α2
ei(kx1 −ωt)
=
0
=
0
=
0
=
0
=
0
En la última linea, hemos usado ω = ck, donde c es la velocidad aparente de
la onda en la dirección x1 , es decir por la superficie (si existe esta onda).
Universidad de Concepción, Geofı́sica, 513430 Sismologı́a Aplicada y de Exploración, Clase 2 – p. 4/18
2.1.2 La ecuación de ondas
Introducimos
rα =
s
c2
−1
α2
rβ =
s
c2
−1
β2
Entonces, la función f (x3 ) tiene que satisfacer
2
f =0
f ′′ + k2 rα
(2.3)
y similarmente g ′′ + k 2 rβ2 g = 0 y h′′ + k 2 rβ2 h = 0. La solución entonces es
f (x3 ) = A′ e−ikrα x3 + Ae+ikrα x3
(2.5)
con soluciones similares para g(x3 ) y h(x3 ). En la próxima diapositiva
vamos a ver que para una onda de superficie rα y rβ están imaginarias, y que
en este caso A′ = 0 porque conservación de energía requiere que
f (x3 ) lim → 0
x3 →∞
Universidad de Concepción, Geofı́sica, 513430 Sismologı́a Aplicada y de Exploración, Clase 2 – p. 5/18
2.1.2 La ecuación de ondas
Los tres posibles soluciones para f , g y h están:
1. β < α < c. En este caso, rα y rβ están reales. Esta situación representa
ondas de cuerpo que se reflectan de la superficie (otro capítulo).
f
φ
=
∼
A′ e−ikrα x3 + Ae+ikrα x3 etc. para g, h
cte.ei(kx1 −ωt±krα x3 ) etc...
note que rα representa la tasa entre los componentes del vector de
onda vertical:horizontal.
2. β < c < α. En este caso, rα esta imaginaria y rβ esta real. Entonces la
onda P se propaga horizontalmente en la forma de una onda
quasi-evanescente (ruido superficial, o, en inglés, ground roll).
f
φ
=
=
Ae−k|rα |x3
Ae−k|rα |x3 ei(kx1 −ωt)
Se nota que φ decae exponencialmente con profundidad (propiedad
evanescente), pero esta onda continuamente pierde energía a las ondas
SV (condiciones de borde) entonces esta onda no se propaga grandes
distancias.
Universidad de Concepción, Geofı́sica, 513430 Sismologı́a Aplicada y de Exploración, Clase 2 – p. 6/18
2.1.2 La ecuación de ondas
Los tres posibles soluciones (cont...)
3. c < β < α. En este caso ambas rα y rβ están imaginarias, y entonces
φ, ψ, u2 ∼ cte.e−k|rα,β |x3 ei(kx1 −ωt)
El tercer caso entrega una solución que representa una onda que viaja
horizontalmente a una velocidad c, que es evanescente (atrapada en la
superficie) y que es una cierta mezcla de las contribuciones de las ondas
P, SV y SH.
No hemos encontrado la onda Rayleigh todavía. La onda descrita arriba
solamente existe si cumpla las condiciones de borde en la superficie
libre. ¿Podría satisfacer las condiciones de borde? ¡Revisemos!
Universidad de Concepción, Geofı́sica, 513430 Sismologı́a Aplicada y de Exploración, Clase 2 – p. 7/18
2.1.3 Condiciones de borde
Los potenciales están:
φ
ψ
u2
=
=
=
Ae[ikrα x3 +ik(x1 −ct)]
Be[ikrβ x3 +ik(x1 −ct)]
Ce[ikrβ x3 +ik(x1 −ct)]
(2.6)
Y las condiciones de borde en la superficie libre (x3 = 0) están
σ31 = σ32 = σ33 = 0. Recuerde, del capítulo anterior (ver ecuaciones (1.2),
(1.6), (1.16)):
σij
=
ǫij
=
u
=
λδij ǫkk + 2µǫij
∂uj
∂ui
1
+
2 ∂x
∂x
j
i
∇Φ + ∇ × Ψ
Entonces, en la notación de esta clase,
u1
=
u3
=
∂φ
∂x1
∂φ
∂x3
−
+
∂ψ
∂x3
∂ψ
∂x1
Universidad de Concepción, Geofı́sica, 513430 Sismologı́a Aplicada y de Exploración, Clase 2 – p. 8/18
2.1.3 Condiciones de borde
σ31 = 0
2µǫ31
∂u3
+
∂x
1
∂2φ
∂x3 ∂x1
∂u1
∂x3
+
∂2ψ
∂x2
1
∂2φ
∂x1 ∂x3
+
−
∂2ψ
∂x2
3
=
=
0
0
=
0
O, en otra notación
2φ,31 + ψ,11 − ψ,33 = 0
(2.7a)
σ33 = 0
λ(ǫ
) + 2µǫ
11 + ǫ22 + ǫ33
 33
0
1 +
λ  ∂u
∂x
1
✒+
∂u2
∂x2
∂u3 
∂x3
3
+ 2µ ∂u
∂x
3
=
0
=
0
Cambiando la notación de nuevo
λ (φ,11 − ψ,31 + φ,33 + ψ,13 ) + 2µ (φ,33 + ψ,13 )
(λ + 2µ)φ,33 + λφ,11 + 2µψ,13
=
=
0
0
(2.7b)
Universidad de Concepción, Geofı́sica, 513430 Sismologı́a Aplicada y de Exploración, Clase 2 – p. 9/18
2.1.3 Condiciones de borde
σ32 = 0
2µǫ32
=
0
=
0
0
✒+
∂u3
∂x2
∂u2
∂x3
O, en otra notación
u2,3 = 0
(2.7c)
Para cumplir la condición de borde (2.7c), con las ecuaciones (2.6),
tenemos C = 0. Entonces u2 = 0. La primera condición para que
existe una onda de superficie, hecha por la interacción entre ondas P y
S, es que las ondas SH no entran al sistema. (Esta no es una gran
sorpresa, dado que el sistema P-SV es desacoplado del sistema SH).
Universidad de Concepción, Geofı́sica, 513430 Sismologı́a Aplicada y de Exploración, Clase 2 – p. 10/18
2.1.3 Condiciones de borde
Para cumplir las otras condiciones de borde (2.7a) y (2.7b), pongamos las
expresiones para φ y ψ de la ecuación (2.6) dentro de las dos ecuaciones que
dan las condiciones de borde (recuerde que la condición de borde se satisface
en la superficie, es decir x3 = 0):
1.
2φ,31 + ψ,11 − ψ,33
2A(ikrα )(ik) + B(ik)2 − B(ikrβ2 )
−2Ak2 rα − Bk2 + Bk2 rβ2
2rα A + (1 − rβ2 )B
=
=
=
=
0
0
0
0
(2.8a)
2. [Requiere λ + 2µ = α2 ρ, µ = β 2 ρ, λ = (α2 − 2β 2 )ρ]
(λ + 2µ)φ,33 + λφ,11 + 2µψ,13
(λ + 2µ)A(ikrα )2 + λA(ik)2 + 2µB(ik)(ikrβ )
2 − λA − 2µBr
−(λ + 2µ)Arα
β
2
2
2
2
2
α Arα + (α − 2β )A + 2β Brβ
2 2
2
α (rα + 1) − 2β A + 2β 2 rβ B
=
=
=
=
=
0
0
0
0
0
(2.8b)
Buscamos la solución simultanea de (2.8a) y (2.8b) para cumplir las
condiciones de borde.
Universidad de Concepción, Geofı́sica, 513430 Sismologı́a Aplicada y de Exploración, Clase 2 – p. 11/18
2.1.3 Condiciones de borde
Para el sistema de ecuaciones
!
a
c
b
d
A
B
!
=
0
0
!
la solución no-trivial (A 6= 0, B 6= 0) requiere (ad − bc) = 0. En nuestro
caso
2
+ 1) − 2β 2 ](1 − rβ2 ) − 4rα rβ β 2 = 0
[α2 (rα
Usando rα =
q
c2
α2
− 1 y rβ =
ih
h 2
c
2
2
2−
α α2 − 2β
c2
2
2
2 − β2
c − 2β
2
c2
c
− 2 2 − β2
β2
2
c2
2 − β2
2
c
β2
i
q
−
−
=
=
c2
β2
(2.9)
− 1:
q
q
2
c2
4 α2 − 1 βc 2 − 1β 2 = 0
2
1/2 2
1/2
c
c
2 =0
4 β2 − 1
−
1
β
2
α
2
1/2 2
1/2
c
c
4 β2 − 1
−1
α2
1/2 1/2
c2
c2
4 1 − β2
1 − α2
(2.10)
La ecuación (2.10) es el requisito para que existe la onda evanescente que
viaja horizontalmente.
Universidad de Concepción, Geofı́sica, 513430 Sismologı́a Aplicada y de Exploración, Clase 2 – p. 12/18
2.1.4 Para un sólido de Poisson
2
2
Encontraremos la solución para un sólido de Poisson λ = µ ⇒ α = 3β :
2−
2−
c2
β2
c2
β2
2
=
4
=
4
2
6
16 − 32 βc 2 + 24 βc 4 − 8 βc 6 +
2
4
6
8
c8
β8
−32 βc 2 + 24 βc 4 − 8 βc 6 + βc 8
6
c2
c
c4
56 c2
32
− 8 β4 + 3 β2 − 3
β2
β6
=
c2
β2
4 1−
16 1 −
16 1 −
2
1/2 c2
β2
c2
β2
=
c
− 64
+
3 β2
=
0
1−
1−
c2
3β 2
1/2
c2
3β 2
c2
c4
− 3β 2 + 3β 4
16 c4
3 β4
(2.11)
Las soluciones de (2.11) son:
c2 /β 2 = 0. Una solución trivial - el medio en equilibrio sin ondas
presentes cumpla las condiciones de borde.
√
2
2
2
2
c /β = 4 y c /β = 2 + 2/ 3. Significa que β < α < c y entonces,
con rα y rβ números reales, el constraint A′ = 0 puesto en la página 5
no se cumpla. No son soluciones actuales.
√
2
2
c /β = 2 − 2/ 3 = 0.8453. Significa que c < β < α que implica
que existe una onda de superficie que cumpla las condiciones de
borde. Esta onda es la onda Rayleigh.
Universidad de Concepción, Geofı́sica, 513430 Sismologı́a Aplicada y de Exploración, Clase 2 – p. 13/18
2.1.5 Onda Rayleigh: propiedades
c2 /β 2 = 0.8453 ⇒ c = 0.92β
(2.12)
La velocidad horizontal de una onda Rayleigh (en un semi espacio
homogéneo) es independiente de su frecuencia y ∼92% de la velocidad de la
onda S.
rβ =
rα =
q
c2
2
qβ
c2
α2
−1=
√
0.8453 − 1 = 0.393i
p
− 1 = (0.8453/3) − 1 = 0.847i
,
rβ2 = −0.155
,
2 = −0.718
rα
De la ecuación (2.8):
2rα A + (1 − rβ2 )B
α A = −1.694i A
B = −2r
1.155
1−r 2
β
=
≈
0
−1.47iA
Ahora estamos preparados para calcular los desplazamientos u1 y u3
asociados con la onda Rayleigh (recuerde que u2 = 0).
Universidad de Concepción, Geofı́sica, 513430 Sismologı́a Aplicada y de Exploración, Clase 2 – p. 14/18
2.1.5 Onda Rayleigh: propiedades
u1
=
=
=
=
∂ψ
∂x3
[ikr
α x3 +ik(x1 −ct)]
Aike
∂φ
∂x1
−
− Bikrβ e[ikrβ x3 +ik(x1 −ct)]
Aike−0.85kx3 − Bikrβ e−0.39kx3 eik(x1 −ct)
−Ak sin(kx1 − ωt) e−0.85kx3 − 0.58e−0.39kx3
En x3 = 0, la superficie (usando la definición de un nuevo constante
a = −Ak):
u1 = 0.42a sin(kx1 − ωt)
u3
=
=
=
=
∂φ
∂x3
∂ψ
∂x1
e[ikrα x3 +ik(x1 −ct)]
(2.13a)
(2.14a)
+
Aikrα
+ Bike[ikrβ x3 +ik(x1 −ct)]
Aikrα e−0.85kx3 + Bike−0.39kx3 eik(x1 −ct)
−0.85kx
−0.39kx
3
3
−Ak cos(kx1 − ωt) 0.85e
− 1.47e
(2.13b)
Y en la superficie:
u3 = −0.62a cos(kx1 − ωt)
(2.14b)
Universidad de Concepción, Geofı́sica, 513430 Sismologı́a Aplicada y de Exploración, Clase 2 – p. 15/18
2.1.6 Rayleigh: movimiento particular
En nuestro la onda Rayleigh se propaga en la dirección +x̂.
El eje ẑ representa profundidad: apunta hacia abajo.
En la superficie:
u1 = 0.42a sin(kx1 − ωt) , u3 = −0.62a cos(kx1 − ωt)
En una cierta posición fija (como x1 = 0 por ejemplo):
u1 = −0.42a sin(ωt) , u3 = −0.62a cos(ωt)
ωt
0
π/2
π
3π/2
etc.
u1
0
−0.42a
0
0.42a
u3
−0.62a
0
0.62a
0
El movimiento particular es retrogrado elíptico en la superficie de la
Tierra.
Universidad de Concepción, Geofı́sica, 513430 Sismologı́a Aplicada y de Exploración, Clase 2 – p. 16/18
2.1.6 Rayleigh: movimiento particular
La variación de |u1 | y |u3 | con profundidad significa que el movimiento
particular cambia de retrogrado elíptico en la superficie al progrado
elíptico a profundidades.
Universidad de Concepción, Geofı́sica, 513430 Sismologı́a Aplicada y de Exploración, Clase 2 – p. 17/18
2.1.7 Rayleigh: sismograma
La onda Rayleigh llega en los componentes vertical-radial de un
sismograma con movimiento retrogrado elíptico.
Universidad de Concepción, Geofı́sica, 513430 Sismologı́a Aplicada y de Exploración, Clase 2 – p. 18/18