MARCO TEÓRICO: yx yx r

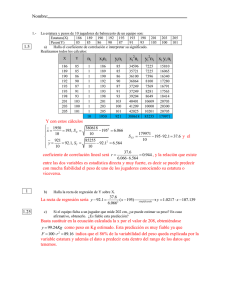
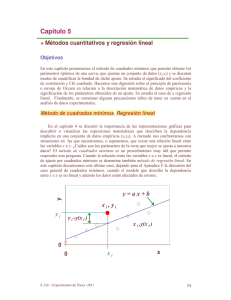
UNIVERSIDAD TECNOLÓGICA DE JALISCO
NO. 4
VERSIÓN: 1 FECHA:
ACADEMIA DE MATEMÁTICAS
TITULO DE LA PRACTICA:
Correlación y mínimos cuadrados
ASIGNATURA:
Matemáticas III
UNIDAD TEMATICA:
HOJA: 1
Correlación y mínimos cuadrados
NUMERO DE PARTICIPANTES RECOMENDABLE:
DURACION :
AGOSTO07
2 HORAS
INDIVIDUAL
LUGAR:
AULA DE CLASE
DE: 2
FECHA DE REALIZACIÓN:
Manuel Ramírez M.
REVISO:
Francisco Chávez
CARRERA:
1
El alumno construirá diagramas de dispersión y utilizará la formula de los mínimos
cuadrados.
OBJETIVO:
-Agosto-2007
ELABORO:
2
3
4
REVISION:
x
MARCO TEÓRICO:
Cuando se miden dos variables en una sola unidad experimental la información obtenida se conoce como
datos divariados. Ambas variables no solo son importantes cuando se estudian de manera separada, sino
que también se podría explorar la relación que existe entre ellas. Si una de las dos variables se puede
clasificar como independiente y si los datos muestran un patrón lineal, entonces la relación que vincula a
las dos variables se puede representar mediante una línea recta.
Conceptos Básicos
-
Diagrama de dispersión: Cuando dos variables se trazan en una grafica, una se traza en el eje
horizontal y la otra en el vertical. La primera variable a menudo se llama X y la segunda Y, de tal forma
que el diagrama toma forma de grafica en el plano cartesiano. Cada par de valores se representa como
un punto.
-
Recta de mínimos cuadrados o regresión lineal: Es la recta de la forma y = a + bx , donde
(
∑ y )(∑ x 2 ) − (∑ x )(∑ x ⋅ y )
a=
2
n ⋅ ∑ x 2 − (∑ x )
-
,
b=
n ⋅ (∑ x ⋅ y ) − (∑ y )(∑ x )
n ⋅ ∑ x 2 − (∑ x )
2
Coeficiente de correlación: Es el coeficiente que mide la intensidad de la relación entre dos variables.
r=
∑x⋅ y
∑ x2 ⋅ ∑ y2
Siempre que se decida calcular el coeficiente de correlación observará que el valor esta entre – 1 y 1.
1
UNIVERSIDAD TECNOLÓGICA DE JALISCO
NO. 4
VERSIÓN: 1 FECHA:
ACADEMIA DE MATEMÁTICAS
AGOSTO07
DESCRIPCIÓN DE LA PRÁCTICA:
1. Para cada uno de los problemas construir la ecuación de mínimos cuadrados y encontrar el coeficiente
de correlación. Trazar la recta de regresión lineal en el diagrama de dispersión correspondiente a cada
problema.
a) La tabla lista el numero de armas automáticas (en la tabla, los números de armas automáticas están
en millares) junto con la tasa de asesinatos (en asesinatos por 100,000) de estados seleccionados al
azar.
Armas automáticas x
11.6
8.3
3.6
0.6
6.9
2.5
2.4
2.6
Tasa de asesinatos y
13.1
10.6
10.1
4.4
11.5
6.6
3.6
5.3
b) La tabla representa el peso y el rendimiento de combustible en una autopista de un automóvil (el
peso esta dado en cientos de libras).
Peso
x
29
35
28
44
25
34
30
33
28
24
Combustible y
31
27
29
25
31
29
28
28
28
33
Calcular el mejor rendimiento de combustible para un automóvil que pesa 4200 lb.
MATERIAL:
• Lápiz y papel, calculadora científica. Bibliografía: Estadística elemental, Mario F. Tripla. Edit. Pearson,
séptima edición.
PRE-REQUISITOS:
•
Aritmética, manejo básico de la calculadora científica.
PROCEDIMIENTO:
1.
Realizar el diagrama de dispersión. 2. Encontrar la recta de regresión lineal. 3. Trazar la recta
en el diagrama de dispersión. 4. Calcular el coeficiente de correlación.
CRITERIOS DE DESEMPEÑO QUE SE EVALUARAN:
1.
Utilización adecuada de las formulas de la regresión lineal. 2. Interpretación del coeficiente de
correlación.
2