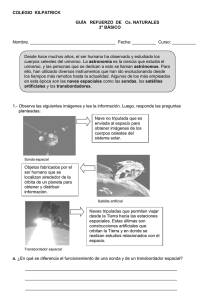
La transposición didáctica de conocimientos lógicos

FACULTAD DE HUMANIDADES Y CIENCIAS DE LAS EDUCACIÓN
UNIVERSIDAD DE JAÉN
Facultad de Humanidades y Ciencias de la Educación
Trabajo Fin de Grado
La transposición didáctica de
conocimientos lógicos,
geométricos y espaciales en
Educación Infantil (3-6 años)
Alumno: Esther Torres Pérez
Tutor:
Dpto:
Prof. Dª. Francisco Javier García García
Didáctica de las Ciencias
Junio, 2014
Índice Índice .......................................................................................................................................... 2 Resumen ..................................................................................................................................... 3 Palabras clave ............................................................................................................................. 3 1. Introducción............................................................................................................................ 3 2. Marco teórico: aprendizaje matemático en la EI y transposición didáctica ........................... 4 2.1. Transposición didáctica ............................................................................................... 6 3. Problema abordado en el TFG: la transposición didáctica de conocimientos lógicos,
geométricos y espaciales en los libros de texto de la EI ............................................................ 8 4. Un modelo epistemológico de referencia: los conocimientos lógicos, geométricos y
espaciales en la EI ...................................................................................................................... 9 5. Un modelo didáctico de referencia: la TSD y la situación fundamental .............................. 13 6. El saber a enseñar: análisis del currículo.............................................................................. 16 7. El saber a enseñar: análisis de una editorial ......................................................................... 19 7.1. Categorías: tipos de tareas ......................................................................................... 19 7.2. Clasificación fichas ................................................................................................... 21 7.3. Clasificación cuantitativa .......................................................................................... 33 8. Síntesis y conclusiones ......................................................................................................... 34 9. Bibliografía........................................................................................................................... 37 Anexos .............................................................................................................................. 40 AnexoI: Ejemplos de tareas en el material curricular “Mundo Flopi”, en relación a los
conocimientos lógicos, geométricos y espaciales ............................................................ 40 Anexo II: clasificación cuantitativa en los diversos cursos del segundo ciclo de
Educación Infantil: 3, 4 y 5 años ...................................................................................... 50 Anexo III: Visto bueno del tutor/a para la entrega del TFG ............................................ 53 Anexo IV: Autorización para la publicación de los Trabajo Fin de Grado en TAUJA ... 54 2 Resumen:En este trabajo mostraremos, en primer lugar, cómo el sistema de enseñanza de
las matemáticas trata los conocimientos lógicos, geométricos y espaciales, pasando por un
breve análisis de cada uno de ellos y teniendo como referente la Teoría de Situaciones
Didácticas de GuyBrousseau y la trasposición didáctica de Yves Chevallard. En segundo
lugar, esbozamos las contemplaciones que aparecen en la legislación vigente en relación a los
contenidos y conocimientos lógicos, geométricos y espaciales.
En tercer lugar, analizamos un determinado material escolar, Mundo Flopi de la editorial
Everest, para establecer las diferentes tareas que propone para trabajar los conocimientos ya
mencionados. Por último, comprobaremos cómo los materiales aún siguen una corriente que
desea ser reducida, la corriente empirista, para dar paso a una corriente de enseñanzaaprendizaje constructivista, que se queda en el aire.
Palabras clave:educación infantil, análisis, conocimientos lógicos, geométricos y
espaciales.
1. Introducción. La principal función de las matemáticas es desarrollar el pensamiento lógico, interpretar la
realidad y la comprensión del
lenguaje lógico-matemático. El acceso a conceptos
matemáticos requiere de un largo proceso de abstracción, y en Educación Infantil se da
inicio a la construcción de nociones básicas.Los conocimientos matemáticos son elementos
esenciales para cualquier conocimiento de la vida cotidiana, por ello es necesario ofrecer una
respuesta educativa de calidad desde el comienzo del colegio, sobre todo cuando los niños
llegan al segundo ciclo de Educación Infantil (3 – 6 años).
El objetivo de este trabajo es analizar un determinado material escolar escogido al azar,
Mundo Flopi de la editorial Everest, para ver el tipo de corriente que se sigue en la actualidad,
ya que la corriente constructivista es olvidada por una amplia mayoría de docentes. Con este
trabajo pretendemos reivindicar la importancia de trabajar la construcción de diferentes
conocimientos espaciales, geométricos y lógicos, esenciales para la adquisición de los demás
conocimientos que les siguen.
La motivación que me ha llevado a la realización de este análisis es la necesidad imperiosa
que deberían tener los docentes, con la finalidad de conocer y estudiar exhaustivamente el
material escolar que van a seleccionar para trabajarlo posteriormente en sus aulas, para
intentar cambiar el modelo de enseñanza tradicional.
3 Considero que este análisis de las diversas editoriales y materiales es una de las primeras
capacidades necesarias que el docente debería adquirir, ya que es el paso para cambiar de
corriente de enseñanza-aprendizaje, además de ser la capacidad que nos informe de lo que
realmente es necesario trabajar en las aulas y nos anime, aún más, a realizar el trabajo por
proyectos, tan necesario para que los alumnos aprendan por si solos a través de las propias
situaciones y la información que estas le apartan cuando los niños ponen en funcionamiento
diferentes acciones y retroacciones1.
2. Marco teórico: aprendizaje matemático en la EI y transposición didáctica Gran parte de las investigaciones en el ámbito de Educación Infantil tratan sobre el
aprendizaje matemático de los alumnos, así como los modelos existentes para la enseñanza de
conocimientos lógico-matemáticos en esta etapa.
El campo de la psicología de la educación es amplio y complejo. Excede de las intenciones de
este trabajo el llevar a cabo una descripción detallada de las teorías del aprendizaje
matemático más usadas. No obstante, esbozaremos dos grandesconcepciones que
consideramos básicos, y hasta cierto punto antagónicos: la concepción empirista y la
constructivista.
El empirismo, bajo el análisis que realizó Ruiz-Higueras (2005a), se fundamenta en una
concepción espontánea, presente en gran parte del profesorado. El alumno aprende lo que el
profesor le explica en clase, y no aprende nada que no es explicado por este. Es una
concepción muy extendida entre los miembros de la comunidad educativa. Piaget la
denominó “empirista” basándose en la concepción filosófica del mismo nombre para la cual,
la experiencia es la única base de conocimientos. En esta concepción, el alumno es
considerado como un sujeto pasivo, el maestro es el sujeto que “todo lo sabe” y el proceso de
enseñanza-aprendizaje se establece como un “trasvase” de conocimientos y saberes. Una de
las consecuencias más importantes que tiene esta construcción de los conocimientos, es el
abuso de la presentación ostensiva de conocimientos por parte del profesor.2
Al contrario en las concepciones constructivistas se postula que el saber no se transmite tal
cual al sujeto, sino que el aprendizaje supone un proceso de construcción activa por parte del
1
En referencia a la Teoría de Situaciones Didácticas de Guy Brousseau.
2
“La ostensión es el procedimiento privilegiado para la introducción precoz de las nociones matemáticas”.
(Brousseau, 1994)
4 sujeto que aprende. En este trabajo, adoptamos una concepción del constructivismo
establecida a partir de una serie de hipótesis, las cuales están basadas en la psicología genética
y social, pero que tiene una idea fundamental: Aprender matemáticas significa construir
matemáticas. Basándonos en Ruiz-Higueras (2005a), esbozamos a continuación los rasgos
más importantes de estas hipótesis:
•
Primera hipótesis: El aprendizaje se apoya en la acción. “Es la acción de la que
procede el pensamiento en su mecanismo esencial, constituido por el sistema de
operaciones lógicas y matemáticas” (Piaget, 1973, p. 26). El término “acción”
significa llevar a cabo manipulaciones, pero dentro del ámbito de las matemáticas, su
significado va más allá, significa anticipar la acción concreta, construir una solución
que nos dispense el manejo incluso de objetos reales. En la Escuela Infantil, estas
acciones concretas y efectivas para adquirir el conocimiento matemático, ayudarán al
niño a apropiarse de los problemas, a comprender la naturaleza de las cuestiones
propuesta y a configurar una representación de la situación propuesta. Además le
ayudará a anticipar resultados matemáticos antes situaciones ausentes o no realizadas,
de las cuales poseen cierta información.
•
Segunda hipótesis: La adquisición, organización e integración de los conocimientos
del alumno pasa por estados transitorios de equilibrio y desequilibrio, en el curso de
los cuales los conocimientos anteriores se ponen en duda. Una vez que el
desequilibrio es superado, se reorganizan los conocimientos y se integran los nuevos,
apoyándose esta secuencia en los procesos de asimilación y acomodación3.
“En el curso de la acción sobre un determinado medio, las contradicciones aparecen en
el sujeto como producto de los desequilibrios, y debe modificar sus representaciones,
se produce lo que Piaget ha denominado acomodación, que supone, básicamente, una
modificación en el sujeto causada por el medio (perturbación). De manera recíproca,
las transformaciones realizadas por el sujeto para dar respuesta a las perturbaciones
modifican su organización del medio, produciéndose entonces un proceso de
asimilación. El doble juego acomodación/asimilación está en el centro de los
mecanismos de los procesos de equilibración.”(Chamorro, 1991, p. 58)
•
Tercera hipótesis: Se conoce en contra de los conocimientos anteriores. Se trata de
una idea fundamental de la epistemología de Bachelard (1983) sobre el conocimiento
científico, tomada por Brousseau para explicar la formación de obstáculos en el
3
Siguiendo la teoría de la equilibración de Piaget.
5 aprendizaje de las Matemáticas: “La utilización y la destrucción de los conocimientos
precedentes forman parte del acto de aprender” (Brousseau, 1998, p. 120). Los
aprendizajes previos de los alumnos se deben tener en cuenta para construir nuevos
conocimientos, ya que éstos no se producen a partir de la nada, su elaboración está
sometida a adaptaciones, rupturas y a reestructuraciones, a veces radicales, de los
conocimientos anteriores. Aprendemos a partir de, y también en contra de, lo que ya
sabemos. Los nuevos conocimientos no pueden hacerse más que modificando los
precedentes y no por simple acumulación de los últimos sobre los ya existentes.
•
Cuarta hipótesis: Los conflictos cognitivos entre miembros de un mismo grupo social
pueden facilitar la adquisición de conocimientos. Idea básica de la psicología social
apoyada en la obra de Vygotsky, quien consideraba preciso tener en cuenta lo que un
individuo puede hacer con la ayuda de otros, ya que el aprendizaje se produce en un
medio social en el que abundan las interacciones, tanto horizontales (niño –
niño)como verticales (niño – adulto). Esta fase es primordial para el aprendizaje
matemático, sobre todo ala hora de poner en público las conclusiones a través del
lenguaje (ya sea oral o escrito).Permite a los niños estructurar la acción, apropiarse de
significaciones nociones y procedimientos, y además les abrirá la vía a la prueba
social, en la que se tratará de responder a los diversos porqués y a los cómo. Estas
respuestas será producidas por los alumnos, y de ellas se beneficiaran el resto de
compañeros, además del profesor.
Empirismo y constructivismo son dos concepciones radicalmente opuestas sobre cómo
aprenden los niños, que dan lugar a modelos de enseñanza diferentes. Siempre que el
profesorado actúa en el aula, asume, de manera más o menos implícita, un modelo de
aprendizaje. Consideramos que una competencia profesional importante del profesorado es,
precisamente, el hacer explícitos los modelos de aprendizaje que usa y, a partir de ellos, llevar
a cabo una elección razonada de las estrategias docentes que pone en juego, en función del
tipo de aprendizaje que desea provocar en sus alumnos.
2.1. Transposición didáctica El término transposición didáctica fue acuñado por Yves Chevallard. La transposición
didáctica designa el conjunto de transformaciones que sufre un saber científico con el fin de
ser enseñado.
“El trabajo que transforma de un objeto de saber a enseñar en un objeto de
enseñanza, es denominado transposición didáctica” (Chevallard, 1991, p. 45).
6 La existencia de estas transformaciones es un hecho conocido aunque aún muy poco
estudiado. Para transmitir un saber es necesario crear todo un proceso de enseñanza. Sin
embargo, en el sistema de enseñanza, el fenómeno de la transposición a veces se oculta y en
muchas ocasiones la "distancia" entre el saber a enseñar y el saber científico tiende a pasar
desapercibida, a ser borrada. La Didáctica de las Matemáticas se interesa en estudiar todo el
complejo sistema de adaptaciones y restricciones que debe sufrir un saber formalizado
científicamente hasta llegar a convertirse en un saber adaptado a la enseñanza escolar.
El profesor en su clase debe enseñar una parte de un saber que Chevallard (1991) denomina
saber sabio; los matemáticos profesionales, universitarios o investigadores puros, son sus
depositarios y sus productores permanentes. Es, normalmente, la sociedad quien solicita que
una determinada parte de este saber se lleve a la enseñanza (la suma de números naturales, de
números decimales, el cálculo de áreas, la resolución de ecuaciones, etc.) porque supone que
será de gran utilidad social. Empieza así un proceso de transformación y adaptación de los
saberes que, según Chevallard (1991), transcurre por diferentes fases, especificadas en el
siguiente esquema:
Saber sabio
Saber a enseñar
Noosfera4
Saber enseñado
Saber
aprendido
Tabla 1: Esquema fases de la trasposición didáctica
Brevemente, la primera fase, la fase del “saber sabio” es en la que se transforma el lenguaje
técnico que solo la comunidad científica conoce, a través de unos determinados mecanismos
como la determinación de los objetos del saber a enseñar, la organización y secuenciación de
los saberes, la temporalización, la división en cursos, en una lenguaje y unos conocimientos
determinados aptos para añadirlos al currículo didáctico. Esta fase es competencia de los
expertos (noosfera), en ella no interviene el profesorado. La fase segunda, el “saber a
enseñar”, es competencia del profesor pero aún fuera del aula, ya que este nivel se aprecia en
los manuales y materiales didácticos o es lo proyectos que realiza el profesor, y es el profesor
el encargado de la elección de este. Diversos materiales didácticos para un mismo curso
4
Chevallard (1991) llama "noosfera" a todo un complejo sistema formado por las personas que en la sociedad
piensan y deciden sobre los contenidos y métodos de enseñanza (matemáticos, diseñadores del currículo,
políticos, formadores de profesores, escritores de libros de textos, asociaciones de profesores, padres de alumnos,
directores y administradores de centros de enseñanza, etc.).
7 pueden presentar variaciones considerables. La siguiente fase, el “saber enseñado”, es
competencia del profesor y ahora sí, dentro del aula. El profesor es el responsable de conocer
el objeto del saber matemático correspondiente y además de representarlo de manera que los
alumnos asimilen los conocimientos a transmitir. Lo más importante de esta fase es la serie de
condicionamientos didácticos que deben seguir los contenidos, al igual que la posibilidad de
ser evaluados. Finalmente, está el “saber aprendido”, que es el que construye el alumno.
3. Problema abordado en el TFG: la transposición didáctica de conocimientos lógicos, geométricos y espaciales en los libros de texto de la EI El presente Trabajo de Fin de Grado aborda algunas etapas del problema de la transposición
didáctica de saberes lógico-matemáticos en el ámbito de la Escuela Infantil. En particular, nos
centramos en los conocimientos que en la Escuela Infantil se denominan como conocimientos
lógicos, conocimientos espaciales y conocimientos geométricos, y en cómo estos son
interpretados en esta institución.
Un análisis completo de la transposición didáctica de saberes lógico-matemáticos en la
Escuela Infantil excedería con creces las intenciones y dimensiones de este trabajo. Por ello,
lo que llevaremos a cabo será:
1. Una aproximación a cómo estos conocimientos se interpretan dentro de la esfera del
saber sabio.
2. Una descripción de cómo estos saberes han sido transpuestos en el currículo vigente
en la Escuela Infantil.
3. Un análisis sobre cómo los libros de texto de una editorial transforman los
conocimientos lógicos, espaciales y geométricos en saberes a enseñar.
Partimos de la hipótesis de que aprender matemáticas es hacer matemáticas, y que en la
actividad matemática llevada a cabo por los niños, los tipos de problemas que abordan juegan
un papel fundamental.
En otros términos, los conocimientos lógico-matemáticos que los niños pueden aprender en la
Escuela Infantil están fuertemente condicionados por la actividad matemática que los niños
lleven a cabo en la misma, y esta queda en gran parte determinada por los tipos de problemas
que son propuestos durante el proceso de enseñanza. Si asumimos que los libros de texto
juegan un papel dominante en muchas aulas de Educación Infantil, es posible postular que el
8 análisis de estos materiales curriculares se convierte en una fuente privilegiada para investigar
sobre el tipo de conocimientos que los niños pueden aprender en la Escuela Infantil.
Además, como futura maestra, este tipo de análisis forma parte de una de las competencia
docentes básicas de la propia profesión, como es la de analizar críticamente y seleccionar los
materiales de enseñanza más adecuados para lograr los aprendizajes deseados en nuestro
alumnado.
4. Un modelo epistemológico de referencia: los conocimientos lógicos, geométricos y espaciales en la EI La lógica clásica fue desarrollada para establecer las bases del razonamiento y para construir
un fundamento teórico de las matemáticas, como afirma Orús (1992); “Se trata de una
disciplina matemática cuyo objeto es el estudio de los tipos de argumentos lógicos y de su
validez”.
La lógica natural es un constituyente esencial del sistema cognitivo de cada sujeto. Cuando
hablamos de los niños que se encuentran en la Etapa de Educación Infantil, es necesario
considerar que los niños de forma innata ponen en funcionamiento procesos lógicos que han
sido descritos como una “lógica natural”, y que son la puerta de entrada a la lógica formal.
Por ello, a este tipo de actividad basada en esta lógica natural del niño en sus comienzos se le
suele denominar como actividad pre-lógica, por oposición con las actividades propias de la
lógica formal.
Según Ruiz-Higueras (2005b), para comprender mejor la posición y el sentido de los
contenidos lógicos-matemáticos en la etapa de Infantil, es conveniente realizar una revisión de
los programas escolares que se han llevado a cabo durante diferentes épocas.
Los programas escolares anteriores a 1971 no hacen ninguna mención explícita a los
conocimientos de tipo lógico, su pretensión es enseñar el recitado y la escritura de los
primeros números, así como su composición y descomposición.
A partir de 1972, los nuevos programas escolares son influenciados por las teorías de Piaget y
por las matemáticas modernas. Este hecho dio paso, por primera vez, a los programas de
Educación Preescolar en los que se tenía en cuenta la enseñanza de conocimientos
“prenuméricos”, es decir, conocimientos considerados como preparatorios para la
construcción del número. Algunos de estos conocimientos son: seriaciones, colecciones,
clasificaciones, ordenaciones, conjuntos…
9 Más tarde, en 1983, surgieron los Programas Renovados para la Educación Preescolar, que
seguían haciendo hincapié en los conocimientos prenuméricos.
En 1992, aparecieron los Diseños Curriculares que pretendían transformar todo el paisaje
prenumérico y su aproximación a la enseñanza. De hecho, no existe en ellos alusión alguna a
los conocimientos designados con dicho término. Pero cabe destacar, que en la propuesta de
secuenciación de contenidos, antes de abordar los aspectos numéricos sí se propone trabajar
con los objetos para formar colecciones y establecer diversos tipos de relaciones.
En la actualidad, no se identifica explícitamente un bloque de conocimientos como saberes
lógicos prenuméricos, aunque sí se propone trabajar con colecciones y diversas relaciones
antes de iniciarse en el número. Además, nos encontramos en un momento en el que la
didáctica de las matemáticas ha evolucionado de manera considerable. Ahora su objetivo es
generar en los niños de este nivel una actividad matemática que promueva el desarrollo de su
pensamiento y razonamiento lógico5.En consecuencia, para llevar a cabo este proceso de
enseñanza-aprendizaje, es necesario realizar un trabajo didáctico que permita la creación de
situaciones de enseñanza que provoquen y hagan evolucionar el lenguaje, el pensamiento y la
actividad lógica en estos niños.
La geometría es otro de los conocimientos más importantes que adquiere el ser humano. Una
de las razones que lleva a esta afirmación es el objeto de estudio de la geometría, “el espacio”.
Además en el estudio de la geometría pueden utilizarse instrumentos de dibujo para la
realización de figuras, se pueden construir sólidos hasta llegar a hacer demostraciones,
pasando por la utilización del cálculo numérico o algebraico, la modelización, la utilización
de situaciones concretas y la resolución de problemas matemáticos no algorítmicos. En
definitiva, la geometría permite a los alumnos poner en práctica todas las dimensiones de la
actividad matemática en su más amplio sentido. Es un campo, que dio lugar a modos de
enseñanza bien diferentes, desde un estudio axiomático hasta una enseñanza de inspiración
constructivista, con un gran apoyo en la resolución de problemas para obtener aprendizajes y
la construcción de significados(De la Torre y Pérez, 2008).
5
El razonamiento lógico es un conjunto de juicios que mantienen entre sí relaciones lógicas de tal forma que
partiendo de algunos juicios dados, denominados premisas, podemos llegar deductivamente a un juicio que no
teníamos anteriormente, denominado conclusión. El Razonamiento lógico-matemático incluye las capacidades
de identificar, relacionar y operar, y aporta las bases necesarias para poder adquirir conocimientos matemáticos
(Canals, 1992). Además, permite desarrollar competencias que se refieren a la habilidad de solucionar
situaciones nuevas de las que no se conoce de antemano el método mecánico de resolución, por lo que podría
considerarse que está relacionado con todos los demás bloques matemáticos (A. Alsina y A. Canals, 2000).
10 Como narra Vecino (2004), la historia reciente de la Geometría como objeto de enseñanza, se
ha visto comprometida debido a dos hechos puntuales:
•
La exclamación de Dieudonné6“¡Abajo el triángulo!”, marcaría decisivamente la
orientación de los programas oficiales y la enseñanza de la geometría en cualquier
nivel de enseñanza. La radicalidad de la propuesta, o la interpretación radical de la
misma, impulsa a la mayoría de las orientaciones oficiales a no incluir la Geometría
como objetivo prioritario de enseñanza, en los distintos niveles de la educación
obligatoria.
•
El ICME7 2 del 1976, registra la intervención de un geómetra (Atyiah) que
determinaría el regreso de la Geometría a su estatus de objetivo prioritario de
enseñanza en los distintos niveles de educación. De su intervención recogemos el
siguiente párrafo, decisivo por los cambios que produciría: "Habéis destronado a
Euclides y en eso estamos de acuerdo. Pero, ¿cómo habéis sustituido la enseñanza de
la geometría? La Matemática que se enseña en la mayor parte de los países está
todavía más alejada de la realidad, pues carece del apoyo geométrico. Daros cuenta
de que la intuición geométrica sigue siendo la fuente más poderosa para la
comprensión de muchos ternas; y por tanto se debería estimular lo más posible, y en
todos los niveles escolares, el pensamiento geométrico". (Vecino, 2004).
Estos sucesos han hecho que la Geometría vuelva a ser un objetivo prioritario en la enseñanza
de las matemáticas. Concretamente en el nivel de Educación Infantil, ha cambiado la visión
de la geometría en general, ahora se realiza una visualización más amplia de esta y a su vez se
introducen los distintos tipos de geometría.
A la hora de introducir estos conocimientos geométricos en las aulas, es el maestro el que
debe realizar con anterioridad un esfuerzo en la revisión de materiales y el cambio de
concepto que ha supuesto la geometría.
6
Esta exclamación de Dieudonne, insigne matemático francés, se oye en el Seminario organizado por la OECE
(Organización Europea de Cooperación Económica) en Royamont (Francia), en el ya un tanto lejano 959, para
coordinar los programas de matemáticas de los distintos países. No se trata de una exclamación individual, es
una exclamación apoyada por toda una serie de representantes del "saber sabio" no menos ilustres que su
portavoz, allí estaban apoyándole otros matemáticos como Choquet, Stone,...
7
Este congreso (Congreso Internacional para la Enseñanza de las Matemáticas) contribuye a agitar las tranquilas
aguas en que se había emplazado la enseñanza de las Matemáticas. Debemos tener en cuenta que se celebra en
un momento en que los programas oficiales de enseñanza no se habían visto afectados por el torbellino de Mayo
del 68 (quizás el movimiento revolucionario no veía la transformación de las enseñanza de esa disciplina como
un objetivo prioritario al considerarla sumamente abstracta).
11 La mayoría de los autores sostienen que los niños se sumergen en un espacio que les rodea,
expresando sus relaciones con él de diversas formas (topológicas, proyectivas o métricas), sin
que pueda establecer claramente una preeminencia de una forma de relación sobre otra
(Vecino, 2005, p. 284).
Como señala Fiol (1996), es necesario realizar algunas preguntas claves para tomar
conciencia del nuevo planteamiento sobre la enseñanza de la Geometría, buscando así la
reflexión y las consideranciones a tener en cuenta al a hora de llevar estos conocimientos al
aula. Estas preguntas claves son las siguientes: “¿cómo construyen (los niños) y actualizan su
comprensión del espacio?, ¿cómo identifican, reconocen propiedades y clasifican diferentes
formas?, ¿cómo desarrrollan sus representaciones externas o internas de forma que resulten
potenciadoras de lo creativo?”.
Actualmente, a nivel de centros educativos y de editoriales, se pretende introducir la
geometría en los niños de edades tempranas de manera diversificada en otros tipos de
aspesctos8 (topológico, proyectivo y métrico) para dar lugar a las ideas de clasificación de
Klein9 y desarrollados en las construcciones teórcias matemáticas.
Los conocimientos espaciales son otros de los elementos fundamentales en todo sujeto, es
necesaria conocer la posición espacial que ocupamos en todo momento así como la
orientación del resto de personas y objetos en nuestra vida diaria, ya que estos conocimientos
espaciales que se comienzan a adquirir a una edad temprana, son muy importantes aunque una
vez adquiridos pasen a convertirse en procedimientos ya mecanizados de los que parece que
nos olvidamos. Por ello, “la representación mental del espacio que nos rodea nos es
imprescindible” (Berdonneau, 2008, p. 141).
Ruiz-Higueras, García y Lendínez (2013, p. 96), consideran que “La representación y el
tratamiento de la información espacial constituyen las funciones primeras de los “grafismos”
del espacio. Planos, mapas, dibujos técnicos, dibujos geométricos, conservan, para quienes
los saben utilizar, informaciones de naturaleza espacial. Estas informaciones se consideran
necesarias para la realización de tareas profesionales y también son imprescindibles para el
correcto desenvolvimiento de todo ciudadano en su vida corriente”.
Esta construcción del espacio, se inicia desde el desarrollo infantil. Sauvy (1980) señala que
el niño pequeño se interesa desde muy pronto por el espacio, ya que desde sus pocos meses de
8
Centrándose en los tres aspectos propios de la geometría y no exclusivamente en el aspecto métrico, como hasta
hace relativamente poco tiempo.
9
Geómetra alemán de finales del siglo XIX. En su clasificación surgen la Geometría proyectiva, la Geometría
afín y la Geometría métrica.
12 vida, recorre porciones del mismo y lo explora activamente. Comienza diferenciando su
cuerpo del espacio exterior, para después, explorar su propio cuerpo. Conforme aumentan sus
posibilidades de movimiento, también lo hace la exploración que realiza del espacio, y por
tanto, su conocimiento del mismo.
Haciendo un breve análisis del tratamiento que han recibido los conocimientos espaciales a lo
largo de la historia, podemos comprobar en la última investigación realizada por Gálvez
(1985) cómo estos se excluyen casi sistemáticamente de los de la enseñanza de las
matemáticas escolares. Consecuentemente, no aparecen reflejados en el currículo como un
bloque de conocimientos independientes, prueba de ello es la afirmación de Alsina (2012)
cuando se refiere a la necesidad de trabajar procesos y contenidos en la escuela infantil, estos
últimos se categorizan en razonamiento lógico-matemático, numeración y cálculo, geometría,
medida y estadística y probabilidad. Sin embargo, cuando propone una serie de actividades
para llevar a cabo en el aula, si se pueden apreciar tareas con presencia de conocimientos
espaciales, los cuales aparecen integrados en el bloque de conocimientos geométricos.
Según Berthelot y Salin (1992), por “espacial” entendemos aquello que es relativo al espacio
en el que todo individuo debe saber desenvolverse de forma pertinente, aprovechando y/o
anticipando las retroacciones del entorno.
5. Un modelo didáctico de referencia: la TSD y la situación fundamental La Teoría de Situaciones Didácticas, a partir de este momento la nombraremos TSD, fue la
teoría consolidada por Guy Brousseau en Francia. A partir de 1970 comenzó a tratar de
construir el modelo de las situaciones utilizadas para la enseñanza de nociones matemáticas,
como consecuencia de situaciones tradicionales de enseñanza, en las cuales, la relación
didáctica se interpreta como una comunicación de informaciones.
Guy Brousseau (1998) parte de un modelo general del conocimiento matemático: Saber
Matemáticas no es solamente saber definiciones y teoremas para reconocer la ocasión de
utilizarlos y de aplicarlos, es “resolver problemas”, que en un sentido amplio incluye tanto
encontrar buenas preguntas como encontrar soluciones.
El aprendizaje por adaptación al medio es el supuesto básico del constructivismo de Piaget.
En este modelo el papel de la interacción entre los propios alumnos y el profesor queda en
cierta medida en un segundo plano.
13 Siguiendo a Ruiz-Higueras (2013), “enseñar un conocimiento matemático concreto es, en una
primera aproximación, hacer posible que los alumnos desarrollen con dicho conocimiento
una actividad matemática en el sentido anterior. El profesor debe imaginar y proponer a los
alumnos situaciones matemáticas que ellos puedan vivir, que provoquen la emergencia de
genuinos problemas matemáticos y en las cuales el conocimiento en cuestión aparezca como
una solución óptima a dichos problemas, con la condición adicional de que dicho
conocimiento sea construible por los propios alumnos. Es decir, que no sea el profesor quien
dé el conocimiento al alumno para que, posteriormente, lo aplique (aplicacionismo), sino que
realmente sea el alumno el que, enfrentándose aun verdadero problema, buscando su
solución, lo construya”.
En la TSD, como bien el nombre hace referencia, se basan en diferentes situaciones que hacen
al alumno resolver problemas cotidianos por sí solos además de que aprendan nuevos
conocimientos. Al hablar de situaciones didácticas, existen dos grandes categorías: las
situaciones didácticas (las que se han llevado siempre a cabo en las aulas, en las cuales el
profesor transmite su conocimiento al alumno dentro de un medio, sin interacción con él por
parte del alumnado) y las situaciones a-didácticas.
Según la definición que nos aporta Ruiz-Higueras (2013), una situación a-didáctica es aquella
en la que el alumno hace frente, de manera autónoma, a la resolución del problema,
construyendo para ello un conocimiento. Hay una serie de condiciones indispensables para
convertir la situación en a-didáctica, entre las cuales encontramos que el alumno debe poder
entrever una respuesta (estrategia de base) al problema planteado, la estrategia de base debe
mostrarse rápidamente como insuficiente y antieconómica, el alumno debe poder validar sus
estrategias interactuando con la situación, el “medio” (la situación problema) debe permitir
retroacciones que informen al alumno sobre la validez de sus estrategias, la situación debe ser
repetible y el conocimiento buscado debe aparecer como la estrategia óptima que permita
resolver el problema, haciendo, así, que el alumno abandone la estrategia de base.
“En la didáctica actual, la enseñanza es la devolución a un alumno de una situación
a-didáctica correcta, el aprendizaje es una adaptación a esta situación.” (Brousseau,
1998, p. 60).
Brousseau establece, en su TSD, lo que denominamos “situación fundamental” como la
situación optima para la transmisión de los conocimientos matemáticos. Una situación
fundamental es un conjunto de situaciones a-didácticas de la misma familia, específica está de
un conocimiento matemático.
14 Brousseau (1998), propone el diseño de diferentes situaciones a-didácticas, las situaciones de
formulación y comunicación, las situaciones de validación y las situaciones de
institucionalización, como complementos imprescindibles de las situaciones de acción o
investigación personal.
1. Las situaciones de acción, en las que se genera una interacción entre los alumnos y el
medio físico. Los alumnos deben tomar las decisiones que hagan falta para organizar
su actividad de resolución del problema planteado.
Las situaciones de acción deben estar basadas en problemas genuinos que atraigan el
interés de los alumnos a fin de que los asuman como propios y deseen resolverlos;
constituyen un primer encuentro de los alumnos con los objetos matemáticos
implícitos, en el que se les ofrece la oportunidad de investigar por sí mismos posibles
soluciones, bien individualmente o en pequeños grupos.
2. Las situaciones de formulación, cuyo objetivo es la comunicación en informaciones
entre alumnos. Para eso deben modificar el lenguaje que utilizan habitualmente,
precisándolo y adecuándolo a las informaciones que deben comunicar.
El tipo de discurso, o sea la comunicación oral o escrita en el aula, realizada por el
profesor y los alumnos es un aspecto central determinante de lo que los alumnos
aprenden sobre matemáticas. Si el núcleo de la comunicación sólo se produce del
profesor hacia los alumnos, de forma escrita a través de la pizarra, los alumnos
aprenderán unas matemáticas distintas, y adquirirán una visión diferente de las
matemáticas, que si tiene lugar una comunicación más rica entre profesor y alumnos y
entre éstos entre sí.
3. Las situaciones de validación, en las que se trata de convencer a uno o a varios
interlocutores de la validez de las afirmaciones que se hacen. En este caso los alumnos
deben elaborar pruebas para demostrar sus afirmaciones. No basta la comprobación
empírica de que lo que dicen es cierto; hay que explicar que necesariamente debe ser
así.
4. Las situaciones de institucionalización, destinadas a establecer convenciones sociales.
En estas situaciones se intenta que el conjunto de alumnos de una clase asuma la
significación socialmente establecido de un saber que ha sido elaborado por ellos en
situaciones de acción, de formulación y de validación.
15 6. El saber a enseñar: análisis del currículo En el momento actual, la Educación Infantil tiene como marco de referencia la Ley Orgánica
de Educación 2/2006 (03-05-06)10, ya que la Ley Orgánica para la Mejora de la Calidad
Educativa 8/2013 (09-12-13)11 no ha derogado a la Ley Orgánica de Educación, y en lo que
respecta a la etapa de Educación Infantil, no se han realizado cambios.
La Ley Orgánica de Educación establece en su Capítulo I, artículo 13, los objetivosgenerales
para esta etapa educativa:
La Educación Infantil contribuirá a desarrollar en las niñas y los niños las capacidades queles
permitan:
a) Observar y explorar su entorno familiar, natural y social.
b) Adquirir progresivamente autonomía en sus actividades habituales.
c) Desarrollar sus capacidades afectivas.
d) Relacionarse con los demás y adquirir progresivamente pautas elementales de
convivencia, relación social y ejercitarse en la resolución pacífica de conflictos.
e) Desarrollar habilidades comunicativas en diferentes lenguajes y formas de expresión.
f) Iniciarse en las habilidades numéricas básicas y en la lecto-escritura.
g) Conocer su propio cuerpo y el de los otros, sus posibilidades de acción yaprender a
respetar las diferencias.
Para conseguir estos objetivos el Real Decreto 1630/2006 (20-12-06)12, por el que se
establecen las enseñanzas mínimas del Segundo ciclo de educación infantil, concreta en su
artículo 6.1:
Las áreas del segundo ciclo de la Educación Infantil son las siguientes:
•
Conocimiento de sí mismo y autonomía personal.
•
Conocimiento del entorno.
•
Lenguajes: Comunicación y representación.
La Comunidad Autónoma de Andalucía ostenta la competencia compartida para el
establecimiento de los planes de estudio, incluida la ordenación curricular, de conformidad
con lo dispuesto en el artículo 52.2 del Estatuto de Autonomía para Andalucía y
10
Boletín Oficial del Estado, nº 106, 2006, pp. 17158-17207.
11
Boletín Oficial del Estado, nº 295, 2013, pp. 97858-97921.
12
Boletín Oficial del Estado nº 4, 2006, p. 474-482.
16 laLey17/2007, de 10 de diciembre, de Educación de Andalucía13 en el título II, capítulo II,
sobre la Educación Infantil.
En el ejercicio de esta competencia, el Decreto oficial de la Junta de Andalucía ha establecido
la ordenación y las enseñanzas correspondientes a la educación infantil en ambos ciclos de la
etapa. En el artículo 5.2 dispone que los objetivos, contenidos, orientaciones metodológicas y
criterios de evaluación del currículo de esta etapa educativa sean regulados por Orden de la
Consejería competente en materia de educación.
Entre los objetivos generales de etapa en esta Orden de 5 de agosto de 2008, por la que se
desarrolla el Currículo correspondiente a la Educación Infantil en Andalucía, en relación a los
conocimientos que nos abordan a lo largo de esta investigación, conocimientos lógicos,
espaciales y geométricos, destaca el siguiente objetivo:
“Comprender y representar algunas nociones y relaciones lógicas y matemáticas
referidas a situaciones de la vida cotidiana, acercándose a estrategias de resolución
de problemas”.
Con este objetivo se pretende contribuir a que niñas y niños desarrollen las habilidades
lógicas y el conocimiento matemático que están generando al interaccionar con los elementos
del medio e intervenir, de manera reflexiva, en acciones y situaciones que se les van
presentando en su cotidianeidad.
En el área que se refiere al conocimiento del entorno, consecuentemente entendido como una
realidad donde se integran, de manera sistémica, las dimensiones física, natural, social y
cultural, que componen el medio donde vivimos. En la etapa de Educación Infantil el entorno
es la realidad en la que se aprende y sobre la que se aprende.
Los contenidos de esta área se organizan en tres bloques, entre los que destaca por su relación
con las matemáticas:
“Conocimiento del medio físico y se denomina Medio físico: elementos, relaciones y
medidas”.
Los conocimientos o las actividades matemáticas de esta área que se trabajan en el segundo
ciclo de la etapa de Educación Infantil y que se abordan en esta investigación, son los que se
muestran esquematizados y categorizados en cuanto a las tres grandes actividades
matemáticas que analizamos en estas páginas, a continuación en la siguiente tabla, para
facilitar su lectura:
13
Boletín Oficial del Estado nº 20, 2007, p. 4467-4501.
17 Conocimientos matemáticos. Segundo ciclo
Conocimientos lógicos
-
Acercamiento comprensivo a las nociones y
relaciones lógicas y matemáticas que pueden
establecerse entre los elementos de la realidad.
Controlar las rutinas de la vida diaria. Secuenciar
rutinas, acciones y situaciones.
Verbalizar estas relaciones, codificarlas e
interpretar dichos códigos.
Identificación de la ley de una serie ya formada.
-
Formar
parejas
por
asociación/contraste/
discriminación de propiedades de los objetos.
-
Desarrollar
estrategias
para
establecer
clasificaciones, relaciones de orden y seriaciones
atendiendo al grado de posesión de una
determinada cualidad en objetos y colecciones.
-
Organizar y ordenar espacial y temporalmente
objetos, momentos y situaciones.
Conocimientos espaciales
-
Representar en el plano acciones realizadas en el - Aplicación de las nociones de direccionalidad que
espacio. (Y, recíprocamente, realizar en el espacio
nacen del propio cuerpo: hacia un lado- hacia
esquemas representados en el plano).
otro, arriba, abajo, hacia delante-hacia atrás,...
Situación de los objetos en el espacio en relación - Situación de objetos en el espacio inmediato con
con el propio cuerpo, de uno mismo con los
relación al propio cuerpo: hacia delante, hacia
objetos, de un objeto con otro.
atrás, arriba, abajo,...
Aproximación las nociones topológicas básicas: dentro, fuera, proximidad, cercanía, interior, exterior,
borde, frontera,…
Conocimientos geométricos
-
Identificar formas planas presentes en el entorno
y explorar algunos cuerpos geométricos.
-
Aproximación a las nociones proyectivas y
euclideas básicas.
Tabla 2: Conocimientos lógicos, espaciales y geométricos de la Orden de 5 de agosto de 2008
En este segundo ciclo, los niños y niñas serán capaces de ordenar colecciones de manera
seriada con un número cada vez mayor de elementos siempre que el atributo sea claramente
perceptibles y los elementos le sean familiares o cotidianos. La reflexión sobre estas
experiencias y la verbalización sobre las mismas, unidas a la observación interesada del uso
cultural que de ellos se hace en nuestro medio, aproximarán a los niños al uso contextualizado
de los números ordinales.
Es importante que se ayude a los niños y niñas a que relacionen unas acciones con otras ya
que vayan descubriendo algunas de las leyes lógicas que subyacen a éstas, dando lugara las
operaciones.
También en este ciclo se acercarán los niños y niñas a las nociones temporales a través de sus
propias vivencias. Ha de considerarse que las nociones temporales son, en la primera infancia,
tan importantes como difíciles de aprehender por ellos. Los niños y niñas de estas edades
tienen dificultades para tomar conciencia del paso del tiempo y mucho más para entender que
el tiempo sea común a todos, que sea continuo, objetivo y cuantificable. La noción de cambio,
tan vinculada al tiempo, tampoco es percibida por los niños y niñas desde el principio y de
manera espontánea. Estas vivencias les llevarán a intuir nociones temporales básicas como:
periodicidad, frecuencia, ciclo, duración, intervalo...
18 Especial importancia se dará a la realización de desplazamientos orientados a través de juegos
y vivencias cotidianas: desplazarse desde... hacia... hasta... son experiencias que llevarán a los
niños y niñas a estimar la situación de sí mismo y de los objetos y las relaciones espaciales
que entre ellos pueden establecerse. Las posteriores y progresivas representaciones que de
estas acciones en el espacio hagan niños y niñas sobre el plano irán ayudándolos a
comprender las relaciones espaciales. Se les acercará, así mismo, a la identificación de las
formas planas presentes en el entorno y a la exploración de algunos cuerpos geométricos.
La importancia de trabajar con los niños y niñas de esta edad las nociones temporales radica
en que éstas, junto a las nociones espaciales constituyen las coordenadas en las que el niño y
la niña se ubica a sí mismo, situando sobre estos ejes elementos y hechos, lo que le permite
avanzar en su conocimiento y comprensión.
7. El saber a enseñar: análisis de una editorial La editorial que se ha analizado en esta investigación es EVEREST. Es un método
globalizado, titulado “Mundo Flopi” destinado al segundo ciclo de Educación Infantil. Los
autores son Carmen Calvo Rojo, Ana Mª Díez Torío y Aurora Estébanez y es del año 2008.
Para cada curso se dispone de una carpeta por trimestre, es decir, tres carpetas por curso
escolar. Estas carpetas contienen los siguientes materiales:
•
Tres Unidades didácticas.
•
Tres cuentos populares (uno por Unidad).
•
Un boletín de Evaluación Trimestral.
•
Un folleto de información para la familia.
•
Láminas de plástica.
•
Pegatinas y gomettes.
•
CD de canciones y sonidos.
7.1. Categorías: tipos de tareas El análisis realizado a lo largo de este documento sobre el material citado anteriormente, ha
tenido que clasificarse atendiendo a diferentes tareas, las cuales implican una determinada
técnica que el alumno debe poner en funcionamiento con la finalidad de resolver el problema
que se plantea.
En un primer momento, la intención era realizar dicha clasificación atendiendo a los
diferentes conocimientos geométricos, lógicos y espaciales que se trabajan a lo largo del
19 material. El principal inconveniente de esta clasificación era la presencia de diferentes tareas
en una misma ficha, como por ejemplo, el hecho que se aprecia en el caso de las seriaciones,
que son una tarea complementaria a la tarea principal que aparecen siguiendo una secuencia
de repetición en los diferentes libros. Estas aparecen cada cinco fichas, como actividad
complementaria.
A continuación, en el siguiente esquema (tabla 3) se puede apreciar la clasificación realizada
sobre los distintos tipos de tareas existentes en “Mundo Flopi”, atendiendo a conocimientos
concretos:
Conocimientos
geométricos
Tipos de
tareas
Conocimientos
lógicos
Conocimientos
espaciales
Π1: Dada una figura geométrica plana presentada de manera
ostensiva, decir el nombre de la figura.
Π2: Dada una figura geométrica plana que sirve de modelo,
reproducir (por copiado) figuras similares.
Π3: Establecer asociaciones (correspondencias) entre figuras
geométricas similares en forma, aunque con distintos tamaños
(transformaciones proyectivas).
Π4: Dada una cuadricula con diferentes figuras geométricas
colocadas en distintas posiciones dentro de ella, reproducir la
configuración espacial bidimensional.
Π5: Completar puzles, atendiendo a criterios lógicos y espaciales.
Π6: Dada una serie espacial, continuarla siguiendo el criterio
establecido para ello
Π7: Dada una colección de imágenes de manera aleatoria,
ordenarlas cronológicamente tras la narración/lectura compresiva
sobre unos hechos determinados, llevando a cabo una seriación
temporal.
Π8: Asociar imágenes sobre las que ha operado una simetría axial
de eje vertical
Π9: Completar una figura poniendo en funcionamiento una
simetría axial de eje vertical.
Π10: Trazar una trayectoria en un “laberinto”, con el fin de llegar
a un objeto o posición determinada.
Π11: Dado una colección de figuras y/o dibujos orientados a la
izquierda o la derecha, identificar aquellos que tienen la misma
orientación.
Π12: Dados uno o varios objetos que actúan como representantes
de un conjunto, identificar la propiedad o propiedades
características que definen dicho conjunto y, en función de las
mismas
Π13: Dado un conjunto de proposiciones lógicas,
identificar/construir objetos que cumplan varias de ellas de
manera simultánea.
Π14: Situar objetos en una configuración espacial poniendo en
funcionamiento relaciones espaciales (del tipo delante de, detrás
de, junto a, dentro de, encima de, debajo de…).
Π15: Poner en funcionamiento relaciones topológicas (dentro,
fuera, interior, exterior, frontera, abierto, cerrado, cerca, lejos,
entre…) en contextos determinados.
Tabla 3: Esquema presentación clasificación de tareas.
20 7.2. Clasificación fichas Las tareas en las que se transmiten y trabajan conocimientos matemáticos relacionados con
los conocimientos lógicos, geométricos y espaciales en los tres cursos del segundo ciclo de
Educación Infantil, se agrupan a continuación en diferentes categorías según las tareas
diseñadas y visualizadas en el esquema anterior. A continuación de cada tarea, se muestra la
técnica que el alumnado debe poner en funcionamiento y una serie de imágenes que
ejemplifican dichas tareas. El resto de tareas encontradas en dicho material en relación a los
conocimientos matemáticas que nos ocupa aquí, se encuentra en el Anexo I.
Las diferentes categorías de fichas que se encuentran en esta editorial son:
Conocimientos geométricos:
•
Π1: Dada una figura geométrica plana presentada de manera ostensiva, decir el nombre
de la figura.
Técnica: Reconocer la figura presentada y producir la palabra que la designa.
Figura2: Presentación ostensiva triángulo
Figura 1: Presentación ostensiva
cuadrado
Figura 3: Presentación ostensiva
triángulos para recortar y pegar.
Figura 4: Presentación ostensiva
de triángulo en objeto cotidiano.
•
Π2: Dada una figura geométrica plana que sirve de modelo, reproducir (por copiado)
figuras similares.
Técnica: Repasar las formas geométricas siguiendo la línea de puntos-rayas, y copiar
figuras geométricas similares.
o Π2.1: Dada la figura en línea continua, reproducir figuras similares en su
interior.
Figura5: Realizar formas geométricas similares en su interior.
o Π2.2: Dada la figura en línea discontinua, producir una figura repasando el
modelo dado.
Figura6: Repasar los
rectángulos.
•
Figura7: Repasar los círculos,
cuadrados y triángulos.
Figura8: Repasar el rombo.
Π3: Establecer asociaciones (correspondencias) entre figuras geométricas similares en
forma, aunque con distintos tamaños (transformaciones proyectivas).
Técnica: Los niños tienen que poner en funcionamiento procesos de centración,
respecto a características específicas de cada figura geométrica, y de decantación, para
discriminar entre diferentes formas geométricas presentadas.
o Π3.1: Establecer asociaciones entre figuras geométricas en el contexto de
colorear un dibujo atendiendo a un modelo forma-color dado como referencia.
22 Figura9: Asociación para colorear un dibujo
(ejemplo 1).
Figura10: Asociación para colorear un dibujo
(ejemplo 2).
o Π3.2: Dado un dibujo con diferentes formas geométricas planas asociar (por
coloreo, pegando gomettes) aquellas que son similares.
Figura11: Relacionar y reconocer formas
cuadradas y circulares.
Figura13: Identificar el cuadrado. Esta tarea
es doble, en ella interviene también la tarea Π15
(dentro, fuera).
Figura12: Relacionar formas geométricas
similares. Círculo y cuadrado.
Figura14: Relacionar círculo, cuadrado y
triángulo.
23 o Π3.3: Dado un dibujo con diferentes cuerpos geométricos asociar (por coloreo,
pegando gomettes) aquellas que son similares según el criterio mismo cuerpo
geométrico.
Figura15: Asociar cuerpos geométricos (ejemplo
1).
•
Figura16: Asociar cuerpos geométricos
(ejemplo 2).
Π4: Dada una cuadricula con diferentes figuras geométricas colocadas en distintas
posiciones dentro de ella, reproducir la configuración espacial bidimensional.
Técnica: Los niños tienen que poner en funcionamiento, por un lado, relaciones
espaciales (debajo de, encima de, al lado de….) pero también el número cardinal (dos
cuadritos debajo, 1 cuadrito al lado,….).
Figura17: Reproducir cuadriculas modelo con figuras geométricas.
Conocimientos lógicos:
•
Π5: Completar puzles, atendiendo a criterios lógicos y espaciales.
Técnica: Dada una representación (escena, dibujo) con unos huecos libres, recortar y
pegar en ellos las piezas correspondientes, poniendo en funcionamiento relaciones
espaciales (al lado de, encima de, debajo de, junto a, entre…).
24 Figura18: Ejemplo de puzle 1.
Figura19: Ejemplo de puzle 2.
Figura20: Ejemplo de puzle 3.
Figura21: Ejemplo de puzle 4. Además presenta
relación con la tarea Π12, ya que los niños tienen que
poner en funcionamiento los procesos de centración
y decantación para seleccionar cada pieza.
•
Π6: Dada una serie espacial, continuarla siguiendo el criterio establecido para ello.
Técnica: Comparar objetos y ordenarlos en función de sus diferencias.
o Π6.1: Dados los elementos iniciales de una serie, reproducirla siguiendo otra
serie que actúa como modelo y que está presente en todo momento.
!
Π6.1.1: Reproducir una serie algorítmica siguiendo un modelo presente.
Figura22: Producir serie algorítmica con modelo.
!
Π6.1.2: Reproducir una serie no algorítmica siguiendo un modelo
presente.
25 Figura23: Producir serie no algorítmica con modelo.
o Π6.2: Extender una serie algorítmica, de la que se conoce su periodo.
Figura 25: Ejemplo 2 serie algorítmica con
pegatinas
Figura 24: Ejemplo serie
algorítmica.
Figura 26: Ejemplo 3 serie algoritmia con
pegatinas.
Figura 27: Continuar serie algorítmica.
Figura 28: Continuación serie algorítmica.
Figura 29: Continuar serie
algorítmica, con ayuda del
modelo.
•
Π7 :
Dada
una
cronológicamente
colección
tras
la
de
imágenes
narración/lectura
de
manera
compresiva
aleatoria,
sobre
ordenarlas
unos
hechos
determinados, llevando a cabo una seriación temporal.
Técnica: Comprender oralmente los sucesos de una narración, y discriminar y
seleccionar las diferentes viñetas con el fin de realizar una seriación temporal.
26 •
Figura30: Secuenciación temporal ejemplo 1.
Figura31: Secuenciación temporal ejemplo 2.
Además, en esta ficha se pide repasar los cuadrados
siguiendo la línea punteada, como en la tarea Π2.2.
Figura32: Secuenciación temporal ejemplo 3.
Figura33: Secuenciación temporal ejemplo 4.
Π8: Asociar imágenes sobre las que ha operado una simetría axial de eje vertical
Técnica: Llevar a cabo centraciones sobre características de las imágenes que
permanecen invariantes.
Figura34: Unir una figura con su correspondiente una vez aplicada la simetría axial de eje vertical.
•
Π9: Completar una figura poniendo en funcionamiento una simetría axial de eje
vertical.
Técnica: Conservar relaciones espaciales y métricas tomando como referencia el eje
de simetría.
27 Figura35: Completar la figura a partir del eje de simetría.
•
Π10: Trazar una trayectoria en un “laberinto”, con el fin de llegar a un objeto o
posición determinada.
Técnica: Realizar un trayecto a través de un laberinto, poniendo en funcionamiento
nociones topológicas básicas como dentro/fuera, interior/exterior, borde, frontero,
continuidad…
Figura36: Ejemplo de laberinto. En él destaca el
interior/exterior.
Figura38: Ejemplo de laberinto.
•
Figura37: Ejemplo laberinto. Destaca la frontera.
Figura39: Laberinto en el que destaca la
continuidad.
Π11: Dado una colección de figuras y/o dibujos orientados a la izquierda o la derecha,
identificar aquellos que tienen la misma orientación.
Técnica: Seleccionar y discriminar aquellos objetos que presentan la misma
orientación espacial que el modelo, o establecida por el criterio, operando procesos de
centración y de decantación sobre diferentes cualidades de los mismos.
28 o Π11.1: Con modelo presente: dada una figura orientada hacia la derecha o hacia
la izquierda, localizar aquellas que tienen la misma orientación.
Figura40: Localizar las figuras dirigidas a la derecha.
o Π11.2: Sin modelo: dada un colección de figuras, identificar todas las que tienen
la misma orientación, según el criterio izq./dcha.
Figura41: Localizar las figuras orientadas siguiendo un criterio dado.
•
Π12: Dados uno o varios objetos que actúan como representantes de un conjunto,
identificar la propiedad o propiedades características que definen dicho conjunto y, en
función de las mismas determinar relaciones de pertenencia o no a dicho conjunto.
Técnica: Operar centraciones para identificar la propiedad o propiedades que
caracterizan el conjunto. Operar decantaciones para separar los objetos que pertenecen
a dicho conjunto de los que no pertenecen.
29 Figura42: Busca el intruso. Ejemplo aplicación
procesos de centración y decantación.
Figura44: Ejemplo 3 centración y decantación.
Mismos elementos, con diferentes formas en su
interior.
•
Figura43: Centración y decantación ejemplo 2.
Elementos del mismo grupo de objetos con
características diferentes.
Figura45: Ejemplo 4 centración y decantación.
Diferentes elementos.
Π13: Dado un conjunto de proposiciones lógicas, identificar/construir objetos que
cumplan varias de ellas de manera simultánea.
Técnica: Operar centraciones sobre las diferentes características de los objetos a
identificar/construir, y conjunciones lógicas, de manera que el objeto cumpla las
propiedades 𝑝! ∩ 𝑝! ∩ ⋯
30 Figura46: Ejemplo 1 de construcción de objetos
según varias proposiciones lógicas (formas, tamaños
y color).
Figura47: Ejemplo 2 de construcción de objetos
según varias proposiciones lógicas (formas y color).
o Π13.1: Dado un “objeto” caracterizado por una amalgama de predicados lógicos,
y dada una “lista” de algunos de estos predicados, determinar cuáles de ellos
los cumple (valor de verdad).
Figura48: Ejemplo 1 de determinar predicados
lógicos de una figura plana.
Figura49: Ejemplo 2 de determinar predicados
lógicos de una figura geométrica en
combinación con figuras planas.
Conocimientos espaciales:
•
Π14: Situar objetos en una configuración espacial poniendo en funcionamiento
relaciones espaciales (del tipo delante de, detrás de, junto a, dentro de, encima de,
debajo de…).
Técnica: Poner en funcionamiento las relaciones espaciales siguiendo un sistema de
referencias.
o Π14.1: Situar los objetos en la configuración espacial con diferentes referentes
externos.
31 Figura50: Ejemplo 1.
Contextualizar objetos
en torno a un elemento
central. Representación
espacial a trabajar
encima de/debajo de.
Figura51: Ejemplo 2.
Representación espacial a
trabajar delante de/detrás de.
Figura52: Ejemplo 5.
Representación espacial a trabajar
a un lado de/ a otro lado de en
combinación con arriba/abajo.
Además, también se trabaja en esta
tarea la lateralidad a través de unos
criterios que aporta la ficha
"Colorea el pájaro que se encuentra
arriba a la derecha”. Esta tarea
tiene relación con Π11.
Figura53: Ejemplo 3.
Representación espacial
a trabajar delante
de/detrás de y encima
de/debajo de.
Figura54: Ejemplo 4.
Representación espacial a
trabajar dentro de/fuera de.
o Π14.1: Situar los objetos en la configuración espacial en ausencia de referentes
externos.
Figura55: Ejemplo 1. Recortar y
pegar cada pala donde se indica.
Encima, debajo, a un lado y a
otro lado.
•
Figura56: Ejemplo 2. Terminar
de enrollas cuerda "alrededor"
de la peonza.
Π15: Poner en funcionamiento relaciones topológicas (dentro, fuera, interior, exterior,
frontera, abierto, cerrado, cerca, lejos, entre…) en contextos determinados.
Técnica: Poner en funcionamiento los conocimientos sobre las relaciones topológicas
básicas.
32 Figura57: Ejemplo 1. Relación
topológica "entre".
Figura 58: Ejemplo 2. Relación
topológica "arriba/abajo, a un lado/a
otro lado". Además, en esta tarea se
trabaja el eje vertical de simetría
axial de la anterior tarea π9.
Figura60: Ejemplo 4. Relación
topológica "entre".
Figura63: Ejemplo 7. Relación
topológica "abierto/cerrado".
Figura61: Ejemplo 5. Relación
topológica "arriba/abajo".
Figura64: Ejemplo 8. Relación
topológica "dentro/fuera".
Figura59: Ejemplo 3.
Relación topológica
"cerca/lejos".
Figura62: Ejemplo 6.
Relación topológica "a una
lado y a otro".
Figura65: Ejemplo 9.
Relación topológica
"dentro/fuera". Esta tarea
presenta una particularidad,
y es que los elementos de
verano hay que añadirlos
dentro de la maleta mediante
flechas. Por otro lado,
presenta relación con la tarea
de los procesos de centración
y decantación π12.
7.3. Clasificación cuantitativa En múltiples ocasiones, dejamos de lado la importancia de las cosas hasta que no nos llaman
la atención por su cantidad. Como afirman Hurtado y Toro (1998),“La investigación
cuantitativa tiene una concepción lineal, es decir, que haya claridad entre los elementos que
conforman el problema, que tenga definición, limitarlos y saber con exactitud donde se inicia
33 el problema, también le es importante saber qué tipo de incidencia existe entre sus
elementos".
A continuación se muestra un gráfico en el que se aprecia la descripción cuantitativa de las
tareas analizadas anteriormente. En él podemos apreciar las tareas en su totalidad, teniendo en
cuenta los tres cursos que componen el segundo ciclo de Educación Infantil, cada cual con sus
tres trimestres correspondientes. En el Anexo II, podemos observar las gráficas de cada uno
de estos cursos de manera independiente.
π1: Presentación ostensiva
40 π2: Reproduccir de figuras geomtétricas similares
π3: Establecer asociaciones entre figuras geométricas
35 π4: Reproducir la configuración espacial bidimensional
30 π5: Puzzles
π6: Continuar la serie espacial
25 π7: Seriación temporal
20 π8: Asociar imágenes con eje de simetría axial
15 π9: Construit objeto con eje de simetría axial
π10: Trazar trayectoria en un laberinto
10 π11: Figuras orientadas izquierda/derecha
5 π12: Identificar la/s propiedad/es características que
definen un conjunto
π13: Construir/identificar un objeto con diferentes
proposiciones lógicas
0 Conocimientos geométricos Conocimientos lógicos Conocimientos espaciales π14: Situar objetos en una configuración espacial
poniendo en funcionamiento relaciones espaciales
π15: Relaciones topológicas
Tabla 4: Cuantificación de las tareas en total de los tres cursos que conforman el segundo ciclo de Educación Infantil
8. Síntesis y conclusiones Como he podido ir comprobando a lo largo de la realización de este análisis exhaustivo de los
conocimientos geométricos, lógicos y espaciales, he llegado a la conclusión de que mis
primeras impresiones al ver de pasada el material analizado se corroboran.
34 Es aquí donde me doy cuenta de que a pesar de la importancia que tiene el modelo
constructivista para la transmisión de conocimientos en las aulas (esta importancia ha sido
remarcada en numerosas investigaciones), sigue estando muy presente la corriente empirista.
A pesar del cambio y la evolución que ha sufrido el campo de la educación desde hace
bastante tiempo, hoy en día sigue existiendo una amplia mayoría de centros educativos y
editoriales que siguen modelos de enseñanza un tanto antiguos, como la corriente empirista, y
que realmente no dejan lugar a que conviva en la rutina diaria del alumnado una serie de
problemas matemáticos preparados con la finalidad de que los niños sean capaces de poner en
funcionamiento determinadas acciones que les permitan resolver dicho problema, obteniendo
así verdadera situaciones didácticas en las que se provocan y buscan la evolución por parte
del alumno. Es necesario esta evolución y cambio por completo a la corriente constructivista,
debido a que los niños tienen un reducido margen de actuación a la hora de aplicar las
estrategias previas que poseen a la hora de resolver problemas, en diversas ocasiones porque
el profesor termina rápidamente con las acciones emprendidas por los alumnos al darles las
soluciones o también como podemos observar a simple vista en diversos manuales
curriculares, porque los materiales destinados a Educación Infantil implican una actividad
nula o escasa para sus destinatarios.
Creo conveniente añadir la siguiente afirmación de Chamorro ya que me parece toda una
realidad con respecto a los momentos que vivimos actualmente en la educación, en concreto a
los procesos de enseñanza-aprendizaje que conviven hoy día en las aulas. “El combate contra
el fracaso escolar en Matemáticas debe empezar, de forma preventiva, en estos niveles14, y no
desaprovechar el inmenso regalo que supone la curiosidad infantil, cualidad indispensable,
que, junto con la perseverancia y la disciplina, son imprescindibles para avanzar en los
aprendizajes matemáticos a los que el niño, ahora preescolar, tendrá que enfrentarse a lo
largo de una dilatada escolaridad” (Chamorro, 2005, p. 15).
En relación a los resultados obtenidos en el análisis del material escolar “Mundo Flopi”,
podemos deducir que muchas de las tareas de estos conocimientos se emplean de manera
descontextualizada ya que el alumnado se limita a observar una serie de ilustraciones que les
dicen lo que son o lo que representa (como es el caso de las figuras geométricas mediante la
presentación ostensiva) en lugar de aportarle una serie de experiencias y situaciones adidácticas en las que tengan que resolver determinados problemas, los cuales contengan estos
conocimientos geométricos por sí solos o en relación a otros conocimientos matemáticos.
14
Haciendo referencia a la etapa de Educación Infantil.
35 Pero mayormente la importancia radica en presentarles a los niños problemas relacionados
con su vida diaria.
De las tareas que hemos clasificado, algunos de los ejemplos de ellas (una minoría, ya que se
trata de tres tareas en total de todas las analizadas) tenían relación con dos conocimientos
diferentes, como en el caso de la tarea de la maleta. En esta tarea se trabaja la noción
topológica básica de dentro/fuero, ya que los niños tienen que llevar con una flecha las ropas
de verano dentro de la maleta. El otro conocimiento que se aborda en la tarea en la operación
por parte del alumnado de centraciones y decantaciones para identificar la propiedad que
caracteriza al conjunto de verano y separarlos estos de los objetos que pertenecen al conjunto
de invierno.
Figura66: Añade dentro de la maleta las ropas que usamos en verano.
Otro ejemplo muy claro y repetitivo a lo largo del análisis es la tarea π2, la de dada una figura
geométrica plana que sirve de modelo, reproducir (por copiado) figuras similares en relación
con la tarea π6, dada una serie espacial, continuarla siguiendo el criterio establecido para ello,
puesto que encontramos 13 tareas en las cuales se relacionan. Algunas de ellas son las que
observamos en las siguientes figuras:
Figura 67: Relación π2 con π6
(ejemplo 1)
Figura 68: Relación π2 con π6
(ejemplos 2)
Figura 69: Relación π2 con π6
(ejemplo 3)
En estos ejemplos, la intención de la editorial es repasar la grafomotricidad de las distintas
figuras geométricas, además de continuar una serie algorítmica ya comenzada. Considero que
está no es la mejor manera para que el alumnado entre en contactos con estas figuras, ni
muchos menos para que aprenda las propiedades que cada una de ellas posee. Si queremos
que aprendan bien este conocimiento geométrico, es necesario que los niños interactúen
directamente con diferentes objetos de la vida cotidiana que posean que presenten dichas
figuras. Además, en relación al conocimiento lógico de la serie, no supone interés al
alumnado, ya que los elementos incluidos en estas series no suponen una motivación
intrínseca a los niños en el momento de realizarlas.
36 Como comentaba en el problema abordado en el desarrollo del TFG, considero que una de las
habilidades imprescindibles y más necesarias que debe formar parte de una competencia
básica de la profesión docente, es la de analizar críticamente y seleccionar los materiales de
enseñanza más adecuados para lograr los aprendizajes deseados en nuestro alumnado. Esta
competencia docente no se aprende por sí sola, sino que es necesario tener en cuenta una serie
de criterios para llevar a cabo este análisis detallado, para ello sería conveniente que las
autoridades competentes formasen a los docentes en este aspecto, puesto que la elección del
material escolar a trabajar en el aula va a influir decisivamente en el modelo de enseñanzaaprendizaje que se trabaje, así como el papel que va a ir jugando el profesor a lo largo del
curso académico. Así, su rol será de guía dando paso a la resolución de problemas por parte
de los niños, o será el conocedor de todos los conocimientos y se limitará a transmitirlos a los
sujetos pasivos (los niños) y a que estos, se dediquen a aplicar (aplicacionismo) los
conocimientos que han “adquirido” sin cabida para la aplicación de diferentes y nuevas
estrategias que evolucionan su aprendizaje.
9. Bibliografía
Alsina, A. (2004).Desarrollo de competencias matemáticas con recursos lúdicomanipulativos. Madrid: Narcea ediciones
Alsina, A. (2012). Más allá de los contenidos, los procesos matemáticos en Educación
InfantilEdma 0-6: Educación Matemática en la Infancia,1 (1), 1-14.
Bachelard, G. (1983). La formación del espíritu científico. Buenos Aires: Siglo XXI
Berdonneau, C. (2008). Matemáticas activas (2-6 años). Barcelona: GRAÓ.
Berthelot, R. ySalin, M. (1992). L'enseignement de l'espace et de la geometrie dans
l'escolarité obligatoire. Thése de doctorat . Université de Bordeaux.
Boletín Oficial del Estado nº 4 (2006), pp. 474-482. Madrid
Boletín Oficial del Estado nº 20 (2007) pp. 4467-4501. Madrid
Boletín Oficial del Estado, nº 106 (2006) pp. 17158-17207. Madrid
Boletín Oficial del Estado, nº 295 (2013)pp. 97858-97921. Madrid
Brousseau, G. (1994). La mémorie du système éducatif et la mémorie de l'enseignant.Paris:
Copilerem
Brousseau, G. (1998).Théorie des situations didactiques. Grenoble: La Pensée Sauvage
Brousseau, G. (2007). Iniciación a la teoría de situaciones didácticas. Buenos Aires: Libros
del Zorzal .
37 Chevallard, Y. (1991). La transposition didactique du savoir savant au savoir enseigné.
Grenoble: La Pensée Sauvage.
Chevallard, Y. (1998). La trasposición didáctica: del saber sabio al saber enseñado. Buenos
Aires: Aique.
Canals, M.A. (2001). Vivir las matemáticas. Barcelona: Ediciones Octaedro
Chamorro, M.C. (2005). Didáctica de las matemáticas. Madrid: Pearson Educación
Chamorro, M.C. (1991). El aprendizaje significativo en el área de las matemáticas. Madrid:
Alhambra-Logman
De la Torre, E. y Pérez, M. (2008). Paradigmas y espacios de trabajo geométricos en los
libros
de
texto
de
la
ESO.
Recuperado
el
10
de
Junio
de
2014:http://www.uv.es/gutierre/aprengeom/archivos2/DelaTorrePerez08.pdf
Fiol, M.L.(1996). Proyecto docente para T.U. Bellaterra: Universidad Autónoma de
Barcelona.
Gálvez, G. (1985). Aprendizaje de la orientación espacial en el espacio urbano. Una propuesta
para la enseñanza de la geometreía en la educación primaria. Tesis doctoral. México:
CINVESTAD
Hurtado, I. y Toro, J. (1998). Paradigmas y Métodos de investigación en tiempos de cambio.
Venezuela: Episteme Consultores Asociados C.A.
Orús, P. (1992). Le raisonnement des élèves dans la relation didactique; effects d´une
invitation à l´analyse classificatoire dans la scolarité obligatoire. Thése de doctorat.
Universidad de Bordeaux
Piaget, J. (1973). Introduction à l'épistemologie genetique. Paris: PUF
Ruiz-Higueras, L. (2005a). Aprendizaje y matemáticas. La construcción del conocimiento
matemático en la Escuela Infantil. En C. Chamorro (Coord.), Didáctica de las matemáticas
para Educación Infantil (pp. 1-38). Madrid: Pearson Educación.
Ruiz-Higueras, L. (2005b). La actividad lógica en la Escuela Infantil. En C. Chamorro
(Coord.), Didáctica de las matemáticas para Educación Infantil (pp. 101-140). Madrid:
Pearson Educación.
Ruiz-Higueras, L. (2013). Didáctica de las Matemáticas en Educación Infantil. Apuntes de
clase (no publicados).
Ruiz-Higueras, L., García, F. J. y Lendínez, E. (2013). La actividad de modelización en el
ámbito de las relaciones. Edma 0-6: Educación Matemática en la Infancia , 2 (1), 95-118.
Sánchez, R.; Sánchez, E. (s.f.). La construcción del espacio en la educación infantil.
Recuperado
el
17
de
Junio
de
2014,
de
Universidad
de
38 Murcia:
http://www.um.es/c/document_library/get_file?uuid=95970414-be18-4270-add4
aa968ef0f0a6&groupId=299436
Sauvy, J. y Sauvy, S. (1980). El niño ante el espacio: iniciación a la topología intuitiva -de la
rayuela a los laberintos-. Madrid: Pablo del Río.
Vecino, F. (2004). La consideración de distintas representaciones geométricas y su influencia
en la proposición de una didáctica coherente de la geometría. En J. López Ruiz (Coord.),
Números, formas y volúmenes en el entorno del niño (pp. 9-36). Madrid: Ministerio de
Educación.
Vecino, F. (2005). El espacio como modelo teórico para el desarrollo de las geometrías.
Situaciones de introducción a las mismas. En C. Chamorro (Coord.), Didáctica de las
matemáticas para Educación Infantil (pp. 279-313). Madrid: Pearson Educación.
Vygotsky (1978). Los conflictos cognitivos. CIRADE
39 Anexos Anexo I: Ejemplos de tareas en el material curricular “Mundo Flopi”, en relación a los conocimientos lógicos, geométricos y espaciales A continuación, se muestran el resto de las tareas correspondientes a los conocimientos
geométricos, lógicos y espaciales que hemos clasificado con anterioridad, agrupadas y
ordenadas en sus correspondientes categorías.
En el proyecto “Mundo Flopi”, hemos encontrado un total de 153 tareas, en las que la
editorial Everest pretende trabajar los conocimientos geométricos, lógicos y espaciales.
Π1: Dada una figura geométrica plana presentada de manera ostensiva, decir el nombre de la
figura.
Figura 70: Presentación ostensiva círculo
Π2: Dada una figura geométrica plana que sirve de modelo, reproducir (por copiado) figuras
similares
Figura 72: Repasar rombos
Figura 71: Repasar triángulos
40 Figura 73: Repasar óvalos y círculos
Figura 74: Repasar rectángulos
Figura 76: Repasar círculos en serie. Relación con la
tarea π6 debido a la serie
Figura 75: Repasar cuadrados, triángulos y círculos en una
serie. Relación con la tarea π6 debido a la serie
Figura 77: Repasar círculos en serie. Relación con la tarea π6
debido a la serie
Figura 79: Repasar cuadrados y rectángulos. Relación con la
tarea π6 debido a la serie
Figura 81: Misma serie y repasado de figuras geométricas que
en la figura 72, con menos elementos.
Figura 78: Repasar óvalos. Relación con la tarea π6
debido a la serie
Figura 80: Repasar círculos. Relación con la tarea π6
debido a la serie
Figura 82: Repasar círculos y óvalos. Relación con la
tarea π6 debido a la serie
Figura 83: Repasar círculos, óvalos y triángulos. Relación con la tarea π6 debido a la serie
41 Π5: Completar puzles, atendiendo a criterios lógicos y espaciales.
Figura 84: Puzle nueve piezas
Figura 85: Puzle ocho piezas
Figura 86: Puzle para pegar los triángulos recortados anteriormente
Figuras 87: Triángulos para recortar
Π6: Dada una serie espacial, continuarla siguiendo el criterio establecido para ello.
Π6.2: Extender una serie algorítmica, de la que se conoce su periodo.
Figura 88: Serie círculos y óvalos.
Figura 89: Serie formas geométricas, color y repasar figuras
42 Figura 91: Serie círculos
Figura 90: Serie círculos según color y tamaño.
Figura 92: Serie óvalos y círculos. Tamaños y color
Figura 94: Serie color y repasar círculo. Sólo una
mancha de color para continuar
Figura 93: Serie formas geométricas diferenciadas por
colores. Más elementos que figura 86
Figura 95: Serie con pegatinas
Figura 97: Serie coche
Figura 96:Serie gusano
Figura 98: Serie círculos de dos colores
Figura 99: Serie coches con diferente referencia espacial
Figura 100: Serie en cuadrícula
Figura 102: Serie en cuadrícula 2
Figura 104: Serie en cuadrícula 4
Figura 101: Serie trazos oblicuos
Figura 103: Serie en cuadrícula 3
Figura 105: Serie con pegatinas de formas geométricas
Figura 107: Serie gotas
Figura 106: Serie con pegatinas de objetos variados
43 Figura 109: Serie en cuadrícula 6
Figura 108: Serie cuadrícula 5
Figura 110: Serie exclusiva para repasar cuadrados y
rectángulos
Figura 111: Serie cuadrados y rectángulos con atributos
de color y tamaño.
Figura 113: Serie en cuadrícula 8
Figura 112: Serie en cuadrícula 7
Figura 115: Serie en cuadrícula 9
Figura 114: Serie óvalos, triángulos y círculos
Π7: Dada una colección de imágenes de manera aleatoria, ordenarlas cronológicamente tras
la narración/lectura compresiva sobre unos hechos determinados, llevando a cabo una
seriación temporal.
Figura 116: Secuencia rutina
Figura 117: Secuencia panadero
44 Figura 118: Secuencia obtención miel
Figura 119: Secuencia compra
Figura 120. Secuencia crecimiento de una planta
Figura 121: Secuencia crecimiento de una planta 2
Figura 122: Secuencia una nueva vida
45 Π10: Trazar una trayectoria en un “laberinto”, con el fin de llegar a un objeto o posición
determinada.
Figura123: Laberinto con semáforos
Figura 124: Laberinto navidad
Figura 125: Laberinto sin distinción dentro/fuera de la
frontera
Figura 126: Laberinto asociar objetos
Figura 127: Laberinto asociación
Π11: Dado una colección de figuras y/o dibujos orientados a la izquierda o la derecha,
identificar aquellos que tienen la misma orientación.
Figura 128: Identificar delfines orientados a la derecha
46 Π12: Dados uno o varios objetos que actúan como representantes de un conjunto, identificar
la propiedad o propiedades características que definen dicho conjunto y, en función de las
mismas determinar relaciones de pertenencia o no a dicho conjunto.
Figura 129: Eliminar el intruso en la categoría
Figura 130: Identificar y seleccionas las hojas con la
misma posición
Π13: Dado un conjunto de proposiciones lógicas, identificar/construir objetos que cumplan
varias de ellas de manera simultánea.
Figura 131: Construir objetos según proposiciones lógicos
Π13.1: Dado un “objeto” caracterizado por una amalgama de predicados lógicos, y dada una
“lista” de algunos de estos predicados, determinar cuáles de ellos los cumple (valor de
verdad).
Figura 132: Identificar objetos dados
47 Π14: Situar objetos en una configuración espacial poniendo en funcionamiento relaciones
espaciales (del tipo delante de, detrás de, junto a, dentro de, encima de, debajo de…).
Figura 133: Delante de/ detrás de
Figura 134: Delante de / detrás de 2
Π15: Poner en funcionamiento relaciones topológicas (dentro, fuera, interior, exterior,
frontera, abierto, cerrado, cerca, lejos, entre…) en contextos determinados.
Figura 135: Colocar árbol en pegatina lejos del árbol
dibujado
Figura 136: Alrededor de
Figura 137. Abierto/Cerrado
Figura 138: Cerca/Lejos
48 Figura 140: Alrededor de 2
Figura 139: Cerca/Lejos 2
Figura 141: Dentro/Fuera
49 Anexo II: clasificación cuantitativa en los diversos cursos del segundo ciclo de Educación Infantil: 3, 4 y 5 años 16 π1: Presentación ostensiva
14 π2: Reproduccir de figuras
geomtétricas similares
π3: Establecer asociaciones entre
figuras geométricas
12 π4: Reproducir la configuración
espacial bidimensional
10 π5: Puzzles
π6: Continuar la serie espacial
8 π7: Seriación temporal
6 π8: Asociar imágenes con eje de
simetría axial
4 π9: Construit objeto con eje de
simetría axial
π10: Trazar trayectoria en un laberinto
2 π11: Figuras orientadas izquierda/
derecha
0 Conocimientos geométricos Conocimientos lógicos Conocimientos espaciales π12: Identificar la/s propiedad/es
características que definen un conjunto
π13: Construir/identificar un objeto
con diferentes proposiciones lógicas
π14: Situar objetos en una
configuración espacial poniendo en
funcionamiento relaciones espaciales
π15: Relaciones topológicas
Tabla 5: Descripción cuantitativa de las tareas en el curso 3 AÑOS
50 π1: Presentación ostensiva
16 π2: Reproduccir de figuras geomtétricas
similares
14 π3: Establecer asociaciones entre figuras
geométricas
12 π4: Reproducir la configuración espacial
bidimensional
10 π5: Puzzles
8 π6: Continuar la serie espacial
π7: Seriación temporal
6 π8: Asociar imágenes con eje de simetría
axial
4 π9: Construit objeto con eje de simetría
axial
2 π10: Trazar trayectoria en un laberinto
0 Conocimientos Conocimientos Conocimientos geométricos lógicos espaciales π11: Figuras orientadas izquierda/derecha
π12: Identificar la/s propiedad/es
características que definen un conjunto
π13: Construir/identificar un objeto con
diferentes proposiciones lógicas
π14: Situar objetos en una configuración
espacial poniendo en funcionamiento
relaciones espaciales
π15: Relaciones topológicas
Tabla 6: Descripción cuantitativa de las tareas en el curso 4 AÑOS
51 π1: Presentación ostensiva
25 π2: Reproduccir de figuras
geomtétricas similares
π3: Establecer asociaciones entre
figuras geométricas
20 π4: Reproducir la configuración
espacial bidimensional
π5: Puzzles
15 π6: Continuar la serie espacial
π7: Seriación temporal
10 π8: Asociar imágenes con eje de
simetría axial
π9: Construit objeto con eje de
simetría axial
5 π10: Trazar trayectoria en un laberinto
0 Conocimientos geométricos Conocimientos lógicos Conocimientos espaciales π11: Figuras orientadas izquierda/
derecha
π12: Identificar la/s propiedad/es
características que definen un
conjunto
π13: Construir/identificar un objeto
con diferentes proposiciones lógicas
π14: Situar objetos en una
configuración espacial poniendo en
funcionamiento relaciones espaciales
π15: Relaciones topológicas
Tabla 7: Descripción cuantitativa de las tareas en el curso 5 AÑOS
52