Método de nudos

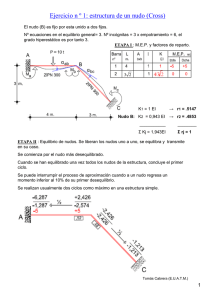
6.2 Método de nudos
Este método, resulta de aplicar la primera ley de Kirchhoff a un circuito, estimando como incógnitas las tensiones en los nudos. Como
sabemos, la citada ley, no se puede aplicar a todos los nudos sino a (n-1) nudos, por lo que en un circuito que tenga "n" nudos
tendremos (n-1) incógnitas. El nudo no considerado, nos servirá para ser tomado como referencia de los anteriores, entendiendo que
cuando hablamos de un potencial de un nudo, en realidad, estamos expresando la diferencia de potencial de ese nudo respecto al
tomado como referencia, que se suele conectar a tierra para indicar que su potencial es nulo.
Consideremos el circuito de la fig. 2.48. Aplicando la 1ª ley de Kirchhoff:
Nudo 1:
Nudo 2:
1 Iz2
I a = I Z1 + I Z 2
Iz1
I Z2 = I Z3 + I b
Ia
V1 −V 3
I Z2 =
I Z3 =
Z1
=
V1
=
V2
2
Iz3
Z3
Z1
Pongamos I Z1 , I Z 2 e I Z 3 en función de los potenciales, teniendo en cuenta que
V3 = 0:
I Z1 =
Z2
Ib
3
Fig. 2.48
Z1
V1 −V 2
Z2
V 2 −V 3
Z3
Z3
Sustituyendo estos valores en las ecuaciones obtenidas para los nudos 1 y 2, tendremos:
Ia =
V1 V1 −V 2
+
Z1
Z2
V1 −V 2 V 2
=
+ Ib
Z2
Z3
Distinguiremos ahora, entre corrientes debidas a fuentes, y corrientes en los elementos pasivos, debidamente ordenado:
Ia =
1
V1 V1 −V 2
 1
 1
+
= V 1
+
 + V 2  −  = V 1 Y 1 + Y 2 + V 2 −Y 2
 Z2 
 Z1 Z 2 
Z1
Z2
−I b =
(
)
( )
1
V 2 V1 −V 2
 1
 1
−
= V 1−  + V 2 
+
 = V 1 −Y 2 + V 2 Y 2 + Y 3



Z3
Z2
Z2
Z2 Z3 
( )
(
)
Estudiaremos a fondo las últimas expresiones tratando de generalizar.
En el miembro de la izquierda, hemos situado las corrientes debidas a fuentes de intensidades, que serán positivas, cuando se acerquen
al nudo, y negativas, cuando se alejen. Esto nos puede hacer suponer que el método de los nudos, sólo sirve si las fuentes son de
intensidad, y no es así, ya que si se tratara de fuentes tensión, se transformarían en fuentes de intensidad. Obviamente resulta más
cómodo operar con fuentes de intensidad que con fuentes de tensión.
En el miembro de la derecha, están ordenadamente expuestos los productos de las tensiones en los nudos por las inversas de las
impedancias (admitancias). Es evidente que en la ecuación del nudo 1, V 1 , multiplicaría a la suma de las admitancias que concurren
en el nudo 1 y V 2 , a la admitancia comprendida entre el nudo 1 y el nudo 2. Si mantenemos V 2 positiva, esta admitancia habría que
expresarla negativamente en todos los casos, ya que una corriente será la diferencia de potenciales multiplicada por la admitancia.
Generalizando las ecuaciones, para los sistemas de (n+1) nudos, es decir, con “n” incógnitas:
I 1 = Y 11 ⋅ V 1 + Y 12 ⋅ V 2 +!!+ Y 1n ⋅ V n
I 2 = Y 21 ⋅ V 1 + Y 22 ⋅ V 2 +!!+Y 2 n ⋅ V n
"""""""""""""""
I n = Y n1 ⋅ V 1 + Y n 2 ⋅ V 2 +!!+ Y nn ⋅ V n
(Y ) ⋅ (V ) = (I )
que expresado en forma matricial, será.
 Y 11

 Y 21
"

 Y n1
Y 12
Y 22
"
Y n2
" Y 1n   V 1   I 1 
    
" Y 2 n  V 2   I 2 
=
⋅
" "   "   "
    
" Y nn  V n   I n 
()
La matriz I , es una matriz columna, de “n” filas, en las que cada termino expresa la suma de corrientes debidas a fuentes, con el
convenio de que serán positivas las que entren en el nudo y negativas, las que salen.
()
La matriz V , es otra matriz columna que expresa los potenciales de los “n” nudos, respecto al de referencia, considerándolos como
incógnitas.
()
La matriz Y , del sistema está formada por dos tipos de términos:
Y hh , que significa suma de admitancias que concurren en el nudo h y siempre estos términos serán positivos. Se
denomina admitancia propia del nudo en cuestión.
Y hk , que significa admitancia que une el nudo h y el nudo k, que siempre serán negativas. Se denomina comitancia ó
coadmitancia de los nudos h y k.
Resolviendo por Cramer, tendríamos:
I1
Y 12
I 2 Y 22
" "
V1 =
In
" Y 1n
" Y 2n
" "
Y 11 Y 12 " I 1
Y 21 Y 22 " I 2
" " " "
Y n 2 " Y nn
Vn =
∆Y
Y n1 Y n 2 " I n
∆Y
()
llamando ∆Y al determinante de la matriz Y .
Si desarrollamos por los adjuntos de las intensidades:
∆11
∆
∆
+ I 2 ⋅ 21 +!!+ I n ⋅ n1
∆Y
∆Y
∆Y
∆12
∆ 22
∆
+ I2 ⋅
+!!+ I n ⋅ n 2
V 2 = I1 ⋅
∆Y
∆Y
∆Y
""""""""""""""""
∆
∆
∆
V n = I 1 ⋅ 1n + I 2 ⋅ 2 n +!!+ I n ⋅ nn
∆Y
∆Y
∆Y
V 1 = I1 ⋅
Los coeficientes ∆ hk , tienen la dimensión de una impedancia y se denominan impedancias generalizadas.
∆Y