Antenas de apertura
Anuncio
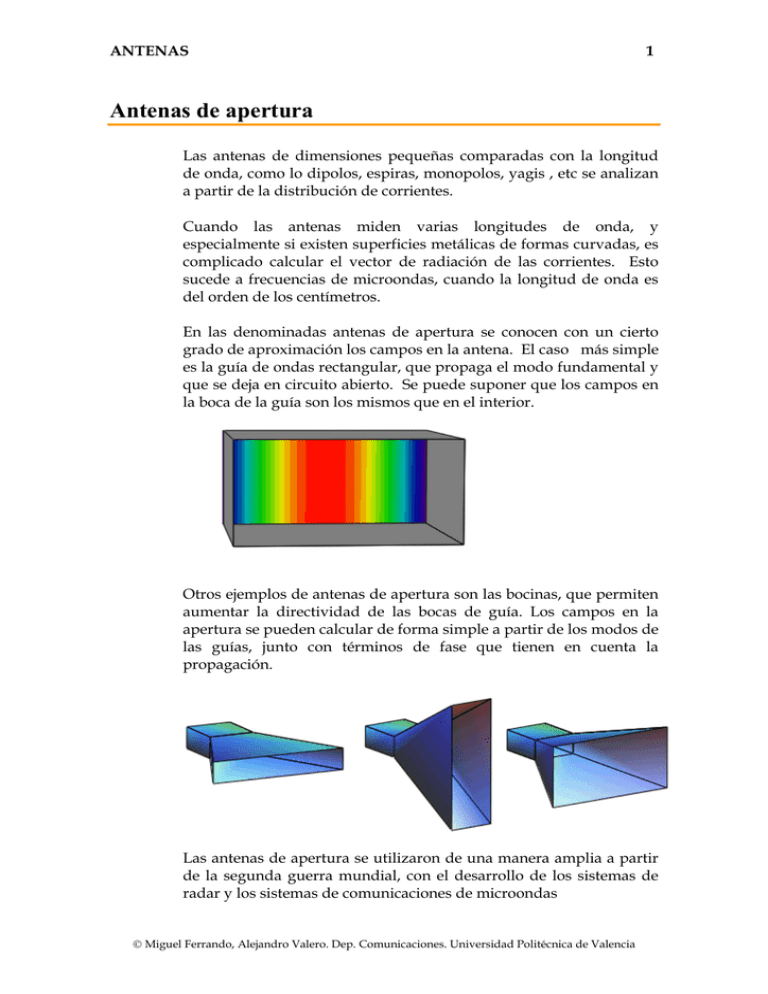
ANTENAS 1 Antenas de apertura Las antenas de dimensiones pequeñas comparadas con la longitud de onda, como lo dipolos, espiras, monopolos, yagis , etc se analizan a partir de la distribución de corrientes. Cuando las antenas miden varias longitudes de onda, y especialmente si existen superficies metálicas de formas curvadas, es complicado calcular el vector de radiación de las corrientes. Esto sucede a frecuencias de microondas, cuando la longitud de onda es del orden de los centímetros. En las denominadas antenas de apertura se conocen con un cierto grado de aproximación los campos en la antena. El caso más simple es la guía de ondas rectangular, que propaga el modo fundamental y que se deja en circuito abierto. Se puede suponer que los campos en la boca de la guía son los mismos que en el interior. Otros ejemplos de antenas de apertura son las bocinas, que permiten aumentar la directividad de las bocas de guía. Los campos en la apertura se pueden calcular de forma simple a partir de los modos de las guías, junto con términos de fase que tienen en cuenta la propagación. Las antenas de apertura se utilizaron de una manera amplia a partir de la segunda guerra mundial, con el desarrollo de los sistemas de radar y los sistemas de comunicaciones de microondas © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 2 Principio de Huygens El comportamiento de las antenas de microondas se puede explicar a partir de conceptos generales de óptica geométrica (trazado de rayos). Aunque dicha teoría tiene limitaciones importantes. Por ejemplo se podría analizar la incidencia de una onda plana sobre un cilindro metálico mediante trazado de rayos. Las reflexiones en la superficie supondrían una dispersión de las ondas, y un efecto de sombra como el indicado en la figura. Dicho análisis lleva a conclusiones incorrectas. Un análisis electromagnético exacto, basado en la resolución de las ecuaciones de onda para los campo lleva a la siguiente solución para un cilindro de 3 longitudes de onda de diámetro. Se puede observar la interferencia entre la onda incidente y las reflejadas y el efecto de sombra . Los fenómenos básicos de difracción de la luz fueron explicados por Huygens en el año 1690. En el principio de Huygens se plantea que cada punto de un frente de onda se comporta como un radiador secundario de ondas esféricas, de forma que la envolvente de estas ondas forman a su vez un nuevo frente de onda. © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 3 Mediante el principio de Huygens se puede explicar la formación de franjas de interferencia en una cámara oscura con una pequeña abertura. También se puede explicar el efecto de las zonas de penumbra en los eclipses. Una antena se puede encerrar en un volumen que contenga todas las fuentes, aplicando a continuación los conceptos de superposición de ondas a cada punto de la superficie. Desde un punto de vista matemático la solución de una ecuación diferencial en un volumen sin fuentes es única si se conocen las condiciones de contorno en la superficie. En los fenómenos electromagnéticos es necesario fijar las condiciones de contorno para las componentes tangenciales del campo eléctrico y el campo magnético, equivalentes desde un punto de vista circuital a generadores de tensión y de corriente. Ecuaciones de Maxwell generalizadas con fuentes magnéticas En las ecuaciones de Maxwell los campos se relacionan con las cargas y corrientes eléctricas, pero no existen los equivalentes de cargas y corrientes magnéticas de conducción. Las ecuaciones permiten explicar la totalidad de fenómenos de radiación, pero en algunos casos, como en el de las antenas de apertura conviene sustituir los campos eléctricos y magnéticos por unas fuentes equivalentes. La introducción del concepto de corriente magnética simplifica los cálculos, como por ejemplo en las espiras, donde el problema del hilo eléctrico circular podría estudiarse como una corriente magnética perpendicular a la superficie que contiene a la espira. Las ecuaciones de Maxwell generalizadas, con cargas τ y corrientes G magnéticas M serían. G ρ ∇⋅E = ε G τ ∇⋅H = µ G G G ∇ × H = jωε E + J G G G ∇ × E = − jωµ H − M Las ecuaciones se pueden descomponer en los dos casos, eléctricos y magnéticos y resolverlas por analogía. © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 4 Soluciones generalizadas Ecuaciones eléctricas Ecuaciones magnéticas Ecuaciones de Maxwell G ∇⋅E = 0 G τ ∇⋅H = G ρ ∇⋅E = ε G ∇⋅H = 0 G G G ∇ × H = jωε E + J G G ∇ × E = − jωµ H µ G G ∇ × H = jωε E G G G ∇ × E = − jωµ H + M Definición de los potenciales G 1 G E = ∇× F ε G G H = − jω F − ∇Ψ G G 1 H = ∇× A µ G G E = − jω A − ∇Φ Solución de los potenciales Φ= G G 1 G G (r , r ') ρ (r ')dv ' ε ∫∫∫ v' G G G G G A = µ ∫∫∫ G (r , r ') J (r ')dv ' v' Ψ= G G 1 G G (r , r ')τ (r ')dv ' µ ∫∫∫ v' G G G G G F = ε ∫∫∫ G (r , r ') M (r ')dv ' v' Vector de radiación G µ e − jkr G A= N 4π r G G G G N = ∫∫∫ J (r ')e jkrˆ⋅r ' dv ' v' G ε e − jkr G F= L 4π r G G G G L = ∫∫∫ M (r ')e jkrˆ⋅r ' dv ' v' Campos radiados G G jk H = − rˆ × A G G jk E = − rˆ × F G G G G E = − jω ( A − rˆ ⋅ A) = jω (rˆ × (r × A)) G G E = η ( H × rˆ) G G G G H = − jω ( F − rˆ ⋅ F ) = jω (rˆ × (r × F )) G G E = η ( H × rˆ) µ µ © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 5 Condiciones de contorno generalizadas La aplicación de las ecuaciones de Maxwell en su forma integral a la discontinuidad entre dos medios permite obtener las condiciones que deben cumplir los campos G G G nˆ × H1 − H 2 = J s G G nˆ ⋅ D1 − D2 = ρ s ( ( ) ) Es decir, en el caso de tener una lámina de corriente eléctrica aparece un salto en el campo magnético. En las ecuaciones generalizadas aparecen contorno adicionales las condiciones de G G G nˆ × E1 − E2 = − M s G G nˆ ⋅ B1 − B2 = τ s ( ( ) ) Es decir que para tener un salto en el valor del campo eléctrico entre dos regiones, es necesario que exista una corriente magnética laminar. Dualidad Las ecuaciones anteriores son duales, es decir que si se conoce la solución del caso eléctrico se puede pasar a la solución del caso magnético intercambiado los valores del campo eléctrico por el magnéticos, o en general las siguientes parejas de valores G E G H G H G −E G A G F φ ψ G J G M ρ τ ε µ µ ε G D G B G B G −D El dual del plano conductor perfecto, es el plano conductor magnético. Las condiciones de contorno duales son G nˆ × E = 0 G nˆ × H = 0 © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 6 Radiación de corrientes eléctricas y magnéticas laminares Supongamos una lámina de corriente eléctrica constante situada en un plano en el espacio libre. La solución para los campos serán dos ondas que se propagarán en las direcciones perpendiculares al plano. El problema es equivalente a una línea de transmisión en la que se conecta una fuente de corriente. G H G E G Js G H G 1G H = J s × nˆ 2 G G E = ηH × nˆ G η G E = − Js 2 n̂ G E I 2 ∞ I 2 V = I () I Z 2 0 ∞ Si la lámina fuese de corriente magnética, la solución también serían dos ondas planas, y el equivalente sería una línea de transmisión con una fuente de tensión. G E ∞ G H G Ms G H G E G 1 G E = M s × nˆ 2 G G 1 H = nˆ × E η G 1 G H = − Ms 2η I ( ) n̂ I V V = IZ 0 2 ∞ © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 7 La superposición de los dos problemas anteriores crea una onda plana de amplitud 2 que se propaga en un solo sentido. En la línea de transmisión aparece propagación en un solo sentido. G H G G E, H = 0 G G 1 G H = J s × nˆ = − M s η G G G E = nˆ × M s = −ηJ s n̂ G E ∞ V = IZ 0 I V,I = 0 I ∞ V Si se desea que haya propagación en un solo sentido utilizando sólo fuentes de tensión o de corriente es necesario añadir un cortocircuito (plano conductor eléctrico) o un circuito abierto (plano conductor magnético). I I =0 ∞ ∞ I I I =0 ∞ V = IZ 0 V V = IZ 0 ∞ Las anteriores consideraciones nos llevan a las tres formulaciones del teorema de equivalencia. © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 8 Teorema de unicidad El teorema de unicidad establece las condiciones que se deben cumplir para garantizar que la solución a un problema regido por las ecuaciones de Maxwell es única. Esto es siempre importante y especialmente ahora que vamos a empezar a resolver problemas sin emplear las fuentes reales y empleando en su lugar un conjunto de corrientes equivalentes, cuyas características quedarán claras en el punto siguiente cuando enunciemos el teorema de equivalencia. El teorema establece la siguiente condición: Dado un volumen V encerrado por una superficie S en cuyo interior no hay fuentes de G ningún tipo, si se conocen las componentes tangenciales a S de E G y/o H producidas por las fuentes exteriores a V, entonces la solución que se obtenga para cualquier punto de V es única. Para demostrar el teorema, se emplea el método de reducción al absurdo, partiendo de la suposición de que existen dos soluciones posibles en el interior de V, dado un conjunto de componentes tangenciales de los campos en S. G G G G Sean dos soluciones ( E1 , H1 ) y ( E2 , H 2 ) que satisfacen las ecuaciones de Maxwell en V G ∇ ⋅ E1 = 0 G ∇ ⋅ H1 = 0 G G ∇ × H1 = (σ + jωε ) E1 G G ∇ × E1 = − jωµ H1 G ∇ ⋅ E2 = 0 G ∇ ⋅ H2 = 0 G G ∇ × H 2 = (σ + jωε ) E2 G G ∇ × E2 = − jωµ H 2 Además ambas soluciones toman el mismo valor en la superficie S, G G n̂ × E y n̂ × H Si construimos una solución nueva, combinación de ambas, tal como G G G G E2 − E1 y H 2 − H1 también debe satisfacer las ecuaciones de Maxwell. Si tomamos la divergencia del vector de Poynting asociado a esta nueva solución, G G G G * G G * G G G G G G ∇ ⋅ ⎡ E2 − E1 × H 2 − H1 ⎤ = H 2 − H1 ⋅∇ × E2 − E1 − E2 − E1 ⋅∇ × H 2 − H1 ⎢⎣ ⎥⎦ G G 2 G G 2 − jωµ H 2 − H1 − (σ − jωε ) E2 − E1 ( ) ( ) ( ) ( ) ( ) ( © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ) * = ANTENAS 9 Si ahora integramos en todo el volumen V y aplicamos el teorema de la divergencia al lado izquierdo de la identidad anterior G G G G * ⎡ µ HG − HG 2 − ε EG − EG 2 ⎤ dV + σ EG − EG 2 dV ˆ E H H n dS j ω − × − ⋅ = 2 1 2 1 2 1 ⎥ ∫ ⎢⎣ 2 1 ∫ 2 1 ⎦ V V ∫(E S ) ( ) Sobre S, ambos conjuntos de campos son iguales por lo que la integral de superficie es nula. G G 2 G G 2 G G 2 jω ∫ ⎡ µ H 2 − H1 − ε E2 − E1 ⎤ dV + σ ∫ E2 − E1 dV = 0 ⎣⎢ ⎦⎥ V V G G G G 2 Dado que E2 − E1 > 0 , necesariamente E1 = E2 para que la integral sea nula, y análogamente con el campo magnético. Teorema de equivalencia El teorema de equivalencia permite sustituir las fuentes originales por otras equivalentes que conducen a la misma solución de las ecuaciones de Maxwell en una región determinada. El teorema de equivalencia se apoya en el teorema de unicidad cuando establece cómo son estas corrientes equivalentes ya que deben elegirse de modo que se obtenga la misma solución que con las fuentes originales. Observando la figura, y suponiendo que las únicas fuentes presentes son las encerradas por la superficie S, los campos eléctricos y magnéticos en el exterior de S se pueden calcular a partir de las G corrientes J , o bien, por el teorema de unicidad, si se conocen las componentes tangenciales a S de los campos eléctrico y magnético, también será posible obtener dicha solución en el exterior de S. Por eso, si eliminamos las fuentes originales y añadimos unas nuevas, éstas deben asegurar que se satisfacen las condiciones de contorno existentes en S. Con este propósito podemos escoger precisamente como corrientes equivalentes las proporcionadas por las condiciones de contorno generalizadas, y que están asociadas a la existencia de una discontinuidad en el campo eléctrico y magnético tangencial, G G G G G G M s = −nˆ × E1 − E2 y J s = nˆ × H1 − H 2 , siendo 1 el medio externo y 2 ( ) ( ) el medio interno y n̂ un vector unitario que apunta a la región donde se desea obtener la solución; en este caso la 1. Dado que sólo estamos interesados en obtener la solución en el medio 1, es posible simplificar la obtención de las corrientes equivalentes obligando a © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS q u e e l 10 G G E, H G J G G Et , H t G J =0 G G E, H = 0 G G E, H campo en la región 2 (región interna) sea nulo. En cuyo caso podemos escribir las corrientes equivalentes más sencillamente como G G J s = nˆ × H t G G M s = − nˆ × Et Alternativamente también es posible utilizar un modelo de equivalencia en el que la región interna se rellena de un conductor perfecto, lo que cortocircuita las corrientes eléctricas equivalentes G G J s = nˆ × H G G M s = − nˆ × E G G M s = −nˆ × E G J =0 G G E, H = 0 G G En el primer caso las corrientes equivalentes J s , M s radian en espacio G libre, en el segundo caso las corrientes M s radian en presencia de un cuerpo metálico de superficie S. el teorema de equivalencia asegura que eligiendo las corrientes como se ha indicado, ambos problemas proporcionan la misma solución y que además ésta es igual a la que proporciona el problema original en la región ¡. © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 11 Aperturas planas El teorema de equivalencia permite determinar las corrientes equivalentes a los campos de la apertura de la figura n̂ G G J s = nˆ × H G G M s = − nˆ × E G G Ea, H a Los vectores de radiación eléctrico y magnético se calculan a partir de las corrientes equivalentes G G G G G N = ∫∫∫ Je jkrˆ⋅r ' ds ' = ∫∫ J s e jkrˆ⋅r ' ds ' v' s' G G G G G L = ∫∫∫ Me jkrˆ⋅r ' ds ' = ∫∫ M s e jkrˆ⋅r ' ds ' v' s' Los campos radiados se calculan a partir de las componentes tangenciales de los vectores de radiación. Los campos radiados de las corrientes eléctricas son G E = − jω Aθθˆ + Aφφˆ ( ) G ω − Aφθˆ + Aθ φˆ H =−j ( η ) Y los campos radiados por las corrientes magnéticas son G H = − jω Fθθˆ + Fφφˆ G E = − jωη Fφθˆ − Fθ φˆ ( ( ) ) La superposición de ambos efectos es e − jkr Eθ = − j (η Nθ + Lφ ) 2λ r e − jkr Eφ = − j (η Nφ + Lθ ) 2λ r Eφ Hθ = − η Hφ = Eθ η © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 12 Campos radiados por una apertura plana (polarización horizontal) ŷ G Ea x̂ En una apertura con campos polarizados horizontalmente G E = Ex xˆ G E H = H y yˆ = x yˆ Z0 Las corrientes equivalentes son G G E J s = nˆ × H = zˆ × yˆ x Z0 G G ˆ x = − Ex yˆ M s = −nˆ × E = − zˆ × xE Los vectores de radiación ⎛ E N x = ∫∫ ⎜ − x Z0 s' ⎝ ⎞ jkx x ' jk y y ' ⎟ e e dx ' dy ' ⎠ Ly = ∫∫ ( − Ex ) e jkx x 'e jk y y ' dx ' dy ' s' Para determinar los campos radiados es necesario realizar un cambio del sistema de coordenadas cartesiano al esférico. G G Nθ = N ⋅θˆ = N ⋅ ( cos θ cos φ xˆ + cosθ sin φ yˆ − sin θ zˆ ) G G Nφ = N ⋅ φˆ = N ⋅ ( − sin φ xˆ + cos φ yˆ ) G Lθ = L ⋅θˆ G L = L ⋅ φˆ φ Las componentes del vector de radiación se obtienen a partir de la proyección en los vectores unitarios en esféricas © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 13 Los campos radiados, en función de los potenciales vectores eléctrico y magnético son Eθ = − j e − jkr (η N x cosθ + Ly ) cos φ 2λ r e − jkr Eφ = j (η N x + Ly cosθ ) sin φ 2λ r Finalmente, la expresión final para los campos radiados por una apertura plana de forma arbitraria, con polarización horizontal es Eθ = j ⎛η ⎞ e − jkr jk y ' cos φ ⎜ cos θ + 1⎟ ∫∫ E ( x ', y ') e jk x x 'e y dx ' dy ' 2λ r ⎝ Z0 ⎠ s' ⎛η ⎞ e − jkr jk y ' sin φ ⎜ + cos θ ⎟ ∫∫ E ( x ', y ' ) e jkx x 'e y dx ' dy ' Eφ = − j 2λ r ⎝ Z0 ⎠ s' Campos radiados por una apertura plana (polarización vertical) En una apertura con campos polarizados verticalmente G E = E y yˆ G E H = H x xˆ = − y xˆ Z0 Se puede realizar el desarrollo equivalente, o de una forma más simple realizar un giro de 90 grados en los ejes coordenados en cartesianas. La solución para los campos radiados es Eθ = j ⎛η ⎞ e − jkr jk y ' sin φ ⎜ cos θ + 1⎟ ∫∫ E ( x ', y ' ) e jkx x 'e y dx ' dy ' 2λ r ⎝ Z0 ⎠ s' Eφ = j ⎛η ⎞ e − jkr jk y ' cos φ ⎜ + cos θ ⎟ ∫∫ E ( x ', y ') e jkx x 'e y dx ' dy ' 2λ r ⎝ Z0 ⎠ s' © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 14 Apertura elemental En una apertura elemental en el espacio libre, con polarización horizontal G E = E0 xˆ G E H = H y yˆ = 0 yˆ η Los campos se pueden calcular teniendo en cuenta que los desfases son despreciables ⎛η ⎞ e − jkr jk y ' cos φ ⎜ cos θ + 1⎟ ∫∫ E ( x ', y ') e jk x x 'e y dx ' dy ' 2λ r ⎝ Z0 ⎠ s' − jkr ⎛η ⎞ e jk y ' sin φ ⎜ + cos θ ⎟ ∫∫ E ( x ', y ' ) e jkx x 'e y dx ' dy ' Eφ = − j 2λ r ⎝ Z0 ⎠ s' Eθ = j Calculando las integrales y sustituyendo la impedancia de la onda por la del espacio libre, queda e − jkr cos φ (1 + cosθ ) E0 ∆s Eθ = j 2λ r e − jkr sin φ (1 + cosθ ) E0 ∆s Eφ = − j 2λ r La densidad de potencia radiada es máxima en la dirección perpendicular a la apertura, con un nulo en la dirección opuesta. El diagrama es tipo cardioide. © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 15 ( E ∆s ) ( E ∆s ) 2 P (θ , φ ) = 0 2 2 (1 + cosθ ) = 0 2 2 2 η 4λ r 2 ηλ r cos 4 θ 2 La potencia total radiada se calcula a partir de la integral de la densidad de potencia en una esfera que encierre a las fuentes ( E ∆s ) 2π π 2 Wt = ∫∫ P (θ , φ )ds ' = 0 2 ∫ ∫ (1 + cosθ ) sin θ dθ dφ η 4λ 2 s' 0 0 ( E0 ∆s ) 4π 2 Wt = ηλ 2 3 La Directividad, calculada a partir de la densidad de potencia y la potencia total radiada es D=3 Aperturas uniformes de forma arbitraria En general los campos radiados por una apertura se pueden expresar como el producto de una onda esférica, el diagrama de la apertura elemental y un término de interferencia que es proporcional a la transformada de Fourier bidimensional de los campos en la apertura. G Eθ , Eφ ∝ ∫∫ E ( x ', y ' ) e jkrˆ⋅r ' dx ' dy ' = ∫∫ E ( x ', y ' ) e jkx x 'e s' jk y y ' dx ' dy ' s' Si el campo en la apertura es constante el diagrama se puede calcular a partir de la integral F ( k x , k y ) = ∫∫ e jk x x ' e jk y y ' dx ' dy ' = xmax ∫ − xmin s' f2 ( x ) e jk x x ' ⎛ f2 ( x ) jk y ' ⎞ ⎜ ∫ e y dy ' ⎟ dx ' ⎜ f ( x) ⎟ ⎝ 1 ⎠ ŷ G Ea f1 ( x ) xmin x̂ xmax © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 16 Transformadas de Fourier de la iluminación uniforme Cuadrado de lado a Hexágono de lado a Cuadrado girado 450 © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 17 Margen visible de las aperturas Se ha visto que los campos radiados son directamente proporcionales a la transformada de Fourier bidimensional. El diagrama de radiación será función de las variables de frecuencia espacial k x = k sin (θ ) cos (φ ) k y = k sin (θ ) sin (φ ) Los valores máximos y mínimos de las variables kx,ky son –k y +k. En general los valores de k estarán en el interior de un círculo de radio k en el plano kx,ky, El círculo corresponde a la intersección de la esfera con el plano kx,ky k x2 = k 2 sin 2 θ cos 2 φ k y2 = k 2 sin 2 θ sin 2 φ k x2 + k y2 = k 2 sin 2 θ ≤ k 2 © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 18 Los cortes del diagrama de radiación corresponden, para aperturas con fase constante a planos φ = cte . Los valores en el plano frecuencial corresponden a la recta k y = k x tan (φ ) La zona que se encuentra fuera del margen visible no contribuye a la radiación, pero supone una energía reactiva almacenada. Se cumple la condición k x2 + k y2 > k 2 La posición del máximo de la transformada de Fourier bidimensional determina la dirección del espacio del diagrama k ym tan (φm ) = m kx 2 ⎛ k ⎞ ⎛ ky ⎞ sin (θ m ) = ⎜ x ⎟ + ⎜ ⎟ ⎝k ⎠ ⎝ k ⎠ 2 © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 19 Apertura rectangular Los campos radiados por una apertura rectangular de dimensiones a,b con campos con polarización horizontal son Eθ = j ⎛η ⎞ e − jkr jk y ' cos φ ⎜ cos θ + 1⎟ ∫∫ E ( x ', y ') e jk x x 'e y dx ' dy ' 2λ r Z ⎝ 0 ⎠ s' Eφ = − j ⎛η ⎞ e − jkr jk y ' sin φ ⎜ + cos θ ⎟ ∫∫ E ( x ', y ' ) e jkx x 'e y dx ' dy ' 2λ r ⎝ Z0 ⎠ s' En el caso de una apertura con distribución de campos separables en el producto de dos funciones las expresiones de los campos se pueden simplificar ∫∫ E ( x ', y ') e jk x x ' e jk y y ' dx ' dy ' s' E ( x ', y ' ) = E0 f ( x ' ) g ( y ' ) ∫∫ E ( x ', y ') e jk x x ' e jk y y ' s' dx ' dy ' = E0 ∫ f ( x ' ) e jkx x ' dx ' ∫ g ( y ')e x' jk y y ' dy ' y' Las dos integrales unidimensionales son transformadas de Fourier de la distribución de campos F (k x , a) = a 2 ∫ f ( x ') e jk x x ' dx ' jk y y ' dy ' a − 2 G ( k y , b) = b 2 ∫ g ( y ') e b − 2 Diagrama de radiación en el plano E El plano E está definido por la dirección de máxima radiación (eje z) y el campo eléctrico en dicha dirección (eje x) Por lo tanto el plano E es el plano XZ, las números de onda son k x = k sin (θ ) cos (φ ) = k sin (θ ) cos ( 0 ) = k sin (θ ) k y = k sin (θ ) sin (φ ) = k sin (θ ) sin ( 0 ) = 0 © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 20 El diagrama de radiación es e − jkr Eθ = j 2λ r ⎛η ⎞ ⎜ cos θ + 1⎟ E0 F ( k x , a ) G ( 0, b ) ⎝ Z0 ⎠ Eφ = 0 Diagrama de radiación en el plano H El plano H está definido por la dirección de máxima radiación (eje z) y el campo magnético en dicha dirección (eje y) Por lo tanto el plano H es el plano YZ, las números de onda son ⎛π ⎞ k x = k sin (θ ) cos (φ ) = k sin (θ ) cos ⎜ ⎟ = 0 ⎝2⎠ ⎛π ⎞ k y = k sin (θ ) sin (φ ) = k sin (θ ) sin ⎜ ⎟ = k sin (θ ) ⎝2⎠ El diagrama de radiación es Eθ = 0 e − jkr Eφ = − j 2λ r ⎛η ⎞ ⎜ + cos θ ⎟ E0 F ( 0, a ) G ( k y , b ) ⎝ Z0 ⎠ Campo radiado en la dirección del máximo La dirección del máximo de radiación es el eje z, para una apertura plana de forma arbitraria es Em = ⎞ 1 ⎛η ⎜ + 1⎟ ∫∫ Ea ds ' 2λ r ⎝ Z 0 ⎠ s ' En el caso particular de una apertura rectangular con distribución de campo separable el campo en la dirección del máximo es Em = ⎞ 1 ⎛η ⎜ + 1⎟ E0 ∫ f ( x ') dx ' ∫ g ( y ' ) dy ' 2λ r ⎝ Z 0 ⎠ x ' y' Em = ⎞ 1 ⎛η ⎜ + 1⎟ E0 F ( 0, a ) G ( 0, b ) 2λ r ⎝ Z 0 ⎠ © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 21 Potencia total radiada La potencia total radiada en una apertura arbitraria es Wt = 1 E η ∫∫ 2 a ds s' En el caso de una apertura separable Wt = E02 η ∫ f ( x ') dx ' ∫ g ( y ') dy ' 2 x' 2 y' Transformadas de aperturas rectangulares Las aperturas rectangulares separables pueden tener distribuciones de campos distintas de la uniforme, por ejemplo los diversos modos una guía de onda. F (k x , a) = a 2 ∫ f ( x ') e jk x x ' dx ' jk y y ' dy ' a − 2 G ( k y , b) = b 2 ∫ g ( y ') e b − 2 Las transformadas de algunas funciones (uniforme, triangular, coseno, coseno cuadrado) se detallan en la siguiente tabla, para las a transformadas según x: u = k x . El cálculo de los anchos de haz y 2 nivel de lóbulo pricipal a secundario se calcula de forma similar al proceso seguido para distribuciones lineales de corrientes. Los valores de u máximo y mínimo para el eje x, son umax=ka/2 , umin=-ka/2. Al igual que en antenas unidimensionales o agrupaciones el ancho de haz disminuye proporcionalmente a las dimensiones de la apertura. © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 22 Distribución Ancho haz –3 dB 50.6 ⎛a⎞ ⎜ ⎟ ⎝λ ⎠ Transformada 1 a sin ( u ) u NLPS (dB) 13.2 2 ⎛ ⎛u⎞⎞ sin a ⎜ ⎜⎝ 2 ⎟⎠ ⎟ ⎜ ⎟ 2⎜ ⎛u⎞ ⎟ ⎜ ⎜2⎟ ⎟ ⎝ ⎝ ⎠ ⎠ π cos ( u ) a 2 ⎛ π ⎞2 2 ⎜ ⎟ −u 2 ⎝ ⎠ ⎛ 2 ⎞ ⎜1 − x ' ⎟ ⎝ a ⎠ ⎛π ⎞ cos ⎜ x ' ⎟ ⎝a ⎠ 26.4 68.8 ⎛a⎞ ⎜ ⎟ ⎝λ ⎠ 83.2 ⎛a⎞ ⎜ ⎟ ⎝λ ⎠ a sin ( u ) ⎛ π 2 ⎞ ⎜ ⎟ 2 u ⎝ π 2 − u2 ⎠ ⎛π ⎞ cos ⎜ x ' ⎟ ⎝λ ⎠ 2 0 73.4 ⎛a⎞ ⎜ ⎟ ⎝λ ⎠ 23.2 31.5 0 10 t1( u) t2( u) 20 t3( u) 30 − 40 40 0 0 2 4 6 u 8 10 10 Gráfica comparativa de las transformadas de las funciones uniforme, coseno y triangular, en escala logarítmica. Las dimensiones de las aperturas están relacionadas directamente con el ancho de haz. En la siguiente gráfica se comparan los diagramas de radiación para una apertura cuadrada uniforme en función de sus dimensiones normalizadas a la longitud de onda. © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 23 También se comparan los diagramas 3D para distintas dimensiones de una apertura rectangular. 1x1 2x2 b=8 a=8 a=4 b=4 3x3 © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 24 Directividad de las aperturas La directividad se puede obtener a partir del campo radiado en la dirección de máxima radiación y de la potencia total radiada, en el caso de aperturas en el espacio libre 2 P 4π r 2 Eθ + Eφ D= m = Wt η Wt 4π r 2 2 2 ⎛ ⎞ ⎜ ∫∫ Ea ( x ', y ') ds ' ⎟ 4π ⎠ D = 2 ⎝ s' 2 λ ∫∫ Ea ( x ', y ') ds ' s' La directividad en caso de aperturas separables es ⎛ a2 ⎞ ⎜ ⎟ ⎜ ∫ f ( x ' ) dx ' ⎟ a ⎟ 4π ⎜ − ⎠ D = 2 ⎝a2 λ ⎛2 ⎞ ⎜ ⎟ 2 ⎜ ∫ f ( x ') dx ' ⎟ ⎜ −a ⎟ ⎝ 2 ⎠ 2 2 ⎛ b2 ⎞ ⎜ ⎟ ⎜ ∫ g ( y ' ) dy ' ⎟ ⎜ −b ⎟ ⎝ 2 ⎠ b ⎛2 ⎞ ⎜ ⎟ 2 ⎜ ∫ g ( y ') dy ' ⎟ ⎜ −b ⎟ ⎝ 2 ⎠ Las integrales se pueden expresar de forma más compacta utilizando los cambios de variable 2 s= x' a ⎛ a2 ⎞ ⎛ 12 ⎞ ⎜ ⎟ ⎜ ⎟ ⎜ ∫ f ( x ' ) dx ' ⎟ ⎜ ∫ f ( s ) ds ⎟ ⎜ −a ⎟ ⎜ 1 ⎟ ⎝ 2 ⎠ = a ⎝ −2 ⎠ 1 a ⎛2 ⎞ ⎛2 ⎞ ⎜ ⎟ ⎜ ⎟ 2 2 ⎜ ∫ f ( x ' ) dx ' ⎟ ⎜ ∫ f ( s ) ds ⎟ ⎜ −a ⎟ ⎜ −1 ⎟ ⎝ 2 ⎠ ⎝ 2 ⎠ y' b ⎛ b2 ⎞ ⎛ 12 ⎞ ⎜ ⎟ ⎜ ⎟ ⎜ ∫ g ( y ' ) dy ' ⎟ ⎜ ∫ g ( t ) dt ⎟ ⎜ −b ⎟ ⎜ 1 ⎟ ⎝ 2 ⎠ = b ⎝ −2 ⎠ b 1 ⎛2 ⎞ ⎛2 ⎞ ⎜ ⎟ ⎜ ⎟ 2 2 ⎜ ∫ g ( y ' ) dy ' ⎟ ⎜ ∫ g ( t ) dt ⎟ ⎜ −b ⎟ ⎜ −1 ⎟ ⎝ 2 ⎠ ⎝ 2 ⎠ 2 t= 2 2 La fórmula final para la directividad es © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 25 D= 4π λ 2 abηilxηily = 4π λ 2 abηil = 4π λ2 Aef Las eficiencias de iluminación se calculan a partir de las distribuciones 2 ⎛ 12 ⎞ ⎜ ⎟ ⎜ ∫ f ( s ) ds ⎟ ⎜ −1 ⎟ ⎠ ηilx = ⎝ 12 ⎛2 ⎞ ⎜ ⎟ 2 ⎜ ∫ f ( s ) ds ⎟ ⎜ −1 ⎟ ⎝ 2 ⎠ 2 ⎛ 12 ⎞ ⎜ ⎟ ⎜ ∫ g ( t ) dt ⎟ ⎜ −1 ⎟ ⎠ b ηily = ⎝ 12 ⎛2 ⎞ ⎜ ⎟ 2 ⎜ ∫ g ( t ) dt ⎟ ⎜ −1 ⎟ ⎝ 2 ⎠ 2 ⎛ 12 ⎞ ⎜ ⎟ 2 ⎜ ∫ f ( s ) ds ⎟ ⎜ −1 ⎟ ⎝ 2 ⎠ ηilx 1 1 1 f ( s ) = (1 − 2 s ) 1/4 1/3 3/4 f ( s ) = (1 − 2 s ) 1/144 1/80 0.55 (2/π)2 1/2 8/π2 ⎛ 12 ⎞ ⎜ ⎟ ⎜ ∫ f ( s ) ds ⎟ ⎜ −1 ⎟ ⎝ 2 ⎠ 1 1 − <s< 2 2 f (s) = 1 2 f ( s ) = cos (π s ) © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 26 Tabla comparativa de diagramas de radiación de aperturas cuadradas en función de la distribución de campos. coseno triangular triangular coseno uniforme uniforme © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia