Transparencias - Universidad de Sevilla

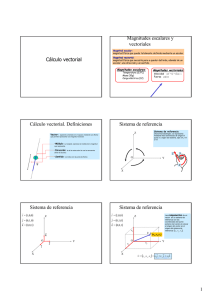
Álgebra vectorial
Dpto.
p de Física Aplicada
p
III
Universidad de Sevilla
Las magnitudes físicas se dividen en
escalares, vectores y tensores
z
Las diferentes magnitudes pueden ser:
z
Escalares
z
z
Vectoriales
z
z
z
z
Se caracterizan sólo por un número (con signo)
Módulo (cantidad escalar positiva)
Dirección
Sentido
Tensores de orden superior
z
Representables por matrices
2
Todas las leyes físicas poseen
homogeneidad en sus expresiones
z
En todas las ecuaciones debe haber homogeneidad:
z
z
z
z
Los dos miembros son del mismo tipo
Todos los sumandos son del mismo tipo
Un escalar nunca puede ser igual a un vector
Un escalar nunca puede sumarse a un vector
G
G
G G G
A= B+C
A= B+C
G G
A= B+C
A= B+C
Correcto
z
Incorrecto
G
Para distinguirlos, es importante incluir las flechas ( A ). En
l libros,
los
lb
los
l escalares
l
van en cursiva (A)
( ) y los
l vectores
3
en negrita (A)
Operaciones internas con cantidades
escalares: suma y producto
z
Pueden sumarse
z
z
z
z
El resultado es un escalar
Requiere que los sumandos tengan las mismas unidades
El resultado tiene las mismas unidades que los sumandos
Ejemplo: masa de un sistema
n
M = m1 + m2 + m3 + " = ∑ mi
i =1
z
V
Pueden multiplicarse
z
z
z
M = ∫ dm
El resultado es un escalar
Sus unidades son el producto de las de los factores
La suma y el producto poseen las propiedades asociativa y
conmutativa.
4
Vector: ente que posee una dirección y
un sentido
z
z
Es un ente que además de su valor escalar (módulo)
posee dirección y sentido. Ej.: Fuerza
Un vector puede darse indicando
z
z
Módulo y dos ángulos con los ejes (un ángulo en 2D)
C
Componentes
respecto a una base
b
(siempre
( i
h que indicar
hay
d
la
l
base)
G G G
G
F = 3ι + 2 j + k
z
( N)
Los vectores pueden ser libres o ligados
z
z
Los ligados requieren dar el origen (ej. campo eléctrico)
Los libres pueden trasladarse de un punto a otro (ej. resultante de
un conjunto de fuerzas)
5
Los vectores pueden sumarse,
empleando la regla del paralelogramo
z
z
z
z
Los vectores pueden sumarse, resultando un vector. Ej.
Resultante de dos fuerzas
JG
B
JG
JG
JG JG JG
JG JG
JG
A
A
A A+ B
A+ B
B
JG
B
P d emplearse
Puede
l
la
l regla
l del
d l paralelogramo
l l
o poner uno
a continuación del otro.
Para que se puedan sumar deben ser libres o tener el
mismo origen
La suma verifica la propiedad asociativa y la conmutativa
6
Los vectores pueden multiplicarse por
cantidades escalares
z
z
Un vector puede multiplicarse por un número. Ej. fuerza
eléctrica sobre una carga puntual
G
G
F = qE
JG
G
3A
A
×3=
El resultado es otro vector
z
z
z
Misma dirección
Mismo sentido, si q>0. Opuesto, si q<0
Módulo igual a
G
G
F =q E
7
Combinaciones lineales: unen suma y
productos por escalares
z
Reuniendo la suma de vectores y la multiplicación por
escalares se obtienen las combinaciones lineales. Ej.
Cantidad
d d de
d movimiento de
dn un sistema
G
G
G
G
G
G
G
p = m1v1 + m2 v2 + m3v3 = ∑ mi vi
p = ∫ v dm
i =1
G
A
z
G
B
G
2A
M
G
G
2 A + 3B
G
3B
Al expresar las componentes de un vector en función de
una base se hace una combinación lineal
G
G
G G
A = 2i + 3 j + k
8
Producto escalar: Operación entre
vectores que produce un número
Dos vectores pueden multiplicarse, resultando un escalar
(ej. Trabajo realizado
fuerza constante)
G G porG una
G
F ·Δr = F Δr cos α
G
G
F
donde α es el ángulo que forman
y Δr
z El producto escalar se anula si los vectores son
ortogonales.
z Si tenemos las componentes en una base ortonormal
G
G
G
G
⎫⎪ G G
F = Fx i + Fy j + Fz k
G ⎬ F ·Δr = Fx Δx + Fy Δy + Fz Δz
G
G
G
Δr = ( Δx ) i + ( Δy ) j + ( Δz ) k ⎪⎭
z
9
Producto escalar: propiedades
z
z
El producto escalar es conmutativo
El producto escalar NO es asociativo
z
z
No se puede definir el producto escalar de tres vectores
Se verifica la desigualdad
G G G G G G
A·B C ≠ A B·C
( )
z
(
)
El producto escalar es lineal (se pueden “quitar
quitar
paréntesis”)
G G
G G G G G
F1 + F2 ·Δr = F1 ·Δr + F2 ·Δr
(
)
10
Producto vectorial: operación entre
vectores que produce otro vector
z
Dos vectores se pueden multiplicar dando como resultado
un vector. Ej. momento de una fuerza
G G G
M = r ×F
z
Módulo
G
G G G G
M = r × F = r F sen α
(Área del paralelogramo
definido por los vectores)
z
G
G
Dirección: la perpendicular a r y a F
z
Sentido: el dado por la regla de la mano derecha
G
M
Gα
r
G
F
G
M
11
Producto vectorial: expresión a partir de
las componentes
z
z
El producto vectorial se anula si los vectores son paralelos
Si se conocen las componentes cartesianas, puede
calcularse mediante un determinante
G
G
G
G
i
G
r = xi + y j + zk ⎫⎪ G G
G⎬ r × F = x
G
G
G
F = Fx i + Fy j + Fz k ⎪⎭
Fx
G
j
y
Fy
G
k
z =
Fz
z G x z G x y G
i−
j+
k=
Fz
Fx Fy
Fx Fz
G
G
G
= ( yFz − zFy ) i + ( zFx − xFz ) j + ( xFy − yFx ) k
y
=
Fy
12
Producto vectorial: propiedades
z
z
El producto vectorial es anticonmutativo
G G
G G
r × F = −F × r
El producto vectorial NO es asociativo
G G G
G G G
A× B × C ≠ A× B × C
G G G
El doble p
producto vectorial
AG× B × C es una
G
combinación lineal de B y C
G G G
G G G
G G G
A × B × C = A·C B − A·B C
G G G
G G G
G G G
G G G
A × B × C = −C × A × B = A·C B − C ·B A
(
z
) (
)
(
(
)
(
) (
(
)
) ( )
) ( ) (
)
13
Producto mixto: unión de un producto
escalar y uno vectoriales
z
z
Dados tres vectores puede calcularse su producto mixto
G G G
G G
G
( A, B, C ) = A·( B × C )
Representa el volumen (con signo) del paralelepípedo
definido por los tres vectores
z Pueden intercambiarse los signos
de producto
G G G
G G G
(
) (
)
A· B × C = A × B ·C
z
B C
A
Puede hallarse como un
d t
determinante
i
t
Ax Ay
Az
G G G
A· B × C = Bx
By
Bz
Cx
Cy
Cz
(
)
14
Componentes de un vector
z
z
Cada vector puede escribirse como combinación lineal de
una base
G
G
G
G
r = x ι + y j + zk
Al cambiar de base cambian las componentes, pero NO
cambia el vector
G
G
G
G
r = x′ι ′ + y′ j ′ + z ′k ′
Y
Y′
z Por eso no se deben indicar
′
y
G G
X′
los vectores como (x,y,z)
j r
G
G
ι′ y
j′
G
15
X
ι
Observaciones finales
z
Los vectores y los escalares son entes diferentes que no
deben igualarse ni sumarse
z
z
z
Al hacer
h
un producto
d t debe
d b observarse
b
qué
é factores
f t
y de
d
que tipo de producto se trata
z
z
z
z
z
Suma de escalares: escalar
Suma de vectores: vector
Producto de escalares: escalar
Escalar por un vector: vector
Producto escalar de vectores: escalar
Producto vectorial de vectores: vector
Los vectores son independientes de la base
16