Derivadas parciales y direccionales

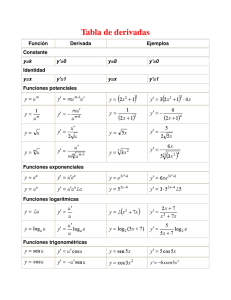
Derivadas parciales
Derivadas direccionales
Derivadas parciales de orden superior
Derivadas parciales y direccionales
Derivadas parciales
Derivadas direccionales
1
Derivadas parciales
2
Derivadas direccionales
3
Derivadas parciales de orden superior
Derivadas parciales de orden superior
Derivadas parciales
Derivadas direccionales
Derivadas parciales de orden superior
Derivadas parciales (de campos escalares de dos
variables)
Sea A = [a1 , b1 ] × [a2 , b2 ] un rectángulo de R2 , es decir,
n
o
[a1 , b1 ] × [a2 , b2 ] = (x, y ) ∈ R2 : x ∈ [a1 , b1 ], y ∈ [a2 , b2 ]
y sea f una función
f : A ⊆ R2 −→ R
Sea (x0 , y0 ) un punto perteneciente a (a1 , b1 ) × (a2 , b2 ) (es decir, al interior
de A). Fijando cada una de las variables se obtienen dos funciones de 1
variable:
Fijado y0 ∈ [a2 , b2 ], podemos definir la función
fy0 : [a1 , b1 ] −→ R,
fy0 (x) = f (x, y0 ).
Fijado x0 ∈ [a1 , b1 ], podemos definir la función
fx0 : [a2 , b2 ] −→ R,
fx0 (y) = f (x0 , y).
Derivadas parciales
Derivadas direccionales
Derivadas parciales de orden superior
Derivadas parciales (de campos escalares de dos
variables)
Sea A = [a1 , b1 ] × [a2 , b2 ] un rectángulo de R2 , es decir,
n
o
[a1 , b1 ] × [a2 , b2 ] = (x, y ) ∈ R2 : x ∈ [a1 , b1 ], y ∈ [a2 , b2 ]
y sea f una función
f : A ⊆ R2 −→ R
Sea (x0 , y0 ) un punto perteneciente a (a1 , b1 ) × (a2 , b2 ) (es decir, al interior
de A). Fijando cada una de las variables se obtienen dos funciones de 1
variable:
Fijado y0 ∈ [a2 , b2 ], podemos definir la función
fy0 : [a1 , b1 ] −→ R,
fy0 (x) = f (x, y0 ).
Fijado x0 ∈ [a1 , b1 ], podemos definir la función
fx0 : [a2 , b2 ] −→ R,
fx0 (y) = f (x0 , y).
Derivadas parciales
Derivadas direccionales
Derivadas parciales de orden superior
Derivadas parciales (de campos escalares de dos
variables)
Sea A = [a1 , b1 ] × [a2 , b2 ] un rectángulo de R2 , es decir,
n
o
[a1 , b1 ] × [a2 , b2 ] = (x, y ) ∈ R2 : x ∈ [a1 , b1 ], y ∈ [a2 , b2 ]
y sea f una función
f : A ⊆ R2 −→ R
Sea (x0 , y0 ) un punto perteneciente a (a1 , b1 ) × (a2 , b2 ) (es decir, al interior
de A). Fijando cada una de las variables se obtienen dos funciones de 1
variable:
Fijado y0 ∈ [a2 , b2 ], podemos definir la función
fy0 : [a1 , b1 ] −→ R,
fy0 (x) = f (x, y0 ).
Fijado x0 ∈ [a1 , b1 ], podemos definir la función
fx0 : [a2 , b2 ] −→ R,
fx0 (y) = f (x0 , y).
Derivadas parciales
Derivadas direccionales
Derivadas parciales de orden superior
Ejemplo: f (x, y ) = 5 − x 2 − 3y 2 , P = (−2, 1/3, 2/3)
Derivadas parciales
Derivadas direccionales
Derivadas parciales de orden superior
Ejemplo: f (x, y ) = 5 − x 2 − 3y 2 , P = (−2, 1/3, 2/3)
f1/3 (x) = 5 − x 2 − 3(1/3)2
Derivadas parciales
Derivadas direccionales
Derivadas parciales de orden superior
Ejemplo: f (x, y ) = 5 − x 2 − 3y 2 , P = (−2, 1/3, 2/3)
f−2 (y) = 5 − (−2)2 − 3y 2
Derivadas parciales
Derivadas direccionales
Derivadas parciales de orden superior
Ejemplo: f (x, y ) = 5 − x 2 − 3y 2 , P = (−2, 1/3, 2/3)
Derivadas parciales
Derivadas direccionales
Derivadas parciales de orden superior
Derivada parcial respecto de x
fy0 : [a1 , b1 ] −→ R,
fy0 (x) = f (x, y0 )
es una función de una variable (la x). Si fy0 es diferenciable en
el punto x0 ∈ (a1 , b1 ), es decir, si existe el
fy0 (x0 + h) − fy0 (x0 )
f (x0 + h, y0 ) − f (x0 , y0 )
= lı́m
h
h
h→0
h→0
lı́m
a ese lı́mite lo llamamos Derivada Parcial Primera de primer
orden de f en (x0 , y0 ) o Derivada Parcial respecto de x de f en
(x0 , y0 ), y se representa por D1 f (x0 , y0 ) o bien en notación
∂f
clásica por ∂x
(x0 , y0 ).
Derivadas parciales
Derivadas direccionales
Derivadas parciales de orden superior
Derivada parcial respecto de x
fx0 : [a2 , b2 ] −→ R,
fx0 (y) = f (x0 , y),
que es una función real de una variable real (la y ). Si fx0 es
diferenciable en el punto y0 ∈ (a2 , b2 ), es decir, si existe el
fx0 (y0 + h) − fx0 (y0 )
f (x0 , y0 + h) − f (x0 , y0 )
= lı́m
h
h
h→0
h→0
lı́m
a ese lı́mite lo llamamos Derivada Parcial Segunda de primer
orden de f en (x0 , y0 ) o Derivada Parcial respecto de y de f en
(x0 , y0 ) , y se representa por D2 f (x0 , y0 ) o bien, en notación
∂f
clásica, por ∂y
(x0 , y0 ).
Derivadas parciales
Derivadas direccionales
Derivadas parciales de orden superior
Ejemplo: f (x, y ) = 5 − x 2 − 3y 2 , P = (−2, 1/3, 2/3)
∂f
(x, y ) = −2x
∂x
∂f
(−2, 1/3) = −2(−2) = 4
∂x
Derivadas parciales
Derivadas direccionales
Derivadas parciales de orden superior
Ejemplo: f (x, y ) = 5 − x 2 − 3y 2 , P = (−2, 1/3, 2/3)
∂f
(x, y ) = −6y
∂y
∂f
(−2, 1/3) = −6(1/3) = −2
∂y
Derivadas parciales
Derivadas direccionales
Derivadas parciales de orden superior
Ejemplo
Si f (x) = 2x sen(x 2 + y 2 ), entonces sus derivadas parciales en
un punto (x, y ) ∈ R2 son:
∂f
(x, y ) = 2 sen(x 2 + y 2 ) + 2x cos(x 2 + y 2 )2x
∂x
∂f
(x, y) = 2x cos(x 2 + y 2 )2y
∂y
Todo esto se generaliza a funciones de n variables . . .
Derivadas parciales
Derivadas direccionales
Derivadas parciales de orden superior
Ejemplo
Si f (x) = 2x sen(x 2 + y 2 ), entonces sus derivadas parciales en
un punto (x, y ) ∈ R2 son:
∂f
(x, y ) = 2 sen(x 2 + y 2 ) + 2x cos(x 2 + y 2 )2x
∂x
∂f
(x, y) = 2x cos(x 2 + y 2 )2y
∂y
Todo esto se generaliza a funciones de n variables . . .
Derivadas parciales
Derivadas direccionales
Derivadas parciales de orden superior
Generalización
En general, para funciones con n variables, f (x1 , x2 , . . . , xn ), se
define su derivada parcial k -ésima en el punto (x1 , x2 , . . . , xn ),
que denotamos por Dk f (x1 , x2 , . . . , xn ) o bien por
∂f
∂xk (x1 , x2 , . . . , xn ) al lı́mite
f (x1 , . . . , xk + h, . . . , xn ) − f (x1 , x2 , . . . , xn )
h
h→0
lı́m
Derivadas parciales
Derivadas direccionales
1
Derivadas parciales
2
Derivadas direccionales
3
Derivadas parciales de orden superior
Derivadas parciales de orden superior
Derivadas parciales
Derivadas direccionales
Derivadas parciales de orden superior
Derivada direccional
La pendiente de la recta tangente (si existe) a la superficie
definida por f en la dirección dada por v es
Dv f (x0 , y0 ) = lı́m
h→0
f ((x0 , y0 ) + h(v1 , v2 )) − f (x0 , y0 )
h
o bien
f (x0 + hv1 , y0 + hv2 ) − f (x0 , y0 )
h
h→0
Dv f (x0 , y0 ) = lı́m
y se llama derivada direccional de f en el punto (x0 , y0 ) en la
dirección dada por v .
Observación:
∂f
(x0 , y0 )
∂x
∂f
D(0,1) f (x0 , y0 ) =
(x0 , y0 )
∂y
D(1,0) f (x0 , y0 ) =
Derivadas parciales
Derivadas direccionales
Derivadas parciales de orden superior
Derivada direccional
La pendiente de la recta tangente (si existe) a la superficie
definida por f en la dirección dada por v es
Dv f (x0 , y0 ) = lı́m
h→0
f ((x0 , y0 ) + h(v1 , v2 )) − f (x0 , y0 )
h
o bien
f (x0 + hv1 , y0 + hv2 ) − f (x0 , y0 )
h
h→0
Dv f (x0 , y0 ) = lı́m
y se llama derivada direccional de f en el punto (x0 , y0 ) en la
dirección dada por v .
Observación:
∂f
(x0 , y0 )
∂x
∂f
D(0,1) f (x0 , y0 ) =
(x0 , y0 )
∂y
D(1,0) f (x0 , y0 ) =
Derivadas parciales
Derivadas direccionales
Derivadas parciales de orden superior
Casos
Dada una función f : A ⊆ R2 −→ R y un punto (x0 , y0 ) interior
de su dominio A puede ocurrir,
(a) que no existan las rectas tangentes en
direcciones (ejemplo: cono) o
(b) que sı́ existan las rectas tangentes en
direcciones.
TODAS
TODAS
las
En este segundo caso, puede ocurrir,
(b.1) que no estén todas las rectas tangentes en un
mismo plano (superficies regladas), o
(b.2) que sı́ estén todas las rectas tangentes en un
mismo plano.
las
Derivadas parciales
Caso (a)
Derivadas direccionales
Derivadas parciales de orden superior
Derivadas parciales
Derivadas direccionales
Caso (b.1): esculturas de Alfaro
Derivadas parciales de orden superior
Derivadas parciales
Caso (b.2)
Derivadas direccionales
Derivadas parciales de orden superior
Derivadas parciales
Derivadas direccionales
Derivadas parciales de orden superior
Plano tangente
En el último caso (existen las rectas tangentes en TODAS las
direcciones y están todas en un mismo plano), a éste plano se
le llama plano tangente a f en el punto (x0 , y0 ), y puede verse
que su ecuación es
z = f (x0 , y0 ) + D1 f (x0 , y0 )(x − x0 ) + D2 f (x0 , y0 )(y − y0 )
Derivadas parciales
Derivadas direccionales
Derivadas parciales de orden superior
Derivadas direccionales y continuidad
La existencia de las derivadas parciales en un punto o, más
aún, de todas las derivadas direccionales, no implica la
continuidad de la función en ese punto.
2
Ejemplo: f (x, y) = x 2xy+y 4 si (x, y ) 6= (0, 0) y f (0, 0) = 0. Existen
todas las derivadas direccionales en (0, 0) pero no es continua.
Derivadas parciales
Derivadas direccionales
1
Derivadas parciales
2
Derivadas direccionales
3
Derivadas parciales de orden superior
Derivadas parciales de orden superior
Derivadas parciales
Derivadas direccionales
Derivadas parciales de orden superior
Derivadas parciales de orden superior
Si f (x) = 2x sen(x 2 + y 2 ), entonces su derivada parcial
primera en cada (x, y ) es
∂f
(x, y ) = 2 sen(x 2 + y 2 ) + 2x cos(x 2 + y 2 )2x
∂x
que es también una función de dos variables y tiene derivadas
parciales que son derivadas parciales de f de segundo orden:
∂2f
(x, y ) = 12x cos(x 2 + y 2 ) − 8x 3 sen(x 2 + y 2 )
∂x 2
∂2f
(x, y ) = 4y cos(x 2 + y 2 ) − 8x 2 y sen(x 2 + y 2 )
∂y∂x
Derivadas parciales
Derivadas direccionales
Derivadas parciales de orden superior
Derivadas parciales de orden superior
Del mismo modo, como
∂f
(x, y ) = 4xy cos(x 2 + y 2 )2x
∂y
sus derivadas parciales son
∂2f
(x, y ) = 4y cos(x 2 + y 2 ) − 8x 2 y sen(x 2 + y 2 )
∂x∂y
∂2f
(x, y) = 4x cos(x 2 + y 2 ) − 8xy 2 sen(x 2 + y 2 )
∂y 2
Derivadas parciales
Derivadas direccionales
Derivadas parciales de orden superior
Derivadas parciales de orden superior
En general, se definen las 4 derivadas parciales de f de
segundo orden como:
∂
∂2f
(x, y) =
∂x 2
∂x
∂2f
∂
(x, y) =
∂y 2
∂y
∂
∂2f
(x, y ) =
∂y ∂x
∂y
∂2f
∂
(x, y ) =
∂x∂y
∂x
∂f
∂x
(x, y )
∂f
(x, y )
∂y
∂f
(x, y )
∂x
∂f
(x, y )
∂y
o bien
D11 f (x, y ) = D1 (D1 f ) (x, y )
o bien
D22 f (x, y ) = D2 (D2 f ) (x, y )
o bien
D12 f (x, y ) = D2 (D1 f ) (x, y )
o bien
D21 f (x, y ) = D1 (D2 f ) (x, y )
Derivadas parciales
Derivadas direccionales
Derivadas parciales de orden superior
Teorema de Schwarz
Teorema
∂2f
∂f
es continua en un punto (x, y) y si
existe en un
∂y ∂x
∂y
∂2f
∂2f
entorno de (x, y ), entonces existe
(x, y) =
(x, y)
∂x∂y
∂y ∂x
Si
Derivadas parciales
Derivadas direccionales
Derivadas parciales de orden superior
Todo lo anterior puede generalizarse a funciones de n
variables. Ası́, por ejemplo, una función f (x1 , x2 , . . . , xn ) tiene n
derivadas parciales en cada punto (x1 , x2 , . . . , xn ) ∈ Rn , que
denotamos por
∂f
(x1 , x2 , . . . , xn ), k = 1, 2, . . . , n
Dk f (x1 , x2 , . . . , xn ) o por
∂xk
y tiene n2 derivadas parciales de segundo orden, que
denotamos por
Dij f (x1 , x2 , . . . , xn ) o por
∂2f
(x1 , x2 , . . . , xn ), i, j = 1, 2, . . . , n
∂xj ∂xi
El Teorema de Schwartz nos asegura que, bajo ciertas
condiciones de continuidad, las derivadas cruzadas coinciden:
Dij f (x1 , x2 , . . . , xn ) = Dji f (x1 , x2 , . . . , xn )
∂2f
∂xj ∂xi
(x1 , x2 , . . . , xn ) =
∂2f
(x1 , x2 , . . . , xn )
∂xi ∂xj