La búsqueda de los grandes equilibrios entre

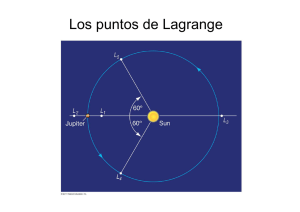
La búsqueda de los grandes equilibrios
entre fuerzas está escrita: los puntos de
Lagrange.
Alejandro Vidal Crespo
Director de Estrategia de Mercados
INFORME MENSUAL DE ESTRATEGIA
Febrero 2016
Informe mensual de estrategia. Febrero 2016
La búsqueda de los grandes equilibrios entre fuerzas está
escrita: los puntos de Lagrange.
Vivimos tiempos convulsos, con grandes fuerzas buscando equilibrios perdidos, distancias y
posiciones dentro de un sistema que debe ser estable. Algo parecido ocurre en los sistemas
orbitales, donde cuerpos más pequeños pueden coexistir en situación estable. Nada nuevo,
conocemos esos equilibrios desde el siglo XVIII, cuando el matemático francés Jean Louis
Lagrange describió esos puntos óptimos para situar satélites artificiales doscientos años
antes de su existencia.
A finales del siglo XVIII, la comunidad científica todavía se encontraba digiriendo las implicaciones
para la observación del Universo que supuso la formulación de la mecánica de Newton y sus leyes
de gravitación. Si bien la teoría de Newton describía perfectamente el movimiento de un sistema
formado por dos cuerpos, se complicaba enormemente cuando eran tres o más los objetos a dinamizar
formando un sistema estable a partir de sus masas, velocidades y posiciones iniciales, algo conocido
como Problema de los Tres Cuerpos.
Y precisamente en esta labor se encontraba Jean Louis Lagrange, teorizando acerca de cómo conseguir
estabilizar sistemas donde más de dos cuerpos se movieran en un sistema estable sin degenerar en
el caos. Parte de este caos lo genera la tercera ley formulada por otro clásico de la ciencia, Johannes
Kepler: es imposible que dos planetas giren sincrónicamente alrededor de una misma estrella a
distancias diferentes, si solamente tenemos en cuenta la interacción entre cada planeta y la estrella.
Más distancia es menos velocidad, si no nos salen las cuentas.
Lagrange avanzó considerablemente en el campo de la resolución del problema (no lo resolvió, pasó
el testigo a otro ilustre, Henri Poincaré) mediante el desarrollo de la mecánica lagrangiana, cuya
explicación física y múltiples aplicaciones no procede desarrollar en este artículo, sino más bien una
de sus consecuencias más naturales e inmediatas: podemos desdecir a Kepler, y situar un objeto
que se mueva sincrónicamente con La Tierra en una órbita diferente, buscando los puntos donde la
atracción gravitatoria entre nuestro planeta y el Sol se compensen. De hecho, existen cinco puntos
teóricos donde esto ocurre. Vean el siguiente diagrama:
Todos ellos son teóricamente posibles (L3 es puramente
teórico, de hecho), pero nos centraremos en L1, L4 y L5.
El punto 1 (L1) es quizás el más intuitivo. En algún punto entre
las dos masas, la fuerza de atracción de Tierra y Sol se igualan,
y un objeto se estabiliza entre ambos. Este punto de hecho
existe y se utiliza para situar los satélites de observación solar
como SOHO. Es perfecto para estos usos, porque se encuentra
más allá de la órbita de la Luna, por lo que el satélite nunca se
ve eclipsado y puede mantener una visión constante del Sol y
controlar su actividad desde un sitio privilegiado.
Sin embargo, aun siendo más intuitivo, L1 no es el punto más estable. Los más estables son L4 y L5,
que se encuentran en el vértice del triángulo equilátero que forma el sistema. Y de hecho, en esos dos
puntos se forman curiosos fenómenos de forma natural.
Por ejemplo, en los puntos L4 y L5 del sistema Sol-Júpiter se encuentran dos grupos de asteroides
conocidos desde hace mucho tiempo. Los L4, que preceden a Júpiter en su órbita, se conocen como
Informe mensual de estrategia. Febrero 2016
Los Griegos, mientras que los del punto L5, que le suceden, se conocen como Los Troyanos.
Acercándonos un poco más, la teoría del Gran Impacto se basa en que un cuerpo planetario se formó en
los puntos L4 o L5 del sistema Tierra-Sol, y que al ganar masa, se desestabilizó y terminó impactando
contra nuestro planeta, formando la Luna.
Imaginemos ahora otro tipo de sistema inestabilizado, como por ejemplo un Parlamento, en busca
de nuevos equilibrios que eviten una situación tendente al desorden. De nuevo, como le ocurrió al
maestro Lagrange, deberíamos partir de conocer las masas, velocidades y posiciones actuales. En base
a eso, el cuerpo menor podría optar por dos opciones estables:
Situarse entre las dos fuerzas mayores y tratar de compensar los fuertes efectos de marea que tendría
en uno y otro sentido, porque finalmente ese equilibrio se basa en que dos tiran de ti con una fuerza
titánica (tanto mayor cuanto menor sea la distancia), pero en sentido opuesto. Eso presupone que el
cuerpo en cuestión es lo bastante resistente como para no partirse en dos (por eso no existen muchos
ejemplos de orbitas en puntos L1 en la naturaleza) y además, que mide muy bien la distancia real que
existe entre los dos cuerpos entre los que quiere situarse. La fuerza que sufrirá es función inversa de
la distancia al cuadrado: cada aproximación entre los grandes será elevada al cuadrado en términos de
fuerza a soportar por el interpuesto.
Otra opción es buscar una triangulación que permita situarte en equilibrio con las dos masas principales,
pero sin alinearse entre ellas. Esto ofrece dos sub alternativas, que es tender a preceder, como los
Griegos de Júpiter, o tender a suceder, como hacen los Troyanos. Iniciativa o control, en términos más
sociales. En cualquier caso, esta posición más alejada de las fuerzas de marea, es la que ha usado la
naturaleza para estabilizarse.
Y en esto, el cosmos tiene bastante experiencia.