Teoría de Control Automático

81
Sistemas físicos
3.4. :BtplÍsito de sección cog~~Il~;'C'U" f:,gultlcióndel
:catl~#l de salida
:.,";"
,:~."-,::':(::
,O",}'
",- '.:<-.,
.::;::\::::,;:/,;,;.,}:;.:, ..... ' "."
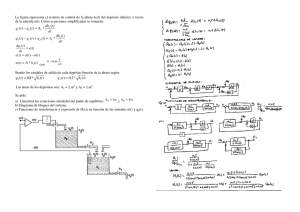
La figura representa el sistema de control de nivel
de un depósito de sección constante A y altura .
máxima 1 metro, alimentado por un caudal qe' La
salida de líquido del depósito se regula por medio
de una válvula, de modo que el caudal de salida qf
depende del producto de la velocidad de escape
libre del líquido v por el factor de apertura de la ,.. ,,' ,
válvula w. Este factor de apertura responde a la
señal eléctrica proporcionada por un amplificador
diferencial que amplifica, con una ganancia K, la
diferencia entre la medida eléctrica n proporcional
(con constante N) al nivel de líquido en el depósito .
h Ya la señal de mando r.
~
n
r
Figura 3.4-1: Depósito.
Datos:
N
=
g
=
V
m
10-
K
10 m
A = 0.5m 2
=
m2
0.005­
V
S2
Se pide:
l°)
2°)
3°)
4°)
Obtener las ecuaciones físicas del sistema y linealizarlas en torno al punto de equilibrio
definido por qeO = 0.02 m 3/s y r 0= 7 V. (Si se procede por tanteo se admitirá un error en h de
±0.2 m).
Diagrama de bloques del sistema.
Función de transferencia entre la altura h y el caudal de entrada qe'
Partiendo del punto de equilibrio y utilizando el modelo linealizado, calcular el máximo
caudal qe que puede aplicarse para que el depósito no rebose. Repetir el cálculo para que
no rebose en un tiempo de 2 segundos.
82
Control de sistemas continuos. Problemas resueltos.
Solución al problema 3.4
lO)
Las ecuaciones físicas del sistema son:
q..
w
= N·h
= w·v
= K(n - r)
v
= V2 g h
n
qe -q.< = A·Ji
Cinco ecuaciones que resultan suficientes, al ser siete las variables del sistema (n, h, q,,, w, v,
qe' r) y dos las variables de entrada (q., r).
Sustituyendo los valores conocidos, las ecuaciones quedan:
n(t) = 10· h(t)
q .< (t)
= w(t)· v(t)
= O.OOS(n(t)-r(t))
v(t) = V20h(t)
w(t)
Ji(t)
=
2 (q/t) -q..(t))
En el equilibrio, dado que el volumen del depósito es constante, la altura h no sufrirá
variación, por lo que el caudal de entrada y el de salida serán iguales:
r =7
no = lOho
{}
q..o
= wo.vo
Wo
= O.ooS (no -7)
Vo
= J20.h o
= qsO = 0.02
qeO
Con lo que:
-V
0.02 = wo' Vo = O.OOS (lOho -7) 20ho =>
=>
4.10-4 = 2S'1O-6(looh~ +49 -140ho)(20ho)
=>
3
2
0.8 = 100ho -140ho +49ho
=>
Sistemas físicos
83
Ecuación de tercer grado que puede resolverse por iteración:
1
3
2
hO == --[100hO -140ho -0.8]
49
Se puede comenzar suponiendo ha=1
(h o
==
1)
ho
__
1 [100-140-0.8]
49
(h o
==
0.833)
ho
__
1 [100.0.833 3 -140.0.833 2 -0.8]
49
==
0.819
(h o
==
0.819)
ho
__
1 [100.0.821 3 -140.0.821 2 -0.8]
49
==
0.812
(h o
==
0.812)
ho
__
1 [100.0.814 3 -140.0.814 2 -0.8]
49
==
0.807
==
0.833
Este resultado puede tomarse como suficientemente aproximado. Por otra parte, la solución
numérica proporciona que las tres raíces están en:
- 0.034
(1) ho == 0.01716 =
no == 0.1716 =
(2)
ho
==
0.582
=
no
==
5.82
(3)
ho
==
0.8
=
no
==
8
- 0.006
=
W
o
==
0.005
Las dos primeras soluciones resultan absurdas al ser w negativo (correspondería a un qs
entrante), por lo que puede tomarse como solución ho == 0.8.
Por tanto, se toma como punto de equilibrio:
3
ro == 7V
qeo == qso == 0.02m 1s
no == 8 V
W
vo
o == 0.005 m 2
ho
==
==
0.8m
4mls
Linealizando en torno a este punto se obtiene:
n(t) == lOh(t)
q/t) == 0.005v(t) +4w(t)
w(t)== 0.005 (n(t) - r(t))
v(t) == 2.5 h(t)
lÍ(t)
==
2 (qeCt) -q/!))
Donde todas las variables representan incrementos respectos al punto de equilibrio l .
'En adelante, y salvo indicación expresa, las variables utilizadas en las ecuaciones linealizadas representan
incrementos respecto del punto de equilibrio, prescindiéndose del símbolo "/1" para indicar esta circunstancia.
84
2°)
Control de sistemas continuos. Problemas resueltos.
Transformando por Laplace las ecuaciones del sistema se obtiene:
N(s) = lOR(s)
Q/s) = 0.005 Ves) +4 W(s)
W(s) = 0.005 (N(s)-R(s»
Ves) = 2.5R(s)
sRes) = 2(Qe(s) - QS(s»
Con lo que el diagrama de bloques es el representado en la Figura 3.4-2:
-0.005
w
2
s
4
N
H
v
0.005
2.5
10
Figura 3.4-2: Diagrama de bloques.
Como se observa en el diagrama de bloques, este sistema de control posee dos entradas Qis)
y R(s) correspondientes a sus dos posibles objetivos: a) mantener constante el nivel h a pesar
de posibles variaciones incontroladas del caudal de entrada qe' y b) seguir las consignas de
mando r ajustando el nivel real h lo mejor posible a la referencia. Pueden combinarse
simultáneamente ambos modos de funcionamiento (normalmente se fijará r y su valor sólo
será modificado en raras ocasiones).
Sistemas físicos
3°)
85
Suponiendo R(s)=O se obtiene el siguiente diagrama de bloques simplificado:
H
2
s
1
tJ
12.5.0.005
I
1---110.0.005.4
H
2
s
-1
-_o
0.2125
~I
~
Figura 3.4-3: Diagrama de bloques simplificado.
2
s
R(s)
2
s +0.425
2
s
Q/s)
1 +-·0.2125
que corresponde a un sistema de primer orden.
4°)
Para que el depósito rebose debe cumplirse que:
h( 00)
=
ho + flh( 00)
=
1m
=
flh( 00)
=
0.2 m
Por ser el sistema estable, podrá aplicarse el teorema del valor final:
flh(oo)
=
0.2 = lim sRes) = lim s' flqe.
s-
=
o
s-
o
s
2
S
=
+0.425
flqe = 0.425 0 .2 = 0.0425
2
luego:
q e(00) = q eO + flq e
= 0.0625 m 3/S
Este valor de qe asegurará que el depósito no rebose en un tiempo infinito.
.''fI~
Para asegurar que el depósito no rebose en un tiempo de 2 segundos se deberá calcular el valor
de h(t) para t =2.
86
Control de sistemas continuos. Problemas resueltos.
Puesto que:
H(s)
= s
2
+0.425 Qe(s)
SI:
s
entonces:
H(s) =
t1h(t)
=
~-1[
t1qe
2
s +0.425 s
~]
t1qe
s +0.425 s
=
=$
_2_(1 -e
0.425
-0.425~ t1q
e
Con lo que:
t1h(2)
=
0.2
=$
t1qe
-0.425
-2- -1 --e0.2
--0.425. 2
=
0.0742
Luego:
;M(;t~(
0.35
:, 0.2
tes)
Figura 3.4-4
La Figura 3.4-4 muestra la evolución temporal de Jh(t) ante una variación en escalón de
0.0742 unidades de qe'
- - - - - - ~------