PDF2

Intnumer.nb
1
Integración numérica
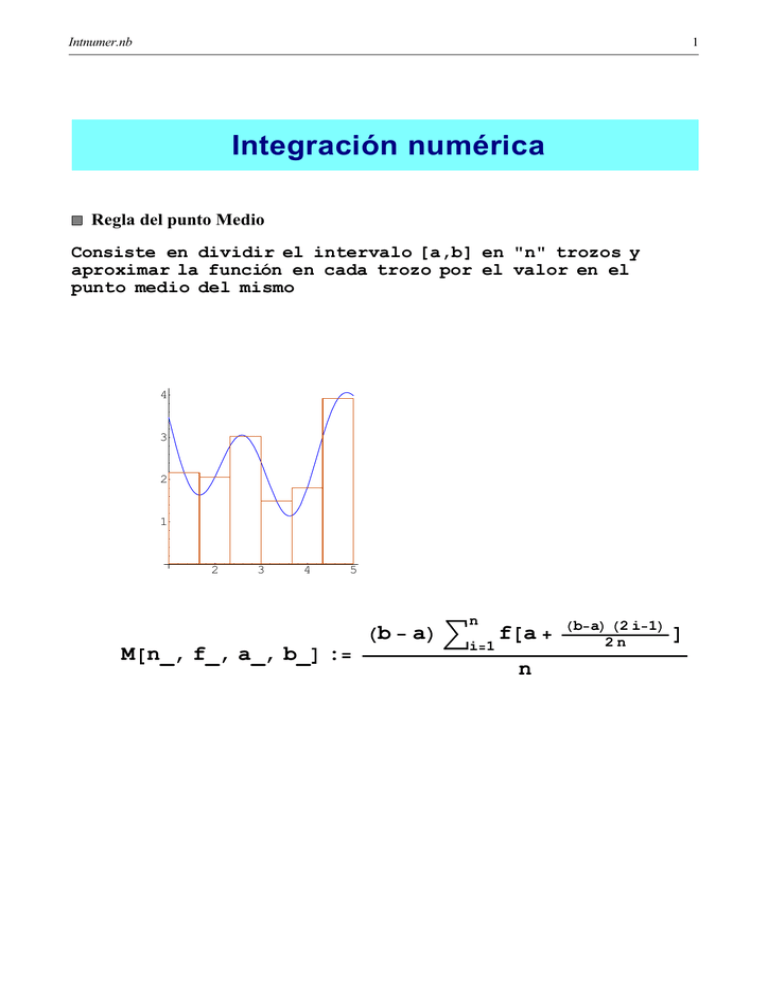
Regla del punto Medio
Consiste en dividir el intervalo [a,b] en "n" trozos y
aproximar la función en cada trozo por el valor en el
punto medio del mismo
4
3
2
1
2
3
4
5
b a
M n_, f_, a_, b_ :
n
b a
f a
i 1
2i 1
2n
n
Intnumer.nb
2
Regla del trapecio
Consiste en dividir el intervalo [a,b] en "n" trozos y
aproximar el área bajo la gráfica en cada trozo por el
área del trapecio que tiene por base el subintervalo y por
alturas los valores de la función en cada uno de los
trozos:
4
3
2
1
2
4
3
5
T n_, f_, a_, b_ :
b a
n
b a
f a
"
i 1
"
"
"
"
"
"
"
i 1
!
"
"
"
"
"
"
"
"
"
"
"
f a
"
"
"
n
b a i
n
(
*
%
#
*
&
*
*
'
$
*
)
*
*
*
*
*
*
*
*
*
-
+
,
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
2n
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Intnumer.nb
3
Estimación del error cuando
|f''(x)|< K2
para x en (a,b)
Para la regla del punto medio el error EM que
mide la diferencia entre el valor real de la
integral I[f,{a,b}] y el aproximado M[n,f,a,b]
está acotado por la expresión:
EM=|Integral[f,{a,b}]-M[n,f,a,b]|
<
(K2/24)(b-a)^3/(n^2)
Para la regla del trápecio el error ET que mide
la diferencia entre el valor real de la integral
I[f,{a,b}] y el aproximado T[n,f,a,b] está
acotado por la expresión:
ET=|Integral[f,{a,b}]-T[n,f,a,b]|
<
(K2/12)(b-a)^3/(n^2)
OBSERVACION: LOS ERRORES DE LA REGLA DEL PUNTO
MEDIO Y DE LA
REGLA DEL TRAPECIO SON DEL MISMO ORDEN. En un
principio con la regla del punto medio tenemos
una acotación menor del error que con la regla
del trapecio, en la práctica depende de cada
caso el que un método pueda ser mejor que otro.
Más adelante vamos a comparar estos dos métodos
en dos ejemplos concretos, justo después de la
regla de Simpson que sigue a continuación.
Intnumer.nb
4
Regla de Simpson
La REGLA DE SIMPSON se basa en la observación de
que la integral de un polinomio de segundo o
tercer grado en un intervalo se puede expresar en
terminos de los valores del polinomio en los
extremos y el punto medio del intervalo.
Concretamente,
.
s
p
r 3
3
x
1 6
0
1
4
5
x
s r
2
/
6
7
8
f r
9
9
8
4f
:
r s
2
f s
<
=
=
;
=
=
=
=
=
=
@
>
A
A
?
La regla de Simpson consiste en dividir el
intervalo [a,b] en "k"
trozos y aproximar el
área bajo la gráfica en cada trozo [x2 k 1 , x2 k]
por el área bajo el polinomio interpolador de
tercer grado que pasa por los puntos
{x2 k 1 , f x2 k 1 },{x2 k 1, f x2 k 1 }, y
{x2 k, f x2 k } que tiene por base el subintervalo,
Expresando esta área por la regla de Simpon:
(1/6)(x2 k x2 k 1 )(f x2 k 1 +4f x2 k 1 +f x2 k )
B
G
E
F
C
D
M
D
H
I
J
K
L
N
O
M
O
T
P
Q
R
Y
S
U
V
W
4
3
2
1
2
3
4
5
X
\
Z
[
[
Intnumer.nb
5
S k_, f_, a_, b_ :
]
^
k
abc
`
1
6k
`
`
`
`
`
`
`
_
c
b a
i
c
c
d
m
b a
`
e
f
f a
g
q
j
q
q
k
q
q
q
q
q
q
q
q
q
q
q
q
n
i 1
o
q
q
q
q
q
p
q
q
q
q
q
q
q
q
q
q
q
q
q
n
q
q
q
l
k
i 1
r
s
h
|}
b a
w
4f a
t
u
y
y
v
y
y
y
y
y
y
y
y
y
y
y
y
y
x
2i 1
2k
y
w
y
y
y
y
y
y
y
y
y
y
y
y
y
y
y
y
y
y
y
y
y
b a i
k
w
y
x
y
y y
v
u
f a
t
y
u
z
y
v
y
y
y
y
y
y
y
y
y
y
y
y
y
y
y
y
y
y
y
y
~
~
y
z
{
Estimación del error cuando
|f''''(x)|< K4 para x en (a,b)
La acotación del error para la regla de Simpson
se puede
hacer en terminos del tamaño de la derivada
cuarta.
ES=|Integral[f,{a,b}]-S[k,f,a,b]|
< (K4/180)(b-a)^5/(2k)^4
Ejemplo: aproximar numéricamente el valor de la integral
Int[ e^(-x^2) , {x,0,1}]
utilizando las reglas del punto medio, de los trapecios y de
Simpson.
f x_ : E

€

x2
‚
~
~
x
Intnumer.nb
6
Table N "k", k, M 2 k, f, 0, 1 ,
T 2 k, f, 0, 1 , S k, f, 0, 1 , 10 ,
k, 1, 10
ƒ
ƒ
„
…
‡
ˆ
†
‡
ˆ
‰
Š
‹
Œ
Ž
k
k
k
k
k
k
k
k
k
k
Ž
‘
‘
‘
‘
‘
‘
‘
‘
‘

1, 0.754597943772,̀ 0.731370251828,̀ 0.747180428909`,
2, 0.748747131891,̀ 0.742984097800,̀ 0.746855379790`,
3, 0.747677083350,̀ 0.745119412436,̀ 0.746830391489`,
4, 0.747303578730,̀ 0.745865614845,̀ 0.746826120527`,
5, 0.747130877747,̀ 0.746210796131,̀ 0.746824948254`,
6, 0.747037112217,̀ 0.746398247893,̀ 0.746824526379`,
7, 0.746980590677,̀ 0.746511256970,̀ 0.746824345350`,
8, 0.746943912516,̀ 0.746584596788,̀ 0.746824257435`,
9, 0.746918769042,̀ 0.746634874950,̀ 0.746824210629`,
10, 0.746900785538,̀ 0.746670836939,̀ 0.746824183875`


’

’

’

’

’

’

’

’

’


1
N
“
f x
”
•
–
x, 12
—
˜
0
0.7468241328124271
Ejemplo: aproximar numéricamente el valor de la integral
Log[2]= Int[ 1/(1+x) , {x,0,1}]
utilizando las reglas del punto medio, de los trapecios y de
Simpson.
g x_ :
™
š
1
œ
œ
œ
œ
œ
œ
œ
œ
œ
œ
œ
œ
œ
›
1 x

Intnumer.nb
7
Table N "k", k, M 2 k, g, 0, 1 ,
T 2 k, g, 0, 1 , S k, g, 0, 1 , 10 ,
k, 1, 10
ž
ž
Ÿ
¢
¡
¢
¡
¡
£
¤
¥
£
¦
¤
"k", 1.`, 0.685714285714285765,̀
0.708333333333333392,̀ 0.694444444444444464`,
"k", 2.`, 0.691219891219891202,̀
0.697023809523809489,̀ 0.693253968253968189`,
"k", 3.`, 0.692284320874979108,̀
0.694877344877344871,̀ 0.693169793169793191`,
"k", 4.`, 0.692660554043203369,̀
0.694121850371850346,̀ 0.69315453065453072`,
"k", 5.`, 0.692835360409960188,̀
0.69377140317542798,̀ 0.693150230688930335`,
"k", 6.`, 0.69293049507839548,̀
0.693580832876162034,̀ 0.69314866220910094`,
"k", 7.`, 0.692987919229683591,̀
0.693465855261184316,̀ 0.693147983875089401`,
"k", 8.`, 0.69302521433097084,̀
0.693391202207526902,̀ 0.693147652819419057`,
"k", 9.`, 0.693050794950824577,̀
0.693340007487214471,̀ 0.693147475981006877`,
"k", 10.`, 0.693069098225587065,̀
0.69330338179269404,̀ 0.693147374665116089`
¦
§
¨
§
¨
§
¨
§
¨
§
¨
§
¨
§
¨
§
¨
§
¨
§
N Log 2 , 10
©
©
ª
ª
0.6931471805599453
§