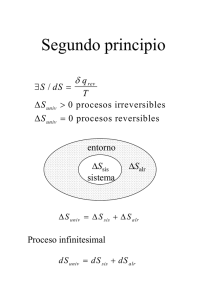
Entropía, 2da Ley

0.5 setgray0 0.5 setgray1
acements
0. Inicio
IV. Entropı́a
(use los comandos de su visor pdf para navegar las fichas)
FICHAS GUÍA: Entropı́a – p. 1/2
1. desigualdad de Clausius
δQ
I
δQ
≤0
T
T
PSfrag replacements
T es la temperatura de la superficie de control en el punto donde
ingresa el calor δQ
todo proceso cı́clico la verifica
se cumple la igualdad si y sólo si el ciclo es internamente reversible
es la base de la definición termodinámica de entropı́a
FICHAS GUÍA: Entropı́a – p. 2/2
2. entropı́a
Para un ciclo internamente reversible, se cumple
I δQ
T
=0
int rev
y (δQ/T )int rev es un diferencial exacto (aunque δQ no lo es, y
δQ/T en un camino no internamente reversible tampoco).
Esto permite definir la variable de estado entropı́a, como
dS ≡
δQ
T int rev
el cambio de entropı́a entre dos estados de equilibrio es
∆S =
Z
2
dS =
1
Z
1
2
δQ
= S 2 − S1
T int rev
[sigue]
FICHAS GUÍA: Entropı́a – p. 3/2
2a. entropı́a
el concepto de entropı́a admite una definición fundamental en
términos del número de microestados accesibles al sistema. Este
enfoque se desarrolla en el módulo de Termodinámica Estadı́stica.
desde este punto de vista, se usa la entropı́a para definir la
temperatura en un estado de equilibrio térmico
1
=
T
∂S
∂E
,
V,N
es decir que la tasa de incremento de la entropı́a con la energı́a es la
temperatura inversa.
esta es una definción fundamental de temperatura.
FICHAS GUÍA: Entropı́a – p. 4/2
3. cambio de entropı́a en general
δQ
¿Cuando puede determinarse la variación de entropı́a integrando T ?
en un proceso A: 1 → 2, regresando a 1 por un proceso B
internamente reversible,
I
δQ
=
T
Z
R2
2
1,A
δQ
+
T
Z
2
1
2,B
δQ
≤0
T
PSfrag replacements
δQ
Dado que 1,B δQ/T
A
1
B (int rev)
= S2 − S1 = ∆S , resulta que siempre
∆S ≥
Z
2
1,A
δQ
δQ
⇒ dS ≥
T
T
vale la igualdad si el proceso A también es internamente reversible.
En general, el cambio de entropı́a es mayor que δQ/T .
FICHAS GUÍA: Entropı́a – p. 5/2
4. entropı́a y segundo principio
La entropı́a de un sistema aislado (δQ
= 0) no puede decrecer,
∆Saislado ≥ 0
y no cambia si el proceso es internamente reversible.
Si consideramos al universo (sistema+ambiente) como un sistema
aislado, en todo proceso posible, la entropı́a del universo
∆Suniv ≡ ∆Ssistema + ∆Sambiente
no puede disminuir
∆Suniv ≥ 0
FICHAS GUÍA: Entropı́a – p. 6/2
5. reversibilidad
¿Cuál es la diferencia entre un proceso internamente reversible y un
proceso reversible?
Un proceso que sufre cierta masa de control es
internamente reversible si
∆S =
Z
δQ
T
un proceso es reversible si
∆Suniv = 0
un proceso internamente reversible no es necesariamente reversible.
FICHAS GUÍA: Entropı́a – p. 7/2
6a. relaciones TdS
A partir de tres elementos:
1. primera ley para un proceso diferencial en una masa de control,
dU = δQ − δW
2. trabajo es de tipo δW
= P dV (sustancia compresible simple)
3. el proceso es internamente reversible, δQ
= T dS
entonces,
T dS = dU + P dV
además, dado que dH
primera TdS
= dU + P dV + V dP , se tiene
T dS = dH − V dP
segunda TdS
[sigue]
FICHAS GUÍA: Entropı́a – p. 8/2
6b. relaciones TdS
T ds = du + P dv
primera TdS
T ds = dh − vdP
segunda TdS
estas ecuaciones, expresadas por unidad de masa, son relaciones
entre propiedades de una sustancia pura compresible simple
valen para una masa de control, aún cuando el proceso no sea
internamente reversible. Por ejemplo, valen entre los
estados de entrada y salida de un flujo RPFE.
integrando, permiten expresar cambios de entropı́a en t érminos de
otras variables.
[sigue]
FICHAS GUÍA: Entropı́a – p. 9/2
6c. trabajo reversible en proceso RPFE
En un proceso RPFE internamente reversible se cumple
δqint rev = du + P dv = T ds
donde los cambios estan asociados a las condiciones de entrada/salida.
Por sencillez suponemos una entrada y una salida, de modo que el Primer
Principio para un proceso diferencial es
δqint rev = dh̃ + δw = d(u + ec + ep + P v) + δw = du + P dv
de donde despejamos la expresión para el trabajo en un proceso int. rev.
RPFE,
δwint rev = −vdP − dec − dep
[sigue]
FICHAS GUÍA: Entropı́a – p. 10/2
6d. realciones TdS: en suma
despreciando variaciones de energı́a cinética y potencial de
ecuación
orı́gen
(1)
δq = du + δw primera ley
(2)
δq = du + P dv primera ley
≈ du,
restricciones
cerrado
cerrado, cuasiestático.
sólo trabajo Pdv
(3)
T ds = du + δw primera y segunda ley
(4) T ds = du + P dv primera y segunda ley
cerrado, int. rev.
sust. comp. simple, int. rev
(2) puede aplicarse en procesos RPFE internamente reversibles, pero
entonces δw
= −vdP 6= P dv .
(3) para procesos con irreversibilidades internas, T ds
> δq .
[sigue]
FICHAS GUÍA: Entropı́a – p. 11/2
6e. relaciones TdS: en suma
La diferencia entre la primera ley y la primera TdS, ecs. (1) y (4), se ilustra
aplicándolas en el siguiente ejemplo: Un recipiente rı́gido de paredes
adiabáticas contiene un gas. El gas recibe trabajo δW de un agente
externo a través de la hélice.
Las ecs. (1) y (4) muestran que
la energı́a y la entropı́a del gas
gas
aumentan en proporción al trabajo recibido,
δW
PSfrag replacements
(1)
(4)
y el proceso es irreversible, ya que:
dU = −δW
T dS = dU
dS = −δW/T > δq/T = 0.
FICHAS GUÍA: Entropı́a – p. 12/2
7. cambio de entropı́a
a partir de las relaciones TdS, expresando el cambio por unidad de
masa,
∆s = s2 − s1 =
=
Z
Z
2
1
2
1
cV
dT
T
cP
dT
T
+
V
P
−
Z
Z
2
P dv
T
2
vdP
T
1
1
las integrales que involucran los calores especı́ficos, son en caminos
a V o P constantes, donde duV
= cV dTV y dhP = cP dTP .
Para evaluar las integrales, es necesario conocer la ecuaci ón de
estado f (P, v, T )
= 0 y la dependencia de los calores especı́ficos
cP (T ) y cv (T ) con la temperatura para la sustancia.
FICHAS GUÍA: Entropı́a – p. 13/2
8. cambio de entropı́a: gas ideal
Para un gas ideal, P v
= RT , y
T2
T2
v2
P2
∆s = s2 −s1 ≈ c̄V ln
+R ln
= c̄P ln
−R ln
T1
v1
T1
P1
donde c̄V y c̄P son valores medios adecuados para la sustancia y el
intervalo de integración. Están tabulados para los gases más comunes.
Como primera aproximación, para gases mono o diátomicos se puede usar
5
c̄V ≈ R
2
7
c̄P ≈ R
2
(diatómico)
y
3
c̄V ≈ R
2
5
c̄P ≈ R
2
(monoatómico)
donde R es la constante del gas.
FICHAS GUÍA: Entropı́a – p. 14/2
9. Proceso isentrópico en gas ideal
a partir de las TdS, para un proceso isentrópico diferencial en gas ideal,
T ds = cV dT + P dv = 0
T ds = cP dT − v dP = 0
eliminando la temperatura, resulta la relación entre las variables (P, v) en
el proceso isentrópico,
dP
dv
=
γ
v
P
con γ
= cP /cV , esto para cualquier sustancia.
Para un gas ideal, γ ≈ 1.40 para gases diatómicos (γ ≈ 1.67 para
monoatómicos). Integrando, con P v = RT ,
γ
P v = cte
T
P R/cP
= cte0
T v γ−1 = cte00
FICHAS GUÍA: Entropı́a – p. 15/2
10. cambio de entropı́a:
sustancia incompresible
Para un cambio de estado en una sustancia incompresible a , dv
= 0, y
T ds = du = c dT
por lo que el cambio de entropı́a depende sólo del cambio de temperatura
∆s = s2 − s1 = c̄ ln(T2 /T1 )
donde c̄ es el calor especı́fico medio para la sustancia, en el intervalo de
= T 2 − T1 ,
Z T2
1
c̄ ≡
c(T ) dT
∆T T1
temperatura relevante ∆T
a
sustancias en fase lı́quida o sólida se pueden considerar como aproximada-
mente incompresibles.
FICHAS GUÍA: Entropı́a – p. 16/2
11. balance de entropı́a
sistemas abiertos
en un volumen de control abierto en el cual entra calor a tasas
Q̇k por
= 1, 2 . . . de la superficie de control (en cada uno de
los cuales la temperatura de frontera es Tk ), la entropı́a cambia a una
varios puntos k
Q̇k
tasa
Ṡvc ≥
ṁs
X
e
ṁe se −
X
s
ṁs ss +
X Q̇k
Tk
PSfrag replacements
k
Tk
V.C.
ṁe
sistema abierto
la igualdad se cumple si el proceso es internamente reversible.
se puede escribir el balance como una igualdad, incluyendo la
entropı́a generada en el volumen de control
[sigue]
FICHAS GUÍA: Entropı́a – p. 17/2
11a. confusiones y dudas usuales
1. la entropı́a generada por un proceso en el volumen de control, se
define por
gen
Ṡvc
≡ Ṡvc −
X
ṁe se +
e
X
s
ṁs ss −
X Q̇k
k
Tk
2. ¿adiabático e internamente reversible ⇒ isentrópico?
No siempre. Sólo para sistemas cerrados o en abiertos para los
cuales
P
e
ṁe se −
P
s
ṁs ss = 0
3. ¿isentrópico ⇒ adiabático e internamente reversible?
No. La entropı́a generada en el VC puede ser evacuada por el flujo
másico.
4. ¿un proceso RPFE puede aumentar la entropı́a del VC?
Nunca. RPFE implica propiedades en el VC constantes.
FICHAS GUÍA: Entropı́a – p. 18/2
12. balance de entropı́a: modelo EUFU
en el modelo EUFU, integrando entre el estado inicial y final,
∆S = mf sf − mi si ≥
X
e
me s̄e −
X
ms s̄s +
s
XZ
k
i
f
δQk
Tk
-
i (f ) indica un estado de equilibrio inicial (final) en el VC.
-
me (ms ) es la masa que entra (sale) del VC durante el proceso en la
entrada e (salida s).
-
s̄e (s̄s ) es la entropı́a promedio asociada a la masa que entra (sale)
durante el proceso en la entrada (salida) correspondiente.
- la suma en k es sobre los intercambios de calor y la integral es a lo largo
del proceso, donde la temperatura Tk puede variar.
FICHAS GUÍA: Entropı́a – p. 19/2
13. balance de entropı́a: masa de control
Para una masa de control (sistema cerrado), simplemente se anulan los
términos de entrada y salida de masa del modelo EUFU,
XZ
∆S = m(sf − si ) ≥
k
i
f
δQk
Tk
y la suma en k tiene sentido si hay regiones aisladas en el VC
intercambiando calor a diferentes temperaturas. La entropı́a generada en
el VC en el proceso es
SVgen
C
≡ ∆S −
XZ
k
i
f
δQk
≥0
Tk
es decir, la parte del cambio de entropı́a del VC que no se debe al
intercambio reversible de calor.
FICHAS GUÍA: Entropı́a – p. 20/2
14. balance de entropı́a: RPFE
en el modelo RPFE, Ṡvc
X
s
= 0 y resulta
dms ss −
para un proceso diferencial, o
X
s
X
ṁs ss −
e
dme se ≥
X
e
ṁe se ≥
X δQk
k
Tk
X Q̇k
k
Tk
para un proceso instantáneo. Para una sola entrada y salida, expresado
por unidad de masa circulante,
X qk
∆ s ≡ s s − se ≥
Tk
k
0
qk = Q̇k /ṁ
FICHAS GUÍA: Entropı́a – p. 21/2
15a. transferencia de calor:
entropı́a generada
En una transferencia de calor entre un ambiente a T0 y un sistema a
T 6= T0 , se genera entropı́a.
T0
dSvc
dSamb
δQ
gen
= dme se − dms ss +
+ dSvc
T
δQ
gen
= −dme se + dms ss −
+ dSamb
T0
PSfrag replacements
δQ
dms
T
V.C.
dme
sistema abierto
sumando ambos balances se obtiene la entropı́a generada por la
transferencia de calor,
dSuniv
1
1
gen
gen
= δQ
+ dSamb
−
+ dSvc
T
T0
[sigue]
FICHAS GUÍA: Entropı́a – p. 22/2
15b. transferencia de calor:
entropı́a generada
gen
si suponemos un proceso lento (internamente reversible, dS vc
gen
ambiente se comporta como una reserva térmica, (dSamb
Entonces,
S
gen
= ∆Suniv =
Z
2
1
1
1
−
δQ
T
T0
= 0) y el
= 0).
la entropı́a generada se debe sólo a la transferencia de calor.
No se genera en el VC ni en el ambiente,
→ se localiza en la frontera sistema-ambiente.
evidentemente, si T
= T0 la transferencia de calor serı́a reversible, pero
tomarı́a un tiempo infinito transferir un calor finito
FICHAS GUÍA: Entropı́a – p. 23/2