Clase_termo 3

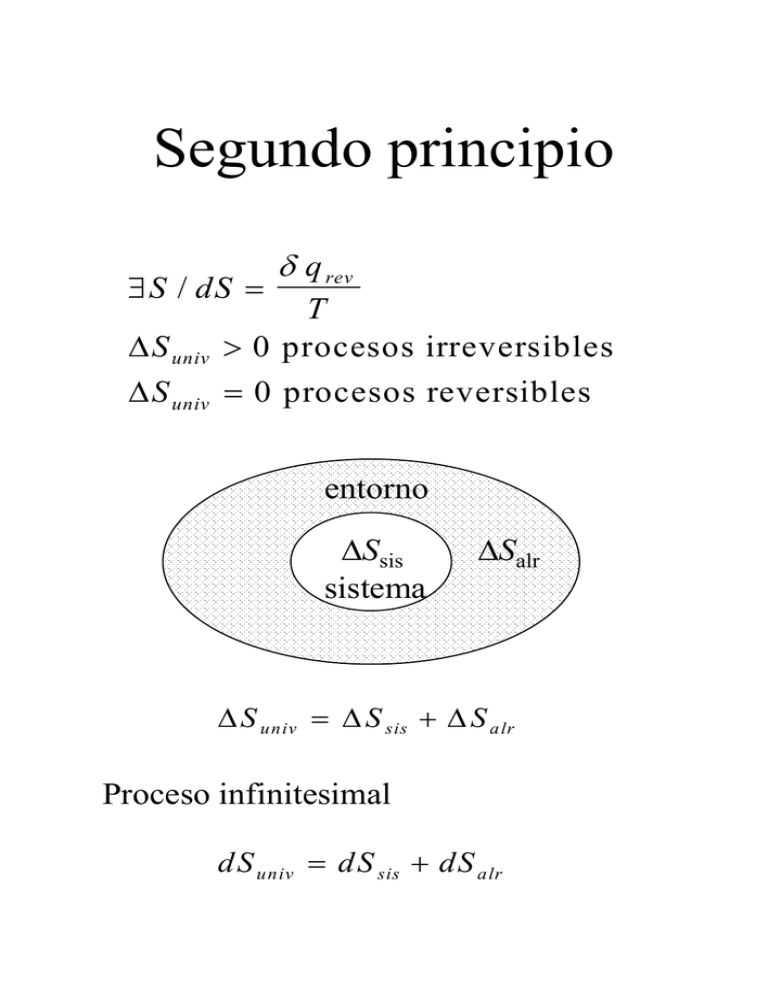
Segundo principio
 S / dS 
 S univ
 S univ
 q rev
T
 0 procesos irreversibles
 0 procesos reversibles
entorno
Ssis
sistema
Salr
 S univ   S sis   S alr
Proceso infinitesimal
dS univ  dS sis  dS alr
Calculando S
Proceso cíclico
 S  0 porque S es función de estado
Proceso adiabático reversible
 q rev
S  
,  q rev  0   S  0
T
Proceso isotérmico reversible
S  
 qrev
T

Qrev
1

q

rev
T
T
Cambio de fase reversible
H
S 
T
Proceso reversible de un gas ideal
 q rev  d E   w rev
 q rev  CV dT  PdV
T2
V
T2
V
2
dT
P
 S   CV
  dV
T
T
T1
V1
2
dT
dV
 S   CV
  nR
T
V
T1
V1
 T2 
 V2 
 S  CV ln    nR ln  
 T1 
 V1 
Proceso irreversible de un gas ideal
 T2 
 V2 
S  CV ln    nR ln  
 T1 
 V1 
Calentamiento a presión constante
S 

 q rev
T
T2


T1
C P dT
T
Entropía y equilibrio
Entropía del universo a lo largo
de un proceso
Suniverso
25
20
15
10
5
0
1
2
3
4
5
6
7
8
9 10 11 12
Tiem po
Suniv máxima en el equilibrio
dS univ = 0
en el equilibrio
er
1
Combinación del
y el
do
2 principio
Desigualdad de Clausius
dS 
q
T
(1)
Primer principio
dE   q   w
(2)
Reemplazando (1) en (2)
dE  TdS   w
(3)
A P=cte., si sólo hay trabajo PV
dE  TdS  PdV
(4)
Energía libre
Consideramos un sistema en equilibrio térmico
y mecánico con su entorno:
dE  TdS  PdV
dE  d (TS )  d ( PV )
porque T y P son ctes.
dE  d (TS )  d ( PV )  0
d ( E  TS  PV )  0
Definimos G  E  PV  TS
dG  0
Eq. térmico y mecánico.
Sólo hay trabajo PV.
Resumiendo
 S / dS 
dS 
 qirrev
 qrev
T
Desigualdad de Clausius
T
dSuniv  0
Proceso irreversible
dSuniv  0
Proceso reversible o equilibrio
dG  0
Proceso irreversible a T y P
constante. Sólo trabajo PV.
dG  0
Proceso reversible o equilibrio a T y P
constante. Sólo trabajo PV.