Clase 11 - MOSFET (III) Modelo equivalente de peque˜na se˜nal

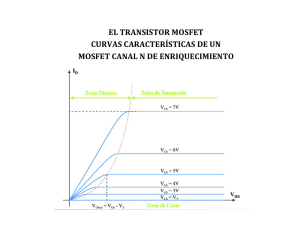
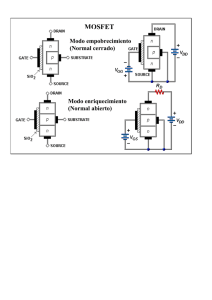
86.03/66.25 - Dispositivos Semiconductores - 2015
Clase 11-1
Clase 11 1 - MOSFET (III)
Modelo equivalente de pequeña señal
Abril de 2015
Contenido:
1. Modelo de pequeña señal del MOSFET para baja frecuencia
2. Modelo de pequeña señal del MOSFET para alta frecuencia
3. Modelo de SPICE
Lectura recomendada:
P. Julian Cap. 5
1
Esta clase es una traducción, realizada por los docentes del curso ”66.25 - Dispositivos Semiconductores - de la FIUBA”, de la correspondiente hecha por el prof. Jesus A. de Alamo para el curso ”6.012 Microelectronic Devices and Circuits” del MIT. Cualquier error debe adjudicarse a la traducción.
86.03/66.25 - Dispositivos Semiconductores - 2015
Clase 11-2
Preguntas disparadoras:
• ¿Por qué necesitamos modelar el MOSFET?
• ¿Cuál es la topologı́a del circuito eléctrico del modelo
de pequeña señal del MOSFET?
• ¿Cuales son las principales dependencias de los elementos fundamentales del modelo de pequeña señal
para saturación?
86.03/66.25 - Dispositivos Semiconductores - 2015
Clase 11-3
Modelado del MOSFET
Hasta ahora tenemos un modelo del MOSFET válido
para ”cualquier” señal de entrada:
• Corte o Cut-off:
ID = 0
• Lineal o triodo:
VDS
W
− VT )VDS
ID = µnCox(VGS −
L
2
• Saturación:
W
ID = IDsat =
µnCox(VGS −VT )2[1+λ(VDS −VDSsat)]
2L
Efecto del Back bias:
r
r
VT (VBS ) = VT o + γ( −2φp − VBS − −2φp)
Pero, ¿Qué pasa si tenemos una señal que varı́a en el
tiempo?
86.03/66.25 - Dispositivos Semiconductores - 2015
Clase 11-4
Modelado del MOSFET para una señal que
varı́a en el tiempo
Suponiendo que el MOSFET está en saturación resulta:
ID =
W
µnCox(VGS − vgssen(2πf · t)) − VT )2
2L
Obtenemos una ecuación que puede ser resuelta por una
computadora, pero que no es práctica para cálculos a
mano.
Imagı́nense si además el MOSFET está un circuito real,
rodeado de resistores, capacitores, otros MOSFETs, generadores de señal, etc.
Es necesario obtener algún tipo de modelo simplificado.
86.03/66.25 - Dispositivos Semiconductores - 2015
Clase 11-5
Hipótesis del modelo simplificado:
• Si las variaciones de vgs son grandes, no hay más remedio que usar las ecuaciones completas.
• Pero si vgs ”no varı́a demasiado”, podemos suponer
que hay una relación lineal entre la variación vgs y la
variación id resultante:
Y buscar un modelo simple que modele esta situación:
iD = f1(VGS ) + f2(vgs)
86.03/66.25 - Dispositivos Semiconductores - 2015
Clase 11-6
Es decir, se pretende partir al problema en dos partes:
De modo tal que al final obtengamos:
iD = ID + id
Donde la notación utilizada es:
VGS ,ID = señal de contı́nua (polarización o gran señal)
vgs,id = señal de alterna (pequeña señal)
vGS ,iD = VGS + vgs, ID + id (señal total)
86.03/66.25 - Dispositivos Semiconductores - 2015
Clase 11-7
Modelo linealizado del MOSFET
¿Cómo hacemos esto?
Por supuesto, desarrollando iD (vGS ) en serie de Taylor:
∂ID
1 ∂ 2ID
2
iD (VGS + vgs) = ID (VGS ) +
|Q · vgs +
|
·
v
gs
2 Q
∂VGS
2 ∂VGS
Evaluando las derivadas para regimen de saturación:
2
iD (vGS ) = k(VGS − VT )2 + 2k(VGS − VT ) · vgs + k · vgs
El modelo linealizado del MOSFET en saturación resulta:
iD (vGS ) '
W
W
µnCox(VGS −VT )2 + µnCox(VGS −VT )vgs
2L
L
iD (vGS ) ' ID (VGS ) + gm(VGS ) · vgs
donde definimos la transconductancia gm [S] como:
W
gm = µnCox(VGS − VT )
L
86.03/66.25 - Dispositivos Semiconductores - 2015
Clase 11-8
Veamos mediante un ejemplo cómo funciona esta idea:
W
Para VGS = 2V, VT = 1.5V, 2L
µnCox = 1mA/V 2,
vgs = 0.1sen(2π · 1kHz · t) y VDS tal que estamos en
saturación,
• Tenemos por un lado el modelo ”completo”:
W
iD (vGS ) =
µnCox((VGS + vgs) − VT )2
2L
iD (vGS ) = 1mA/V 2·((2V +0.1sen(2π·1kHz·t))−1V )2
• Y por otro el modelo aproximado para ”pequeña señal”:
iD (vGS ) = ID + gmvgs
W
ID =
µnCox(VGS − VT )2 = 250µA
2L
gm =
W
µnCox(VGS − VT ) = 250µS
L
iD (vGS ) = 250µA + 250µS · 0.1sen(2π · 1kHz · t)
¿Podemos usar el modelo aproximado? ¿Es útil?
86.03/66.25 - Dispositivos Semiconductores - 2015
Clase 11-9
Comparemos los resultados obtenidos con el ”modelo completo” y con el ”modelo aproximado”:
Para vgs = 100mV los resultados son parecidos.
⇒ ¡Pero el modelo linealizado es mucho más simple (apto
para cálculos a mano)!
⇒ Puedo pensar las variaciones id como resultado de una
fuente de corriente controlada por vgs:
¿Qué pasa con valores más chicos o más grandes de vgs?
86.03/66.25 - Dispositivos Semiconductores - 2015
Clase 11-10
Dejamos los demás parámetros constantes y varı́amos vgs:
• Para vgs=50mV la aproximación es excelente:
• Para vgs=200mV la aproximación es mala
Esto ocurre porque estamos haciendo Taylor en el entorno
de VGS .
86.03/66.25 - Dispositivos Semiconductores - 2015
Clase 11-11
Rango de validez del modelo linealizado del
MOSFET
¿Cuando es válido el modelo linealizado?
Si aceptamos un 10% de error en la linealización:
2
k · vgs
< 0.1 · 2k(VGS − VT ) · vgs
o sea,
vgs < 0.2(VGS − VT )
Ejemplo:
Si VGS = 2V y VT = 1.5V, resulta vgs ≤ 100mV
Si VGS = 3V y VT = 1.5V, resulta vgs ≤ 300mV
La linealización del ”modelo completo” es útil para diferentes dispositivos (MOSFET, diodo, TBJ, etc.) en diferentes regimenes de operación (saturación, lineal, etc.) y
es válida dentro de cierto rango acotado.
86.03/66.25 - Dispositivos Semiconductores - 2015
Clase 11-12
2. Modelo de pequeña señal del MOSFET en
baja frecuencia
Aplicamos la misma idea a pequeñas señales aplicadas
sobre cualquiera de las fuentes de polarización:
Puntos fundamentales:
• Podemos separar la respuesta del dispositivo a la polarización y a la pequeña señal.
• Las señales son pequeñas
⇒ la respuesta de los dispositivos es aprox. lineal
⇒ se puede usar el principio de superposición
⇒ los efectos de diferentes señales son independientes.
86.03/66.25 - Dispositivos Semiconductores - 2015
Clase 11-13
Matemáticamente:
iD (VGS + vgs, VDS + vds, VBS + vbs) '
∂ID
∂ID
∂ID
ID (VGS , VDS , VBS )+
| vgs +
| vds +
| vbs
∂VGS Q
∂VDS Q
∂VBS Q
Donde Q ≡ punto de polarización (VGS , VDS , VBS )
Corriente id de pequeña señal:
id ' gmvgs + govds + gmbvbs
Definimos:
gm ≡ transconductancia [S]
go ≡ salida o conductancia del drain [S]
gmb ≡ transconductancia del backgate [S]
Luego:
∂ID
|
gm '
∂VGS Q
∂ID
go '
|
∂VDS Q
gmb
∂ID
'
|
∂VBS Q
86.03/66.25 - Dispositivos Semiconductores - 2015
Clase 11-14
2 Transconductancia
En regimen de saturación:
W
ID =
µnCox(VGS − VT )2[1 + λ(VDS − VDSsat)]
2L
Luego (despreciando la modulación del largo del canal):
∂ID
W
gm =
|Q ' µnCox(VGS − VT )
∂VGS
L
Lo reescribimos en términos de ID :
v
u
u
u
u
t
gm = 2
W
µnCoxID
L
86.03/66.25 - Dispositivos Semiconductores - 2015
Clase 11-15
Trasconductancia de un nMOSFET (VDS = 2 V ):
Modelo circuital equivalente de gm:
86.03/66.25 - Dispositivos Semiconductores - 2015
Clase 11-16
2 Conductancia de salida
En regimen de saturación:
W
ID =
µnCox(VGS − VT )2[1 + λ(VDS − VDSsat)]
2L
Luego:
go =
∂ID
W
ID
|Q =
µnCox(VGS − VT )2λ ' ID λ ∝
∂VDS
2L
L
La resistencia de salida es:
1
L
ro = ∝
go ID
86.03/66.25 - Dispositivos Semiconductores - 2015
Conductancia de salida de un nMOSFET:
Modelo circuital equivalente de go:
Clase 11-17
86.03/66.25 - Dispositivos Semiconductores - 2015
Clase 11-18
2 Transconductancia de Backgate
En régimen de saturación (despreciando la modulación
del canal):
W
ID '
µnCox(VGS − VT (VBS ))2
2L
Luego:
gmb
∂ID
W
∂VT
=
| = µnCox(VGS − VT )(−
| )
∂VBS Q
L
∂VBS Q
∂VT
|Q )
gmb = gm(−
∂VBS
Dado que:
r
r
VT (VBS ) = VT o + γ( −2φp − VBS − −2φp)
Resulta:
gmb =
γgm
2 −2φp − VBS
r
gmb hereda las dependencias de gm
86.03/66.25 - Dispositivos Semiconductores - 2015
Clase 11-19
El Body del MOSFET es un terminal de control: caracterı́sticas de salida para un barrido de VBS desde VBS =
0V hasta VBS = −3V con ∆VBS = −0.5 V y VGS = 2 V :
Modelo circuital equivalente de gmb:
86.03/66.25 - Dispositivos Semiconductores - 2015
Clase 11-20
Modelo completo del MOSFET para pequeña señal:
86.03/66.25 - Dispositivos Semiconductores - 2015
Clase 11-21
3. Modelo de pequeña señal del MOSFET en
alta frecuencia
Tenemos que incorporar las capacidades. En saturación:
Cgs ≡ capacidad intrı́nseca del gate
+ capacidad de overlap, Cov (+fringe)
Cgd ≡ capacidad de overlap, Cov (+fringe)
Cgb ≡ (sólo capacidades parásitas)
Csb ≡ capacidad zona vaciamiento source
+ sidewall (+capacidad canal-substrato)
Cdb ≡ capacidad zona vaciamiento drain + sidewall
Los términos entre paréntesis son menores y se descartan.
86.03/66.25 - Dispositivos Semiconductores - 2015
Clase 11-22
Modelo de pequeña señal del MOSFET para alta frecuencia:
Plan para obtener las capacidades del modelo:
• Empezamos con Cgs,i
– calculamos la carga del canal QG = −(QN + QB )
– calculamos cómo QG cambia con VGS
• Sumamos las capacidades Cj de las junturas PN
86.03/66.25 - Dispositivos Semiconductores - 2015
Clase 11-23
Carga de la capa de inversión en saturación
QN (VGS ) = W
L
0 Qn (y)dy
Z
=W
VGS −VT
0
Z
Qn(Vc)
dy
dVc
dVc
Siendo:
ID
dVc
= −Ey (y) = −
dy
W µnQn(Vc)
Luego:
W 2µn Z VGS −VT 2
QN (VGS ) = −
Qn(Vc)dVc
0
ID
Recordando:
Qn(Vc) = −Cox(VGS − Vc − VT )
Entonces:
2 Z
W 2µnCox
VGS −VT
2
QN (VGS ) = −
(V
−
V
−
V
)
dVc
GS
c
T
0
ID
86.03/66.25 - Dispositivos Semiconductores - 2015
Clase 11-24
Integramos y substituimos ID para saturación:
2
QN (VGS ) = − W LCox(VGS − VT )
3
La carga del canal es:
QG(VGS ) = −QN (VGS ) − QB,max|indepV GS
Capacidad gate-source debido a la capa de inversión (i):
Cgs,i =
2
dQG
= W LCox
dVGS 3
Debemos incluir la capacidad de overlap:
2
Cgs = W LCox + W Cov
3
Capacidad gate-drain - sólo capacidad de overlap:
Cgd = W Cov
86.03/66.25 - Dispositivos Semiconductores - 2015
Clase 11-25
Capacidad body-source = Capacidad de juntura del source:
Csb = Cj +Cjsw = W L
v
u
u
u
u
t
dif f u
qsNa
+(2Ldif f +W )CJSW
2(φB − VBS )
Capacidad body-drain = Capacidad de juntura del drain:
Cdb = Cj +Cjsw = W L
v
u
u
u
u
t
dif f u
qsNa
+(2Ldif f +W )CJSW
2(φB − VBD )
86.03/66.25 - Dispositivos Semiconductores - 2015
Clase 11-26
Principales conclusiones
Modelo de pequeña señal del MOSFET para alta frecuencia:
En saturación:
gm ∝
v
u
u
u
u
t
W
ID
L
ID
go ∝
L
Cgs ∝ W LCox
86.03/66.25 - Dispositivos Semiconductores - 2015
Clase 11-27
4. Modelo de simulación del SPICE
SPICE es el acrónimo de Simulation Program with Integrated Circuits Emphasis y fue desarrollado por la Universidad de California, en Berkeley, en 1975.
Es un estándar de simulación de circuitos electrónicos.
Para eso hay que describir el circuito y elegir el tipo de
simulación (temporal, en frecuencia, continua, etc.)
Vs 1 0
Ra 1 2
Rb 2 0
Rc 3 0
Is 3 2
.DC Vs
.PRINT
.PRINT
.END
DC 20.0V ; Se indica la fuente
5.0k
4.0k
1.0k
DC 2.0mA
20 20 1 ; Se pide simulación DC
DC V(1,2) I(Ra) ; Calculo V,I para Ra
DC V(2) I(Rb)
86.03/66.25 - Dispositivos Semiconductores - 2015
Clase 11-28
Y se obtiene un resultado como este:
**** DC TRANSFER CURVES
Vs V(1,2) I(Ra)
20 6.667 1.333E-03
Vs V(2) I(Rb)
20 13.33 3.333E-03
JOB CONCLUDED
TOTAL JOB TIME .13
Hoy en dı́a hay muchas implementaciones de SPICE:
• Software no libre: LTSPICE (freeware), PSpice/OrCAD,
HSpice, MicroCad, Dr. Spice, Proteus, etc.
• Software libre: ASCO tool, GEDA (GPL), MacSpice,
Oregano (GPL), Qucs, TclSpice, etc.
Todas se basan en los mismos modelos de SPICE y cada
una agrega su entorno visual y herramientas propias.
86.03/66.25 - Dispositivos Semiconductores - 2015
Clase 11-29
Modelos de SPICE de MOSFETs
Para MOSFETs con L ≥ 1.5µm funciona bien el modelo
elemental ”Level 1” de SPICE:
Level 1 MOSFET model:
.MODEL MODN NMOS LEVEL=1 VTO=1 KP=50u
+ LAMBDA=.033 GAMMA=.6 PHI=0.8 TOX=1.5E-10
+ CGDO=5E-10 CGSO= 5e-10 CJ=1E-4 CJSW=5E-10
+ MJ=0.5 PB=0.95 W=5u L=1u
Por ejemplo, en Level 1 para calcular la corriente de Drain
se usan las ecuaciones:
86.03/66.25 - Dispositivos Semiconductores - 2015
Clase 11-30
Para calcular las capacidades el Level 1 usa por ejemplo:
Y las ecuaciones:
86.03/66.25 - Dispositivos Semiconductores - 2015
Clase 11-31
Existen muchos modelos SPICE de MOSFETs
Hay una modelos de MOSFETs desde Level 1 a Level 14.
El uso, complejidad y precisión de cada uno es diferente.
Permiten simular transitorios, temperatura, ruido, etc.
Por ejemplo, para MOSFETs sub-µm se usan modelos
como el BSIM, ”Berkeley Short-Channel IGFET Model”.
Ejemplo: AMI 0.5um Level 3 (AMI Semiconductor Inc.,
L=0.5um)
Para más información ver:
⇒ ”OrCAD PSpice A/D Reference Manual”
⇒ http://ltspice.linear.com/software/scad3.pdf