Electrónica Digital (ED) Primer parcial 1. CURSO 1.999-2.000

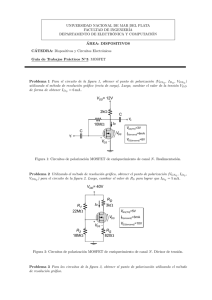
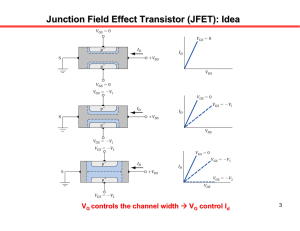
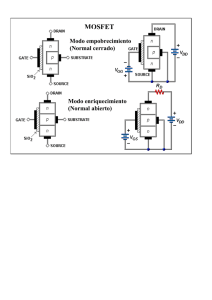
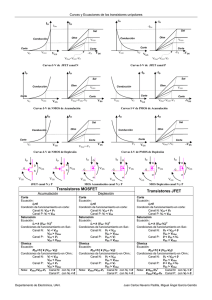
Electrónica Digital (ED)
CURSO 1.999-2.000
1 de febrero de 2.000
Primer parcial
1. Se dispone de dos cristales de semiconductor extrínseco homogéneamente dopados, no degenerados,
uno tipo n puro y otro tipo p puro, con las siguientes características:
NA = 1016 cm-3
ND = 1018 cm-3
EA = EV + 0.045 eV (dopado con B)
ED = EC - 0.044 eV (dopado con P)
EG = 1.115 eV (Si)
1mm
p
n
p
1mm
1mm
x
1.1. Dibujar los diagramas de bandas de energía para ambos cristales, indicando los valores energéticos
de cada banda o nivel discreto de energía. Se debe situar en los diagramas el nivel de Fermi
intrínseco Ei y el nivel de Fermi EF y explicar porqué se encuentra donde se haya representado. (Se
tomará como referencia de energías (E=0) la posición de Ei)
1.2. Calcular las concentraciones de portadores mayoritarios y minoritarios en cada cristal a la
temperatura indicada (300ºK). Con los datos obtenidos recalcule los niveles de Fermi de cada
cristal. Vuelva a dibujar los diagramas de bandas situando el nivel de Fermi en su lugar exacto. Con
los nuevos valores de los niveles de Fermi vuelva a calcular las concentraciones de portadores en
cada cristal y observe si hay diferencias significativas.
1.3. Sobre el semiconductor tipo p se aplica un campo eléctrico Ex=103 V/cm. Calcular las corrientes de
arrastre Ia y de difusión Id que circularán por el cristal. Razone como variará la corriente si sube la
temperatura 50º C.
2. Se unen idealmente los cristales n y p del problema anterior, formándose un diodo de unión abrupta
plana.
1.1. Dibujar el diagrama de bandas de energía resultante y calcular gráficamente, a partir de éste, el
potencial termodinámico de la unión, Φ T.
1.2. Haga un dibujo del cristal indicando la longitud de la zona de deplexión a cada lado de la unión y el
tipo de cargas existentes en esta zona, en situación de equilibrio y cuando se aplica una tensión de
polarización inversa de 10 V. Analice los resultados obtenidos.
1.3. Se aplica una tensión de polarización directa de 0.3V. Calcular las concentraciones de portadores
minoritarios en ambos bordes de la zona dipolar y representar los perfiles de minoritarios según el
eje x. Tenga en cuenta que las longitudes físicas de ánodo y cátodo son mucho mayores que las
longitudes de difusión en ambas regiones.
1.4. Calcular la corriente ID que circulará por el diodo bajo una tensión de polarización directa de 0.3V.
¿La corriente en el diodo será predominantemente de huecos o de electrones? ¿ En qué porcentaje?
Represente el perfil de las diferentes corrientes una vez conocido este dato.
3. Se tiene el circuito de la figura 2, en el que hay un transistor MOSFET de deplexión de canal n, con
los siguientes parámetros constitutivos: VT = -2 V, K=10-5A·V-2. El conmutador se abre y cierra
periódicamente cada T0 =10-3 s.
3.1. Dibujar una sección transversal de un NMOS de deplexión. Indicar si existe o no el canal para una
tensión VGS= 0V. Representar la característica de transferencia, IDS(VGS)|VDS=cte de un transistor de
este tipo (sin hacer ningún cálculo).
3.2. Calcular VGS, IDS y VDS cuando VGG = +3V y cuando VGG = -3V. ¿En que región de
funcionamiento se encuentra el transistor en cada caso?
3.3. Representar la forma de onda de la tensión de salida VO. Suponga para ello que el período de
conmutación del interruptor T0 es muy superior a los tiempos de acumulación-vaciamiento de
carga bajo la puerta del transistor. Razonar que sucedería si el transistor fuese un JFET de canal n
con idéntica tensión umbral VT. Representar la forma de onda de la tensión a la salida V0.
RD, RS, RG=103Ω; W/L=10;
K=10-5 A·V-2;
VDD=+10V
RD
RG
VGG
3V
-3V
RS
VT= -2V
Constantes de interés:
k = 1,381·10-23 J·oK-1 , 1eV = 1,602·10-19 J , Τ = 300 oK, ni |T=300 K=1,5·1010 cm-3
µn=1300 cm2V-1s-1 , µp=500 cm2V-1s-1 , ε0=8,854·10-12 Fm-1, εrs=11,7, εs=εrs·ε0,
τn=10-6s, τp=2·10-6s
Fórmulas de interés:
σ n = e·n·µ n
σ p = e· p·µ p
kT
µn
e
L p = D pτ p
Dp =
kT
µp
e
Ln = Dnτ n
Dn =
J d = e·(Dn ·∇n − D p ·∇p )
→
J a = σ ·E
→ →
I = ∫∫ J dS
I = J · A en problemas unidimensionales
S
N A− = N A · f FD ( E A )
E F = Ei + kT ·ln
f FD ( E ) =
n
ni
N D+ = N D ·(1 − f FD ( E A ))
E F = Ei − kT ·ln
p
ni
1
E − EF
1 + exp
kT
1
 2ε
2
1
1
)(φT − V )
l= s (
+
 e N A ND

lp =
ND
l
NA + ND
eV 
x

pn' ( x ) = p neq exp
− 1 exp( − )
kT 
Lp

eV 
x

n 'p ( x) = n peq exp
− 1 exp( − )
kT 
Ln

W 
I DS = K  (VGS − VT ) 2 (región de saturación)
L
[
NA
l
NA + ND
 eL p pneq eLn n peq 

J SAT = 
+
 τ

τ
p
n


eV


J D = J SAT  exp
− 1
kT


W
I DS = K 
L
ln =
]

2
 2(VGS − VT )VDS − VDS (región óhmica)
