Trabajo de Cálculo X

Matemáticas
Trabajo de Cálculo
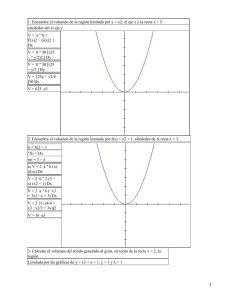
1. Encuentre el volumen de la región limitada por y = x2, el eje x y la recta x = 5
alrededor del el eje y
V = π a∫
b
{ F(x)2 – G(x)2 } Dx
V=π
0
∫
50
[(25 - √ y/2)2 ] Dy
V=π
0
∫
50
[(25 - y/2 ] Dy
V = π [25y - y2/4 ]50 Dy
V = 625 π u3
2. Encuentre el volumen de la región limitada por f(x) = x2 + 1, alrededor de la recta x
=3
h = Xi2 + 1
∆Xi = Dx
rm = 3 - x
a) V = 2 π a ∫
b
(x) (f(x)) Dx
V = 2 π 0∫
2
(3 - x) (x2 + 1) Dx
V = 2 π a∫
b
(-x3 + 3x2 –x + 3) Dx
V = 2 π [(-x4/4 + x3 –x2/2 + 3x)]2
V = 16 π u3
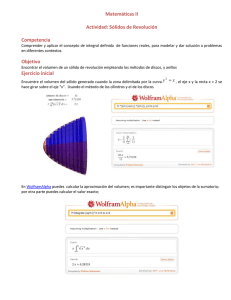
3. Calcular el volumen del sólido generado al girar, en torno de la recta x = 2, la región
Limitada por las gráficas de y = x3 + x + 1, y = 1 y
x=1
V = 2 π a ∫ b p(x)h(x)Dx
V = 2π 0∫
1
(2 – x ) (x3 + x +1 –1 )Dx
V = 2π 0∫
1
(-x4 + 2x3 –x2 + 2x ) Dx
V = 2 π [-x5/5 + x4/2 –x3/3 +x2 ]10
V = 2 π (-1/5 + ½ -1/3 +1 )
V = 29 π /15 u3
4. Calcular el volumen del sólido generado al girar la región acotada por las gráficas de
y = x2 +1 , y = 0 , x = 0 , y x = 1 en torno al eje y
Método de capas
V = 2 π a ∫ b p(x)h(x)Dx
V = 2 π 0∫
1
x(x2 +1)Dx
V = 2 π [x4/4 + x2/2]1
V = 3 π /2 u3
5. Calcular el volumen de un sólido de revolución engendrado por la región limitada
y = 1/ (x2 + 1)2 y el eje x ( x menor e igual a 1 y x mayor e igual a 0 )
V = 2 π a ∫ b p(x)h(x)Dx
V = 2 π 0∫1 x /(x2 + 1)2
Dx
V = [-π /x2 + 1 ]10
V = π /2 u3
6. Calcular el volumen del sólido de revolución que se genera al girar la región limitada
por
Y = x – x3 y el eje x ( x menor e igual q 1 y x mayor e igual q 0)
V = 2 π a ∫ b p(x)h(x) Dx
V = 2 π 0∫
1
x(x – x3) Dx
V = 2 π 0 ∫ 1 (-x4 +x2) Dx
V = 2 π [-x5/5 + x3/3]
V = 4 π /15 u3
7. Encontrar el volumen del sólido de revolución generado al hacer girar sobre el eje x
la
región encerrada en el primer cuadrante por la elipse 4x² + 9y ²=36 y los ejes
coordenados.
Y = ⅔ √(9-x²)
V= 4π/9 0∫³ [(9-x²)] Dx
V= 4π/9 [9x - ⅓x3]3
V = 8 π u3
8. Encontrar el volumen del sólido generado al girar sobre el eje y la región limitada
por la
curva y = x³, el eje y y la recta y = 3
V = π 0∫³ [y
V = [3/5 y
2/3
5/3 3
V = 3.74 u3
]
] Dy
9. Encontrar el volumen generado al girar sobre el eje x la región encerrada por las
parábolas y = x ² , y ² = 8x
V = π 0∫² [(8x – x4)] dx
V = π [4x2 – 1/5 x5]2
V = 48π / 5 u3
10. Encontrar el volumen generado por las gráficas x = y2 , x = y + 6 haciendo rotar el
eje y.
V = π a∫
b
{ F(x)2 – G(x)2 } Dx
V=π
-2
∫3 [(y + 6)
2
– (y2) 2 ] Dy
V=π
-2
∫3 (y2 + 12y + 36 – y4 ) Dy
V = π [ ⅓y3+ 6y2 + 36y – 1/5 y5]
V = 500 π / 3 u3
-2
3
11. Encontrar el volumen generado por la gráfica y = x3 – x , el eje x al rotar y = 0
V=π
-1
V = 2π
0
∫ 1[(x3 – x )2 ] Dy
∫ 1[x6 – 2x4 + x2 ] Dy
V = 2π [1/7 x7 – 2/5 x5 + 1/3 x3]
V = 16π /105 u3
12. Calcular el volumen del sólido generado al girar, alrededor de la recta x = 1, la
región
Limitada por la curva (x – 1)2 = 20 – 4y y las rectas x = 1, y = 1, y = 3
V = π 1∫3 [(√ 20 – 4y + 1) – 1]2 Dx
V = π 1∫3 [ 20 – 4y ] Dx
V = π [ 20y – 2y2 ]31
V = 24π u3
13. Hallar el volumen al girar el área limitada por la parábola y2 = 8x y la
ordenada correspondiente a x = 2 con respecto al eje y
V=
-4
∫ 4 4 π Dy -
-4
∫ 4 Πx2 Dy
V = 2π 0 ∫
4
(4 – x2) Dy
V = 2π 0 ∫
4
(4 – y4/64) Dy
V = 2π [4y – y5/320]40
V = 128π /5 u3
14. Hallar el volumen generado el la rotación del área comprendida entre la parábola
y = 4x – x2 y el eje x con respecto a la recta y = 6
V = π 0∫
4
[62 – (6 - y)2 ] Dx
V = π 0∫
4
(12y – y2) Dx
V = π 0∫
4
(48x – 28x2 +8x3 –x4) Dx
V = π [24x2 – 28x3/3 + 2x4 –x5/5]40
V = 1408π /15 u3
15. Hallar el volumen generado el la rotación del área comprendida entre la parábola
y2 = 8x y la ordenada correspondiente a x = 2 con respecto a esa recta (método de
anillo)
V = 8 (2)
½
π 0∫
2
(2 – x ) (x)1/2 Dx
V = 8 (2)
½
π 0∫
2
(2x1/2 – x3/2) Dx
V = 256π /15 u3
16. Encontrar el Volumen engendrado al girar sobre el eje y, la región del primer
cuadrante
Situada por encima de la parábola y = x2 y por debajo de la parábola y = 2 – x2
V = 4π
1
0∫
V = 4π
0[
V = π u3
(x – x3) Dx
½ x2 – ¼ x4]1
17. Encontrar el volumen de un sólido de revolución engendrado al girar sobre el eje y
la región limitada por la curva y = (x – 1)3, el eje x, y la recta x = 2
V = 2π 1∫2 x(x – 1)3Dx
V = 2π 1∫2 (x4 – 3x3 + 3x2 –x)Dx
V = 2π [x5/5 – 3x4/4 + x3 - x2/2]21
V = 9π/10
18. Encontrar el volumen del sólido generado por las gráficas y = 4 – x2 , 4y = 4 – x2 al
hacer rotar el eje x.
V=π
2
-2∫
[(4 – x2) 2 – (1 - ¼ x2 ) 2 ]Dx
V = 2π 0∫2 (16 - 8x2 + x4 – 1 + ½ x2 +
1/16x4)Dx
V = 2π [15x – 5/2 x2 – 3/16 x4]2
V = 32π u3
18. Encontrar el volumen del sólido generado por las gráficas y = x2 , y2 = 8x al
hacer rotar el eje x.
V=π
2
-2∫
[(4 – x2) 2 – (1 - ¼ x2 ) 2 ]Dx
V = 2π 0∫2 (16 - 8x2 + x4 – 1 + ½ x2 +
1/16x4)Dx
V = 2π [15x – 5/2 x2 – 3/16 x4]2
V = 32π u3
20.. Encontrar el volumen generado en la rotación del área del primer cuadrante
limitada
Por la parábola y2 = 8x y la ordenada correspondiente a x = 2 con respecto al eje x
V = π a∫
b
y2 D x
V = π 0 ∫ 2 8x Dx
V = 4π [x2]20
V = 16 π u3
http://www.loseskakeados.com