Geometr´ıa Anal´ıtica II 1 Formando un cono hacia una superficie
Anuncio
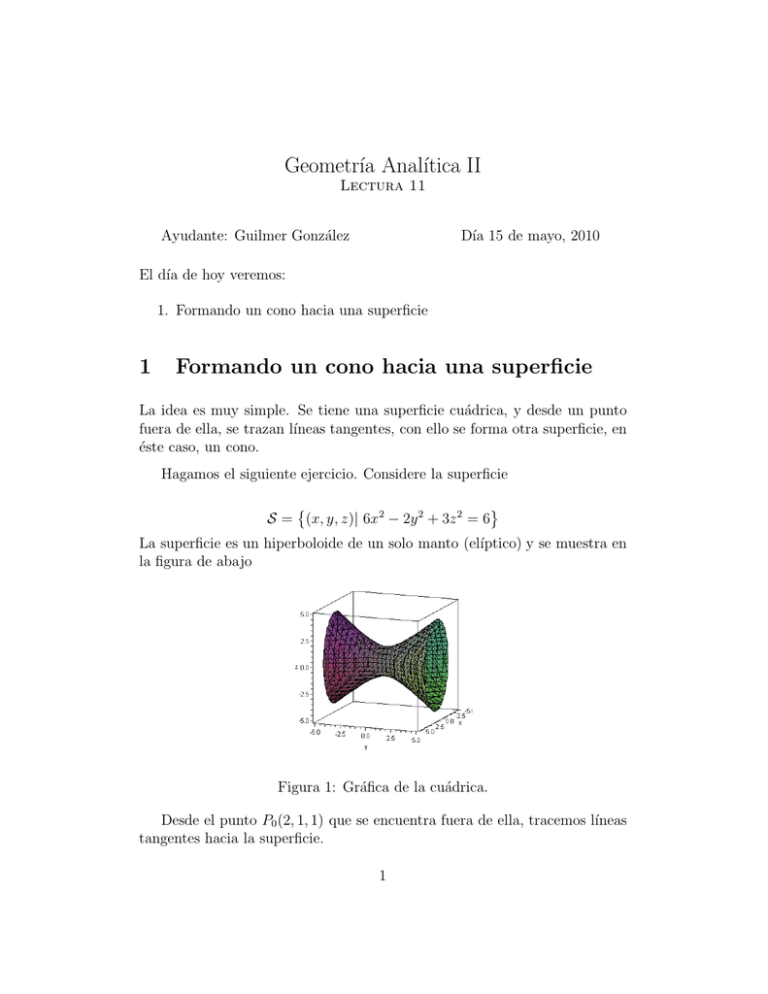
Geometrı́a Analı́tica II Lectura 11 Ayudante: Guilmer González Dı́a 15 de mayo, 2010 El dı́a de hoy veremos: 1. Formando un cono hacia una superficie 1 Formando un cono hacia una superficie La idea es muy simple. Se tiene una superficie cuádrica, y desde un punto fuera de ella, se trazan lı́neas tangentes, con ello se forma otra superficie, en éste caso, un cono. Hagamos el siguiente ejercicio. Considere la superficie S = (x, y, z)| 6x2 − 2y 2 + 3z 2 = 6 La superficie es un hiperboloide de un solo manto (elı́ptico) y se muestra en la figura de abajo Figura 1: Gráfica de la cuádrica. Desde el punto P0 (2, 1, 1) que se encuentra fuera de ella, tracemos lı́neas tangentes hacia la superficie. 1 La superficie cuádrica la podemos escribir en forma matricial como S = P t AP + γ = 0 donde 6 0 0 A = 0 −2 0 , 0 0 3 γ = −6 En śte ejercicio no tenemos términos lineales. Si el vector dirección, de la recta a trazar, lo escribimos por sus componentes d~ = (d1 , d2, d3 )t , la recta la escribimos como: 2 + td1 P (t) = P0 + td~ = 1 + td2 1 + td3 Para que la recta pase por la curva, debe satisfacerse que ~ tA(P0 + td) ~ +γ =0 (P0 + td) desarrollando y usando el hecho de que A es simétrica, lo anterior lo escribimos como ~ + γ + P t AP0 = 0 t2d~t Ad~ + 2t(P0t Ad) 0 Ahora bien, para que la recta solo toque tangencialmente a la superficie, debe cumplirse que la cuadrática en t tenga solamente un cero, lo cual ocurre cuando el discriminante asociado es cero: ~ 2 − 4d~t Ad(γ ~ + P t AP0 ) = 0 4(P0t Ad) 0 lo cual se puede escribir de una manera mucho más cómoda en ~ + P t AP0 ) = 0 d~t AP0 P0 Ad~ − d~t Ad(γ 0 y entonces la ecuación que caracteriza a los vectores dirección es 2 d~t [AP0 P0t A − (γ + P0t AP0 )]Ad~ = 0 y la ecuación del cono se escribe como (P − P0 )t[AP0 P0t A − (γ + P0t AP0 )A](P − P0 ) = 0 vamos ahora a revisar que se trata de un cono con centro en P = P0 . Calculemos la matriz AP0 P0t A − (γ + P0t AP0). Primero calculemos AP0 6 0 0 2 12 1 = −2 AP0 = 0 −2 0 1 3 0 0 3 ahora 12 144 −24 36 AP0 P0t A = (AP0 )(AP0 )t = −2 12 −2 3 = −24 4 −6 3 36 −6 9 Por otra parte, 12 γ + P0t AP0 = −6 + 2 1 1 −2 = 19 3 Ahora calculemos la matriz que describimos el supuesto cono 144 −24 36 6 0 0 30 −24 36 AP0 P0t A−(γ+P0tAP0 )A = −24 4 −6−19 0 −2 0 = −24 42 −6 36 −6 9 0 0 3 36 −6 −48 La ecuación del cono se escribe como 30 −24 36 x − 2 x − 2 y − 1 z − 1 −24 42 −6 y − 1 = 0 36 −6 −48 z−1 3 Para comprobar que es un cono, debemos observar los valores propios de la matriz asoaciada, es decir, calcular los ceros del polinomio caracterı́stico 30 −24 36 p(λ) = det −24 42 −6 = 0 36 −6 −48 haciendo las cuentas tenemos que p(λ) = (30−λ)[(42−λ)(−48−λ)−36]+24[24(48+λ)+6·36]+36[24·6−(42−λ)36] En clase haremos los detalles. Los valores propios segun Matlab son >> eig(A) ans = -6.2176e+001 1.8543e+001 6.7633e+001 >> La superficie es un cono con centro en P = P0 . En la gráfica de abajo se observa el cono que se forma al tirar la lı́neas hacia el hiperboloide. Figura 2: Gráfica de la cuádrica y el cono. Use k3dsurf, Matlab o Maple para graficar las superficies de su ejercicio. 4