C 0 M B I N A T 0 R I A

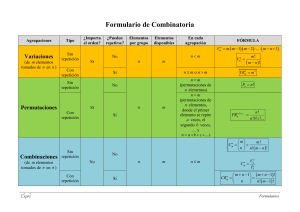
C0MBINAT0RIA
Combinatoria, rama de las matemáticas que estudia las posibles agrupaciones de objetos tomados de un conjunto
dado; es de gran importancia en otras ramas de las matemáticas. Por ejemplo, se utiliza para el desarrollo del binomio
de Newton; en la teoría de la probabilidad y en estadística (para calcular el número de casos posibles de un sistema).
También tiene importantes aplicaciones en el diseño y funcionamiento de ordenadores o computadoras, así como en
las ciencias físicas y sociales. De hecho, la teoría combinatoria es de gran utilidad en todas aquellas áreas en donde
tengan relevancia las distintas maneras de agrupar un número finito de elementos.
►IMPORTA EL ORDEN◄
VARIACIONES ORDINARIAS O SIN REPETICIÓN de m elementos tomados de n en n (n<m) son los distintos grupos que se
pueden formar con los m elementos, de manera que:

En cada grupo entre n elementos distintos.

Dos grupos son distintos si difieren en algún elemento o en el orden de colocación de estos.
El número de variaciones ordinarias de m elementos tomados de n en n se representa por Vm,n.
Vm,n=m(m-1)(m-2)...(m-n+1)=
m!
(m  n)!
VARIACIONES CON REPETICIÓN de m elementos tomados de n en n son los distintos grupos que se pueden formar con los m
elementos, de manera que:

En cada grupo entre n elementos, repetidos o no.

Dos grupos son distintos si difieren en algún elemento o en el orden de colocación de estos.
El número de variaciones con repetición de m elementos tomados de n en n se representa por VRm,n.
VR=mn
PERMUTACIONES ORDINARIAS es el caso particular de las variaciones de n=m. Se representa por Pn.
Pn=n!
PERMUTACIONES CON REPETICIÓN de n elementos donde el primer elemento se repite a veces, el segundo b veces,.... el
último k veces (a+b+...+k=n), son los distintos grupos que se pueden formar, de manera que:

En cada grupo de n elementos el primer elemento está “a” veces; el segundo “b” veces; ...

Un grupo se diferencia de otro únicamente por el orden de colocación de sus elementos.
El número de permutaciones con repetición de n elementos, donde el primer elemento se repite “a” veces, el segundo “b” veces, ...
el último k veces, se representa por Pna,b,...,k
PRna,b,...,k=
n!
a!b!...k!
►NO IMPORTA EL ORDEN◄
COMBINACIONES ORDINARIAS O SIN REPETICIÓN de m elementos tomados de n en n (n<m) son los distintos grupos que se
pueden formar con los m elementos. de manera que:

En cada grupo entre n elementos distintos.

Dos grupos son distintos si difieren en algún elemento pero no el orden de colocación de estos.
El número de combinaciones ordinarias de m elementos tomados de n en n se representa por Cm,n.
Cm,n=
m!
n!(m  n)!
COMBINACIONES CON REPETICIÓN de m elementos tomados de n en n son los distintos grupos que se pueden formar con los
m elementos, de manera que:

En cada grupo entre n elementos, repetidos o no.

Dos grupos son distintos si difieren en algún elemento pero no en orden de colocación de estos.
El número de combinaciones con repetición de m elementos tomados de n en n se representa por:
CRm,n=Cm+n-1,n.
CRm,n=
(m  n  1)!
n!(m  1)!