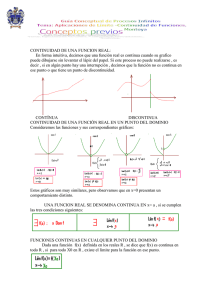
CONTINUIDAD CONTINUIDAD Una función f es continua en un
Anuncio

CONTINUIDAD
José Antonio Sánchez Guillén
CONTINUIDAD
f x =f a
Una función f es continua en un punto de abscisa a si lim
x a
Esta definición lleva implícita las siguientes condiciones:
a) La función está definida en a, es decir, existe f(a)
f x
b) Existe (y es finito) el límite lim
xa
c) El límite anterior coincide con el valor de la función
Continuidad de las funciones usuales
Función Polinómica.- siempre es continua
lim P x =P a
x a
P x P a
=
Q a
x a Q x
Función Racional.- Continua siempre que esté definida lim
si Q(a) # 0
Función Exponencial.- af(x) continua si lo es f(x)
Función Logarítmica.- log f(x) es continua para aquellos valores de x donde f(x) es positiva.
Funciones Trigonométricas.- sen x y cos x sí son continuas, pero tg x no lo es.
Funciones definidas a trozos.- son continuas si lo son en sus intervalos y en los puntos de unión.
En estas funciones hay que ver si la función está definida y si los límites laterales existen y
coinciden.
Estudia la continuidad en x=2 para las funciones:
1
f x =
x−2
{
g x = x , 2 si x2
4x−x , si x≥2
{
x−2
, si x≠2
h x = x 2−4
1 , si x =2
CONTINUIDAD
José Antonio Sánchez Guillén
EJERCICIOS RESUELTOS
1. Halla los puntos de discontinuidad de las siguientes funciones:
x+ 1
x + x− 6
a) f ( x) =
3x
x +1
b) g ( x) =
c) h( x) =
1
sen x
d) p x =e−x
2
2
Solución:
a) f(x) es continua siempre, pues el denominador nunca se hace cero
b) Discontinua en los ceros del denominador; es decir, cuando x2+x-6=0, cuyas soluciones son x=2 y x=3.
c) Discontinua cuando sen x=0. Por tanto, si x = k·π siendo k un número entero
d)
p( x) = e − x = 1
ex
es continua siempre porque la función exponencial ex nunca se hace cero.
2. Estudia la continuidad de la función:
{
2
x 1 , si x0
f x = −x1 , si 0≤x≤2
2
x −4x2 , si x2
Solución:
La función está definida para todo número real. En cada trozo viene dada por un polinomio y, por
tanto, será continua en cada uno de ellos. Entonces, los únicos puntos que pueden presentar
dificultades son los de unión de los respectivos trozos.
En cada uno de los puntos (x=0 y x=2) los límites laterales deben coincidir con f(0) y f(2)
respectivamente.
• En x = 0
Límite por la izquierda: Si x → 0 − , f ( x) = x 2 + 1 → 1
Límite por la derecha: Si x → 0 + , f ( x) = − x + 1 → 1
Por tanto, el límite vale 1 y coincide con f(0). Luego f(x) es continua en x=0
• En x = 2
Límite por la izquierda: Si x → 2 − , f ( x ) = − x + 1 → − 1
Límite por la derecha: Si x → 2 + , f ( x) = x 2 − 4 x + 2 → − 2
Por tanto, en x=2 el límite no existe. Luego f(x) es discontinua en x=2
En definitiva, la función f(x) es continua para todo x # 2
CONTINUIDAD
José Antonio Sánchez Guillén
EJERCICIOS
1. Estudia la continuidad de las siguientes funciones:
{
x 2−1 , si x≤0
a) f x =
2x−1 , si x0
{
{
{
2
, si x1
b) f x = x1
2−x , si x≥1
2
1−x
, si x−1
f
x
=
c)
1x
x3 , si x ≥−1
1−x
, si x1
f
x
=
d)
1−x 2
x−1/2 , si x≥1
2. Indica para qué valores de k son continuas las funciones:
{
{
2−x
, si x ≠2
a) f x = 4−x 2
x−k , si x=2
2
x −2x1
, si x ≠1
b) f x =
x −2
k , si x=1
3. Halla el valor de a y b para que sea continua la función:
{
{
x 21 , si x0
a) f x = axb , si 0≤x≤3
x−5 , si x3
x 2a , si x≤−1
b) f x = x1 , si −1x1
2−b , si x≥1