Sistemas de unidades - Mediciones y Errores de medición

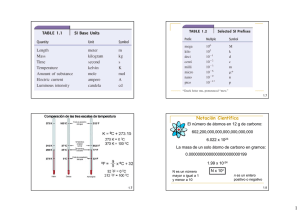
UNIVERSIDAD TECNOLÓGICA NACIONAL
Facultad Regional Rosario
UDB Física
Cátedra FÍSICA I
Sistemas de unidades - Mediciones y Errores de medición
Recordemos que una magnitud es todo aquello que se puede medir. Así longitud, presión, tiempo, velocidad, densidad, etc., son magnitudes. Las magnitudes que quedan determinadas en forma completa
por un número y una unidad se denominan escalares (ejemplo: masa, volumen, etc.). Algunas magnitudes
escalares son adimensionales -es decir, no poseen unidades-, por ejemplo la densidad relativa, el índice
de refracción, etc. Las magnitudes que requieren la especificación de dirección y sentido (y a veces también del punto de aplicación) para quedar completamente definidas, se denominan vectoriales (ejemplo:
velocidad, aceleración, fuerza, etc.)
Medir es comparar una cantidad (X) de cierta magnitud con otra cantidad (U) de la misma especie que
se toma arbitrariamente como unidad, de modo tal que se pueda asociar un número (n) que expresa
cuántas veces está contenida la unidad en la cantidad medida (X/U) = n. De esta manera se dice que n es
la medida de X con respecto a la unidad U. Desde luego que se debe especificar el proceso mediante el
cual se realiza la medición de la magnitud.
Si una unidad se acepta oficialmente, se la llama unidad estándar. Tradicionalmente un gobierno o un
organismo internacional establecen las unidades estándares. Un conjunto de unidades estándar y sus
combinaciones constituye un sistema de unidades. La definición de una unidad queda asociada con un
"modelo oficial", "patrón" o "estándar". A veces el "patrón" o "estándar" es material (como el del kilogramo masa, que es un cilindro de platino e iridio guardado en una oficina de París), y otras veces es descriptivo -cuando no se puede "guardar una muestra" en un laboratorio- (tal es el caso del estándar de
intensidad de corriente eléctrica o el de intensidad luminosa, para los cuales se prescribe el procedimiento y las condiciones que deben reunirse para determinarlos).
Una magnitud fundamental es aquella totalmente independiente de las demás. El Sistema Internacional de Unidades (SI), está basado en 7 unidades fundamentales que sirven para describir todas las magnitudes físicas conocidas hasta la fecha. Las unidades fundamentales en el SI son la masa -cuya unidad es el
kilogramo-, la longitud -cuya unidad es el metro-, el tiempo -cuya unidad es el segundo- y otras. Las magnitudes derivadas resultan de la combinación de las fundamentales a través de operaciones de acuerdo
con definiciones y leyes físicas (así, por ej. la velocidad es una relación entre la longitud y el tiempo).
El SIMELA, Sistema Métrico Legal Argentino, adoptado por nuestro país según la ley N° 19.511 de
1.972, tomó todas las unidades, símbolos, múltiplos y submúltiplos del SI; y le agregó algunas pocas unidades más, tales como el litro (l o L), hora (h), minuto (min), grado sexagesimal (°), etc.
Mediciones directas e indirectas
Para que el proceso de medición quede determinado deben interactuar necesariamente tres componentes o sistemas: el del objeto a medir, el de medición o instrumento de medida y el de comparación o
unidad de medida. Habrá una interacción previa entre el instrumento y la unidad adoptada (calibración),
y luego la medición propiamente dicha al interactuar el instrumento calibrado con el objeto a medir.
Se denomina medición directa a aquella que resulta de leer directamente sobre la escala de un instrumento. Por ejemplo una longitud mediante una regla, un volumen mediante una bureta, etc.
Una medición indirecta es aquella que resulta de operaciones de cálculos realizadas sobre magnitudes
medidas directamente. Por ejemplo, la superficie de un terreno rectangular, a partir de su largo y su anCurso Promoción Directa
1
Año 2011
cho, la densidad de un líquido a partir de su masa -determinada con una balanza- y de su volumen determinado con una probeta-, etc.
Incertezas o errores de medición
Siempre una medición está afectada de incerteza o "error". Por ejemplo, al medir un espesor, por más
refinado que sea el método y el instrumento de medida, el límite estaría impuesto por los átomos superficiales que vibran con respecto a una "posición media".
Se define como error de una medida a la diferencia entre el valor obtenido en la medición y el valor
real de la magnitud medida. Podemos diferenciar por su origen, al menos dos tipos de errores: los errores sistemáticos, y los errores casuales o incidentales. Existe una teoría sobre errores que intenta disminuir y evaluar la influencia de los errores en el resultado final de una medición y, a la vez proveer métodos
de cálculos para estimarlos.
Los errores sistemáticos se deben a diversas causas y son, en muchos casos determinables y corregibles, siempre y cuando se conozca lo suficiente de la física del proceso. Se les llama sistemáticos porque
dan efectos consistentes: siempre tienen el mismo signo al repetirse las mediciones en las mismas condiciones. Estos errores pueden provenir de defectos en el instrumento de medida (una cinta métrica estirada, un instrumento de aguja que no parta de cero), de la acción permanente de una causa exterior (campos magnéticos o eléctricos presentes), o de las características propias del método de medida (medir masas de cuerpos poco densos sin tener en cuenta el empuje del aire). En muchos casos el error sistemático
puede determinarse en valor y signo y corregir el valor obtenido de la medida realizada. Para poder determinar este tipo de errores se debe tener en cuenta la información disponible sobre los instrumentos de
medida (manuales de operación de los mismos), y un buen conocimiento de las hipótesis y limitaciones
propias del método de medida y de las alteraciones que dicho método puede introducir en la medida debido al proceso mismo de medición. Cuando no se tiene forma de evaluar con certeza o incluso de conocer la existencia de un error sistemático, la medida perderá en exactitud; el valor medido discrepará (por
exceso o por defecto) con el valor real de la magnitud en mayor o menor medida según sea la magnitud
(en general desconocida) del error sistemático introducido en la medición.
Dentro de los errores sistemáticos se suelen incluir los llamados errores instrumentales o de apreciación. Estos errores surgen como consecuencia de las limitaciones propias de los instrumentos de medición
y de la perfección con que los mismos fueron construidos. En la mayoría de los casos las mediciones se
concretan con la lectura de una escala graduada en el instrumento de medida. Al valor representado por
la mínima división de la escala se la llama Apreciación de la escala y se la denomina con la letra A.
En general los instrumentos están diseñados de tal modo que el fabricante garantiza que el límite
máximo del error atribuible al instrumento nunca supera la apreciación (A) del mismo. Al efectuar la lectura, el observador “estima”, en general, una fracción de A. El signo de este error clasificado dentro de los
sistemáticos, puede ser positivo o negativo aunque su valor puede ser considerado prácticamente constante para un mismo observador que opera en iguales condiciones. Así por ejemplo cuando se mide una
longitud con una regla milimetrada, un observador no experimentado, o provisto con una regla de mala
calidad podrá estimar fracciones de hasta 0,5 mm mientras que un observador hábil (o el anterior, provisto con una regla de mejor calidad) puede llegar a estimar hasta 0,2 mm. Los errores de apreciación estimados respectivos serán de 0,5 y 0,2 mm. Se define un criterio de tolerancia (t) para determinar este tipo
de error sistemático donde t = A/n. El factor n puede tomar los valores de: n = 1,2,3,4 o 5, dependiendo
de las características del instrumento y del criterio del observador (mayor n, supone un mejor instrumento y/o operador más diestro con menor error de apreciación). Los errores sistemáticos estimados en base
a la apreciación del instrumento fijan una cota a los errores azarosos (que analizaremos a continuación).
Los errores casuales o incidentales son totalmente aleatorios, aparecen distribuidos al azar. Si a una
misma magnitud se la mide varias veces, con el mismo instrumento y en las mismas condiciones, los resulCurso Promoción Directa
2
Año 2011
tados obtenidos seguramente diferirán entre sí. Esto es natural en los procesos de mediciones de los fenómenos físicos. Si así no ocurriera hay que pensar que se eligieron inadecuadamente instrumentos y/o el
método muy poco sensibles para la medición. Estas discrepancias pueden deberse a varias causas: fluctuaciones en el medio físico en que se realiza la medición (cambios de temperatura, de la presión, de la
iluminación, vibraciones en el piso donde se asienta el experimento) y/o a factores personales del operador (estado de stress, cansancio visual, situación anímica) y otras desconocidas. La diferencia en cada caso
entre los distintos valores medidos y el valor considerado como más representativo de la magnitud medida es lo que se llama error casual o incidental. La proximidad entre los valores medidos entre sí, se denomina precisión. No debe confundirse precisión con exactitud; una serie de mediciones puede ser muy
precisa (valores muy semejantes) pero poco exacta (valores alejados del valor exacto o real).
Los errores casuales pueden predecirse, o al menos ser acotados, a través de teorías o modelos físicos,
lo cual se justifica cuando se realiza una gran cantidad de veces la determinación de una misma magnitud.
Lo que se dispone al finalizar una serie de experiencias, es un conjunto de “n” medidas de la magnitud
“x”, y debemos adoptar un valor como resultado. De acuerdo con la teoría de errores de medición, el mejor valor es la media artimética del conjunto de valores de las medidas. Se representa con el símbolo x y
se lo denomina simplemente valor medio:
n
x = ( ∑ xi )/n
(1)
i =1
A partir de este valor medio (el más próximo al verdadero), de acuerdo al modelo estadístico de Gauss
y a través de hipótesis y aproximaciones razonables para la mayoría de las experiencias en física, se puede
demostrar que la desviación estándar de una medida (Sx), se puede calcular a partir de un conjunto finito
n
de “n” medidas según:
∑ (δxi )2
Sx =
i =1
n −1
(2)
Donde δxi =(xi – x ), se conoce como desviación aparente de la medida xi. La desviación estándar de
una medida está relacionada con la desviación estándar del valor medio (S x ), de acuerdo con:
S x = Sx / n
(3)
¿Cuál es la diferencia entre desviación estándar de una medida y desviación estándar del valor medio? El modelo predice que si efectuamos un conjunto de n medidas y adoptamos como resultado del
mismo, el valor de “una” de ellas, el error azaroso estimado es Sx. Si en cambio adoptamos no ya uno de
los n valores, sino la media aritmética de esos valores ( x ), el error azaroso adjudicable es S x .
En general en un proceso de medición se busca que ambos tipos de errores –de apreciación y casualessean de un mismo orden de magnitud, por lo que se deben tener en cuenta ambos al diseñar una medición y planificar el número de mediciones a realizar.
Cifras significativas
El resultado de una medida o cálculo debe explicitarse correctamente en función de las cifras significativas de las cantidades que intervienen en su determinación. Las cifras exactas y significativas dependen
de los errores correspondientes con que se expresan los resultados, y con ello la representatividad de
dichos resultados. Así por ejemplo, la aritmética nos dice que 9 mm = 9,0 mm, pero la física nos dice que
9 mm ≠ 9,0 mm
Para entender estas afirmaciones haremos uso del concepto de estimación de una lectura. Cuando un
observador escribe: L = 9,0 mm ± 0,1 mm, está afirmando que L puede valer entre 8,9 mm y 9,1 mm, lo
cuál significa que el cero tiene una información sobre la cifra de las décimas.
Otro observador, menos hábil, o con la vista no tan buena, o trabajando con menor iluminación, puede
Curso Promoción Directa
3
Año 2011
informar sólo hasta 1 mm. Entonces su lectura de la misma cantidad será, por ejemplo L = 9 mm + 1 mm.
El número de cifras significativas de la medida de una magnitud es el número de dígitos conocidos confiablemente que contiene. Los ceros son significativos sólo cuando se encuentran a la derecha de un número, de lo contrario sólo sirven para ubicar la como decimal.
La última cifra significativa es la insegura -la primera afectada de incerteza o error-. Por ejemplo:
0,1200 kg ó 120,0 g ó 1,200 x 10 kg, tienen cuatro cifras significativas. Las décimas de gramos son inseguras (las potencias de diez no alteran el número de cifras significativas).
Redondeo de cifras significativas
Cuando se realizan cálculos es conveniente arrastrar todas las cifras durante las operaciones intermedias, hasta obtener el resultado final, y entonces en este último efectuar el redondeo. El criterio que se
aplica es el siguiente:
1) Si la primera cifra a eliminar es mayor que 5 se suma 1 a la última cifra retenida (ejemplo: 4,3267,
suponiendo redondeo a tres cifras significativas: 4,33)
2) Si la primera cifra a eliminar es menor que 5, la última cifra retenida se deja tal cual (ejemplo:
7,5649, suponiendo redondeo a tres cifras significativas: 7,56)
3) Si la primera cifra a eliminar es 5, hay dos casos diferentes según que la última cifra retenida sea par
o impar, si es par se deja tal cual, y si es impar se incrementa en 1. (Ejemplo: 6,2458, suponiendo redondeo a tres cifras significativas: 6,24; 2,4759, suponiendo redondeo a tres cifras significativas: 2,48)
Expresión correcta del resultado de una medición
Para tener en cuenta el hecho que toda medición está afectada de incertezas o errores, se conviene en
expresar los resultados como intervalos de confianza. En otras palabras, se da el valor más probable "valor representativo" o "valor observado"- y el margen de error que lo afecta. Por ejemplo, para una
magnitud M (masa): M = "valor representativo" ± error. Ejemplo: M = (34,56 ± 0,01) g
Adviértase que no tendría sentido expresar: M = (34,56376 ± 0,01) g porque la 2º cifra decimal del valor
representativo ya está afectada de error.
A su vez, el error que afecta a una medición se debe expresar con una sola cifra significativa (algunas
pocas veces se suele aceptar el uso de hasta dos cifras significativas). La cantidad de decimales del "valor
representativo" debe coincidir con la del error informado. Ejemplos:
M = 34,56 ± 0,015........incorrecto
M = 34,56 ± 0,02..........correcto
M =27,79 + 0,5...........incorrecto
M = 27,8 ± 0,5..............correcto
Errores en una medición directa
Supongamos el caso de una sola medición. Convengamos los siguientes símbolos y significados:
X = valor exacto de una magnitud (siempre desconocido)
X' = valor representativo de la magnitud medida
Ea = ∆X = X - X' = error absoluto (siempre desconocido)
En la práctica ∆X se estima como igual al error de apreciación (dijimos, a su vez, que este último puede
llegar a tomarse igual a la apreciación del instrumento utilizado, o a la tolerancia).
Er = ∆X/X = ∆X(estimado)/X' = error relativo
Er % = (∆X/X).100 = (∆X(estimado)/X').100 = error relativo porcentual
Propagación de errores en mediciones indirectas
Supongamos dos magnitudes medidas directamente: A = A' ± ∆A
Curso Promoción Directa
4
y
B = B' ± ∆B
Año 2011
Veamos cómo se procede al trabajar con ellas mediante las operaciones matemáticas más comunes:
Suma:
Para efectuar la operación:
C=A+B
Y lograr la expresión de un resultado así:
C = C´ ± ∆C
Se puede demostrar que resulta:
C' = A' + B'
El valor "representativo" de la suma se obtiene sumando los valores "representativos" individuales.
Por otra parte, se puede demostrar que el error absoluto resulta:
∆C = ∆A + ∆B
Es decir, el error absoluto de la suma es igual a la suma de los errores absolutos individuales.
Resta:
Para efectuar la operación:
C=A-B
Y lograr la expresión de un resultado así:
C = C´ ± ∆C
Se puede demostrar que resulta:
C' = A' - B'
El valor "representativo" de la resta se obtiene restando los valores "representativos" individuales.
Por otra parte, se puede demostrar que el error absoluto resulta:
∆C = ∆A + ∆B
Es decir, el error absoluto de la resta es igual a la suma de los errores absolutos individuales (se calcula
del mismo modo que para las sumas, como vimos antes).
Ej: Supongamos que se desea determinar una cierta masa de agua ma, para lo cual se pesa ésta en un
recipiente, obteniéndose el siguiente valor de masa total mt = (583,2 + 0,1) g. Luego se pesa el recipiente
vacío obteniéndose el valor: mr = (30,285 + 0,005) g. La masa de agua calculada por diferencia, resulta:
ma = mt – mr = 583,2 g - 30,285 g = 552,915 g
Notemos que las dos últimas cifras son cifras al azar, pues podríamos haber puesto cualquier cifra (y no
necesariamente ceros), por poner algo, después del 2 en el valor de mt para poder restar, de modo que
carecen de sentido y el resultado debe expresarse en este caso con solamente la primera cifra decimal. El
mismo resultado se obtiene calculando el error como la suma de los errores absolutos, que en el ejemplo
es 0,1 g. El resultado debe expresarse entonces como: ma = (552,9 ± 0,1) g.
Concluimos que, como regla práctica, cuando se suman o restan cantidades no enteras, el resultado
debe ser expresado con un número de cifras decimales igual al del sumando de menor número de cifras
decimales.
Producto:
Para efectuar la operación:
C=AxB
Y lograr la expresión de un resultado así:
C = C´ ± ∆C
Se puede demostrar que resulta:
C´ = A' x B'
El valor "representativo" del producto se obtiene multiplicando los valores "representativos" de los factores. Para este caso se puede demostrar la siguiente relación entre los errores relativos:
∆C/C´ = ∆A/A' + ∆B/B'
Es decir, el error relativo del producto es igual a la suma de los errores relativos individuales.
De la expresión anterior despejamos entonces el error absoluto -que necesitamos para expresar el resultado- y nos queda:
∆C = (∆A/A' + ∆B/B') x C'
Cociente:
Para efectuar la operación:
Curso Promoción Directa
C=A/B
5
Año 2011
Y lograr la expresión de un resultado así:
C = C´ ± ∆C
Se puede demostrar que resulta:
C' = A'/ B'
El valor "representativo" del cociente se obtiene dividiendo los valores "representativos" individuales.
También en este caso -al igual que para el producto- se puede demostrar la siguiente relación entre los
errores relativos:
∆C/C´ = ∆A/A' + ∆B/B'
Es decir, el error relativo del cociente es igual a la suma de los errores relativos individuales.
De la expresión anterior despejamos entonces el error absoluto -que necesitamos para expresar el resultado- y nos queda:
∆C = (∆A/A' + ∆B/B') x C'
Ej: Supongamos que debemos calcular la rapidez media V de un cuerpo que realizó un desplazamiento
L = (2586 + 1) m en un tiempo t = (1,54 + 0,01) s. El cociente realizado con la calculadora resulta:
V = L / t = 2586 m / 1,54 s = 1679,2208 m/s
Este valor se obtuvo considerando que todas las cifras decimales del valor de L son ceros, y que t =
1,54000…, lo cual no es correcto. Si calculamos el error relativo del cociente, sumando los errores relativos de L y de t, tenemos: ErL = 1 m / 1585 m = 3,8 x 10-4 y Ert = 0,01 s /1,54 s = 6,5 x 10-3 y ∆V = (3,8 x
10-4 + 6,5 x 10-3) 1679,2208 m/s = 11,5 m/s. Esto significa que el error de V afecta la decena con lo cual
todos las cifras que le siguen están indeterminadas y carecen de valor. El resultado deberá expresarse,
entonces, según: V = (16,7 ± 0,1) x 102 m/s o bien: V = (1,67 ± 0,01) km/s.
El resultado queda expresado con el mismo número de cifras significativas que tiene el valor de t, que
es la magnitud con mayor error relativo. Concluimos que, como regla práctica, cuando se multiplican o
dividen cantidades, el resultado debe ser expresado con un número de cifras significativas igual al del
factor de menor número de cifras significativas.
Potencia:
Para efectuar la operación:
C = An
Y lograr la expresión de un resultado así:
C = C´ ± ∆C
Se puede demostrar que resulta:
C' = A'n
El valor "representativo" de la potencia se obtiene elevando al exponente n el valor "representativo"
individual. Se puede demostrar la siguiente relación entre los errores relativos:
∆C/C´ = n . ∆A/A'
Es decir, el error relativo de la potencia es igual al producto del exponente por el error relativo de la
base. De la expresión anterior resulta el error absoluto -que necesitamos para expresar el resultado- expresado como un caso particular del producto de n factores iguales, según: ∆C = (n . ∆A/A' ) x C´
Curso Promoción Directa
6
Año 2011