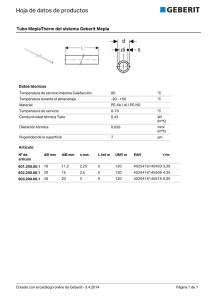
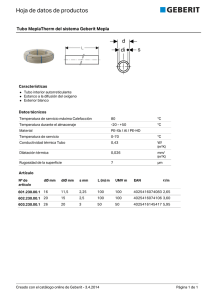
DILATACIÓN TÉRMICA DE SÓLIDOS

DILATACIÓN TÉRMICA DE SÓLIDOS
1.- Objetivo:
Cálculo de la dilatación lineal de varios sólidos; por ejemplo: acero, aluminio, etc.
2.- Principio:
Se determina la dilatación lineal de varios sólidos elevando su temperatura utilizando vapor.
3.- Materiales:
- 1 soporte de dos piezas
- 1 tubo de muestra
- 1 amplificador de ángulos
- 1 regla (precisión: 0,5 mm)
- 1 termómetro (precisión: 0,5 ºC)
- Termopares de superficie (precisión: 1ºC)
- 1 calibre (precisión: 0,05 mm)
- 2 tubos de silicona
- 2 aros soporte
- 1 soporte vertical
- 1 rejilla
- 1 matraz erlenmeyer
- 1 tapón de goma perforado
- 1 vaso de precipitados
- Agua
4.- Montaje:
Se realiza un montaje como el esquematizado en la figura 1. De los extremos del tubo de
muestra (se utiliza un tubo para simplificar el problema) salen dos tubos de silicona. Uno de ellos va hasta
un matraz y el otro hasta un vaso de precipitados. Conviene que ambos estén situados en posición vertical
para evitar que se acumule agua de la condensación en su interior. Por esta misma razón es preferible que
el extremo del tubo de muestra que conecta con el matraz esté más bajo que el otro extremo.
El tubo de muestra se monta sobre un soporte de forma que uno de sus extremos permanezca
solidario al soporte y el otro se apoya sobre un índice que sirve de amplificador de ángulos.
Se coloca una regla solidaria al soporte y paralela a éste a una distancia igual a la longitud del índice.
Sobre la superficie del tubo de muestra se colocan varios termopares de superficie cuyas lecturas se
toman en un PC.
Dilatación térmica de sólidos
1
PC
Tubo de muestra
Figura 1. Esquema del montaje
5.- Procedimiento:
Se anotan las condiciones iniciales: temperatura inicial del tubo ( t0 ), y la longitud desde la fijación
del tubo hasta el índice ( l0 ). Se miden los radios del índice para calcular su grado de amplificación ( R1 y R2
).
Se calienta agua en el matraz hasta llegar a la ebullición. Por el paso de vapor a lo largo del tubo,
éste llega hasta una temperatura ( t f ).
Por último, se mide sobre la regla la distancia que se ha movido el extremo del índice sobre ella ( L
).
6.- Fundamento teórico:
Con algunas pocas excepciones, las dimensiones de los sólidos y en especial de los metales
aumentan cuando se eleva su temperatura.
Se define el coeficiente de expansión de volumen como:
αv =
FG IJ
H K
1 ∂V
V ∂T
(1)
p
Que es mayor que cero en la mayoría de los casos.
Considerando una única dimensión se obtiene el coeficiente de expansión lineal:
αl =
FG IJ
H K
1 ∂l
l ∂T
(2)
p
Como se demuestra a continuación, la relación entre ambos coeficientes es la siguiente: α v = 3α l .
Dilatación térmica de sólidos
2
Sea V = Cte • abc , siendo a, b y c las dimensiones indicativas del volumen del sólido, entonces:
αv =
FG IJ
H K
1 ∂V
V ∂T
=
p
FG b
H
1 ∂ Cte • abc
V
∂T
gIJ
K
=
p
FG IJ
H K
1 ∂a
a ∂T
+
p
FG IJ
H K
1 ∂b
b ∂T
+
p
FG IJ
H K
1 ∂c
c ∂T
= 3α l
p
En este caso se mide α l dado que en sólidos con una dimensión predominante frente a las otras
resulta más sencillo medir la variación de esta, dado que son variaciones en general pequeñas.
Dado que el incremento de longitud ∆l = l f − l0 es pequeño comparado con la longitud inicial l0 ,
se puede poner:
αl =
∆l 1
l0 ∆T
(3)
Y entonces:
d
l = l0 1 + α l t f − t0
i
(4)
Para medir ∆l se usa un procedimiento indirecto; conocidas las distancias de la punta de la aguja
del índice a su eje y del tubo al eje de la aguja, R1 y R2 respectivamente, se calcula como:
R2
L
R1
∆l =
(5)
Siendo L el incremento de longitud amplificado.
7. Cálculo de errores
El error, partiendo de ( 3 ) y ( 5 ) se calcula como sigue:
FG ∂α ∆R IJ + FG ∂α ∆R IJ + FG ∂α ∆LIJ + FG ∂α ∆l IJ + FG ∂α ∆b∆T gIJ
H ∂R K H ∂R K H ∂L K H ∂l K H ∂∆T K
2
∆α =
2
2
2
2
2
1
1
0
2
(6)
0
Siendo estos valores:
∂α
1 L 1
=
∂R2 R1 l0 ∆T
(7)
∂α
R L 1
= − 22
∂R1
R1 l0 ∆T
(8)
Dilatación térmica de sólidos
3
∂α R2 1 1
=
∂L R1 l0 ∆T
(9)
∂α
R L 1
=− 2 2
∂l0
R1 l0 ∆T
( 10 )
FG IJ
H K
∂α
R L 1
=− 2
∂∆T
R1 l0 ∆T
2
( 11 )
8. Realización del ensayo
Se realiza un ensayo con una muestra de acero siendo los valores obtenidos:
t0
21 ºC
tf
87 ºC
∆T = t f − t0
66 K
R1
205,0 mm
R2
3,00 mm
l0
424,5 mm
L
19,0 mm
Así, de ( 3 ), de ( 5 ) y ( 6 ) se obtiene:
α = 10 ⋅10−6 ± 4,32 ⋅10−7 K-1
Se realiza un ensayo con una muestra de acero siendo los valores obtenidos:
t0
19 ºC
tf
88 ºC
∆T = t f − t0
69 K
R1
205,0 mm
R2
3,00 mm
l0
421 mm
L
4 mm
Así, de ( 3 ), de ( 5 ) y ( 6 ) se obtiene:
α = 2 ⋅10−6 ± 2,67 ⋅10-7 K-1
Se realiza un ensayo con una muestra de acero siendo los valores obtenidos:
t0
21 ºC
tf
87 ºC
∆T = t f − t0
66 K
R1
205,0 mm
R2
3,00 mm
l0
421 mm
L
4,5 mm
Así, de ( 3 ), de ( 5 ) y ( 6 ) se obtiene:
α = 2 ⋅10−6 ± 2,67 ⋅10-7 K-1
Se realiza un ensayo con una muestra de acero siendo los valores obtenidos:
t0
21 ºC
tf
87 ºC
∆T = t f − t0
66 K
Dilatación térmica de sólidos
R1
205,0 mm
R2
3,00 mm
l0
421 mm
L
3,5 mm
4
Así, de ( 3 ), de ( 5 ) y ( 6 ) se obtiene:
α = 2 ⋅10−6 ± 2,67 ⋅10-7 K-1
Se muestra en la figura 2 el proceso de toma de datos de temperaturas que corresponden a esta última
experiencia.
Figura 2
9. Cálculo estadístico
Para una muestra de n valores de la variable α i su media y su desviación típica vienen dadas
respectivamente por:
n
α=
∑α i
i =1
( 12 )
n
∑ bα i − α g
n
∆α =
i =1
2
n −1
Dilatación térmica de sólidos
( 13)
5
En nuestro caso tenemos una muestra de cuatro valores. Sustituyéndolos en ( 12 ) y ( 13 ):
α = 4 ⋅10−6 K-1
∆α = 4 ⋅10−6 K-1
Quedando como resultado:
α = 4 ⋅10−6 ± 4 ⋅10−6 K-1
Dilatación térmica de sólidos
6