Termodinámica: Método de Newton–Raphson
Anuncio
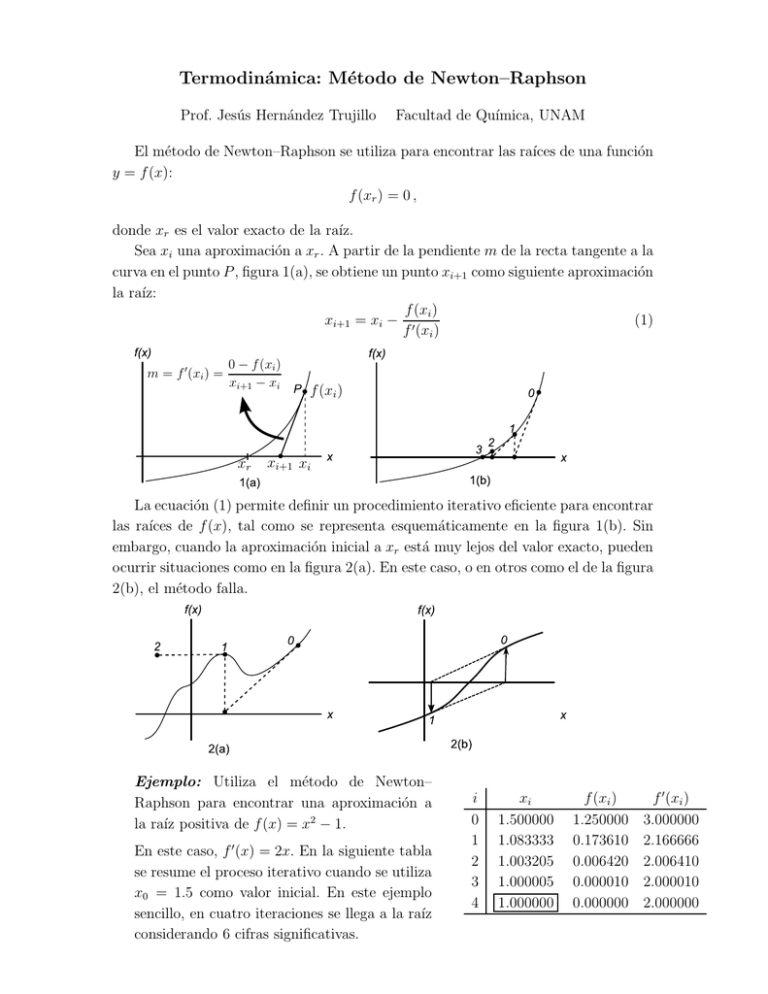
Termodinámica: Método de Newton–Raphson Prof. Jesús Hernández Trujillo Facultad de Quı́mica, UNAM El método de Newton–Raphson se utiliza para encontrar las raı́ces de una función y = f (x): f (xr ) = 0 , donde xr es el valor exacto de la raı́z. Sea xi una aproximación a xr . A partir de la pendiente m de la recta tangente a la curva en el punto P , figura 1(a), se obtiene un punto xi+1 como siguiente aproximación la raı́z: f (xi ) xi+1 = xi − ′ (1) f (xi ) m = f ′ (xi ) = 0 − f (xi ) xi+1 − xi xr f (xi ) xi+1 xi La ecuación (1) permite definir un procedimiento iterativo eficiente para encontrar las raı́ces de f (x), tal como se representa esquemáticamente en la figura 1(b). Sin embargo, cuando la aproximación inicial a xr está muy lejos del valor exacto, pueden ocurrir situaciones como en la figura 2(a). En este caso, o en otros como el de la figura 2(b), el método falla. Ejemplo: Utiliza el método de Newton– Raphson para encontrar una aproximación a la raı́z positiva de f (x) = x2 − 1. En este caso, f ′ (x) = 2x. En la siguiente tabla se resume el proceso iterativo cuando se utiliza x0 = 1.5 como valor inicial. En este ejemplo sencillo, en cuatro iteraciones se llega a la raı́z considerando 6 cifras significativas. i 0 1 2 3 4 xi 1.500000 1.083333 1.003205 1.000005 1.000000 f (xi ) 1.250000 0.173610 0.006420 0.000010 0.000000 f ′ (xi ) 3.000000 2.166666 2.006410 2.000010 2.000000



![[Prac03-Práctica]](http://s2.studylib.es/store/data/003990524_1-e393ff5943abb13aea6916f6b05f51e4-300x300.png)



![[Prac03-Prepráctica]](http://s2.studylib.es/store/data/003990523_1-ce5e214aaa06ad3b618169833fcf4c9e-300x300.png)



