DE LA GRÁFICA A LA EXPRESIÓN ALGEBRAICA LA RECTA

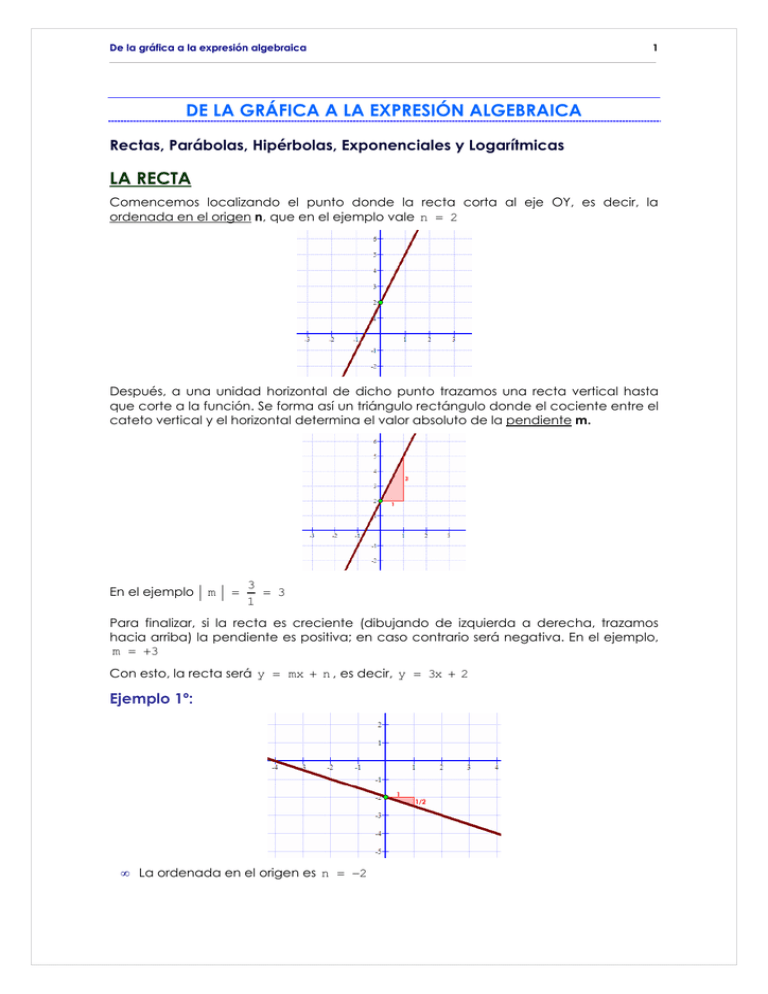
De la gráfica a la expresión algebraica
1
DE LA GRÁFICA A LA EXPRESIÓN ALGEBRAICA
Rectas, Parábolas, Hipérbolas, Exponenciales y Logarítmicas
LA RECTA
Comencemos localizando el punto donde la recta corta al eje OY, es decir, la
ordenada en el origen n, que en el ejemplo vale n = 2
Después, a una unidad horizontal de dicho punto trazamos una recta vertical hasta
que corte a la función. Se forma así un triángulo rectángulo donde el cociente entre el
cateto vertical y el horizontal determina el valor absoluto de la pendiente m.
En el ejemplo
m
=
3
= 3
1
Para finalizar, si la recta es creciente (dibujando de izquierda a derecha, trazamos
hacia arriba) la pendiente es positiva; en caso contrario será negativa. En el ejemplo,
m = +3
Con esto, la recta será y = mx + n , es decir, y = 3x + 2
Ejemplo 1º:
• La ordenada en el origen es n = −2
2
De la gráfica a la expresión algebraica
• El triángulo tiene de cateto vertical
m
=
1
y de cateto horizontal 1, por lo que
2
1
2
• La recta es decreciente (de izquierda a derecha se dibuja hacia abajo) y así la
1
pendiente ha de ser negativa, m = −
2
y = −
1
x − 2
2
Ejemplo 2ª:
• La ordenada en el origen es n = −1
• El triángulo tiene de cateto vertical 4 y de cateto horizontal 1, por lo que
4
m =
= 4
1
• La recta es creciente (de izquierda a derecha se dibuja hacia arriba) y así la
pendiente ha de ser positiva, m = +4
y = 4x − 1
LA PARÁBOLA
En primer lugar deberemos localizar el vértice, que se encuentra en el punto
V ( x0 , y 0 ) = V ( 3 , − 1 ) :
A partir del vértice debemos construir un triángulo de lados paralelos a los ejes, cuya
base debe medir 1, y cuya altura alcance la curva:
3
De la gráfica a la expresión algebraica
• El cociente entre el cateto vertical y el horizontal determina el valor absoluto del
1
coeficiente principal, es decir, a =
= 1
1
• Por último, observar el sentido de las ramas. Si se dirigen hacia arriba, el
coeficiente principal será positivo, mientras que si se dirigen hacia abajo, en
coeficiente principal será negativo. Así, en nuestro caso a = +1
• Con estos datos, la parábola es y − y0 = a(x − x0 )2 ⇒ y − (− 1) = +1(x − 3)2
y = (x − 3)2 − 1
Ejemplo 1º:
• El vértice se encuentra en V( − 2 , 3
)
• EL triángulo tiene de cateto vertical 3 y cateto horizontal 1:
• Las ramas se dirigen hacia abajo, a = −3
•
y − 3 = −3(x − (−2))2
y = −3(x + 2)2 + 3
Ejemplo 2º:
a
=
3
= 3
1
4
De la gráfica a la expresión algebraica
• El vértice se encuentra en V ( 3 , 2
)
1
• EL triángulo tiene de cateto vertical
y cateto horizontal 1:
2
• Las ramas se dirigen hacia arriba, a = +
•
y − 2 =
a
=
1
2
1
=
1
2
1
2
1
(x − 3)2
2
y =
1
(x − 3)2 + 2
2
LA HIPÉRBOLA
Lo primero que debemos hacer es localizar y dibujar las asíntotas. Donde se corten
ambas tendremos en centro de la hipérbola C( x0 , y0 ) . En nuestro caso, las asíntotas
son y = 2 ; x = 1 , por lo que el centro está en C( 1 , 2 ) .
Seguidamente, a una unidad del centro, trazamos una vertical hasta que corte a la
función, formándose así un rectángulo de base b y altura a. Estos dos valores
b
3
determinan k =
=
= 3
a
1
5
De la gráfica a la expresión algebraica
Para finalizar, las asíntotas determinan cuatro sectores similares a los cuatro cuadrantes
del plano. Si la función ocupa los sectores I y III, el valor de k será positivo, mientras que
si ocupa los sectores II y IV la k será negativa, por lo que en nuestro caso k = +3
Con todo esto, la hipérbola será y − y0 =
k
3
, es decir: y − 2 =
x − x0
x −1
Ejemplo 1º:
x = 0
• Las asíntotas están en 
⇒ C( 0 , − 2)
y = −2
1
• El rectángulo tiene de base 1 y altura
por lo que k
2
=
1
2
1
=
1
2
• Las ramas de la hipérbola ocupan los sectores I y III, por lo que k es positiva:
1
k = +
2
•
1
2
y − (−2) =
x −0
y = 2+
1
2x
6
De la gráfica a la expresión algebraica
Ejemplo 2º:
x = −2
• Las asíntotas están en 
⇒ C( − 2 , − 2)
y = −2
• El rectángulo tiene de base 1 y altura 2 por lo que k
=
2
1
= 2
• Las ramas de la hipérbola ocupan los sectores II y IV, por lo que k es negativa:
k = −2
•
y − (−2) =
−2
x − (−2)
y = −2 −
2
x + 2
LA EXPONENCIAL
Localizamos y dibujamos la asíntota horizontal
Buscamos un punto de la gráfica que se encuentre a una unidad de la asíntota (en
vertical), P( 1 , − 2)
De la gráfica a la expresión algebraica
7
Trazamos un eje vertical que pase por dicho punto
Donde se corta este eje vertical con la asíntota se encuentra el “centro” de la
exponencial C( x0 , y0 ) = C( 1 , − 3)
Si la función es creciente, trazamos una vertical desde la asíntota hasta la función, a
una unidad la derecha del centro, formándose así un triángulo; dividiendo el cateto
vertical entre el horizontal quedará determinada la base de la exponencial, que en
2
nuestro caso es a =
= 2
1
Con todo esto, la exponencial es y − y0 = a (x − x0 ) , es decir, y + 3 = 2(x − 1)
Ejemplo 1ª:
8
De la gráfica a la expresión algebraica
• Asíntota: y = −1
• Punto P de la función a una unidad de la asíntota: P( − 2 , 0
)
• Eje vertical x = −2
• Centro, intersección del eje con la asíntota: C( − 2 , − 1
)
• A una unidad a la derecha del centro, se forma un triángulo de cateto vertical
y cateto horizontal 1, por lo que la base de la exponencial es a =
1
• La exponencial es y − (−1) =  
 2
1
2
1
2
x −(−2)
1
y =  
 2
, es decir:
x+2
−1
Ejemplo 2º:
• Asíntota: y = −3
• Punto P de la función a una unidad de la asíntota: P( 2 , − 2
)
• Eje vertical x = 2
• Centro, intersección del eje con la asíntota: C( 2 , − 3
)
• A una unidad a la derecha del centro, se forma un triángulo de cateto vertical 4
y cateto horizontal 1, por lo que la base de la exponencial es a = 4
• La exponencial es y − (−3) = 4x − 2 , es decir:
y = 4x − 2 − 3
De la gráfica a la expresión algebraica
9
LA LOGARÍTMICA
En primer lugar, debemos trazar la asíntota vertical de la función logarítmica, que en
nuestro ejemplo tiene de ecuación x = 1
En segundo lugar, trazar un eje horizontal que corte a la gráfica a una unidad de la
asíntota. Llamaremos dicho punto P( 2 , 4)
Determinamos el punto donde se cortan dicho eje y la asíntota,
C( x0 , y0 ) = C( 1 , 4)
A una unidad hacia arriba del centro, trazamos una horizontal hasta que corte a la
gráfica, formándose así un triángulo rectángulo cuyo cateto horizontal nos determina
la base del logaritmo a = 3
10
De la gráfica a la expresión algebraica
Con todo esto, la función es y − y0 = Log a ( x − x0
) , es decir, y
− 4 = Log3 ( x − 1
)
Ejemplo 1º:
• Asíntota: x = 3
• Punto P sobre la curva a una unidad de la asíntota: P( 4 , − 2)
• Eje horizontal por P: y = −2
• Punto C intersección del eje anterior y la asíntota: C( 3 , − 2)
• A una unidad hacia arriba del centro, trazamos una horizontal hasta la gráfica.
Formamos un triángula que tiene por cateto horizontal a = 2
• Con esto, y − (−2) = Log2 ( x − 3
)
y = Log2 ( x − 3
)−2
Ejemplo 2º:
• Asíntota: x = −4
• Punto P sobre la curva a una unidad de la asíntota: P( − 3 , 4)
• Eje horizontal por P: y = 4
• Punto C intersección del eje anterior y la asíntota: C( − 4 , 4)
• A una unidad hacia arriba del centro, trazamos una horizontal hasta la gráfica.
Formamos un triángula que tiene por cateto horizontal a = 3
• Con esto, y − 4 = Log3 ( x − (−4) )
y = Log3 ( x + 4
)+4