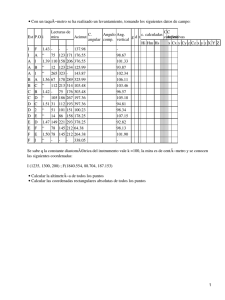
Espacios Métricos

Espacios Métricos
El concepto de k k (norma) nos da una noción de distancia, el tener una noción de distancia en
R o más generalmente en Rn , es lo que nos permite hablar de limite o de convergencia.
Consideremos la noción común de distancia entre dos puntos en R3 .
Si x̄ = (x1 , x2 , x3 )
ȳ = (y1 , y2 , y3 )
kx̄ − ȳk =
p
(x1 − y1 )2 + (x2 − y2 )2 + (x3 − y3 )2
Esta distancia la denominamos métrica euclidiana y la generalizamos en Rn en la siguiente
definición.
Definición: Sean x̄ = (x1 , . . . , xn ) y ȳ = (y1 , . . . , yn ) elementos cualesquiera de Rn definimos la
distancia euclidiana entre ellos como
d(x̄, ȳ) = kx̄ − ȳk =
p
(x1 − y1 )2 + . . . + (xn − yn )2
La función d : Rn × Rn → R se denomina distancia o métrica euclidiana.
Proposición: Para cualequiera vectores x̄, ȳ, z̄ Rn se tiene:
i. d(x̄, ȳ) ≥ 0
ii. d(x̄, ȳ) = d(ȳ, x̄)
iii. d(x̄, ȳ) ≤ d(x̄, z̄) + d(z̄, ȳ)
iv. d(x̄, ȳ) = 0
⇒
x̄ = ȳ
Demostración :
1. Como d(x, y) = kx̄ − ȳk ≥ 0 entonces d(x̄, ȳ) ≥ 0 tambien si d(x, y) = 0
kx̄ − ȳk = 0
⇒
x̄ = ȳ
2. d(x̄, ȳ) = kx̄ − ȳk = kx̄ − ȳk = kȳ − x̄k = d(ȳ, x̄)
1
⇒
3. d(x̄, ȳ) = kx̄ − ȳk = kx̄ − z̄ + z̄ − ȳk ≤ kx̄ − z̄k + kz̄ − ȳk = d(x̄, z̄) + d(z̄, ȳ)

 0 a=b
Métrica discreta.- Demostrar que la metrica definida por d(a, b) =
satisface los
 1 a 6= b
axiomas de métrica
Demostración :
1. Sean a, b Rn entonces d(a, b) = 1 ó d(a, b) = 0 ∴ d(a, b) ≥ 0
2. Sean a, b Rn Si ā 6= b̄
d(ā, b̄) = 1 y si b̄ 6= ā
d(b, a) = 1 ∴ d(a, b) = 1 =
d(b, a)
Ahora bien si a = b entonces d(a, b) = 0 = d(b, a)
∗
* Si a = b entonces b = a por lo tanto d(b, a) = 0
3. Sean ā, b̄, c̄ Rn
ā 6= b̄ 6= c̄
d(ā, b̄) = 1, d(b̄, c̄) = 1 y
d(ā, b̄) = 1
∴ d(a, c) = 1 ≤ 1 + 1 = d(a, b) + d(b, c)
Métrica C[a, b].- Sea C[a, b] el conjunto de las funciones reales contunias en el intervalo cerrado
[a, b]. Sean f, g C[a, b] definimos
d(f, g) = máx {|f (x) − g(x)|}
x [a,b]
demostrar que d es una métrica.
Demostración :
1. Como |f (x) − g(x)| ≥ 0 para todo x [a, b] entonces máx{|f (x) − g(x)|} ≥ 0
por lo tanto d(f, g) ≥ 0
2. d(f, g) = 0
⇒
máx {|f (x) − g(x)|} = 0
x [a,b]
⇒
|f (x) − g(x)| = 0
⇒
f (x) = g(x)
∀ x [a, b]
2
3. d(f, g) = máx {|f (x) − g(x)|} = máx {|g(x) − g(x)|} = d(g, f )
∗ x [a,b]
x [a,b]
* |f (x) − g(x)| = |g(x) − f (x)|
∀x
4. d(f, g) = máx {|f (x) − g(x)|}
x [a,b]
máx {|f (x) − g(x)|} = máx {|f (x) − h(x) + h(x) − g(x)|}
x [a,b]
x [a,b]
≤ máx {|f (x) − h(x)| + |h(x) − g(x)|}
x [a,b]
≤ máx {|f (x) − h(x)|} + máx {|h(x) − g(x)|}
x [a,b]
x [a,b]
∴ d(f, g) ≤ d(f, h) + d(h, g)
Probar que en el espacio de sucesiones {an } de números reales tales que
La aplicación d(xn , yn ) =
∞
X
∞
X
1
|xn − yn | es una distancia.
1
Prueba :
1. Como |xn − yn | ≥ 0 ∀ n N entonces
∞
X
|xn − yn | ≥ 0
1
por lo tanto d(xn , yn ) ≥ 0
2. d(xn , yn ) = 0
∞
X
|xn − yn | = 0
⇒
1
⇒
|xn − yn | = 0
⇒
xn − yn = 0
⇒
xn = yn
3. d(xn , yn ) =
∞
X
∀nN
∀nN
|xn − zn |
1
∞
X
|xn − zn | ≤
1
=
∞
X
1
∞
X
1
|xn − yn | + |yn − zn |
|xn − yn | +
∞
X
|yn − zn |
1
= d(xn , yn ) + d(yn , zn )
3
|an | < ∞.
Ejercicio: Sea d una métrica de un conjunto no vacio X. Demostrar que la función e definida
por e(a, b) = mı́n(1, d(a, b)) donde a, b X tambien es una métrica de X.
Solución :
1. Sean a, b X. Puesto que d es una métrica d(a, b) ≥ 0 entonces e(a, b) = 1
ó e(a, b) = d(a, b) ≥ 0, en cualquier caso e(a, b) ≥ 0
2. Si a = b entonces e(a, b) = mı́n(1, d(a, b)) = mı́n(1, 0) = 0
3. Sea a, b X. Por definición e(a, b) = d(a, b) ó e(a, b) = 1
Supongamos e(a, b) = d(a, b)) entonces d(a, b) < 1.
Puesto que d(a, b) es una métrica d(a, b) = d(b, a) < 1. En consecuencia e(b, a) =
d(a, b) = e(a, b), por otro lado supóngase que e(a, b) = 1, entonces d(a, b) ≥ 1
∴ d(b, a) ≥ 1
por lo tanto e(a, b) = 1 = e(b, a)
Sean ahora a, b, c X. Demostremos la desigualdad triangular. Por demostrar e(a, c) ≤
e(a, b) + e(b, c)
Observese que e(a, c) = mı́n{1, d(a, c)} ≤ 1 de donde e(a, b) = 1 ó e(b, c) = 1
∴ e(a, c) ≤ e(a, b) + e(b, c) pero puede ocurrir e(a, b) < 1 y e(b, c) < 1
∴ e(a, b) = d(a, b)
e(b, c) = d(b, c)
por lo tanto e(a, c) = mı́n(1, d(a, c)) ≤ d(a, c) ≤ d(a, b) + d(b, c) = e(a, b) + e(b, c).
Z 1
Sea d(f, g) =
|f (x) − g(x)|
¿Es d una métrica?
0
Solución: No, ya que si consideramos f (x) = 0
kf (x) − g(x)k = 0 pero f 6= g
∴ d no es una métrica.
4

 0 0≤x≤1
∀ x, g(x) =
 1 x=1
entonces
CALCULO DIFERENCIAL E INTEGRAL III
TAREA 5
Profa. Ana Belem Zavaleta Ramos, Profa. Pamela Villamil Sapién, Prof. Esteban Rubén Hurtado Cruz
1.- Demostrar la fórmula para calcular la torsión de una funcion vectorial f (t)
τ=
[f 0 (t)xf 00 (t)] · f 000 (t)
kf 0 (t)xf 00 (t)k2
2.- Si f (s) es la reparametrización por longitud de arco de una función f (t), demostar que
[f 0 (t)xf 00 (t)] · f 000 (t)
τ=
kf 0 (t)xf 00 (t)k2
1
3.- Calcular la torsión de la hélice f (t) = √ (cos(t) sin(t), t)
2
4.- Mostar que si una trayectoria está en un plano, entonces su torsión es cero.
5.- Demostrar la desigualdad de Minkowski: Dados un par de puntos cualesquiera p = (a1 , . . . , an )
pP
pP
pP
y q = (b1 , . . . , bn ) de Rn , kp + qk ≤ kpk + kqk es decir
|ai + bi |2 ≤
|ai |2 +
|bi |2
(Sugerencia: Desarrolle kp + qk2 y use la desigualdad de Schwarz demostrada en clase)
6.- Demostar la desigualdad de Minkowski para sumas infinitas: Si {an }, {bn } son
v sucesiones
u∞
∞
∞
X
X
uX
tales que
|an | < ∞,
|bn | < ∞, entonces kan +bn k ≤ kan k+kbn k es decir t
|an + bn |2 ≤
1
1
1
v
v
u∞
u∞
uX
uX
2
t
|an | + t
|bn |2
1
1
7.- Sea d una métrica de un conjunto no vacio X. Demostrar que la función e definida por
d(a, b)
e(a, b) =
, donde a, b ∈ X, es una métrica de X.
1 + d(a, b)
fecha de entrega 22 de marzo.
5