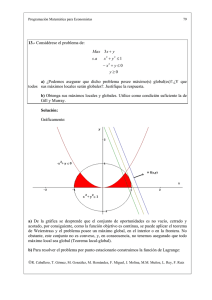
3.-Una compañía aérea tiene dos clases de aviones Boeing 757 y

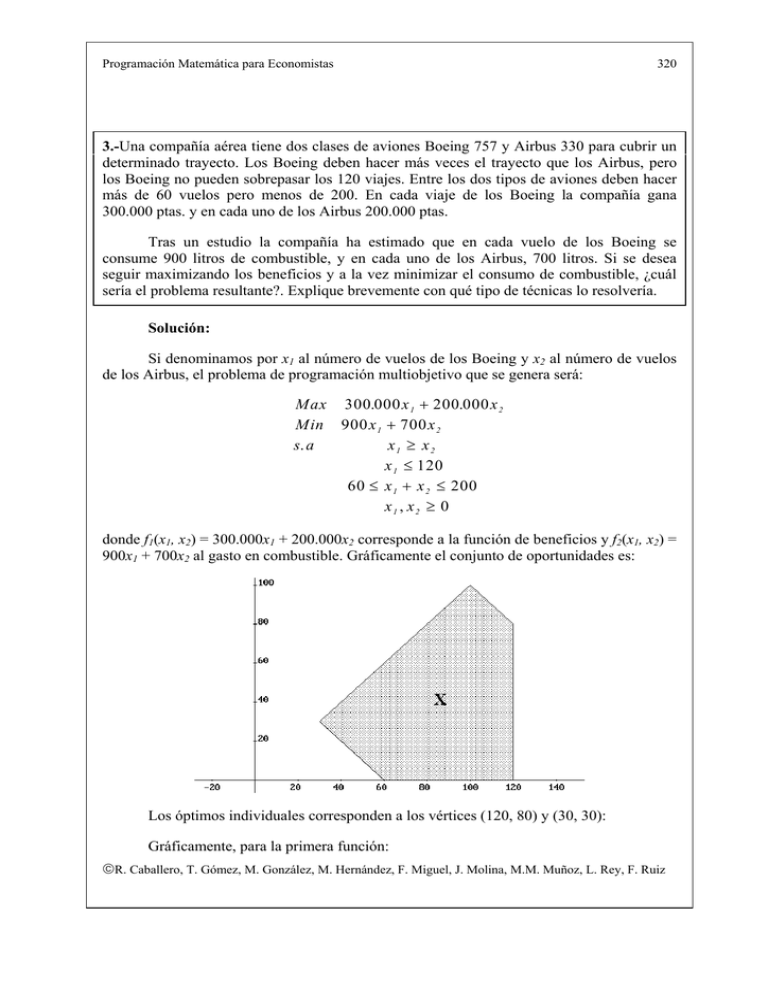
Programación Matemática para Economistas
320
3.-Una compañía aérea tiene dos clases de aviones Boeing 757 y Airbus 330 para cubrir un
determinado trayecto. Los Boeing deben hacer más veces el trayecto que los Airbus, pero
los Boeing no pueden sobrepasar los 120 viajes. Entre los dos tipos de aviones deben hacer
más de 60 vuelos pero menos de 200. En cada viaje de los Boeing la compañía gana
300.000 ptas. y en cada uno de los Airbus 200.000 ptas.
Tras un estudio la compañía ha estimado que en cada vuelo de los Boeing se
consume 900 litros de combustible, y en cada uno de los Airbus, 700 litros. Si se desea
seguir maximizando los beneficios y a la vez minimizar el consumo de combustible, ¿cuál
sería el problema resultante?. Explique brevemente con qué tipo de técnicas lo resolvería.
Solución:
Si denominamos por x1 al número de vuelos de los Boeing y x2 al número de vuelos
de los Airbus, el problema de programación multiobjetivo que se genera será:
Max 300.000 x 1 + 200.000 x 2
Min 900 x 1 + 700 x 2
s. a
x1 ≥ x2
x 1 ≤ 120
60 ≤ x 1 + x 2 ≤ 200
x1 , x2 ≥ 0
donde f1(x1, x2) = 300.000x1 + 200.000x2 corresponde a la función de beneficios y f2(x1, x2) =
900x1 + 700x2 al gasto en combustible. Gráficamente el conjunto de oportunidades es:
Los óptimos individuales corresponden a los vértices (120, 80) y (30, 30):
Gráficamente, para la primera función:
©R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz
Programación Matemática para Economistas
321
y para la segunda:
La matriz de pagos, tras evaluar los óptimos individuales en cada uno de los bjetivos
nos quedaría:
*
1
*
2
x = (120, 80)
x = (30, 30)
f1
52.000.000
15.000.000
-f2
-164.000
-48.000
Hemos considerado -f2 para tener los dos objetivos bajo máximo. Una vez
determinada la matriz de pago obtenemos el rango de variación de las correspondientes
funciones.
©R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz
Programación Matemática para Economistas
322
Para los beneficios f1 tomaremos valores en [15.000.000, 52.000.000] y para la
contaminación f2 o los tomamos en [48.000, 164.00], si lo mantenemos en mínimo, o en [164.000, -48000] si consideramos -f2.
Para resolver el problema podríamos utilizar la programación por metas, debiendo
imponer niveles de prioridad y metas sobre el planteamiento del problema.
Para ello, supongamos que: la empresa cuenta tan sólo con 75.000 litros de
combustible, y estima unos costes de 24 millones que es evidente que desea cubrirlos. Con
esta información del problema podemos construir las metas y determinar las funciones de
realización.
El combustible está limitado a 75.000 litros, por tanto:
900x1 + 700x2 ≤ 75.000
entonces 900x1 + 700x2 +n1 - p1 = 75.000 y h1(n1, p1) = p1
Como queremos cubrir los costes los beneficios deberán de ser superiores luego,
300.000x1 + 200.000x2 ≥ 24.000.000, y, la meta:
300.000x1 + 200.000x2 + n2 - p2 = 24.000.000
la función de realización h2(n2, p2) = n2.
El problema de metas correspondería a:
lexmin ( p 1 , n 2 )
s. a − x 1 + x 2 ≤ 0
x 1 ≤ 120
x 1 + x 2 ≥ 60
x 1 + x 2 ≤ 200
900 x 1 + 700 x 2 + n 1 − p 1 = 75.000
300000 x 1 + 200000 x 2 + n 2 − p 2 = 24.000.000
x 1 , x 2 , n1 , p1 , n 2 , p 2 ≥ 0
Nivel 1:
©R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz
Programación Matemática para Economistas
323
Min
p1
-x1 + x2 ≤ 0
s.a
x1 ≤ 120
x1 + x2 ≥ 60
x1 + x2 ≤ 200
900x1 + 700x2+ n1 - p1 = 75000
x1, x2, n1, p1 ≥ 0
Aplicando el programa LINDO para programación lineal obtenemos:
LP OPTIMUM FOUND AT STEP
2
OBJECTIVE FUNCTION VALUE
1)
0.000000
VARIABLE
P1
X1
X2
N1
VALUE
0.000000
30.000000
30.000000
27.000.000000
NO. ITERATIONS=
REDUCED COST
1.000000
.000000
.000000
.000000
2
Como p1 = 0, pasamos al siguiente nivel.
Gráficamente:
©R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz
Programación Matemática para Economistas
324
Nivel 2:
Min
n2
-x1 + x2 ≤ 0
s.a
x1 ≤ 120
x1 + x2 ≥ 60
x1 + x2 ≤ 200
900x1 + 700x2+ n1 - p1 = 75000
p1 = 0
300000x1 + 200000x2 + n2 - p2 = 24.000.000
x1, x2, n1, p1, n2, p2 ≥ 0
LP OPTIMUM FOUND AT STEP
2
OBJECTIVE FUNCTION VALUE
1)
0.000000000
VARIABLE
N2
P2
X1
X2
P1
N1
VALUE
0.000000
0.000000
80.000000
0.000000
0.000000
3000.000000
NO. ITERATIONS=
REDUCED COST
1.000000
0.000000
.000000
.000000
.000000
.000000
2
A la vista del resultado, la compañía debe realizar 80 vuelos con los aviones Boeing
y ninguno con los Airbus.
El conjunto de soluciones satisfactorias sería:
©R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz
Programación Matemática para Economistas
325
©R. Caballero, T. Gómez, M. González, M. Hernández, F. Miguel, J. Molina, M.M. Muñoz, L. Rey, F. Ruiz