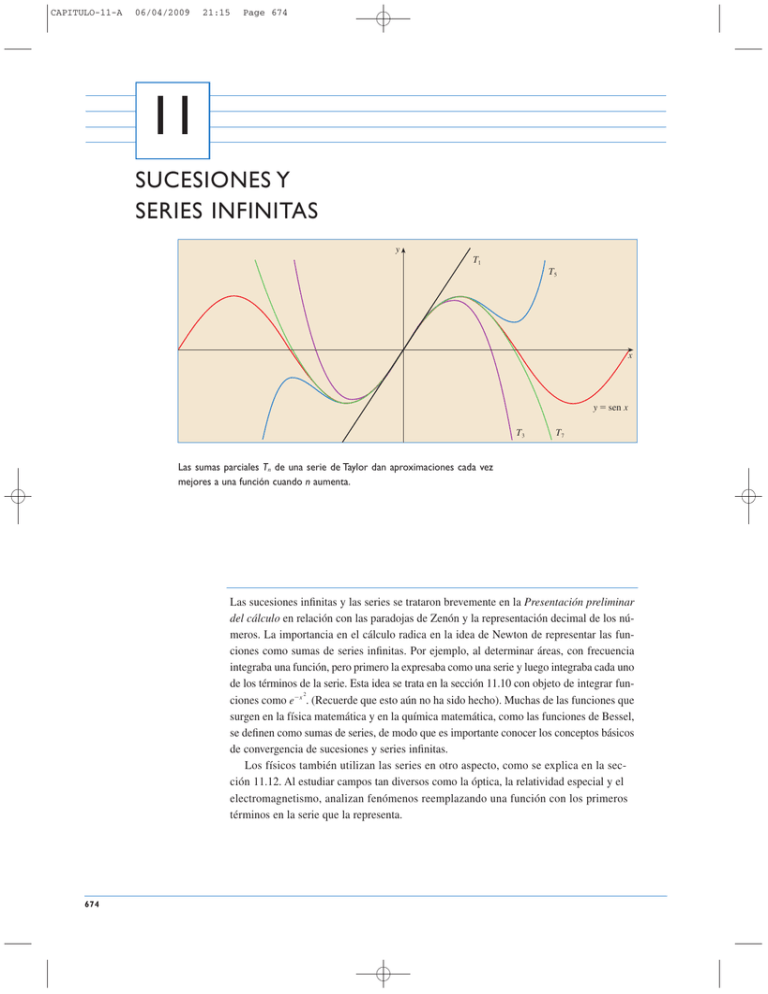
SUCESIONES Y SERIES INFINITAS

CAPITULO-11-A
06/04/2009
21:15
Page 674
11
SUCESIONES Y
SERIES INFINITAS
y
T¡
T∞
x
y=sen x
T£
T¶
Las sumas parciales Tn de una serie de Taylor dan aproximaciones cada vez
mejores a una función cuando n aumenta.
Las sucesiones infinitas y las series se trataron brevemente en la Presentación preliminar
del cálculo en relación con las paradojas de Zenón y la representación decimal de los números. La importancia en el cálculo radica en la idea de Newton de representar las funciones como sumas de series infinitas. Por ejemplo, al determinar áreas, con frecuencia
integraba una función, pero primero la expresaba como una serie y luego integraba cada uno
de los términos de la serie. Esta idea se trata en la sección 11.10 con objeto de integrar fun2
ciones como ex . (Recuerde que esto aún no ha sido hecho). Muchas de las funciones que
surgen en la física matemática y en la química matemática, como las funciones de Bessel,
se definen como sumas de series, de modo que es importante conocer los conceptos básicos
de convergencia de sucesiones y series infinitas.
Los físicos también utilizan las series en otro aspecto, como se explica en la sección 11.12. Al estudiar campos tan diversos como la óptica, la relatividad especial y el
electromagnetismo, analizan fenómenos reemplazando una función con los primeros
términos en la serie que la representa.
674
CAPITULO-11-A
06/04/2009
21:15
Page 675
11.1 SUCESIONES
Se puede considerar que una sucesión es una lista de números escritos en un orden definido:
a1, a2, a3, a4, . . . , an, . . .
El número a1 recibe el nombre de primer término, a2 es el segundo término y, en general,
an es el n-ésimo término. Aquí se trata exclusivamente con sucesiones infinitas, por lo que
cada término an tiene un sucesor an1.
Observe que para todo entero positivo n hay un número correspondiente an, por lo que
una sucesión se puede definir como una función cuyo dominio es el conjunto de enteros
positivos. Por lo regular, se escribe an en lugar de la notación de función f(n) para el valor
de la función en el número n.
NOTACIÓN
La sucesión {a1, a2, a3, . . .} también se denota mediante
an
o
a n n1
EJEMPLO 1 Algunas sucesiones se pueden definir dando una fórmula para el término
n-ésimo. En los ejemplos siguientes se ofrecen tres descripciones de la sucesión: Una
en la que se aplica la notación anterior, en otra se aplica una fórmula definida y en la
tercera se escriben los términos de la sucesión. Observe que la n no tiene que empezar
en 1.
(a)
(b)
n
n1
1nn 1
3n
cos
n
6
n
n1
an 1nn 1
3n
n1
(c) {sn 3 }n3
(d)
an a n sn 3, n 3
a n cos
n0
V EJEMPLO 2
n
, n0
6
1 2 3 4
n
, , , ,...,
,...
2 3 4 5
n1
2 3
4 5
1nn 1
, , ,
,...,
,...
3 9
27 81
3n
{0, 1, s2, s3, . . . , sn 3, . . .}
1,
n
s3 1
, , 0, . . . , cos
,...
2 2
6
Encuentre una fórmula para el término general an de la sucesión
4
5
6
7
3
, ,
,
,
,...
5
25 125
625 3125
y suponga que el patrón de los primeros términos continúa.
SOLUCIÓN Se sabe que
a1 3
5
a2 4
25
a3 5
125
a4 6
625
a5 7
3125
Observe que los numeradores de estas fracciones empiezan con 3 y se incrementan una
unidad al pasar al siguiente término. El segundo término tiene numerador 4, el siguiente
numerador es 5; en general, el n-ésimo término tendrá como numerador n 2. Los
denominadores son las potencias de 5, de modo que an tiene por denominador 5n. El
signo de los términos es alternadamente positivo y negativo, por lo que es necesario
675
CAPITULO-11-A
676
||||
06/04/2009
21:15
Page 676
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
multiplicar por una potencia de 1. En el ejemplo 1(b) el factor 1n significa que
empieza con un término negativo. Como aquí se busca iniciar con un término positivo,
se usa 1n1, o bien, 1n1. Por lo tanto,
a n 1 n1
n2
5n
EJEMPLO 3 En este caso hay algunas sucesiones que no tienen una ecuación que las defina en forma simple.
(a) La sucesión pn, donde pn es la población mundial el uno de enero del año n.
(b) Si an es el n-ésimo dígito en la expansión decimal del número e, entonces an es una
sucesión bien definida cuyos primeros términos son
7, 1, 8, 2, 8, 1, 8, 2, 8, 4, 5, . . .
(c) Las condiciones siguientes definen en forma recursiva la sucesión de Fibonacci f n
f1 1
f2 1
fn fn1 fn2
n3
Cada uno de los términos es la suma de los dos anteriores. Los primeros términos son
1, 1, 2, 3, 5, 8, 13, 21, . . .
Esta sucesión surgió cuando el matemático italiano del siglo XIII, a quien se conoce como Fibonacci, resolvió un problema que se relacionaba con la cría de conejos (véase
ejercicio 71).
a¡
1
2
0
a™ a£
Una sucesión como la del ejemplo 1(a), an nn 1, se puede representar dibujando
sus términos en una recta numérica como en la figura 1, o trazando la gráfica como en
la figura 2. Observe que, como una sucesión es una función cuyo dominio es el conjunto de
los enteros positivos, su gráfica consta de puntos aislados con coordenadas
a¢
1
FIGURA 1
1, a1
an
2, a2
3, a3
n, an
...
De acuerdo con la figura 1 o la 2, parece que los términos de la sucesión
an nn 1 se aproximan a 1 cuando n se incrementa. En efecto, la diferencia
1
1
7
a¶= 8
0
...
1 2 3 4 5 6 7
n
n
1
n1
n1
se puede hacer tan pequeña como se quiera al incrementar a n. Se indica lo anterior
escribiendo
FIGURA 2
lím
nl
n
1
n1
En general, la notación
lím a n L
nl
quiere decir que los términos de la sucesión an se aproximan a L cuando n se incrementa suficientemente. Observe que la definición siguiente del límite de una sucesión
es muy parecida a la definición de límite de una función en el infinito dada en la sección 2.6.
CAPITULO-11-A
06/04/2009
21:15
Page 677
SECCIÓN 11.1 SUCESIONES
||||
677
1 DEFINICIÓN Una sucesión an tiene como límite L, y se escribe
lím a n L
a n l L cuando n l o
nl
si podemos aproximar los términos an tanto como se quiera cuando n es suficientemente grande. Si existe lím n l an , se dice que la sucesión converge (o
que es convergente). De lo contrario se dice que la sucesión diverge (o es divergente).
En la figura 3 se ilustra la definición 1 mostrando las gráficas de las dos sucesiones que
tienen como límite a L.
an
an
L
L
FIGURA 3
Gráficas de las
dos sucesiones
lím an= L
0
0
n
n
n `
Una versión más exacta de la definición 1 es como se indica a continuación.
2
DEFINICIÓN Una sucesión an tiene por límite a L y se escribe
lím an L
an l L cuando n l o bien
nl
Compare esta definición con la
definición 2.6.7.
&
si para todo 0 hay un entero correspondiente N tal que
si
nN
an L entonces
La definición 2 se ilustra mediante la figura 4, en la cual los términos a1, a2, a3, . . . se
localizan en la recta numérica. No importa qué tan pequeño se escoja al intervalo L ,
L , existe una N tal que todos los términos de la sucesión desde aN 1 en adelante
deben estar en el intervalo.
a¡
FIGURA 4
0
a£
a™
aˆ
aN+1 aN+2
L -∑
L
a˜
aß
a∞
a¢
a¶
L+∑
Otra ilustración de la definición 2 es la figura 5. Los puntos sobre la gráfica de an
deben estar entre las rectas horizontales y L y y L si n N. Esta imagen debe ser válida, no importa qué tan pequeño se haya escogido , pero por lo regular un más
pequeño requiere una N más grande.
y
y=L+∑
L
y=L-∑
FIGURA 5
0
1 2 3 4
N
n
CAPITULO-11-A
678
||||
06/04/2009
21:15
Page 678
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
La comparación de la definición 2 y la definición 2.6.7 señala que la única diferencia entre lím n l an L y lím x l fx L es que se requiere que n sea entero. En estos términos está el siguiente teorema, el cual se ilustra en la figura 6.
3 TEOREMA Si lím x l fx L y fn an, cuando n es un entero, entonces
lím n l an L.
y
y=ƒ
L
0
FIGURA 6
x
1 2 3 4
En particular, puesto que ya se sabe que límx l 1x r 0, cuando r 0 (teorema
2.6.5), se tiene
1
0
nr
lím
4
nl
si r 0
Si an tiende a ser muy grande cuando n lo es, se usa la notación lím n l an . La
siguiente definición exacta es parecida a la definición 2.6.9.
5
DEFINICIÓN lím n l an significa que para todo número positivo M hay un
entero N tal que
an M
siempre que n N
Si lím n l an , entonces la sucesión an es divergente pero de una manera especial.
Se dice que an diverge a .
Las leyes de los límites que se estudian en la sección 2.3 también se cumplen para los
límites de sucesiones y sus demostraciones son similares.
LEYES DE LOS LÍMITES PARA LAS SUCESIONES.
Si an y bn son sucesiones convergentes y c es una constante, entonces
lím a n bn lím a n lím bn
nl
nl
nl
lím a n bn lím a n lím bn
nl
nl
nl
lím ca n c lím a n
nl
lím c c
nl
nl
lím a n bn lím a n lím bn
nl
lím
nl
nl
lím a n
an
nl
si lím bn 0
nl
bn
lím bn
nl
[
lím a np lím a n
nl
nl
nl
]
p
si p 0 y a n 0
CAPITULO-11-A
06/04/2009
21:15
Page 679
SECCIÓN 11.1 SUCESIONES
||||
679
El teorema de la compresión también se puede adaptar a las sucesiones como sigue (véase figura 7).
Si an bn cn para n n0 y lím a n lím cn L , entonces lím bn L .
TEOREMA DE LA COMPRESIÓN
PARA LAS SUCESIONES.
nl
nl
nl
Otro hecho útil con respecto a los límites de sucesiones se proporciona en el teorema siguiente cuya demostración se deja como ejercicio (ejercicio 75).
cn
bn
6
Si lím a n 0, entonces lím a n 0.
TEOREMA
nl
nl
an
0
n
EJEMPLO 4 Determine lím
nl
FIGURA 7
La sucesión hbnj es comprimida
entre las sucesiones hanj y hcnj
n
.
n1
SOLUCIÓN El método es similar al que se presenta en la sección 2.6: Se divide tanto el numerador como el denominador entre la potencia más alta de n y luego se aplican las leyes de los límites.
lím
nl
n
lím
nl
n1
Esto demuestra que la conjetura que
se hizo antes a partir de las figuras 1 y 2
era correcta.
&
1
1
1
n
lím 1
nl
lím 1 lím
nl
nl
1
n
1
1
10
En este caso se aplica la ecuación 4 con r 1.
EJEMPLO 5 Calcule lím
nl
ln n
.
n
SOLUCIÓN Observe que tanto el numerador como el denominador tienden al infinito cuando
n l . No se puede aplicar directamente la regla de l’Hospital porque no se aplica a
sucesiones, sino a funciones de una variable real. No obstante, se puede aplicar la regla
de l’Hospital a la función relacionada fx ln xx y obtener
lím
xl
ln x
1x
lím
0
xl
1
x
Por lo tanto, de acuerdo con el teorema 3
lím
nl
an
EJEMPLO 6 Determine si la sucesión an 1n es convergente o divergente.
1
0
ln n
0
n
SOLUCIÓN Si escribe los términos de la sucesión obtiene
1
_1
FIGURA 8
2
3
4
n
1, 1, 1, 1, 1, 1, 1, . . .
La gráfica de esta sucesión se muestra en la figura 8. Como los términos oscilan entre
1 y 1 en forma infinita, an no se aproxima a ningún número. Por lo tanto, lím n l 1n
no existe; es decir, la sucesión 1n es divergente.
CAPITULO-11-A
680
||||
06/04/2009
21:15
Page 680
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
EJEMPLO 7 Evaluar lím
La gráfica de la sucesión del ejemplo 7 se
muestra en la figura 9 y apoya la respuesta.
&
nl
an
1
1n
si es que existe.
n
SOLUCIÓN
lím
nl
1n
n
lím
nl
1
0
n
Por lo tanto, de acuerdo con el teorema 6,
0
n
1
lím
nl
_1
1n
0
n
El siguiente teorema dice que al aplicar una función continua a los términos de una
sucesión convergente, el resultado también es convergente. La prueba se deja como ejercicio 76.
FIGURA 9
7
TEOREMA Si lím an L y la función f es continua en L, entonces
nl
lím f an f L
nl
EJEMPLO 8 Encuentre lím senpn .
nl
SOLUCIÓN Como la función seno es continua en 0, el teorema 7 hace posible
escribir
lím senpn sen lím pn sen 0 0
nl
nl
Analice la convergencia de la sucesión an n!nn, donde
n! 1 2 3 n .
V EJEMPLO 9
& GRAFICACIÓN DE SUCESIONES
Algunos sistemas algebraicos computacionales
contienen comandos especiales que permiten
crear sucesiones y dibujarlas directamente. Sin
embargo, con la mayoría de las calculadoras para
trazar gráficas se pueden dibujar sucesiones
usando ecuaciones paramétricas. Por ejemplo,
la sucesión del ejemplo 9 se puede dibujar
introduciendo las ecuaciones paramétricas
xt
y t!t t
y dibujando en el modo punto (dot mode) iniciando
con t 1; se establece el paso t-ésimo igual a 1.
El resultado se muestra en la figura 10.
SOLUCIÓN Tanto el numerador como el denominador tienden al infinito cuando n l , pero
en este caso no hay función correspondiente para usar la regla de l’Hospital (x! no está definida cuando x no es un entero). Se escriben algunos de los términos para ver qué pasa
con an cuando n es grande:
a1 1
8
a2 an a3 123
333
1 2 3 n
n n n n
Al parecer, por estas expresiones y la gráfica de la figura 10, los términos son decrecientes y
quizá se aproximen a 0. Para confirmarlo, observe que según la ecuación 8
an 1
12
22
1
n
2 3 n
n n n
Observe que la expresión entre paréntesis es cuando mucho 1 porque el numerador es
menor que (o igual) al denominador. De este modo
0 an 0
FIGURA 10
1
n
10
Sabe que 1n l 0 cuando n l . Por lo tanto, an l 0 cuando n l por el teorema de
la compresión.
CAPITULO-11-A
06/04/2009
21:15
Page 681
SECCIÓN 11.1 SUCESIONES
V EJEMPLO 10
||||
681
¿Para qué valores de r es convergente la sucesión r n?
SOLUCIÓN Sabe por la sección 2.6 y las gráficas de las funciones exponenciales de la sección 1.5 que lím x l a x para a 1 y lím x l a x 0 para 0 a 1. Por lo tanto, si
hace a r y aplica el teorema 3 llega a
lím r n nl
0
si r 1
si 0 r 1
Es obvio que
lím 1n 1
y
nl
lím 0 n 0
nl
Si 1 r 0, por lo tanto 0 r 1, de modo que
lím r n lím r
nl
nl
n
0
y, debido a eso, lím n l r n 0 de acuerdo con el teorema 6. Si r 1, entonces r n diverge como en el ejemplo 6. En la figura 11 se ilustran las gráficas de varios valores de r.
(El caso de r 1 se muestra en la figura 8.)
an
an
r>1
1
1
_1<r<0
0
r=1
n
1
0
FIGURA 11
1
n
0<r<1
r<_1
La sucesión an=r
n
Los resultados del ejemplo 10 se resumen para uso futuro como sigue.
La sucesión r n es convergente si 1 r 1 y divergente para todos los
otros valores de r.
9
lím r n nl
0
1
si 1 r 1
si r 1
10 DEFINICIÓN Una sucesión an se llama creciente si a n a n1 para toda n 1,
es decir, a1 a2 a3 . Se denomina decreciente si a n a n1 para toda
n 1. Recibe el nombre de monótona si es creciente o decreciente.
EJEMPLO 11 La sucesión
& El lado derecho es menor porque tiene un
denominador mayor.
3
n5
es decreciente porque
3
3
3
n5
n 1 5
n6
y por lo tanto an an1 para toda n 1.
CAPITULO-11-A
682
||||
06/04/2009
21:15
Page 682
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
EJEMPLO 12 Demuestre que la sucesión a n n
es decreciente.
n 1
2
SOLUCIÓN 1 Es necesario demostrar que a n1 a n , es decir,
n1
n
2
2
n 1 1
n 1
Esta desigualdad equivale a la obtenida por multiplicación cruzada:
n1
n
2
2
n 1 1
n 1
&? n 1n 2 1 nn 12 1
&?
n 3 n 2 n 1 n 3 2n 2 2n
&?
1 n2 n
Puesto que n 1, ya sabe que la desigualdad n 2 n 1 es verdadera. Por lo tanto,
a n1 a n y también an es decreciente.
SOLUCIÓN 2 Considere la función f x f x x
:
x2 1
x 2 1 2x 2
1 x2
0
x 2 1 2
x 2 1 2
cuando x2 1
En estos términos, f es decreciente en 1, y por eso f n f n 1. Por lo tanto
an es decreciente.
11 DEFINICIÓN Una sucesión an está acotada por arriba si hay un número
M tal que
an M
para toda n 1
Se dice que está acotada por abajo si hay un número m tal que
m an
para toda n 1
Si está acotada por arriba y por abajo, en tal caso an es una sucesión acotada.
an
M
L
0 1 23
FIGURA 12
n
Por ejemplo, la sucesión an n está acotada por abajo an 0, pero no por arriba. La
sucesión an nn 1 está acotada porque 0 an 1 para toda n.
Ya sabe que no toda sucesión acotada es convergente [por ejemplo, la sucesión
an 1n cumple con 1 an 1, pero es divergente del ejemplo 6] y no toda sucesión monótona es convergente an n l . Pero si una sucesión es tanto acotada como
monótona, entonces tiene que ser convergente. Este hecho se demuestra en la forma del teorema 12, pero intuitivamente se entiende por qué es cierto viendo la figura 12. Si an es
creciente y an M para toda n, después los términos están forzados a aglomerarse y a
aproximarse a un número L.
La demostración del teorema 12 se apoya en el axioma de completitud para el conjunto de los números reales, que dice que si S es un conjunto no vacío de números reales
que tiene una cota superior M (x M para toda x en S), luego S tiene una cota superior
mínima b. [Esto quiere decir que b es una cota superior para S, pero si M es cualquier otra
cota superior, por lo tanto b M]. El axioma de completitud expresa el hecho de que no
hay brecha o agujero en la recta de los números reales.
CAPITULO-11-A
06/04/2009
21:15
Page 683
SECCIÓN 11.1 SUCESIONES
||||
683
12 TEOREMA DE LA SUCESIÓN MONÓTONA Toda sucesión acotada y monótona es
convergente.
DEMOSTRACIÓN Suponga que an es una sucesión creciente. Puesto que an está acotada, el
conjunto S a n n 1 posee una cota superior. De acuerdo con el axioma de completitud, tiene una cota mínima superior L. Dado 0, L no es una cota superior
para S (puesto que L es la cota superior mínima). Por lo tanto,
aN L para un entero N
Pero la sucesión es creciente de modo que an aN para toda n N. En estos términos,
si n N
an L 0 L an de tal manera
puesto que an L. Así que,
L a n
cuando n N
así lím n l a n L .
Una demostración similar (aplicando la cota inferior más grande) funciona si an es
decreciente.
La demostración del teorema 12 demuestra que una sucesión que es creciente y
acotada por arriba es convergente. (De igual manera, una sucesión decreciente que está acotada por abajo es convergente.) Este hecho se aplica muchas veces al trabajar con
series infinitas.
EJEMPLO 13 Investigue la sucesión an definida por la relación de recurrencia
a1 2
a n1 12 a n 6
para n 1, 2, 3, …
SOLUCIÓN Para empezar se calculan los primeros términos:
& Con frecuencia, la inducción matemática
se aplica cuando se trabaja con sucesiones
recursivas. Véase página 77 donde se encuentra
un análisis del principio de inducción matemática.
a1 2
a 2 12 2 6 4
a 3 12 4 6 5
a 4 12 5 6 5.5
a5 5.75
a6 5.875
a7 5.9375
a8 5.96875
a9 5.984375
Estos términos iniciales hacen pensar que la sucesión es creciente y que los términos se
aproximan a 6. Para confirmar que la sucesión es creciente, aplique la inducción matemática para demostrar que an1 an para toda n 1. Esto es válido para n 1 porque
a2 4 a1. Si supone que se cumple para n k, después tiene
a k1 ak
a k1 6 ak 6
de modo que
y
Por esto,
1
2
a k1 6 12 a k 6
a k2 ak1
CAPITULO-11-B
684
06/04/2009
||||
21:17
Page 684
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
Ya se dedujo que an1 an es válida para n k 1. Por lo tanto, la desigualdad se cumple
para toda n por inducción.
Luego de verificar que an está acotada demostrando que an 6 para toda n.
(Puesto que la sucesión es creciente, se sabe que tiene una cota inferior: an a1 2
para toda n.) Se tiene que a1 6, de modo que la aseveración es válida para n 1.
Suponga que se cumple para n k. En tal caso
ak 6
a k 6 12
de este modo
1
2
a k 6 12 12 6
a k1 6
Por eso,
Esto demuestra por inducción matemática que an 6 para toda n.
Como la sucesión an es creciente y acotada, el teorema 12 garantiza que tiene un
límite. El teorema no dice cuál es el valor del límite, pero ahora que sabe que L lím n l an existe, puede aplicar la relación de recurrencia para escribir
lím a n1 lím 12 a n 6 12 lím a n 6 12 L 6
nl
(
nl
nl
)
Como an l L, se infiere que an 1 l L, también (cuando n l , n 1 l , también). De este modo
& Una demostración de este hecho se pide
en el ejercicio 58.
L 12 L 6
Al resolver esta ecuación, determina que L 6, tal como había
predicho.
11.1
EJERCICIOS
11. 2, 7, 12, 17, . . .
1. (a) ¿Qué es una sucesión?
(b) ¿Qué significa decir que lím n l an 8?
(c) ¿Qué significa decir que lím n l an ?
13.
12.
{1, 23 , 49 , 278 , . . .}
{ 14 , 29 , 163 , 254 , . . .}
14. 5, 1, 5, 1, 5, 1, . . .
2. (a) ¿Qué es una sucesión convergente? Proporcione dos
ejemplos.
(b) ¿Qué es una sucesión divergente? Dé dos ejemplos.
3–8 Proporcione los primeros cinco términos de la sucesión.
3. an 1 0.2n
5. a n 31n
n!
7. a1 3,
a n1 2an 1
9.
{1,
, , , , . . .}
finida por
an n1
4. a n 3n 1
6. 2 4 6 2n
8. a1 4, a n1 an
an 1
9–14 Encuentre una fórmula para el término general an de la sucesión, suponiendo que se mantenga el patrón de los primeros
términos.
1 1 1 1
3 5 7 9
15. Haga una lista de los seis primeros términos de la sucesión de-
10.
{1,
, , , , . . .}
1 1 1 1
3 9 27 81
n
2n 1
¿Parece que la sucesión tiene un límite? Si es así, hállelo.
16. Haga una lista de los nueve primeros términos de la sucesión
cosnp3. ¿Parece que esta sucesión tiene un límite? Si es
así, hállelo; si no es así, explique por qué.
17–46 Determine si la sucesión converge o diverge. Si converge,
calcule el límite.
17. an 1 0.2n
18. an n3
n 1
3
CAPITULO-11-B
06/04/2009
21:17
Page 685
SECCIÓN 11.1 SUCESIONES
19. a n 3 5n 2
n n2
21. an e1n
23. a n tan
25. a n 2np
1 8n
1 n1n
n2 1
27. an cosn2
29.
31.
20. an n3
n1
22. a n 3n2
5n
24. an 26. a n 1 n n3
n 2n2 1
n1
9n 1
3
28. an cos2n
2n 1 !
2n 1!
30. arctan 2n
e n e n
e 2n 1
32.
33. n 2en
35. a n ln n
ln 2n
34. n cos np
cos 2n
2n
36. an lnn 1 ln n
1
2
n
n
43. 0, 1, 0, 0, 1, 0, 0, 0, 1, . . . 40. a n n!
2n
44.
sen 2n
1 sn
ln n2
n
{11 , 13 , 12 , 14 , 13 , 15 , 14 , 16 , . . .}
46. a n 3n
n!
; 47–53 Con la ayuda de una gráfica de la sucesión, establezca si és-
ta es convergente o divergente. Si la sucesión es convergente,
deduzca el valor del límite a partir de la gráfica, y luego demuestre su
conjetura. (Véase una advertencia sobre las gráficas de sucesiones
en la nota al margen de la página 680).
47. an 1 2en
49. an 3 2n2
8n2 n
n2 cos n
51. a n 1 n2
1 3 5 2n 1
52. a n n!
53. a n 54. (a) Determine si la sucesión definida como sigue es convergen-
te o divergente:
a1 1
a n1 4 an
para n 1
(b) ¿Qué ocurre si el primer término es a1 2?
55. Si se invierten 1000 dólares a 6% de interés, compuesto anual-
mente, por lo tanto n años después la inversión tiene un valor
de an 10001.06n dólares.
(a) Determine los primeros cinco términos de la sucesión an.
(b) ¿La sucesión es convergente o divergente? Explique
56. Determine los primeros 40 términos de la sucesión definida por
a n1 1
2
an
si a n es un número par
3a n 1 si a n es un número impar
y a1 11. Haga lo mismo para a1 25. Conjeture con respecto al tipo de sucesión.
57. ¿Para qué valores de r es convergente la sucesión nr n ?
58. (a) Si an es convergente, demuestre que
1 3 5 2n 1
n!
nl
n 13n
38. an s2
41. an ln2n2 1 lnn2 1 42. an 45. a n 685
lím a n1 lím a n
37. an n sen1n
39. a n ||||
48. an sn sen(psn )
nl
(b) Una sucesión an se define con a1 1 y
a n1 11 an para n 1. Si supone que an es convergente, calcule el límite.
59. Suponga que sabe que an es una sucesión decreciente y que to-
dos sus términos están entre los números 5 y 8. Explique por
qué la sucesión tiene un límite. ¿Qué puede decir con respecto
al valor del límite?
60–66 Determine si la sucesión es creciente, decreciente, o no es
monótona. ¿Está acotada la sucesión?
60. an 2n1
61. a n 1
2n 3
63. an n1n
65. a n n
n2 1
62. a n 2n 3
3n 4
64. an nen
66. a n n 1
n
n
3n 5n
50. a n s
67. Determine el límite de la sucesión
{s2, s2s2, s2s2s2, . . .}
68. Una sucesión an está dada por a 1 s2, a n1 s2 a n .
(a) Mediante inducción u otro método, demuestre que an es
creciente y que su cota superior es 3. Aplique el teorema
de sucesión monótona para demostrar que sí existe
lím n l an.
(b) Determine lím n l an.
CAPITULO-11-B
686
||||
06/04/2009
21:17
Page 686
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
69. Demuestre que la sucesión definida por
a1 1
an1 3 1
an
es creciente y que an 3 para toda n. Deduzca que an es
convergente y determine su límite.
(e) Mediante los incisos (c) y (d) demuestre que an 4 para
toda n.
(f) Aplique el teorema 12 para demostrar que existe
lím n l 1 1nn. (El límite es e. Vea la ecuación 3.6.6)
79. Sean a y b números positivos con a b. Sea a1 la media arit-
mética y b1 la media geométrica:
70. Demuestre que la sucesión definida por
a1 2
1
a n1 3 an
cumple con 0 an 2 y es decreciente. Deduzca que la sucesión es convergente y encuentre el límite.
71. (a) Fibonacci planteó el problema siguiente: Suponga que los
conejos viven toda la vida, que cada mes todas las parejas
tiene un nuevo par de conejitos, los cuales empiezan a ser
productivos a la edad de dos meses. Si empieza con una pareja de recién nacidos, ¿cuántas parejas de conejos tendrá en
el n-ésimo mes? Demuestre que la respuesta es fn, donde f n
es la sucesión de Fibonacci que se define en el ejemplo 3(c).
(b) Sea a n fn1fn y demuestre que a n1 1 1a n2. Suponiendo que an es convergente, determine el límite.
72. (a) Sea a1 a, a 2 f a, a 3 f a 2 f f a, . . . ,
a n1 f a n , donde f es una función continua. Si
lím n l a n L , demuestre que fL L.
(b) Ilustre el inciso (a) haciendo f x cos x, a 1, y calculando el valor de L con cinco cifras decimales.
; 73. (a) Mediante una gráfica, deduzca el valor del límite
lím
nl
n5
n!
(b) Con una gráfica de la sucesión del inciso (a) calcule los
valores más pequeños de N que corresponden a 0.1 y
0.001 en la definición 2.
ab
2
a1 Repita el proceso de modo que, en general,
a n1 a n bn
2
75. Demuestre el teorema 6.
[Sugerencia: Aplique la definición 2 o el teorema de la compresión].
76. Demuestre el teorema 7
77. Demuestre que si lím n l 0 y bn es acotada, entonces
lím n l anbn 0
1 n
.
n
(a) Demuestre que si 0 a b, en tal caso
78. Sea a n 1
b n1 a n1
n 1b n
ba
(b) Deduzca que b n n 1a nb
a n1.
(c) Aplique a 1 1n 1 y b 1 1n en el inciso
(b) para demostrar que an es creciente.
(d) Use a 1 y b 1 12n en el inciso b) para demostrar
que a2n 4.
bn1 sa n bn
(a) Mediante la inducción matemática demuestre que
a n a n1 bn1 bn
(b) Deduzca que tanto an como bn son convergentes.
(c) Demuestre que límn l an límn l bn. Gauss llamó al valor común de estos límites media aritmética-geométrica
de los números a y b.
80. (a) Demuestre que si lím n l a 2n L y lím n l a2n1 L , en-
tonces an es convergente y lím n l a n L .
(b) Si a1 1 y
an1 1 1
1 an
calcule los primeros ocho términos de la sucesión an. Luego use el inciso (a) para demostrar que lím n l a n s2 .
Esto da el desarrollo en fracción continua
1
s2 1 2
74. Aplique directamente la definición 2 para demostrar que
lím n l r n 0 cuando r 1.
b1 sab
1
2 81. El tamaño de una población de peces inalterada está modelado
mediante la fórmula
pn1 bpn
a pn
donde pn es la población de peces después de n años y
a y b son constantes positivas que dependen de las especies
y su medio. Suponga que la población en el año 0 es p0 0.
(a) Demuestre que si pn es convergente, después los únicos valores posibles de este límite son 0 y b a.
(b) Demuestre que p n1 bapn.
(c) Mediante el inciso (b) demuestre que si a b, en seguida
lím n l pn 0 , en otras palabras, la población muere.
(d) Ahora suponga que a b. Demuestre que si p0 b a, por
lo tanto pn es creciente y 0 pn b a. Asimismo, demuestre que si p0 b a, en tal caso pn es decreciente
y pn b a. Deduzca que si a b, por lo tanto
lím n l pn b a .
CAPITULO-11-B
06/04/2009
21:17
Page 687
SECCIÓN 11.2 SERIES
P ROY E C TO D E
LA B O R AT O R I O
CAS
||||
687
SUCESIONES LOGÍSTICAS
Una sucesión que surge en ecología como un modelo para el crecimiento poblacional se define
por medio de la ecuación logística en diferencias
pn1 kpn1 pn
donde pn es el tamaño de la población de la n-ésima generación de una sola especie. Para poder
trabajar con los números, pn es una fracción del tamaño máximo de la población, de modo
que 0 pn 1. Observe que la forma de la ecuación es similar a la ecuación logística en
diferencias de la sección 9.4. El modelo discreto, con sucesiones en lugar de funciones continuas,
es preferible para modelar las poblaciones de insectos, donde el apareamiento y la muerte ocurren
de un modo periódico.
Un ecologista se interesa en predecir el tamaño de la población a medida que el tiempo avanza, y plantea estas preguntas: ¿Se estabilizará en un valor límite? ¿Cambiará de manera cíclica? O
bien, ¿mostrará un comportamiento aleatorio?
Escriba un programa para calcular los primeros n términos de esta sucesión con una población inicial p0, donde 0 p0 1. Con este programa efectúe lo siguiente.
1. Calcule 20 o 30 términos de la sucesión para p0 2 y para dos valores de k tales que 1 k
1
3. Dibuje las sucesiones. ¿Convergen? Repita para un valor distinto de p0 entre 0 y 1.
¿El límite depende del valor de p0 escogido? ¿Depende del valor elegido de k?
2. Calcule términos de la sucesión para un valor de k entre 3 y 3.4 y dibújelos. ¿Qué observa
con respecto al comportamiento de los términos?
3. Experimente con valores de k entre 3.4 y 3.5. ¿Qué sucede con los términos?
4. Para valores de k entre 3.6 y 4, calcule y dibuje por lo menos 100 términos y comente el
comportamiento de la sucesión. ¿Qué sucede si cambia p0 por 0.001? Este tipo de comportamiento se llama caótico y lo muestran poblaciones de insectos en ciertas condiciones.
11.2 SERIES
Si trata de sumar los términos de una sucesión infinita a n n1, obtiene una expresión de
la forma
1
a1 a2 a3 an que se denomina serie infinita, o sólo serie, y se denota con el símbolo
a
n1
n
o
a
n
Pero, ¿tiene sentido hablar de suma de una cantidad infinita de términos?
Sería imposible encontrar la suma finita de la serie
1 2 3 4 5 n porque si empieza a sumar los términos, obtiene sumas acumulativas 1, 3, 6, 10, 15,
21, . . . y después del n-ésimo término, llega a nn 12, lo cual se vuelve muy grande cuando n se incrementa.
Sin embargo, si empieza por sumar los términos de la serie
1
1
1
1
1
1
1
n 2
4
8
16
32
64
2
CAPITULO-11-B
688
||||
06/04/2009
21:17
Page 688
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
n
obtiene 2 , 4 , 8 , 16 , 32 , 63
64 , . . . , 1 12 , . . . . En la tabla se puede ver que cuando suma más
y más términos, estas sumas parciales se vuelven más y más cercanas a 1. (Véase también
la figura 11 en Presentación preliminar del cálculo en la página 7). De hecho, al sumar
suficientes términos de la serie es posible hacer que las sumas parciales sean tan cercanas
a 1 como se quiera. Por eso es razonable decir que la suma de esta serie infinita es igual a
1 y escribir
1
n
Suma de los primeros
n términos
1
2
3
4
5
6
7
10
15
20
25
0.50000000
0.75000000
0.87500000
0.93750000
0.96875000
0.98437500
0.99218750
0.99902344
0.99996948
0.99999905
0.99999997
3
7
15 31
n1
1
1
1
1
1
1
n 1
2n
2
4
8
16
2
Se aplica una idea similar para determinar si una serie general (1) tiene o no tiene una
suma. Considere las sumas parciales
s1 a1
s2 a1 a2
s3 a1 a2 a3
s4 a1 a2 a3 a4
y, en general,
n
sn a 1 a 2 a 3 a n a
i
i1
Estas sumas parciales forman una nueva sucesión sn, la cual puede tener o no tener un límite. Si existe lím nl sn s (como un número finito), después, como en el ejemplo anterior, se llama suma de la serie infinita an.
2
DEFINICIÓN Dada una serie
n1 a n a 1 a 2 a 3 , denote con sn la
n-ésima suma parcial:
n
sn a
i
a1 a2 an
i1
Si la sucesión sn es convergente y lím n l sn s existe como un número real, entonces la serie an se dice convergente y se escribe
a1 a2 an s
a
o
n
s
n1
El número s se llama suma de la serie. Si no es así, la serie se dice divergente.
&
Compare con la integral impropia
y
1
f x dx lím
tl
y
t
1
f x dx
Para determinar esta integral integre desde 1
hasta t y hacemos que t l . En el caso de
series, sume desde 1 hasta n y hacemos que
n l .
Así, la suma de una serie es el límite de la sucesión de sumas parciales. Cuando escribe n1 a n s quiere decir que al sumar suficientes términos de la serie puede llegar tan
cerca como quiera al número s. Observe que
a
n1
n
n
lím
a
n l i1
i
EJEMPLO 1 Un ejemplo importante de una serie infinita es la serie geométrica
a ar ar 2 ar 3 ar n1 ar
n1
n1
a0
CAPITULO-11-B
06/04/2009
21:17
Page 689
SECCIÓN 11.2 SERIES
La figura 1 proporciona una demostración
geométrica del resultado del ejemplo 1. Si los
triángulos se construyen como se indica y s es
la suma de la serie, después, por triángulos
semejantes
&
s
a
a
a ar
s
por lo que
a
1r
||||
689
Cada término se obtiene a partir del término precedente y se multiplica por la razón
común r. (Ya se consideró el caso especial cuando a 12 y r 12 de la página 687).
Si r 1, en consecuencia sn a a a na l . Puesto que
lím n l sn no existe, la serie geométrica diverge en este caso.
Si r 1,
sn a ar ar 2 ar n1
rsn y
ar ar 2 ar n1 ar n
ar#
Al restar estas ecuaciones obtiene
ar@
ar@
sn rsn a ar n
ar
a-ar
ar
s
sn 3
a1 r n 1r
Si 1 r 1, sabe por (11.1.9) que rn l 0 cuando n l , de modo que
a
a
lím sn lím
nl
a
FIGURA 1
nl
a1 r n a
a
a
lím r n n
l
1r
1r
1r
1r
Por esto, cuando r 1, la serie geométrica es convergente y su suma es a1 r.
Si r 1 o bien, r 1, la sucesión r n es divergente de acuerdo con (11.1.9) y de
ese modo, según la ecuación 3, lím n l sn no existe. Por lo tanto, la serie geométrica di
verge en esos casos.
El resumen de los resultados del ejemplo 1 es como se señala a continuación.
4
La serie geométrica
ar
n1
a ar ar 2 n1
& En palabras: la suma de la serie
geométrica convergente es
es convergente si r 1 y su suma es
primer término
1 razón común
ar
n1
n1
a
1r
r 1
Si r 1, la serie geométrica es divergente.
V EJEMPLO 2
Calcule la suma de la serie geométrica
5 103 209 40
27 SOLUCIÓN El primer término es a 5 y la razón común es r 3 . Como r 3 1, la
2
serie es convergente según (4) y su suma es
5
10
20
40
5
5
5 3
2
3
9
27
1 ( 3 )
3
2
CAPITULO-11-B
690
||||
06/04/2009
21:17
Page 690
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
& ¿Qué se quiere dar a entender en realidad
cuando se dice que la suma de la serie del
ejemplo 2 es 3? Naturalmente, no puede sumar
uno más uno una cantidad infinita de términos.
Pero, de acuerdo con la definición 2, la suma
total es el límite de la sucesión de sumas
parciales. De este modo, al efectuar la suma
de suficientes términos, se acerca tanto como
quiera al número 3. La tabla muestra las
primeras diez sumas parciales sn, y en la gráfica
de la figura 2 se ilustra cómo la sucesión de las
sumas parciales se aproxima a 3.
sn
n
sn
1
2
3
4
5
6
7
8
9
10
5.000000
1.666667
3.888889
2.407407
3.395062
2.736626
3.175583
2.882945
3.078037
2.947975
3
0
20 n
FIGURA 2
EJEMPLO 3 ¿Es convergente o divergente la serie
2
2n
3 1n?
n1
SOLUCIÓN Escriba el n-ésimo término de la serie en la forma arn1:
Otra manera de identificar a y r es escribir los
primeros términos:
&
2
2n
3 1n n1
4 163 649 2 3
2 n
n1
n1
n1
4n
4 n1
n1 4( 3 )
3
n1
Identifique esta serie como una serie geométrica con a 4 y r 43 . Como r 1, la serie
diverge, de acuerdo con (4).
V EJEMPLO 4
Escriba el número 2.317 2.3171717. . . como una razón de enteros.
SOLUCIÓN
2.3171717. . . 2.3 17
17
17
3 5 10
10
10 7
Después del primer término tiene una serie geométrica con a 17103 y
r 1102. Debido a eso,
17
10 3
17
1000
2.317 2.3 2.3 1
99
1 2
10
100
23
17
1147
10
990
495
EJEMPLO 5 Encuentre la suma de la serie
x
n
donde x 1.
n0
SOLUCIÓN Observe que esta serie inicia con n 0 y por eso el primer término es
TEC En Module 11.2 se estudia una
serie que depende del ángulo u en un
triángulo y permite ver qué tan rápido
converge la serie cuando varía u.
x0 1. (En las series, se adopta la convención de que x0 1 aun cuando x 0). De este
modo,
x
n
1 x x2 x3 x4 n0
Ésta es una serie geométrica con a 1 y r x. Puesto que r x 1, converge, y de
acuerdo con (4) se tiene
5
x
n0
n
1
1x
CAPITULO-11-B
06/04/2009
21:17
Page 691
SECCIÓN 11.2 SERIES
EJEMPLO 6 Demuestre que la serie
||||
691
1
es convergente, y determine su suma.
nn 1
n1
SOLUCIÓN No es una serie geométrica, de modo que regrese a la definición de una serie
convergente y calcule las sumas parciales.
n
sn i1
1
1
1
1
1
ii 1
12
23
34
nn 1
Puede simplificar esta expresión si la descompone en fracciones parciales
1
1
1
ii 1
i
i1
(véase sección 7.4). Así que,
n
sn i1
Observe que los términos se cancelan
por pares. Éste es un ejemplo de una suma
telescópica. Debido a las cancelaciones, la
suma se colapsa, al igual que un telescopio
de pirata que se colapsa, en dos términos.
&
n
1
ii 1
i1
1
1
i
i1
1
1
1
2
1
1
2
3
1
1
3
4
1
1
n
n1
1
n1
lím sn lím
y de este modo
& En la figura 3 se ilustra el ejemplo 6 y
se muestra la gráfica de la sucesión de
términos an 1nn 1
y la sucesión
sn de sumas parciales. Observe que an l 0
y sn l 1. Refiérase a los ejercicios 62 y 63, en
donde se tratan dos interpretaciones
geométricas del ejemplo 6.
nl
nl
1
1
n1
101
Por lo tanto, la serie dada es convergente y
n1
V EJEMPLO 7
1
1
nn 1
Demuestre que la serie armónica
1
n1
1
1
1
1
1 n
2
3
4
es divergente.
sn SOLUCIÓN Para esta serie particular, es conveniente considerar las sumas parciales s2, s4, s8,
s16, s32, . . . y demostrar que se hacen grandes.
s1 1
a n 0
n
s2 1 12
s4 1 12 ( 13 14 ) 1 12 ( 14 14 ) 1 22
FIGURA 3
s8 1 12 ( 13 14 ) ( 15 16 17 18 )
1 12 ( 14 14 ) ( 18 18 18 18 )
1 12 12 12 1 32
s16 1 12 ( 13 14 ) ( 15 18 ) ( 19 161 )
1 12 ( 14 14 ) ( 18 18 ) ( 161 161 )
1
1
1
1
4
1222212
CAPITULO-11-B
692
||||
06/04/2009
21:17
Page 692
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
En forma similar, s32 1 52 , s64 1 62 , y, en general,
s2 n 1 & El método usado en el ejemplo 7 para
demostrar que la serie armónica diverge es
original del francés Nicole Oresme (1323-1382).
n
2
Esto demuestra que s2 n l cuando n l y por eso sn es divergente. Debido a eso, la
serie armónica es divergente.
6
TEOREMA Si la serie
a
n
es convergente, entonces lím an 0.
nl
n1
DEMOSTRACIÓN Sea sn a 1 a 2 a n . En tal caso, a n sn sn1. Puesto que an
es convergente, la sucesión sn es convergente. Sea lím n l sn s. Como n 1 l cuando n l , también se tiene lím n l sn1 s. Por lo tanto,
lím a n lím sn sn1 lím sn lím sn1
nl
nl
nl
nl
ss0
NOTA 1 Con cualquier serie an se asocian dos sucesiones: la sucesión sn de sus sumas
parciales y la sucesión an de sus términos. Si an es convergente, entonces el límite de
la sucesión sn es s, (la suma de la serie) y, como establece el teorema 6, el límite de la
sucesión an es 0.
|
NOTA 2 En general, el inverso del teorema 6 no se cumple. Si lím n l an 0, no
puede concluir que an es convergente. Observe que para la serie armónica 1n
tiene an 1n l 0 cuando n l , pero ya demostró en el ejemplo 7 que 1n es
divergente.
7
LA PRUEBA DE LA DIVERGENCIA Si lím a n no existe o si lím a n 0, entonces
la serie
nl
a
n
nl
es divergente.
n1
La prueba de la divergencia se infiere del teorema 6 porque si la serie no es divergente,
entonces es convergente y por lo tanto lím n l an 0.
EJEMPLO 8 Demuestre que la serie
n1
n2
es divergente.
5n 2 4
SOLUCIÓN
lím a n lím
nl
nl
n2
1
1
lím
0
2
2
n l 5 4n
5n 4
5
De modo que la serie diverge de acuerdo con la prueba de la divergencia.
NOTA 3 Si encuentra que lím n l an 0, sabe que an es divergente. Si tiene que
lím nl an 0, no sabe nada con respecto a la convergencia o la divergencia de an. Recuerde la advertencia de la nota 2: si lím nl an 0, la serie an podría ser convergente o
divergente
CAPITULO-11-B
06/04/2009
21:17
Page 693
SECCIÓN 11.2 SERIES
||||
693
8 TEOREMA Si an y bn son series convergentes, entonces también lo son las
series can (donde c es una constante), an bn y an bn, y
(i)
ca
n
c
n1
a
a
(ii)
n
n1
(iii)
a
n
bn n1
n
a
bn n1
a
n
n1
n
n1
b
n
n1
b
n
n1
Estas propiedades de las series convergentes se infieren de las leyes de los límites correspondientes a las sucesiones de la sección 11.1. Por ejemplo, aquí se demuestra la
parte (ii) del teorema 8:
Sea
n
sn a
a
s
i
i1
n
tn n
n1
b
t
i
i1
b
n
n1
La n-ésima suma parcial de la serie an bn es
n
un a
bi i
i1
y, a través de la ecuación 5.2.10, tiene
n
lím u n lím
nl
a
n l i1
bi lím
nl
n
lím
n
i
n
b
ai i1
i
i1
n
ai lím
n l i1
b
n l i1
i
lím sn lím tn s t
nl
nl
Por lo tanto, an bn es convergente y su suma es
a
n
bn s t n1
a
n
n1
EJEMPLO 9 Determine la suma de la serie
n1
b
n
n1
3
1
n .
nn 1
2
SOLUCIÓN La serie 12n es una serie geométrica con a 2 y r 2 , de modo que
1
n1
1
1
1
2
1
n 2
1 12
En el ejemplo 6 encuentra que
n1
1
1
nn 1
Así, por el teorema 8, la serie dada es convergente y
n1
1
3
n
nn 1
2
3
n1
1
1
n 3114
nn 1
n1 2
NOTA 4 Una cantidad finita de términos no afecta la convergencia o divergencia de una
serie. Por ejemplo, suponga que es capaz de demostrar que la serie
n4
n
n3 1
CAPITULO-11-C
694
06/04/2009
||||
21:19
Page 694
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
es convergente. Puesto que
n1
n
1
2
3
n
3
n 1
2
9
28
n
1
n4
3
se infiere que la serie completa n1 nn 3 1 es convergente. Asimismo, si sabe que la
serie nN1 a n es convergente, entonces la serie completa
a
N
n
a
n1
n
n1
an
nN1
es también convergente.
11.2
EJERCICIOS
1. (a) ¿Cuál es la diferencia entre una sucesión y una serie?
(b) ¿Qué es una serie convergente? ¿Qué es una serie
divergente?
2. Explique qué significa decir que n1 a n 5.
17.
n1
19.
n0
3 n1
4n
18.
n
3 n1
20.
1
(s2 )
n
n0
n1
en
3 n1
; 3–8 Calcule por lo menos 10 sumas parciales de las series. Dibuje
tanto la sucesión de los términos como la sucesión de las sumas
parciales en la misma pantalla. ¿Cómo parece ser la serie? ¿Convergente o divergente? Si es convergente, determine la suma. Si es
divergente, explique la razón.
3.
n1
12
5n
4.
n1
5.
n1
7.
n1
6.
tan n
2n 2 1
n2 1
1
1
n 1
sn
0.6
n1
21–34 Determine si la serie es convergente o divergente. Si es convergente, encuentre su suma.
21.
n1
23.
8.
1
nn 1
n2
24.
12
32
26.
k1
2n
.
9. Sea a n 3n 1
(a) Determine si a n es convergente.
(b) Diga si n1 a n es convergente.
n1
n
31.
n
y
i1
j1
(b) Explique la diferencia entre
33.
n
a
a
y
i1
13. 3 4 8
16
3
6(0.9 )
n1
n1
n1
0.3 n 30.
cos 1
k1
32.
n1
34.
n1
k
3
2
5n
n
en
n2
12.
1
8
14 12 1 35–40 Determine si la serie es convergente o divergente al expresar sn como suma extensible (como en el ejemplo 6). Si es convergente,
encuentre su suma.
649 35.
14. 1 0.4 0.16 0.064 15.
1
1
n e
n(n 1
0.8
i1
divergente. Si es convergente, calcule la suma.
4
1 3n
2n
j
11–20 Determine si la serie geométrica es convergente o
11. 3 2 3 9 n1
n
i
n2 1
2n2 1
arctan n
n1
aj
kk 2
k 32
n1
10. (a) Explique la diferencia entre
ai
ln
n1
2n 3
28.
n
29.
n1
s2
n1
n1
n
27.
n1
2
k
k2 1
k2
25.
22.
n1
1
2n
n2
16.
n1
10 n
(9) n1
37.
n1
2
n 1
36.
3
n(n 3)
38.
2
n1
2
n2 4n 3
ln
n1
n
n1
CAPITULO-11-C
06/04/2009
21:19
Page 695
SECCIÓN 11.2 SERIES
39.
(e
n1
40.
n1
cos
1
1
cos
n2
(n 1)2
sn 3 n 2 n, determine a n y n1 an .
57. Cuando el dinero se gasta en bienes y servicios, los que reci-
41–46 Exprese el número como una razón de enteros.
41. 0,2 0.2222. . .
42. 0.73 0.73737373. . .
43. 3.417 3.417417417. . .
44. 6.254 6.2545454. . .
45. 1.5342
46. 7.12345
47–51 Calcule los valores de x para los cuales la serie converge.
Determine la suma de la serie para dichos valores de x.
47.
n1
xn
3n
48.
4x
n
n
50.
n0
51.
n0
x 4
n
n1
49.
695
56. Si la n-ésima suma parcial de una serie n1 an es
e1/(n1))
1/n
||||
n0
x 3 n
2n
n
cos x
2n
52. Puesto que la serie armónica es una serie divergente cuyos tér-
ben el dinero también gastan un poco de él. Las personas que
reciben algo del dinero gastado dos veces, gastarán algo de dicho dinero, y así sucesivamente. Los economistas llaman a esta reacción en cadena efecto multiplicador. En un hipotético
pueblo aislado, el gobierno local inicia el proceso gastando D
dólares. Suponga que cada persona que recibe dinero gasta
100c% y ahorra 100s% del dinero. Los valores c y s se denominan propensión marginal al consumo y propensión marginal
al ahorro y, naturalmente, c s 1.
(a) Sea Sn el total de lo gastado que ha sido generado después de
n transacciones. Determine una ecuación para Sn.
(b) Demuestre que lím n l Sn kD , donde k 1s. La cantidad k se llama multiplicador. ¿Cuál es el multiplicador si la
propensión marginal al consumo es 80%?
Nota: El gobierno federal de Estados Unidos usa este principio
para justificar el gasto que muestra déficit. Los bancos utilizan
el principio para justificar los préstamos de un gran porcentaje
del dinero que reciben como depósito.
58. Una cierta pelota tiene la característica de que cada vez que cae
desde una altura h sobre una superficie nivelada y dura, rebota
hasta una altura rh, donde 0 r 1. Suponga que la pelota
cae desde una altura inicial de H metros.
(a) Suponga que la pelota continúa rebotando de manera
indefinida y calcule la distancia total que recorre.
(Use el hecho de que la pelota cae 12 tt 2 metros en
t segundos).
(b) Calcule el tiempo total que la pelota viaja.
(c) Suponga que cada vez que la pelota golpea la superficie
con velocidad v rebota con velocidad k v, donde
0 k 1. ¿Cuánto tiempo le tomará a la pelota llegar al
reposo?
minos se aproximan a 0. Demuestre que
59. ¿Cuál es el valor de c si
1
ln 1 n
n1
1 c
es otra serie con esta propiedad.
CAS
n
60. Encuentre el valor de c tal que
53–54 Aplique el comando de las fracciones parciales en su siste-
ma algebraico computacional para determinar la suma parcial, y
luego aplique esta expresión para determinar la suma de la serie.
Compruebe su respuesta usando directamente el sistema algebraico
a la suma de la serie.
53.
n1
3n 2 3n 1
n 2 n3
54.
n2
1
n3 n
55. Si la n-ésima suma parcial de una serie n1 an es
sn determine a n y n1
an .
2?
n2
n1
n1
e
nc
10
n0
61. En el ejemplo 7 se demostró que la serie armónica es divergente.
Aquí se resume otro método, haciendo uso del hecho de que
ex 1 x para cualquier x 0. (Vea el ejercicio 4.3.76.)
Si sn es la n-ésima suma parcial de la serie armónica, demuestre que esn n 1. ¿Por qué esto implica que la serie armónica es divergente?
n
; 62. Dibuje las curvas y x , 0 x 1, para n 0, 1, 2, 3, 4, . . .
sobre una misma pantalla. Determine las áreas entre las curvas
sucesivas y mediante geometría demuestre el hecho siguiente,
demostrado en el ejemplo 6,
n1
1
1
nn 1
CAPITULO-11-C
696
||||
06/04/2009
21:19
Page 696
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
63. En la figura se ilustran dos círculos C y D de radio 1 que se to-
can en P. T es una tangente común; C1 es el círculo que toca C,
D y T; C2 es el círculo que toca C, D y C1; C3 es el círculo que
toca C, D y C2. Este procedimiento puede continuar en forma
indefinida y produce una sucesión infinita de círculos Cn . Determine una expresión para el diámetro de Cn y, de ese modo,
proporcione otra demostración geométrica del ejemplo 6.
69. Si a n es convergente y bn es divergente, demuestre que la
serie a n bn es divergente. [Sugerencia: aplique el razonamiento de contradicción.]
70. Si a n y bn son divergentes, ¿necesariamente a n bn es
divergente?
71. Suponga que una serie a n consta de términos positivos y sus
sumas parciales sn cumplen con la desigualdad sn 1000 para
toda n. Explique por qué a n debe ser convergente.
72. La sucesión de Fibonacci se define en la sección 11.1 mediante
las ecuaciones
P
f1 1,
C£
C™
1
C
1
D
C¡
T
ma perpendicular a BC, EF AB, y este procedimiento continúa en forma indefinida como se ilustra en la figura. Determine
la longitud total de todas las perpendiculares
(a)
1
1
1
fn1 fn1
fn1 fn
fn fn1
(b)
1
1
fn1 fn1
fn
2
fn1 fn1
n2
(c)
n2
CD DE EF FG en términos de b y .
A
D
¨
F
H
B
b
G
E
C
65. ¿Qué es lo que está mal en el cálculo siguiente?
0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 1
(Guido Ubaldus pensaba que esto demostraba la existencia de
Dios, porque “se había creado algo de la nada”).
66. Suponga que se sabe que n1 a n a n 0 es una serie conver-
gente. Demuestre que n1 1a n es una serie divergente.
67. Demuestre la parte (i) del teorema 8.
a n es divergente y c 0, demuestre que ca n es
divergente.
68. Si
fn fn1 fn2
n3
Demuestre que cada uno de los siguientes enunciados es
válido.
64. Un triángulo rectángulo ABC está definido con A y
AC b. CD se traza perpendicular a AB, DE se traza en for-
f2 1,
73. El conjunto de Cantor, nombrado así en honor al matemáti-
co alemán Georg Cantor (1845-1918), se construye como se
señala a continuación. Empiece con el intervalo cerrado [0, 1]
y retire el intervalo abierto ( 13 , 23 ). Esto deja los dos intervalos
[0, 13 ] y [ 23, 1] y luego elimine el intervalo abierto constituido
por el tercio medio de cada uno. De este modo quedan cuatro
intervalos y de nuevo elimine el tercio medio de cada uno de
ellos. Continúe este procedimiento de manera indefinida eliminando en cada paso el tercio medio de cada intervalo que
queda del paso anterior. El conjunto de Cantor consiste en los
números que quedan en [0, 1] después de que todos esos intervalos se han eliminado.
(a) Demuestre que la longitud total de todos los intervalos que
se eliminan es 1. A pesar de eso, el conjunto de Cantor contiene una cantidad infinita de números. Proporcione ejemplos de algunos números del conjunto de Cantor.
(b) El tapete de Sierpinski es un equivalente en dos dimensiones del conjunto de Cantor. Se construye eliminando el
noveno central de un cuadrado de lado 1, y luego se elimina el centro de cada uno de los ocho cuadrados restantes,
y así sucesivamente. (En la figura se ilustran los primeros
tres pasos de la construcción). Demuestre que la suma de
las áreas de los cuadrados eliminados es 1. Esto significa
que el área del tapete de Sierpinski es cero.
CAPITULO-11-C
06/04/2009
21:19
Page 697
SECCIÓN 11.3 LA PRUEBA DE LA INTEGRAL Y ESTIMACIONES DE LAS SUMAS
74. (a) Una sucesión a n se define recursivamente mediante la
||||
697
76. En la figura hay una cantidad infinita de círculos que se aproxi-
ecuación a n 12 a n1 a n2 para n 3, donde a 1 y a 2
son números reales. Experimente con varios valores de
a 1 y a 2 y con la ayuda de su calculadora adivine el límite
de la sucesión.
(b) Encuentre lím n l a n en términos de a 1 y a 2 escribiendo
a n1 a n en función de a 2 a 1 y sume la serie.
man a los vértices de un triángulo equilátero. Cada círculo toca
a otros círculos y a los lados del triángulo. Si el triángulo tiene
lados que miden una unidad de longitud, calcule el área total
que ocupan los círculos.
75. Considere la serie
n1
n
n 1!
(a) Calcule las sumas parciales s1, s2, s3 y s4. ¿Reconoce los
denominadores? Mediante el patrón conjeture una fórmula para sn.
(b) Aplique la inducción matemática para demostrar su conjetura.
(c) Demuestre que la serie infinita dada es convergente y
calcule la suma
11.3 LA PRUEBA DE LA INTEGRAL Y ESTIMACIONES DE LAS SUMAS
En general, es difícil determinar la suma exacta de una serie. Se es capaz de lograrlo en el
caso de series geométricas y las series 1nn 1
porque en cada uno de estos casos es
posible encontrar una fórmula simple para la n-ésima suma parcial sn . Pero por lo regular no
es fácil calcular lím n l sn. Por lo tanto, en las siguientes secciones se tratan varias pruebas
que permiten determinar si una serie es convergente o divergente sin que se tenga que encontrar en forma explícita su suma. (En algunos casos, los métodos permiten determinar unas
buenas estimaciones de la suma.) El primer método utiliza integrales impropias.
Empiece por investigar las series cuyos términos son los recíprocos de los cuadrados de
los enteros positivos:
n
n
sn i1
5
10
50
100
500
1000
5000
1
i2
n1
1
1
1
1
1
1
2 2 2 2 2 n
1
2
3
4
52
No hay una fórmula sencilla para la suma sn de los primeros n términos, pero la tabla generada mediante una computadora de los valores, dados en el margen sugiere que las sumas parciales se aproximan a un número cercano a 1.64 cuando n l y de este modo parece como si la serie fuera convergente.
Se confirma esta impresión con un razonamiento geométrico. En la figura 1 se ilustra la
curva y 1x 2 y algunos rectángulos que se encuentran abajo de la curva. La base de cada uno de los rectángulos es un intervalo de longitud igual a 1; la altura es igual al valor
de la función y 1x 2 en el extremo derecho del intervalo de este modo, la suma de las
áreas de los rectángulos es
1.4636
1.5498
1.6251
1.6350
1.6429
1.6439
1.6447
1
1
1
1
1
1
2
2
2
2
2
2
1
2
3
4
5
n1 n
y
y= 1
≈
área= 1
1@
0
FIGURA 1
1
2
área= 1
2@
4
área= 1
3@
área= 1
4@
5
área= 1
5@
x
CAPITULO-11-C
698
||||
06/04/2009
21:19
Page 698
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
Si excluye el primer rectángulo, el área total de los rectángulos restantes es menor que el
área bajo la curva y 1x2 para x 1, que es el valor de la integral x1
1x 2 dx. En la
sección 7.8 descubrió que esta integral impropia es convergente y que tiene un valor de 1. De
modo que la figura muestra que todas las sumas parciales son menores que
1
1
dx 2
2 y
1
1
x2
En estos términos, las sumas parciales están acotadas. También sabe que las sumas parciales son crecientes porque todos los términos son positivos. Por lo tanto, las sumas parciales convergen, de acuerdo con el teorema de la sucesión monótona, y de esa manera la
serie es convergente. La suma de la serie (el límite de las sumas parciales) es también
menor que 2:
n1
n
n
sn i1
5
10
50
100
500
1000
5000
1
1
1
1
1
2 2 2 2 2
n2
1
2
3
4
[El matemático suizo Leonhard Euler (1707-1783) calculó que la suma exacta de esta serie es 26, pero la demostración de esto es muy difícil. Véase el problema 6 en los Problemas adicionales después del capítulo 15].
Ahora estudie la serie
1
si
1
1
1
1
1
1
sn
s1
s2
s3
s4
s5
3.2317
5.0210
12.7524
18.5896
43.2834
61.8010
139.9681
n1
La tabla de valores de sn hace pensar en que las sumas parciales no se aproximan a un número finito, de modo que se sospecha que la serie dada podría ser divergente. Una vez más
use una imagen para confirmarlo. En la figura 2 se ilustra la curva y 1sx, pero esta
vez se usan rectángulos cuya parte superior queda por encima de la curva.
FIGURA 2
y
y= 1
œx
œ„
0
1
2
área= 1
œ1
œ„
3
área= 1
œ2
œ„
4
área= 1
œ3
œ„
5
x
área= 1
œ4
œ„
La base de cada uno de los rectángulos es un intervalo de longitud 1. La altura es igual
al valor de la función y 1sx en el extremo izquierdo del intervalo. Así, la suma de las
áreas de todos los rectángulos es
1
1
1
1
1
1
s1
s2
s3
s4
s5
n1 sn
Esta área total es mayor que el área bajo la curva y 1sx para x 1, que es igual a la
integral x1
(1sx ) dx. Pero según la sección 7.8, esta integral impropia es divergente. En
otras palabras, el área bajo la curva es infinita. Por eso, la suma de la serie debe ser infinita;
es decir, la serie es divergente.
El mismo tipo de razonamiento geométrico aplicado para estas dos series, se puede hacer para demostrar la prueba siguiente. (La demostración se encuentra al final de esta
sección.)
CAPITULO-11-C
06/04/2009
21:19
Page 699
SECCIÓN 11.3 LA PRUEBA DE LA INTEGRAL Y ESTIMACIONES DE LAS SUMAS
||||
699
PRUEBA DE LA INTEGRAL Suponga que f es una función continua, positiva y decreciente en 1, y sea a n f n. En tal caso la serie n1 a n es convergente si y
sólo si la integral impropia x1
f x dx es convergente. En otras palabras:
(i) Si y f x dx es convergente, entonces
1
(ii) Si y f x dx es divergente, entonces
1
a
n
es convergente.
n1
a
n
es divergente.
n1
NOTA Cuando use la prueba de la integral no es necesario iniciar la serie o la integral
en n 1. Por ejemplo, al probar la serie
n4
1
n 32
use
y
4
1
dx
x 32
Asimismo, no es necesario que f sea siempre decreciente. Lo importante es que f sea decreciente por último, es decir, decreciente para x más grande que algún número N. En consecuencia nN a n es convergente, de modo que n1 a n es convergente de acuerdo con la
nota 4 de la sección 11.2.
EJEMPLO 1 Aplique la prueba de la integral para saber si la serie
1
es convern2 1
n1
gente o divergente.
SOLUCIÓN La función f x 1x 2 1 es continua, positiva y decreciente en 1, de
modo que aplique la prueba de la integral:
y
1
t
1
dx lím y 2
dx lím tan1x
t
l
tl
1
x 1
x 1
]
2
1
lím tan1t tl
4
t
1
2
4
4
Por lo tanto, x1
1x 2 1 dx es una integral convergente y si es así, de acuerdo con la
prueba de la integral, la serie 1n 2 1 es convergente.
V EJEMPLO 2
¿Para qué valores de p es la serie
n1
Para usar la prueba integral necesita
evaluar x1
fx dx y, por lo tanto, tiene
que hallar una antiderivada de f. Es frecuente que esto sea difícil o imposible,
de modo que también necesita otras
pruebas para convergencia.
&
1
convergente?
np
SOLUCIÓN Si p 0, entonces lím n l 1n . Si p 0, entonces lím n l 1n p 1. En
p
cualquier caso lím n l 1n p 0, por lo que la serie dada es divergente de acuerdo con
la prueba de la divergencia (11.2.7).
Si p 0, entonces la función f x 1x p evidentemente es continua, positiva y decreciente en 1, . Según el capítulo 7 [véase (7.8.2)],
y
1
1
dx converge si p 1 y diverge si p 1
xp
Se infiere de la prueba de la integral que la serie 1n p converge si p 1 y diverge si
0 p 1. (En el caso de p 1, esta serie es la serie armónica estudiada en el ejem
plo 7 de la sección 11.2).
La serie del ejemplo 2 se llama serie p. Es importante en el resto de este capítulo, de
modo que se resumen los resultados del ejemplo 2 para referencia futura como se indica a
continuación.
CAPITULO-11-C
700
||||
06/04/2009
21:19
Page 700
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
1
La serie p,
1
es convergente si p 1 y divergente si p 1.
np
n1
EJEMPLO 3
(a) La serie
n1
1
1
1
1
1
3 3 3 3 n3
1
2
3
4
es convergente porque es una serie p con p 3 1.
(b) La serie
n1
1
1
1
1
1
1 3 3 3 13 3
n
s2
s3
s4
n1 sn
es divergente porque es una serie p con p 13 1.
NOTA No debe inferir que, de acuerdo con la prueba de la integral, la suma de la serie es igual al valor de la integral. En efecto,
1
2
n2
6
n1
en tanto que
Por lo tanto,
a
n1
V EJEMPLO 4
Determine si la serie
n1
y
1
1
dx 1
x2
n
y f x dx
1
ln n
es convergente o divergente.
n
SOLUCIÓN La función f x ln xx es positiva y continua para x 1 porque la función
logaritmo es continua. Pero no es obvio si f es decreciente o no lo es, de modo que al
calcular su derivada:
f x 1xx ln x
1 ln x
x2
x2
Por lo tanto, f x 0 cuando ln x 1, es decir, x e. Se infiere que f es decreciente
cuando x e y así aplicar la prueba de la integral:
y
1
ln x
t ln x
ln x2
dx lím y
dx lím
tl
1
tl
x
x
2
t
1
ln t
2
2
lím
tl
Puesto que esta integral impropia es divergente, la serie ln nn también es divergente
de acuerdo con la prueba de la integral.
ESTIMACIÓN DE LA SUMA DE UNA SERIE
Suponga que pudo aplicar la prueba de la integral para demostrar que una serie a n es
convergente y que quiere encontrar una aproximación a la suma s de la serie. Claro, cualquier suma parcial sn es una aproximación a s porque lím n l sn s. Pero, ¿qué tan buena
es esa aproximación? Para saberlo, necesita estimar el tamaño del residuo.
Rn s sn a n1 a n2 a n3 CAPITULO-11-C
06/04/2009
21:19
Page 701
SECCIÓN 11.3 LA PRUEBA DE LA INTEGRAL Y ESTIMACIONES DE LAS SUMAS
y=ƒ
0
701
El residuo Rn es el error que se comete cuando sn, la suma de los primeros n términos, se
usa como una aproximación a la suma total.
Se usa la misma notación y las ideas que en la prueba de la integral, suponiendo que f
es decreciente en n, . Al comparar las áreas de los rectángulos con el área bajo y f x
para x n en la figura 3
y
an+1 a
n+2
||||
...
Rn a n1 a n2 y f x dx
n
x
n
Asimismo, en la figura 4
FIGURA 3
Rn a n1 a n2 y
y
y=ƒ
n1
f x dx
De este modo se demuestra la siguiente estimación de error.
an+1 an+2
0
n+1
2 ESTIMACIÓN DEL RESIDUO PARA LA PRUEBA DE LA INTEGRAL Suponga f k a k,
donde f es una función continua, positiva y decreciente para x n y a n es convergente. Si Rn s sn , entonces
...
x
FIGURA 4
y
n1
f x dx Rn y f x dx
n
V EJEMPLO 5
(a) Obtenga un valor aproximado de la suma de la serie 1n 3 usando la suma de los
primeros 10 términos. Estime el error originado en esta aproximación.
(b) ¿Cuántos términos se requieren para asegurar que la suma no difiere en más
de 0.0005?
SOLUCIÓN En los incisos (a) y (b) necesita conocer xn
f x dx. Con f x 1x 3,
que satisface las condiciones de la prueba integral, tiene
y
n
t
1
1
2
3 dx tlím
l
x
2x
n
lím tl
1
1
2 2t
2n 2
1
2n 2
(a)
n1
1
1
1
1
1
s10 3 3 3 3 1.1975
n3
1
2
3
10
De acuerdo con el residuo estimado en (2) tiene
R10 y
10
1
1
1
3 dx 2 x
210
200
De modo que el tamaño del error es cuanto mucho de 0.005.
(b) La precisión de 0.0005 quiere decir que debe encontrar un valor de n tal que
Rn 0.0005. Puesto que
Rn y
n
se quiere que
1
1
dx x3
2n 2
1
0.0005
2n 2
CAPITULO-11-C
702
||||
06/04/2009
21:19
Page 702
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
Al resolver la desigualdad, sabe que
n2 1
1000
0.001
o bien,
n s1000 31.6
Necesita 32 términos para tener la seguridad de que no habrá una diferencia mayor que
0.0005.
Si suma sn a cada miembro de las desigualdades en (2), obtiene
3
sn y
n1
f x dx s sn y f x dx
n
porque sn Rn s. Las desigualdades en (3) dan una cota inferior y una cota superior
para s. Proporcionan una aproximación más certera a la suma de la serie que la suma parcial sn.
EJEMPLO 6 Use (3) con n 10 para estimar la suma de la serie
n1
1
.
n3
SOLUCIÓN Las desigualdades en (3) se vuelven
s10 y
11
1
1
dx s s10 y 3 dx
10 x
x3
Del ejemplo 5 sabe que
y
n
s10 de modo que
1
1
3 dx x
2n 2
1
1
2 s s10 211
2102
Si usa s10 1.197532, obtiene
1.201664 s 1.202532
Si obtiene la aproximación de s por medio del punto medio de este intervalo, en este
caso el error es cuanto mucho la mitad de la longitud del intervalo. Así,
n1
1
1.2021
n3
con error 0.0005
Si compara el ejemplo 6 con el ejemplo 5, se observa que la estimación en (3) es
mucho mejor que la estimación s sn . Para que el error sea menor que 0.0005 tiene que
usar 32 términos en el ejemplo 5, pero sólo 10 términos en el ejemplo 6.
DEMOSTRACIÓN DE LA PRUEBA DE LA INTEGRAL
Ya se trató la idea básica en la que se apoya la demostración de la prueba de la integral
en las figuras 1 y 2 para la serie 1n 2 y 1sn. En el caso de la serie general a n examine las figuras 5 y 6. El área del primer rectángulo sombreado de la figura 5 es el valor
de f en el extremo derecho de [1, 2], es decir, f 2 a 2 . De esta manera, al comparar
CAPITULO-11-C
06/04/2009
21:19
Page 703
SECCIÓN 11.3 LA PRUEBA DE LA INTEGRAL Y ESTIMACIONES DE LAS SUMAS
y
a
a£
¢
703
las áreas de los rectángulos sombreados con el área bajo y f x desde 1 hasta n observa que
y=ƒ
a 2 a 3 a n y f x dx
n
4
0
||||
∞
an
...
1
n x
1
(Observe que esta desigualdad depende del hecho de que f es decreciente.) De manera similar, en la figura 6 se muestra que`
FIGURA 5
y
5
y
n
1
y=ƒ
f x dx a 1 a 2 a n1
(i) Si y f x dx es convergente, en este caso (4) da
1
an-1
a¡ a™
0
£
n
a
¢
n
1
i2
...
1
n x
y f x dx y f x dx
i
1
puesto que f x 0. Por lo tanto
FIGURA 6
n
sn a 1 a
i2
i
a 1 y f x dx M
1
Como sn M para toda n, la sucesión sn está acotada por arriba. Asimismo,
sn1 sn a n1 sn
como a n1 f n 1 0. En estos términos, sn es una sucesión acotada creciente y, de
este modo, es convergente de acuerdo con el teorema de la sucesión monótona (11.1.12).
Esto quiere decir que a n es convergente.
(ii) Si x1
f x dx es divergente, entonces x1n f x dx l cuando n l porque f x 0.
Pero con (5) se obtiene
y
n
1
n1
f x dx a
i
sn1
i1
y también sn1 l . Esto quiere decir que sn l entonces a n diverge.
11.3
EJERCICIOS
1. Dibuje una imagen para demostrar que
n2
3–8 Mediante la prueba de la integral determine si la serie es convergente o divergente.
1
1
y 1.3 dx
1 x
n 1.3
3.
n1
¿Qué puede concluir con respecto a la serie?
2. Suponga que f es una función continua, positiva y decreciente
para x 1 y an f n. En una imagen acomode las tres cantidades siguientes en orden creciente.
y
6
1
5
f x dx
a
i1
a
i2
5.
n1
7.
6
i
i
4.
1
(2n 1)3
6.
ne
n1
1
sn
5
n
n1
n1
8.
n1
1
n5
1
sn 4
n2
n1
CAPITULO-11-D
704
||||
06/04/2009
21:21
Page 704
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
9–26 Determine si la serie es convergente o divergente.
9.
n1
2
10.
n 0.85
n
1.4
33. (a) Mediante la suma de los primeros 10 términos, estime
la suma de la serie n1 1n 2. ¿Qué tan buena es la estimación?
(b) Mejore esta estimación usando (3) con n 10.
(c) Encuentre un valor de n que dé la certeza de que el error en
la aproximación s sn es menor que 0.001.
3n 1.2 n1
1
1
1
1
8
27
64
125
11. 1 34. Calcule la suma de la serie n1 1n 5 correcta en tres cifras
12. 1 1
1
1
1
2 s2
3 s3
4 s4
5 s5
13. 1 1
1
1
1
3
5
7
9
36. ¿Cuántos términos de la serie n2 1nln n 2
se necesitarían
14.
1
1
1
1
1
5
8
11
14
17
37. Demuestre que si busca obtener un valor aproximado de la su-
15.
n1
17.
n1
19.
n1
21.
n2
23.
n1
25.
n1
16.
1
n 4
18.
ln n
n3
20.
1
n ln n
22.
n1
n1
n1
n2
1/n
e
n2
24.
1
n n
26.
n3
3
35. Estime n1 2n 16 correcta a cinco lugares decimales.
sumar para calcular la suma que no difiera de 0.01?
5 2 sn
n3
2
decimales.
n1
n2
n3 1
3n 2
nn 1
1
n 2 4n 5
1
n(1n n)2
2
n
en
n
n4 1
ma de la serie n1 n1.001 de modo que el error sea menor de 5
en la novena cifra decimal, en este caso ¡necesita sumar más
de 1011,301 términos!
CAS
38. (a) Demuestre que la serie n1 ln n2n 2 es convergente.
(b) Encuentre una cota superior para el error en la aproximación s sn.
(c) ¿Cuál es el valor más pequeño de n tal que esta cota superior sea menor que 0.05?
(d) Encuentre sn para este valor de n.
39. (a) Mediante (4) demuestre que si sn es la n-ésima suma parcial
de la serie armónica, entonces
sn 1 ln n
(b) La serie armónica diverge, pero muy lentamente.
Con ayuda del inciso (a) demuestre que la suma del primer millón de términos es menor que 15 y que la suma
de los primeros mil millones de términos es
menor que 22.
40. Siga los pasos siguientes para demostrar que la sucesión
27–30 Determine los valores de p para los cuales la serie es con-
1
1
1
ln n
2
3
n
tn 1 vergente.
27.
n2
29.
1
nln n p
n1 n
28.
n3
2 p
30.
n1
n1
1
n ln n lnln n
p
ln n
np
31. La función zeta de Riemann z se define como
- x n1
1
nx
y se usa en teoría de los números para estudiar la distribución
de los números primos. ¿Cuál es el dominio de z?
32. (a) Calcule la suma parcial s10 de la serie
n1 1n 4. Estime el
error al usar s10 como una aproximación a la suma de la
serie.
(b) Use (3) con n 10 para conseguir una estimación
mejorada de la suma.
(c) Calcule un valor de n tal que sn no difiera más de 0.00001
del valor de la suma.
tiene un límite. (El valor del límite se denota con g y se denomina constante de Euler.)
(a) Dibuje un diagrama como la figura 6 con f x 1x e interprete tn como un área, o bien use (5), para demostrar
que tn 0 para toda n.
(b) Interprete
tn tn1 lnn 1 ln n
1
n1
como una diferencia de áreas para demostrar que
tn tn1 0. Por lo tanto, tn es una sucesión decreciente.
(c) Aplique el teorema de sucesión monótona para demostrar
que tn es convergente.
41. Determine todos los valores positivos de b para los cuales la
serie n1 b ln n converge.
42. Encuentre todos los valores de c para los que converge la si-
guiente serie.
n1
c
1
n
n1
CAPITULO-11-D
06/04/2009
21:21
Page 705
SECCIÓN 11.4 PRUEBAS POR COMPARACIÓN
||||
705
11.4 PRUEBAS POR COMPARACIÓN
En las pruebas por comparación, la idea es comparar una serie dada con una serie que ya se
sabe que es convergente o divergente. Por ejemplo, la serie
1
2n 1
1
n1
recuerde la serie n1 12 n, la cual es una serie geométrica con a 12 y r 12 por lo tanto,
es convergente. Como la serie (1) es similar a la serie convergente, se presiente que también
debe ser convergente. De hecho, así es. La desigualdad
1
1
n
2 1
2
n
demuestra que la serie dada (1) tiene términos menores que los de la serie geométrica y, por
lo tanto, todas las sumas parciales son también más pequeñas que 1 (la suma de la serie
geométrica). Esto quiere decir que las sumas parciales forman una sucesión creciente acotada, la cual es convergente. Asimismo, se infiere que la suma de la serie es menor que la
suma de la serie geométrica:
n1
1
1
2 1
n
Un razonamiento similar se puede hacer para demostrar la prueba siguiente, la cual se
aplica sólo a series cuyos términos son positivos. La primera parte dice que si tiene una
serie cuyos términos son menores que los de una serie conocida convergente, por lo tanto
la serie también es convergente. La segunda parte establece que si empieza con una serie
cuyos términos son mayores que los de una serie divergente conocida, en tal caso también
es divergente.
PRUEBA POR COMPARACIÓN Suponga que an y bn son series con términos
positivos.
(i) Si bn es convergente y an bn para toda n, entonces an es convergente.
(ii) Si bn es divergente y an bn para toda n, entonces an es divergente.
& Es importante estar atento a la distinción entre sucesión y serie. Una sucesión es un listado de
números, y una serie es una suma. Con toda
serie an hay dos sucesiones asociadas: la sucesión an de términos y la sucesión sn de
sumas parciales.
DEMOSTRACIÓN
n
(i) Sea
sn a
i1
n
i
tn b
t
i
i1
b
n
n1
Puesto que ambas series tienen términos positivos, las sucesiones sn y tn son crecientes sn1 sn an1 sn. Asimismo, tn l t, así que tn t para toda n. Como
ai bi, sn tn. De este modo, sn t para toda n. Esto quiere decir que sn es creciente
y está acotada superiormente, por el teorema de sucesiones monótonas la serie an
es convergente.
(ii) Si bn es divergente, después tn l (puesto que tn es creciente). Pero ai bi
de modo que sn tn. Así que sn l . Por lo tanto an diverge.
Naturalmente, al usar la prueba por comparación es necesario tener alguna serie conocida
bn para los fines de la comparación. La mayor parte de las veces se usan las series:
La serie estándar se usa
con la prueba por comparación
&
&
p [ 1n p que convergen si p 1 y divergen si p 1; véase (11.3.1)] o bien,
series geométricas [ ar n1 es convergente si r 1 y es divergente si r 1;
véase (11.2.4)].
CAPITULO-11-D
706
||||
06/04/2009
21:21
Page 706
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
V EJEMPLO 1
Determine si la serie
n1
5
es convergente o divergente.
2n 4n 3
2
SOLUCIÓN En el caso de n grandes el término dominante en el denominador es 2n2 de modo que compare la serie dada con la serie 52n2. Observe que
5
5
2n 4n 3
2n 2
2
porque el lado izquierdo tiene un denominador más grande. (En la notación de la prueba
por comparación, an está en el lado izquierdo y bn en el lado derecho). Ya sabe que
5
5
2 2n
2
n1
n1
1
n2
es convergente porque es una constante por una serie p con p 2 1. Por lo tanto,
n1
5
2n 4n 3
2
es convergente de acuerdo con el inciso (i) de la prueba por comparación.
NOTA 1 La condición an bn o bien, an bn de la prueba por comparación es para
toda n, es necesario comprobar sólo que se cumple para n N, donde N es un entero
establecido, porque la convergencia de una serie no está afectada por un número finito de
términos. Lo anterior se ilustra con el ejemplo siguiente.
V EJEMPLO 2
Pruebe si la serie
n1
ln n
es convergente o divergente.
n
SOLUCIÓN Esta serie se probó (usando la prueba de la integral) en el ejemplo 4 de la
sección 11.3, pero también es posible probarla por comparación con la serie armónica.
Observe que ln n 1 para n 3 y de esa manera
ln n
1
n
n
n3
Ya sabe que 1n es divergente (serie p con p 1). De esta manera la, serie dada es
divergente de acuerdo con la prueba por comparación.
NOTA 2 Los términos de la serie que se está probando deben ser menores que los de una
serie convergente, o mayores que los de una serie divergente. Si los términos son más grandes que los términos de una serie convergente, o bien, menores que los de una serie divergente, en tal caso la prueba por comparación no se aplica. Por ejemplo, considere la serie
n1
1
2n 1
La desigualdad
1
1
n
2n 1
2
es inútil en cuanto a la prueba por comparación porque bn ( 12 ) es convergente y
an bn. Sin embargo, la impresión es que 12n 1 tiene que ser convergente porque
n
es muy parecida a la serie geométrica convergente ( 12 ) . En tal caso se puede aplicar la
prueba siguiente.
n
CAPITULO-11-D
06/04/2009
21:21
Page 707
SECCIÓN 11.4 PRUEBAS POR COMPARACIÓN
||||
707
PRUEBA POR COMPARACIÓN EN EL LÍMITE Suponga que an y bn son series con
términos positivos. Si
lím
Los ejercicios 40 y 41 tratan los casos
c 0 y c .
&
nl
an
c
bn
donde c es un número finito y c 0, en seguida ambas series convergen o ambas
divergen.
DEMOSTRACIÓN Sea m y M números positivos tales que m c M. Como anbn está cer-
cano a c para n grande, hay un entero N tal que
m
an
M
bn
mbn an Mbn
y así
cuando n N
cuando n N
Si bn es convergente también lo es Mbn. Así an es convergente según el inciso (i)
de la prueba por comparación. Si la serie bn diverge también mbn es divergente y por
el inciso (ii) de la prueba por comparación la serie an diverge.
EJEMPLO 3 Pruebe si la serie
n1
1
es convergente o divergente.
2n 1
SOLUCIÓN Aplique la prueba por comparación en el límite con
an 1
2n 1
bn 1
2n
y obtiene
lím
nl
an
12 n 1
2n
1
lím
lím
lím
10
n
n
nl
nl
2 1
n l 1 12 n
bn
12
Puesto que existe este límite y 12n es una serie geométrica convergente, la serie dada
converge de acuerdo con la prueba por comparación en el límite.
EJEMPLO 4 Determine si la serie
n1
2n 2 3n
es convergente o divergente.
s5 n 5
SOLUCIÓN La parte dominante del numerador es 2n2 y la parte dominante del denominador
es sn5 n 52. Esto recomienda efectuar
an lím
nl
2n 2 3n
s5 n 5
bn 2n 2
2
52 n
n 12
an
2n 2 3n n 12
2n 52 3n 32
lím
lím
n l s5 n 5
nl
bn
2
2s5 n 5
2
lím
nl
2
3
n
5
1
n5
20
1
2s0 1
CAPITULO-11-D
708
||||
06/04/2009
21:21
Page 708
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
Puesto que bn 2 1n12 es divergente (es una serie p con p 12 1), la serie dada
diverge de acuerdo con la prueba por comparación en el límite.
Observe que al probar muchas series se encuentra una serie conveniente bn conservando sólo las potencias más altas en el numerador y en el denominador.
ESTIMACIÓN DE SUMAS
Si ha usado la prueba por comparación para demostrar que una serie an es convergente comparando con la serie bn, entonces se puede hacer una estimación de la serie an al
comparar los residuos. Como en la sección 11.3, considere el residuo
Rn s sn an1 an2 En cuanto a la serie de comparación bn considere el residuo correspondiente
Tn t tn bn1 bn2 Puesto que an bn para toda n, Rn Tn. Si bn es una serie p, estime su residuo Tn como
en la sección 11.3. Si bn es una serie geométrica, por lo tanto Tn es la suma de una serie
geométrica y puede sumarla exactamente (véanse ejercicios 35 y 36). En cualquier caso,
sabe que Rn es menor que Tn.
V EJEMPLO 5 Con la suma de los primeros 100 términos obtenga un valor aproximado
de la suma de la serie 1n 3 1. Estime el error de esta aproximación.
SOLUCIÓN Como
1
1
3
n3 1
n
la serie dada es convergente de acuerdo con la prueba por comparación. El residuo Tn de la
serie de comparación 1n 3 ya se estimó en el ejemplo 5 de la sección 11.3 por medio de
la estimación del residuo para la prueba de la integral. Allí se encontró que
Tn y
n
1
1
dx x3
2n 2
Por lo tanto, el residuo Rn de la serie dada cumple con
Rn Tn 1
2n 2
Con n 100
R100 1
0.00005
21002
Con una calculadora programable o una computadora, resulta que
n1
100
1
1
3
0.6864538
n 1
n1 n 1
3
con un error menor que 0.00005.
CAPITULO-11-D
06/04/2009
21:21
Page 709
SECCIÓN 11.4 PRUEBAS POR COMPARACIÓN
11.4
que se sabe que bn es convergente.
(a) Si an bn para toda n, ¿qué puede decir con respecto a
an? ¿Por qué?
(b) Si an bn para toda n, qué puede decir con respecto
a an? ¿Por qué?
2. Suponga que an y bn son series con términos positivos y
que se sabe que bn es divergente.
(a) Si an bn para toda n, ¿qué puede decir de an? ¿Por qué?
(b) Si an bn para toda n, ¿que puede decir con respecto a
an? ¿Por qué?
3–32 Determine si la serie es convergente o divergente.
n1
5.
n1
7.
9.
13.
n1
15.
n1
17.
n1
19.
n1
21.
n1
23.
n1
25.
n1
27.
n1
29.
n1
31.
8.
n1
n2sn
n1
cos n
n2 1
10.
n1
n4n
12.
arctan n
n1.2
14.
n1
n0
16.
n1
1
sn 2 1
18.
14
1 3n
20.
sn 2
2n n 1
22.
5 2n
1 n 2 2
24.
2
n3
n1
1 n n2
s1 n 2 n 6
26.
e n
n1
2
28.
n1
1
n!
30.
1
n
n1
32.
43
2n
n1
n1
35.
n1
1
sn 1
34.
1
1 2n
36.
4
n1
n1
sen2n
n3
n
n 13 n
37. El significado de la representación decimal de un número
0.d1d2d3 . . . (donde el dígito di es uno de los números 0, 1,
2, . . . , 9) es que
d2
d1
d3
d4
0.d1 d2 d3 d4 . . . 2 3 10
10
10
10 4
Demuestre que esta serie siempre es convergente.
39. Demuestre que si an 0 y an converge, por lo tanto a n2
también converge.
n 1
3n 4 1
2
40. (a) Suponga que an y bn son series con términos positivos y
que bn es convergente. Demuestre que si
1 sen n
10 n
lím
nl
1
3 1
sn
(i)
n1
ln n
n3
n2
n 1 3
n 2 5n
3
n n1
n5
3
n7 n2
s
n!
nn
1
n 11n
(ii)
n1
ln n
sne n
41. (a) Suponga que an y bn son series con términos positivos y
que bn es divergente. Demuestre que si
lím
nl
n
e1n
n
an
0
bn
entonces an también es convergente.
(b) Mediante el inciso (a) demuestre que la serie converge.
sn
n1
n4
n 6n
33.
convergente?
n
valor aproximado de la suma de la serie. Estime el error.
38. ¿Para qué valores de p la serie n2 1n p ln n es
n1
33–36 Mediante la suma de los primeros 10 términos, obtenga un
4
1
2n 3
n1
n
1
1
n
n2
2 1 n
n sn
sen
n1
n
2
n1
n3
n 1
n1
n2
6.
9
3 10 n
11.
4.
n1
nsn
n
2n 1
3
n1
n1
709
EJERCICIOS
1. Suponga que an y bn son series con términos positivos y
3.
||||
an
bn
entonces an también es divergente.
(b) Use el inciso (a) para demostrar que la serie es divergente.
(i)
n2
1
ln n
(ii)
n1
ln n
n
42. Proporcione un ejemplo de un par de series an y bn con tér-
minos positivos donde lím nl anbn 0 y bn diverge, pero
an converge. [Compare con el ejercicio 40.]
43. Demuestre que si an 0 y lím nl nan 0, en tal caso an es
divergente.
44. Demuestre que si an 0 y an es convergente, por lo tanto
ln1 an es convergente.
45. Si an es una serie convergente con términos positivos, ¿es
cierto que senan también es convergente?
46. Si an y bn son series convergentes con términos positivos,
¿es cierto que a n b n también es convergente?
CAPITULO-11-D
710
||||
06/04/2009
21:21
Page 710
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
11.5 SERIES ALTERNANTES
Las pruebas de convergencia que se han examinado hasta este momento se aplican sólo a
series con términos positivos. En esta sección y en la siguiente, se estudia cómo tratar a series cuyos términos no son necesariamente positivos. De particular importancia son las
series alternantes, cuyos términos se alternan en signo.
Una serie alternante es una serie cuyos términos son alternadamente positivos y negativos. Aquí hay dos ejemplos:
1
1
1
1
1
1n1
2
3
4
5
6
n
n1
1
1
2
3
4
5
6
n
1n
2
3
4
5
6
7
n1
n1
De acuerdo con los ejemplos, el n-ésimo término de una serie alternante es de la forma
an 1n1bn
an 1n bn
o bien,
donde bn es un número positivo. (En efecto, bn an .)
La prueba siguiente establece que si los términos de una serie alternante decrecen hacia 0 en valor absoluto, en este caso la serie converge.
PRUEBA DE LA SERIE ALTERNANTE Si la serie alternante
1
bn b1 b2 b3 b4 b5 b6 n1
bn 0
n1
cumple con
(i) bn1 bn
(ii) lím bn 0
para toda n
nl
entonces la serie es convergente.
Antes de proporcionar la demostración vea la figura 1, la cual es una representación de
la idea en la que se apoya la demostración. Primero dibuje s1 b1 en una recta numérica.
Para determinar s2 reste b2, de modo que s2 está a la izquierda de s1. Luego, para determinar s3 sume b3, de modo que s3 está a la derecha de s2. Pero como b3 b2, s3 está a la
izquierda de s1. Al continuar de esta manera, se observa que las sumas parciales oscilan
hacia un lado y hacia el otro. Puesto que bn l 0, los pasos siguientes se vuelven más y
más pequeños. Las sumas parciales pares s2, s4, s6, . . . se incrementan, y decrecen las
sumas parciales impares s1, s3, s5, . . . En estos términos, es posible que ambas converjan
en el mismo número s, el cual es la suma de la serie. Por consiguiente, en la demostración
siguiente se consideran por separado las sumas parciales pares e impares.
b¡
-b™
+b£
-b¢
+b∞
-bß
FIGURA 1
0
s™
s¢
sß
s
s∞
s£
s¡
CAPITULO-11-D
06/04/2009
21:21
Page 711
SECCIÓN 11.5 SERIES ALTERNANTES
||||
711
DEMOSTRACIÓN DE LA PRUEBA DE LA SERIE ALTERNANTE Primero considere las sumas parciales
pares:
s2 b1 b2 0
puesto que b2 b1
s4 s2 b3 b4 s2
puesto que b4 b3
s2n s2n2 b2n1 b2n s2n2
En general,
puesto que b2n b2n1
0 s2 s4 s6 s2n Por esto,
Pero también puede escribir
s2n b1 b2 b3 b4 b5 b2n2 b2n1 b2n
Todos los términos entre paréntesis son positivos, de modo que s2n b1 para toda n. Por
lo tanto, la sucesión s2n de las sumas parciales pares se incrementa y está acotada por
arriba. Debido a eso, de acuerdo con el teorema de la sucesión monótona es convergente.
Llame s a su límite, es decir,
lím s2n s
nl
Ahora calcule el límite de las sumas parciales impares:
lím s2n1 lím s2n b2n1 nl
nl
lím s2n lím b2n1
nl
nl
s0
[según la condición ii)]
s
Puesto que tanto la suma parcial par como la suma parcial impar convergen en s, lím n l sn s (véase el ejercicio 80(a) de la sección 11.1), por lo que la serie es convergente. & En la figura 2 se ilustra el ejemplo 1; se muestran las gráficas de los términos an 1n1n
y las sumas parciales sn. Observe cómo los valores de sn van en zigzag dentro del límite, el cual al
parecer está alrededor de 0.7. De hecho, la
suma exacta de la serie es ln 2 0.693 (véase
ejercicio 36).
V EJEMPLO 1
La serie armónica alternante
1
1
1n1
1
1
2
3
4
n
n1
cumple con
(i) bn1 bn
1
sn porque
(ii) lím bn lím
nl
nl
1
1
n1
n
1
0
n
de modo que la serie es convergente de acuerdo con la prueba de la serie
alternante.
an 0
n
V EJEMPLO 2
La serie
n1
1n 3n
es alternante pero
4n 1
lím bn lím
nl
FIGURA 2
nl
3n
lím
nl
4n 1
3
4
1
n
3
4
CAPITULO-11-D
712
06/04/2009
||||
21:21
Page 712
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
por lo que la condición (ii) no se cumple. En cambio, vea el límite del n-ésimo término
de la serie:
lím a n lím
nl
nl
1n 3n
4n 1
Este límite no existe, de modo que la serie es divergente de acuerdo con la prueba de la
divergencia.
EJEMPLO 3 Pruebe si la serie
1
n1
n1
n2
es convergente o divergente.
n 1
3
SOLUCIÓN La serie dada es alternante, de modo que trate de comprobar las condiciones (i)
y (ii) de la prueba de la serie alternante.
Al contrario de la situación en el ejemplo 1, no es obvio que la sucesión dada por
bn n2n3 1 sea decreciente. Sin embargo, si considera la función relacionada f x
x 2x 3 1, encuentre que
x2 x 3 x 3 12
3
Puesto que se consideran sólo x positivas, fx 0 si 2 x3 0, es decir, x s
2. De
3
esta manera, f es decreciente en el intervalo (s2, ). Esto quiere decir que fn 1 fn y, por lo tanto, bn1 bn cuando n 2. (La desigualdad b2 b1 se puede comprobar
de manera directa, pero lo que realmente importa es que la sucesión bn decrece con el
tiempo.)
La condición (ii) se comprueba rápidamente:
f x & En lugar de verificar la condición (i) de la
prueba de la serie alternante calculando una
derivada, puede comprobar que bn1 bn
directamente usando la técnica de la solución 1
del ejemplo 12 de la sección 11.1.
1
n
2
lím bn lím
nl
nl
n
lím
nl
n3 1
1
1 3
n
0
Por esto, la serie dada es convergente de acuerdo con la prueba de la serie
alternante.
ESTIMANDO SUMAS
Una suma parcial de sn de cualquier serie convergente se puede usar como una aproximación a una suma total s, pero no es muy utilizado, a menos que estime la exactitud de
la aproximación. El error generado al usar s sn es el residuo Rn s sn. El teorema
siguiente establece que para las series que cumplen con la condición de la prueba de la
serie alternante, el tamaño del error es menor que bn1, lo cual es el valor absoluto del
primer término ignorado.
& Desde el punto de vista de la geometría,
puede ver por qué el teorema de estimación
para series alternantes es verdadero al examinar
la figura 1 en la página 710. Observe que
s s4 b5, s s5 b6, y así sucesivamente. Note también que s queda entre dos sumas
parciales consecutivas.
TEOREMA DE ESTIMACIÓN PARA SERIES ALTERNANTES Si s 1n1bn es la
suma de una serie alternante que cumple con
(i) 0 bn1 bn
entonces
y
(ii) lím bn 0
nl
Rn s sn bn1
DEMOSTRACIÓN Sabemos de la demostración para la prueba de series alternantes que s queda
entre dos sumas parciales consecutivas sn y sn1. Se infiere que
s sn sn1 sn bn1
CAPITULO-11-D
06/04/2009
21:21
Page 713
SECCIÓN 11.5 SERIES ALTERNANTES
Calcule la suma de la serie n0
(Por definición, 0! 1.)
V EJEMPLO 4
||||
713
1n
con tres cifras decimales.
n!
SOLUCIÓN Primero observe que la serie es convergente de acuerdo con la prueba de la serie
alternante porque
(i)
1
1
1
n 1!
n!n 1
n!
(ii)
0
1
1
1
l 0 conforme n l l 0 de modo que
n!
n
n!
Para ver cuántos términos necesitamos usar en la aproximación, escriba los primeros
términos de la serie
s
1
1
1
1
1
1
1
1
0!
1!
2!
3!
4!
5!
6!
7!
1
1
1
1 1 12 16 241 120
720
5040
1
1
b 7 5040
5000 0.0002
Observe que
1
1
s6 1 1 12 16 241 120
720
0.368056
y
De acuerdo con el teorema de la estimación de la serie alternante, se sabe que
s s6 b7 0.0002
& En la sección 11.10 se demuestra que
e x n0 x nn! para toda x, de modo que
el resultado del ejemplo 4 es en realidad una
aproximación al número e1.
11.5
Este error de menos de 0.0002 no afecta la tercera cifra decimal, de modo que tenemos
s 0.368 que es correcta hasta la tercera cifra decimal.
|
NOTA La regla de que el error (al usar sn para aproximarse a s) es menor que el primer término ignorado es en general válida sólo para series alternantes que cumplen con las
condiciones del teorema de la estimación de la serie alternante. La regla no se aplica a
otros tipos de series.
EJERCICIOS
1. (a) ¿Qué es una serie alternante?
(b) ¿En qué condiciones una serie alternante converge?
(c) Si estas condiciones se cumplen, ¿qué puede decir con respecto al residuo después de n términos?
9.
1
n
n1
11.
1
n1
n1
2–20 Pruebe las series para ver si son convergentes o divergentes.
2. 1
3
3.
4
7
2
4
3
5
4
6
5
7
48 49 104 114 15.
5.
n1
1
2n 1
3n 1
7. 1
2n 1
n1
n
n1
n
8. 1
sn3 2
n1
19.
n1
cos n
n 34
1
lnn 4
6.
n1
n
1
n
sen
n1
1
n
n1
nn
n!
1
n
n1
n2
3
n 4
sn
1 2sn
12.
1
n1
n1
n
13. 1n
ln
n
n2
17.
n1
10.
1
1
1
1
1
4.
s2
s3
s4
s5
s6
n
10n
14.
1
n1
n1
16.
n
n1
1
n
n1
n
5
cos
n1
20.
ln n
n
senn2
n!
18.
e 1n
n
n
n
CAPITULO-11-D
714
||||
06/04/2009
21:21
Page 714
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
31. ¿Es la 50a. suma parcial s50 de la serie alternante
; 21–22 Calcule las 10 primeras sumas parciales de la serie y
n1 1n1n una estimación excesiva o una subestimación de
la suma total? Explique.
dibuje tanto la sucesión de términos como la sucesión de las sumas parciales en la misma pantalla. Estime el error al usar la décima suma parcial para aproximarse a la suma total.
21.
n1
1n1
n 32
22.
n1
32–34 ¿Para qué valores de p es convergente cada serie?
1n1
n3
32.
n1
23.
n1
24.
n1
25.
n0
26.
1n1
n6
error 0.0001
1n
10n n!
error 0.000005
n1
29.
n1
ln n
n
36. Siga los pasos siguientes para demostrar que
n1
1 n1
n5
1 n1 n 2
10 n
28.
n1
30.
1n1
ln 2
n
Sean hn y sn las sumas parciales de las series armónica y
armónica alternante.
(a) Demuestre que s2n h2n hn.
(b) Según el ejercicio 40 de la sección 11.3
error 0.01
hn ln n l .
27–30 Obtenga un valor aproximado de la suma de la serie que sea
correcta hasta la cuarta cifra decimal.
n1
1n
np
p
1n1nen
bn 1n si n es impar y bn 1n 2 si n es par. ¿Por qué no se
aplica la prueba de la serie alternante?
n1
27.
33.
35. Demuestre que es divergente la serie 1n1bn , donde
error 0.00005
1 n
n 5n
n1
n2
de la serie necesita sumar para determinar la suma con la exactitud
señalada?
1
34.
23–26 Demuestre que la serie es convergente. ¿Cuántos términos
1n1
np
n1
cuando n l y, por lo tanto,
1 n n
8n
h2n ln2n l .
1 n
3 n n!
cuando n l Apoyándose en estos hechos y el inciso (a), demuestre que
s2n l ln 2 cuando n l .
11.6 CONVERGENCIA ABSOLUTA Y LAS PRUEBAS DE LA RAZÓN Y LA RAÍZ
Dada una serie an, considere las series correspondientes
a a a a n
1
2
3
n1
cuyos términos son los valores absolutos de los términos de la serie original.
& Hay pruebas para la convergencia para
series con términos positivos y para series
alternantes. Pero, ¿y si los signos de los
términos cambian de manera irregular? En
el ejemplo 3, se observa que la idea de la
convergencia absoluta ayuda a veces en
tales casos.
1 DEFINICIÓN Una serie an es llamada absolutamente convergente si la serie
de valores absolutos an es convergente.
Observe que si an es una serie con términos positivos, entonces an an y por lo tanto
la convergencia absoluta es lo mismo que la convergencia.
EJEMPLO 1 La serie
n1
1n1
1
1
1
1 2 2 2 n2
2
3
4
CAPITULO-11-D
06/04/2009
21:21
Page 715
SECCIÓN 11.6 CONVERGENCIA ABSOLUTA Y LAS PRUEBAS DE LA RAZÓN Y LA RAÍZ
||||
715
es absolutamente convergente porque
n1
1n1
1
1
1
1
2 1 2 2 2 2
n
n
2
3
4
n1
es una serie p convergente p 2.
EJEMPLO 2 Ya sabe que la serie armónica alternante
n1
1n1
1
1
1
1 n
2
3
4
es convergente (véase ejemplo 1 de la sección 11.5), pero no es absolutamente convergente porque la serie correspondiente de valores absolutos es
n1
1n1
1
1
1
1
1 n
2
3
4
n1 n
que es la serie armónica (serie p con p 1) y, por lo tanto, es divergente.
2 DEFINICIÓN Una serie an se llama condicionalmente convergente si es
convergente pero no absolutamente convergente.
En el ejemplo 2 se muestra que la serie armónica alternante es condicionalmente convergente. En estos términos, es posible que una serie sea convergente, pero no absolutamente
convergente. No obstante, el teorema siguiente muestra que la convergencia absoluta significa convergencia.
3
TEOREMA Si una serie an es absolutamente convergente, entonces es convergente.
DEMOSTRACIÓN Observe la desigualdad
0 an an 2 an
es cierta porque an es an o bien, an. Si an es absolutamente convergente, entonces
an es convergente, así que 2an es convergente. Por lo tanto, según la prueba de
la comparación, (a n a n ) es convergente. Entonces,
En la figura 1 se ilustran las gráficas de los
términos an y las sumas parciales sn de la serie del
ejemplo 3. Observe que la serie no es alternante,
pero tiene términos positivos y negativos.
a
n
&
es la diferencia de dos series convergentes y, por lo tanto, convergente.
V EJEMPLO 3
Determine si la serie
n1
0.5
cos n
cos 1
cos 2
cos 3
2
2
2
n
1
2
32
es convergente o divergente.
sn an 0
n
SOLUCIÓN La serie posee términos tanto positivos como negativos, pero no es alternante.
(El primer término es positivo, los siguientes tres son negativos, y los otros tres que siguen son positivos. Los signos no siguen un patrón regular.) Entonces puede aplicar la
prueba de comparación a la serie de valores absolutos
FIGURA 1
an an an n1
cos n
cos n
2
n
n2
n1
CAPITULO-11-E
716
||||
06/04/2009
22:22
Page 716
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
Puesto que cos n 1 para toda n, entonces
cos n n
2
1
n2
Sabemos que 1n 2 es convergente (serie p con p 2) y, por lo tanto, cos n n 2 es
convergente según la prueba por comparación. De esta manera, la serie dada cos nn 2
es absolutamente convergente y, debido a eso, convergente de acuerdo con el teorema 3. La prueba siguiente es muy útil para determinar si una cierta serie es absolutamente
convergente
PRUEBA DE LA RAZÓN
a n1
L 1, entonces la serie a n es absolutamente convergente
nl
an
n1
(y, en consecuencia, convergente).
(i) Si lím
a n1
a n1
L 1, o bien, lím
, entonces la serie a n
nl
nl
an
an
n1
es divergente.
(ii) Si lím
a n1
1, la regla de comparación no es concluyente; es decir, no se
an
puede sacar conclusión alguna con respecto a la convergencia o a la
divergencia de an.
(iii) Si lím
nl
DEMOSTRACIÓN
(i) La idea es comparar la serie dada con una serie geométrica convergente. Puesto
que L 1, puede escoger un número r tal que L r 1. Como
lím
nl
a n1
L
an
y
Lr
el cociente an1an eventualmente será menor que r; es decir, existe un entero N tal que
a n1
r
an
cuando n N
que equivale,
4
a a r
n1
cuando n N
n
Al hacer a n sucesivamente igual a N, N 1, N 2, . . . en (4), se obtiene
a a r
a a r a r
a a r a r
N1
N
N2
N1
N
N3
N2
N
2
3
y, en general,
5
a a r
Nk
N
k
para toda k 1
CAPITULO-11-E
06/04/2009
22:22
Page 717
SECCIÓN 11.6 CONVERGENCIA ABSOLUTA Y LAS PRUEBAS DE LA RAZÓN Y LA RAÍZ
||||
717
Ahora la serie
a r
N
k
aN r aN r 2 aN r 3 k1
es convergente porque es una serie geométrica con 0 r 1. De modo que la desigualdad 5), junto con la prueba de la comparación demuestran que la serie
a a a a a n
Nk
nN1
N1
N2
N3
k1
también es convergente. Se infiere que la serie n1 a n es convergente. (Recuerde que
una cantidad finita de términos no afecta la convergencia.) Por lo tanto, an es absolutamente convergente.
(ii) Si a n1a n l L 1, o bien, a n1a n l , entonces el cociente a n1a n eventualmente será mayor que 1; es decir, existe un entero N tal que
a n1
1
an
siempre que n N
Esto significa que a n1 a n siempre que n N y de este modo,
lím a n 0
nl
En consecuencia, an es divergente según la prueba de la divergencia.
NOTA La parte (iii) de la regla de comparación establece que si lím nl an1an 1,
la prueba no proporciona información. Por ejemplo, en cuanto a la serie convergente
1n2
1
a n1
n 12
n2
an
1
n 12
n2
1
1
1
n
2
l1
cuando n l pero para la serie divergente 1n
a n1
an
1
n1
n
1
l1
1
1
n1
1
n
n
cuando n l Por lo tanto, si lím nl
an1an 1, la serie an podría ser convergente o divergente. En este caso, la regla de comparación no funciona, razón por la cual debe aplicar otra prueba.
1
n
EJEMPLO 4 Pruebe si la serie
ESTIMACIÓN DE SUMAS
En las tres últimas secciones estudió varios
métodos para estimar la suma de la serie, y
el método dependía de cuál prueba se usaba
para demostrar la convergencia. ¿Qué sucede
con las series para las cuales sí funciona la
regla de comparación? Hay dos posibilidades: si
la serie es alternante, como en el ejemplo 4,
entonces es mejor aplicar los métodos de la
sección 11.5. Si todos los términos son positivos,
en este caso aplique los métodos especiales que
se explican en el ejercicio 34.
n1
n3
es absolutamente convergente.
3n
&
SOLUCIÓN Aplique la regla de comparación con a n 1n n 33 n:
a n1
an
1n1n 13
3 n1
n 13 3 n
3
n 3
1 n
3 n1
n
n
3
|
1
3
|
n1
n
3
1
3
1
1
n
3
l
1
1
3
CAPITULO-11-E
718
||||
06/04/2009
22:22
Page 718
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
De esta manera, de acuerdo con la regla de comparación, la serie dada es absolutamente
convergente y, en consecuencia, convergente.
nn
es convergente.
n1 n!
SOLUCIÓN Puesto que los términos a n n nn! son positivos, no necesita los signos del valor absoluto.
V EJEMPLO 5
Pruebe si la serie
a n1
n 1n1 n!
n 1n 1n n!
n n
an
n 1!
n
n 1n!
n
n1
n
n
1
n
1
n
le
cuando n l (Véase ecuación 3.6.6.) Puesto que e 1, la serie dada es divergente según la prueba
de la razón.
NOTA La prueba de la razón funciona en el ejemplo 5, pero un método más fácil es la
prueba de la divergencia. Como
an nn
n n n n
n
n!
1 2 3 n
se infiere que an no tiende a 0 cuando n l . Por lo tanto, la serie dada es divergente según la prueba de la divergencia.
Es conveniente aplicar la siguiente prueba cuando hay potencias n-ésimas. Su demostración es similar a la de la prueba de la razón y se deja en el ejercicio 37.
PRUEBA DE LA RAÍZ
n
(i) Si lím s
a n L 1, entonces la serie
nl
a
n
es absolutamente convergente
n1
(y, por lo tanto, convergente).
nl
(iii)
a
Si lím s a 1, la prueba de la raíz no es concluyente.
n
n
(ii) Si lím s
a n L 1 o lím s
a n , entonces la serie
nl
n
nl
n
es divergente.
n1
n
n
Si lím n l s
a n 1, entonces la parte (iii) de la prueba de la raíz establece que la
prueba no proporciona información. La serie an podría ser convergente o divergente.
(Si L 1 en la prueba de la razón no intente con la prueba de la raíz porque L será una
vez más 1. Y si L 1 en la prueba de la raíz, no intente la prueba de la razón porque
también fallará.)
V EJEMPLO 6
Pruebe la convergencia de la serie
n1
SOLUCIÓN
an n
an
s
2n 3
3n 2
2n 3
3n 2
n
.
2n 3
3n 2
n
3
n
2
l 1
2
3
3
n
2
Así, la serie dada converge según la prueba de la raíz.
CAPITULO-11-E
06/04/2009
22:22
Page 719
SECCIÓN 11.6 CONVERGENCIA ABSOLUTA Y LAS PRUEBAS DE LA RAZÓN Y LA RAÍZ
||||
719
REORDENAMIENTOS
La pregunta de si una serie dada que es convergente es absolutamente convergente o condicionalmente convergente, tiene relación con la pregunta si las sumas infinitas se comportan como sumas finitas.
Naturalmente, si reordena los términos en una suma finita, pues el valor de la suma
no cambia. Pero esto no siempre sucede en las series infinitas. Con reordenamiento de
una serie infinita an se da a entender una serie obtenida simplemente al cambiar el orden de los términos. Por ejemplo, un reordenamiento de an podría ser el siguiente:
a1 a2 a5 a3 a4 a15 a6 a7 a20 Resulta que
si an es una serie absolutamente convergente de suma s,
en tal caso cualquier reordenamiento de an tiene la misma suma s.
Sin embargo, cualquier serie condicionalmente convergente se puede reordenar, con lo
cual la suma será distinta. Para ilustrar este hecho considere la serie armónica alterna
1 12 13 14 15 16 17 18 ln 2
6
(Véase ejercicio 36 en la sección 11.5.) Si multiplica la serie por 12 , obtiene
1
2
14 16 18 12 ln 2
Si inserta ceros entre los términos de esta serie, tiene
Sumar ceros no afecta la suma de la serie;
se repite cada uno de los términos de la sucesión
de sumas parciales, pero el límite es el mismo.
&
0 12 0 14 0 16 0 18 12 ln 2
7
Ahora sume la serie de las ecuaciones 6 y 7 usando el teorema 11.2.8:
1 13 12 15 17 14 32 ln 2
8
Observe que la serie en (8) consta de los mismos términos que en (6), pero reordenados de
modo que haya un término negativo después de cada par de términos positivos. Pero las sumas de estas series son diferentes. De hecho, Riemann demostró que
si an es una serie condicionalmente convergente y r es cualquier número real, por
lo tanto hay un reordenamiento de an que tiene una suma igual a r.
Una demostración de este hecho se plantea en el ejercicio 40.
11.6
EJERCICIOS
1. ¿Qué puede decir acerca de la serie an en cada uno de los ca-
sos siguientes?
a n1
8
(a) lím
nl
an
(c) lím
nl
5.
n1
a n1
0.8
(b) lím
nl
an
7.
a n1
1
an
n1
3.
n0
2 k
3
n1
4.
1
n1
n1
2n
n4
13.
n1
n1
n
n1
8.
1
n1
11.
n2
2n
10 n
n!
6.
k( )
9.
nalmente convergente o divergente.
2.
1n1
4
n
s
k1
2–28 Determine si la serie es absolutamente convergente, condicio
1.1n
n4
1n
n4
n!
100 n
10.
1
n
n1
1ne 1n
n3
12.
10 n
n 142n1
14.
n1
n
sn3 2
sen 4n
4n
1
n1
n1
n 22n
n!
CAPITULO-11-E
720
||||
15.
n1
17.
n2
19.
n1
n1
23.
22:22
Page 720
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
1n arctan n
n2
16.
1
ln n
18.
cosn3
n!
20.
n1
n 1
2n2 1
n1
n1
n
22.
n2
n2
1
n
24.
2n
nn
n2
2n
n1
5n
n
ln nn
135
1357
13
25. 1 3!
5!
7!
1 3 5 2n 1
1n1
2n 1!
26.
2
26
2 6 10
2 6 10 14
5
58
5 8 11
5 8 11 14
27.
n1
2 4 6 2n
n!
28.
1
n
n1
según la prueba de la razón. Como es lo usual, Rn sea el residuo
después de n términos, es decir,
Rn a n1 a n2 a n3 n!
nn
n1
2
1
3 cos n
n 23 2
n
21.
06/04/2009
2 n n!
5 8 11 3n 2
(a) Si rn es una sucesión decreciente y rn1 1, demuestre
con la suma de una serie geométrica que
a n1
Rn 1 rn1
(b) Si rn es una sucesión creciente, demuestre que
a n1
Rn 1L
35. (a) Calcule la suma parcial s5 de la serie n1 1n2n. Con ayu-
da del ejercicio 34 estime el error al usar s5 como una
aproximación a la suma de la serie.
(b) Determine un valor de n de tal modo que sn no difiera
0.00005 de la suma real. Use este valor de n para obtener
un valor aproximado de la suma de la serie.
36. Use la suma de los primeros 10 términos para obtener un valor
aproximado de la suma de la serie
n
n
n1 2
Aplique el ejercicio 34 para estimar el error.
37. Demuestre la prueba de la raíz.
[Sugerencia para la
parte (i): tome cualquier número r tal que L r 1 y
n
aplique el hecho de que hay un entero N tal que s
an r
cuando n N.]
29. Los términos de una serie se definen en forma recursiva me-
diante las ecuaciones
38. Hacia 1910, Srinivasa Ramanujan, matemático de la India, des-
a1 2
a n1 5n 1
an
4n 3
Determine si an es convergente o divergente.
30. Una serie an está definida de acuerdo con las ecuaciones
a1 1
a n1 2 cos n
an
sn
Determine si an converge o diverge.
31. ¿Para cuáles de las series siguientes la prueba de la razón
no es concluyente (es decir, no proporciona una respuesta
definida)?
(a)
n1
(c)
n1
1
n3
(b)
n1
3
sn
n1
(d)
n1
n
2n
sn
1 n2
32. ¿Para cuáles enteros positivos k la serie siguiente es conver-
gente?
n1
n!2
kn!
33. (a) Demuestre que n0 x nn! converge para toda x.
(b) Deduzca que lím n l x nn! 0 para toda x.
34. Sea an una serie con términos positivos y sea rn a n1 a n. Su-
ponga que lím n l rn L 1, de modo que an es convergente
cubrió la fórmula
2s2
1
p
9801
n0
4n!1103 26390n
n!4 3964n
William Gosper utilizó esta serie en 1985 para calcular los primeros 17 millones de dígitos de p.
(a) Verifique que la serie sea convergente.
(b) ¿Cuántos lugares decimales correctos de p obtiene el lector
si usa sólo el primer término de la serie? ¿Qué pasa si usa
dos términos?
39. Dada cualquier serie an define una serie a n si todos sus térmi-
nos son positivos de an y una serie a n si todos sus términos
son negativos de an. Para ser específicos,
an an an
2
an a n an
2
Observe que si an 0, por lo tanto an a n y a n 0, siempre
que an 0, después an a n y an 0.
(a) Si an es absolutamente convergente, demuestre que tanto
la serie a n como la a n son convergentes.
(b) Si an es condicionalmente convergente, demuestre que
tanto la serie a n como la a n son divergentes.
40. Demuestre que si an es una serie condicionalmente convergen-
te y r es cualquier número real, en este caso hay un
reordenamiento de an cuya suma es r. [Sugerencias: utilice la
notación del ejercicio 39. Tome sólo suficientes términos positivos an de modo que su suma sea mayor que r. Luego sume sólo
suficientes términos negativos an para que la suma acumulativa
sea menor que r. Continúe así y aplique el teorema 11.2.6.]
CAPITULO-11-E
06/04/2009
22:22
Page 721
SECCIÓN 11.7 ESTRATEGIA PARA PROBAR SERIES
||||
721
11.7 ESTRATEGIA PARA PROBAR SERIES
Ya conoce varias maneras de probar la convergencia o divergencia de una serie. Ahora el
problema es decidir cuál prueba aplicar en cada serie. En este aspecto, probar series es parecido a integrar funciones. No hay reglas rígidas y rápidas con respecto a qué prueba aplicar a una serie dada, pero puede seguir las recomendaciones siguientes, puesto que le pueden
ser útiles.
No es prudente aplicar una lista de pruebas en un orden específico hasta que una acaba por
funcionar. Eso sería un desperdicio de tiempo y esfuerzo. En lugar de eso, al igual que en la integración, la estrategia principal es clasificar las series de acuerdo con su forma.
1. Si la serie es de la forma 1n p, es una serie p, lo cual significa que es convergente
2.
3.
4.
5.
6.
si p 1 y divergente si p 1.
Si la serie es de la forma ar n1 o ar n, es una serie geométrica, la cual converge
si r 1 y diverge si r 1. Se podrían requerir algunas operaciones algebraicas para hacer que la serie alcance esta forma.
Si la serie posee una forma similar a la de una p-serie o a una serie geométrica, entonces se debe considerar una de las pruebas por comparación. En particular, si an
es una función racional o una función algebraica de n (es decir, que contiene raíces
de polinomios), por lo tanto, la serie se debe comparar contra una p-serie. Observe
que la mayoría de las series de los ejercicios 11.4 poseen esta forma. (El valor de
p se debe escoger como en la sección 11.4, y conservar sólo las potencias más altas
de n en el numerador y en el denominador.) Las pruebas por comparación se aplican sólo en series con términos positivos, pero si an tiene algunos términos negativos, en seguida puede aplicar la prueba por comparación a an y probar si hay
convergencia absoluta.
Si es fácil ver que lím n l a n 0, entonces se debe aplicar la prueba para la divergencia.
Si la serie es de la forma 1n1bn, o bien, 1nbn , entonces una posibilidad
obvia es la prueba de la serie alternante.
Las series que contienen factoriales u otros productos (incluso una constante elevada
a una potencia n-ésima) se prueban en forma aceptable usando la prueba de la
razón. Siempre piense que a n1a n l 1 cuando n l para todas las p-serie y,
por lo tanto, todas las funciones racionales o algebraicas de n. En estos términos,
la prueba de la razón no se debe aplicar para dichas series.
Si an es de la forma bn n, entonces la prueba de la raíz podría ser útil.
Si a n f n, donde x1
f x dx se puede evaluar con facilidad, entonces la prueba de la
integral es efectiva (suponiendo que la hipótesis de esta prueba se cumple).
7.
8.
En los ejemplos siguientes no se presenta todo el desarrollo, sino que simplemente se
indica qué prueba se debe usar.
V EJEMPLO 1
n1
n1
2n 1
Puesto que a n l 12 0 cuando n l , debe usar la prueba de la divergencia.
EJEMPLO 2
n1
sn 3 1
3n 3 4n 2 2
Como an es una función algebraica de n, compare la serie dada con la p-serie.
CAPITULO-11-E
722
06/04/2009
||||
22:22
Page 722
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
La serie de comparación de la prueba de comparación en el límite es bn, donde
bn V EJEMPLO 3
n 32
1
sn 3
3
3n
3n 3
3n 32
ne
n 2
n1
Puesto que la integral x1
xex dx se evalúa con facilidad, use la prueba de la integral.
La prueba de la razón también funciona.
2
n3
n 1
n1
Como la serie es alternante, aplique la prueba de la serie alternante.
EJEMPLO 4
1
n
V EJEMPLO 5
k1
4
2k
k!
Como la serie contiene k!, se aplica la prueba de la razón.
1
2 3n
La serie está estrechamente relacionada con la serie geométrica 13 n, por lo que se
aplica la prueba por comparación.
EJEMPLO 6
n1
11.7
EJERCICIOS
1–38 Pruebe si las series son convergentes o divergentes.
1.
n1
1
n 3n
2.
n1
n
3. 1
n2
n1
n
5.
n1
7.
n2
n
4. 1 2
n 2
n1
n
6.
1
nsln n
8.
n1
1
2n 1
k
k1
21.
n1
2 k!
k 2!
23.
9.
k
2 k
10.
e
k1
11.
25.
n2
13.
n1
15.
n0
28.
1n
cosh n
30.
5k
3 4k
32.
sen1n
sn
34.
n
3 n
n!
14.
1 2
n
1
n1
sen 2n
1 2n
n2 1
n3 1
33.
16.
1n1
sn 1
35.
n
n1
1n
18.
n2
ln n
sn
20.
31.
n1
n1
19.
sen n
k1
n1
n1
2
n!
2 5 8 3n 2
29.
12.
17.
ne
k5
5k
k1
n1
n1
n2 1
5n
e 1n
n2
1
j
j1
n1
n1
n2
(s2 1)
n1
n1
n
n1
n
n1
k
37.
k ln k
k 13
27.
n sen1n
n1
26.
n1
sn 2 1
n 2n 2 5
3
24.
n!
2
en
n1
n1
2 n 3
n1
1 n1
n ln n
22.
tan1n
k1
22n
nn
n2 2n1
5n
2n 1
n2n
n
n
36.
n2
n!n
n4n
1
n n cos2 n
1
ln nln n
38.
sj
j5
(s2 1)
n
n1
CAPITULO-11-E
06/04/2009
22:22
Page 723
SECCIÓN 11.8 SERIES DE POTENCIAS
||||
723
11.8 SERIES DE POTENCIAS
Una serie de potencias es una serie de la forma
cx
1
n
n
c0 c1 x c2 x 2 c3 x 3 n0
donde x es una variable y las cn son constantes que se denominan coeficientes de la serie. Para cada x establecida, la serie (1) es una serie de constantes que puede probar para ver si son
convergentes o divergentes. Una serie de potencias podría ser convergente para algunos valores de x y ser divergente para otros. La suma de la serie es una función
SERIES TRIGONOMÉTRICAS
Una serie de potencias es una serie en la cual
cada uno de los términos es una función con
potencias. Una serie trigonométrica
f x c0 c1 x c2 x 2 cn x n &
a
n
cos nx bn sen nx
n0
es una serie cuyos términos son funciones trigonométricas. Este tipo de serie se analiza en la
página web
cuyo dominio es el conjunto de todas las x para las cuales la serie es convergente. Observe
que f es parecida a un polinomio. La única diferencia es que f tiene una cantidad infinita
de términos.
Por ejemplo, si hace cn 1 para toda n, la serie de potencias se transforma en una serie geométrica
x
n
1 x x2 xn n0
www.stewartcalculus.com
Dé un clic en Additional Topics y luego en
Fourier Series.
que es convergente cuando 1 x 1 y es divergente cuando x 1 (véase ecuación 11.2.5).
En general, una serie de la forma
2
c x a
n
n
c0 c1x a c2x a2 n0
se denomina serie de potencias en x a, o bien, serie de potencias centrada en a, o
también, serie de potencias con respecto a a. Observe que al escribir el término correspondiente a n 0 en las ecuaciones 1 y 2, se ha adoptado la convención de x a0 1
aun cuando x a. Asimismo, note que cuando x a todos los términos son 0 para n 1 y
de este modo la serie de potencias (2) siempre es convergente cuando x a.
V EJEMPLO 1
¿Para qué valores de x la serie
n!x
n
es convergente?
n0
SOLUCIÓN Aplique la prueba de la razón. Si denota con an, como se acostumbra, el n-ésimo
término de la serie, entonces a n n! x n. Si x 0,
& Nótese que
n 1! n 1nn 1 3 2 1
n 1n!
lím
nl
an1
n 1!x n1
lím
lím n 1 x nl
nl
an
n!x n
Según la prueba de la razón, la serie es divergente cuando x 0. En estos términos, la
serie dada converge sólo cuando x 0.
V EJEMPLO 2
¿Para qué valores de x la serie
x 3n
es convergente?
n
n1
SOLUCIÓN Sea a n x 3 n. En tal caso
n
an1
x 3n1
n
an
n1
x 3n
1
1
1
n
x 3
l x3
cuando n l CAPITULO-11-F
724
||||
06/04/2009
21:24
Page 724
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
De acuerdo con la regla de comparación, la serie dada es absolutamente convergente y, por
lo tanto, convergente cuando x 3 1 y divergente cuando x 3 1. Ahora
x 3 1 &?
1 x 3 1 &?
2x4
National Film Board of Canada
de modo que la serie converge cuando 2 x 4 y diverge cuando x 2 o bien x 4.
La prueba de la razón no proporciona información cuando x 3 1 de modo que
debe considerar x 2 y x 4 por separado. Si pone x 4 en la serie, se vuelve 1n,
la serie armónica, la cual es divergente. Si x 2, la serie es 1nn, la cual es convergente de acuerdo con la prueba de la serie alternante. Por lo tanto, la serie de potencias
dada converge para 2 x 4.
Ya verá que el uso principal de las series de potencias es proporcionar una manera de representar algunas de las funciones más importantes que surgen en matemáticas, física y química. En particular, la suma de la serie de potencias del ejemplo siguiente se llama función de Bessel, en honor al astrónomo alemán Friedrich Bessel (1784-1846), y la función
dada en el ejercicio 35 es otro ejemplo de la función de Bessel. En efecto, estas funciones
surgieron primero cuando Bessel resolvió la ecuación de Kepler para describir el movimiento de los planetas. Desde esa época, estas funciones se aplican en diversas situaciones físicas, sin olvidar la distribución de temperaturas en una lámina circular y las vibraciones
de una membrana de un tambor.
EJEMPLO 3 Determine el dominio de la función de Bessel de orden 0 definida por
J0x n0
1n x 2n
2 2nn!2
SOLUCIÓN Sea a n 1n x 2n2 2nn!2
. En tal caso
an1
1n1x 2n1
2 2nn!2
2n1
an
2
n 1!
2 1nx 2n
& Observe cómo la aproximación del modelo
generado por computadora (el cual utiliza
funciones de Bessel y de cosenos) coincide
con la fotografía de una membrana vibratoria
de hule.
x 2n2
2 2nn!2
2 2n2n 12n!2
x 2n
x2
l 01
4n 12
para toda x
De este modo, de acuerdo con la prueba de la razón, la serie dada converge para
todos los valores de x. En otras palabras, el dominio de la función de Bessel J0 es
, .
Recuerde que la suma de una serie es igual al límite de la sucesión de las sumas parciales. De esa manera, cuando se define la función de Bessel del ejemplo 3 como la suma de
una serie quiere decir que, para todo número real x,
n
J0x lím snx
nl
donde
snx i0
1ix 2i
2 2ii!2
Las primeras sumas parciales son
s0x 1
s3x 1 s1x 1 x2
x4
x6
4
64
2304
x2
4
s2x 1 s4x 1 x2
x4
4
64
x2
x4
x6
x8
4
64
2304
147 456
CAPITULO-11-F
06/04/2009
21:24
Page 725
SECCIÓN 11.8 SERIES DE POTENCIAS
y
s™
s¸
1
s¢
0
x
1
s¡ s£
J¸
||||
725
En la figura 1 se muestran las gráficas de estas sumas parciales, las cuales son polinomios.
Todas son aproximaciones de la función J0, pero observe que la aproximación es mejor
cuando se incluyen más términos. En la figura 2 se ilustra una gráfica más completa de la
función de Bessel.
En lo que respecta a la serie de potencias examinadas hasta el momento, el conjunto de
valores de x para los cuales la serie es convergente ha resultado ser siempre un intervalo [un intervalo finito de la serie geométrica y la serie del ejemplo 2, el intervalo infinito , del
ejemplo 3 y un intervalo colapsado 0, 0
0 del ejemplo 1. El teorema siguiente, demostrado en el apéndice F, establece que esto es válido en general.
FIGURA 1
Sumas parciales de la función
de Bessel J¸
1
y=J¸(x)
10
0
n
n
n0
y
_10
TEOREMA Para una serie de potencias dada
c x a
hay sólo tres posibilidades:
(i) La serie converge sólo cuando x a.
(ii) La serie converge para toda x.
(iii) Hay un número positivo R tal que la serie converge si x a R y diverge
si x a R.
3
x
FIGURA 2
El número R en el caso (iii) se llama radio de convergencia de la serie de potencias.
Por convención, el radio de convergencia es R 0 en el caso (i) y R en el caso
(ii). El intervalo de convergencia de una serie de potencias es el intervalo que consiste
en todos los valores de x para los cuales la serie converge. En el caso (i) el intervalo
consta de un solo punto a. En el caso (ii) el intervalo es , . Observe que en el caso
(iii) la desigualdad x a R se puede escribir de nuevo como a R x a R.
Cuando x es un extremo del intervalo, es decir, x a R, cualquier cosa puede suceder:
la serie podría ser convergente en uno o en ambos extremos, o podría ser divergente en
ambos extremos. Por lo tanto, en el caso (iii) hay cuatro posibilidades para el intervalo de
convergencia:
a R, a R
a R, a R
a R, a R
a R, a R
La situación se ilustra en la figura 3.
convergencia para | x-a |<R
a-R
FIGURA 3
a+R
a
divergencia para | x-a |>R
Se resumen a continuación el radio y el intervalo de convergencia para cada uno de los
ejemplos ya considerados en esta sección.
Serie
Radio de convergencia
Intervalo de convergencia
R1
1, 1
n
R0
0
x 3n
n
R1
2, 4
1nx 2n
2 2nn!2
R
, Serie geométrica
x
n
n0
Ejemplo 1
n! x
n0
Ejemplo 2
n1
Ejemplo 3
n0
CAPITULO-11-F
726
||||
06/04/2009
21:24
Page 726
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
En general, la prueba de la razón (o a veces, la prueba de la raíz) se debe usar para determinar el radio de convergencia R. Las pruebas de la razón y la raíz siempre fracasan
cuando x es un extremo del intervalo de convergencia, de modo que es necesario verificar
los extremos por medio de alguna otra prueba.
EJEMPLO 4 Determine el radio de convergencia y el intervalo de convergencia de la serie
3n x n
sn 1
n0
SOLUCIÓN Sea a n 3n x nsn 1. Por lo tanto
an1
3n1x n1 sn 1
3x
an
3nx n
sn 2
3
1 1n
x l 3 x
1 2n
n1
n2
cuando n l De acuerdo con la prueba de la razón, la serie dada converge si 3 x 1 y es divergente si 3 x 1. En estos términos, es convergente si x 13 y diverge si x 13 .
Esto quiere decir que el radio de convergencia es R 13 .
Sabemos que la serie converge en el intervalo ( 13 , 13 ), pero ahora es necesario probar
si hay convergencia en los extremos de este intervalo. Si x 13 , la serie se
transforma en
n0
n
3n(13 )
1
1
1
1
1
sn 1
s1
s2
s3
s4
n0 sn 1
la cual es divergente. (Aplique la prueba de la integral o simplemente observe que es una
p-serie con p 12 1.) Si x 13 , la serie es
n0
n
3n( 13 )
1n
sn 1
n0 sn 1
la cual converge de acuerdo con la prueba de la serie alternante. Por lo tanto, la
serie dada de potencias converge cuando 13 x 13 , de modo que el intervalo de
convergencia es (13 , 13 ].
V EJEMPLO 5
Determine el radio de convergencia y el intervalo de convergencia de la
serie
n0
nx 2n
3 n1
SOLUCIÓN Si a n nx 2n3 n1, entonces
an1
n 1x 2n1
3 n1
n2
an
3
nx 2n
1
1
n
x2
3
l
x 2
3
cuando n l Al aplicar la prueba de la razón, se ve que la serie es convergente si x 2 3 1 y
que es divergente si x 2 3 1. De modo que es convergente si x 2 3 y divergente si x 2 3. Así que, el radio de convergencia es R 3.
CAPITULO-11-F
06/04/2009
21:24
Page 727
SECCIÓN 11.8 SERIES DE POTENCIAS
||||
727
La desigualdad x 2 3 se puede escribir como 5 x 1, así que probamos
la serie en los extremos 5 y 1. Cuando x 5, la serie es
n0
n3n
1
1nn
3
3 n1
n0
la cual es divergente según la prueba de la divergencia [1n n no converge en 0].
Cuando x 1, la serie es
n0
n3n
1
n1 3 n
3
n0
la cual también es divergente según la prueba de la divergencia. Por esto, la serie converge
sólo cuando 5 x 1, de modo que el intervalo de convergencia es (5, 1).
11.8
EJERCICIOS
1. ¿Qué es una serie de potencias?
2. (a) ¿Cuál es el radio de convergencia de una serie de poten-
cias? ¿Cómo se determina?
(b) ¿Cuál es el intervalo de convergencia de una serie de potencias? ¿Cómo se calcula?
3–28 Determine el radio de convergencia y el intervalo de conver-
23.
n1
5.
n1
7.
n0
xn
sn
4.
n0
1 x
n3
n1
11.
25.
n1
27.
nx
2n
2n x n
4
n
s
17.
n1
19.
n1
21.
n1
xn
n n
x 3n
16. 1
2n 1
n0
3nx 4n
sn
18.
x 2n
nn
20.
n
n1
b0
22.
n1
n
(b)
n
x 1n
4n
3x 2n
n3 n
nx 4n
n3 1
c 4
n
n
n0
diverge cuando x 6. ¿Qué puede decir con respecto a la convergencia o divergencia de la serie siguiente?
(c)
n1
n
30. Suponga que n0 c n x n es convergente cuando x 4 y
x 2n
14. 1
2n!
n0
n
c 2
n0
n2
convergente?
(a)
x2n
nln n2
n
x 2n
n2 1
n
x an,
bn
n1
xn
5nn5
n1
26.
n!x n
1 3 5 2n 1
12.
4x 1
n2
10 x
n3
n1
xn
13. 1 n
4 ln n
n2
n0
n
n1
n
x
1 3 5 2n 1
10.
n
15.
n
2 n
28.
n2xn
2 4 6 2n
24.
n1
(a)
n1
n
sn x
n1
8.
1
n1
6.
n
29. Si n0 c n 4 n es convergente, ¿se infiere que la serie siguiente es
n
n1
1nx n
n1
n
xn
n!
9.
n!2x 1
n1
gencia de la serie.
3.
c
(b)
n
n0
n
n
n0
c 3
n
c8
n
(d)
n0
1 c 9
n
n
n
n0
31. Si k es un entero positivo, encuentre el radio de convergencia
de la serie
n0
n!k n
x
kn!
32. Sean p y q números reales con p q. Encuentre una serie de
potencias cuyo intervalo de convergencia sea
(a) p, q
(b) p, q
(c) p, q
(d) p, q
33. ¿Es posible hallar una serie de potencias cuyo intervalo de con-
vergencia sea 0, ? Explique.
CAPITULO-11-F
728
||||
06/04/2009
21:24
Page 728
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
n
; 34. Dibuje las primeras sumas parciales snx de la serie n0 x ,
junto con la función suma fx 11 x, sobre una misma
pantalla. ¿En qué intervalo parece que convergen estas sumas
parciales y fx?
CAS
(c) Si su CAS tiene incorporadas las funciones de Airy, dibuje
A en la misma pantalla que las sumas parciales del inciso
b), y observe cómo las sumas parciales se aproximan a A.
37. Una función f está definida mediante
35. La función J1 definida por
J1x n0
;
CAS
f x 1 2x x 2 2x 3 x 4 es decir, sus coeficientes son c2n 1 y c2n1 2 para toda n 0.
Determine el intervalo de convergencia de la serie y plantee
una fórmula explícita para fx.
1n x 2n1
n!n 1!2 2n1
se llama función de Bessel de orden 1.
(a) Determine el dominio.
(b) Dibuje las primeras sumas parciales en una misma pantalla.
(c) Si su CAS tiene incorporadas las funciones de Bessel,
dibuje J1 en la misma pantalla que las sumas parciales
del inciso (b) y observe cómo se aproximan las sumas
parciales a J1.
38. Si f x mine el intervalo de convergencia de la serie y una fórmula
para fx.
n
39. Muestre que si lím n l s
cn c , donde c 0, en tal caso el radio
de convergencia de la serie de potencias cn x n es R 1c.
40. Suponga que la serie de potencias c nx a n
satisface cn 0 para toda n. Demuestre que si existe
lím n l cncn1 , por lo tanto es igual al radio de convergencia
de la serie de potencias.
36. La función A se define mediante
Ax 1 ;
x3
x6
x9
23
2356
235689
que se llama función de Airy en honor al matemático y astrónomo inglés sir George Airy (1801-1892).
(a) Determine el dominio de la función de Airy.
(b) Dibuje las primeras sumas parciales snx en una misma
pantalla.
n0 cn x n, donde cn4 cn para toda n 0, deter-
41. Suponga que el radio de convergencia de la serie c n x n es 2 y
que el radio de convergencia de la serie d n x n es 3. ¿Cuál es el
radio de convergencia de la serie c n d n x n ?
42. Suponga que el radio de convergencia de la serie de potencias
c n x n es R. ¿Cuál es el radio de convergencia de la serie de potencias cn x 2n?
11.9 REPRESENTACIONES DE LAS FUNCIONES COMO SERIES DE POTENCIAS
& Una ilustración geométrica de la ecuación 1
se muestra en la figura 1. Como la suma de una
serie es el límite de la sucesión de las sumas
parciales
1
lím snx
nl
1x
donde
En esta sección aprenderá a representar ciertos tipos de funciones como sumas de series de potencias mediante la manipulación de series geométricas, o mediante derivación o integración
de dichas series. Quizá se pregunte por qué siempre se busca expresar una función conocida
como una suma de una cantidad infinita de términos. Más adelante se explica la utilidad de
esta estrategia en la integración de funciones que no tienen antiderivadas elementales, en la solución de ecuaciones diferenciales y para aproximar funciones mediante polinomios. (Los científicos lo hacen así para simplificar las expresiones con las que trabajan; los especialistas en
computación lo hacen así para representar funciones en calculadoras y computadoras.)
Inicie con una ecuación que estudió antes:
1
1 x x2 x3 xn
x 1
1
1x
n0
Ya encontró esta ecuación en el ejemplo 5 de la sección 11.2, donde la obtuvo al observar
que es una serie geométrica con a 1 y r x. Pero en este caso la opinión es distinta.
Ahora considere la ecuación 1 como expresión de la función f x 11 x como una
suma de una serie de potencias.
snx 1 x x2 xn
s¡¡
y
es la n-ésima suma parcial. Observe que cuando
n se incrementa, snx se vuelve una mejor aproximación para fx en 1 x 1.
sˆ
s∞
f
s™
FIGURA 1
1
ƒ=
y algunas sumas parciales
1-x
_1
0
1
x
CAPITULO-11-F
06/04/2009
21:24
Page 729
SECCIÓN 11.9 REPRESENTACIONES DE LAS FUNCIONES COMO SERIES DE POTENCIAS
& Cuando se pide una serie de potencias
en esta sección, se supone que la serie está
centrada en 0, a menos que se indique de
otra forma.
||||
729
Exprese 11 x2 como la suma de una serie de potencias, y determine
el intervalo de convergencia.
V EJEMPLO 1
SOLUCIÓN Al reemplazar x por x2 en la ecuación 1, queda
1
1
x 2 n
1 x2
1 x 2 n0
1 x
n 2n
1 x2 x4 x6 x8 n0
Como es una serie geométrica, es convergente cuando x 2 1, es decir, x2 1, o
bien, x 1. Por lo tanto, el intervalo de convergencia es 1, 1. Naturalmente, podría haber determinado el radio de convergencia aplicando la prueba de la razón, pero
esa cantidad de trabajo es innecesaria en este caso.
EJEMPLO 2 Determine una representación para 1x 2.
SOLUCIÓN Con objeto de poner esta función en la forma del lado izquierdo de la ecuación 1, primero se factoriza un 2 del denominador:
1
2x
1
1
x
2 1
2
1
2
n0
2 1 x
2
n
n0
x
2
1n n
x
2 n1
Esta serie converge cuando x2 1, es decir, x 2. De modo que el intervalo de
convergencia es 2, 2.
EJEMPLO 3 Obtenga una representación como serie de potencias de x3x 2.
SOLUCIÓN Puesto que esta función es justamente x3 veces la función del ejemplo 2, todo lo
que debe hacer es multiplicar esa serie por x3:
3
Es válido pasar x al otro lado del signo de
la suma porque no depende de n. [Aplique el
teorema 11.2.8(i) con c x 3.]
&
1
1n
1n
x3
x3 x 3 n1 x n n1 x n3
x2
x2
n0 2
n0 2
12 x 3 14 x 4 18 x 5 161 x 6 Otra forma de escribir esta serie es como sigue:
x3
1n1 n
x
x2
2 n2
n3
Como en el ejemplo 2, el intervalo de convergencia es 2, 2.
DERIVACIÓN E INTEGRACIÓN DE SERIES DE POTENCIAS
La suma de una serie de potencias es una función f x n0 cnx an cuyo dominio
es el intervalo de convergencia de la serie. Para ser capaces de derivar e integrar estas
funciones, el siguiente teorema (el cual no será demostrado) establece que es posible hacerlo derivando o integrando cada uno de los términos de la serie, justo como se haría
para un polinomio. Esto se denomina derivación e integración término a término.
CAPITULO-11-F
730
||||
06/04/2009
21:24
Page 730
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
2
TEOREMA Si la serie de potencias cnx an posee un radio de convergencia
R 0, entonces la función f definida por
f x c0 c1x a c2x a2 c x a
n
n
n0
es derivable (y, por lo tanto, continua) en el intervalo a R, a R y
(i) f x c1 2c2x a 3c3x a2 nc x a
n
n1
n1
En el inciso (ii), x c0 dx c0 x C1 se
escribe como c0x a C, donde
C C1 ac0, de modo que todos los términos
de la serie tienen la misma forma.
&
(ii)
y f x dx C c x a c
0
C
1
x a2
x a3
c2
2
3
x an1
n1
c
n
n0
Los radios de convergencia de la serie de potencias en las ecuaciones (i) y (ii) son R.
NOTA 1
(iii)
Las ecuaciones (i) y (ii) del teorema 2 se pueden volver a escribir en la forma
y d
dx
n0
(iv)
n0
cnx an n0
d
cnx an dx
cnx an dx y c x a dx
n
n
n0
Se sabe que, por lo que toca a las sumas finitas, la derivada de una suma es la suma de las
derivadas y la integral de una suma es la suma de las integrales. Las ecuaciones (iii) y (iv)
aseguran que lo mismo se cumple para sumas infinitas, siempre que esté trabajando con series de potencias. (En el caso de otros tipos de series de funciones la situación no es tan
simple; véase ejercicio 36.)
NOTA 2 Aunque el teorema 2 establece que el radio de convergencia es el mismo
cuando una serie de potencias es derivada o integrada, esto no quiere decir que el intervalo de
convergencia siga siendo el mismo. Podría suceder que la serie original converja en el extremo, y que la serie derivada sea divergente aquí. (Véase ejercicio 37.)
La idea de derivar una serie de potencias término a término es la base de un
método eficaz para resolver ecuaciones diferenciales. Estudiará este método en el capítulo 17.
NOTA 3
EJEMPLO 4 En el ejemplo 3 de la sección 11.8 vio que la función de Bessel
J0x n0
1n x 2n
2 2nn!2
se define para toda x. De esta manera, de acuerdo con el teorema 2, J0 es derivable para
toda x y su derivada se encuentra derivando término a término como sigue:
J0x n0
d 1nx 2n
1n 2nx 2n1
2 2nn!2
dx 2 2nn!2
n1
CAPITULO-11-F
06/04/2009
21:24
Page 731
SECCIÓN 11.9 REPRESENTACIONES DE LAS FUNCIONES COMO SERIES DE POTENCIAS
||||
731
Exprese 11 x2 como una serie de potencias derivando la ecuación 1.
¿Cuál es el radio de convergencia?
V EJEMPLO 5
SOLUCIÓN Al derivar cada miembro de la ecuación
1
1 x x2 x3 xn
1x
n0
1
2
1
2x
3x
nx n1
1 x2
n1
se obtiene
Si quisiera podría reemplazar n por n 1 y escribir la respuesta como
1
n 1x n
1 x2
n0
De acuerdo con el teorema 2, el radio de convergencia de la serie derivada es el mismo
que el radio de convergencia de la serie original, R 1.
EJEMPLO 6 Determine una representación como serie de potencias para ln1 x y su
radio de convergencia.
SOLUCIÓN Observe que, excepto en el caso de un factor de 1, la derivada de esta función
es 11 x. Por eso integre ambos miembros de la ecuación 1:
ln1 x y
1
dx y 1 x x 2 dx
1x
x
x2
x3
x n1
xn
C C C
2
3
n0 n 1
n1 n
x 1
Para determinar el valor de C haga x 0 en esta ecuación y obtenga
ln1 0 C. Por lo tanto, C 0 y
ln1 x x x2
x3
xn
2
3
n1 n
x 1
El radio de convergencia es el mismo que el de la serie original: R 1.
Observe qué sucede si hace x 12 en el resultado del ejemplo 6. Puesto que
ln ln 2,
1
2
ln 2 V EJEMPLO 7
1
1
1
1
1
n
2
8
24
64
n2
n1
Encuentre una representación como serie de potencias para
f x tan1x.
SOLUCIÓN Observe que f x 11 x2 y encuentre la serie requerida integrando la se-
rie de potencias para 11 x2 determinada en el ejemplo 1.
tan1x y
1
dx y 1 x 2 x 4 x 6 dx
1 x2
Cx
x3
x5
x7
3
5
7
CAPITULO-11-F
732
||||
06/04/2009
21:24
Page 732
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
1
& La serie de potencias para tan
x obtenida
en el ejemplo 7 se llama serie de Gregory en
honor al matemático escocés James Gregory
(1638-1675), quien pronosticó algunos de los
descubrimientos de Newton. Ya se demostró
que la serie de Gregory es válida cuando
1 x 1, pero resulta que (aunque no es
fácil de demostrar) también es válida cuando
x 1. Observe que cuando x 1 la serie
se transforma en
1
1
1
1 4
3
5
7
Este admirable resultado se conoce como fórmula
de Leibniz para p.
Para determinar C haga x 0 y obtiene C tan1 0 0. Por lo tanto,
tan1x x x3
x5
x7
x 2n1
1n
3
5
7
2n 1
n0
Puesto que el radio de convergencia de la serie para 11 x2 es 1, el radio de conver
gencia de esta serie para tan1x es también 1.
EJEMPLO 8
(a) Evalúe x 11 x 7 dx como una serie de potencias.
(b) Mediante el inciso (a) obtenga una aproximación de x00.5 11 x 7 dx que no difiera
en 107 del valor real.
SOLUCIÓN
(a) El primer paso es expresar la integral, 11 x7, como la suma de una serie de potencias. Como en el ejemplo 1, inicie con la ecuación 1 y reemplace x por x7:
1
1
7 n
7 7 x 1x
1 x n0
1 x
n 7n
1 x 7 x 14 n0
& Este ejemplo demuestra una manera útil de
las representaciones como series de potencias.
Integrar 11 x7 a mano es increíblemente
difícil. Diferentes sistemas algebraicos computacionales dan respuestas de distintas formas, pero
son extremadamente complicadas. (Si tiene un
CAS, inténtelo usted mismo.) La respuesta de la
serie infinita que se obtiene en el ejemplo 8(a) es
realmente mucho más fácil de manejar que
la respuesta finita que proporciona un CAS.
Ahora integre término a término:
1
y 1x
7
dx y
1 x
n 7n
dx C n0
Cx
1
n
n0
x 7n1
7n 1
x8
x 15
x 22
8
15
22
Esta serie converge para x7 1, es decir, para x 1.
(b) Si aplica el teorema fundamental del cálculo no importa qué antiderivada use, de modo
que utilice la antiderivada del inciso (a) con C 0:
y
0.5
0
1
x8
x 15
x 22
dx
x
1 x7
8
15
22
12
0
1
1
1
1
1n
8 15 22 2
82
15 2
22 2
7n 12 7n1
Esta serie infinita es el valor exacto de la integral definida, pero como es una serie alternante, puede obtener una aproximación de la suma aplicando el teorema de la estimación
de la serie alternante. Si deja de sumar después del término n 3, el error es menor que
el término con n 4:
1
6.4 1011
29 2 29
De modo que
y
0.5
0
1
1
1
1
1
0.49951374
7 dx 8 15 1x
2
82
15 2
22 2 22
CAPITULO-11-F
06/04/2009
21:24
Page 733
SECCIÓN 11.9 REPRESENTACIONES DE LAS FUNCIONES COMO SERIES DE POTENCIAS
11.9
||||
733
EJERCICIOS
1. Si el radio de convergencia de la serie de potencias n0 cn x n es
10, ¿cuál es el radio de convergencia de la serie n1 ncn x n1?
¿Por qué?
2. Suponga que sabe que la serie
n0
n
bn x es convergente para
x 2. ¿Qué puede decir de la serie siguiente?
¿Por qué?
bn
x n1
n
1
n0
3–10 Encuentre una representación como serie de potencias para la
función y determine el intervalo de convergencia.
15–18 Encuentre una representación como serie de potencias para
la función, y determine el radio de convergencia.
15. f x ln5 x
17. f x x3
x 22
4. f x 3
1 x4
19. f x 5. f x 2
3x
6. f x 1
x 10
21. f x ln
7. f x x
9 x2
8. f x x
2x 2 1
11–12 Exprese la función como la suma de una serie de potencias
usando primero fracciones parciales. Determine el intervalo de convergencia.
11. f x 3
x2 x 2
12. f x x2
2x 2 x 1
13. (a) Use la derivación para determinar una representación como
1
1 x2
¿Cuál es el radio de convergencia?
(b) Por medio del inciso (a) determine una serie de potencias
para
f x 1
1 x3
(c) Mediante el inciso (b) determine una serie de potencias para
x
x 2 16
20. f x lnx2 4
1x
1x
22. f x tan12x
23–26 Evalúe la integral indefinida como una serie de potencias.
¿Cuál es el radio de convergencia?
t
23.
y 1t
25.
y
8
dt
x tan 1 x
dx
x3
ln1 t
dt
t
24.
y
26.
y tan
1
x 2 dx
27–30 Use una serie de potencias para aproximar la integral definida con seis cifras decimales.
27.
y
0.2
29.
y
0.1
0
serie de potencias para
f x 18. f x arctanx3
f, y dibuje f y varias sumas parciales snx en la misma pantalla.
¿Qué sucede cuando n se incrementa?
1
1x
x2
10. f x 3
a x3
x2
1 2x2
; 19–22 Encuentre una representación como serie de potencias para
3. f x 1x
9. f x 1x
16. f x 0
1
dx
1 x5
28.
y
0.4
x arctan3x dx
30.
y
0.3
0
0
ln1 x 4 dx
x2
dx
1 x4
31. A través del resultado del ejemplo 6, calcule ln 1.1 con cinco
cifras decimales.
32. Demuestre que la función
f x n0
1n x 2n
2n!
es una solución de la ecuación diferencial
2
f x x
1 x3
14. (a) Determine una representación como serie de potencias para
f x ln1 x. ¿Cuál es el radio de convergencia?
(b) Mediante el inciso (a) determine una serie de potencias
para f x x ln1 x.
(c) Mediante el inciso (a) determine una serie de potencias para
f x lnx 2 1
f x f x 0
33. (a) Demuestre que J0 (la función de Bessel de orden 0 dada
en el ejemplo 4) cumple con la ecuación diferencial
x 2J 0x xJ0x x 2J0x 0
(b) Evalúe x01 J0x dx con tres cifras decimales.
CAPITULO-11-G
734
||||
06/04/2009
22:24
Page 734
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
38. (a) Empezando con la serie geométrica n0 x n, calcule la suma
34. La función de Bessel de orden 1 se define con
de la serie
J1x n0
1n x 2n1
n!n 1!2 2n1
nx
x 1
n1
n1
(a) Demuestre que J1 satisface la ecuación diferencial
x 2J1x x J1x x 2 1J1x 0
(b) Calcule la suma de cada una de las series siguientes.
n
(i) nx n, x 1
(ii) n
2
n1
n1
(c) Determine la suma de cada una de las series siguientes.
(b) Demuestre que J0x J1x.
(i)
n
n2
35. (a) Demuestre que la función
f x nn 1x , x 1
n0
(ii)
n
x
n!
n2
n2 n
2n
(iii)
n1
n2
2n
39. Utilice la serie de potencias para tan 1 x para demostrar que la
expresión siguiente para como la suma de una serie infinita:
es una solución de la ecuación diferencial
f x f x
2s3
n0
(b) Demuestre que f x e .
x
1 n
2n 1 3 n
40. (a) Aplique el método de completar cuadrados para demostrar
36. Sea fnx sen nxn 2 . Demuestre que la serie
fnx es
convergente para todos los valores de x, pero la serie de derivadas f nx es divergente cuando x 2n, n es un entero.
¿Para qué valores de x la serie f nx es convergente?
37. Sea
f x n1
xn
n2
Determine los intervalos de convergencia para f, f y f .
que
y
12
0
dx
x2 x 1
3s3
(b) Mediante la factorización de x 3 1 como una suma de cubos, escriba de nuevo la integral del inciso (a). Luego exprese 1x 3 1 como la suma de una serie de potencias y
úsela para demostrar la fórmula siguiente para :
3s3
4
n0
1n
8n
1
2
3n 1
3n 2
11.10 SERIES DE TAYLOR Y DE MACLAURIN
En la sección anterior, se representaron como series de potencias una cierta clase restringida de funciones. En esta sección se tratan problemas más generales: ¿Qué funciones se
pueden representar como series de potencias? ¿Cómo es posible hallar esa representación?
Empiece por suponer que f es cualquier función que se puede representar mediante una
serie de potencias
1
f x c0 c1x a c2x a2 c3x a3 c4x a4 x a R
Trate de determinar qué coeficientes cn tienen que estar en función de f. Para empezar, observe que si hace x a en la ecuación 1, en tal caso todos los términos después del
primero son 0 y obtiene
f a c0
De acuerdo con el teorema 11.9.2, puede derivar la serie de la ecuación 1 término a término:
2
f x c1 2c2x a 3c3x a2 4c4x a3 y al sustituir x a en la ecuación 2 tiene
f a c1
x a R
CAPITULO-11-G
06/04/2009
22:24
Page 735
SECCIÓN 11.10 SERIES DE TAYLOR Y DE MACLAURIN
||||
735
En seguida derive ambos miembros de la ecuación 2 y obtiene
3
f x 2c2 2 3c3x a 3 4c4x a2 x a R
Una vez más haga x a en la ecuación 3. El resultado es
f a 2c2
Aplique el procedimiento una vez más. La derivación de la serie de la ecuación 3 origina
4
f x 2 3c3 2 3 4c4x a 3 4 5c5x a2 x a R
y la sustitución de x a en la ecuación 4 da
f a 2 3c3 3!c3
Ahora ya puede ver el patrón. Si continúa derivando y sustituyendo x a, obtendrá
f na 2 3 4 ncn n!cn
Al resolver esta ecuación para el n-ésimo coeficiente cn , tiene
cn f na
n!
Esta fórmula sigue siendo válida incluso para n 0 si adopta la convención de que 0! 1
y f 0 f . En estos términos, ha demostrado el teorema siguiente:
5 TEOREMA Si f se puede representar como una serie de potencias (expansión)
en a, es decir, si
f x c x a
n
n
n0
x a R
entonces sus coeficientes los da la fórmula
cn f na
n!
Si sustituye esta fórmula de cn de nuevo en la serie, observe que si f tiene un desarrollo
en serie de potencias en a, después debe ser de la forma siguiente:
6
f x n0
f na
x an
n!
f a f a
f a
f a
x a x a2 x a3 1!
2!
3!
CAPITULO-11-G
736
||||
06/04/2009
22:24
Page 736
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
TAYLOR Y MACLAURIN
La serie de Taylor lleva este nombre en honor
al matemático inglés Brook Taylor (1685-1731) y
la serie de Maclaurin se llama así para recordar al
matemático escocés Colin Maclaurin (1698-1746)
a pesar del hecho de que la serie de Maclaurin es
realmente un caso especial de la serie de Taylor.
Pero la idea de representar funciones particulares
como sumas de series de potencias se remonta a
Newton, y el matemático escocés James Gregory
conoció la serie general de Taylor en 1668 y el
matemático suizo John Bernoulli la conoció por
1690. Al parecer, Taylor no conocía el trabajo de
Gregory ni de Bernoulli cuando publicó sus descubrimientos relacionados con las series en 1715 en
su libro Methodus incrementorum directa et inversa.
Las series de Maclaurin se llaman así porque
Colin Maclaurin las popularizó en su libro de
texto Treatise of Fluxions que se publicó en 1742.
&
La serie de la ecuación 6 se denomina serie de Taylor de la función f en a (o bien,
con respecto a a o centrada en a). Para el caso especial a 0 la serie de Taylor se
transforma en
f x 7
n0
f n0 n
f 0
f 0 2
x f 0 x
x n!
1!
2!
Como este caso surge con bastante frecuencia, se le da el nombre especial de serie de
Maclaurin.
NOTA Ya se demostró que si f se puede representar como una serie de potencias con
respecto a a, después f es igual a la suma de sus series de Taylor. Pero hay funciones que no
son iguales a la suma de sus series de Taylor. Un ejemplo de tales funciones se presenta en
el ejercicio 70.
V EJEMPLO 1
Determine la serie de Maclaurin de la función f x e x y su radio de
convergencia.
SOLUCIÓN Si f x e x, entonces f nx e x, por lo que f n0 e 0 1 para toda n. Por
lo tanto, la serie de Taylor para f en 0, (es decir, la serie de Maclaurin), es
n0
f n0 n
xn
x
x2
x3
x 1
n!
1!
2!
3!
n0 n!
Para determinar el radio de convergencia haga a n x nn! En tal caso
a n1
x n1
n!
x
n l 01
an
n 1! x
n1
por esto, según la prueba de la razón, la serie converge para toda x y el radio de conver
gencia es R .
La conclusión que obtiene del teorema 5 y el ejemplo 1 es que si e x tiene un desarrollo
de serie en potencias en 0, por lo tanto
ex n0
xn
n!
x
Por eso, ¿cómo se puede decir si e tiene una representación como serie de potencias?
Investigue la cuestión más general: ¿en qué circunstancias es una función igual a la
suma de su serie de Taylor? En otras palabras, si f tiene derivadas de todos los órdenes,
cuándo es cierto que
f na
f x x an
n!
n0
Como sucede con cualquier serie convergente, esto quiere decir que f x es el límite de la
sucesión de sumas parciales. En el caso de la serie de Taylor, las sumas parciales son
n
Tnx i0
f ia
x ai
i!
f a f a
f a
f na
x a x a2 x an
1!
2!
n!
CAPITULO-11-G
06/04/2009
22:24
Page 737
SECCIÓN 11.10 SERIES DE TAYLOR Y DE MACLAURIN
y
737
Observe que Tn es un polinomio de grado n llamado polinomio de Taylor de n-ésimo grado, de f en a. Por ejemplo, en el caso de la función exponencial f x e x, el resultado del
ejemplo 1 muestra que los polinomios de Taylor en 0 (o polinomios de Maclaurin), con
n 1, 2 y 3 son
y=´
y=T£(x)
y=T™
T (x)
||||
y=T™
T (x)
(0,
0
T1x 1 x
y=T¡
T (x)
x
y=T£
T (x)
T2x 1 x x2
2!
T3x 1 x x2
x3
2!
3!
Las gráficas de la función exponencial y estos tres polinomios de Taylor se ilustran en la
figura 1.
En general, f x es la suma de su serie de Taylor si
FIGURA 1
f x lím Tnx
nl
Si hace
& Cuando n se incrementa, Tnx parece aproximarse a e x en la figura 1. Esto hace pensar que
e x es igual a la suma de su serie de Taylor.
Rnx f x Tnx
f x Tnx Rnx
de modo que
entonces Rnx se llama residuo de la serie de Taylor. Si puede de alguna manera demostrar que lím n l Rnx 0, entonces se sigue que
lím Tnx lím f x Rnx
f x lím Rnx f x
nl
nl
nl
Por lo tanto, ha demostrado lo siguiente:
8 TEOREMA Si f x Tnx Rnx, donde Tn es el polinomio de Taylor de
n-ésimo grado de f en a y
lím Rnx 0
nl
para x a R, entonces f es igual a la suma de su serie de Taylor en el intervalo
x a R.
Al tratar de demostrar que lím n l Rnx 0 para una función específica f, se usa por
lo regular el hecho siguiente.
9
DESIGUALDAD DE TAYLOR Si f n1x M para x a d, entonces el
residuo Rnx de la serie de Taylor cumple con la desigualdad
M
R x n 1! x a n
para x a d
n1
Para entender por qué es cierto para n 1, suponga que f x M . En particular, se
tiene f x M , y de tal manera para a x a d
y
x
a
f t dt y M dt
x
a
Una antiderivada de f es f , por lo que según la parte 2 del teorema fundamental del
cálculo tenemos
f x f a Mx a
o bien,
f x f a Mx a
CAPITULO-11-G
738
||||
06/04/2009
22:24
Page 738
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
& Otras opciones aparte de la desigualdad de
Taylor son las fórmulas siguientes para el residuo. Si f n1 es continua en un intervalo I y
x I , por lo tanto
1 x
R nx y x tn f n1 t dt
n! a
Esta expresión recibe el nombre de forma integral
del término del residuo. Otra fórmula, que se llama
forma de Lagrange del término del residuo, establece que hay un número z entre x y a tal que
f n1z
R nx x a n1
n 1!
Esta versión es una generalización del teorema
del valor medio, que es el caso n 0).
Las demostraciones de estas fórmulas, además del análisis de cómo usarlas para resolver
los ejemplos de las secciones 11.10 y 11.11, se
encuentran en la página web
y
En estos términos,
x
a
f t dt y f a Mt a
dt
x
a
f x f a f ax a M
x a2
2
M
x a2
2
f x f a f ax a Pero R1x f x T1x f x f a f ax a. De modo que
R1x M
x a2
2
Un razonamiento similar, aplicando f x M , demuestra que
R1x www.stewartcalculus.com
Dé un clic en Additional Topics y luego en Formulas
for the Remainder Term in Taylor series.
R x De donde
1
M
x a2
2
M
xa
2
2
Aunque hemos supuesto supuesto que x a, cálculos similares muestran que esta desigualdad es válida también para x a.
Esto demuestra la desigualdad de Taylor para el caso donde n 1. El resultado para
cualquier n se demuestra de manera parecida integrando n 1 veces. (Véase el ejercicio 69 para el caso n 2.)
NOTA En la sección 11.11 se explora el uso de la desigualdad de Taylor en funciones
que se aproximan. Aquí, el uso inmediato es junto con el teorema 8.
Con frecuencia, al aplicar los teoremas 8 y 9 es útil recurrir al hecho siguiente.
lím
10
nl
xn
0
n!
para todo número real x
Es verdadero porque de acuerdo con el ejemplo 1, la serie x nn! es convergente para toda x y de este modo su n-ésimo término se aproxima a 0.
V EJEMPLO 2
Demuestre que e x es igual a la suma de su serie de Maclaurin.
SOLUCIÓN Si f x e x, entonces f n1x e x para toda n. Si d es cualquier número
ed
x
n 1!
positivo y x d , después f n1x e x e d . Por eso, la desigualdad de Taylor,
con a 0 y M e d , establece que
Rnx n1
para x d
Observe que la misma constante M e d funciona para todo valor de n. Pero, según la
ecuación 10,
lím
nl
ed
x
n 1!
n1
x
n1
e d lím
nl
n 1!
0
CAPITULO-11-G
06/04/2009
22:24
Page 739
SECCIÓN 11.10 SERIES DE TAYLOR Y DE MACLAURIN
||||
739
Se infiere entonces del teorema de la compresión que el lím n l Rnx 0 y, por lo
tanto, lím n l Rnx 0 para todos los valores de x. De acuerdo con el teorema 8, e x es
igual a la suma de la serie de Maclaurin, es decir,
ex 11
n0
& En 1748, Leonhard Euler aplicó la ecuación 12
para determinar el valor de e con 23 dígitos
decimales. En 2003 Shigeru Kondo, de nuevo
usando la serie en (12), calculó e a más de
50,000 millones de lugares decimales. Las
técnicas especiales que utilizaron para acelerar
el cálculo se explican en la página web
xn
n!
para toda x
En particular, si hace x 1 en la ecuación 11, obtiene la expresión siguiente para el
número e como una suma de una serie infinita:
e
12
n0
1
1
1
1
1
n!
1!
2!
3!
www.numbers.computation.free.fr
EJEMPLO 3 Determine la serie de Taylor para f x e x en a 2.
SOLUCIÓN Se tiene f n2 e 2 y, de este modo, al hacer a 2 en la definición de la serie
de Taylor (6) obtiene
n0
f n2
e2
x 2n x 2n
n!
n0 n!
También se puede verificar, como en el ejemplo 1, que el radio de convergencia es
R . Como en el ejemplo 2 puede comprobar que lím n l Rnx 0, de modo que
ex 13
n0
e2
x 2n
n!
para toda x
Hay dos desarrollos de series de potencias para e x, la serie de Maclaurin de la ecuación
11 y la serie de Taylor de la ecuación 13. El primero es mejor si está interesado en valores de x cercanos a 0 y el segundo funciona muy bien si x es cercano a 2.
EJEMPLO 4 Determine la serie de Maclaurin para sen x y demuestre que representa a
sen x para toda x.
SOLUCIÓN Acomode los cálculos en dos columnas como sigue:
f x sen x
f 0 0
f x cos x
f 0 1
f x sen x
f 0 0
f x cos x
f 0 1
f 4x sen x
f 40 0
Puesto que la derivada se repite en un ciclo de cuatro, puede escribir la serie de Maclaurin
como sigue:
f 0 f 0
f 0 2
f 0 3
x
x x 1!
2!
3!
x
x3
x5
x7
x 2n1
1n
3!
5!
7!
2n 1!
n0
CAPITULO-11-G
740
06/04/2009
||||
22:24
Page 740
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
Puesto que f n1x es sen x o bien, cos x, sabe que f n1x 1 para toda x. De
este modo puede tomar a M 1 en la desigualdad de Taylor
& En la figura 2 se ilustra la gráfica de
sen x junto con su polinomio de Taylor
(o de Maclaurin)
T1x x
M
x
R x n 1! x n 1!
n1
x3
T3x x 3!
T5x x 14
x3
x5
3!
5!
n1
n
De acuerdo con la ecuación 10 el lado derecho de esta desigualdad tiende a 0 cuando
n l , de modo que Rnx l 0 según el teorema de compresión. Se infiere entonces
que Rnx l 0 cuando n l , de modo que sen x es igual a la suma de su serie de Ma
claurin de acuerdo con el teorema 8.
Observe que cuando n se incrementa, Tnx se
vuelve una mejor aproximación para sen x.
y
Se establece el resultado del ejemplo 4 para referencia futura.
T
T¡
1
T
T∞
sen x x 15
y=sen x
0
x
1
x3
x5
x7
3!
5!
7!
x 2n1
2n 1!
1
n
n0
para toda x
T
T£
FIGURA 2
EJEMPLO 5 Determine la serie de Maclaurin para cos x.
SOLUCIÓN Podría proceder en forma directa como en el ejemplo 4, pero es más fácil derivar la serie de Maclaurin para sen x dada por la ecuación 15:
cos x d
d
sen x dx
dx
1
x
& La serie de Maclaurin para e , sen x y cos x
que determinó en los ejemplos 2, 4 y 5 la descubrió Newton aplicando métodos distintos.
Estas ecuaciones son notables porque se
conoce todo con respecto a cada una de estas
funciones si conoce todas sus derivadas en el
número 0.
x3
x5
x7
3!
5!
7!
x
3x 2
5x 4
7x 6
x2
x4
x6
1 3!
5!
7!
2!
4!
6!
Puesto que la serie de Maclaurin para sen x converge para toda x, el teorema 2 de la
sección 11.9 señala que la serie derivada para cos x converge también para toda x. En
estos términos,
16
cos x 1 x2
x4
x6
2!
4!
6!
1
n
n0
x 2n
2n!
para toda x
EJEMPLO 6 Determine la serie de Maclaurin para la función f x x cos x.
SOLUCIÓN En lugar de calcular las derivadas y sustituir en la ecuación 7, es más fácil multiplicar la serie para cos x, ecuación 16, por x:
x cos x x
1
n
n0
x 2n
2n!
1
n
n0
x 2n1
2n!
EJEMPLO 7 Represente f x sen x como la suma de su serie de Taylor centrada
en 3.
CAPITULO-11-G
06/04/2009
22:24
Page 741
SECCIÓN 11.10 SERIES DE TAYLOR Y DE MACLAURIN
SOLUCIÓN Primero acomode los valores en columnas
Ha obtenido dos diversas series de
representaciones para sen x, la serie de
Maclaurin en el ejemplo 4 y la serie de Taylor
en el ejemplo 7. Es mejor utilizar la serie de
Maclaurin para los valores de x cerca a 0 y la
serie de Taylor para x cerca a p/3. Observe
que el tercer polinomio de Taylor T3 en la
figura 3 es una buena aproximación al sen x
cerca de p/3, mas no así cerca de 0.
Compárelo con el tercer polinomio de Maclaurin T3 en la figura 2, donde está el polinomio
opuesto verdadero.
&
y
0
f x cos x
f
3
f x sen x
f
3
f x cos x
f
3
f
3
f
3
1!
x
1
s3
2
2 1!
f
3
x
s3
2
1
2
s3
2
1
2
3
3
2!
s3
2 2!
x
x
3
3
f
2
2
3
3!
1
2 3!
3
x
x
3
3
3
La demostración de que esta serie representa sen x para toda x es muy similar a la del
ejemplo 4. [Sólo reemplace x por x 3 en (14).] Puede escribir la serie con la notación sigma o suma si separamos los términos que contienen s3 :
x
π
3
3
f
741
y este patrón se repite en forma indefinida. Por lo tanto, la serie de Taylor en 3 es
y=sen x
f x sen x
||||
sen x n0
1ns3
x
22n!
3
T£
2n
n0
1n
x
22n 1!
3
2n1
La serie de potencias obtenidas mediante métodos indirectos en los ejemplos 5 y 6 y en la
sección 11.9 son realmente la serie de Taylor o de Maclaurin de las funciones dadas porque
el teorema 5 así lo establece, ya que no importa cómo una representación de una serie de
potencias f x cnx an se obtenga, siempre es cierto que cn f nan! En otras palabras, la determinación de los coeficientes es única.
En la tabla siguiente están reunidas, para referencia futura, algunas de las series importantes de Maclaurin deducidas en esta sección y en la anterior.
EJEMPLO 8 Encuentre la serie de Maclaurin para f(x) (1 x)k, donde k es cualquier
número real.
SOLUCIÓN Al ordenar el trabajo en columnas
f(x) (1 x)k
f(0) 1
k1
f (x) k(1 x)
f(0) k
f (x) k(k 1)(1 x)k 2
f(x) k(k 1)(1 2)(1 x)
f(0) k(k 1)
k3
f(0) k(k 1)(k 2)
f (n)(x) k(k 1) (k n 1)(1 x)k n
f (n)(0) k(k 1) (k n 1)
Por lo tanto, la serie de Maclaurin de f(x) (1 x)k es
n0
f (n)(0) n
k(k 1) (k n 1) n
x x
n!
n!
n0
CAPITULO-11-G
742
||||
06/04/2009
22:24
Page 742
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
Esta serie se denomina serie binomial. Si su n-ésimo término es an, entonces
a n1
k(k 1) (k n 1)(k n)xn1
n!
an
n 1!
k(k 1) (k n 1)xn
k
n
x 1
1
n
kn
n1
1
x l x
es n l Entonces, por la prueba de la razón, la serie binomial converge si x 1 y diverge
si x 1.
La notación tradicional para los coeficientes de la serie binomial es
k
k(k 1)(k 2) (k n 1)
n
n!
y los números se llaman coeficientes del binomio.
El siguiente teorema expresa que (1 x)k es igual a la suma de su serie Maclaurin. Es
posible demostrar esto al probar que el término restante Rn(x) se aproxima a 0, pero esto
resulta ser muy difícil. La prueba resumida en el ejercicio 71 es mucho más fácil.
17 SERIE BINOMIAL Si k es cualquier número real y x 1, entonces
(1 x)k n0
k n
k(k 1) 2
k(k 1)(k 2) 3
x 1 kx x x n
2!
3!
Aun cuando la serie binomial siempre converge cuando x 1, la pregunta de si converge o no en los extremos, 1, depende del valor de k. Resulta que la serie converge
en 1 si 1 k 0 y en ambos extremos si k 0. Nótese que si k es un entero positivo
y n k, entonces la expresión para nk contiene un factor (k k), de modo que nk 0
para n k. Esto significa que la serie termina y reduce el teorema del binomio ordinario
cuando k es un entero positivo. (Véase la página de referencia 1.)
1
Encuentre la serie de Maclaurin para la función f(x) y su
s4 x
radio de convergencia.
V EJEMPLO 9
SOLUCIÓN Escriba f(x) de forma que pueda usar la serie binomial:
1
s4 x
1
1
4 1
x
4
2
4 1
x
4
1
2
1
x
4
12
CAPITULO-11-G
06/04/2009
22:24
Page 743
SECCIÓN 11.10 SERIES DE TAYLOR Y DE MACLAURIN
||||
743
Y al usar la serie binomial con k 12 y donde x fue reemplazada por x4, tenemos
1
1
2
s4 x
1
2
1
12
x
4
1 1
2
1
2
1
1
2
n0
x
4
12
n
x
4
1232
2!
n
x
4
2
123252
x
3!
4
123252 12 n 1
x
n!
4
n
3
1
13 2
135 3
1 3 5 2n 1 n
x
x x x 8
2!82
3!83
n!8n
Sabe de (17) que esta serie converge con x4 1, es decir, x 4, de modo que el ra
dio de convergencia es R 4.
En la tabla siguiente están reunidas, para referencia futura, algunas de las series importantes de Maclaurin que ha deducido en esta sección y en la anterior..
TABLA 1
Series importantes de Maclaurin y
sus radios de convergencia.
1
xn 1 x x2 x3 1x
n0
ex xn
x
x2
x3
1
n!
1!
2!
3!
n0
1
sen x n
n0
cos x 1
n
n0
tan1x R
x 2n
x2
x4
x6
1
2n!
2!
4!
6!
R
n
n0
n0
TEC Module 11.10/11.11 permite
ver cómo polinomios sucesivos de Taylor
se aproximan a la función original.
x 2n1
x3
x5
x7
x
2n 1
3
5
7
R1
R
x 2n1
x3
x5
x7
x
2n 1!
3!
5!
7!
1
1 xk R1
k n
kk 1 2
kk 1k 2 3
x 1 kx x x R1
n
2!
3!
Una razón de que las series de Taylor sean importantes, es que permiten integrar funciones que no se podían manejar antes. En efecto, en la introducción de este capítulo
mencionamos que Newton integraba a menudo funciones expresándolas primero como series de potencias, y que después integraba la serie término a término. No es posible in2
tegrar la función f x ex por medio de las técnicas conocidas hasta este momento,
porque su antiderivada no es una función elemental (véase sección 7.5). En el ejemplo
siguiente se aplica la idea de Newton para integrar esta función.
CAPITULO-11-G
744
||||
06/04/2009
22:24
Page 744
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
V EJEMPLO 10
(a) Evalúe x ex dx como una serie infinita.
2
(b) Evalúe x01 ex dx de tal manera que no difiera 0.001 del valor real.
2
SOLUCIÓN
2
(a) Primero encuentre la serie de Maclaurin de f x ex . Aunque es posible usar el
método directo, determinémosla simplemente mediante el reemplazo de x con x 2 en la
serie de e x dada en la tabla 1. Por esto, para todos los valores de x,
2
ex n0
x 2 n
n!
1n
n0
x 2n
x2
x4
x6
1
n!
1!
2!
3!
Ahora integre término a término
ye
x 2
dx y 1 x2
x4
x6
x 2n
1n
dx
1!
2!
3!
n!
Cx
x3
x5
x7
x 2n1
1n
3 1!
5 2!
7 3!
2n 1n!
2
Esta serie es convergente para toda x porque la serie original para ex converge para
toda x.
(b) El teorema fundamental del cálculo
y
1
0
2
ex dx x Es posible hacer C 0 en la antiderivada
del inciso (a).
x3
x5
x7
x9
3 1!
5 2!
7 3!
9 4!
1
0
1
1 13 101 421 216
&
1
1 13 101 421 216
0.7475
El teorema de estimación de la serie alternante demuestra que el error que hay en esta
aproximación es menor que
1
1
0.001
11 5!
1320
Otra aplicación de la serie de Taylor se ilustra en el ejemplo siguiente. El límite podría ser calculado con la regla de l’Hospital, pero en lugar de hacerlo así se recurre a
las series.
EJEMPLO 11 Evalúe lím
xl0
ex 1 x
.
x2
SOLUCIÓN Al utilizar la serie de Maclaurin para e x
& Algunos sistemas algebraicos computacionales calculan los límites de esta manera.
x
x2
x3
1 x
e 1x
1!
2!
3!
lím
lím
xl0
xl0
x2
x2
2
3
4
x
x
x
2!
3!
4!
lím
xl0
x2
1
x
x2
x3
1
lím
xl0
2
3!
4!
5!
2
x
1
porque las series de potencias son funciones continuas.
CAPITULO-11-G
06/04/2009
22:24
Page 745
SECCIÓN 11.10 SERIES DE TAYLOR Y DE MACLAURIN
||||
745
MULTIPLICACIÓN Y DIVISIÓN DE SERIES DE POTENCIAS
Si las series de potencias se suman o restan, se comportan como polinomios; (el teorema 11.2.8 lo ilustra). En efecto, como lo ilustra el ejemplo siguiente, las series también se
pueden multiplicar y dividir como los polinomios. Primero determine los primeros términos porque los cálculos para los siguientes se vuelven tediosos y los términos iniciales son
los más importantes.
EJEMPLO 12 Calcule los primeros tres términos no cero de la serie de Maclaurin para (a)
e x sen x y (b) tan x.
SOLUCIÓN
(a) Mediante la serie de Maclaurin para e x y sen x en la tabla 1
e x sen x 1 x
x2
x3
1!
2!
3!
x
x3
3!
Al multiplicar esta expresión y agrupar por términos semejantes, al igual que con los polinomios:
1 x 12 x 2 16 x 3 x
16 x 3 x x 2 12 x 3 16 x 4 16 x 3 16 x 4 x x 2 13 x 3 Así,
e x sen x x x 2 13 x 3 (b) Al utilizar la serie de Maclaurin en la tabla 1
x3
x5
sen x
3!
5!
tan x cos x
x2
x4
1
2!
4!
x
Aplique un procedimiento como el de la división larga
x 13 x 3 1 12 x 2 241 x 4 x 16 x 3 x 12 x 3 1
3
1
3
Por consiguiente,
x3 x3 2
15
1
120
1
24
x5 x5 x 5 1
30
1
6
x5 x5 2
15
x5 tan x x 13 x 3 152 x 5 No se ha intentado justificar las manipulaciones formales que se utilizaron en el ejemplo
12, pero son legítimas. Hay un teorema que establece que si tanto f x cn x n como
tx bn x n convergen para x R y las series se multiplican como si fueran polinomios,
en tal caso la serie resultante también converge para x R y representa f xtx. En
cuanto a la división es necesario que b0 0; la serie resultante converge para x suficientemente pequeña.
CAPITULO-11-G
746
||||
11.10
06/04/2009
22:24
Page 746
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
EJERCICIOS
1. Si f x n0 bnx 5 n para toda x, escriba una fórmula
para b 8.
2. Se proporciona la gráfica de f.
17. f x cos x,
a
18. f x sen x , a 2
19. f x 1sx,
a9
20. f x x 2,
a1
y
21. Demuestre que la serie obtenida en el ejercicio 7 representa sen
f
px para toda x.
22. Demuestre que la serie obtenida en el ejercicio 18 representa
1
sen x para toda x.
0
x
1
23. Demuestre que la serie obtenida en el ejercicio 11 representa
senh x para toda x.
(a) Explique por qué la serie
24. Demuestre que la serie obtenida en el ejercicio 12 representa
cosh x para toda x.
1.6 0.8x 1 0.4x 12 0.1x 13 25–28 Use la serie binomial para expandir la función como una se-
no es la serie de Taylor de f centrada en 1.
rie de potencias. Exprese el radio de convergencia.
(b) Explique por qué la serie
2.8 0.5x 2 1.5x 2 0.1x 2 2
3
25. s1 x
27.
no es la serie de Taylor de f centrada en 2.
26.
1
(2 x)3
1
(1 x)4
28. (1 x)23
3. Si f (n)(0) (n 1)! para n 0, 1, 2,…, encuentre la serie de
Maclaurin para f y su radio de convergencia.
29–38 Utilice la serie de Maclaurin que paracere en la tabla 1 para
4. Encuentre la serie de Taylor para f con centro en 4 si
f (n)4 1n n!
3nn 1
¿Cuál es el radio de convergencia de la serie de Taylor?
5–12 Encuentre la serie de Maclaurin para f x usando la defini-
ción de la serie de Maclaurin. [Suponga que f tiene un desarrollo
en serie de potencias. No demuestre que Rnx l 0.] Determine
también el radio asociado con la convergencia.
5. f x 1 x2
6. f x ln1 x
7. f x sen px
8. f x cos 3x
9. f x e 5x
30. f x cos(x2)
31. f x e x e2x
32. f x e x 2ex
33. f x x cos2 x2
33. f x x2 tan1 (x)3
1
35. f x x
s4 x2
37. f x sen2 x
38. f x 36. f x x2
s2 x
[Sugerencia: utilice sen 2x 12 1 cos 2x.]
x sen x
x3
1
6
isif x 0
isif x 0
; 39–42 Determine la serie de Maclaurin de f (mediante cualquier
12. f x cosh x
13–20 Calcule la serie de Taylor para f x centrada en el valor dado
de a. [Suponga que f tiene un desarrollo de serie de potencias. No
demuestre que Rnx l 0.]
13. f x x4 3x2 1 ,
14. f x x x3 ,
15. f x e ,
29. f x sen x
10. f x xe x
11. f x senh x
x
obtener la serie de Maclaurin para la función dada.
a1
a 2
a3
método), y su radio de convergencia. Dibuje f y sus primeros
polinomios de Taylor en la misma pantalla. ¿Qué observa con
respecto a la correspondencia entre estos polinomios y f ?
2
39. f x cosx 2 40. f x ex cos x
41. f x xex
42. f x 1n(1 x2)
43. Mediante la serie de Maclaurin para e x calcule e 0.2 con cinco
16. f x 1x ,
a 3
posiciones decimales.
CAPITULO-11-G
06/04/2009
22:24
Page 747
SECCIÓN 11.10 SERIES DE TAYLOR Y DE MACLAURIN
44. Utilice la serie de Maclaurin para sen x a fin de calcular sen 3
61. y con cinco posiciones decimales.
x
sen x
||||
747
62. y e x ln1 x
45. (a) Use la serie binomial para expandir 1s1 x2
(b) Use la parte (a) para hallar la serie de Maclaurin para
sen1x.
63–68 Calcule la suma de la serie.
4
46. (a) Expanda 1 s1
x como una serie de potencias.
(b) Use el inciso (a) para estimar correctamente
posiciones decimales.
1
4
s1.1
63.
con tres
47.
y x cosx
49.
y
3
dx
cos x 1
dx
x
y
1
52.
y
0.2
53.
y
0.4
54.
y
0.5
0
x cos x 3 dx
0
0
48.
y
0
2
50.
y arctan(x ) dx
57. lím
sen x x x
x5
x l0
27
81
9
2!
3!
4!
R x (cinco decimales)
2
M
xa
6
x l0
para x a d
3
70. (a) Demuestre que la función definida por
f x 56. lím
1
6
ln 23
ln 22
2!
3!
muestre que si f x M para x a d, en tal caso
55–57 Mediante las series evalúe el límite.
x l0
n0
3n
5n n!
69. Demuestre la desigualdad de Taylor para n 2, es decir, de-
( error 0.001)
x tan1x
x3
1n 2n
6 2n2n!
2
( error 5 106)
55. lím
n0
2n1
68. 1 ln 2 tan 1 x 3 senx 3
dx
x 2ex dx
66.
67. 3 (tres decimales);
s1 x4 dx
x
51–54 Utilice series para obtener un valor aproximado de la integral definida con la exactitud indicada.
51.
1n 2n1
4
2n 1!
n0
n0
e 1
dx
x
64.
n
65.
47–50 Evalúe la integral indefinida como una serie infinita.
x 4n
n!
1
;
1 cos x
1 x ex
3
tan x x
lím
x l0
x3
2
si x 0
si x 0
no es igual a la serie de Maclaurin.
(b) Dibuje la función del inciso (a) y comente su comportamiento cerca del origen.
71. Use los pasos siguientes para demostrar (17).
(a) Sea gx n0nkxn . Derive esta serie para demostrar que
gx 58. Utilice la serie del ejemplo 12(b) para evaluar
e1x
0
kgx
1x
1 x 1
(b) Sea h(x) (1 x)kg(x) y demuestre que h(x) 0.
(c) Deduzca que g(x) (1 x)k.
72. En el ejercicio 53 de la sección 10.2 se demostró que la longi-
tud de la elipse x a sen , y b cos , donde a b 0, es
Este límite se calculó en el ejemplo 4 de la sección 4.4 utilizando la regla de l’Hospital tres veces. ¿Cuál método prefiere?
L 4a y
2
0
59–62 Utilice la multiplicación o la división de series de potencias
para determinar los primeros tres términos diferentes de cero en la
serie de Maclaurin para cada función.
2
59. y ex cos x
60. y sec x
s1 e2 sen2 d
donde e sa2 b2 a es la excentricidad de la elipse.
Expanda el integrando como serie binomial y use el resultado
del ejercicio 46 de la sección 7.1 para expresar L como una serie en potencias de la excentricidad hasta el término en e6.
CAPITULO-11-G
748
||||
06/04/2009
22:24
Page 748
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
P ROY E C TO D E
LA B O R AT O R I O
CAS
UN LÍMITE ESCURRIDIZO
Este proyecto es sobre la función
f x sentan x tansen x
arcsenarctan x arctanarcsen x
1. Utilice su sistema algebraico computacional para evaluar f x para x 1, 0.1, 0.01, 0.001,
y 0.0001. ¿Parece tener f un límite cuando x l 0?
2. Use el CAS para dibujar f cerca de x 0. ¿Parece tener f un límite cuando x l 0?
3. Intente evaluar lím x l 0 f x con la regla de l’Hospital, usando el CAS para hallar las deri-
vadas del numerador y el denominador. ¿Qué descubrió? ¿Cuántas aplicaciones de la
regla de l’Hospital se requieren?
4. Evalúe lím x l 0 f x con ayuda del CAS para encontrar la cantidad suficiente de términos de
la serie de Taylor del numerador y el denominador. (Utilice el comando taylor en Maple o
Series en Mathematica).
5. Utilice el comando límite en su CAS para calcular directamente lím x l 0 f x (La mayor
parte de los sistemas algebraicos computacionales utilizan el método del problema 4 para
calcular límites.)
6. En vista de las respuestas a los problemas 4 y 5, ¿cómo explica los resultados de los
problemas 1 y 2?
R E DAC C I Ó N
D E P ROY E C TO
CÓMO DESCUBRIÓ NEWTON LA SERIE BINOMIAL
El Teorema Binomial, que proporciona el desarrollo de a bk, ya lo conocían los matemáticos
chinos muchos siglos antes de que naciera Newton, en especial para el caso donde el exponente k
es un entero positivo. En 1665, cuando Newton tenía 22 años, descubrió por primera vez el desarrollo de la serie infinita a bk cuando k es un exponente fraccionario, positivo o negativo. No publicó sus descubrimientos, pero los planteó y proporcionó ejemplos de cómo usarlos en una carta
de fecha 13 de junio de 1676, carta que (ahora se llama epistola prior), que envió a Henry
Oldenburg, secretario de la Royal Society of London, para que la transmitiera a Leibniz. Cuando
éste contestó, le preguntó a Newton cómo había descubierto las series binomiales. Newton escribió una segunda carta, la epistola posterior, del 24 de octubre de 1676, en la cual explica con lujo
de detalles la manera como llegó a su descubrimiento mediante una ruta muy indirecta. Estaba
investigando las áreas bajo las curvas y 1 x 2 n2 de 0 a x para n 0, 1, 2, 3, 4, . . . . Son fáciles de calcular si n es par. Al observar patrones y al interpolar, Newton fue capaz de adivinar
las respuestas de valores impares de n. Por lo tanto se dio cuenta de que podía obtener las mismas respuestas expresando 1 x 2 n2 como una serie infinita.
Escriba un ensayo sobre el descubrimiento de Newton. Inicie dando el enunciado de serie
binomial en la notación de Newton (véase epistola prior en la página 285 de [4] o la página 402
de [2]). Explique por qué la versión de Newton es equivalente al teorema 17 de la página 742.
Luego lea la epistola posterior de Newton (página 287 de [4] o página 404 de [2]) y explique los
patrones que descubrió Newton en las áreas bajo las curvas y 1 x 2 n2. Muestre cómo
podía él calcular el área bajo las curvas restantes y cómo comprobó su respuesta. Para finalizar, explique cómo estos descubrimientos llevaron a las series binomiales. Los libros de
Edwards [1] y Katz [3] contienen comentarios de las cartas de Newton.
1. C. H. Edwards, The Historical Development of the Calculus, Nueva York: Springer-Verlag,
1979, pp. 178-187.
2. John Fauvel y Jeremy Gray, eds., The History of Mathematics: A Reader, Londres:
MacMillan Press, 1987.
3. Victor Katz, A History of Mathematics: An Introduction, Nueva York: HarperCollins, 1993,
pp. 463-466.
4. D. J. Struik, ed., A Sourcebook in Mathematics, 1200-1800, Princeton, N.J.: Princeton Uni-
versity Press, 1969.
CAPITULO-11-G
06/04/2009
22:24
Page 749
SECCIÓN 11.11 APLICACIONES DE LOS POLINOMIOS DE TAYLOR
||||
749
11.11 APLICACIONES DE LOS POLINOMIOS DE TAYLOR
En esta sección se exploran dos tipos de aplicaciones de los polinomios de Taylor. Primero
se examina cómo se usan para aproximar funciones; a los científicos de la computación les
gustan porque los polinomios son los más sencillos de las funciones. Luego investigamos
cómo los físicos y los ingenieros los usan en campos como la relatividad, óptica, radiación de cuerpos negros, dipolos eléctricos, la velocidad de las ondas en el agua y la construcción de carreteras en el desierto.
APROXIMACIÓN DE FUNCIONES MEDIANTE POLINOMIOS
Suponga que f x es igual a la suma de su serie de Taylor en a:
f x n0
f na
x an
n!
En la sección 11.10 se presentó la notación Tnx para la n-ésima suma parcial de esta serie y se le llamó polinomio de n-ésimo grado de Taylor de f en a. Así,
n
Tnx i0
f ia
x ai
i!
f a f a
f a
f na
x a x a2 x an
1!
2!
n!
Puesto que f es la suma de su serie de Taylor, sabe que Tnx l f x cuando n l y de
este modo Tn se puede usar como una aproximación de f : f x Tnx.
Observe que el polinomio de primer grado de Taylor
y
y=´
T1x f a f ax a
y=T£(x)
y=T™
T (x)
y=T™
T (x)
(0,
y=T¡
T (x)
0
x
y=T£
T (x)
FIGURA 1
x 0.2
x 3.0
T2(x)
T4(x)
T6(x)
T8(x)
T10(x)
1.220000
1.221400
1.221403
1.221403
1.221403
8.500000
16.375000
19.412500
20.009152
20.079665
ex
1.221403
20.085537
es lo mismo que la linealización de f en a que estudió en la sección 3.10. Note también
que T1 y su derivada tienen los mismos valores en a que f y f . En general, se puede demostrar que las derivadas de Tn en a concuerdan con las de f hasta las derivadas de orden
n, inclusive (véase ejercicio 38).
Con el fin de ilustrar estas ideas, vea una vez más las gráficas de y e x y sus primeros polinomios de Taylor, como se ilustran en la figura 1. La gráfica de T1 es la tangente a y e x en 0, 1; esta tangente es la mejor aproximación lineal a e x cerca de (0,
1). La gráfica de T2 es la parábola y 1 x x 22, y la gráfica de T3 es la curva cúbica y 1 x x 22 x 36, que es un ajuste más cercano a la curva exponencial
y e x que T2. El polinomio siguiente de Taylor T4 sería una aproximación mejor, y así
sucesivamente.
Los valores de la tabla proporcionan una demostración numérica de la convergencia de los
polinomios de Taylor Tnx a la función y e x. Cuando x 0.2 la convergencia es muy rápida, pero cuando x 3 es un poco más lenta. De hecho, entre más lejos esté x de 0 es un
poco más lenta. Tnx converge más despacio hacia e x.
Cuando usa un polinomio de Taylor Tn para aproximar una función f , debe preguntarse: ¿qué tan buena es una aproximación? ¿Qué tan grande quiere que sea n con objeto de
que alcance una precisión deseada? Para responder estas preguntas, es necesario que examine el valor absoluto del residuo:
R x f x T x n
n
CAPITULO-11-G
750
||||
06/04/2009
22:24
Page 750
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
Hay tres métodos posibles para estimar el tamaño del error:
1. Si cuenta con una calculadora que trace gráficas o una computadora, la puede usar
para dibujar Rnx y de ahí estimar el error.
2. Si sucede que la serie es alternante, puede aplicar el teorema de estimación de la
serie alternante.
3. En todos los casos puede aplicar la desigualdad de Taylor (Teorema 11.10.9), el
cual establece que si f n1x M , por lo tanto
M
R x n 1! x a n1
n
V EJEMPLO 1
3
(a) Obtenga una aproximación de la función f x s
x por medio del polinomio de
Taylor de grado 2 en a 8.
(b) ¿Qué tan exacta es esta aproximación cuando 7 x 9?
SOLUCIÓN
3
f x s
x x 13
(a)
f 8 2
f x x23
f 8 121
1
3
f x 29 x53
1
f 8 144
83
f x 10
27 x
En estos términos, el polinomio de Taylor de segundo grado es
f 8
f 8
x 8 x 82
1!
2!
T2x f 8 1
2 121 x 8 288
x 82
La aproximación deseada es
1
3
x T2x 2 121 x 8 288
x 82
s
(b) La serie de Taylor no es alternante cuando x 8, de modo que no puede aplicar el
teorema de estimación de la serie alternante en este ejemplo. Pero sí puede usar la desigualdad de Taylor con n 2 y a 8:
M
R x 3! x 8 2
3
donde f x M . Como x 7, tiene x 83 7 83 y de esa manera
f x 10
1
10
1
0.0021
27 x 83
27 7 83
Por lo tanto, puede hacer M 0.0021. Asimismo, 7 x 9, de modo que
1 x 8 1 y x 8 1. Después la desigualdad de Taylor da
R x 2
0.0021
0.0021
13 0.0004
3!
6
En estos términos, si 7 x 9, la aproximación en el inciso (a) no difiere en más
de 0.0004 del valor real.
CAPITULO-11-G
06/04/2009
22:24
Page 751
SECCIÓN 11.11 APLICACIONES DE LOS POLINOMIOS DE TAYLOR
2.5
751
Con la ayuda de una calculadora para trazar gráficas o de una computadora compruebe
3
el cálculo del ejemplo 1. En la figura 2 se muestra que las gráficas de y s
x y y T2x
están muy cercanas entre sí cuando x está cerca de 8. En la figura 3 se ilustra la gráfica de
R2x calculada a partir de la expresión
T
T™
#x
y=œ
œ
„
R x sx T x 3
2
15
0
||||
2
A partir de la gráfica:
FIGURA 2
R x 0.0003
2
0.0003
cuando 7 x 9. Así, la estimación de error mediante métodos gráficos es ligeramente
mejor que cuando se hace a partir de la desigualdad de Taylor, en este caso.
y=|R™(x)|
V EJEMPLO 2
(a) ¿Cuál es el error máximo posible al utilizar la aproximación
7
9
sen x x 0
FIGURA 3
x3
x5
3!
5!
cuando 0.3 x 0.3? Utilice esta aproximación para calcular sen 12 con seis cifras
decimales.
(b) ¿Para qué valores de x esta aproximación no difiere en más de 0.00005 del valor
real?
SOLUCIÓN
(a) Observe que la serie de Maclaurin
x5
x7
x3
3!
5!
7!
es alternante para todos los valores no cero de x, y los términos sucesivos decrecen en tamaño porque x 1, de modo que puede usar el teorema de estimación de la serie
alternante. El error en la aproximación de sen x por medio de los tres términos de su
serie de Maclaurin es cuando mucho
sen x x x7
x 7
7!
5040
Si 0.3 x 0.3, entonces x 0.3, de modo que el error es más pequeño que
0.37
4.3 108
5040
Para calcular sen 12° primero convierta a radianes.
sen 12 sen
12
180
15
15
sen
3
1
3!
15
15
Por esto, con seis dígitos decimales, sen 12 0.207912.
(b) El error será menor que 0.00005 si
x
7
5040
0.00005
5
1
0.20791169
5!
CAPITULO-11-G
752
06/04/2009
||||
22:24
Page 752
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
Al resolver la desigualdad y encontrar x
x
7
0.252
x 0.252
17
o bien,
0.821
De modo que la aproximación dada no difiere en más de 0.00005 cuando x 0.82.
TEC En Module 11.10/11.11 se muestran
en forma gráfica los residuos de las aproximaciones de los polinomios de Taylor.
¿Qué sucede si recurre a la desigualdad de Taylor para resolver el ejemplo 2? Puesto
que f 7x cos x, tiene f 7x 1 y de esa manera
1
R x 7! x 7
6
De este modo llegamos a la misma estimación que con el teorema de la estimación de la
serie alternante.
¿Qué hay con respecto a los métodos gráficos? En la figura 4 se ilustra la gráfica de
R x sen x ( x x x ) y observe que R x 4.3 10 cuando x 0.3. Es la misma estimación que obtuvo en el ejemplo 2. En el caso del inciso (b) quiere R x 0.00005, de modo que
dibuja tanto y R x como y 0.00005 en la figura 5. Si coloca el cursor en el punto de intersección derecho, verá que la desigualdad se cumple cuando x 0.82. Una
1
6
6
4.3 10–*
1
120
3
5
8
6
6
y=| Rß(x)|
6
_0.3
0.3
0
FIGURA 4
0.00006
y=0.00005
vez más llega a la misma estimación que obtuvo en la solución del ejemplo 2.
Si se hubiera pedido que aproximara sen 72° en lugar de sen 12° en el ejemplo 2, habría sido prudente utilizar los polinomios de Taylor en a p3 (en lugar de a 0),
porque son mejores aproximaciones de sen x para valores de x cercanos a p3. Observe
que 72° es cercano a 60°, es decir, p3 radianes, y las derivadas de sen x son fáciles de
calcular en p3.
La figura 6 muestra las gráficas de las aproximaciones de los polinomios de Maclaurin
y=| Rß(x)|
T5x x _1
x3
3!
x3
x5
x7
T7x x 3!
5!
7!
T1x x
1
0
FIGURA 5
T3x x x3
x5
3!
5!
a la curva seno. Puede ver que cuando n se incrementa, Tnx es una buena aproximación
a sen x en un intervalo más y más grande.
y
T
T¡
T
T∞
x
0
y=sen x
T
T£
FIGURA 6
T
T¶
Las calculadoras y computadoras aplican el tipo de cálculo hecho en los ejemplos 1
y 2. Por ejemplo, cuando usted presiona la tecla sen o ex de su calculadora, o bien, cuando un programador de computadoras utiliza una subrutina en el caso de una función trigonométrica o exponencial o de Bessel, en muchas máquinas se calcula una aproximación polinomial. Con frecuencia, el polinomio es uno de Taylor que ha sido modificado
de modo que el error se extiende más uniformemente en todo el intervalo.
APLICACIONES EN LA FÍSICA
Los polinomios de Taylor también se usan con mucha frecuencia en la física. Con objeto
de entender una ecuación, los físicos simplifican a menudo una función considerando sólo
los dos o tres términos de su serie de Taylor. En otras palabras, los físicos usan un polino-
CAPITULO-11-G
06/04/2009
22:24
Page 753
SECCIÓN 11.11 APLICACIONES DE LOS POLINOMIOS DE TAYLOR
||||
753
mio de Taylor como una aproximación de la función. La desigualdad de Taylor se puede
usar para medir la exactitud de la aproximación. En el ejemplo siguiente, se muestra una
manera en la cual esta idea se usa en la relatividad especial.
V EJEMPLO 3 En la teoría de Einstein de la relatividad especial, la masa de un objeto
que se desplaza con velocidad v es
m0
s1 v 2c 2
m
donde m0 es la masa del objeto cuando está en reposo y c es la velocidad de la luz. La energía cinética del objeto es la diferencia entre su energía total y su energía en reposo:
K mc 2 m0 c 2
(a) Demuestre que cuando v es muy pequeña comparada con c, esta expresión para K
concuerda con la física clásica de Newton: K 12 m0v 2.
(b) Aplique la desigualdad de Taylor para estimar la diferencia en estas expresiones para
K cuando v 100 ms.
SOLUCIÓN
(a) Mediante las expresiones dadas para K y m obtiene
K mc 2 m0 c 2 m0 c 2
m0 c 2
s1 v 2c 2
m0 c 2
& La curva superior de la figura 7 es la gráfica de
la expresión de la energía cinética K de un objeto con velocidad v en la relatividad especial. La
curva inferior muestra la función usada para K
en la física clásica newtoniana. Cuando v es mucho más pequeña que la velocidad de la luz, las
curvas son prácticamente idénticas.
c
1 x12 1 12 x K m0 c 2
m0 c 2
K=mc@-m¸c@
0
FIGURA 7
c
√
1
y
K = 21 m ¸ √ @
2
Con x v 2c 2, la serie de Maclaurin para 1 x12 es más fácil de calcular que una
serie binomial con k 12 . (Observe que x 1 porque v c.) Por lo tanto
( )( 32 ) x 2 ( 12 )( 32 )( 52) x 3 1
2
2!
1 x x2 K
12
v2
1
1
2
3
8
1
3!
5
16
x3 1 v2
3 v4
5 v6
1
2 c2
8 c4
16 c 6
1 v2
3 v4
5 v6
2 4 2 c
8 c
16 c 6
Si v es mucho más pequeña que c, entonces todos los términos después del primero
son muy pequeños cuando se les compara con el primer término. Si los omite,
obtiene
1 v2
K m0 c 2
12 m0 v 2
2 c2
(b) Si x v 2c 2, f x m0 c 2 1 x12 1
y M es un número tal que
f x M , entonces aplica la desigualdad de Taylor para escribir
M
R x 2! x
1
2
Tiene f x 34 m0 c 21 x52 y sabe que v 100 ms, de modo que
3m0 c 2
f x 41 v c
2
2 52
3m0 c 2
41 100 2c 2 52
M
CAPITULO-11-G
754
||||
06/04/2009
22:24
Page 754
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
Así, con c 3 10 8 ms,
3m0 c 2
1
R x 2 41 100 c
1
2
2 52
100 4
4.17 1010 m0
c4
De modo que cuando v 100 ms, la magnitud del error al usar la expresión newtoniana para la energía cinética es cuanto mucho 4.2 1010 m0.
Estos conceptos también se aplican en el campo de la óptica. La figura 8 es una adaptación de Optics, 4a. ed. de Eugene Hecht, Reading, MA: Addison-Wesley, 2002, p. 153.
Representa una onda de la fuente puntual S que se encuentra una interfaz esférica de radio
R centrado en C. El rayo SA se refracta hacia P.
¨r
Lo
h
R
V
˙
¨t Li
S
C
so
si
n¡
FIGURA 8
n™
Refracción en una interfaz esférica
P
Cortesía de Eugene Hecht
A
¨i
Al aplicar el principio de Fermat de que la luz viaja en el menor tiempo posible, Hecht
deduce la ecuación
1
n1
n2
1
ᐉo
ᐉi
R
n2si
n1so
ᐉi
ᐉo
donde n1 y n2 son índices de refracción y ᐉo , ᐉi , so y si son las distancias indicadas en la
figura 8. De acuerdo con la ley de los cosenos aplicada en los triángulos ACS y ACP,
tiene
2
&
En este caso utilice la identidad
ᐉo sR 2 so R2 2Rso R cos *
ᐉi sR 2 si R2 2Rsi R cos *
cos * cos *
Como es un poco complicado trabajar con la ecuación 1, Gauss, en 1841, la simplificó
usando la aproximación lineal cos * 1 para valores pequeños de *. (Esto equivale a usar
el polinomio de Taylor de grado 1.) Por lo tanto la ecuación se transforma en la siguiente
ecuación más sencilla, que se le pide demostrar en el ejercicio 34(a):
3
n1
n2
n2 n1
so
si
R
La teoría óptica resultante se conoce como óptica de Gauss u óptica de primer orden, y se
ha vuelto la herramienta teórica básica para diseñar lentes.
Una teoría más exacta se obtiene al aproximar cos * por medio de su polinomio de Taylor de grado 3 (que es el mismo que el polinomio de Taylor de grado 2). Esto considera
los rayos para los cuales * no es tan pequeña, es decir, rayos que golpean la superficie
CAPITULO-11-G
06/04/2009
22:24
Page 755
SECCIÓN 11.11 APLICACIONES DE LOS POLINOMIOS DE TAYLOR
||||
755
a mayores distancias h por arriba del eje. En el ejercicio 34(b) se le pide usar esta aproximación para deducir la ecuación más exacta
4
n1
n2
n2 n1
n1
h2
so
si
R
2so
1
1
so
R
2
n2
2si
1
1
R
si
2
La teoría óptica resultante se conoce como óptica de tercer orden.
Otras aplicaciones de los polinomios de Taylor a la física y la ingeniería se exploran en los
ejercicios 32, 33, 35, 36 y 37 y en el proyecto de aplicación de la página 757.
11.11
EJERCICIOS
; 1. (a) Encuentre los polinomios de Taylor hasta de grado 6 para
f x cos x centrada en a 0. Dibuje f y estos polinomios en una misma pantalla.
(b) Evalúe f y estos polinomios en x 4, 2 y p.
(c) Explique cómo los polinomios de Taylor convergen
en f x.
; 2. (a) Encuentre los polinomios de Taylor hasta de grado 3 para
f x 1x centrada en a 1. Dibuje f y estos polinomios en una misma pantalla.
(b) Evalúe f y estos polinomios en x 0.9 y 1.3.
(c) Explique cómo los polinomios de Taylor convergen
en f x.
; 3–10 Determine los polinomios de Taylor Tnx para la función f
en el número a. Dibuje f y Tn en la misma pantalla.
3. f x l x ,
a2
4. f x x ex ,
5. f x cos x ,
x
6. f x e
a 2
a0
7. f x arcsen x ,
a0
9. f x xe
2x
de Rnx .
13. f x sx,
a 4,
n 2,
4 x 4.2
14. f x x ,
a 1,
n 2,
0.9 x 1.1
15. f x x
a 1,
n 3,
0.8 x 1.2
2
23
,
16. f x sen x ,
a 6 , n 4,
17. f x sec x ,
a 0,
18. f x ln1 2x,
x2
19. f x e ,
20. f x x ln x,
n 2 , 0.2 x 0.2
a 1,
a 0,
0 x 3
n 3,
a 1,
n 3,
0.5 x 1.5
0 x 0.1
n 3,
0.5 x 1.5
21. f x x sen x ,
a 0,
n 4,
1 x 1
22. f x senh 2x ,
a 0,
n 5,
1 x 1
a0
sen x ,
ln x
8. f x ,
x
; (c) Compruebe el resultado del inciso (b) mediante la gráfica
a1
, a0
10. f x tan1x, a 1
23. Mediante la información del ejercicio 5 estime cos 80° con cin-
co cifras decimales.
24. Mediante la información del ejercicio 16 estime sen 38° con
cinco cifras decimales.
25. Aplique la desigualdad de Taylor para determinar el número
de términos de la serie de Maclaurin para ex que se debe usar
para estimar e 0.1 de tal manera que no difiera de 0.00001 del
valor real.
26. ¿Cuántos términos de la serie de Maclaurin para ln1 x son
necesarios para estimar ln 1.4 con 0.001 de precisión?
CAS
11–12 Use un sistema algebraico computacional para encontrar los
polinomios de Taylor Tn con centro en a para n 2, 3, 4, 5. Luego
dibuje estos polinomios y f en la misma pantalla.
11. f x cot x ,
a 4
12. f x s3 x ,
3
2
n0
13–22
(a) Encuentre un valor aproximado de f mediante un polinomio de
Taylor con grado n en el número a.
(b) Con la desigualdad de Taylor estime la exactitud de la aproximación f x Tnx cuando x está en el intervalo dado.
; 27–29 Aplique el teorema de estimación de la serie alternante o la desigualdad de Taylor para estimar los valores de x para los cuales la
aproximación dada es exacta y está dentro del error establecido.
Compruebe gráficamente su respuesta.
27. sen x x x3
6
28. cos x 1 x2
x4
2
24
29. arctan x x ( error 0.01)
x3
x5
3
5
( error 0.005)
( error 0.005)
CAPITULO-11-G
756
||||
06/04/2009
22:24
Page 756
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
30. Suponga que
f n4 de tercer orden. [Sugerencia: utilice los dos primeros
1
términos de la serie binomial para ᐉ1
o y ᐉi . Aplique también * sen *.]
1)n n!
3nn 1
y la serie de Taylor de f con centro en 4 converge a f (x) para
toda x en el intervalo de convergencia. Demuestre que el polinomio de Taylor de quinto grado aproxima f (5) con error menor a 0.0002.
35. Si una onda de agua de longitud L se desplaza con una velocidad v a través de un cuerpo de agua de profundidad d como en
la figura, por lo tanto
tL
2 d
tanh
2
L
v2 31. Un vehículo se desplaza a una velocidad de 20 ms y a una
aceleración de 2 ms2 en un instante dado. Mediante un polinomio de Taylor de segundo grado, estime qué tanto se desplazará
el automóvil en el siguiente segundo. ¿Sería razonable utilizar
este polinomio para estimar la distancia recorrida durante el
minuto siguiente?
32. La resistividad de un conductor es el recíproco de la conduc-
tividad y se mide en unidades ohm-metros ( -m). La resistividad de un metal dado depende de la temperatura de acuerdo
con la ecuación
(a) Si el agua es profunda, demuestre que v stL2.
(b) Si el agua es poco profunda, aplique la serie de Maclaurin
para tanh para demostrar que v std. (Así, en agua poco
profunda, la velocidad de una onda tiende a ser independiente de la longitud de la onda).
(c) Mediante el teorema de estimación de la serie alternante,
demuestre que si L 10d, entonces la estimación v 2 td
es exacta dentro de 0.014tL.
L
t 20 e t20
;
;
d
donde t es la temperatura en °C. Hay tablas que dan los valores de (llamado coeficiente de temperatura) y 20 (la resistividad a 20°C) para varios metales. Excepto a temperaturas
muy bajas, la resistividad varía casi en forma lineal con la
temperatura, por lo que es común aproximar la expresión para
t mediante su polinomio de Taylor de primero o segundo
grados en t 20.
(a) Encuentre expresiones para estas aproximaciones lineales
y cuadráticas.
(b) Por lo que se refiere al cobre, las tablas dan 0.0039C
y 20 1.7 10 8 -m. Dibuje la resistividad del cobre
y las aproximaciones lineales y cuadráticas para 250
C t 1000C.
(c) ¿Para qué valores de t la aproximación lineal concuerda
con la expresión exponencial de tal manera que no difiera
1% del valor real?
33. Un dipolo eléctrico consiste en dos cargas eléctricas de igual
magnitud y signos opuestos. Si las cargas son q y q y hay una
distancia d entre ellas, en tal caso el campo eléctrico E en el punto P en la figura es
E
36. El periodo de un péndulo con longitud L que subtiende un án-
gulo máximo 0 con la vertical es
L
t
T 2
L
t
1
q
_q
P
ecuación 1 aproximando cos * en la ecuación 2 mediante
su polinomio de Taylor de primer grado.
(b) Demuestre que si cos * es reemplazado por su polinomio
de Taylor de tercer grado en la ecuación 2, en tal caso la
ecuación 1 se transforma en la ecuación 4 para una óptica
dx
s1 k 2 sen 2x
Si 0 no es demasiado grande, se usa a menudo la aproximación T 2 sLt, obtenida usando sólo el primer término de la serie. Se obtiene una mejor aproximación si se
usan sólo dos términos:
L
(1 14 k 2 )
t
(b) Observe que todos los términos de la serie después del primero tienen coeficientes que son cuanto mucho 14. Aplique
este hecho para comparar esta serie con una serie geométrica
y demuestre que
d
34. (a) Deduzca la ecuación 3 para la óptica de Gauss a partir de la
2
0
12 2
12 3 2 4
12 3 25 2 6
k 2 k 2 2 k 2
24
2 2426 2
T 2
Al expandir esta expresión para E como serie en potencias de
dD, demuestre que E es aproximadamente proporcional a
1D 3 cuando P está alejada del dipolo.
y
donde k sen( 12 0 ) y t es la aceleración debida a la gravedad.
En el ejercicio 40 de la sección 7.7 se aproximó esta integral
usando la regla de Simpson.
(a) Desarrolle el integrando como una serie binomial y use el resultado del ejercicio 46 de la sección 7.1 para demostrar que
q
q
D2
D d 2
D
T4
2
L
(1 14 k 2 ) T 2
t
L 4 3k 2
t 4 4k 2
(c) Mediante las desigualdades del inciso (b), estime el
periodo de un péndulo con L 1 m y 0 10. ¿Cómo es
si se le compara con la estimación T 2 sLt ? ¿Cómo
es si 0 42 ?
CAPITULO-11-G
06/04/2009
22:25
Page 757
PROYECTO DE APLICACIÓN RADIACIÓN PROVENIENTE DE LAS ESTRELLAS
37. Si un topógrafo mide diferencias en la altitud cuando hace planos
para una carretera que cruza un desierto, se deben hacer correcciones tomando en cuenta la curvatura de la Tierra.
(a) Si R es el radio de la Tierra y L es la longitud de la carretera, demuestre que la corrección es
orden n.
39. En la sección 4.9 utilizó el método de Newton para obtener un
valor aproximado de una raíz r de la ecuación f x 0, y a
partir de una aproximación inicial x1 obtuvo aproximaciones sucesivas x 2 , x 3 , . . . , donde
f x n
x n1 x n f x n
C R secLR R
L2
5L 4
2R
24R 3
(c) Compare las correcciones dadas por las fórmulas en los incisos (a) y (b) para una carretera que mide 100 km de longitud. Tome como radio de la Tierra 6 370 km
C
R
© Luke Dodd, Photo Researchers, Inc.
P ROY E C TO D E
A P L I C AC I Ó N
757
38. Demuestre que Tn y f tienen las mismas derivadas en a hasta el
(b) Mediante un polinomio de Taylor demuestre que
C
||||
Aplique la desigualdad de Taylor con n 1, a x n y x r
para demostrar que si f x existe en un intervalo I que contiene r, x n y x n1, y f x M , f x K para toda x I ,
por lo tanto
M
x n1 r xn r 2
2K
[Esto quiere decir que si x n es exacta con d cifras decimales,
en tal caso x n1 es exacta con alrededor de 2d cifras
decimales. Más exactamente, si el error en la etapa n es cuanto
mucho 10m, por lo tanto el error en la etapa n 1
es cuanto mucho M2K 102m.]
RADIACIÓN PROVENIENTE DE LAS ESTRELLAS
Cualquier objeto emite radiaciones cuando se calienta. Un cuerpo negro es un sistema que absorbe
toda la radiación que le llega. Por ejemplo, una superficie negra mate o una cavidad grande con un
pequeño agujero en su pared, (como un alto horno), es un cuerpo negro y emite radiación de cuerpo
negro. Incluso la radiación que llega del Sol está cerca de ser radiación de un cuerpo negro.
La ley de Rayleigh-Jeans, propuesta a fines del siglo XIX, expresa la densidad de energía de radiación de cuerpo negro de longitud de onda l como
8 kT
"4
donde l se mide en metros, T es la temperatura en kelvins (K) y k es la constante de Boltzmann. La ley de Rayleigh-Jeans concuerda con las mediciones experimentales para longitudes de
onda largas, pero no sucede lo mismo con las longitudes de onda cortas. [La ley predice que
f " l cuando " l 0 pero los experimentos han demostrado que f " l 0.] Este hecho
recibe el nombre de catástrofe ultravioleta.
En 1900, Max Planck encontró un mejor modelo, (que se conoce ahora como ley de Planck),
para la radiación de cuerpo negro:
8 hc"5
f " hc" kT e
1
f " donde l se mide en metros, T es la temperatura en kelvins, y
h constante de Planck 6.6262 1034 Js
c velocidad de la luz 2.997925 10 8 ms
k constante de Boltzmann 1.3807 1023 JK
1. Con ayuda de la regla de l’Hospital demuestre que
lím f " 0
" l 0
y
lím f " 0
"l
para la ley de Planck. De este modo, esta ley modela la radiación de cuerpo negro mejor que la
ley de Rayleigh-Jeans para longitudes de onda cortas.
CAPITULO-11-G
758
||||
06/04/2009
22:25
Page 758
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
2. Use un polinomio de Taylor para demostrar que, en el caso de las longitudes de onda
largas, la ley de Planck da aproximadamente los mismos valores que la ley de
Rayleigh-Jeans.
; 3. Dibuje f de acuerdo con ambas leyes en una misma pantalla y comente sobre las similitu-
des y las diferencias. Use T 5 700 K (la temperatura del Sol). (Quizá quiera cambiar de
metros a la unidad más conveniente de micrómetros: 1 m 106 m.)
4. Use la gráfica del problema 3 para estimar el valor de " para el cual f " es un máximo
según la ley de Planck.
; 5. Investigue cómo la gráfica de f cambia cuando T varía. (Utilice la ley de Planck). En particular, dibuje f para las estrellas Betelgeuse (T 3 400 K ), Proción (T 6 400 K ) y Sirio
(T 9 200 K ) así como para el Sol. ¿Cuál es la variación de la radiación total emitida, es
decir (el área bajo la curva), con T? Apóyese en las gráficas y explique por qué a Sirio se le
conoce como estrella azul y a Betelgeuse como una estrella roja.
11
REPASO
R E V I S I Ó N D E C O N C E P TO S
1. (a) ¿Qué es una sucesión convergente?
(b) ¿Qué es una serie convergente?
(c) ¿Qué significa lím n l an 3?
(d) ¿Qué significa n1 an 3?
2. (a) ¿Qué es una sucesión acotada?
(b) ¿Qué es una sucesión monótona?
(c) ¿Qué puede decir con respecto a una sucesión monótona
acotada?
3. (a) ¿Qué es una serie geométrica? ¿En qué circunstancias es
convergente? ¿Cuál es su suma?
(b) ¿Qué es una p-serie? ¿En qué circunstancias es convergente?
4. Suponga que an 3 y sn es la n-ésima suma parcial de la se-
rie. ¿Qué es lím n l an? ¿Qué es lím n l sn?
5. Enuncie lo siguiente.
(a)
(b)
(c)
(d)
(e)
(f)
(g)
Prueba de la divergencia
Prueba de la integral
Prueba por comparación
Prueba por comparación en el límite
Prueba de la serie alternante
Prueba de la razón
Prueba de la raíz
6. (a) ¿Qué es una serie absolutamente convergente?
(b) ¿Qué puede decir acerca de dicha serie?
(c) ¿Qué es una serie condicionalmente convergente?
7. (a) Si una serie es convergente de acuerdo con la prueba de la
integral, ¿cómo estima su suma?
(b) Si una serie es convergente según la prueba por comparación, ¿cómo estima su suma?
(c) Si una serie es convergente según la prueba de la serie
alternante, ¿cómo estima su suma?
8. (a) Escriba la forma general de una serie de potencias.
(b) ¿Qué es el radio de convergencia de una serie de potencias?
(c) ¿Qué es el intervalo de convergencia de una serie de
potencias?
9. Suponga que f x es la suma de una serie de potencias con ra-
dio de convergencia R.
(a) ¿Cómo deriva f ? ¿Cuál es el radio de convergencia de la
serie para f ?
(b) ¿Cómo integra f ? ¿Cuál es el radio de convergencia de la
serie para x f x dx?
10. (a) Escriba una expresión para el polinomio de Taylor de
n-ésimo grado de f centrada en a.
(b) Escriba una expresión para la serie de Taylor de f centrada
en a.
(c) Escriba una expresión para la serie de Maclaurin de f .
(d) ¿Cómo demuestra que f x es igual a la suma de su serie
de Taylor?
(e) Enuncie la desigualdad de Taylor.
11. Escriba la serie de Maclaurin y el intervalo de convergencia
para cada una de las funciones siguientes.
(a) 11 x
(d) cos x
(b) e x
(e) tan1x
(c) sen x
12. Escriba el desarrollo de la serie binomial de 1 x k. ¿Cuál es
el radio de convergencia de esta serie?
CAPITULO-11-G
06/04/2009
22:25
Page 759
CAPÍTULO 11 REPASO
||||
759
P R E G U N TA S D E V E R DA D E R O - FA L S O
Determine si el enunciado es verdadero o falso. Si es verdadero, explique
por qué. Si es falso, dé la razón o proporcione un ejemplo que contradiga
el enunciado.
1. Si lím n l a n 0, entonces a n es convergente.
11. Si 1 1, en tal caso lím n l n 0.
12. Si a n es divergente, luego a n es divergente.
13. Si f x 2x x 2 3 x 3 converge para toda x,
1
2. La serie n1 n sen 1 es convergente.
por lo tanto f 0 2.
3. Si lím n l a n L, entonces lím n l a 2n1 L.
4. Si cn6 n es convergente, entonces cn2n es convergente.
5. Si cn6 es convergente, entonces cn6 es convergente.
n
n
6. Si cn x n diverge cuando x 6, entonces diverge cuando
x 10.
14. Si a n y bn son divergentes, en consecuencia a n bn es
divergente.
15. Si a n y bn son divergentes, entonces a n bn es divergente.
16. Si a n es decreciente y a n 0 para toda n, entonces a n es convergente.
7. La prueba de la razón se puede usar para determinar si
converge 1n 3.
17. Si a n 0 y a n converge, por lo tanto converge 1n a n.
8. La prueba de la razón se puede usar para determinar si
converge 1n!
9. Si 0 a n bn y bn diverge, entonces la serie a n diverge.
10.
n0
1
1n
n!
e
18. Si a n 0 y lím n l a n1a n 1, entonces lím n l a n 0 .
19. 0.99999 . . . 1
20. Si
a
Ay
n
n1
b
n
B, entonces
n1
ab
n n
AB.
n1
EJERCICIOS
1–8 Determine si la sucesión es convergente o divergente. Si es
convergente, determine su límite.
2n
1 2n 3
n3
3. a n 1 n2
n sen n
5. a n 2
n 1
17.
n1
3
n1
1. a n 9
10 n
2. a n 19.
7. 1 3n 20.
n1
ln n
sn
6. a n n1
4. a n cosn2
cos 3n
1 1.2n
n
a 1 1, a n1 13 a n 4. Demuestre que a n es creciente y
a n 2 para toda n. Deduzca que a n es convergente y determine su límite.
n1
n 2n
1 2n 2 n
1
n1
sn
n1
22.
n1
sn 1 sn 1
n
23–26 Determine si la serie es condicionalmente convergente, ab-
solutamente convergente o divergente.
23.
1
n 13
n1
24.
n1
4 n
0 y mediante una gráfica determine el valor más pequeño de N que corresponde a 0.1
en la definición exacta de límite.
52n
n 29n
n1
9. Una sucesión se define recursivamente mediante las ecuaciones
18.
1 3 5 2n 1
5 nn!
21.
8. 10 n!
4n
; 10. Demuestre que lím n l n e
25.
n1
1
n 3
n1
n1
1nn 13 n
2 2n1
26.
n2
1nsn
ln n
11–22 Determine si la serie es convergente o divergente.
11.
n1
13.
n1
15.
n2
n
n 1
12.
n3
5n
14.
1
nsln n
16.
3
n1
n1
n2 1
n3 1
27–31 Calcule la suma de la serie.
1n
sn 1
27.
ln
n1
n
3n 1
n1
29.
3 n1
23n
tan
n1
1
n 1 tan1n
28.
1
nn 3
1n n
3 2n 2n!
n1
30.
n0
CAPITULO-11-G
760
06/04/2009
||||
22:25
Page 760
CAPÍTULO 11 SUCESIONES Y SERIES INFINITAS
31. 1 e e2
e3
e4
2!
3!
4!
49. f x ln1 x
50. f x xe 2x
51. f x senx 4 52. f x 10 x
4
16 x
53. f x 1s
54. f x 1 3x5
32. Exprese el decimal periódico 4.17326326326 . . . como una
fracción.
55. Evalúe y
33. Demuestre que cosh x 1 2 x 2 para toda x.
1
34. ¿Para qué valores de x converge la serie n1 ln xn?
35. Calcule la suma de la serie
n1
decimales.
el error al usarla como aproximación de la suma de la serie.
(b) Calcule la suma de esta serie con cinco dígitos decimales.
37. Use la suma de los primeros ocho términos para aproximarse a la
suma de la serie n1 2 5 n 1. Estime el error que se origina
en esta aproximación.
38. (a) Demuestre que la serie
n1
56. Mediante series aproxime x01 s1 x 4 dx con dos dígitos
decimales.
1n1
con cuatro dígitos
n5
36. (a) Determine la suma parcial s5 de la serie n1 1n 6 y estime
57–58
(a) Obtenga un valor aproximado de f mediante un polinomio de
Taylor de grado n en el número a.
; (b) Dibuje f y Tn en una misma pantalla.
(c) Use la desigualdad de Taylor para estimar la exactitud de la
aproximación f x Tnx cuando x se encuentra en el intervalo dado.
(d)
Compruebe su resultado del inciso (c) mediante la gráfica
;
de Rnx .
n
57. f x sx,
n
es convergente.
2n!
a 1,
58. f x sec x,
nn
0.
(b) Deduzca que lím
n l 2n!
39.
ex
dx como una serie infinita.
x
a 0, n 2,
n1
lím
xl0
n1
an
n
F
gencia de la serie.
n
n1
42.
n1
xn
n 25 n
41.
n1
2 x 2
n 2!
n
n
43.
n0
x 2n
n4 n
2 nx 3n
sn 3
44. Calcule el radio de convergencia de la serie
n1
2n! n
x
n!2
45. Determine la serie de Taylor de f x sen x en a 6.
;
47–54 Encuentre la serie de Maclaurin para f y su radio de convergencia. Puede aplicar el método directo (definición de una serie de
Maclaurin) o las series conocidas, como la serie geométrica, serie binomial o la serie de Maclaurin para e x, sen x y tan1x.
x2
1x
48. f x tan1x 2 mtR 2
R h2
donde R es el radio de la Tierra y g es la aceleración de la
gravedad.
(a) Exprese F como una serie en potencias de hR.
(b) Observe que si aproxima F con el primer término de la serie, obtiene la expresión F mt que se usa por lo común
cuando h es mucho más pequeña que R. Aplique el teorema de la estimación de la serie alternante para calcular
los valores de h para los cuales la aproximación F mt no
difiere 1% (del valor real R 6 400 km).
61. Suponga que f x n0 cn x n para toda x.
(a) Si f es una función impar, demuestre que
46. Determine la serie de Taylor de f x cos x en a 3.
47. f x sen x x
x3
una altura h por encima de la superficie de la Tierra es
40–43 Encuentre el radio de convergencia y el intervalo de conver
0 x 6
60. La fuerza de la gravedad que actúa en un objeto de masa m a
es también absolutamente convergente.
1
0.9 x 1.1
59. Mediante series evalúe el siguiente límite.
Demuestre que si la serie n1 an es absolutamente convergente,
por lo tanto la serie
40.
n 3,
c0 c2 c4 0
(b) Si f es una función par, demuestre que
c1 c3 c5 0
2
62. Si f x e x , demuestre que f 2n0 2n!
n!