COMUNICACIÓN INTERIOR

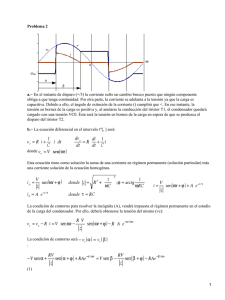
Ecuación de difusión.
INTRODUCCIÓN
La ecuación de difusión es de la forma
u
2 u
 2 · 2
(1)
t
x
Esta ecuación describe la conducción de calor a través de sólidos. Por ejemplo, si se
considerara una barra de sección transversal, uniforme y de material homogéneo,
eligiendo el eje x como eje horizontal de la barra y haciendo coincidir los extremos
de la barra con los puntos x = 0 y x = , la ecuación anterior describiría la variación
de temperatura a lo largo de la barra. La función incógnita u = u(x,t) depende de la
coordenada x de la barra, que variará entre 0 y y del tiempo t, que tomará valores
mayores que 0.
Para resolver la ecuación (1), es preciso imponer ciertas condiciones iniciales y de
contorno sobre los extremos, que surgirán del estudio de algunos de los fenómenos
de naturaleza física en relación con estos procesos de difusión. Algunos tipos de
condiciones de contorno sobre los extremos que pueden imponerse son los
siguientes:
1) Que uno o los dos extremos de la barra se mantienen a temperatura constante,
lo que da lugar a las condiciones
u ( 0, t )  T1
u( , t )  T2 t  0
o bien
2) Que uno o los dos extremos de la barra se aíslen para que no pase calor a través
de ellos, lo que da lugar a las condiciones
u x ( 0, t )  0
u x ( , t )  0 t  0
o bien
3) Otro tipo más general de condiciones de contorno surgen de imponer que el flujo
de calor a través de uno o de ambos extremos de la barra es proporcional a la
temperatura en él, que se expresa en la forma
u x ( 0, t )  h1 · u( 0, t )  0 t  0
u x ( , t )  h 2 · u( , t )  0 t  0
donde h 1 y h 2 son constantes no negativas de proporcionalidad.
Por último, para determinar completamente el flujo de calor en la barra es
necesario conocer la distribución de temperatura en un instante fijo, por ejemplo en
el instante t = 0. Esta es una condición inicial que puede expresarse en la forma
u(x,0) = h(x) 0  x 
Los problemas que se van a resolver en este tema van a consistir en determinar la
solución de la ecuación diferencial (1), sujeta a alguna de las condiciones de
contorno comentadas en cada uno de los extremos y a una condición inicial del tipo
anterior.
MÉTODO DE SEPARACIÓN DE VARIABLES
Sea la ecuación
u
2 u
 2 · 2
(1)
t
x
con 0 < x < y t > 0. Supóngase conocida la distribución inicial de temperatura
u(x,0) = h(x) 0  x 
(2)
y supóngase que los extremos de la barra se mantienen a temperaturas fijas
u ( 0, t )  T1
u( , t )  T2 t  0
(3)
Copyright © 2006 by Tecnun (University of Navarra)
Se comenzará resolviendo el caso homogéneo, es decir, cuando los extremos se
mantienen a temperatura nula, para a continuación centrarse en el caso más
general, que podrá reducirse a éste.
Para resolverlo, se considera en primer lugar la ecuación junto con las condiciones
de contorno sobre los extremos y a continuación se impondrá la condición inicial. El
método de resolución empleado es el de separación de variables, que consiste en
buscar soluciones de la forma
u(x,t) = f(x)·g(t)
Derivando y sustituyendo en la ecuación se obtiene
f · g   2 · f  · g
dividiendo por el producto f·g
f 
1 g
 2·
f
 g
pero como f es sólo función de x y g es sólo función de t, entonces para que la
igualdad anterior sea cierta el cociente debe ser constante. Llamando  a tal
constante
f 
1 g
 2· 
f
 g
se obtienen las dos ecuaciones diferenciales siguientes
f  ( x)   · f ( x)  0
g ( t )   ·  2 · g( t )  0
Pero como u(x,t) debe ser tal que
u(0,t) = 0 y u( ,t) = 0  t
la función f(x) debe verificar las condiciones de contorno
f(0) = 0 y f( ) = 0
Luego, para hallar la solución de la ecuación (1), es preciso resolver el problema de
Sturm-Liouville regular homogéneo para f:
f"(x) - ·f = 0
f(0) = 0 y f( ) = 0
Al resolver este problema hay que tener en cuenta los tres casos que pueden
presentarse en cuanto a los valores de 
i)  = 0
ii)  > 0
iii)  < 0
Puede observarse fácilmente que la única solución que puede obtenerse en los dos
primeros casos es la solución trivial, por lo que habrá que restringirse al caso iii) en
que     2  0 . La solución general de la ecuación es
f ( x)  C1 ·cos(  · x)  C2 · sin (  · x)
pero al imponer f(0) = 0, se llega a que C1 = 0, y como también f( ) = 0 se tiene
que
n ·
n2 · 2
 ·  n ·   
 2
n  1, 2,...
Las soluciones asociadas a estos autovalores son
 n •  • x
f n ( x)  sin
 n  1,2,...


Resolviendo ahora la ecuación diferencial para g
n2 ·  2 · 2
g( t ) 
·g( t )  0
2
se obtienen como soluciones
Copyright © 2006 by Tecnun (University of Navarra)
gn  Kn ·en · · ·t
Los productos de estas funciones f n y g n constituyen una familia infinita de
soluciones de la ecuación de difusión (1), junto con las condiciones de contorno
homogéneas. A tales soluciones
 n •  • x   n2 • 2 • 2 •t 2
u n  sin
n  1,2,...
 •e


se les llama soluciones fundamentales. Pero como la ecuación (1) es una ecuación
lineal y las condiciones de contorno son homogéneas, cualquier combinación lineal
finita de estas soluciones sigue siendo también solución. Procediendo formalmente
también será solución la serie infinita

 n •  • x   n2 • 2 • 2 •t 2
(4)
u( x, t )   C n • sin
 •e


n 1
Las constantes C n se determinarán imponiendo la condición inicial que falta por
considerar:

 n •  • x
u( x,0)  h( x)   C n • sin



n 1
Es decir, los coeficientes C n deben ser los coeficientes del desarrollo de la función
h(x) en serie de las autofunciones f n del problema de Sturm-Liouville. Por los
resultados vistos en temas anteriores se sabe que tales coeficientes vienen dados
por las fórmulas
1
 n •  • x
Cn 
•  h( x) • sin
 • dx =
0


2  n •  • x
 • dx
0sin 

2

2
2
2
2
 n •  • x
•  h( x) • sin
 • dx n  1,2,...
0


(5)
Por tanto, la solución de la ecuación de difusión, junto con las condiciones de
contorno homogéneas y la inicial (2), viene dada por la serie (4), siendo los
coeficientes C n los establecidos en las fórmulas (5).
En principio, esta solución obtenida es una serie formal, pero puede demostrarse
que en el intervalo 0 < x < y para todos los valores de t > 0, la serie converge a
una función continua cuyas derivadas u t y u xx pueden computarse por derivación
término a término, y que verifica la ecuación del calor y las condiciones de contorno
e iniciales establecidas. Además
lim u( x, t )  0
t
Ejemplo :
Un ejemplo donde surge un problema de este tipo es en el calentamiento súbito de
un bloque definido geométricamente por
0x
- < y <  , - < z < 
En el instante inicial está a una temperatura uniforme T0 . En un cierto instante se
eleva la temperatura de los planos x = 0, x = a la temperatura T , que se
mantendrá constante a lo largo de todo el proceso. Denotando por T(x,t) a la
temperatura, la ecuación que verifica es
T
2T
 2 · 2
0x
(6)
t
x
Copyright © 2006 by Tecnun (University of Navarra)
Para eliminar algunas constantes se hace un cambio de escala de la forma
siguiente. Se considera como nueva variable dependiente
T( x, t )  T1
( x, t ) 
T0  T1
Esta nueva variable dependiente sigue verificando la ecuación difusión (6), pero con
las condiciones iniciales y de contorno siguientes
(x,0)=1
0x
(7)
(0,t)=0=( ,t)
(8)
t > 0
Si se efectúa ahora un cambio de las variables independientes de la forma
x  x ·

t = ·t'
donde  se elegirá convenientemente
entonces, considerando la función (x',t') la relación entre las derivadas parciales es
2 2  2

·
x 2 x  2 2
  1

·
t t  
quedando la ecuación
 1
 2  2
·  2 · 2 · 2
t  
x 
eligiendo  de forma que
 · 2 ·  2
1
2
la ecuación queda reducida a
  2 

0  x  
(9)
t  x  2
y las condiciones iniciales y de contorno se transforman en
( x  , 0)  1 0  x   
(10)
( 0, t  )  (  , t  )  0 t   0
(11)
quedando un problema análogo al que se acaba de resolver. Se busca la solución
por el método de separación de variables de la forma
( x  , t  )  f ( x  ) · g ( t  )
derivando y sustituyendo en la ecuación, se llega a
g  ( t ) f  ( x  )


g( t )
f ( x )
donde  es una constante, lo queda lugar a las ecuaciones
g'(t) - ·g(t) = 0
f"(x') - ·f(x') = 0
Las condiciones de contorno implican
f(0) = 0 = f()
quedando el problema de contorno homogéneo de Sturm-Liouville para f
f"(x') - ·f(x') = 0
f(0) = 0 = f()
razonando como se ha hecho antes se llega a la conclusión de los únicos valores de
 que permiten obtener soluciones no nulas son los negativos  = -  2 < 0, siendo la
solución general
f ( x )  C1 • cos  • x   C 2 • sin  • x 
Al imponer las condiciones de contorno, se deduce que C1 = 0 y que
  n     n2
n = 1, 2,... son los autovalores
Copyright © 2006 by Tecnun (University of Navarra)
siendo las autofunciones correspondientes
n = 1, 2,...
f n  sin n • x 
Para los valores de  anteriores la ecuación para g queda
g  n 2 · g  0
cuya solución general es
g t   C n • e  n •t 
Luego, las soluciones fundamentales son
2
 n (x, t )  Cn • e  n •t  • sin n • x n = 1, 2, .....
Considerando la serie infinita
2

( x , t )   C n • e  n
2
•t 
• sin n • x 
n 1
e imponiendo finalmente la condición inicial, se determinan los coeficientes C n :

( x ,0)  1   C n • sin n • x 
0 < x' < 
n 1
es decir, los C n son los coeficientes del desarrollo en serie de las autofunciones f n
de la función h(x') = 1
Cn 
1


0

sin 2  n • x  • dx 

•  h( x ) • sin n • x  • dx  
0
2 
• h( x ) • sin n • x  • dx 
 0

2
n
1    1
n = 1, 2,...
n•
Si n es par C n = 0
4
Si n es impar Cn 
n ·
Por tanto, la solución es
2
4 
1
( x , t )  • 
• e  2•n 1 •t  • sin2 • n  1 • x 
 n 1 2 • n  1
Deshaciendo los cambios de variable efectuados, se obtendría finalmente la
solución T(x,t) buscada.

CONDICIONES DE CONTORNO NO HOMOGÉNEAS
Supóngase ahora que uno de los extremos de la barra se mantiene a una
temperatura constante T1 y el otro a una temperatura T2 . El problema a resolver es
u
2 u
 2 · 2
0x
t  0
t
x
u ( 0, t )  T0
t  0
u( , t )  T1 t  0
u(x,0) = h(x) 0  x 
Para resolver este problema se utiliza la siguiente técnica. Cuando el tiempo t se
hace suficientemente grande, cabe esperar que se alcance una distribución de
temperatura estable que sea independiente del tiempo y de la condición inicial. A
una tal función se la denotará por v(x). Entonces, la solución u = u(x,t) buscada se
descompone en
u(x,t) = v(x) + w(x,t)
(1)
de modo que
w(0,t) = 0
w( ,t) = 0
Copyright © 2006 by Tecnun (University of Navarra)
v(0) = T0
v( ) = T1
y como además u(x,t) es solución de la ecuación de difusión
  2 v  2 w  w
2
 • 2  2  
x  t
 x
pero v(x) debe seguir verificando esta ecuación, luego cumplirá
2 v
 0  v  C1x  C2
x 2
y al imponer las condiciones de contorno
v ( 0)  T0
v ( )  T1
se obtiene
T T
(2)
v( x)  1 0 x  T0
Finalmente, falta obtener w(x,t) que sigue verificando la ecuación de difusión,
 2 w w
2 · 2 
x
t
con condiciones de contorno nulas,
w(0,t) = 0
w( ,t) = 0
y con la condición inicial
w(x,0) = h(x) - v(x)
Este problema es el que se ha resuelto ya en el apartado anterior, quedando de
esta forma perfectamente determinada la función u(x,t), como suma de la función
v(x) obtenida en (2) y de esta w(x,t).
EXTREMOS AISLADOS
Supóngase ahora que los extremos de la barra están aislados, es decir que no hay
trasvase de calor a través de ellos. Esto se expresa mediante las siguientes
condiciones de contorno
u0, t 
0
x
u , t 
0
x
supuesto que se aíslan ambos extremos.
Por tanto, el problema a resolver ahora es
u
2 u
 2 · 2
0x
t  0
t
x
u0, t 
u , t 
0
0
t  0
x
x
u(x,0) = h(x) 0  x 
Buscando de nuevo la solución por separación de variables
u(x,t) = f(x)·g(t)
se obtienen las dos ecuaciones diferenciales ordinarias siguientes
f" - ·f = 0
g   2 ·  · g  0
Pero en este caso las condiciones de contorno implican que
Copyright © 2006 by Tecnun (University of Navarra)
f'(0) = 0 = f'( )
por lo que f debe ser solución del problema homogéneo de Sturm-Liouville
f" - ·f = 0
f'(0) = 0 = f'( )
Supuesto en primer lugar  = 0, la solución general de la ecuación es
f ( x)  C1 · x  C2
Como f'(0) = 0  C1  0 , quedando f ( x)  C2 , función que ya verifica la otra
condición de contorno. Luego,  = 0 es autovalor.
Puede observarse fácilmente que  no puede ser positivo, por lo que nos
restringiremos al caso en que  = -  2  0 :
f ( x)  C1 • cos  • x  C2 • sin  • x
f ( x)   • C1 • sin  • x   • C 2 • cos  • x
como f'(0) = 0  C 2  0
n 2 ·  2
n ·
y como f'( ) = 0   ·  n ·   
 
n = 1, 2,...
2
Para estos autovalores, las correspondientes autofunciones son
n · ·x
n = 1, 2,...
fn  cos
Resolviendo la ecuación diferencial para g:
para  = 0 g' = 0  g(t) = C
n 2 ·  2
para  
2
g 
 2 · n2 · 2
2
·g  0 
g( t )  Kn ·e ·n · ·t
Por tanto, se obtiene la familia de soluciones fundamentales
u0  C0
2 2 2
2
n · ·x
n = 1, 2,...
u n  Cn ·e ·n · ·t ·cos
2
2
2
2
La suma infinita de estas soluciones seguirá siendo solución de la ecuación y de las
condiciones de contorno homogéneas. Falta imponer únicamente la condición
inicial:

2 2 2
2
n · ·x
u( x, t )  C0   C n · e  ·n · ·t ·cos
n 1

u( x, 0)  h( x)  C0   C n ·cos
n · ·x
n 1
Luego, los C n son los coeficientes del desarrollo en serie de las autofunciones
obtenidas, de la función h(x), y vienen dados por
1
1
C0 
•  h( x) • dx  •  h( x) • dx
0
0
 1 • dx
0
Cn 
2
 n •  • x
•  h( x) • cos
 dx
0


n = 1, 2,..
quedando así resuelto completamente el problema.
Puede observarse que la solución obtenida es suma de una distribución de
temperatura estable independiente del tiempo (la constante C 0 ), y de una
distribución transitoria (la constituída por el resto de los términos de la serie
infinita), que tiende a cero para valores grandes de t. El que la distribución de
Copyright © 2006 by Tecnun (University of Navarra)
temperatura estacionaria sea constante, en este caso, es consistente con el hecho
de que al no existir trasvase de calor por los extremos, cabe esperar que el proceso
de conducción de calor suavice gradualmente la temperatura de la barra.
Nota:
El método de separación de variables puede utilizarse también para resolver la
ecuación de difusión con otro tipo de condiciones de contorno, diferentes a las
vistas aquí. Se podrá emplear incluso con ecuaciones en derivadas parciales más
generales, describiendo fenómenos de difusión más complejos en los que existen
otras fuentes de calor. En general, se podrá utilizar, siempre que las ecuaciones
diferenciales a las que da lugar, junto con las condiciones de contorno e inicial
fijadas constituyan un problema homogéneo de Sturm-Liouville.
Copyright © 2006 by Tecnun (University of Navarra)