Apuntescentroides
Anuncio

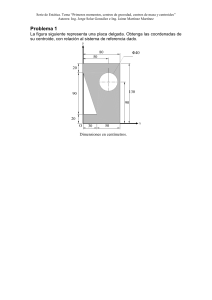
Complementario Centroides y Centro de gravedad R. Lagos Centroides y Centros de Gravedad 1.- Introducción En términos generales, hemos estado trabajando con sistemas homogéneos para los cuales la fuerza que ejerce la tierra sobre ellos, denominada Fuerza de Gravedad o Peso del cuerpo actúa en un punto que corresponde al Centro de gravedad. En esta sección aprenderemos a determinar dicho centro de gravedad para cuerpos homogéneos con formas diferentes. En un principio se analizarán los casos de placas y alambres o filamentos que se encuentran en un plano definido. El concepto de Centro de Gravedad está vinculado estrechamente con los conceptos de Centroide y Primer Momento de Área o Línea. 2.- Áreas y Líneas: Centro de gravedad de un cuerpo bidimensional. Para comenzar, considere una placa plana que se encuentra en un plano x,y; como se muestra en la figura 1. Existirá un punto que identificamos con (Xc,Yc) con respecto al origen del sistema de referencia que represente el punto donde actúa la fuerza debida a la gravedad denominada fuerza peso. z Xc z O O Yc C x (xi , yi) x x x ΔWi W El momento de esta fuerza con respecto al origen del sistema de referencia se determina a partir de la expresión: Mo rW X C î YC ĵ W k̂ (1) Realizando el producto cruz, se obtiene Mo W YC î W XC ĵ (2) 1 Complementario Centroides y Centro de gravedad R. Lagos De la ecuación (2) se ve que el momento de la fuerza peso con respecto al origen del sistema de referencia tiene dos componentes que se encuentran en el plano (x,y). Estos momentos tienen un valor correspondiente a: Mx = YC W ; My = X C W (3) Considere ahora, que el objeto está formado por un gran número de elementos ubicados en las coordenadas (x,y), cada uno de estos elementos tiene un área ΔA pequeña. Las componentes del pequeño momento que se produce por el peso de este elemento con respecto al origen del sistema de referencia corresponde a: ΔMx = y ΔW ΔMy = x ΔW (4) Si cada pequeño elemento tiene coordenadas (x1,y1) ; (x2,y2) ; (x3,y3) ; ……… ; (xi,yi), entonces el momento total corresponde a la suma de las contribuciones de cada uno de esos pequeños elementos ubicados en dichas posiciones, es decir, Mx y i Wi ; My x i Wi (5) Igualando los resultados de la ecuación (5) con los de la ecuación (3), se obtiene: YC W y i Wi XC W ; x i Wi (6) Cuando los elementos se hacen cada vez más pequeños, el número de partes aumenta. Si se piensa que los elementos son infinitamente pequeños, entonces, el número de ellos tiende a infinito; para ese caso la sumatoria en las expresiones anteriores se transforma en una integral y el peso del pequeño elemento se representa por un diferencial de peso dW, lo que permite escribir la ecuación (6) como: YC W y dW XC W ; x dW (7) Si la distribución corresponde a un filamento o alambre (su sección transversal uniforme es pequeña comparada con su longitud) situado en un plano definido, entonces, se pueden obtener de la misma forma las coordenadas del centro de gravedad usando las siguientes relaciones: YC W y dW XC W ; x dW (8) Para un alambre de cualquier forma, es posible encontrar que el centro de gravedad no se encuentra dentro del alambre. z O W Yc y Xc x C 2 Complementario 3.- Centroides y Centro de gravedad R. Lagos Centroides de Áreas y de Líneas. Es posible vincular el peso de un objeto con los conceptos de volumen, área y línea, para ello se establece que cuando un objeto se define como homogéneo, es decir, la masa es proporcional ya sea a su volumen, superficie o línea que describe al objeto; en ese caso, la magnitud del peso del pequeño elemento ΔW, se puede escribir en función del concepto de densidad de masa o en términos del concepto de peso específico. ΔW = ΔM g = Δ V g = t ΔA g = ( g) t A = t ΔA (9) Donde es la densidad volumétrica de masa, t es el espesor de la placa, ΔA es la pequeña superficie y se define como el producto de la densidad de masa por la gravedad, denominada peso específico. Usando la expresión (9), entonces, el peso del objeto se puede escribir como: W=tA (10) Reemplazando este resultado en las ecuaciones (7) y (8), da como resultado las coordenadas de lo que se define como Centroide de área. YC t A y t dA XC t A ; x t dA (11) Finalmente eliminando el producto t, de ambas ecuaciones, las coordenadas del centroide son: YC A y dA ; XC A x dA (12) Si la distribución corresponde a un filamento o alambre (su sección transversal es pequeña comparada con su longitud) situado en un plano definido, se puede obtener de la misma forma las siguientes relaciones: YC L y dL ; XC L x dL (13) Para un alambre de cualquier forma, es posible encontrar que el centroide no se encuentra dentro del alambre. 3 Complementario 4.- Centroides y Centro de gravedad R. Lagos Primeros Momentos de Áreas y Líneas. Las expresiones (12) y (13) representan los Primeros momentos de Áreas y Primeros momentos de Líneas respectivamente. Estas cantidades se expresan habitualmente con la letra Q, es decir: y Qx Qx YC A dA ; Qy x dA (14) ; Qy XC A (15) Las coordenadas del centroide se pueden obtener al dividir los primeros momentos y el área del objeto. Si el centroide de un área está localizado sobre el eje de coordenadas, entonces el primer momento con respecto de ese eje es igual a cero. Si el primer momento de área con respecto de un eje coordenado es igual a cero, entonces, el centroide del área está localizado sobre el eje. Simetría Se dice que un área es simétrica con respecto de un eje BB’ si para todo punto P del área existe un punto P’ de esa misma área tal que la línea PP’ es perpendicular a BB’ y dicha línea está dividida en dos partes iguales por el eje en cuestión. Cuando un área A o una Línea L posee un eje de simetría BB’ su primer momento con respecto a BB’ es igual a cero y su centroide está localizado sobre dicho eje. Si un área o línea posee dos ejes de simetría, su centroide C debe estar localizado en la intersección de esos ejes. Ejemplo son los cuadrados, círculos, elipses, rectángulos, triángulos equiláteros u otras formas simétricas. Se dice que un área es simétrica con respecto a un centro O, si para cada elemento dA de coordenadas x,y; existe un elemento de área dA’ de igual superficie con coordenadas x’ = - x ; y’ = -y. A partir de ello se concluye que Qx = 0 ; Qy = 0; XC = 0 ; YC = 0 Una figura que tiene un centro de simetría, no necesariamente posee un eje de simetría. Una figura con dos ejes de simetría no necesariamente tiene un centro de simetría. Si una figura posee dos ejes de simetría que son perpendiculares entre sí, el punto de intersección de dichos ejes es un centro de simetría. 4 Complementario Centroides y Centro de gravedad R. Lagos Tabla para Centroides de Áreas y Líneas Forma x y Área 1 (a b) 3 h 3 bh 2 Un cuarto de área circular 4r 3 4r 3 r2 4 Área semicircular 0 4r 3 r2 2 3a 8 3h 5 2a h 3 0 3h 5 4a h 3 3a 8 3h 10 ah 3 2 r sen 3 0 r2 Un cuarto de Arco Circular 2 r 2 r r 2 Arco Semicircular 0 2 r r Arco de un Círculo 2 r sen 3 0 Área triangular Área semiparabólica Área parabólica Enjuta o Tímpano parabólico Sector circular Representación 2r 5 Complementario Centroides y Centro de gravedad n 1 h 4n2 n 1 a n2 Enjuta General 5.- R. Lagos ah n 1 Placas y alambres compuestos. En algunas situaciones particulares las placas planas se pueden representar análogamente como formada por distintas formas geométricas tales como rectángulos, triángulos, círculos, cuadrados, etc; en estos casos es posible hallar las coordenadas del centroide, determinando primero las coordenadas de los centros de gravedad de cada uno de los componentes del sistema y luego expresando los momentos de cada uno de ellos con respecto de un sistema de referencia. Se suman los momentos respectivos y se divide por el área total que es la suma de las áreas de sus componentes. Si cada parte tiene coordenadas (xC1,yC1) ; (xC2,yC2) ; (xC3,yC3) ; ……… ; (xCi,yCi) de sus propios centroides con respecto del origen del sistema de referencia, entonces el momento total corresponde a la suma de las contribuciones de cada una de esas partes ubicadas en dichas posiciones, es decir, Mx y Ci Wi ; My x Ci Wi (16) Wi (17) Si la suma de los pesos se representa por WT, la ecuación (16) puede escribirse como: YC WT y Ci Wi ; XC WT x Ci Si a su vez la placa es homogénea y de espesor uniforme, el centro de gravedad coincide con el centroide C de su área. Las coordenadas del centroide serán obtenidas a partir de los primeros momentos, es decir: y Qx Qx YC A Ci Ai ; ; Qy Qy x Ci XC A Ai (18) (19) Donde A es la suma de las áreas parciales. Note que los primeros momentos de área al igual que los momentos de las fuerzas, pueden ser positivos o negativos. Por ejemplo, un área de un centroide que esté localizado a la izquierda del eje y, tendrá un primer momento negativo con respecto de dicho eje. Del mismo modo al área de un agujero se le debe asignar un signo negativo. 6