Ejemplos tema 1

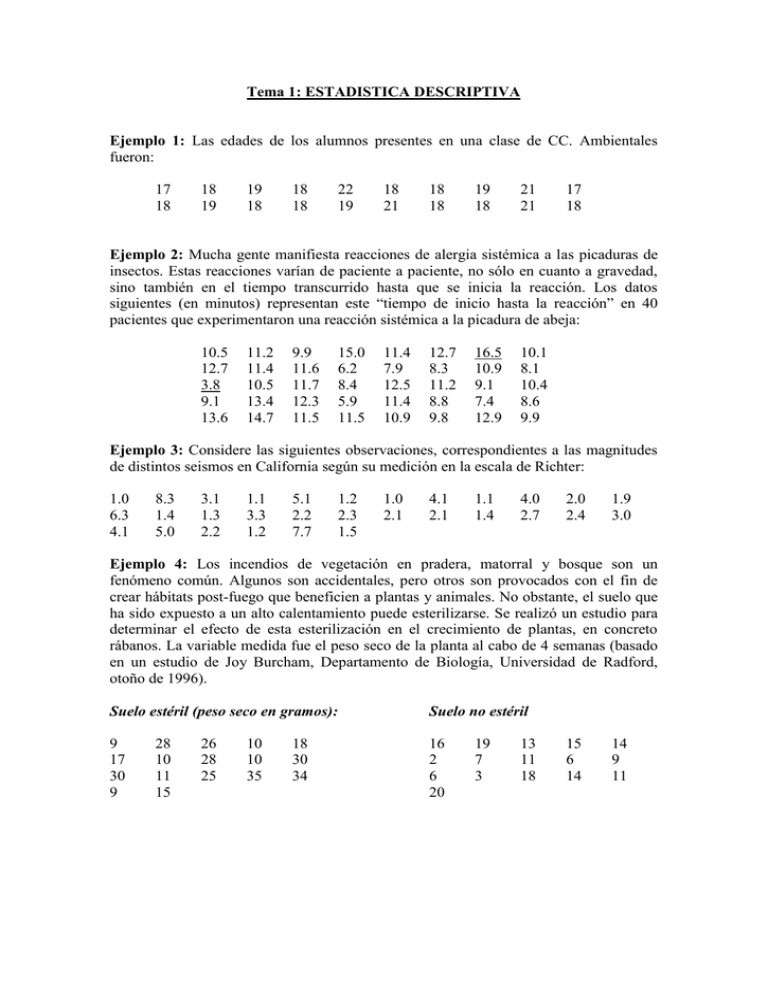
Tema 1: ESTADISTICA DESCRIPTIVA
Ejemplo 1: Las edades de los alumnos presentes en una clase de CC. Ambientales
fueron:
17
18
18
19
19
18
18
18
22
19
18
21
18
18
19
18
21
21
17
18
Ejemplo 2: Mucha gente manifiesta reacciones de alergia sistémica a las picaduras de
insectos. Estas reacciones varían de paciente a paciente, no sólo en cuanto a gravedad,
sino también en el tiempo transcurrido hasta que se inicia la reacción. Los datos
siguientes (en minutos) representan este “tiempo de inicio hasta la reacción” en 40
pacientes que experimentaron una reacción sistémica a la picadura de abeja:
10.5
12.7
3.8
9.1
13.6
11.2
11.4
10.5
13.4
14.7
9.9
11.6
11.7
12.3
11.5
15.0
6.2
8.4
5.9
11.5
11.4
7.9
12.5
11.4
10.9
12.7
8.3
11.2
8.8
9.8
16.5
10.9
9.1
7.4
12.9
10.1
8.1
10.4
8.6
9.9
Ejemplo 3: Considere las siguientes observaciones, correspondientes a las magnitudes
de distintos seismos en California según su medición en la escala de Richter:
1.0
6.3
4.1
8.3
1.4
5.0
3.1
1.3
2.2
1.1
3.3
1.2
5.1
2.2
7.7
1.2
2.3
1.5
1.0
2.1
4.1
2.1
1.1
1.4
4.0
2.7
2.0
2.4
1.9
3.0
Ejemplo 4: Los incendios de vegetación en pradera, matorral y bosque son un
fenómeno común. Algunos son accidentales, pero otros son provocados con el fin de
crear hábitats post-fuego que beneficien a plantas y animales. No obstante, el suelo que
ha sido expuesto a un alto calentamiento puede esterilizarse. Se realizó un estudio para
determinar el efecto de esta esterilización en el crecimiento de plantas, en concreto
rábanos. La variable medida fue el peso seco de la planta al cabo de 4 semanas (basado
en un estudio de Joy Burcham, Departamento de Biología, Universidad de Radford,
otoño de 1996).
Suelo estéril (peso seco en gramos):
Suelo no estéril
9
17
30
9
16
2
6
20
28
10
11
15
26
28
25
10
10
35
18
30
34
19
7
3
13
11
18
15
6
14
14
9
11
Ejemplo 5: En una investigación sobre deficiencias medioambientales encontradas en
plantas industriales, se seleccionaron aleatoriamente 25 plantas de dos comunidades
diferentes. Se obtuvieron los siguientes datos sobre el número de deficiencias
encontradas:
Nº deficiencias com. A Frecuencia
1
1
2
3
3
5
4
7
5
5
6
3
7
1
Nº deficiencias com. B Frecuencia
1
6
2
4
3
2
4
1
5
2
6
4
7
6
Algunas observaciones teóricas:
1.- Número de clases sugerido para subdividir datos numéricos en función del
tamaño de la muestra (“Estadística para Biología y Ciencias de la Salud”, Susan
Milton, pág. 22)
Tamaño de la muestra
Menos de 16
16-31
32-63
64-127
128-255
256-511
512-1023
1024-2047
2048-4095
4096-8190
Número de clases
Datos insuficientes
5
6
7
8
9
10
11
12
13
2.- Procedimientos habituales para agrupar datos en clases.
1.- El nº de clases se puede aproximar como k  1 3.322log10 n , donde n es el tamaño
de la muestra; k se redondea hacia abajo, p. ej. 6.82 a 6.
2.- Localizamos el mayor y menor dato, respectivamente. Diferencia entre ambos:
RANGO de los datos.
3.- Amplitud mínima de clase: cociente entre el rango y el nº de clases.
- Redondeamos por arriba el nº obtenido hasta la precisión de los datos; si el
cociente tiene ya esa precisión, la incrementamos en una unidad.
- El extremo inferior de la primera clase es el menor de los datos, disminuido en
0.5 si los datos son enteros, en 0.05 si tienen 1 decimal, en 0.005 si tienen 2
decimales…
(Así ningún dato coincide con un extremo de un intervalo)
4.- Si hay datos atípicos (outliers), la técnica se modifica (S. Milton, p. 25)
3.- Construcción de un diagrama de tallo y hojas simple (“Estadística para Biología
y Ciencias de la Salud”, Susan Milton, pág. 14)
a.- Elija algunos números oportunos que puedan servir de tallos. Se necesitan al menos
5 tallos. Los tallos elegidos generalmente son el primero o los dos primeros dígitos de
los números del conjunto de datos.
b.- Etiquete las filas con los tallos elegidos.
c.- Reproduzca gráficamente los datos anotando el dígito que sigue al tallo, como hoja
del tallo adecuado.
d.- Si los datos son muy similares, de modo que resulta difícil elegir 5 tallos distintos, se
pueden utilizar tallos “dobles” (por ejemplo, 33 y 33, de modo que en el primero se
consignen desde 33.0 hasta 33.4, y en el segundo desde 33.5 hasta 33.9), “triples”, etc.
e.- Para comparar grupos de datos, se pueden utilizar diagramas de tallo y hojas
“dobles” (un mismo tallo, distintas hojas).
(Ampliar en páginas 15, 16, 17 de S. Milton)
EJEMPLO FINAL: Se midieron los niveles de ozono en una zona boscosa
cerca de Seattle, Washington. Los datos recogidos fueron los siguientes:
160
165
170
172
161
176
163
196
162
160
162
185
167
180
168
163
161
167
173
162
169
164
179
163
178
a) Calcula la media, la mediana, la desviación típica, y los cuartiles.
b) Dibuja el diagrama de caja.
c) En otra zona, la media es de 169’12 y la desviación típica de 19’05. ¿En cuál de
las dos zonas es mayor la variabilidad? ¿Resulta fiable en esta segunda zona una
previsión de nivel de ozono en torno a 169?
d) En una ciudad próxima a la zona de estudio, el nivel de ozono medio registrado
fue de 220, con una desviación típica de 12’32. ¿Podemos decir que en la ciudad
la variabilidad es mayor que en la zona boscosa de estudio?
e) ¿Hay algún dato atípico? ¿Qué deberíamos hacer con él? ¿A qué parámetro de
centralización afecta más?