Laboratorio6REV1MyMGuia03

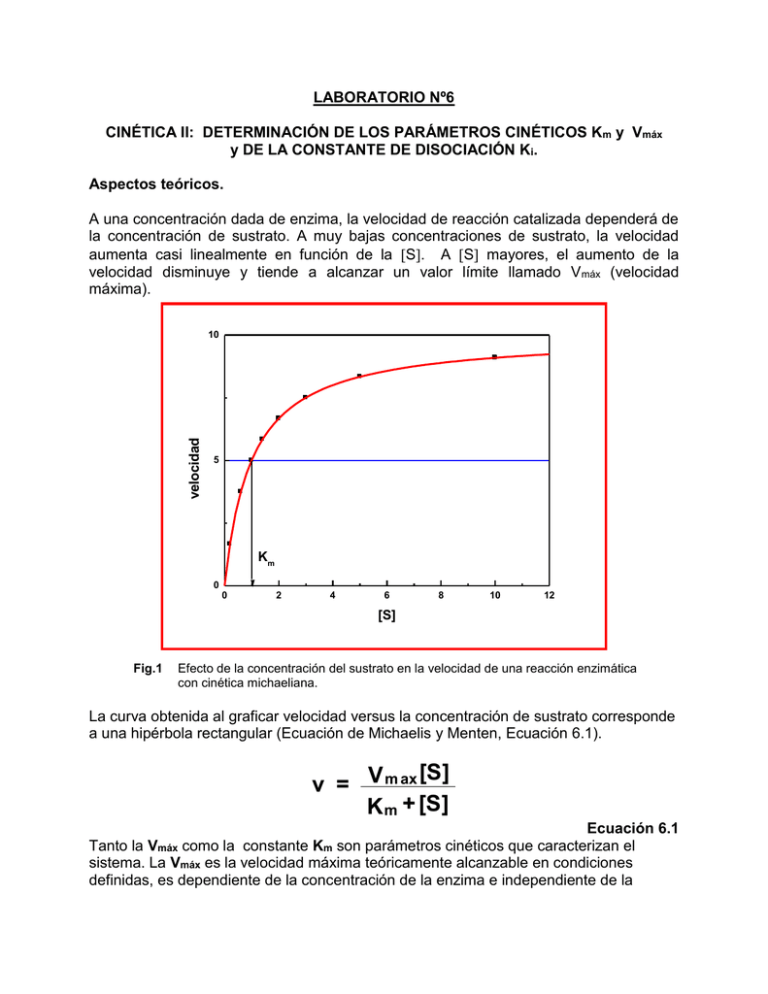
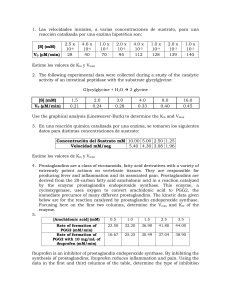
LABORATORIO Nº6
CINÉTICA II: DETERMINACIÓN DE LOS PARÁMETROS CINÉTICOS Km y Vmáx
y DE LA CONSTANTE DE DISOCIACIÓN Ki.
Aspectos teóricos.
A una concentración dada de enzima, la velocidad de reacción catalizada dependerá de
la concentración de sustrato. A muy bajas concentraciones de sustrato, la velocidad
aumenta casi linealmente en función de la S. A S mayores, el aumento de la
velocidad disminuye y tiende a alcanzar un valor límite llamado V máx (velocidad
máxima).
velocidad
10
5
Km
0
0
2
4
6
8
10
12
[S]
Fig.1
Efecto de la concentración del sustrato en la velocidad de una reacción enzimática
con cinética michaeliana.
La curva obtenida al graficar velocidad versus la concentración de sustrato corresponde
a una hipérbola rectangular (Ecuación de Michaelis y Menten, Ecuación 6.1).
[S]
v = V m ax
K m + [S]
Ecuación 6.1
Tanto la Vmáx como la constante Km son parámetros cinéticos que caracterizan el
sistema. La Vmáx es la velocidad máxima teóricamente alcanzable en condiciones
definidas, es dependiente de la concentración de la enzima e independiente de la
concentración del sustrato, sus unidades son las de velocidad. La Km se conoce como
constante de Michaelis y Menten, es numéricamente igual a la concentración de
sustrato que da una velocidad igual a la mitad de la Vmax, es independiente de la
concentración de enzima, sus unidades son de concentración.
Condiciones que deben cumplirse para que en una reacción con cinética
michaeliana los datos experimentales se ajusten a esta ecuación:

Velocidad inicial (vo)
tiempo  0
tiempo  0

[E] <<< [S]
Curva progreso de la reacción enzimática.
10
8
[P]
6
[S]O = 1 KM
vo
4
2
0
0
100
200
300
400
500
600
tiempo
Fig.2
Típica curva progreso de una reacción enzimática. En este caso la disminución de la
concentración de sustrato en el tiempo explica la disminución de la pendiente de la curva
(velocidad). En la zona donde la pendiente tiende a cero se ha alcanzado el equilibrio.
La velocidad de una reacción enzimática disminuye en el tiempo. Esta disminución se
debe a varios factores dependientes del tiempo de la reacción; como la disminución de la
concentración del sustrato a medida que éste se transforma, el aumento de la
concentración del producto que puede traducirse en una mayor inhibición de la reacción
directa, como también en una mayor velocidad de la reacción inversa. Además la posible
inactivación de la enzima aumenta con el tiempo de ensayo. Se han obtenido ecuaciones
integradas que dan cuenta de la disminución de la concentración del sustrato y del
aumento de la inhibición por producto en el tiempo, sin embargo, no hay ecuaciones que
consideren todos los factores que pueden estar involucrados.
30
Por ello, normalmente se mide la velocidad inicial de la reacción a partir de la tangente
obtenida a tiempos cortos en la curva progreso de la reacción enzimática (concentración
de producto (o de sustrato) versus tiempo de reacción).
Experimentalmente, se mide la velocidad inicial a diferentes concentraciones de
sustrato. El rango adecuado de concentración de sustrato a utilizar es de 0,2 Km  3,0
Km.
La ecuación de Michaelis y Menten puede ser linealizada, con la ventaja que Vmáx y Km
pueden determinarse fácilmente por regresión lineal utilizando una calculadora.
Si un sistema enzimático sigue una cinética tipo Michaeliana, las transformaciones
lineales dan origen a rectas del tipo y = mx + b.
Ecuación de Lineweaver y Burk.
1
v
Km
Vmax

1
1

S
Vmax
Ecuación 6.2
0,6
0,4
1/v
1.
0,2
0,0
-1
0
1
2
3
4
5
1/[S]
Fig. 3 Gráfica de Lineweaver y Burk para una reacción que sigue la cinética michaeliana.
La pendiente es igual a Km/Vmax y el intercepto en el eje x es –1/Km.
31
Ecuación de Hanes – Woolf.
S
v

Km
Vmax
S

Vmax
Ecuación 6.3
1,2
1,0
Vmax= 1/pendiente
0,8
[S]/v
2.
0,6
0,4
0,2
0,0
-2
0
-Km
2
4
6
8
10
[S]
Fig. 4 Gráfica de Hanes y Woolf para una reacción que sigue la cinética michaeliana.
La pendiente es igual a 1/Vmax y el intercepto en el eje x es – Km.
32