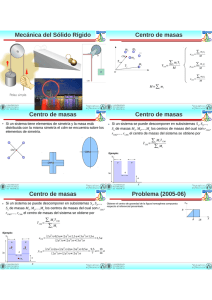
El movimiento de rodadura

El movimiento de rodadura
Consideremos el movimiento de los objetos que ruedan tales como una rueda de
bicicleta o una pelota. Cuando ruedan sin deslizamiento hay una relación sencilla entre
la velocidad lineal del centro de masas y la velocidad angular con respecto a un eje que
pasa por su centro de masas.
VCM= ω R
Donde ω es la velocidad angular y R el radio del objeto rodante
De la misma forma la velocidad de un punto de la periferia se puede expresar, en el
movimiento de rodadura como:
V= ω R
Donde ω es de nuevo la velocidad angular y R el radio del objeto rodante.
Por tanto la velocidad de una partícula del objeto rodante puede considerarse
como el resultado de una traslación pura más una rotación pura del objeto.
En consecuencia la expresión de la energía cinética de un objeto rodante se puede
expresar como la suna de dos términos, uno correspondiente a la rotación con
respecto a un eje que pasa por el centro de masas y otro correspondiente a la
traslación del centro de masas.
EC=
1
1
ICM ω2 + M VCM2
2
2
Observar la animación del movimiento de rodadura en plano horizontal y
responder a las siguientes preguntas:
1
a) En cada instante del movimiento la velocidad de un punto del objeto
rodante, en este caso una rueda de bicicleta, será la suma vectorial de
su velocidad con respecto al C.M. (flecha azul) y la velocidad del CM
(flecha verde). Dibuja la velocidad absoluta del punto situado en la
periferia en las siguientes situaciones:
 cuando se encuentra en la parte inferior
 cuando se encuentra en la parte superior
 cuando se encuentra en un punto intermedio
b) Suponiendo que la masa de los radios es despreciable frente a la llanta
y la cubierta de caucho y por tanto se puede asimilar a un aro de radio
R y masa M ¿Cuál es su momento de inercia con respecto al eje que
pasa por el C.M.?
c) ¿Cuál será el momento de inercia si consideramos la masa de cada
radio m? Para calcularlo parar la imagen y contar el número de radios
de la rueda
d) Si el movimiento es uniforme y recorre 1m, con ayuda de un
cronómetro calcula la velocidad del C.M.
2
e) Si la rueda no desliza (observa atentamente la animación) ¿Cuál será
su radio?
f) ¿Cuál será la velocidad angular?
g) ¿Cuál será su energía cinética? Si la masa de la rueda es de 1500 g.
h) Si el cuerpo rodante es un disco homogéneo ¿Cuál será su momento de
inercia en función de su masa y de su radio?
i) Si el disco no es uniforme ya que la densidad aumenta linealmente con
el radio de la forma ρ=κ.r donde r es la distancia al centro y κ es una
cte ¿Cuánto vale el nuevo momento de inercia en función de la masa y
el radio?
Si el cuerpo rodante esta sometido a fuerzas exteriores el movimiento no será
uniforme y tanto la velocidad del C.M. como la velocidad angular cambiaran
con el tiempo.
Si el cuerpo rueda sin deslizar hay una relación sencilla entre la aceleración del
C.M. y la aceleración angular con respecto al eje que pasa por el C.M.
aCM= α R
Donde α es la aceleración angular y R el radio.
Esta situación se produce cuando el objeto rodante rueda sin deslizar sobre un
plano inclinado. La componente tangencial del peso y la fuerza de rozamiento
estático que se produce en el punto de contacto, provocan la aceleración del
C.M. y por tanto el cambio en la velocidad del C.M. la fuerza de rozamiento
estática efectúa un momento sobre el C.M. que produce una aceleración
angular que cambia la velocidad angular. Si rueda sin deslizar se cumple la
relación anterior entre las aceleraciones.
La fuerza de rozamiento estática actúa siempre en el punto de contacto, se
trata de una fuerza instantánea (en cada instante actúa en un punto diferente)
en consecuencia no sufre deslizamiento y por tanto no realiza trabajo, al no
realizar trabajo se conserva la energía en la rodadura.
Como se trata de una fuerza de rozamiento estático su valor será:
Fr  μe N
Donde μe es el coeficiente de rozamiento estático y N la normal
Observar la animación del movimiento de rodadura en un plano inclinado,
identificar los vectores que representan fuerzas y velocidades y tener en cuenta
su dirección en cada fase del movimiento.
Observa cuidadosamente como la fuerza de rozamiento (de color rojo) actúa en
cada instante en un punto distinto, en cambio las otras fuerzas presentes se
encuentran aplicadas en el C.M.
3
Contestar a las siguientes preguntas:
1) Aplicando la conservación de la energía, obtener la expresión de la
velocidad del C.M. de la rueda después de descender en el plano
inclinado una “altura” h partiendo del reposo. Expresar el resultado en
función del momento de inercia I y la masa M.
2) Aplicando las leyes de la Dinámica obtener la expresión de la
aceleración del C.M en función del ángulo del plano inclinado β.
3) A partir de la aceleración, calcular la velocidad del C.M. y comprobar
que el resultado es el mismo que en el apartado 1.
4) Si el cuerpo rodante es una esfera maciza y homogénea de masa M y
radio R ¿Cuál es su velocidad? ¿Cuál es su aceleración?
5) Si se trata de una esfera hueca pero de la misma masa y radio ¿Cuál es
su velocidad? ¿Cuál es su aceleración?
6) Si es una lata vacía y sin tapas de la misma masa y radio ¿Cuál será su
velocidad? ¿Cuál es su aceleración?
7) Si es un yo-yo (dos conos unidos por el vértice) con la misma masa y
radio ¿Cuál es su velocidad? ¿Cuál es su aceleración?
4
8) Si se sueltan al mismo tiempo todos los objetos anteriores por el plano
inclinado ¿Quién llegara el primero a la base del plano? ¿Quién llegara
el último? Razonar la respuesta.
9) Si consideramos una esfera de 50 g de masa y 20 cm. de radio ¿Cuál
será el mínimo coeficiente de rozamiento estático compatible con la
rodadura si β =30º ; β= 45º, β=60º ¿Qué conclusiones puedes obtener
del resultado?
Resuelve un problema similar:
Se enrolla una cuerda a un cilindro macizo y homogéneo de masa M y radio R
y se cuelga como indica la figura y se suelta partiendo del reposo:
1º) ¿Qué fuerzas actúan sobre el
cilindro?
2º) ¿Cómo describirías el movimiento
del cilindro?
3º) Demuestra que la tensión de la
cuerda es un tercio del peso del
cilindro.
4º) Demuestra que la aceleración del
centro de masas es dos tercios de la
aceleración de la gravedad.
5º) Calcular la aceleración angular
6º) Después de que el cilindro haya
descendido una distancia h ¿Cuál es la
velocidad del centro de masas? ¿Y la
velocidad angular?
7º) Calcular lo mismo pero aplicando el
principio de conservación de la energía
8º) Al cabo de un cierto tiempo la
cuerda se ha desenrollado completamente, y el cilindro queda en libertad ¿Qué
fuerzas actúan ahora sobre el cilindro? ¿Cómo será su movimiento?
5