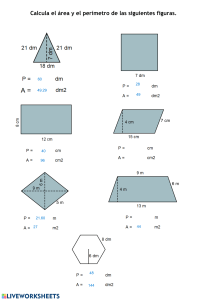
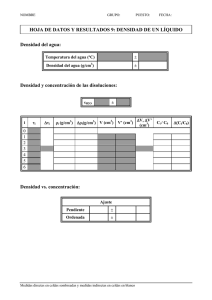
ALGORITMO PARA EL CALCULO DE AREAS Y VOLUMENES. GA2-240201528-AA4-EV01 Aprendiz: DIANA MABEL BERMÚDEZ JAIMES EDISSON ESTEBAN ALVARADO Instructora Área Matemáticas SERVICIO NACIONAL DE APRENDIZAJE (SENA) CENTRO DE MATERIALES Y ENSAYOS BOGOTÁ (DC) Tecnología en Análisis y Desarrollo de Software Ficha: 2977399 2024 – 2026 INTRODUCCION En esta actividad el cálculo de áreas y volúmenes desempeña un papel importante en la resolución de problemas geométricos. Un algoritmo para calcular áreas y volúmenes de formas geométricas combina principios matemáticos con técnicas computacionales. Dado que hay muchas figuras geométricas desde las básicas como círculos y cubos hasta estructuras mas avanzadas como prismas irregulares y solidos de revolución y estos algoritmos requieren una comprensión profunda de conceptos como el calculo integral, la trigonometría, y la geometría analítica. ÁREA Y VOLUMEN DE LAS FIGURAS GEOMÉTRICAS Triangulo: Área: A=b*h/2 Perímetro: P= a + b + c Cuadrado: Área: A= L*L = L2 Perímetro: P= L+L+L+L Rectangulo: Área: A=b*h Perímetro: P= b+b+h+h Circulo: Área: A = π*r2 Perímetro: P= 2*π*r Rombo: Área: A = d * D / 2 Perímetro: P= a+a+a+a Exagono: Área: A = Perímetro + apotema / 2 Perímetro: P= 6*L Cubo: Para sacar el volumen del cubo, multiplica la longitud de sus lados por si misma tres veces. Área: Para calcular el área de un cubo se multiplica el área de una cara por 6, ya que tiene 6 caras cuadradas Volumen: ancho * largo + alto V= a˄3 Pirámide: Área total: Se calcula sumando el área lateral y el área de la base. Volumen: Se calcula multiplicando el área de la base por la altura de la pirámide y dividiendo el resultado entre 3. Esfera: Podemos calcular el área superficial de una esfera al multiplicar por 4 al producto de pi y el cuadrado del radio de la esfera. Entonces, la fórmula del área superficial de una esfera está dada por: V=4* π*r˄2/3 Problema planteado Si tuviera un sólido irregular ¿Qué método utilizaría para calcular el volumen? Quiero saber el volumen de un tornillo: Para calcular el volumen de un tornillo utilizaría el método de Arquímedes el cual nos indica que todo cuerpo sumergido dentro de un fluido experimenta una fuerza ascendente llamada empuje, equivalente al peso del fluido desalojado por el cuerpo. 1. Utilizamos un recipiente y lo llenamos con 500 cm3 de agua. 2. Introducimos el tornillo en el recipiente y notamos que el agua sube a los 600 cm3. 3. La diferencia de la cantidad de agua desplazada es equivalente al volumen del tornillo. Volumen = cm3 de agua final – cm3 agua inicial V = 600 cm3 – 500 cm3 = 100 cm3 Volumen del tornillo es igual a 100 cm3 Ejemplo del Principio de Arquímedes: El volumen adicional en la segunda probeta corresponde al volumen desplazado por el sólido sumergido (que naturalmente coincide con el volumen del sólido). CONCLUSIONES En esta actividad se estudió sobre las áreas y perímetros de las figuras geométricas y se realizo un problema planteado por la actividad, nos queda claro el tema estudiado en el nivel avanzado de matemáticas y todos los conceptos sobre la competencia.