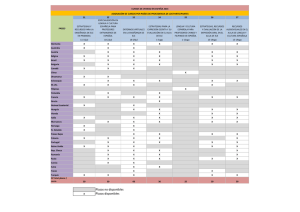
Universidad Nacional de Loja Facultad de la Energı́a, las Industrias y los Recursos Naturales no Renovables CARRERA DE ELECTRICIDAD CIRCUITOS ELÉCTRICOS II INFORME: Mejoramiento del Factor de Potencia con MATLAB DOCENTE: Ing. Diego Iñiguez ESTUDIANTES: Antuan Isaac Agurto Arciniegas Cristian David Alulima Garrido Marilin Alondra Vásquez Benalcázar GRUPO: Nro 3 FECHA: 3 de Julio del 2024 Índice general 1. 2. 3. 4. 5. 6. 7. Introducción . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 Marco Teórico . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 2.1. Potencias . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 2.2. Factor de Potencia . . . . . . . . . . . . . . . . . . . . . . . . . . . 4 2.3. MATLAB Simulink . . . . . . . . . . . . . . . . . . . . . . . . . . . 5 Planteamiento . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 Resultados . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7 Discusión . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9 Referencias Bibliográficas . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10 Anexos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 2 3 1. Introducción El factor de potencia (FP) es un indicador de la eficiencia con la que un sistema eléctrico utiliza la energı́a. La relación entre la potencia activa y la potencia aparente, que oscila entre 0 y 1, se conoce como potencia. Un FP bajo indica una alta presencia de potencia reactiva, lo que puede conducir a ineficiencia, pérdidas en la red y posibles sanciones económicas. Para maximizar el rendimiento de los sistemas eléctricos, se debe mejorar el factor de potencia. Para contrarrestar la potencia reactiva, se instalan condensadores y se utilizan sistemas de compensación automática. Estas mejoras pueden aumentar la capacidad del sistema, reducir las pérdidas de energı́a y reducir los costos operativos. 2. Marco Teórico 2.1. Potencias Figura 1: Relación de Potencias Recuperado de: https://n9.cl/2yy8a Potencia Activa La potencia activa, también conocida como potencia real o potencia verdadera, es la cantidad de energı́a que se consume en un circuito eléctrico para realizar un trabajo útil. Se mide en vatios (W) y representa la energı́a que se convierte en formas útiles como luz, calor, o trabajo mecánico.[1] La potencia activa se calcula utilizando la siguiente fórmula: P = V · I · cos(ϕ) (1) donde: P es la potencia activa en vatios (W), V es la tensión eficaz en voltios (V), I es la corriente eficaz en amperios (A), cos(ϕ) es el factor de potencia, que es el coseno del ángulo de fase (ϕ) entre la tensión y la corriente. 4 En un circuito puramente resistivo, la potencia activa es igual al producto de la tensión y la corriente, ya que el factor de potencia es 1 (cos(0) = 1). Sin embargo, en circuitos con componentes reactivos (inductores o capacitores), el ángulo de fase (ϕ) no es cero, y la potencia activa será menor que el producto de la tensión y la corriente debido a la presencia de potencia reactiva.[1] Potencia Reactiva La potencia reactiva es la cantidad de energı́a en un circuito eléctrico que alterna entre la fuente y los componentes reactivos del sistema (como inductores y capacitores) sin realizar un trabajo útil neto. Se calcula utilizando voltio-amperios reactivos (VAR). Aunque no se transforma en trabajo, esta energı́a es necesaria para el funcionamiento de dispositivos como motores y transformadores. La potencia reactiva es la parte de la potencia aparente que no hace trabajo efectivo en el sistema y es responsable de crear los campos magnéticos y eléctricos necesarios para que los componentes inductivos y capacitivos funcionen.[2] Potencia Aparente La potencia aparente es la combinación vectorial de la potencia activa y la potencia reactiva en un circuito de corriente alterna (AC). Se mide en voltio-amperios (VA) y representa la carga total que el sistema eléctrico debe soportar. La potencia aparente se calcula como el producto de la tensión eficaz (rms) y la corriente eficaz (rms) en el circuito.[3] La relación entre la potencia aparente (S), la potencia activa (P ) y la potencia reactiva (Q) se puede expresar mediante el triángulo de potencias: S 2 = P 2 + Q2 (2) donde: S es la potencia aparente en voltio-amperios (VA), P es la potencia activa en vatios (W), Q es la potencia reactiva en voltio-amperios reactivos (VAR). Esta relación muestra que la potencia aparente es la hipotenusa del triángulo formado por la potencia activa y la potencia reactiva. 2.2. Factor de Potencia Figura 2: Triangulo se Potencias Recuperado de: https://n9.cl/6if0dc 5 El factor de potencia es una medida de la eficiencia con la que se utiliza la potencia aparente en un sistema eléctrico. Se define como la relación entre la potencia activa (P ) y la potencia aparente (S) y se expresa como un número adimensional entre 0 y 1 o como un porcentaje. Un factor de potencia de 1 (o 100 %) indica que toda la potencia aparente se está utilizando eficazmente como potencia activa, mientras que un factor de potencia menor indica la presencia de potencia reactiva en el sistema.[1] Matemáticamente, el factor de potencia se puede expresar como: FP = P = cos(ϕ) S (3) donde: FP es el factor de potencia, P es la potencia activa en vatios (W), S es la potencia aparente en voltio-amperios (VA), ϕ es el ángulo de fase entre la tensión y la corriente. Un factor de potencia bajo significa que se está utilizando más corriente para la misma cantidad de potencia útil, lo cual puede resultar en mayores pérdidas en los conductores y transformadores, y puede llevar a mayores costos operativos y tarifas de energı́a. 2.3. MATLAB Simulink MATLAB MATLAB es un entorno de programación y un lenguaje especializado en cálculo numérico, análisis de datos y visualización. Desarrollado por MathWorks, es ampliamente utilizado en ingenierı́a, ciencias de la computación y otras disciplinas técnicas para el desarrollo de algoritmos, modelado y simulación. Ofrece capacidades avanzadas para el manejo de matrices, visualización de datos y una interfaz interactiva para resolver problemas matemáticos y técnicos.[4] Simulink MathWorks también desarrolló Simulalink, una plataforma de simulación basada en modelos. Se utiliza para modelar, simular y analizar sistemas dinámicos de múltiples dominios, como sistemas de control, eléctricos, mecánicos e hidráulicos. La interfaz gráfica proporcionada por Simulación facilita la representación y simulación de sistemas complejos al permitir la creación de modelos mediante bloques de funciones predefinidos. Para la simulación de procesos en tiempo real y el diseño y verificación de sistemas de control, es particularmente útil.[4] 6 Figura 3: Logo de MATLAB Simulink Recuperado de: https://recluit.com/que-es-matlab/ 3. Planteamiento Figura 4: Diagrama Esquemático del Experimento de Mejoramiento de Factor de Potencia Recuperado de: (espol,2022) 1. Determine teóricamente el valor del capacitor (C1) de tal manera que el factor de potencia sea igual a 0,95. 2. Coloque el capacitor (C1) en paralelo a la fuente variable de voltaje AC, y realice lo siguiente: a. Conecte el vatı́metro digital, mida la potencia activa (PR1 ) que consume el resistor R1 y repórtelo en la Tabla 1. 7 b. Realice los cálculos teóricos necesarios para completar la Tabla 1 y que validen los resultados simulados c. Realice el triángulo de potencia del circuito RL-serie propuesto con los datos de la Tabla 1 4. Resultados Figura 5: Circuito Completo Esquematizado en Simulink Elaborado por: Agurto, A., Alulima, C., & Vasquez, M. (2024) 8 Figura 6: Subsistema de Medición I Esquematizado en Simulink Elaborado por: Agurto, A., Alulima, C., & Vasquez, M. (2024) Figura 7: Subsistema de Medición II Esquematizado en Simulink Elaborado por: Agurto, A., Alulima, C., & Vasquez, M. (2024) 9 5. Discusión En la Figura 4 se presenta un circuito básico que consta de una resistencia y una inductancia en serie. La configuración inicial de este circuito genera un factor de potencia que necesita ser corregido para mejorar la eficiencia del sistema. Para lograr esta corrección, se ha añadido un capacitor en paralelo al circuito. Al agregar un capacitor se tiene como objetivo principal compensar el desfase entre el voltaje y la corriente, reduciendo ası́ el componente reactivo de la potencia y mejorar el factor de potencia. Sin embargo, cuando se introduce únicamente el capacitor, se puede observar que las mediciones iniciales de corriente pueden resultar en valores nulos, lo que es incoherente con el comportamiento esperado del circuito. Para solucionar este problema, se coloco una resistencia denominada como RShunt en serie con el capacitor como se muestra en la Figura 5. La resistencia RShunt, aunque sea de un valor realmente pequeño, es crucial para estabilizar las mediciones iniciales. Su presencia permite que haya una pequeña corriente de fuga inicial que facilita la correcta medición y evita los resultados incoherentes que se obtendrı́an si solo estuviera presente el capacitor. En la Figura 6, también se muestra un subsistema diseñado para realizar mediciones detalladas del circuito. Este subsistema es capaz de medir la potencia activa (P), la potencia reactiva (Q), la potencia aparente (S), ası́ como la fase entre el voltaje y la corriente. Además, calcula el factor de potencia, que es una medida de la eficiencia con la que se utiliza la energı́a eléctrica en el circuito. En resumen, la inclusión del capacitor junto con la resistencia RShunt permite una corrección efectiva del factor de potencia y asegura la coherencia de las mediciones iniciales. El subsistema de medición proporciona una evaluación completa de los parámetros eléctricos del circuito, lo que es indispensable para el análisis y la optimización del desempeño del sistema. 10 6. Referencias Bibliográficas Referencias 1. BARRERO GONZALEZ, FERMIN. Sistemas de energı́a eléctrica. Ediciones Paraninfo, SA, 2004. 2. GRAINGER, Jonh y STEVENSON, W. Análisis de sistemas de potencia. De. 1997, vol. 15. 3. CAMPOMANES, José Gómez. Circuitos eléctricos. Vol. 2. Universidad de Oviedo, 1990. 4. MOORE, H. MATLAB for Engineers. Pearson, 2018. isbn 9780134589640. Disponible también desde: https://books.google.com.ec/books?id=tyk9vgAACAAJ. 11 7. Anexos 12