diseno y calculo estructural de una casa

INSTITUTOTECNOLÓGICO DELA
CONSTRUCCIÓN
cmic
<S
ESTUDIOS CON RECONOCIMIENTO DE VALIDEZ OFICIAL DE LA SECRETARIA DE
EDUCACIÓN PUBLICA CONFORME AL ACUERDO No. 952359 DE FECHA 15 DE
NOVIEMBRE DE 1995
DISEÑO Y CÁLCULO ESTRUCTURAL DE UNA CASA-HABITACIÓN,
UBICADA EN LA CALLE VICENTE VILLADA No. 77. COL. AHUIZOTLA.
NAUCALPAN DE JUÁREZ, EDO. DE MEX.
T
E
S
PARA
OBTENER
I
EL
S
TITULO
DE :
INGENIERO CONSTRUCTOR
P
R
E
S
E
N
T
A
VÍCTOR ENRIQUE SEGURA TORRES
(TITULACIÓN POR TESIS)
ING. ALFONSO D'ABBWRTT PANTOJA
ASESOR
04 DEAGOSTO DE2003
A mis padres, por el apoyo que me han brindado en el transcurso de mi
vida y especialmente durante mi camino en mi carreraprofesional. Gracias.
A mi esposa Raquel, con todo mi amor y agradecimiento quiero dedicar
este logroa ti y a nuestra querida e inteligente hija Edith, porque gracias a
ustedes he logrado uno de mis más grandes anhelos. Asimismo quiero
desearles que logren culminar sus metas académicas más anheladas y
cuando esos momentos lleguen a nuestras indas los compartamos juntos con
la bendición de dios.
A mi hermana Viridiana con el deseo de que este logro sea una
inspiración para ti y logres ser una persona productiva para nuestra familia
ypara la sociedad.
A mi primo el Ing. Rafael Baca Torres, por ser el ejemplo de la familia,
inspirándome a estudiar una carrera de ingeniería.
Al Instituto Tecnológico de la Construcción que me dio la oportunidad
de ser alguien en la vida, les doy mi más profundo agradecimiento a todos y
cada uno de los que conforman a ese Instituto. Gracias.
IV
Al Ing. Alfonso D'abbwrtt Pantoja por ser mi asesor y apoyarme en la
correcta elaboración delpresente trabajo. Gracias.
Al Capitán l/o. Ing. Ind. Ignacio Berna! Tapia, mi más sincero y
profundo agradecimiento por su apoyo incondicional, por las experiencias
adquiridas, por los conocimientos brindados y por fomentarme el sentimiento
de la superación durante mi estancia en la Unidad de Ingeniería y
Mantenimiento Eléctrico de la Dirección General de Fábricas de la Defensa
Nacional. De todo corazón. Gracias.
Al Teniente A.M.G. José Alberto Reyes Sánchez por las todas las pautas
brindadas y experiencias laborables que pasamos en la U.I.M.E.
A mi tía Gloria, por el gran apoyo que recibíde Usted durante mi
adolescencia. Gracias.
V
TESIS PROFESIONAL
índice
Registro de tesis
Oficio de terminación de tesis
Reconocimiento y dedicatorias
Índice de tablas, figuras y planos
Introducción
II
III
IV
VI
1
Capitulo 3
Materiales de construcción
3.1.
Capitulo 1
El diseño estructural
1.1.
1.2.
1.3.
1.4.
Objetivos del diseño estructural
Proceso del diseño estructural
Criterios de diseño estructural
1.3.1. Seguridad estructural
1.3.2. Criterio reglamentario de diseño
estructural
Reglamentos de diseño
3.2.
2
2
4
4
6
7
Capitulo 2
Acciones
2.1.
2.2.
2.3.
Clasificación de las acciones
9
Combinación de acciones
10
Determinación de las acciones
12
2.3.1. Cargas permanentes (cargas
muertas)
12
2.3.2. Cargas variables (cargas vivas).... 14
2.3.3. Cargas accidentales
17
3.3.
3.4.
Mampostería
3.1.1. Piedras naturales
3.1.2. Piedras artificiales
3.1.3. Tabiques
3.1.4. Pruebas de mampostería
Concreto simple
3.2.1. Cemento
3.2.2. Mezclas
3.2.3. Pruebas en el concreto
3.2.4. Aditivos para concreto
Acero de refuerzo
Concreto reforzado
18
20
22
24
26
30
30
33
35
36
37
41
Capitulo 4
Diseño estructural de
elementos de casa habitación
4.1.
4.2.
4.3.
Estructuración
42
Transmisión y bajada de cargas
45
Diseño de la cimentación
49
4.3.1. Cimientos de concreto reforzado.. 51
4.3.2.1. Zapatas corridas de concreto
reforzado
51
4.3.2.2. Zapatas aisladas de concreto
reforzado
53
TESIS PROFESIONAL
4.4.
4.5.
4.6.
5.2.4.4. Bajada
de
cargas
transmitidas por muros de
carga y concentraciones
108
5.2.5. Diseño de cimentación
113
5.2.5.1. Diseño dezapata corridade
concreto reforzado
113
5.2.5.2. Diseño dezapata aisladade
concreto reforzado
126
5.2.6. Revisión de muros
136
5.2.6.1. Verificación de muros a
cargas verticales
136
5.2.6.2. Verificación de muros a
cargas horizontales (sismo).... 137
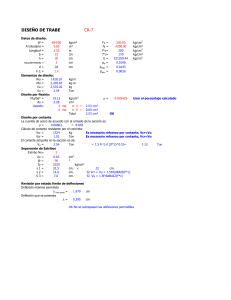
5.2.7. Diseño de trabes
142
5.2.7.1. Diseño de trabes de azotea.... 142
5.2.7.2. Diseño
de trabes de
entrepiso
155
5.2.8. Diseño de losas
170
5.2.8.1. Diseño de losas de azotea
170
5.2.8.2. Diseño de losas de entrepiso.. 186
Diseño y revisión de muros
55
4.4.1. Muros sujetos acargas verticales 55
4.4.2. Muros
sujetos
a
cargas
horizontales
57
4.4.2.1. Clasificación
de
las
estructuras
58
4.4.2.2. Zonificación del Distrito
Federal
58
4.4.2.3. Método
simplificado de
análisis del RCDF
61
Diseño de trabes de concreto reforzado
66
Diseño de losas de concreto reforzado
70
4.6.1. Losas macizas perimetralmente
apoyadas
70
Capitulo 5
Proyecto de aplicación de cálculo
estructural
para
una casahabitación, ubicada en la Calle
Vicente Villada No. 77. Col.
Ahulzotla. Naucalpan de Juárez,
Edo. de Méx.
5.1.
5.2.
Descripción de la obra
76
Desarrollo del proyecto
78
5.2.1. Proyecto arquitectónico
78
5.2.2. Proyecto estructural
78
5.2.3. Análisis de cargas unitarias
85
5.2.3.1. Losa de azotea
85
5.2.3.2. Losa de entrepiso
89
5.2.4. Transmisión y bajada de cargas.. 95
5.2.4.1. Transmisión de cargas a
perímetro de tableros de losa
de azotea
95
5.2.4.2. Transmisión de cargas a
perímetro de tableros de losa
de entrepiso
100
5.2.4.3. Cálculo de reacciones de
trabes
105
Proyecto arquitectónico
Proyecto de cimentación
Proyecto estructural
199
: 200
201
Conclusiones
202
Bibliografía
204
Glosario de términos
205
TESIS PROFESIONAL
, figuras y
índice de
planas
Tablas
Figuras
2.1.
2.1.
2.2.
2.3.
2.2.
3.1.
3.2.
3.3.
3.4.
3.5.
3.6.
3.7.
4.1.
4.2.
Tabla de pesos volumétricos de algunos materiales,
según el RCDF
13
Cargas unitarias, en kg/m 2
16
Propiedades de algunas piedras naturales
21
Resistencia a la compresión y cortante de piedras
naturales
21
Resistencia a lacompresión y velocidad de fraguado
de los morteros
23
Proporcionamiento de morteros
24
Resistencia de diseño a compresión de la
manipostería f*m para algunos tipos de piezas sobre
área bruta
28
Esfuerzo cortante resistente de diseño v* para
algunos tipos de manipostería sobre área bruta
29
Diámetro, peso y área de varillas
40
Coeficientes sísmicos reducidos por ductilidad para el
método simplificado (Estructuras grupo B)
62
Cuantías máximas y mínimas reglamentarias
68
Primera combinación de acciones
11
Segunda combinación de acciones
11
Distribución de ocurrencia de eventos sísmicos en el
tiempo
17
3.1. Prueba de compresión de las piezas de mampostería.. 26
3.2. Ensaye acompresión de muretes
27
3.3. Obtención de esfuerzo resistente v*.
28
3.4. Resistencia contra tipo de vibrado
34
4.1. Nomenclatura para el proyecto estructural
43
4.2. Colocación de trabe de azotea que refleja lade
entrepiso
44
4.3 Áreas tributarias y transmisión decarga en tableros
rectangulares con carga perimetral
45
4.4. Carga por metro lineal en base de muros
46
4.5. Bajada de cargas sobre cimentación
47
4.6. Diversos casos de transmisión deconcentración en
muros
49
4.7. Zapata aislada
50
4.8. Distribución de aceleraciones sísmicas en una
construcción
63
4.9. Flexión en vigas de concreto reforzado
66
4.10. Disposición de dobleces en losas
74
VI
TESIS PROFESIONAL
Planos
T-l
T-2
T-3
T-4
T-5
T-6
T-7
T-8
T-9
T-10
T-11
T-12
T-13
T-14
T-15
T-16
T-17
T-18
T-19
T-20
T-21
T-22
T-23
T-24
T-25
T-26
T-27
T-28
T-29
Planta baja
Planta alta
Planta de azotea
Fachada principal
Estructuración de losa de azotea
Estructuración de losa de entrepiso
Pendiente de azotea
Cargas lineales en losa de azotea
Cargas lineales en losa de entrepiso
Magnitud de concentraciones en losa de azotea
Magnitud de concentraciones en losa de entrepiso
Transmisión de cargas de eje 1, tramo B-F
Transmisión de cargas de eje 2, tramo B-F
Transmisión de cargas de eje 3, tramo B-D
Transmisión de cargas de eje C, tramo 1-3
Planta de cimentación
Cortes de zapatas corridas
Cortes de zapatas aisladas
Estimación de peso de planta baja
Estimación de peso de planta alta
Trabes de azotea B(l-3), D(l-3) y E(l-2)
Trabes de azotea F(l-2) y 2(D-F)
Trabes de entrepiso B(1-3), D(1-3) y E(1-2)
Trabes de entrepiso F(l-2) y 2(D-F)
Diseño de losas de azotea
Diseño de losas de entrepiso
Proyecto arquitectónico
Proyecto de cimentación
Proyecto estructural
79
80
81
82
83
84
88
99
104
106
107
109
110
111
112
133
134
135
138
139
153
154
168
169
185
198
199
200
201
VII
TESIS PROFESIONAL
Introducción
El objetivo de este trabajo es demostrar que mediante procedimientos de cálculo racionalmente sencillos, podemos lograr cuando
menos disminuir los factores de riesgo involucrados y, de reducir el costo de la obra. Asimismo se busca también, que sea un documento
de apoyo en el área de estructuras para estudiantes del Instituto Tecnológico de la Construcción.
Con el fin de cumplir con las expectativas del presente trabajo, se estudiarán una serie de objetivos específicos que a la postre nos
lleve a un entendimiento claro y conciso de los temas aquí a tratar. Siendo estos objetivos los siguientes:
a).
Se definirán los objetivos, proceso, criterios y reglamentos del diseño estructural.
b).
Se conocerán las características mecánicas de los diferentes materiales a emplearse, como es la manipostería,
concreto y acero de refuerzo principalmente.
c).
Se clasificarán los diferentes tipos de acciones que afectan a la construcción en sí, las cuales deberán de tomarse en
consideración para el diseño.
d).
Se estudiará el proceso para el diseño estructural de una casa-habitación.
e).
Se aplicarán los conceptos estudiados en un problema real de un diseño estructural para una casa-habitación,
ubicada en la Calle Vicente Villada No. 77. Col. Ahuizotla. Naucalpan de Juárez. Edo. de Méx.
Finalmente se dan a conocer las conclusiones del trabajo, en las que se resaltan algunos aspectos técnicos de los capítulos aquí
tratados.
1
TESIS PROFESIONAL
Eldiseño estructura/
1.1.
O B J E T I V O S D E LD I S E Ñ O E S T R U C T U R A L
Podemos definir aldiseño estructural como unconjunto deactividades a desarrollar para determinar las características físicas
de una estructura, detal manera que nos permita garantizar laabsorción de las cargas a las que ésta va estar sujeta en las diferentes
etapas de vida útil, sin sufrir daño alguno; es decir, la función adecuada de una estructura en condiciones de servicio.
A unaobra determinada la debemos concebir como un sistema global, elcual, a su vez, está integrado porun conjunto de
subsistemas que se deben combinar en forma precisa para cumplir con la función a la que fueron destinados.
Todos estos subsistemas deben interactuar detalmanera que eneldiseño tomen encuenta larelación existente entre ellosy
así, poder lograr elobjetivo final del diseño estructural, elcual es: producir estructuras que den unmejor rendimiento, esdecir, que
sean seguras y económicas.
Usualmente, elencargado deeste diseño trabaja tratando desatisfacer elproyecto arquitectónico y muchas veces notomaen
cuenta los diferentes subsistemas (como instalaciones, acabados, etc.), loque lleva alapostre a corregir sobre lamarcha los diseños,
provocado incluso alteraciones importantes en las especificaciones; por lo tanto, es necesario que el proyectista conozca con
profundidad sutrabajo ytome en cuenta, en sus diseños, todo locorrespondiente para hacerlos correctamente.
1.2.
P R O C E S O D E LD I S E Ñ O E S T R U C T U R A L
1.-
Estructuración.
2 . - Análisis.
A.
B.
C.
Modelación.
Determinación de las acciones de diseño.
Obtención de los elementos mecánicos1de diseño.
3.-
Dimensionamiento.
2
TESIS PROFESIONAL
1.-
E s t r u c t u r a c i ó n .En esta fase del diseño se seleccionan los materiales que compondrán la estructura para poder conocer el peso de
la misma y sus resistencias, así como la forma general de ésta, es decir, el tipo de estructura que en particular esa obra
requiere o debe tener. En esta etapa se necesita que el proyectista tenga un grado de experiencia y conocimientos de la
teoría estructural, ya que es necesario realizar el llamado predimensionamiento
de los elementos que compondrán
la estructura.
2.-
Análisis.Dentro de la actividad se tendrá que determinar la respuesta de la estructura ante las diferentes acciones a las
cuales será sometida y, para realizar esta etapa, será necesario considerar lo siguiente:
A.
Modelar la estructura.- Aquí se idealizará la estructura por medio de un modelo teórico factible de
ser analizado mediante los procedimientos y métodos conocidos de análisis estructural. Para ello
es necesario establecer las propiedades de los materiales y características geométricas de las
secciones. Podemos mencionar también algunos modelos clásicos, los cuales se emplean en la
modelación de estructuras como puentes, edificios, etc. Ejemplos de estos modelos son: vigas,
columnas, losas, armaduras, cables, etc., los cuales combinados, forman marcos, vigas continuas,
etc.
B.
Determinación de las acciones de diseño.- En esta parte del análisis se determinan las acciones
que obrarán en la estructura y, para ello, será necesario conocer los sistemas constructivos, la
ubicación de la estructura y, en general, toda la información que ayude a la determinación de las
solicitaciones que puedan, eventual o permanentemente, actuar sobre la estructura, ya que de esta
manera podemos obtener el mayor grado de aproximación en la valuación de las acciones. Es obvio
que tendremos que recurrir a los códigos y reglamentos existentes en el medio.
C.
Determinación de los elementos mecánicos de diseño.- Aquí se aplican los diferentes
procedimientos y métodos de cálculo para la obtención de las fuerzas internas, o elementos
mecánicos, tales como las fuerzas axiales, los cortantes, los momentos flexionantes y de torsión a
los que van a estar sometidos los diferentes componentes de la estructura (muros, vigas,
columnas, etc.). Cabe hacer una aclaración; al aplicar los métodos de cálculo, se obtendrán
resultados exactos, pero sólo para el modelo teórico elegido, no así para la estructura real; de ahí la
importancia de evaluar adecuadamente las acciones y el modelo que la estructura en cuestión
tendrá.
3
TESIS PROFESIONAL
3.-
Dimensionamiento.En esta etapa se obtienen las dimensiones correspondientes al detallar los elementos estructurales
conforman la estructura, además de verificar si ésta cumple con los requisitos de seguridad establecidos.
que
Estos resultados se vacían en los planos constructivos definiendo en ellos las especificaciones correspondientes.
Es importante resaltar la necesidad de transmitir adecuadamente a los constructores la información de los resultados
obtenidos, en forma clara, precisa y sencilla; es decir, los planos deberán contener toda la información procurando que
ésta sea lo más detallada posible sin olvidar nada, de tal forma que se pueda entender y la obra pueda desarrollarse
según el criterio con el cual se desarrollo el proyecto.
Una vez que el proyecto está terminado, el siguiente paso es la construcción del mismo, pero en esta fase se tendrá especial
cuidado con un aspecto que es fundamental para lograr la calidad de la obra esperada. Este aspecto es la supervisión, ya que ésta
será responsable de la buena ejecución de los trabajos a desarrollar al vigilar y controlar que se cumplan todas las especificaciones y
normas que del proyecto resultaron. Es común que en esta última etapa existan descuidos, por lo que debemos ser extremadamente
escrupulosos en la verificación del cumplimiento del proyecto en lo tocante a la calidad de los materiales y la propia obra.
Una etapa final es la puesta en servicio, ya que es la culminación de los objetivos que inicialmente se marcaron para atender
una necesidad; es decir, realizar una construcción con algún propósito específico.
1.3.
CRITERIO
1.3.1.
Seguridad
DE
DISEÑO
ESTRUCTURAL
estructural
El diseño estructural tiene como objetivo proporcionar soluciones que, por medio del aprovechamiento óptimo de las
propiedades de los materiales y de las técnicas de construcción, den lugar a un buen comportamiento en condiciones normales de
funcionamiento, con una seguridad adecuada contra la posible ocurrencia de una falla.
Hemos dicho que la estructura es un subsistema dentro del sistema global, que deberá soportar las cargas que le van a
ocasionar deformaciones, desplazamientos y otro tipo de posibles daños, lo que representa la respuesta de la estructura ante las
acciones a las que está sometida.
Respuesta
ACCIÓN ESTRUCTURAL
FIGURA 1.1
Acción - r e s p u e s t a
D
•
•
•
•
•
Agrietamientos
Flechas
Vibraciones
Hundimientos
Desplazamientos
horizontales
4
TESIS PROFESIONAL
La respuesta de la estructura está representada por el conjunto de parámetros físicos que describen su comportamiento ante
las acciones. La respuesta, por supuesto, debe estar comprendida dentro de ciertos valores llamados limites para, de esta manera,
garantizar tanto el adecuado funcionamiento como la estabilidad de la estructura.
Con base a lo anterior podemos entonces establecer el concepto de estado límite.
Estado limite.- lo definimos como la etapa del comportamiento a partir de la cual la respuesta de la estructura se considera
inaceptable.
a. Estados límites de falla.- que esta relacionado con la seguridad y corresponden a situaciones de falla parcial o
total de la estructura. Teniendo que soportar la combinación de acciones más desfavorables durante la vida útil de la
estructura.
b. Estados de limite de servicio.- que se relacionan con situaciones que afectan el correcto funcionamiento de la
estructura, pero que no ponen en peligro la estabilidad de la construcción, como pueden ser deformaciones,
vibraciones, etc., es decir, efectos que provocan en el usuario inseguridad e impiden el confiable uso de la estructura
construida. Así mismo contempla que la estructura funcione correctamente ante la acción de las cargas de operación
normales.
En términos de lo anterior reafirmamos que el objetivo que persigue el diseño estructural es no rebasar los estados
limites.
Respecto a esta situación, los reglamentos marcan los parámetros convencionales basados en el bienestar de los usuarios. Una
forma de acercarnos a estos parámetros es comparar los efectos internos que actúan, en las estructuras, contra las resistencias.
Se define como resistencia de un elemento con respecto a un efecto determinado al valor de tal efecto capaz de
conducir la estructura a un estado límite de falla. Puede hablarse de tantas resistencias como estados límites de falla puedan
presentarse.
Por ejemplo, la resistencia a la flexión será el momento flexionante máximo que una sección es capaz de resistir, por
lo tanto, podemos hablar también de una resistencia al cortante, a la torsión y a la fuerza axial.
El estado límite que regirá la falla será aquel que primero se alcance al crecer la intensidad de la acción.
Para impedir que la estructura llegue a un estado límite de falla, el proyectista
valores dependen de varios factores, como son:
a.
La porción de la estructura afectada por la falla.
b.
El costo de lo que pueda dañarse en equipo u otros aspectos.
c.
El número de personas afectadas por la falla.
recurre a factores de seguridad
cuyos
5
TESIS PROFESIONAL
d.
Las consecuencias de la interrupción del servicio de la estructura.
e.
La forma de la falla, dúctil o frágil.
La seguridad se debe ponderar contra el costo de la estructura para, así, lograr una conñabilidad adecuada a un costo de lo
menos posible, especialmente si la estructura se va a repetir muchas veces, es decir, si se van a construir varias edificaciones del
mismo tipo.
Los factores de seguridad se fijan en los códigos para los casos más usuales. Sin embargo, el proyectista deberá juzgar,
de acuerdo a su criterio, si la estructura que se está analizando no difiere de lo usual para decidir entonces si emplea factores
de seguridad mayores. Los valores de diseño de las acciones son especificados por los reglamentos y determinados por razonamientos
estadísticos y probabilísticos.
1.3.2.
Criterio
reglamentario
de diseño
estructural
Para tratar adecuadamente el problema de la seguridad, es necesario plantear el diseño en términos que permitan identificar
claramente contra qué se quiere o pretende tener seguridad, en dónde se deben aplicar estos factores y qué efectos se quieren cubrir.
El planteamiento de estados límite es el indicado en este caso, ya que se puede comparar la resistencia de cada estado límite
contra la sección respectiva.
Si se manejan correctamente el concepto de resistencia y el concepto de acción, se podría llagar a diseñar con un factor
de seguridad óptimo, el que podemos expresar del siguiente modo:
FS~MAS
Donde:
F.S.= es el factor de seguridad.
AR =es la valor de la resistencia esperada.
AS =es el valor de la acción o carga de servicio.
Los reglamentos, por sencillez de presentación, prefieren definir en forma rígida los factores de seguridad mediante factores
parciales. Esto se debe al número de incertidumbres que aparecen al evaluar las resistencias y las acciones.
En este sentido, los reglamentos manejan las incertidumbres a través de factores de reducción aplicados a los valores de los
esfuerzos de los materiales y las incertidumbres en las acciones o cargas, mediante los llamados factores de carga.
El planteamiento de los estados límite conduce en forma directa a lo que denominamos criterio de diseño por
última (Art. 183 del Reglamento de Construcciones para el Distrito Federal); en donde se plantea lo siguiente:
resistencia
6
TESIS PROFESIONAL
FR(AR) >FC(AS)
Donde, las resistencias AR se multiplican por un factor de reducción, el cual genera un valor conservador. En el otro lado de la
desigualdad, se presentan las fuerzas internas AS obtenidas del análisis, y éstas se multiplican por un factor de carga que toma en
cuenta la probabilidad de que el efecto de las acciones se incremente cuando éstas se combinan.
1.4.
R E G L A M E N T O S DE
DISEÑO
De lo anteriormente dicho sobre el cumplimiento eficiente de las estructuras, debemos agregar que, en gran medida, se debe al
buen proyecto realizado con la experiencia del proyectista y con el cabal cumplimiento de las normas establecidas para el efecto.
En este sentido, al conjunto de normas que establecen una serie de disposiciones legales se le denomina reglamento y lo
podemos definir como un documento legal que tiene por objetivo fundamental proteger a la sociedad contra la ocurrencia de un colapso
o del mal funcionamiento de las estructuras. Es obvio que el grado de protección no es absoluto, pero deberá tratarse de obtener al
máximo posible, es decir, que el proyecto sea congruente con las consecuencias de posibles fallas y el costo que representa aumentar la
seguridad.
Los reglamentos, en general, son elaborados por grupos de especialistas, los que a su vez son revisados por personas o
instituciones interesadas; por lo tanto, un reglamento refleja el punto de vista de sus redactores, así como los conocimientos que se
tengan en el momento de su elaboración.
Existen en general dos tipos de reglamentos en lo relativo al diseño estructural:
a.
Reglamentos funcionales: Estos son los que fijan los requisitos de seguridad y funcionamiento; el proyectista tiene la
libertad para cumplirlos de acuerdo a su criterio y su experiencia.
b.
Reglamentos prescriptivos: Estos prescriben en todo detalle los procedimientos que deben seguirse para lograr el
grado de seguridad deseado.
En su gran mayoría, los reglamentos de diseño en vigencia son prescriptivos. Los reglamentos, dependiendo de su alcance,
pueden abarcar diversos aspectos de la ingeniería estructural, ya sean de acuerdo con el tipo de estructura o de material. Ejemplo de
estos reglamentos son los siguientes:
•
•
•
•
Código ACI
Código AISC
Código UBC
Código CEB
American Concrete Institute
American Institute of Steel Construction
Uniform Building Code (proyecto de edificios)
Comité Européen Du Betón (concreto)
Existen, por otro lado, reglamentos que rigen una gran variedad de aspectos industriales y, entre ellos, los estructurales,
ejemplo de éstos son las normas alemanas DIN que regulan una gran cantidad de procesos industriales.
7
TESIS PROFESIONAL
En México existen varios códigos que reglamentan diversos aspectos del diseño estructural; así, tenemos el Manual de obras
civiles editado por la Comisión Federal de Electricidad y la edición en español del código ACI. Sin embargo, el reglamento específico
para las construcciones urbanas más frecuentemente empleado es el Reglamento de Construcciones del Distrito Federal (RCDF), que
además sirve de modelo para reglamentaciones en lugares del interior de la República Mexicana.
El RCDF vigente consta de un cuerpo principal que en su Título VI se refiere a aspectos específicos del diseño estructural. Para
abarcar los diversos materiales estructurales fueron emitidas las Normas Técnicas Complementarias (NTC) de fácil actualización desde
el punto de vista legal.
Estas normas se dividen en:
NTC
NTC
NTC
NTC
NTC
NTC
NTC
NTC
Concreto reforzado.
Acero.
Madera.
Manipostería.
Cimentaciones.
Sismo.
Viento.
Previsión de incendios.
8
TESIS PROFESIONAL
Acciones
Para anticipar las diferentes clases de cargas y fuerzas que puedan llegar a actuar en la estructura que se está diseñando, el
ingeniero cuenta con la ayuda de los códigos de diseño en donde se especifican en general las cargas más usuales para las estructuras.
Sin embargo, en ocasiones se tiene que acudir al criterio u otros métodos para la determinación de los valores de las acciones que no
son tan comunes y que no se encuentran en las normas. Las magnitudes de estas acciones no siempre se pueden valuar con precisión
y, aun cuando así fuera, no es posible protegerse en contra de los valores de las cargas excepto a un costo inaceptable.
Antes del siglo XIX, la mayoría de las estructuras se construían en forma masiva y fundamentalmente resistían su propio peso,
teniendo poca importancia las otras cargas, debido a la calidad de los materiales y a la inexistencia del análisis estructural.
En la actualidad es muy importante definir y, por lo tanto, entender qué es una acción y qué acciones deben considerarse en el
diseño, cómo se clasifican, cuáles son los modelos para analizar sus efectos, cuál es su magnitud y cómo se combinan para, así poder
tomar en cuenta el efecto en su conjunto.
Las acciones se deben a fenómenos físicos complejos, por lo que se requiere de un modelo para evaluarlas. En general, el
modelo consiste en representar a estas acciones como sistemas de fuerzas, concentradas, lineales, distribuidas uniforme o no
uniformemente. También el modelo se constituye por deformaciones impuestas, por sistemas de fuerzas equivalentes o por una
excitación dinámica, en el caso de acciones dinámicas.
De esta forma, podemos modelar las cargas que actúan sobre los diferentes elementos estructurales con una aproximación
aceptable, aunque a veces estas simplificaciones resulten burdas en comparación con el fenómeno real y puedan conducir a errores
importantes.
2.1.
C L A S I F I C A C I Ó N DE LAS
ACCIONES
Una de las tareas iniciales del calculista es la determinar las acciones que afectan la estructura ocasionando en ella efectos
significativos. La clasificación de estas acciones puede hacerse con diferentes criterios, sin embargo, el criterio más conveniente es el
que obran en la estructura, de acuerdo con su máxima intensidad o cercana a ella. Para el efecto, el RCDF las clasifica de la siguiente
forma:
9
TESIS PROFESIONAL
a.
Acciones permanentes: Son aquellas que obran en las estructuras en forma continua y cuya intensidad se puede
considerar no variante con respecto al tiempo. Dentro de esta clasificación entran las cargas muertas, que son debidas
al peso propio de las estructuras y a empujes estáticos ya sea de tierras, líquidos o granos que tengan un carácter
permanente. También aquí se consideran las deformaciones y los desplazamientos impuestos, debidos a efectos del
presfuerzo o a movimientos diferenciales permanentes de los apoyos, del equipo o maquinaría fijos, etc.
b.
Acciones variables: Son aquellas que obran sobre la estructura con una intensidad variable con respecto al tiempo,
pero que alcanzan valores significativos durante períodos grandes. En este grupo tenemos a las cargas vivas, que son
las que se originan por el funcionamiento de la estructura y que no tienen carácter permanente, como pueden ser: las
personas, el mobiliario y el equipo, los cambios de temperatura, etc.
c.
Acciones accidentales: Son aquellas que no se deben al funcionamiento normal de la estructura, pero que toman
valores muy significativos sólo durante breves períodos en la vida útil de la construcción. En este tipo, tenemos al sismo,
al viento, al oleaje, a las explosiones, etc.
2.2.
C O M B I N A C I Ó N DE A C C I O N E S
La clasificación que el reglamento establece de las acciones, antes descritas, se hace considerando en forma independiente cada
acción, pero también considerando que estas acciones deben combinarse dado que, en algún momento, todas pueden actuar al mismo
tiempo. Los reglamentos especifican que debe revisarse la seguridad de una estructura para el efecto combinado de todas las acciones
que tengan una probabilidad no despreciable de ocurrir simultáneamente.
La combinación de acciones la debemos entender como el efecto conjunto de las mismas actuando a un tiempo en una
estructura cuya seguridad deberá revisarse para esta condición.
De acuerdo con lo establecido en el RCDF (Art. 188), en la combinación común de acciones intervendrán todas las acciones
permanentes, una acción accidental y las acciones variables que tengan probabilidad significativa de ocurrir simultáneamente cuando
actuá la acción accidental. Por lo tanto, en edificaciones comunes las acciones pueden identificarse como:
a.
Carga muerta (como acción permanente).
b.
Carga viva (como acción variable).
c.
El sismo o el viento como acción accidental, aunque no actuando al mismo tiempo, ya que la probabilidad de que esto
suceda es casi nula.
Con base en lo anterior, las combinaciones reglamentadas son las siguientes:
Carga muerta +Carga viva (con su máximo valor)
Carga muerta +Carga viva (con su valor reducido) +Sismo o viento
10
TESIS PROFESIONAL
Cada combinación de acciones constituye u n caso p a r a el cual la e s t r u c t u r a debe ser analizada, y el dimensionamiento final de
los elementos de la e s t r u c t u r a se h a c e con base en los efectos m á s desfavorables encontrados.
Acciones últimas
El RCDF establece el empleo de u n o s factores denominados de carga (F.C.), los cuales deberán multiplicar a las combinaciones
de acciones calculadas convirtiéndolas en carga o acciones ú l t i m a s , las que se emplearán en el diseño.
Estos factores de carga t o m a n los siguientes valores u n valor de 1.4 p a r a la combinación de acciones de cargas m u e r t a s m á s
cargas vivas en e s t r u c t u r a s del grupo "B"y, u n valor de 1.5 p a r a e s t r u c t u r a s del grupo "A".
Para combinación de acciones que incluyan cargas m u e r t a s , cargas vivas y cargas accidentales, el valor del factor e s 1.1.
Resistencia
Resistencia
10% de (CM+CV+CA)
40% (CM+CV)
Sismo
Cargavivamáxima
Carga viva instantánea
Carga muerta máxima
Carga muerta
máxima
FIGURA 2.1.
Primera combinación de acciones
FIGURA 2.2.
Segunda combinación de acciones.
11
TESIS PROFESIONAL
2.3.
D E T E R M I N A C I Ó N DE LAS
ACCIONES
La forma de evaluar las cargas está basada en la normatividad que el RCDF establece. Cabe mencionar que, en este capítulo,
sólo valuaremos cargas que aparecen en construcciones habitacionales, particularmente viviendas.
La clasificación que el reglamento establece de las acciones, antes descritas, se hace considerando en forma independiente cada
acción, pero también considerando que estas
2.3.1.
Cargas permanentes {cargas
muertas)
Entenderemos a la carga muerta como el conjunto de acciones básicamente derivadas del peso propio de la construcción. Las
cargas muertas incluyen:
•
•
•
•
•
•
Peso de la estructura.
Muros divisorios.
Acabados en pisos, muros y techos.
Herrería con ventanas.
Instalaciones.
Equipo que estará fijo durante la vida útil de la construcción.
El cálculo de esta carga en general no representa mayor problema, ya que se obtiene mediante la multiplicación de los
volúmenes de los elementos de la construcción por su peso volumétrico respectivo. Estas cargas se representan comúnmente como
cargas distribuidas linealmente o por áreas, o también se representan como concentraciones.
El reglamento y algunos otros códigos nos presentan tablas de pesos volumétricos de distintos materiales, valores con los que
podemos calcular las cargas muertas. Cabe aclarar que, en las tablas, estos pesos volumétricos muestran dos valores, el máximo y el
mínimo, por lo que se recomienda siempre utilizar el máximo para reducir las incertidumbres con respecto a su valor real, si no
especifica el reglamento otra cosa. (Tabla 2.1.).
De lo anterior, podemos mencionar que en todo proyecto van existir elementos estructurales, como losas, vigas, etc., cuyas
dimensiones no conocemos, por lo que tenemos que definir las dimensiones de tales elementos de manera inicial. Aeste proceso se le
denomina predimensionamiento. El predimensionamiento de diferentes elementos se realiza utilizando algunos criterios que los códigos
sugieren, pero también si el proyectista cuenta con suficiente experiencia, podrá proponer de entrada esas dimensiones.
Es necesario hacer esto puesto que se requiere conocer las dimensiones de los elementos estructurales para poder evaluar su
peso y, de esa forma, realizar los cálculos respectivos. Sin embargo, una vez realizado el diseño definitivo existe la posibilidad de que
las dimensiones propuestas inicialmente no coincidan con las finales, problema del desconocimiento del valor real de las cargas.
También suele suceder que en un proyecto arquitectónico no esté completamente detallado, por lo que al realizar el cálculo el
proyectista no cuenta con toda la información y tiene que estimar una serie de cargas que no coinciden con la realidad. Para estar
12
TESIS PROFESIONAL
siempre del lado de la seguridad, el valor de estas cargas deberá ser alto. Por ejemplo, en una vivienda, el tipo de piso en muchas
ocasiones no está definido y para realizar la estimación de la carga muerta de la losa se sugiere considerar un piso pesado, como
granito, cerámica u otro. Con esto, garantizamos estar del lado más favorable, ya que probablemente el piso que los usuarios decidan
tener sea alfombra.
Otro de los problemas que principalmente se presentan en la estimación del peso de las losas de concreto es la irregularidad
derivada del cimbrado, lo que ocasiona huecos, contraflechas, etc. Esto propiciará que el firme que se coloque para nivelar y recibir el
piso no tenga en toda el área el mismo espesor, generando zonas en donde se cumpla el espesor calculado y otras donde no.
Para estos casos, el reglamento especifica que en losas de concreto de peso volumétrico normal se aumenten 20 kg/m 2 al peso
propio y si se coloca un firme, se deberá agregar una cantidad igual, lo que resulta en una sobrecarga total de 40 kg/m 2 . Tratándose de
losas y morteros que posean pesos volumétricos diferentes del normal, estos valores se modificarán en proporción a los pesos
volumétricos.
TABLA2.1.
Tabla depesosvolumétricos dealgunos materiales, según elRCDF.
Peaoe,»t/m»
Mínimo
MAxtano
Piedras naturales
Chilucas y canteras (secas)
Chilucas y canteras (saturadas)
Basalto (piedra braza)
Granito
Mármol
Pizarras
Tepetate (seco)
Tepetate (saturado)
Tezontle (seco)
Tezontle (saturado)
1.75
2.00
2.35
2.40
2.55
2.30
0.75
1.30
0.65
1.15
2.45
2.50
2.60
3.20
2.60
2.80
1.60
1.95
1.25
1.55
Suelos
Arena de mina (seca)
Arena de mina (saturada)
Grava
Arcilla típica delValle de México
Cemento
Mortero
1.40
1.85
1.40
1.20
1.50
1.00
1.75
2.10
1.60
1.50
1.60
1.00
Piedras artificiales y concretos
Concreto simple y agregado normal
Concreto reforzado
Mortero caly arena
Mortero caly arena
Yeso
2.00
2.20
1.40
1.90
1.10
2.20
2.40
1.50
2.10
1.50
Material
I.
II.
III.
13
TESIS PROFESIONAL
Peso en t/m a
Mínimo
>: Máximo
1.30
1.50
1.60
2.20
0.90
1.30
1.30
1.70
2.00
2.20
Material
Tabiquede barromacizorecocido
Tabiquedebarro prensado
Bloque huecodeconcreto (ligero)
Bloque huecodeconcreto (intermedio)
Bloque huecodeconcreto (pesado)
IV.
Varios
Caoba (seca)
Caoba (saturada)
Cedro(seco)
Cedro (saturado)
Oyamel(seco)
Oyamel (saturado)
Pino(seco)
Pino(saturado)
Encino (seco)
Encino (saturado)
Vidrio plano
Azulejo
Mosaicode pasta
Mosaicodeterrazo (20x20)
Mosaicodeterrazo (30x30)
Granitodeterrazo (40x40)
Losetaasfáltica ovinílica
Falso plafón deaplanado (incluye malla)
Mármolde2.5cm. de espesor
Cancelería metálica para oficina
Tablarocade 1.25 cm.
2.3.2.
0.55
0.70
0.40
0.50
0.30
0.55
0.45
0.80
0.80
0.80
0.80
10
25
35
45
55
5
40
52.50
32
8.50
0.65
1.00
0.55
0.70
0.40
0.65
0.65
1.00
0.90
1.00
3.10
Peso ec tkg/ma
15
35
45
55
65
10
Cargas variables (cargas vivas)
En el RCDF considera en su Art. 198a las cargas vivas como lasfuerzas quese producen porelusoy ocupación delas
Edificaciones y queno tienen carácter permanente. A menos quesejustifiquen racionalmente otros valores, estas cargas se tomarán
iguales alas especificadas en el artículo 199.
Las cargas especificadas no incluyen elpeso de muros divisorios demanipostería odeotros materiales, nieldemuebles, equipos
u objetos de peso fuera de lo común, como cajas fuertes degran tamaño, archivos importantes, libreros pesados ocortinajes ensalas de
espectáculos. Cuando seprevean tales cargas deberán de cuantificarse y tomarse encuenta eneldiseño en forma independiente de la
carga viva especificada. Los valores adoptados deberán justificarse enla memoria decálculo eindicarse enlosplanos estructurales.
14
TESIS PROFESIONAL
Modelar este tipo de cargas resulta muy complejo, pero para fines de diseño se emplean modelos muy simples, como son las
cargas uniformes y estáticas distribuidas en áreas a las cuales en ocasiones se les agrega alguna carga concentrada.
Por otro lado el RCDF establece, en su artículo 199, una tabla de cargas vivas que deberán emplearse en los diseños y en
diversos usos de la construcción. Además, define tres valores de cargas vivas:
o.
Carga viva máxima (Wm); Esta carga se deberá emplear en el diseño estructural de los elementos de una estructura
sujeta a la acción de las cargas verticales gravitacionales, así como en el cálculo de asentamientos inmediatos del suelo y
en el diseño de las cimentaciones.
b.
Carga instantánea
y el viento.
c.
Carga media (W); Ésta se deberá emplear para el cálculo de asentamientos diferidos, así como para el cálculo de flechas
diferidas.
(Wa);Ésta se empleará para el diseño de las estructuras cuando estén sujetas a la acción del sismo
Aestas cargas, el reglamento las considera como uniformemente distribuidas en el área tributaria del elemento.
Loanterior implica que la carga viva toma valores diferentes para cada caso de diseño que tengamos que realizar.
La intensidad de las cargas vivas en las tres modalidades depende de dos factores: el destino del área sobre la que actúa y el
tamaño de la misma.
Desde luego, el destino del área es más importante, ya que el tipo de ocupación determina las actividades que se van a realizar
en el lugar, definiendo de esta forma las características de las acciones que puedan presentarse.
Uno de los problemas que se presentan en ocasiones es que el destino de los espacios no está bien definido, lo que genera
dudas sobre el tipo de cargas que actuarán en tal área y nos obliga a utilizar las carga más desfavorables dentro de la operación
normal de la construcción.
De lo anterior, surge un comentario importante; el proyectista debe dejar perfectamente plasmadas las condiciones de operación
que consideró en sus cálculos, de manera que los usuarios o propietarios las conozcan y quede bajo su responsabilidad cualquier otro
uso que se le dé a la edificación y que le llegue a provocar daños.
Por otro lado podemos comentar que entre más pequeña sea el área en donde se desarrolle la actividad se tendrá una mayor
probabilidad de que se presenten cargas vivas muy altas, debido a alguna actividad en particular. Esta probabilidad de ocurrencia
disminuye si el área de trabajo es mayor, ya que se cuenta con mayor espacio para el desarrollo de la actividad, lo que implica que la
carga viva disminuya.
15
TESIS PROFESIONAL
Otro comentario importante respecto a la variabilidad de la carga viva es que no necesariamente el empleo de su valor máximo
aplicado en toda la estructura es el que provocaría los efectos más desfavorables, es decir, se tendría que realizar diferentes análisis
colocando esta carga en diferentes posiciones para identificar las zonas en donde se generen los efectos más desfavorables y así
mediante este estudio, poder diseñar los elementos.
El RCDF, en su artículo 199, presenta la tabla de cargas vivas unitarias en kg/m 2 para áreas tributarias no mayores de 36 m 2 y
establece que puede reducirse esta carga cuando el área sea mayor, calculándola con la siguiente ecuación:
Wcv= 100 + 420/VA
Además de considerar otras observaciones que en el artículo mencionado se indican.
TABLA2.2.
Cargasvivasunitarias, en kg/m2.
D«,tino de pUo o cubierta
a).
b).
c).
d).
e).
Habitación
(casa-habitación,
departamentos,
viviendas, dormitorios, cuartos de hotel, internados
de escuelas, cuarteles, cárceles, correcciones,
hospitales y similares.
Oficinas, despachos y laboratorios.
Comunicación para peatones (pasillos, escaleras,
rampas, vestíbulos y pasajes de acceso libre al
público).
Estadios y lugares de reunión sin asientos
individuales.
Otros lugares de reunión (templos, cines, teatros,
gimnasios, salones de baile, restaurantes,
bibliotecas, aulas, salas dejuego y similares).
g).
Comercios, fábricas y bodegas.
Cubiertas y azoteas con pendiente no mayor de
5%.
h).
Cubiertas y azoteas con pendiente mayor de 5%.
0-
i).
i).
Volados en vía pública (marquesinas, balcones y
similares).
Garajes y estacionamientos (para automóviles
exclusivamente).
W
(C.V.media)
Wft
IC.V. inst.)
Wm
(C.V. Mix.)
70
90
170
100
180
250
40
150
350
40
350
450
40
0.8 Wm
250
0.9 Wm
350
Wm
15
70
100
5
20
40
15
70
300
40
100
250
16
TESIS PROFESIONAL
2.3.3.
Cargas accidentales
Sismo
De l a sacciones accidentales, la m á s importante p a r a el diseño d ecasa-habitación e sel sismo. Elefecto delossismos e n u n a
construcción, a diferencia d e l a s cargas vivas y l a s cargas m u e r t a s , n o puede s e r estudiado como u n a acción p e r m a n e n t e o
semipermanente. E nla figura 2.3 puede observarse laforma e nq u e a c t ú a esta solicitación e nrelación con el tiempo.
Magnitud dela
acción sísmica
Tiempo
FIGURA 2.3.
Distribución de ocurrencia de eventos sísmicos en el tiempo.
El objetivo deldiseño sísmico del a se s t r u c t u r a s e s lograr l a stres características q u e rigen el b u e n comportamiento sísmico:
resistencia, rigidez y ductilidad. E n e s t r u c t u r a s de mampostería, como e s el caso d e u n a casa-habitación, la resistencia e s
proporcionada p o rlos m u r o s alineados e n cada dirección, q u e deben resistir la acción completa debida al sismo. Lasotras d o s
características s o nobtenidas por l a spropiedades intrínsecas delmaterial, a u n q u e e s difícil conciliar rigidez con ductilidad. Als e r la
casa-habitación u n sistema rígido p o rnaturaleza, e n realidad n o e s necesario considerar los d a ñ o s q u e sufran los elementos n o
e s t r u c t u r a l e s debido a los desplazamientos sísmicos. Desgraciadamente loanterior define a lafalla sísmica como frágil.
17
TESIS PROFESIONAL
Q Materiales de
U construcción
Es importante conocer las características de los materiales estructurales. Desde luego, hay que aclarar lo que entendemos por
material estructural y, en este sentido, al acero, concreto, piedras, tabiques, maderas, etc., los conoceremos como materiales utilizados
en laconstrucción para soportar las cargas yproporcionar resistencia yestabilidad, por ejemplo, los edificios de acero o concreto. Otro
tipo de materiales que también se usan en la construcción son para los acabados opara la protección contra el interperismo.
La resistencia esla propiedad más importante del material estructural, yaque eslaque define lafuerza que será capazde
soportar un elemento estructural antes de que falle. Aéste se le conoce como esfuerzo.
Luego entonces, empezaremos aconocer aspectos importantes de algunos materiales empleados en la construcción.
3.1.
MANIPOSTERÍA
Conceptos Generales
Se entiende pormampostería al material de construcción queresulta dela combinación de piedras o piezas naturales o
artificiales, con un mortero que las une para formar un conjunto monolítico.
La mampostería por su escasa resistencia a la tensión es usado principalmente en elementos estructurales sujetos
fundamentalmente a compresiones axiales. Hacen excepción por ejemplo los muros de contención y los muros de rigidez para cargas
laterales en edificios que están sujetos acombinaciones de carga más complejas.
El comportamiento a carga axial delamampostería depende delas propiedades delapiedra yelmortero ydela interacción
entre ambos.
Actualmente, la mampostería seemplea enlaconstrucción deviviendas, tanto unifamiliares como multifamiliares, y se han
encontrado que las estructuras más altas eneste material son del orden decinco niveles, aunque existen algunos casos de mayor
altura. También se emplea en la construcción de muros de contención, muros de división y en la construcción de cimientos,
chimeneas, etc.
18
TESIS PROFESIONAL
La manipostería puede ser de piedras naturales, arcillas y/o concreto, y su presentación es diversa, por ejemplo al natural, en
el caso de piedras, o en forma de tabiques y bloques, tanto macizos como huecos, en el caso de la arcilla y el concreto.
Contar con alternativas diferentes en lo que corresponde a los tipos de piezas de manipostería permite la realización tanto de
elementos estructurales como de no estructurales, es decir, elementos de fachadas, divisorios, etc.; Sin embargo, lo que nos ocupa, en
este caso, son los elementos que tienen una función estructural.
Mencionaremos algunas características típicas de las diferentes maniposterías con la intención de conocer a fondo sus
propiedades.
Después de la tierra, la piedra es el material más natural de todos los utilizados en la construcción. Es razonable suponer que
en aquellas áreas donde existían construcciones de piedra, los hogares del hombre primitivo eran meros amontonamientos de piedras.
Por otro lado, el descubrimiento de materiales cementantes naturales le permitió al hombre construir paredes que podían ser a la vez
más delgadas, más altas y más sólidas.
Como en el caso de la construcción a base de tierra que ha sido usada durante siglos para construir paredes, suelos y tejados,
la piedra puede adquirirse fácilmente, ya que ésta se encuentra en los lechos de los ríos, en minas, canteras y campo abierto, siendo
poco factible, en nuestro medio, una región que no contenga una cantidad de piedra que pueda ser usada para la construcción.
Actualmente, los constructores explotan poco la construcción a base de piedra. Probablemente, esto se deba a que la
construcción de piedra es similar a la de tierra, siendo esta última más económica que la piedra, la que se deja para cimientos, bardas
y muros pequeños.
Existe poca información acerca de la tecnología de albañilería de piedra; Probablemente, ha sido tradicionalmente guardada
como secreto. Alo largo de los siglos, los albañiles que trabajan con piedra han conseguido mantener en la industria de la construcción
un status respetable. Los secretos de su oficio permanecen.
Por otro lado, es obvio que a menor procesamiento de un material, menor el costo del elemento estructural. La tecnología
moderna de construcción ha producido algunos materiales como tabiques y bloques, tanto de tierra como de concreto.
Curiosamente, se ha encontrado que los tabiques o ladrillos son el material de construcción más adecuado para satisfacer las
necesidades de vivienda, ya que su tamaño pequeño presenta gran adaptabilidad a prácticamente cualquier diseño.
Actualmente, persiste el método antiguo y lento de superposición de tabiques. Sin embargo, su utilización es amplia por lo que
la calidad de la construcción depende del trabajo del obrero, por un lado, y de la efectividad de las uniones entre el mortero y los
tabiques, por el otro.
La clave para una colocación adecuada de las piezas es que éstas contengan gran cantidad de agua, ya que son muy
absorbentes y si se colocan secas absorberán el agua del mortero antes de que se realice la unión entre ambos.
19
TESIS PROFESIONAL
3.1.1.
Piedras
naturales
Las piedras o rocas naturales se encuentran en la naturaleza en formaciones de grandes dimensiones, sin forma determinada y
constituyendo el principal componente de la parte sólida de la corteza terrestre.
Características
Por constituir un material natural, la piedra no precisa para su empleo más que la extracción y la transformación en elementos
de forma adecuada. Sin embargo, es necesario que reúna una serie de cualidades que garanticen su aptitud para el empleo a que se
destine. Estas cualidades dependen de su estructura, densidad, compacidad, porosidad, dureza, composición, durabilidad, resistencia
a los esfuerzos a que estará sometida, etc.
Aplicaciones
De tres maneras principales se utilizan las piedras en la construcción:
•
•
•
Como elemento resistente.
Como elemento decorativo.
Como materia prima para la fabricación de otros materiales.
Cada aplicación determina los factores a tener en cuenta para la elección del material. Esta elección se hace atendiendo a
razones de tipo:
•
•
•
Estético: color, textura.
Técnico: resistencia a esfuerzos mecánicos y agentes atmosféricos.
Económico: facilidad de extracción y labra.
Clasificación
La clasificación más corrientemente utilizada es la que agrupa las piedras según su origen, dividiéndolas así:
•
•
•
ígneas o Eruptivas.
Sedimentarias.
Metamórficas.
La resultados experimentales acerca de la resistencia a la compresión de este material son muy escasos. En pruebas efectuadas
con especimenes aproximadamente cúbicos de 40 cm de lado, se han obtenido resistencias del orden de 200 kg/cm 2 para sillería (Se
entiende por sillería a la manipostería de 1/a. Clase que esta formada por piezas perfectamente labradas a dimensiones exactas y
asentadas en hiladas regulares) y de 120 kf/cm ¿ para manipostería ordinaria. Estos valores son muy diferentes, o sea a la resistencia
de la piedra sola, pero mayores que la resistencia del mortero.
20
TESIS PROFESIONAL
El mecanismo de falla no esta muy bien definido. La resistencia puede ser muy sensible a la calidad del mortero, al tamaño de
las piedras y al espesor de las juntas. La variación de la resistencia en una muestra o espécimen nominalmente iguales es
considerable.
TABLA3.1.
Propiedades de algunas piedras naturales
Piedra
Peso volumétrico seco
Ton/m a
Resistencia a la
compresión
Kg/cm*
Resistencia a la
tensión
Kg/cm*
Módulo de elasticidad
Kg/cm 9
Areniscas
1.75 a 2.65
150 a 3 200
60 a 120
40 000 a 200 000
Basaltos (Piedra braza)
2.3 a 3.0
800 a 5 800
200 a 300
100 000 a 300 000
Granito natural
2.4 a 3.2
800 a 3 000
100 a 200
400 000 a 500 000
Mármol
2.4 a 2.85
300 a 3 000
35 a 200
900 000
TABLA 3.2.
Resistencia a la compresión y cortante de piedras naturales
Manipostería de tercera (piedra no labrada).
Tipo de mortero
f*m
Kg/cm a
Kg/cm 3
Manipostería junteada con mortero de resistencia
en compresión no menor que 50 kg/cm 2
20
0.6
Manipostería junteada con mortero de resistencia
en compresión menor que 50 kg/cm 2
15
0.4
V*
21
TESIS PROFESIONAL
3.1.2.
Piedras
artificiales
El uso de este tipo de materiales para la construcción es cada día más frecuente. Este material se compone generalmente de un
concreto a base de cemento Portland, arena o gravilla fina, así como de mortero de cemento y arena, según sea el espesor finura de la
piedra que se quiera.
La calidad de una piedra artificial depende de los materiales que la conforman y tiene tantas aplicaciones como se requiera. En
la actualidad, se utilizan para la fabricación de bloques de construcción de muros, o como elementos decorativos o de división.
Los bloques de concreto, por lo general, son de dimensiones mayores que las de los ladrillos cerámicos, son macizos o huecos y
su fabricación puede ser a mano o con máquinas. Dependiendo del fabricante, podemos encontrar una gran gajaoma de tamaños y
formas, tanto en piezas huecas como en macizas.
Interacción mortero - piedra
La mampostería esta compuesta por dos materiales que tienen distintas características esfuerzo - deformación y que al ser
sometidos a carga axial sufre deformaciones verticales acompañadas por una deformación transversal. Esta debe ser igual en los dos
materiales ya que la fricción y la adherencia entre ellos impiden el desplazamiento relativo en las caras de contacto.
El caso más común es que el mortero sea más deformable que la piedra y por lo tanto, sí los dos materiales pueden deformarse
libremente al ser sometidos al mismo esfuerzo vertical, sufrirán las deformaciones mencionadas.
Morteros
Los morteros son mezclas plásticas aglomerantes que resultan de combinar arena y agua con un cementante que puede ser
cemento, cal, yeso o una mezcla de estos materiales.
Las principales propiedades de los morteros son su resistencia a la compresión y tensión, adherencia con la piedra, módulo de
elasticidad, trabajabilidad, rapidez de fraguado e impermeabilidad. Otra característica importante es su retención de agua, es decir, su
capacidad para evitar que la pieza absorba el agua necesaria para el fraguado del mortero.
La adherencia entre el mortero y las piezas es fundamental para la resistencia por cortante del elemento. Además, es importante
que el mortero tenga una trabajabilidad adecuada para que pueda ser colocado de forma tal que permita el asentamiento correcto de
las piezas y, así, evitar concentraciones de esfuerzos y excentricidades.
La resistencia a la compresión de los morteros no tiene una influencia importante en el comportamiento de la mampostería. Sin
embargo, hay que realizar la prueba de compresión del mortero para verificar su calidad. Esta prueba consiste en la fabricación de
probetas de mortero en forma de cubo de 5 cm. de lado, para la misma proporción de mezcla, fabricadas por el mismo albañil. En la
obra, es obvio que no se tiene el mismo control y, por lo tanto, los resultados se presentan con más dispersión debido a la posible
alteración del proporcionamiento de la mezcla.
22
TESIS PROFESIONAL
Las propiedades mecánicas de los morteros son muy variables y dependen principalmente del tipo de cementante utilizado y de
la relación arena-cementante. (Ver tabla 3.3.)
TABLA3.3.
Resistencia a la compresión yvelocidad de fraguado delosmorteros.
Mortero
compresión
Kg/cm
a
Poso volumétrico
Ton/m 3
*
-
—
*
—
-
Cal
l a 10
lxlO5
2.0
Lento
Cemento
40 a 200
1x105a 5xl0 5
2.1
Rápido
Yeso
Baja
-
-
Rápido
Premezclado con
aditivos plásticos
-
-
-
Cemento de albañilería
Mixto:cemento-cal
Buena
-
-
Buena manejabilidad
Por la restricción en las caras de contacto los dos materiales tendrán una misma deformación lateral intermedia entre la de los
materiales aislados. Para adoptar el estado de deformación, el mortero sufrirá compresiones en ambas direcciones transversales,
quedando sometido a un estado de compresión triaxial, o sea, la piedra estará sometida a tensiones transversales mas una compresión
longitudinal.
Para fines ingenieriles la relación arena-cementante, recomendable está entre 2.5 y 3, ya que se obtienen así mezclas de buena
resistencia, buena adherencia con la piedra y baja contracción.
Por lo anterior el material más deformable incrementará su resistencia sobre la obtenida en un ensayo a compresión simple, ya
que está sometido a compresión triaxial. Por el contrario el material menos deformable verá reducida su resistencia por las tensiones
transversales. Este comportamiento de la manipostería se ha denominado "Fenómeno de junta".
23
TESIS PROFESIONAL
TABLA3.4.
Proporcionamiento para morteros.
Tipode
norteño
i
n
ni
Partee de
cemento
Partee de
Partee de
cal
Partee de
arena
f%en
-
0 - lÁ
-
o- ya
-
-
VA - '/a
Vaa 1
-
Nomenos
de2.25 ni
másde 3
vecesla
suma de
cementant
es en
-
'/=> a 1v«
albaftileria
vohimpn
125
75
40
R e c o m e n d a c i o n e s del RCDF y s u s n o r m a s t é c n i c a s p a r a los m o r t e r o s
a.
b.
c.
d.
3.1.3.
Su resistencia en compresión no será menor de 40 kg/cm 2 .
La relación volumétrica entre la arena y la suma de cementantes se encontrará entre 2.25 y 3.
La resistencia se determinará según lo especificado en la Norma Oficial Mexicana (NOM C61).
Se empleará la mínima cantidad de agua que dé como resultado un mortero fácilmente trabajable.
Tabiques
Los ladrillos y/o tabiques se clasifican entre los materiales que se obtienen mediante la cocción de arcillas naturales,
previamente moldeadas, o de materiales cerámicos.
El arte de la cerámica es una de las actividades más antiguas del mundo. Nació con la elaboración de objetos diversos de arcilla,
como recipientes y piezas de ornato y, al paso del tiempo, surgieron los materiales de construcción ofreciendo grandes ventajas. Se
sabe que en Persia ya se conocían los ladrillos.
Dentro de los productos utilizados en la construcción, el adobe se tiene como uno de los más antiguos y se forma mezclando
pastas de arcilla con arena y paja secada simplemente al sol. Otro de estos productos resulta de la mezcla de agua y varias clases de
arcilla sometida después al fuego.
24
TESIS PROFESIONAL
Las arcillas utilizadas para la fabricación de productos cerámicos pertenecen a dos grandes grupos: arcillas micáceas y arcillas
caolíticas, que son más puras. Frecuentemente se añaden a las arcillas otros materiales que mejoran el producto, los que pueden ser:
desengrasantes, como la arena cuarzosa, cuarcita, bauxita; etc., fundentes, como alquitrán, grafito, etc., y colorantes.
Tabique es toda pieza destinada a la construcción de muros y generalmente son de formas ortoédricas. Los tabiques son
producto de la cocción de la arcilla y otros materiales. Existen, en la actualidad, tabiques macizos y huecos con diferentes tipos de
diseño que dependen del fabricante.
El ladrillo macizo es un elemento que puede tener algunas rebajas de profundidad para mejorar la adherencia de la pieza y
también debe cumplir con ciertas características, como son:
1.2.3.4.5.-
Ser homogéneo.
Estar bien moldeado y tener aristas vivas.
Ser poroso sin exceso, para poder tomar el mortero.
Tener buena sonoridad al ser golpeado.
Poder ser cortado con facilidad.
Una prueba que puede realizarse en la obra para observar la calidad de las piezas consiste en frotar dos piezas y observar que
no se desmoronen. Otra puede ser golpear la pieza contra un objeto duro y escuchar un sonido metálico. Otra es partir un ladrillo y no
se deberán observar manchitas blancas, ya que esto representa contenido de cal, la cual con el tiempo puede disgregar el material.
Propiedades de las piezas de barro
Una de las propiedades importantes que debemos conocer de las piezas es la resistencia a la compresión, la cual se realiza
mediante el ensaye de medio ladrillo en posición horizontal y al cual se le aplica una carga de compresión. La pieza debe estar seca y
las superficies de apoyo deben pintarse con goma de laca, antes de cabecearla, para impedir la absorción de humedad que puede
alterar su resistencia.
La razón de utilizar sólo la mitad de la pieza radica en que las piezas enteras tienen irregularidades que pueden dar origen a
una mayor dispersión de resultados en los ensayes.
Otra propiedad fundamental es la absorción, que es la medida de la porosidad, la cual nos indica la posible filtración a través
del ladrillo y la tendencia a su disgregación. Un ladrillo poroso es menos resistente que uno más denso. La calidad de esta pieza se
logra mediante procesos industrializados que, desde luego, pueden variar en las propiedades dependiendo del tipo de barro utilizado,
su proceso y su horneado.
La prueba de absorción consiste en secar cinco mitades de ladrillo que se pesan al enfriarse. Posteriormente se sumergen en
agua a temperaturas entre 16°y 30° C durante 24 horas. Una vez transcurrido ese tiempo, las piezas se sacan y se secan con un trapo
húmedo para volverse a pesar inmediatamente. La absorción se calcula con base en el peso de las unidades secadas por horneado.
La absorción de los ladrillos presenta variaciones que van del 1% al 25%, aunque en general esta absorción se encuentra
siempre abajo del 20% para un buen ladrillo común.
25
TESIS PROFESIONAL
Es importante aclarar que las diferentes e m p r e s a s que fabrican piezas tienen s u s propias particularidades, e s decir, las
propiedades p u e d e n ser diferentes y todo esto lo expresan en su propaganda.
La durabilidad es otra propiedad y tiene que vef con los cambios en las condiciones de h u m e d a d y t e m p e r a t u r a . E s t a propiedad
se evalúa mediante u n a p r u e b a de congelación-descongelación. Los ladrillos son sometidos a m u c h o s ciclos en condiciones s a t u r a d a s y
a varios ciclos de humedecimiento y secado. La perdida de peso se relaciona con su resistencia.
E s t a s propiedades indican la calidad de la pieza, y a que los valores de resistencia de é s t a s son mayores que los de los elementos
de m a m p o s t e r í a construidos con el mismo tipo de piezas.
En el caso de bloques de concreto y tabiques extruidos, las p r u e b a s son similares a las de las piezas enteras, ya que los huecos
que contienen dificultan la realización de los ensayes. Otra dificultad p a r a e s t a s p r u e b a s es que se requieren m á q u i n a que tengan u n a
g r a n capacidad.
l a c a de apoyo
V/¿//SM/////S/M////////¿
Media pieza
VA>/S/M///SS///////////S/JsA
FIGURA 3.1.
3.1.4.
Prueba de compresión de las piezas de mampostería.
P r u e b a s en
manipostería
Resistencia a la compresión
La forma m á s c o m ú n p a r a determinar la resistencia a compresión de la mampostería, y por lo tanto la m á s confiable, es
e n s a y a r pilas formadas con las piezas del tipo de mampostería a emplear en la construcción, j u n t e a d a s con morteros.
26
TESIS PROFESIONAL
El reglamento establece el procedimiento e s t á n d a r p a r a calcular el esfuerzo a compresión resistente, proponiendo el ensaye de
pilas con u n a relación altura-espesor del orden de cuatro (h/t=4), y así evitar problemas de esbeltez en caso de q u e la relación sea
mayor de cuatro. Lo p r u e b a se realiza por lo m e n o s nueve veces en este tipo de m u r e t e s p a r a d a r confiabilidad a los valores obtenidos.
Los r e s u l t a d o s de las p r u e b a s p r e s e n t a n dispersión, por lo que se aplican procedimientos estadísticos que n o s d a n valores que
s e r á n cubiertos t r a z a n d o u n a línea recta por debajo de la n u b e de resultados.
El valor nominal de diseño en compresión es:
/%.«
fm
(\ + 2.5 cv)
cv = coeficiente de variación de la m u e s t r a .
fm =esfuerzo promedio de todos los ensayes.
También de e s t a s p r u e b a s se p u e d e obtener el módulo de elasticidad p a r a a l g u n o s materiales son:
a). Para manipostería de bloques y tabiques de concreto:
b). Para manipostería de tabiques de barro:
E = 4 0 0 fm para cargas de corta duración.
E - 2 5 0 fm para cargas
sostenidas.
E =6 0 0 fm para cargas de corta duración.
E= 250 fm para cargas
sostenidas.
FIGURA 3.2.
Ensaye a compresión de muretes.
urete
f
«?—
t
—>
p
27
TESIS PROFESIONAL
Valoras def *men Kg/cm3
Tipo de mortero
Mortero I
Mortero JJ
Mortero ni
Tabique de barro recocido
15
15
15
Bloque de concreto tipo A
(pesado).
20
15
15
Tabique de concreto
fP >80 kg/cm 2
20
15
15
Tabiques con huecos verticales
fp > 120 kg/cm 2
40
40
30
TABLA 3.5.
Resistencia de diseño a compresión de la manipostería fm para algunos tipos de piezas, sobre área bruta (La relación área
neta-área bruta no será menor de 0.45.).
Resistencia al cortante
El valor del esfuerzo cortante resistente, v', de la manipostería se obtiene mediante ensayes de muretes aproximadamente
cuadrados, que contienen en cada hilada cuando menos una pieza y media, sometidos a fuerzas diagonales (figura 3.3).
PR
D
PR
FIGURA 3.3.
Obtención de esfuerzo resistentev*.
28
TESIS PROFESIONAL
El RCDF sugiere que se realice u n mínimo de nueve ensayes a partir de los cuales se obtendrá el esfuerzo resistente en cada
prueba, mediante la expresión:
v =-£.
Db
En la cual:
v" =esfuerzo cortante resistente de la mampostería empleada.
PR =fuerza diagonal resistente sobre múrete.
D=distancia diagonal en múrete.
b =espesor del múrete.
Una vez realizadas las pruebas, se determinará el valor del esfuerzo resistente, v", del lote de muretes, ensayando a partir de la
siguiente expresión:
.
v
v ~——
1 + 2.5CV
Donde:
v =promedio de los esfuerzos resistentes de los muros ensayados.
Cy=coeficiente de variación de los esfuerzos resistentes de los muretes ensayados, el que no se tomará
menor que 0.20
v' (kg/cm3)I
Plena
Tipo de mortero I
TABLA3.6.
Tabique de barro recocido
I
IIy III
3.5
3.0
Bloque de concreto tipoA
I
IIy III
3.0
2.5
Tabique de concreto
fp >80 kg/cm 2
I
IIy III
3.0
2.0
Tabique hueco de barro
I
H y ni
3.0
2.0
Esfuerzo cortante dediseño if para algunos tiposde mampostería sobre área bruta.
29
TESIS PROFESIONAL
Modos de falla
La falla de la manipostería sujeta a carga axial, se presenta por aplastamiento de las piezas o por agrietamiento vertical. La falla
nunca se produce atraves del mortero.
La falla por aplastamiento de las piezas ocurre cuando estas son de muy baja resistente y el mortero de buena calidad; También
es típica en piezas con huecos horizontales.
La forma mas usual de falla es atraves de grietas verticales (se estima un ángulo de falla de 45°) y se produce cuando el mortero
es de resistencia igual o menor que la de la pieza. Los otros tipos de falla observados incluyen los efectos de flexión y esbeltez (pandeo).
3.2.
CONCRETO
SIMPLE
El concreto es le material que con mayor frecuencia se utiliza en la construcción de múltiples y diversas edificaciones, tanto en
nuestro país como en el resto del mundo. Dadas sus características, este material es especial ya que ofrece la oportunidad de cambiar
sus propiedades, de ahí la importancia de aprender todo lo posible sobre el concreto.
Una de las situaciones por la que amerita estudios más detallados es que la mayoría de la gente que tiene que ver con el
concreto no ésta debidamente informada sobre él, es decir, se desconoce que la calidad del concreto puede afectarse durante el proceso
de fabricación, esto es, en el mezclado, colocación, curado, transportación, etc.
El concreto, como sabemos, es una mezcla de varios materiales: cemento, agua, agregados finos (arena) y gruesos (grava). A la
arena y a la grava se les denomina agregados inertes, y son utilizados en la mezcla para disminuir la cantidad de cemento y, de esta
manera, poder obtener como resultado un producto más económico.
Al agua y al cemento se les denomina agregados activos, ya que al unirse provocan una reacción química que produce el
fraguado, el cual no es más que el proceso de endurecimiento de la mezcla hasta llegar a la solidez.
La característica más importante del concreto es su alta capacidad a la compresión y su nula resistencia a la tensión. Sin
embargo, esta deficiencia se corrige con la introducción de un material que absorbe las tensiones, como el acero de refuerzo, cuya
combinación produce un material óptimo para la construcción de elementos estructurales que se llama concreto reforzado.
3.2.1.
Cemento
Podemos describir al cemento como un material con propiedades adhesivas y cohesivas las cuales dan la capacidad de aglutinar
otros materiales para formar un todo, sólido y compacto. En nuestra especialidad, que es ramo de la construcción, el término cemento
lo entendemos como el material que aglutina a otros siendo éstos: piedras, tabiques o bloques, grava y arena para, de esta manera,
formar un concreto.
30
TESIS PROFESIONAL
El uso de este material se remonta a la antigüedad. Desde la época de los egipcios, griegos y romanos, se aprendió a mezclar cal
con agua, arena y piedra triturada, por lo que se puede decir que este tipo de producto, fue el primer concreto en la historia.
Actualmente, tenemos perfectamente establecido el uso del cemento, siendo el más común el denominado Portland.
El cemento se obtiene a partir de la mezcla de materiales calcáreos y arcillosos, así como de otros que contengan sílice, aluminio
y óxidos de fierro.
El proceso de fabricación del cemento consiste en moler finamente la materia prima, mezclarla en ciertas proporciones y
calcinarla en un horno rotatorio de gran dimensión, a una temperatura de 1400° C, donde el material se sintetiza y se funde
parcialmente formando bolas conocidas como clinker que, cuando se enfría el material, se trituran hasta obtener un polvo fino al que
se le añade un poco de yeso para obtenerse, como producto final, el cemento Portland, el que es usado en todo el mundo en la
actualidad.
El cemento Portland debe su nombre a la semejanza, en color y calidad, con la piedra de Portland, una caliza obtenida de una
cantera en Dorset, Inglaterra. Este cemento empezó a ser desarrollado pro Joseph Aspin, en 1824.
Hasta nuestros días, este material se ha convertido en un elemento primordial para la construcción de edificaciones de diversa
índole, propiciando grandes obras que, a lo largo y ancho di mundo, podemos observar.
El cemento más común que se emplea actualmente en la fabricación de concretos, morteros y otros elementos es el denominado
cemento Portland. Existe también el cemento Portland Punzolana, empleado para casos especiales.
La definición del cemento Portland, según la Norma Oficial Mexicana, dice que es un conglomerante hidráulico que resulta de la
pulverización del clinker frío, a un grado de finura determinado y al cual se le añade sulfato de calcio natural, o agua y sulfato de calcio
natural. El cemento Portland punzolana además tiene puzolana, que le imparte un calor de hidratación moderado. La cantidad de
punzolana constituirá del 15% al 40% del peso del producto. A opción del producto pueden utilizarse coadyuvantes de molienda, que
no sean nocivos para el comportamiento posterior del producto, para impartir determinadas propiedades al cemento (NOM C-1 y NOM
C-2).
Existen varios tipos de cementos dependiendo de su uso específico. En relación con su color general, se encuentran los
cementos grises y blancos.
Acontinuación, se muestra una clasificación general para diferentes tipos de cementos de acuerdo con su propósito específico.
•
Cemento tipo 1 (Para todos los propósitos); se usa este tipo de cemento para mezclas de concreto en las que no se
requiere de propiedades especiales, sobre todo cuando los elementos estructurales no están expuestos a la acción de
sulfates.
•
Cemento tipo 2 (Resistente a los sulfatas); Este cemento tiene un objetivo más específico. Se recomienda su uso
en estructuras que van estar expuestas a la acción de cantidades no muy importantes de sulfates.
31
TESIS PROFESIONAL
•
Cemento tipo 3 (De resistencia rápida); Este cemento logra alcanzar la resistencia en poco tiempo (una semana o
quizá menos) y nos permite optimizar tiempos de construcción. Se usa en pisos, caminos, banquetas, etc.
•
Cemento tipo 4 (De baja temperatura de hidratación); Este tipo de cemento se usa primordialmente en
estructuras masivas, tales como presas, donde las temperaturas que se desarrollan durante el fraguado pueden
dañarlas.
•
Cemento tipo S (De alta resistencia a los sulfatos); Se usa en estructuras expuestas a la acción de sulfatos como,
por ejemplo, el agua del subsuelo, que tiene gran contenido de este material.
Agregados Inertes
Estos agregados, denominados agregados inertes finos y gruesos, son de tipo mineral y ocupan aproximadamente el 70% del
volumen total de la mezcla de concreto. Su objetivo principal es lograr una disminución en la cantidad de cemento a utilizar, lo cual da
como resultado una mezcla más económica, ya que estos materiales son más baratos. Además, dado el volumen que ocupan en la
mezcla, conocer sus características y calidad es de suma importancia.
No obstante, la economía no es la única razón para utilizar agregados, ya que además de ésta, le proporcionan al concreto
ventajas técnicas, dándole una mayor estabilidad volumétrica y durabilidad que las proporcionadas por el cemento solo.
El tamaño de los agregados utilizados en el concreto varía desde algunos centímetros hasta partículas muy pequeñas de
décimas de milímetro. Por otro lado, el tamaño máximo que se usa varía, pues en cualquier mezcla se incorporan partículas de diversos
tamaños. Ala distribución de las partículas según su tamaño se llama granulometría.
Para fabricar concreto de buena calidad, es común incluir agregados que entren en dos rangos de tamaño máximo. En el caso
del agregado fino (arena), el tamaño no debe ser mayor de 5 mm. y en el agregado grueso (grava), mayor de 5 cm.
Los agregados en general son de materiales naturales. Sin embargo, estos últimos se pueden fabricar con productos
industriales que, en términos generales, pueden ser más ligeros o más pesados.
Grava (agregado grueso); La grava se compone de guijarros de diversos tamaños que suelen encontrarse en depósitos.
Provienen de rocas duras, por lo que sus propiedades dependen de la roca original. La grava se encuentra en abundancia en México y,
de acuerdo con la necesidad de empleo, este material se puede requerir en diferentes dimensiones, las que varían de 1,2 hasta 5 cm.
Arena (agregado fino); Debe garantizarse que este material provenga de rocas disgregadas por la acción del tiempo y del
interperismo y que no tenga residuos de tierra, ya que esto afectaría su trabajo en la elaboración el concreto.
Por otro lado, la adherencia entre la pasta de cemento y los agregados es un factor importante para la resistencia del concreto,
especialmente la resistencia a flexión. La adherencia se debe, en parte, a que el agregado y la pasta se entrelazan debido a la aspereza
de la superficie del primero, es decir, el agregado tiene una superficie más áspera, como la de las partículas trituradas. La
determinación de la calidad de la adherencia de los agregados es muy difícil y no existen pruebas aceptadas.
32
TESIS PROFESIONAL
Un detalle muy importante en los agregados es su almacenamiento, es decir, se deberá hacer un esfuerzo para mantener el
contenido estable con respecto a la humedad, ya que esto es una de las causas más frecuentes de la pérdida de control de la
consistencia del concreto, medida a partir del revenimiento.
3.2.2.
Mezclas
Mezclar tiene como objetivo recubrir todas las partículas de agregado con la pasta de cemento y combinar todos los
componentes del concreto hasta lograr una masa uniforme. La eficiencia de la operación de mezclado radica en los detalles de diseño
de la mezcladora o traspaleado, pero la acción de descarga es siempre buena cuando todo el concreto puede volcarse con rapidez y
como una masa, sin segregación.
En la actualidad, se utiliza el llamado concreto premezclado, el cual se prepara en una planta y se entrega por medio de
camiones (revolvedoras) a la obra, ya listo para colocarse.
Una acción fundamental que debe realizarse en la mezcla del concreto es el proceso de compactación, el cual consiste en
eliminar el aire atrapado en él. Una forma de lograrlo es picando la superficie del concreto para desalojar el aire y lograr acomodar las
partículas adecuadamente, es decir, ocupando los espacios vacíos.
Actualmente, el sistema moderno es el denominado vibrado, el cual se realiza con una herramienta llamada vibrador. Al utilizar
estos vibradores, podemos hacer mezclas más secas que las que pueden compactarse a mano.
El diseño de mezclas se resuelve en el proporcionamiento de los ingredientes, incluida el agua para obtener la resistencia
requerida. Las proporciones de una mezcla de concreto se estipulan por peso o por volumen; por ejemplo, una mezcla de 1:2:3 Vá;
Significa una parte de cemento, dos partes de arena y tres y media partes de grava. Cabe hacer mención que existen varios métodos de
diseño de mezclas.
Relación agua-cemento
La resistencia de un concreto de determinada edad que haya sido curado depende fundamentalmente de dos factores:
a.
b.
La relación agua-cemento.
El grado de compactación.
Debemos recordar que la relación agua-cemento (a/c) determina la porosidad de la pasta de cemento endurecida en cualquiera
de sus etapas de hidratación, por lo que la relación agua/cemento así como el grado de compactación, afecta el volumen de cavidades
del concreto.
Amenor relación agua/cemento, mayor será la resistencia del concreto preparado.
33
TESIS PROFESIONAL
Concreto vibrado
Concretocon
compactación manual
Resistencia ala
compresión
Relación a/c
FIGURA3.4
Resistencia contra tipodevibrado.
Las proporciones del concreto deben seleccionarse para lograr el uso de los materiales disponibles para la producción de
concreto, con la manejabilidad, durabilidad y resistencias requeridas. Se han establecido relaciones fundamentales que proporcionan
guías para aproximarse a las combinaciones óptimas, pero las proporciones finales deben establecerse por medio de pruebas directas y
ajustes en la obra.
Para la estimación de proporciones a partir de relaciones establecidas, son necesarios algunos datos de laboratorio, es decir,
deben determinarse la granulometría, la densidad, y la absorción, tanto de los agregados finos como de los gruesos, y el peso
volumétrico. También debe saberse si el cemento es inclusor de aire o no. En en este sentido, incluir aire, mediante el uso de un
cemento con inclusor de aire o de un aditivo, mejora bastante la trabajabilidad del concreto y su resistencia al interperismo.
El concreto debe colocarse con la cantidad mínima de agua de mezclado, compatible con su manejo adecuado, ya que de ello
dependerá el aprovechamiento en resistencia, durabilidad y otras propiedades.
Para producir un concreto, el proporcionamiento debe seleccionarse:
a.
De la consistencia más seca (menor revenimiento) que permita colocarlo eficientemente hasta obtener una masa
homogénea.
b.
Con el tamaño máximo del agregado disponible, a fin de lograr una mezcla económica y que pueda tener una colocación
satisfactoria.
c.
De durabilidad adecuada para resistir el interperismo y otros agentes destructores.
d.
De la resistencia requerida para resistir, sin peligro de falla, las cargas a las que estará sujeto.
34
TESIS PROFESIONAL
Un mezclado completo es esencial para laproducción de u nconcreto uniforme. Por lo tanto, el equipo ylos métodos empleados
deben ser capaces demezclar eficazmente los materiales componentes del concreto. Esrecomendable controlar tanto el tamaño del
agregado grueso como su revenimiento adecuado, es decir, que sea práctico para el trabajo.
3.2.3.
Pruebas en el concreto
Prácticamente, todas lasramas dela ingeniería, especialmente aquellas que tratan con estructuras y máquinas, conciernen
íntimamente alos materiales cuyas propiedades mecánicas deben ser determinadas por medio de ensayes.
Conocer los resultados delos ensayes esimportante para los ingenieros, aun para los que noseocupan delarealizaciónde
estas pruebas, ya quees fundamental poseer u n acompresión general de losmétodos comunes de ensaye, así como delo que
constituye un ensaye válido.
También esimportante tener idea clara delos aspectos básicos que una prueba requiere, para que los resultados obtenidos
reflejen larealidad lomás aproximadamente que sepueda. En este sentido, podemos establecer los aspectos más importantes queu n
ensaye debe cumplir:
1.- Técnica del ensaye.
2.- Principios físicos ymecánicos involucrados en el aparato.
3.- Teoría de las mediciones.
4.- Variabilidad de los materiales.
5.- Interpretación de los resultados.
Es obvio recalcar que el ensaye de laboratorio no debe usarse como sustituto delpensamiento. Antes de emprenderlo, el
propósito de una prueba de esta naturaleza debe entenderse bien yel carácter general de los resultados debe ser previsto. La magia de
los ensayes noreside eniniciarlos y esperar lo mejor, sino enlos resultados delaplaneación cuidadosa e inteligente, así como en el
proceso de resolver dificultades.
Un experimento oensaye permanece inconcluso hasta que secomprueba einterpreta. Los ensayes siempre están sometidos a
condiciones especiales y losresultados nose pueden informar hasta quese tenga u n ainterpretación práctica. Para el casodel
concreto, yasetienen pruebas perfectamente bien diseñadas para obtener las características importantes que los proyectistas deben
conocer.
Las pruebas más importantes que en el concreto reforzado se realizan son:
1.- Características del concreto fresco.
2.- Ensaye acompresión del concreto.
3.- Ensaye atensión del concreto.
4.- Ensaye de tensión en el acero de refuerzo.
35
TESIS PROFESIONAL
3.2.4
Aditivos para
concreto
Es común que, en lugar de usar un cemento especial para atender un caso particular, a éste se le puedan cambiar algunas
propiedades agregándole un elemento llamado aditivo.'
Un aditivo es un material diferente a los normales en la composición del concreto, es decir, es un material que se agrega
inmediatamente antes, después o durante la realización de la mezcla con el propósito de mejorar las propiedades del concreto, tales
como resistencia, manejabilidad, fraguado, durabilidad, etc.
En la actualidad, muchos de estos productos existen en el mercado, y los hay en estado líquido y sólido, en polvo y pasta.
Aunque sus efectos están descritos por los fabricantes, cada uno de ellos deberá verificarse cuidadosamente antes de usarse el
producto, pues sus cualidades están aún por definirse.
Los aditivos más comunes empleados en la actualidad pueden clasificarse de la siguiente manera:
1.- Inclusores de aire.- Es un tipo de aditivo que, al agregarse a la mezcla de concreto, produce un incremento en su contenido
de aire provocando, por una parte, el aumento en la trabajabilidad y en la resistencia al congelamiento y, por otra, la
reducción en el sangrado y en la segregación.
2.- Fluidizantes.- Estos aditivos producen un aumento en la fluidez de la mezcla, o bien, permiten reducir el agua requerida
para obtener una mezcla de consistencia determinada, lo que resulta en un aumento de la trabajabilidad, mientras se
mantiene el mismo revenimiento. Además, pueden provocar aumentos en la resistencia tanto al congelamiento como a los
sulfatos y mejoran a la adherencia.
3.- Retardantes del fraguado.- Son aditivos que retardan el tiempo de fraguado inicial en las mezclas y, por lo tanto, afectan
su resistencia a edades tempranas. Estos pueden disminuir la resistencia inicial. Se recomienda para climas cálidos,
grandes volúmenes o tiempos largos de transportación.
4.- Acelerantes de la resistencia.- Éstos producen, como su nombre lo indica, un adelanto en el tiempo de fraguado inicial
mediante la aceleración de la resistencia a edades tempranas. Se recomienda su uso en bajas temperaturas para adelantar
descimbrados. Además, pueden disminuir la resistencia final.
5.- Estabilizadores de volumen.- Producen una expansión controlada que compensa la contracción de la mezcla durante el
fraguado y después la de éste. Se recomienda su empleo en bases de apoyo de maquinaría, rellenos y resanes.
6.- Endurecedores.- Son aditivos que aumentan la resistencia al desgaste originado por efectos de impacto y vibraciones.
Reducen formación de polvo.
También se cuenta con otro tipo de aditivos cómo son loa impermeabilizantes, las membranas de curado y los adhesivos.
Dentro de las aplicaciones comunes en donde se utilizan aditivos, se encuentran las siguientes:
36
TESIS PROFESIONAL
a.
Construcción de cisternas y tanques en la que se emplean impermeabilizantes.
b.
Para llevar concreto a alturas elevadas por medio de bombeo, se pueden aplicar aditivos fluidizantes y/o retardadores
del fraguado.
c.
En la reparación de estructuras dañadas, donde se debe ligar concreto viejo con un nuevo, se utilizan aditivos
adhesivos.
d.
En colados, donde las temperaturas son bajas, usamos aditivos Inclusores de aire para obtener concretos resistentes al
efecto del congelamiento.
e.
Para el correcto y eficiente anclaje de equipo y maquinaría se usan aditivos expansores, los cuales proporcionan
estabilidad dimensional a las piezas por anclar.
Es obvio volver a recalcar que el uso de aditivos debe hacerse conociendo, en primera instancia, el requerimiento y, de esta
manera, poder definir adecuadamente el producto a emplear. También es de suma importancia conocer perfectamente las
características del aditivo que deberemos utilizar para obtener los resultados esperados.
3.3.
ACERO DE
REFUERZO
Como ya se vio, la principal función del acero en un elemento de concreto reforzado consiste en remediar la falta de resistencia
a la tensión del concreto simple. Esta función la puede realizar el acero gracias a la adherencia entre este y el concreto, con lo que se
logra una liga íntima entre ambos materiales.
Otra circunstancia que ha hecho posible la combinación de los dos materiales es que sus coeficientes de dilatación térmica
difieren poco.
Aunque el refuerzo de acero suple la escasa resistencia del concreto a la tensión no evita el agrietamiento. El agrietamiento
excesivo es indeseable por razones de apariencia y porque puede afectar la durabilidad de la estructura al permitir la corrosión del
refuerzo. Comúnmente se considera tolerable un ancho de grieta del orden de 0.30 mm.
El acero de refuerzo también realiza otras funciones de interés, por ejemplo: En columnas y en las zonas comprimidas de
algunas vigas, se utiliza el acero para aumentar la resistencia a la compresión del concreto. En la forma del suncho mejora la
ductilidad de los elementos de concreto reforzado. Por último sirve para controlar los agrietamientos producidos en elementos
estructurales restringidos por los cambios volumétricos debidos a temperatura, contracción y dilatación.
37
TESIS PROFESIONAL
Propiedades del a c e r o de refuerzo
El acero para reforzar el concreto se utiliza en distintas formas. La más común es la varilla de distintos diámetros que pueden
ser lisa o tener corrugaciones para mejorar sus características de adherencia.
En México se fabrican con diámetros que varían de lA"a 1 Vi".En muros y losas se utilizan con frecuencia mallas formadas por
retículas de barras soldadas en las intersecciones. En concreto pre-forzado se usan alambres, barras lisas o corrugadas y torones
formados por varios alambres trensados. Ocasionalmente el refuerzo puede consistir en perfiles laminados.
Varillas
Las varillas se pueden hacer laminando el acero en caliente o sometiendo al resultado de este proceso un tratamiento en frío.
Generalmente, el tipo de acero se clasifica en grados de acuerdo con su límite de fluencia mínimo, es decir, 30,42 y 52 kg/mm 2 ,
los que se designan, respectivamente, como de grado 30,42 y 52.
Las pruebas que se realizan en el acero de refuerzo son la de tensión y compresión; sin embargo, la más común es la de tensión
ya que la de compresión presenta un problema en su realización debido a la esbeltez de la probeta. La prueba de tensión se lleva a
cabo mediante el ensaye de una probeta de 25 cm. de longitud sometida a una carga de tensión hasta la ruptura de la varilla (el
diámetro puede ser cualquiera de los conocidos).
De esta prueba, se obtiene la gráfica de la curva de esfuerzo-deformación, en donde se distinguen las siguientes zonas:
ZONA "A*.-Comportamiento elástico. Termina en el límite de proporcionalidad. (Módulo de elasticidad).
ZONA "B" .- Zona de transición (Entre el comportamiento elástico y comportamiento plástico).
ZONA " C .- Zona de fluencia. (fy=kg/cm2).
ZONA"D".- Endurecimiento por deformación.
ZONA"E" .- Estrangulamiento y fractura.
38
TESIS PROFESIONAL
CURVA DE ESFUERZO- DEFORMACIÓN
(Acero laminadoen caliente)
El esfuerzo de fluencia (fy) es el índice mas comúnmente utilizado para caracterizar a un acero. En México se dispone de varillas
laminadas en caliente con esfuerzos de fluencia de:
2 300 - 4 200 kg/cm 2
Los aceros trabajados en frío disponibles en México tienen esfuerzos de fluencias convencionales que varían de:
4 000 - 6 000 kg/cm 2
En otras palabras los aceros laminados en caliente son mas dúctiles que los trabajados en frío. Lo mismo puede decirse de los
aceros de resistencia baja con respecto a los de alta resistencia. Un acero laminado en caliente de resistencia no muy alta puede tener
deformación de ruptura hasta del 20% en una longitud de medición de 20 cm. Mientras que en un acero torcido en frío tiene
comúnmente deformación de ruptura entre el 5 y 12%.
39
^••••••••••••••¡¡^^••^^^^^•^•••^^^•••••^^•^^^•i^^^HBBMBHI
PROFESIONAL
•••IHHHBMMHHi
Otro índice se obtiene mediante la prueba de doblado que consiste en comprobar si la varilla puede doblarse sobre un perno de
diámetro variable según el diámetro de la varilla.
La pendiente de la porción recta inicial de las curvas esfuerzo-deformación, define el Módulo de Elasticidad.
Es= 2 000 000 kg/cm 2 ó Es= 2x10 6 kg/cm 2
Las características esfuerzo-deformación en compresión suelen considerarse iguales a la tensión. Una propiedad importante que
debe tenerse en cuenta en refuerzos con detalles soldados es precisamente la soldabilidad.
Yacero = y s = 7 800 kg/m 3 => Peso volumétrico del acero.
Ctacero = Cts =0.00001/°C => Coeficiente térmico del acero.
Todas las varillas con excepción del alambre de %" tienen corrugaciones en la superficie para mejorar sü adherencia con el
concreto.
TABLA3.7.
Diámetro, pesoyárea devarillas.
Diámetro
Diámetro
Area
(cm?)
Peto
(kg/ml)
2
3/4
6.4
0.32
0.248
2.5
5/16
7.9
0.49
0.388
3
3/8
9.5
0.71
0.559
4
1/2
12.7
1.27
0.993
5
5/8
15.9
1.98
1.552
6
3/4
19.0
2.85
2.235
7
7/8
22.2
3.88
3.042
8
1
25.4
5.07
3.973
10
1 1/4
31.8
7.92
6.207
12
1 1/2
38.1
11.4
8.938
Var.No.
40
TESIS PROFESIONAL
3.4.
CONCRETO
REFORZADO
El concreto reforzado es un material heterogéneo formado por la combinación del concreto simple y el acero. La combinación
permite el aprovechamiento eficiente de las características óptimas de los materiales integrantes; La gran resistencia a la tensión del
acero y la economía con que el concreto simple soporta compresiones.
El acero se utiliza en las zonas de los elementos estructurales sujetas a tensión para suplir la escasa resistencia del concreto
simple a este tipo de esfuerzo.
Aunque el concreto reforzado es un material de construcción relativamente moderno es en la actualidad uno de los usos mas
común. Su naturaleza moldeable permite al proyectista una gran libertad en la elección de formas estructurales.
El concreto se coloca en estado plástico, en moldes a los que es fácil dar las formas mas complejas que caracterizan a la
Arquitectura contemporánea como son: cascarones, arcos, elementos prefabricados para soportar cargas y elementos prefabricados
para fachada.
No existen restricciones propias de las estructuras de acero en que el diseñador esta obligado a usar los elementos laminados
estándar disponibles en el mercado.
El concreto reforzado por acero y adecuadamente distribuido, al endurecer forma un conjunto estructural monolítico en la que
la continuidad con todas sus ventajas se obtienen de una manera natural. El proyectista puede jugar con la dosificación del concreto,
el tamaño de los elementos estructurales y la distribución del acero para resolver los problemas funcionales que se plantean con la
mayor eficiencia posible.
Evidentemente la multitud de opciones que se presentan eleva el costo de diseño. En efecto en los E.U.A. algunos ingenieros
constructores consideraban que el costo de diseñar una estructura de concreto es del 20-40% mayor que el diseñar una estructura de
acero equivalente.
41
^^^^^^•^^^•^^^•^^••^•••••••^•iMHHHHHIHHBHBHHBHBHHHHBMi^^HHH
_
A
^
4.1.
PROFESIONAL
gg^ggggggjgg^gjgg
Diseñoestructural de
elementosde casahabitación
ESTRUCTURACIÓN
El proceso de estructuración consiste en la creación de un modelo teórico que representa aceptablemente ala estructura realy
nos permite desarrollar el proceso de análisis estructural de lamanera más fácil. La manera de expresar gráficamente este procesoes
por medio deu nproyecto estructural, elcual, apartir del empleo decierta simbología, nos indica ladisposición delos elementos
estructurales en la construcción representada. La creación de este modelo teórico implica forzosamente realizar ciertas simplificaciones
a larealidad constructiva, pero no hacerlo acarrearía graves complicaciones alanálisis. Un ejemplo de estas simplificaciones setiene
en u n muro quecontiene aberturas (puertas, ventanas, troneras, etc.) queserán reforzadas concerramientos enlarealidad
constructiva; considerar estas irregularidades nos conduciría au nproblema de difícil solución. La consideración de lallamada línea
resistente, esdecir, elnoconsiderar estas aberturas sisudimensión noesgrande (dos metros enplanta, por ejemplo) simplifica
notablemente el cálculo.
En elproyecto estructural setrabaja endiversos niveles endonde sedisponen los elementos estructurales. Dichos nivelesse
denominan (a partir del inferior): nivel de cimentación, nivel del primer entrepiso, del segundo entrepiso, etc. y, finalmente, azotea.En
contraste, enel proyecto arquitectónico seconsideran volúmenes habitables: planta baja, primer piso oplanta alta, etc. De esta
manera, enuna casa-habitación dedos niveles, elnivel deentrepiso representa latapa delaplanta baja con todos los elementos
estructurales que contiene,yel nivel de azotea representa la tapa de la planta alta.
El criterio para realizar una correcta estructuración (es decir, u n buen proyecto estructural) se adquiere através del tiempo ya
partir de la experiencia; sin embargo, es posible aplicar ciertas reglas sencillas para lograr resultados aceptablemente buenos:
a).
Estudie el plano arquitectónico cuidadosamente. Establezca la disposición de los muros yde los locales que contengala
construcción.
b).
Observe lacoincidencia demuros situados enniveles sucesivos para así plantear los muros que serán de carga ylos
divisorios.
42
TESIS PROFESIONAL
c).
Defina las puertas, ventanas, troneras y, en general, las aberturas que contenga cada muro para juzgar si se considera
la colocación de una trabe que cubra el claro o si se considera una línea resistente. Como regla aproximada, tome como
línea resistente un muro macizo o que tenga aberturas con longitudes menores o iguales a dos metros en planta.
d).
Analice si es posible plantear tableros de mediana dimensión en planta baja para evitar un excesivo gasto en tramos de
cimentación. Un tablero puede cubrir locales pequeños como medios baños, alacenas, etc., mediante la disposición de
muros divisorios entre ellos.
e).
Recuerde que es conveniente repetir en azotea las trabes que se planteen en entrepiso con carga de muro para así
aligerar la carga sobre éstas.
Slmbologia
Para poder dibujar adecuadamente un proyecto estructural, es necesario tener una simbología que no necesariamente
corresponderá ni a la del proyecto arquitectónico ni a la del plano constructivo. Recuérdese que el proyecto estructural sólo lo verá en
la mayoría de los casos el ingeniero calculista.
Una nomenclatura conveniente puede ser la considerada en la figura 4.1.
-ffi%%%%%%^/>&m%k-
INDICA MURODE CARGA
—I
INDICA MURODIVISORIO
I^T^L
m_
INDICA
TRABEPRIMARIA
INDICA LIMITEDELOSA EN VOLADO
jj
INDICA CASTILLO
|
INDICA COLUMNA
FIGURA4.1
Nomenclatura para elproyecto estructural
En la nomenclatura mostrada anteriormente, se mencionan los castillos de carga. En este caso no se refiere a los elementos
constructivos que aparecen en cada intersección de muros y a ciertas distancias contenidas en los muros, sino a los que reciben el
efecto de una concentración.
43
TESIS PROFESIONAL
También se mencionan los muros divisorios. Estos deberán representarse sobre el nivel donde aplican su carga pues su efecto
puede transformarse en una carga equivalente de acuerdo al método reglamentario. La carga mencionada se añadirá a las cargas
permanentes (cargas muertas) y variables (cargas vivas) para su posterior transmisión hacia la cimentación.
La forma practica de realizar el proyecto estructural es colocar un papel albanene o mantequilla sobre cada planta
arquitectónica y dibujar los elementos estructurales que contiene cada nivel (entrepisos, azoteas) siguiendo la nomenclatura
mencionada anteriormente. Se sugiere seguir el siguiente orden:
1.-
Defina provisionalmente los elementos estructurales del nivel de entrepiso. Coloque un albanene sobre la planta
arquitectónica de la planta baja. Defina tableros de tamaño adecuado y haga caso omiso de pequeños locales,
resolviendo mejor estos casos con muros divisorios que se apoyan en el firme de planta baja. Recuerde que los muros de
carga y líneas resistentes definen los tramos de cimentación que soportarán la superestructura. En consecuencia, una
cantidad excesiva de tableros conduce a una cimentación muy congestionada.
2.-
Coloque el albanene anterior con la planta estructural del entrepiso sobre la planta arquitectónica de la planta alta. De
esta manera, establecerá la coincidencia entre muros de planta alta y planta baja, muros que deberán actuar como
divisorios sobre tableros de entrepiso y las trabes que soportarán muros de planta alta.
3.-
Coloque ahora otro albanene sobre la planta arquitectónica de planta alta y defina los tableros de la losa de azotea. De
preferencia, repita en azotea las trabes que coinciden con las de entrepiso y que soportan muros, para aligerar la carga
de las de entrepiso y lograr que no resulten tan voluminosas (figura 4.2.). Recuerde que en la representación de la losa
de azotea no deben colocarse muros divisorios en planta alta, pues estos deben representarse en el nivel de entrepiso.
Verifique que los castillos de las trabes de azotea tengan prolongación hasta la cimentación, condición que es preferible.
Trabe en azotea
Muro divisorio
Trabe en entrepiso
Piso de planta baja
FIGURA 4.2.
Colocación de trabe de azotea que refleja la de entrepiso.
44
TESIS PROFESIONAL
4.2.
T R A N S M I S I Ó N Y BAJADA DE C A R G A S
El objetivo de este proceso es establecer un valor de carga sobre terreno que nos permita calcular las dimensiones de la
cimentación para cada tramo
Transmisión d e c a r g a s
La transmisión de cargas hacia el perímetro de los distintos tableros principia con el cálculo de la carga W por metro cuadrado
de los distintos sistemas constructivos. Una vez resuelto éste punto se deberá calcular la carga que se transmite hacia el borde del
tablero analizado. Este cálculo toma en cuenta el área tributaria (figura 4.3) que le corresponde a cada borde del tablero. De hecho, la
forma de dicha área nos indica la forma en que teóricamente varían las cargas en cada borde (triangularmente en los claros cortos y
trapezoidal en los largos). Sin embargo, se ha demostrado que la carga actúa en forma muy uniforme en el perímetro del tablero, por lo
que el peso del área tributaria se considera uniformemente distribuido en el borde correspondiente.
Para realizar el cálculo mencionado se calculan primero las superficies de las áreas tributarias:
El peso en kg de las distintas áreas tributarias se calcula multiplicando la superficie de cada una de ellas por el peso W en
kg/m 2 del sistema (es decir, el número de metros cuadrados multiplicado por lo que pesa cada uno de ellos).
Finalmente, si se desea realizar la bajada por franja unitaria (un metro de ancho), se calcula la carga w en cada metro lineal
mediante la división del peso obtenido en el paso anterior entre la longitud del tramo analizado, es decir, entre la longitud de la base
del triángulo o trapecio correspondiente.
a2
Area deltriangulo =bxh/2
Area deltrapecio =(B+b)h/2
t
AREADEL
TRAPECIO
ai
i
ANÁLISIS TRAMOCORTO:
WL= WvAi/ai
AREADEL
TRIANGULO
ANÁLISIS TRAMOLARGO:
WL= WvA2/a2
FIGURA 4 . 3 . Áreas tributarias y transmisión de carga en tableros rectangulares con carga perimetral.
45
TESIS PROFESIONAL
Peso por metro lineal de muros.- para realizar este cálculo, nuevamente se recurre al peso Wpor metro cuadrado, correspondiente al
sistema constructivo del tipo de muro que analicemos. Posteriormente, se calcula la carga w por metro lineal mediante la
multiplicación del peso Wpor la altura del muro en cuestión (figura 4.4).
CD = W h
h
<
co;carga (kg/m)
W; peso (kg/m2)
h; altura de muro
•
1m
FIGURA 4.4.
Carga por metro lineal en b a s e de m u r o s .
Peso por metro lineal de volados.- en el caso de volados, la carga w que aplican por medio lineal a todo lo largo de su apoyo equivale
al peso Wpor metro cuadrado multiplicado por la longitud del claro.
B a j a d a d e c a r g a s hacia la cimentación
Este proceso se desarrolla mediante la suma de las cargas por metro lineal que transmite un tablero hacia el borde analizado y
las cargas por metro lineal que transmite un muro. Este proceso se repite tantas veces como pisos se tengan (figura 4.5).
En la figura 4.5 puede observarse la representación de la bajada de cargas. En este caso, la suma mencionada sería la
siguiente:
C a r g a SObre C i m i e n t o = W s / c = W azo te» + W muro l + W entrepiso + W m U ro2
46
TESIS PROFESIONAL
coLosa entrepiso
co Azotea
a Azotea
co Muro p. alta
iQJosaerurepiso
coEntrepiso
coEntrepiso
(oMuro D. baia
co Muro p. baia
Carga sobre cimiento
Carga sobre cimiento
FIGURA 4.5.
Bajada de cargas sobre cimentación.
Esta carga sobre cimiento a c t ú a sobre la parte superior de la cimentación y debe agregársele el peso propio por metro lineal de
dicha cimentación. Si recordamos que el objetivo de este cálculo e s definir las dimensiones de la cimentación, sólo podemos hacer u n a
estimación de dicho peso propio, p a r a lo cual se considera a éste como u n porcentaje de entre el 2 0 % y 2 5 % de la carga sobre la
cimentación:
Carga sobre terreno = w s /t = 1.10 (w s / c )
Este valor e s el que será empleado p a r a calcular las dimensiones de la cimentación.
Manejo de concentraciones:
El manejo de las fuerzas c o n c e n t r a d a s r e p r e s e n t a n u n problema que tradicionalmente se ignora, lo q u e
ocasiona u n diseño deficiente de la cimentación y, por lo t a n t o , posibles a s e n t a m i e n t o s locales. Los esfuerzos en el terreno, producto de
las concentraciones, dependen de la forma que tienen é s t a s p a r a transmitirse a través de la cimentación. Específicamente, los
esfuerzos en el suelo son función de la rigidez del sistema cimentación-dala de repartición, p u e s t o que de lo anterior depende la forma
en que se distribuye la carga.
47
TESIS PROFESIONAL
Existen ciertos casos en que la dala de repartición y la m i s m a cimentación no c u e n t a n con la rigidez como p a r a poder evitar los
a s e n t a m i e n t o s locales. En estos casos, podremos establecer criterios de distribución de las concentraciones considerando que los
esfuerzos en el terreno se i n c r e m e n t a r á n en la vencidad de las cargas debido a la falta de rigidez mencionada.
El primero de estos criterios establece que la fuerza se t r a n s m i t e mediante el empleo del mismo m u r o como medio de
distribución hacia el nivel inferior; p a r a este caso se requerirá u n a u m e n t o en el a n c h o de la cimentación p a r a equilibrar la o las
concentraciones que a c t ú a n sobre el m u r o .
El segundo criterio considera a los castillos como elementos de transmisión; p a r a este caso se requerirá u n a ampliación de base
debajo del p u n t o de concentración, a nivel de terreno, p a r a dicho equilibrio.
Ácontinuación se describirá c a d a criterio de los mencionados anteriormente:
Transmisión
de concentraciones
por medio de muros: el criterio p a r a calcular la carga uniforme en k g / m . , carga c o n c e n t r a d a (wc)
en la b a s e de u n m u r o producida por u n a concentración implica dividir el valor C de la concentración entre u n a distancia que depende
del ángulo de transmisión de la fuerza. E n este caso, se considera u n ángulo de transmisión que equivale al de falla por cortante de la
manipostería empleada en m u r o s . Un valor conveniente de dicho ángulo es de 45°, p u e s n o s permite calcular la distancia como u n a
equivalencia de la a l t u r a del m u r o . De este modo, las expresiones típicas p a r a algunos casos de transmisión de concentraciones se
m u e s t r a n en la figura 4.7
c
\
Caso 1
A
// \\ \
/
\
í
•
/
h
Ü)c
1
//
/
//
/
//
//
/
\
/
Caso 2
\v
\\
(Oc
COc
\\
\\
\\
\
\
2h
Caso 1: CÚC = C/h
Caso 2: Wc = C/2h
48
TESIS PROFESIONAL
Ca
Ci
Caso 3
C2
í
/
í
Caso 4
h
, ' ' (Oc
\
tócl
I
Caso 4: (ÚC= Ci/h =C2/I1
Caso 3:roc= (Ci+C2)/h
FIGURA.4.6.
0)c2
Diversos casos de transmisión de concentración en muros.
Transmisión
de concentraciones
por medio de castillos: este criterio e s m á s sencillo de aplicar p u e s implica transmitir el valor
íntegro de la concentración C directamente h a s t a la cimentación, en el p u n t o donde se aplica. Posteriormente, se deberá diseñar u n a
ampliación de b a s e a nivel de terreno o optar por u n a z a p a t a aislada de concreto.
4.3.
D I S E Ñ O
DE
LA
C I M E N T A C I Ó N
Las cimentaciones son los elementos e s t r u c t u r a l e s encargados de transmitir las c a r g a s de la e s t r u c t u r a a los estratos
resistentes del terreno, con la finalidad de reducir o evitar h u n d i m i e n t o s y el volteo provocado por la acción de las cargas horizontales.
Otra aplicación de las cimentaciones la e n c o n t r a m o s en b a s e s p a r a m á q u i n a s , en donde su función recae en la absorción de las
vibraciones producidas por el equipo.
En general, se puede decir q u e existen dos tipos de cimentaciones a las cuales podemos clasificar en:
1.-
Cimentaciones superficiales.
2.-
Cimentaciones profundas.
49
TESIS PROFESIONAL
Las cimentaciones más comunes para viviendas unifamiliares, duplex, etc. son las del tipo superficial, siendo las más típicas:
las zapatas aisladas, corridas y losas de cimentación, las cuáles generalmente son de mampostería o de concreto reforzado.
Zapatas aisladas: este tipo de cimiento recibe las descargas de la superestructura por medio de columnas, es decir, puntualmente,
asignándose una zapata por columna en la base de ésta (figura 4.9).
COLUMNA
DADO
ZAPATA
FIGURA4.7.
Zapata aislada.
Zapatas corridas: este tipo de cimiento recibe las descargas de la superestructura de manera lineal o puntual, siguiendo la
distribución de ejes de columnas o muros.
Losas de cimentación: cuando una estructura se va a desplantar en terrenos de baja resistencia (alta compresibilidad), y la descarga
de la estructura no es demasiado grande, se puede optar por una losa de cimentación que distribuya el peso de la estructura en toda el
área de desplante de la construcción a través de las contratrabes.
Los materiales más comunes que se emplean en la construcción de las cimentaciones, como ya se dijo anteriormente, son el
concreto reforzado y la mampostería, cuya elección depende entre otras cosas de los materiales existentes en la zona, la profundidad de
desplante, la intensidad de las cargas y, desde luego, la capacidad del terreno.
50
TESIS PROFESIONAL
•4.3.1.
Cimientos de c o n c r e t o
reforzado
4 . 3 . 1 . 1 . Zapata corrida de concreto reforzado
Procedimiento de cálculo
S.C. Momento
TV.- Revisión por momento flexionante,
en donde el momento
flexionante
se analiza como un empotramiento
en
"cantiliver".
S.C. Cortante
C
<
>
i
BaBSCBOBcSES
Wn
S.C.=(B-C)/2
<
>
I.- Clasificación
de la zona geotécnica
del terreno, con el
fin de determinar la capacidad de carga admisible del suelo.
II.- Cálculo de la base, mediante la expresión:
„
B =-
Cara a sobre cimiento
•
-Cap. carga del suelo - Peso propio cimentación
III.- Revisión de esfuerzos,
ton/m
=- - - - - - = m
ton/m
mediante la expresión:
Qu =
Peso
Area
ton
m2
Condición:
la ^Qu
Si no se cumple la condición se deberá proceder a una
ampliación de base hasta que esta cumpla con la condición.
W„l¿
M„
V.- Cálculo de peralte
formula:
Q=-
efectivo
M„
Frbd2 f'c
kg -cm
u
d", utilizando
d=
la
siguiente
M„
Frbf'cQ
El valor de "Q" se obtiene, proponiendo un porcentaje de acero,
con el fin de obtener el valor de "q" y de esta manera utilizar la
gráfica de "Momentos resistentes de secciones
rectangulares".
q =p
IJL
f"c
51
TESISPROFESIONAL
• • • • • • • • • • • • • H
VI.- Cálculo de peralte total "hn
X.-Cálculo de separación de acero
hT =recubrimiento + peralte efectivo +diámetro var illapropuesta
S = — ? — .-. as; es el área de la varilla a utilizar
hT =r +d + </>var
Vll.-Cálculo de área de acero principal,
porcentaje de acero propuesto:
conforme al
min = pbd
Esfuerzo que resiste el concreto =Vc =Fr0.5jf *c
•'• b = 100 cm
Area de acero requerido =As =
cortante
Esfuerzo cortante que resiste la sección de concreto (Vcr) al
cortante en una "zapata corrida"para un "b"y "d" dados.
,•
„
0-7JTc
Porcentaje mínimo de acero =Pmin =———
f'y
As
XI.- Revisión de fuerza
transversal:
ppn,puestbd
Fuerza que resiste la sección =Vcr =bdVc
Condición :
XII.- Cálculo de fuerza cortante exterior o última (Vu)
Vu =VsxF.S. .: Vs =WnxL
Vlll.-Cálculo
de
(longitudinal).
separación
de
acero
principal
Condición :
V
>V
S =~§—- .-. a • es el área de la varilla a utilizar
As
Condición :
Smax <3h
ÍX.-Cálculo de área de acero
transversal:
Asr =0.002bh :. b =100 cm
52
TESIS PROFESIONAL
4 . 3 . 1 . 2 . Zapatas aisladas de concreto reforzado
Procedimiento de cálculo
IV.- Revisión
w
de esfuerzos,
1
mediante la expresión:
<lu
Peso
Area
ton
m
Condición:
Qa ><lu
Si no se cumple la condición se deberá proceder a una
ampliación de base hasta que esta cumpla con la condición.
V.- Revisión
B
I.- Clasificación
de la zona geotécnica
del terreno,
de peralte
por esfuerzo
cortante
con el
losa:
t d/2
fin de determinar la capacidad de carga admisible del suelo.
II.- Cálculo del peralte
como
efectivo:
1.- Se propone un peralte total, considerando
el peralte
mínimo.
B
Km = 15 cm
d =hT-rL<t>var :.
hT; es el peralte
propuesto.
rL; es el recubrimiento libre.
<j>var; es el diámetro de la var illa
1.- Cálculo de esfuerzo
cortante
último.
propuesta.
v,.-~ b„d
III.-
Cálculo de la base, mediante la expresión:
•Carga sobre cimiento
I Cap. de carga suelo
W
W„
,
Vu = (WnxaxB)F.S
b0=4(c + d)
=> La fuerza cortante
última.
53
TESIS PROFESIONAL
2.- Cálculo de esfuerzo
cortante
que resiste el
concreto.
VIL- Revisión por
flexión:
Vcr=FrJf*c
<
C
>
Condición :
Vrr
1
V\,
>
VI.- Revisión por esfuerzo
OQ0O9GUuaOHDa
cortante
como
trabe:
•Wn
S.C.=(B-C)/2
<
>
B
S.C. de cortante
^ como trabe
1.- Cálculo de momento flexionante
M„
B
W„L
2
2.- Cálculo de área de acero
1.- Cálculo de esfuerzo
cortante
:. L = S.C.
B-C
2
principal
último.
A - __. _ JÍ
Bd
Vu =(WnxaxB)F.S.
máximo
:. a =
• a;es un valor que se propone
Frf'y(d-a/2)
B-C
3.- Cálculo de área
mínimo
z
4c
2.- Cálculo de esfuerzo
cortante
que resiste el
concreto.
—
-°- B.d
o.iJrc
f'y
Ver= 0-5 lf*C
Condición :
v„
> v\
54
TESIS PROFESIONAL
4.4
D I S E Ñ O Y R E V I S I Ó N DE
4.4.1.
Muros sujetos a cargas
MUROS
verticales
Las cargas verticales se derivan fundamentalmente del funcionamiento de la construcción, es decir, estas cargas corresponden
al peso propio de la estructura y acabados, así como a las cargas generadas por el uso de la edificación.
En una estructura de manipostería, estas cargas serán soportadas por los muros, los cuales se llaman muros de carga y cuya
función principal es la de soportar y transmitir las cargas a la cimentación. De esta manera simple, se puede establecer la forma de
resistir estas cargas las disposiciones que el reglamento estipula para el análisis y revisión de muros sujetos a la acción de cargas
verticales.
Disposición reglamentarla
El RCDF establece que la resistencia de los muros a cargas verticales debe ser mayor o igual a la carga vertical última en cada
muro de la estructura, es decir:
P R > PU
En donde Pu es la carga vertical actuante debida al peso propio, al peso de las losas y al generado por el funcionamiento de la
construcción, cuya suma será multiplicada por el factor de carga respectivo y que, en este caso, corresponde a FC= 1.4, el cual es el
que debe aplicarse para combinaciones de cargas muertas y cargas vivas.
Por otro lado, el reglamento establece que, para determinar las fuerzas internas en los muros, es necesario hacer un análisis
elástico. Además, considera que la mampostería no resiste tensiones en dirección normal a lasjuntas y, por lo tanto, debe realizarse un
análisis más adecuado en caso de la aparición de tensiones.
Criterio d e análisis d e muros por c a r g a vertical del RCDF
El reglamento establece el criterio para la revisión de muros sometidos a la acción de las cargas verticales, criterio que se indica
a continuación:
Para analizar muros que están sujetos a la acción de cargas verticales, se deberá considerar lo siguiente:
1.-
En las juntas de muros y pisos ocurren rotaciones locales debidas al asentamiento del mortero, por lo que se considera
que la junta tiene capacidad de rotación, lo que genera en ese lugar una articulación que provoca que los momentos
sean nulos.
2.-
Para el diseño solo se tomarán en cuenta los momentos debidos a los efectos siguientes:
55
TESIS PROFESIONAL
a).
Los momentos que deben ser resistidos por condiciones de estática y que no pueden ser distribuidos por la
rotación del nudo, como son los momentos debidos a un voladizo que se empotre en el muro y los debidos a
empujes de viento o sismo normales al plano del muro.
b).
Los momentos debidos a la excentricidad con que se transmite la carga de la losa del piso inmediatamente
superior en muros extremos. Tal excentricidad será tomada como la siguiente expresión:
e =t / 2 - b / 3
donde:
t; es el espesor del muro.
b; es la porción de muro en donde se apoya la losa soportada por el mismo.
Será admisible determinar las cargas verticales que actúan sobre cada muro mediante una bajada de cargas por áreas
tributarias, siempre que se tomen en cuenta los efectos de esbeltez y excentricidad recomendados reglamentariamente, y que además
cumpla con lo siguiente:
1.-
Las deformaciones en los extremos del muro están restringidas por el sistema de piso que se liga a los muros mediante el
refuerzo vertical de éstos.
2.-
No hay excentricidades importantes en la transmisión de las cargas, ya que las losas se apoyan directamente sobre los
muros sin volados ni cargas concentradas.
3.-
La relación altura entre espesor del muro es menor a 20.
h / e m < 20
Criterio d e análisis de muros por c a r g a vertical del RCDF
El reglamento establece una expresión por medio de la cual se puede determinar la carga vertical que un muro puede resistir:
PR =FR FE PmAt
Donde:
PR = Carga vertical resistente
FR = Factor de reducción que vale 0.6 para muros confinados o reforzados y 0.3 para muros que no son ni reforzados,
ni confinados.
FB = Factor de reducción por excentricidad y esbeltez del muro, con un valor de 0.7 para muros interiores que soportan
claros que no difieren entre sí en más del 50% y con un valor de 0.6 para muros extremos o con claros
56
TESIS PROFESIONAL
asimétricos, así como para aquellos casos en que la relación de carga muerta y carga viva sea mayor que 1,
siempre que se cumplan los requisitos antes mencionados.
f*m= Esfuerzo a compresión de diseño de la mampostería.
At = Área del muro en planta.
Cuando no se cumplan las condiciones establecidas del caso anterior, el factor de reducción por esbeltez, FE,se determinará
con el valor menor que resulte de comparar 0.7 y la siguiente expresión:
F E = ( 1- 2 e " / t ) [ l - ( H 7 3 0 t ) 2 ]
Donde:
t = Espesor del muro.
e" = Excentricidad calculada para la carga vertical más una excentricidad accidental que se tomará igual a t/24.
H' = La altura efectiva del muro que se determinará a partir de la altura no restringida, según el criterio siguiente:
H' = 2H para muros sin restricción al desplazamiento lateral en su extremo superior, 0.8H para muros limitados por dos losas
continuas en ambos lados del muro, H para muros extremos en que se apoyan losas.
H =Altura del muro.
Por lo tanto, para garantizar la seguridad de los muros ante la acción de las cargas verticales, bastará con comparar la carga
última actuante (Pu) contra la carga resistente (PR), en donde la resistencia deberá ser mayor que la acción de servicio. En caso de que
esta condición no se cumpla, se tendrán que rediseñar los muros que no la satisfagan.
Para realizar este rediseño, tendremos que tomar como base la expresión de la resistencia, cambiando el espesor del muro
utilizado, ya que con esto el área aumentaría (At), y/o el tipo de material del muro, es decir, buscar una mampostería con mayor
resistencia (f*m).
4.4.2.
M u r o s sujetos a c a r g a s horizontales (sismo)
Las cargas horizontales que actúan sobre estructuras de mampostería pueden ser debidas a diversas causas. Sin embargo, la
causa más frecuente e importante es el sismo. La acción sísmica produce efectos diversos de los cuales, el más trascendente, es la
fuerza cortante en la estructura. Ésta debe resistir mediante los elementos estructurales (marcos rígidos y muros).
57
TESIS PROFESIONAL
4 . 4 . 2 . 1 . Clasificación de las estructuras
De acuerdo con el reglamento, todas las estructuras se clasifican según su uso y destino, conforme a lo establecido en el Art.
174 que establece que las construcciones se clasifican en los siguientes grupos:
L- Grupo A; Edificaciones cuya falla estructural podría causar lapérdida de un número elevado de vidas opérdidas económicas o
culturales excepcionalmente altas, o que constituyan un peligro significativo por contener sustancias tóxicas o explosivas, así como
edificaciones cuyo funcionamiento es esencial a raíz de una emergencia urbana, como hospitales y escuelas, terminales de
transporte, estaciones de bomberos, centrales eléctricas y de telecomunicaciones; estadios, depósitos de sustancias inflamables o
tóxicas; museos y edificios que alojen archivos y registros públicos de particular importancia, ajuicio del Departamento; y
II.- Grupo B; Edificaciones comunes destinadas a vivienda, oficinas y locales comerciales, hoteles y construcciones comerciales e
industriales no incluidas en este grupo y que se subdividen en:
a.
Subgrupo Bl
•
Edificaciones de más de 30 m. de altura o con más de 6000 m2 de área total construida, ubicada en las zonas Iy E a
que se aluden en él artículo 175.
•
Construcciones de más de 15 m. de altura o3000 m2de esta área total construida, en zonaHI.
En ambos casos las áreas se refieren a un solo cuerpo de edificio que cuente con medios propios de desalojo (acceso y
escaleras), incluyen las áreas de anexos, como pueden ser los propios cuerpos de escaleras de área de un cuerpo que no cuente
con medios propios de desalojo se adicionará a la de aquél o a través del cual se desaloje. Además templos, salas de espectáculos
y edificios que tengan sala de reunión que puedan alojar más de 200 personas, y
b.
Subgrupo Bl; Las demás de este grupo.
4 . 4 . 2 . 2 . Zoniflcación del Distrito Federal
Para fines de las disposiciones que marca el RCDF, se considera que el Distrito Federal se encuentra dividido en zonas del I al
III. Las características de las zonas mencionadas según elArt. 219 son:
•
Zona I -Lomas; formadas por rocas osuelos generalmente firmes quefueron depositados juera del ambiente lacustre,
pero en los que puede existir superficialmente o intercalados, depósitos arenosos en estado suelto o cohesivos
relativamente blandos. En esta zona es frecuente la presencia de oquedades en rocas y de cavernas y túneles
excavados en suelo para explotar minas de arena.
58
TESIS PROFESIONAL
•
Zona II - Transición; en la que los depósitos profundos se encuentran a 20 m. de profundidad, o menos, y que está
constituida predominantemente por estratos arenosos y limo-arenosos intercalados con capas de arcilla lacustre; el
espesor de éstas es variable entre decenas de centímetros y pocos metros.
•
Zona III - Lacustre; integrada por potentes depósitos de arcilla altamente compresible, separadas por capas
arenosas con contenido diverso de limo o arcilla. Estas capas arenosas son de consistencia firme a muy dura y de
espesores variables de centímetros a varios metros. Los depósitos lacustres suelen estar cubiertos superficialmente por
suelos aluviales y rellenos artificiales; el espesor de este conjunto puede ser superior a 50 m.
La zona a que corresponda un predio se determinará a partir de las investigaciones que se realicen en el subsuelo del
predio objeto de estudio, tal y como lo establezcan las Normas Técnicas Complementarias. En caso de edificaciones ligeras
o medianas, cuyas características se definan en dichas normas, podrá determinarse la zona mediante el mapa incluido en
las mismas, si elpredio está dentro de laporción zonifícada; lospredios ubicados a menos de 200 m. de lasfronteras entre
dos de las zonas antes descritas se supondrán ubicados en la más desfavorable.
59
I
m
en
en
•o
70
O
-n
m
en
O
z
>
o
Zonifícación Geotécnica de la Cd. de México
TESIS PROFESIONAL
4 . 4 . 2 . 3 . Método simplificado de análisis del RCDF
Este método es aplicable a estructuras cuya altura no exceda de 13 metros y que cumplan ciertas condiciones de regularidad en
carga y rigidez.
Para garantizar que se cumplan las condiciones de regularidad en la distribución de carga y rigideces, el RCDF establece los
siguientes requisitos para la aplicación del método simplificado:
I.- En cada planta, al menos el 75% de las cargas verticales estarán soportadas por muros ligados entre sí mediante losas
monolíticas u otros sistemas de piso suficientemente resistentes y rígidos al corte. Dichos muros tendrán distribución
sensiblemente simétrica con respecto a dos ejes ortogonales y deberán satisfacer las condiciones que establecen las normas
complementarias correspondientes. Será admisible cierta asimetría en la distribución de los muros cuando existan en todos los
pisos dos muros de carga perimetrales y paralelos, cada uno con longitud al menos igual a la mitad de la dimensión mayor en
planta del edificio. Los muros a que se refiere este párrafo podrán ser de manipostería, concreto reforzado o madera.
II.- La relación entre longitud y anchura de la planta del edificio no excederá de dos a menos que, para fines de análisis sísmico, se
pueda suponer dividida dicha planta en tramos independientes cuya relación entre longitud y anchura satisfaga esta restricción
y cada tramo resista según el criterio que marcan las presentas normas.
III.-La relación entre la altura y la dimensión mínima de la base del edificio no excederá de 1.5 y la altura del edificio no será mayor
de 13 metros.
Además, cuando se use dicho método simplificado, la contribución a la resistencia a fuerza cortante de los muros cuya relación
de altura de entrepiso, H; a longitud, L, es mayor que 1.33, se reducirá multiplicándola por el coeficiente (1.33 L/H) 2 .
Una vez verificado que se cumplen las anteriores condiciones, se procede a calcular la fuerza cortante sísmica a partir de los
coeficientes sísmicos que proporciona el mismo RCDF. Para la correcta selección del coeficiente sísmico que corresponde a nuestra
construcción, deberemos considerar:
1.- Tipo de construcción.- anteriormente, se estableció la clasificación de estructuras como grupo Ay grupo B, subdivididas a su
vez en subgrupos Bl y B2.
2.- Tipo de terreno.- este concepto también fue definido anteriormente.
3.- Altura de la construcción.- Los coeficientes del método simplificado se han obtenido a partir del período fundamental estimado
en función de la altura, por lo que, en general, a mayor altura se considera una fuerza sísmica mayor.
4.- Tipo de piezas de manipostería.- el coeficiente sísmico es afectado por un factor de ductilidad que toma en cuanta la
capacidad de disipar energía de los diversos sistemas constructivos. Los tipo de piezas especificados (piezas macizas y piezas
huecas) son los más comunes, por lo que se especifican los valores del coeficiente sísmico afectado por ductilidad para ellos.
61
TESIS PROFESIONAL
TABLA4.1 Coeficientes sísmicos reducidos porductilidad para elmétodo simplificado (estructuras grupoB)
Zona
Murosde piezas macizas
Muro, de piezas hueca.
Altura de la construcción
Altara de la construcción
b<4 m
4<h<7 m
7<h<l3 m
a<4 m
4<h<7 m
7<h<i3 m
Zonal
0.07
0.08
0.08
0.10
0.11
0.11
ZonaH
0.13
0.16
0.19
0.15
0.19
0.23
ZonaIII
0.13
0.16
0.19
0.15
0.19
0.23
Nota:Para estructuras del grupoA,multiplicar coeficientes por1.5
Los coeficientes dela tabla anterior representan la ordena espectral reducida porductilidad; portanto, multiplicados porel peso
total delaconstrucción, proporcionan la fuerza cortante sísmica en la base
2
P2
w
Fi
Vs = csP
Pi
i»
w »l
En donde:
->Vs
es; Coeficiente sísmico dela tabla anterior.
P; Peso total dela construcción enkg(considerando cargas
cargas muertas máximas y cargas vivas accidentales WH).
62
TESIS PROFESIONAL
D e t e r m i n a c i ó n d e la f u e r z a s í s m i c a
El RCDF acepta la hipótesis de la distribución de aceleraciones e n los diferentes niveles de la e s t r u c t u r a es lineal, partiendo de
cero en la b a s e h a s t a u n máximo a m en la parte superior.
a m /g
P
a/g
F,
H
*
h,
mmmm^^w///.
FIGURA 4.8.
Distribución de aceleraciones sísmicas en una construcción
La fuerza lateral en c a d a piso vale:
P
P
h
> a
tFx -- - --a,a - _—r-- a„
9
9 H
Finalmente, sustituyendo a m :
El cortante en la base vale:
'
2P,h,
ZP,h,
(
H
g
Hg
En donde:
F„ es la fuerza sísmica en el nivel deseado.
De donde:
m
ZP,h,
63
TESIS PROFESIONAL
D e t e r m i n a c i ó n d e la f u e r z a c o r t a n t e r e s i s t e n t e
El cortante resistente de los muros se establece mediante la aplicación de la expresión reglamentaria siguiente:
VR=FR(0.5v*bl
+ 0.3P) <
\.5FRv*bl
Donde:
VR= Cortante resistente del elemento analizado.
FR= Factor de reducción de resistencia.
y*=Esfuerzo resistente de la manipostería empleada.
b =Ancho del muro analizado.
L=Longitud del muro analizado.
P =Carga vertical soportada por el muro.
Procedimiento d e revisión sísmica aplicando el método simplificado d e análisis del RCDF.
El procedimiento mencionado implica los siguientes pasos:
a).
Verificar que el local a revisión cumpla con los requisitos de regularidad establecidos por el reglamento.
b).
Determinar la clasificación (grupo) de la construcción de acuerdo con el criterio reglamentario.
c).
Localizar geotécnicamente la construcción empleando para ello la carta geotécnica del D.F.
d).
Calcular el peso "P" de la construcción considerando las cargas muertas máximas totales, apéndices y cargas vivas
accidentales. En el cálculo de este peso puede no considerarse la mitad inferior de los muros de la plana baja.
e).
Seleccionar el coeficiente sísmico correspondiente a partir de la tabla de coeficientes, considerando el grupo, tipo de piezas de
manipostería, altura de la construcción y tipo de terreno.
f).
Obtener el cortante sísmico en la base de la estructura mediante la aplicación de:
Vs =CSP
g).
Obtener el cortante último:
K =i.ivs
64
TESIS PROFESIONAL
Obtener el cortante resistente de los m u r o s en las dos direcciones ortogonales principales mediante las siguientes expresiones:
VRx =FR(0.3PX +0.5y *blx) <l.5FRv * blx
Vyx = FR(Q.3Py + 0.5f *bly) <1.5FRv* bly
Donde:
VRX, VRy= Fuerzas cortantes en las dos direcciones ortogonales principales.
Lx, Ly = Longitudes de m u r o s de planta baja en direcciones xx y yy.
En las expresiones anteriores, puede s u p o n e r s e que la fuerza que soporta cada dirección de m u r o s es proporcional a la
longitud L, de modo que:
L
p __r*_p
r
r
x
j
• pr
y
'
Lu
r
= _ l p
j
Donde:
LT = Longitud total de m u r o s de p l a n t a baja.
P = Carga vertical total sobre m u r o s de planta baja.
Se c o m p a r a el cortante último con el cortante resistente en cada dirección. Las siguientes expresiones, correspondientes a la
revisión en c a d a dirección, deben cumplirse:
VRx
<
vu
65
TESIS PROFESIONAL
4.5
D I S E Ñ O
DE TRABES
DE
C O N C R E T O
REFORZADO
La naturaleza inelástica del concreto reforzado hace mas propios los métodos plásticos de dimensionamiento de vigas que los
métodos pasados en las hipótesis elásticas. Se reconoce así en la mayoría de los reglamentos modernos de concreto reforzado que da
preferencia a métodos basados en la determinación de la resistencia última de elementos bajo diversas acciones.
Estos métodos no requieren el uso del módulo de elasticidad, eliminándose así las incertidumbres que se derivan de la gran
variabilidad de este parámetro en el concreto reforzado. Otra ventaja es que las resistencias no son afectadas significativamente por los
efectos del tiempo que tanto dificultan la aplicación de procedimientos elásticos.
Flexión.
Según la mecánica de materiales, la flexión es el estado interno de esfuerzos cuya acción genera en una sección del elemento
flexionado un par de fuerzas "M" cuya intensidad puede establecerse a partir de las condiciones de equilibrio en vigas isostáticas o de
las condiciones de equilibrio y compatibilidad de desplazamiento en el caso de vigas estáticamente indeterminadas. Siendo la magnitud
de este par de fuerzas una constante de la sección, es posible modificar el valor de las fuerzas componentes C y T mediante la
alteración de la distancia entre ellas. En la figura 4.9 se ilustra el concepto anterior, pues observamos que si se aumenta la distancia
"Z", la magnitud "M"de las fuerzas componentes del par disminuye en la misma proporción. Esta es la razón por la que las vigas en la
práctica se disponen con su mayor dimensión (peralte) de manera vertical. De este modo, los esfuerzos de tensión son absorbidos por el
acero de refuerzo y los de compresión por el concreto.
FIGURA4.9.
Flexión envigasdeconcreto reforzado
La flexión representa el estado límite de servicio que usualmente rige la determinación de las dimensiones de las vigas de
concreto reforzado.
Por otro lado, los elementos más comunes de las estructuras sometidos al efecto de flexión son las vigas y las losas, las que la
tienen como acción principal, generalmente acompañada de la acción de la fuerza cortante.
66
TESIS PROFESIONAL
Criterio básico de diseño.
El diseño por flexión debe cumplir la condición reglamentaria, la cual establece que la resistencia a la flexión de una sección de
concreto reforzado debe tener una magnitud que exceda o cuando menos sea igual a la del momento último producido por las cargas,
es decir:
MR
> Mu
Donde:
MR = Momento resistente de sección.
Mu =Momento último de la viga.
Á r e a de a c e r o máxima y mínima reglamentarias
El RCDF, a través de las Normas Técnicas Complementarias, establece que el comportamiento de las estructuras debe ser dúctil
en zona sísmica y para garantizarlo establece una cantidad máxima de acero equivalente al 75% de la cantidad balanceada, la cual
esta definida por al expresión:
As
-0 75A - ° - 7 5 / " c '
f'y
_4800
'°™ ' bd
f'y +6000
Adicionalmente, las secciones deberán tener una cantidad mínima de acero para también garantizar un comportamiento dúctil.
Tal cantidad mínima es especificada por el RCDF mediante:
Asmm=
0.7¡fe
,
J
" -~ bd
fy
Cuantía de acero de la sección
El término denominado "cuantía de sección", esta dada por la expresión:
p = - s-
bd
Esta cuantía es adimensional y representa la cantidad relativa de acero en relación con la de concreto. Para garantizar la
disposición reglamentaria sobre el comportamiento dúctil de las vigas de concreto reforzado en zona sísmica, es obvio que la cuantía de
una viga se limita también a un 75%de la cuantía balanceadaPb.
67
TESIS PROFESIONAL
Pmax =0J5Pb
Donde:
Pb
~ bd
También en este caso es obvio que la cuantía mínima de acero es establecida, partiendo de la expresión:
1
"•'
mm
r,
fy
En la tabla siguiente se indican los valores de cuantías máxima y mínima para diversas combinaciones de resistencias de acero
y concreto.
RESISTENCIA
Fy DELACERO
150
200
2S0
300
2530-iw
0.0170
0.0226
0.0284
0.0340
2530-pmin
0.0033
0.0039
0.0044
0.0048
4200-po.ax
0.0086
0.0114
0.0143
0.0171
4200-pmin
0.0020
0.0023
0.0026
0.0029
TABLA4.2.Cuantías máximasymínimas reglamentarias.
Por otro lado se puede calcular el momento resistente si consideramos la magnitud del par resistente ahora como producto de la
fuerza de tensión por su brazo de palanca, mediante la expresión:
MR~FRAsf-y(d-0.5a)
Donde:
a =•
bf'c
68
TESIS PROFESIONAL
Sin embargo, es común considerar el brazo del par (d-0.5 a) equivalente a un producto jd, donde " / es una constante menor que
la unidad que cambia su valor en función de la cuantía empleada, pero que puede ser estimada como un valor cercano a 0.9. En este
caso consideraremos a j = 0.89 para evitar que se confunda con el factor de reducción de resistencia, cuyo valor, como sabemos, es
Fr=0.9.
De esta manera, la expresión alternativa para el cálculo de la resistencia por flexión es:
M
R
=FRAsf'yJd
Cortante
La resistencia por cortante VR de vigas de concreto reforzado está representada por la contribución de tres factores: el concreto
simple que conforma la viga, el refuerzo longitudinal y el refuerzo transversal (usualmente anillos de acero, llamados estribos).
1.- Fuerza cortante última (Vu),Sí:
Vu < 2.0FRbd Jf* c =>Se requiere refuerzo transversal
2.- Fuerza cortante que resiste el concreto (Ver),Sí:
Porcentaje = p <0.01 .-. Vcr =FRbd(0.2 + 30p)Jf* c
Porcentaje =p > 0.01 .•. Vcr = 0.5FRbdJ~f*c
3.- Fuerza cortante que toma el refuerzo transversal (V'u):
V =V -V
69
TESIS PROFESIONAL
4.6
D I S E Ñ O DE L O S A S DE C O N C R E T O
REFORZADO
Las losas de concreto reforzado se encuentran entre los elementos estructurales más comunes y, a pesar de que se han
diseñado y además construido un gran número de losas, los detalles de comportamiento no siempre se comprenden debido a la
complejidad de las ecuaciones elásticas de las placas, especialmente en las zonas de apoyo. Sin embargo, existen métodos que
permiten analizar de manera relativamente sencilla este tipo de elementos.
Las losas son elementos estructurales que consisten en tableros que trabajan en dos direcciones y se les conoce como
elementos bidimensionales, ya que dos de sus dimensiones, el largo y el ancho, son mucho mayores que su espesor. Por lo tanto de
observa que ai, a¿ >>h.
Por otro lado, a las losas las podemos dividir en dos categorías:
a).
Losas formadas por tableros apoyados en su perímetro, ya sea por trabes o muros.
b).
Losas planas, o sea, losas formadas por tableros sin apoyo perimetral, esto es, sin vigas ni muros.
El criterio para decidir cuándo usar uno u otro tipo de losa dependerá en gran medida de la magnitud de las cargas y los claros
a cubrir.
Las losas apoyadas en su perímetro se conocen como losas que trabajan en dos direcciones. Sin embargo, se presentan casos de
losas que se consideran trabajando en una dirección, siendo éstas muy alargadas, es decir, en las que la relación del claro corto entre
el claro largo es menor a 0.5.
^!<0.5
a-,
4.6.1.
Losas macizas perimetralmente
apoyadas
Las losas son elementos estructurales cuyas dimensiones en planta son relativamente grandes comparadas con su espesor. Una
losa no es más que una placa apoyada en un conjunto de trabes, muros o líneas resistentes subdividida en tableros. Los bordes de
cada tablero tendrán diversas condiciones de continuidad, dependiendo de si la losa se prolonga hacia el otro lado del apoyo o termina
en dicho borde. Si la relación geométrica entre el lado corto y el lado largo de cada tablero es mayor que 0.5, entonces el tablero
distribuye su carga en dos direcciones, apoyándose en todo el perímetro y el armado estará dispuesto tanto en lado corto como en el
lado largo, contribuyendo a la resistencia por flexión del sistema.
La solución (análisis) de cada tablero de los que conforman la losa es relativamente compleja, puesto que los desplazamientos
en cada punto son distintos, lo que conduce a un sistema altamente indeterminado. Existen, sin embargo, soluciones aproximadas que
están basadas en la teoría de la elasticidad y que consideran a los bordes de cada tablero con una rigidez infinita; de esta manera, los
tableros se suponen perimetralmente apoyados. Usualmente, estos métodos plantean el empleo de coeficientes que conducen a la
70
TESIS PROFESIONAL
obtención de momentos flexionantes en franjas unitarias (de un metro de ancho) que se cruzan en el centro del tablero. Ejemplo de
estos métodos lo tenemos en el método del Reglamento de Construcciones para el D.F.
M é t o d o d e l R C D F p a r a el c á l c u l o d e l m o m e n t o flexionante e n t a b l e r o s d e l o s a s d e c o n c r e t o
reforzado.
La solución de losas se puede llevar a cabo mediante coeficientes que proporciona el reglamento.
El método mencionado puede aplicarse si se satisfacen las siguientes limitaciones:
1.-
Los tableros son aproximadamente rectangulares.
2.-
La distribución de cargas que actúan sobre la losa es aproximadamente uniforme en cad tablero.
3.-
Los momentos negativos en el apoyo común de dos tableros adyacentes no difieren entre sí en más del 50% del menor de
ellos.
4.-
La relación de carga viva a carga muerta no es mayor que 2.5 para losas monolíticas con sus apoyos, ni mayor que 1.5
en otros casos.
Para el establecimiento de dichos coeficientes se toman en cuenta:
a).
La relación "m"de lados del tablero analizado.
b).
La forma de apoyo perimetral del tablero: colado monolítico (caso I) o no monolítico (caso II), que usualmente se refiere a
apoyo sobre viga de acero.
c).
Las condiciones de continuidad de los bordes del tablero.
Dada la naturaleza aproximada del método, se sugiere aproximar la relación al décimo o al medio décimo más cercano (ejemplo:
0.63 a 0.65, 0.88 a 0.90, 0.71 a 0.70) para facilitar el proceso de interpolación si es necesaria ésta.
En caso de una relación m menor que 0.5, se tomarán los coeficientes que correspondan a la relación 0 (cero) de la tabla
reglamentaria.
En la tabla el término borde continuo se refiere a que la losa se prolonga más allá del borde y borde discontinuo a que no se
prolonga. Para obtener los coeficientes, se entra a la tabla con el valor de m, se establece el caso y el tipo de tablero de acuerdo con las
condiciones de apoyo y de continuidad, respectivamente, y se realiza una interpolación, si es necesario, para obtener los coeficientes.
Para establecer el tipo de tablero y el caso correspondiente, se considera la continuidad con los tableros adyacentes, de donde
se definen cinco casos, que se muestra en la tabla 4.3.
71
TESIS PROFESIONAL
Diseño d e losas m a c i z a s .
Las losas deben diseñarse para cumplir con las condiciones de servicio y de seguridad. Para lo primero, se establece un peralte
que les permita funcionar sin excesivas deflexiones y vibraciones; para lo segundo se revisa que la resistencia de la losa por flexión y
cortante sea la adecuada para resistir los efectos últimos correspondientes.
P e r a l t e por d e f l e x i ó n .
El reglamento establece al respecto que para fc>250 kg/cm 2 , el peralte efectivo es:
_ Perímetro
En la obtención de dicho perímetro, la longitud se incrementará:
50%, sí no es monolítico y 25%, sí es monolítico
Además se afectará el peralte efectivo por:
0.034 « f ^
••• / s = 0 . 6 / - t /
Sí no cumple con:
/ s <2000kg/cm2
Ws<380kg/m2
y
En tableros alargados, no es necesario tomar un peralte mayor que el que corresponde a un tablero con a2=2 ai
Revisión d e l p e r a l t e por f u e r z a c o r t a n t e .
La fuerza cortante en un ancho unitario se calcula con la siguiente expresión:
1.4
a,
--d|W„
V = ->¿Í
\
a
1 + Jl
Ka2J
Incrementándose 15%cuando haya bordes continuos y discontinuos en el claro corto del tablero.
72
TESIS PROFESIONAL
Para realizar la revisión de la resistencia por cortante, se considera el cortante resistente calculado con la siguiente expresión:
VR = 0.5FRbdJf*c
:. b = 100cm
Diseño por f l e x i ó n .
Este consiste en calcular la separación necesaria del refuerzo considerando, además de la flexión, los cambios volumétricos y
aspectos prácticos del armado.
Se puede considerar dos soluciones:
1.-
Proponer la varilla a utilizar y calcular la separación de las varillas, mediante la expresión:
_ asbf'yd
,.
, ,
S =—- .-. as;es el area de la varilla propuesta
Mu
2.-
Calcular el área de acero necesario y posteriormente calcular la separación, mediante las expresiones:
FRf'yjd
100a.
As
Se considerarán los cambios volumétricos mediante la disposición de una cuantía mínima por franja unitaria Pmm=0.002 en
entrepiso y Pmm=0.003 en azotea. La separación del refuerzo no debe exceder de 3.5h ni de 50 cm.
Reducción del a r m a d o .
Si el armado resulta demasiado denso, debemos recordar que los momentos de análisis corresponden a la zona central en cad
dirección, por lo que es posible reducirlo un 60% en las franjas extremas, definidas geométricamente.
Doblado d e v a r i l l a .
Para el armado de la losa, se deben tomar en cuenta algunos aspectos constructivos, de los cuales el más importante es el de
garantizar que el acero se coloque en la zona donde se produzcan esfuerzos de tensión bajo el efecto de las cargas. Para ello, se
disponen dobleces del refuerzo denominados columpios, de tal manera que la varilla sea colocada en el lecho superior de la losa en
zonas sobre apoyo y en el lecho inferior en los centros de los claros.
73
TESIS PROFESIONAL
Se acostumbra configurar la parrilla en cada dirección con pares de varillas conformados por una varilla recta, por el lecho
inferior, y la siguiente doblada con los columpios mencionados. De esta manera, se pierde una varilla que debería ir sobre el apoyo de
la zona del momento negativo. Para compensar esta situación, se disponen bastones en esas zonas para subsanar esta pérdida.
En cuanto al doblado de la varilla, se toman en cuenta las distancias a partir del paño del apoyo al punto de inflexión
equivalentes a un séptimo del claro en bordes discontinuos, un quinto del claro en bordes interiores y un cuarto del claro para localizar
el extremo de los bastones.
Var. doblada
Bastones
~^
<r
L/5
L/7
->
<r
L/4
L/5
->
<r
->
<-
L/4
<-
L/4
L
<-
FIGURA4.10. Disposición dedobleces en losas.
->
->
->
TABLA DECOEFICIENTES DEMOMENTOS PASA TAZLE?OS RECTANGULARES,
FRANJAS CENTRALES PARA FRANJAS EXTREMAS MULTIPLIQÚENSE LOS COEFICIENTES POS 0.60)
RELACIÓN DELADOS
TABLERO
MOMENTO
0
CLARO
05
II
m= a , a
06
08
07
1 n*
09
1
II
1
II
1
II
1
II
1
II
1
II
INTERIOR
NEGATIVO
CORTO
998
1 018 553
565
489
498
432
438
381
337
333
338
288
292
TODOS LOS
EN BORDES
LARGO
516
544
409
431
391
412
371
388
34""
361
329
330
2co
2v ^
BORDES
INTERIORES
CONTINUOS
POSITIVO
CORTO
630
088
312
322
268
276
223
236
192
199
158
164
'2o
;
LARGO
175
181
139
144
134
139
130
135
128
133
127
131
12o
13.
1
'
DEBORDE
NEGATIVO EN BORDES
CORTO
998
1 018 568
594
506
533
451
478
403
431
357
388
3'5
24c
UN LADO
INTERIORES
LARGO
516
544
431
391
412
372
392
350
369
326
341
207
3i| '
409
1
CORTO
DISCONTINUO
DISCONTINUOS
LARGO
326
0
258
0
248
0
236
0
222
0
POSITIVO
CORTO
630
668
329
356
292
306
240
261
202
219
167
LARGO
179
187
142
149
137
143
133
140
131
137
129
'
•
DeBORDE
UN LADO LARGO
1
NEGATIVO ENBORDES
206
0
190
0
181
133
144
136
129
135
624
514
548
453
481
397
420
346
364
297
311
LARGO
5S7
687
465
545
442
513
411
470
379
424
317
384
315
346
DISCONTINUOS
CORTO
651
0
362
0
321
0
283
0
250
0
219
0
190
0
POSITIVO
CORTO
751
912
334
366
285
312
241
263
202
218
164
175
129
135
LARGO
185
200
147
158
142
153
138
149
135
146
134
145
133
144
NEGATIVO ENBORDES
INTERIORES
CORTO 1 060 1 143 583
DISCONTINUO
NEGATIVO EN BORDES
DEESQUINA
NEGATIVO EN BORDES
CORTO
1 C60 1 143 598
653
530
582
471
520
419
464
371
412
324
364
DOS LADOS
INTERIORES
LARGO
600
713
475
564
455
541
429
506
394
457
360
410
324
364
NEGATIVO ENBORDES
CORTO
651
0
362
0
321
0
277
0
250
0
219
0
190
0
DISCONTINUOS
LARGO
326
0
258
0
248
0
236
0
222
0
206
0
190
0
POSITIVO
CORTO
751
912
358
416
306
354
259
298
216
247
176
199
137
153
LARGO
19!
212
152
168
146
163
142
158
140
156
138
154
137
153
CORTO
570
0
550
0
530
0
470
0
430
0
380
0
330
0
0
330
0
ADYACENTES
DISCONTINUOS
AISLADO
CUATRO
NEGATIVO ENBORDES
0
330
DISCONTINUOS
LARGO
330
POSITIVO
CORTO
1 100 1 670 830
LARGO
500
0
330
0
330
0
330
0
330
LADOS
DISCONTINUOS
200
250
1 380 800
830
500
1 330 720
830
500
1 190 640
i 070
570
950
500
830
830
830
500
830
500
830
500
CASO I LOSA COLADA MONOLÍTICAMENTE CON SUSAPOYOS
CASO II LOSA N O COLADA MONOLÍTICAMENTE CON SUSAPOYOS
Loscoeficientes multiplicados por ]0~4 wd\ dan momentos por unidad de ancho
Paraelcaso I, a, y a2puedetomarse como losclaros libres entre pañosdevigas;para elcaso IIsetomarán como losclarosentre ejes,pero
sinexceder el claro libre másdosveces elespesor de lalosa
OÍ
••¡^^••••••••^•••^^•••••••••^^^•••••••••••••••••••^••MH
5
5.1.
Proyecto
de
TESIS PROFESIONAL
aplicación
de
^g^gggggg^ggjgggi
cálculo
estructural
para
una casa-habitación,
ubicada en la Calle Vicente Villada No.77.
Col. Ahuizotla. Mun. ñlaucalpan de Juárez,
D E S C R I P C I Ó N D EL A O B R A
Edo.de Méx.
Terreno
El terreno tiene una dimensión de 8.00x19.00 mts., yse encuentra dentro dela Zona deTransición (Zona II), según Ja
Zonificación geotécnica de la Ciudad de México.
Arquitectónico
El proyecto arquitectónico consta de lo siguiente:
Plantabaja
1
1
1
1
1
1
Sala.
Comedor.
Cocina.
Cuarto deestudio.
Toilet.
Patiodeservicio.
Garage.
Planta alta
3
1
2
Recamaras.
Sala de televisión.
Baños.
76
TESIS PROFESIONAL
Estructural
Las plantas de azotea y de entrepiso se estructuraron a base de losas macizas las cuales están soportadas por trabes de
concreto armado y muros de carga de tabique rojo recocido.
Se supusieron castillos en los muros de barro recocido y se localizaron en los extremos de todos ellos al igual que en los cruces
existentes, y en los lugares que nos determinan el RCDF. Los armados de dalas y castillos son de 4 varillas de 3/8" corridas en lechos
inferiores y superiores, con estribos de 1/4" a cada 25 cm. en toda su longitud.
La estructuración en muros de las plantas se dispuso a base de tabique de barro recocido, esto tanto para muros de carga como
para muros divisorios.
La escalera se proyectó a base de rampas inclinadas de concreto reforzado y escalones forjados de tabique de barro recocido.
Los materiales de recubrimientos en los pisos se consideraron que en toda la casa fueran de loseta cerámica, excepto en baños
en los que se colocó azulejo antiderrapante.
Dada la magnitud y distribución de las cargas que son transmitidas al suelo, y a las características mecánicas del mismo, la
cimentación propuesta será a base de zapatas corridas y aisladas de concreto reforzado (tipo superficial).
Dimenslonamiento
Se utilizo para el diseño y análisis de los elementos estructurales, el Reglamento de Construcciones para el Distrito Federal.
Clasificación de la construcción p a r a análisis sísmico
De acuerdo al Reglamento de Construcciones del Distrito Federal, el análisis sísmico de la construcción se efectuó con la
siguiente clasificación:
Clasificación según su uso..
GrupoB
Ubicación del inmueble
ZonaII
Coeficiente sísmico reducido,,..,...,
,
,.,..,
0.16
77
TESIS PROFESIONAL
Análisis de cargas accidentales
Se siguió el criterio de análisis estático sísmico, analizando la estructura bajo la acción de dos componentes horizontales
ortogonales.
5.2.
DESARROLLO DEL
5.2.1.
Proyecto
PROYECTO
arquitectónico
Véanse los siguientes planos:
•
•
•
•
5.2.2.
T-l; Planta baja.
T-2; Planta alta.
T-3; Planta de azotea.
T-4; Fachada principal.
Proyecto
estructural
Véanse los siguientes planos:
•
•
T-5; Estructuración en losa de azotea.
T-6; Estructuración en losa de entrepiso.
78
c
(F;
J
2 00
2 00
¡00
4 00
3
i
p l a n t a i>£tj£i
PLANO
N 111JK í NULOoUlJI I A( NHI C UN
T-01
Casa- Habitación
NC AL No 1 AS WBITPANIJIA
""
V i c t n t c Villdda No 7 7 Col Ahui¿otla M u n N d u o l p in d t Juarez
V lililí
II bl
PII * t
v*V
1 12
2
800
4 00
planta alta
1 90
T-02
MFTTI S
A csrr2[LJ
IN I l l l 10 If N O L O U O D t l A C NSTHU CON
Casa-Habitación
NÜ n
Vicente Villada No 77Col Ahuizotla M u n N sucalpan d( J u a r t z
Nil)
LBvVI IT
V 1I INHIJJE I Ul I w
NTA
no^ e |)
r^\
cr;
D
2 00
f ]
4 00
p l a n t a cl<
'
1 90
T-03
ACOMCQN
MLTrtlS
A jtoTO(LO
IN mure i k N O i u i u i I L I / U J N IHUCUUN
Casa- Habitación
Vicente Villadd No 77 Gol Ahuizotla M u n Naucalpan dp Juarez
INL AltI N U) AUIW i l l I Nl) A
/ U O P I N r i JJL FCURA11l HEo
h
x\o&*-
4 00
4 00
0 50
010
2 50
010
2 50
4?
<#?
|9l~inGlf*Sftl
'
Í.SOJ*
iNoiiij] tiKNt ( u c i r t una HUGHON
1 bb
T-04
METHCb
CH
* n SI (3
HO^^jl
Casa-Habitación
IN( A JN I f AbBM I H\U1JJA
Vicente Villada No
il Col Ahuizotld Mun Nam tlpan dt, J u a r v
v i M NM
i\ i «ir
17 00
4 00
2 00
5 00
6 00
1
( 1
I
^>
y
"l
\HZZZr^ZZZ7Z7^7rC?7TT777?Z-7777777rr7ZW77777^7777.V^
SZYiZáZIZZZZET
TABI
4 00
xSt"'' 800 4
Vr7?Z77Z777-777ZZ>Z'Z>77777777Z'77777,
TAB IV
?m
ZZZZZZZZZZZZZ7M—
TABV
4 00
S I M B O L O G I A
^//
v3;
i ¿
/ / /-^-7~7
J
INDICA MURO DE CARGA
INDICA MURO DIVISORIO
TZZZZZZZ23ZZZ2ZZZ2ZZZZZZ2ZZZZZ¿ZZfi!mZ?ZZZZ3Z2Z2J2L
INDICA TRABb PRIMARIA
INDICA LIMITE DEVOLADOi
V
fB
INDICA CASTILLO
Nota solo serepresentan
loscastillos quedanapoyo
alastrabes
Puwo
INbTIfUTü lEuNOlOQCUDt LALONSThUbClON
T-05
Casa-Habitación
METRUS
ING A L U J N S O D ABBWHTT [ANTOJA
uaotoN
Vicente Villada No 77 Col Ahutzotla Mun Naucatpan deJuarez
V r r O h L N R I Ü U t >FUJHA FORhLo
j
17 00
2 00
r
6 00
T ->7y777V? m7^77r~,V'77777r7^77VT7777777777777Z".
^7777,..
777777^77771 m,7777.->777ZT.yTT.,
^
TAB III
TABU
i
4 00
v
2 )
8 00 <b
4 00
r
3
SIMBOLOGIA
zzzzzz¿zzzz
«
INDICAMURODE CARGA
INDICAMURODIVISORIO
INDICATRABEPRIMARIA ,
INDICALIMITEDE VOLADO,
o
INDICACASTILLO
J
Nota solo se representan
los castillos que dan apoyo
a las trabes
INSTITUTO1 IKNGLÜC ICOl)b LA CONSTRUCCIÓN
1 90
T-06
METROS
Casa-Habitación
V40^¿|
NO A U L N S O O ABBWhTT rANTOJA
V n ente Villada No 71 C o l Ahuizotla M u n N d u c a l p a n de Juarez
VICTOR I N R i a j t
lUrUORRL'?
TESIS PROFESIONAL
2 . 3 . A n á l i s i s de c a r g a s u n i t a r i a s
2.3.1. Losadeazotea
SISTEMA: LOSA DE CONCRETOARMADO COLADA ENELLUGAR CONDIFERENTES RECUBRIMIENTOS.
Cargas muertas.
( L O S A
D B
A
Z O T E
A
PESOVOL.
(kg/m a )
1500
2100
2100
0.03
1300
0.16
2400
0.10
0.015
1500
POR CONCRETO
POR MORTERO
w
ESPESOR
(mts.)
0.02
0.015
-
MATERIAL
ENLADRILLADO
MORTERO
IMPERMEABILIZANTE
MORTERO
RELLENO (TEPETATE)
LOSADECONCRETO
YESO
CARGA MUERTA ADICIONAL
(ART. 197RCDF)
(kg/m*)
30
32
5
63
208
240
23
20
20
Wat*
641
Cargas vivas.
Tabla decargas vivas unitarias (kg/m-*)
Destino de piso o cubierta
a).
g)-
Habitación
(casa-habitación,
departamentos, viviendas, dormitorios,
cuartos de hotel, internados de
escuelas,
cuarteles,
cárceles,
correccionales, hospitalesysimilares.).
Cubiertas y azoteas conpendiente no
mayor de 5%.
W
Wa
(instantánea)
Wn
(maxima)
70
90
170
18
70
100
C a r g a d ediseño.
Cargas VeMcalev =Wv - CM +CV - 641 +100 = 741
kg
m
85
TESIS PROFESIONAL
I.-
Peso del tinaco
Consideraciones:
A
1.-
Se considera que la carga por concepto del tinaco y su base, será repartida uniformemente sobre el á r e a del tablero I
(6.00x4.00=24.00 m 2 ) del cual se e n c u e n t r a soportado.
2.-
Se colocará u n tinaco con capacidad de 1100 Its. con peso propio de 220 kg.
3.-
El tinaco trabajará por gravedad, por lo que se colocará 2.00 m t s . sobre el mueble sanitario m á s alto (Art. 151. Cap. VI.
RCDF).
4.-
Se c o n s t r u i r á n 2 b a s e s de m u r o de tabique macizo con dos c a p a s .
Cargas muertas.
1» K
m o
ESPESOR
MATERIAL
MORTERO
TABIQUE
MORTERO
D
(mts.)
'"
0.02
0.12
0.02
E
B
A
S
E
PESOVOL.
(kg/m 3 )
2100
1500
2100
w
(kg/m 2 )
42
180
42
264
R=0.475m
h= 1.27 m
Area ={bxh)- (
7
Ttr
)=(1.10x1.27)- (
1
7t x 047
:
) =1.05m~
0
Pesototal=• WxA = 264x1.05=277.20kg *280kg
b= l.lOm
86
TESIS PROFESIONAL
p
E
S
O
D
MATERIAL
,
TINACO
AGUA
BASE
,
,„
E
L
1
8
•
CANTIDAD
UNIDAD
1
PZA.
1100
LT.
2
PZA.
T
IB
w
(kg)
220
1100
560
w»
Pesosistema _ 1880¿g
Carga sobre TableroI = - ~"^^^r
=-""" "? = 78.33*80.00
Area tablero 24m2
B
A
M
1880
kg
m~
Carga de diseño.
Carga Verticales =Wv =CM +CV+PS=641+100+80=821-\ =>Sobre Tablero I
m
II.-
Altura promedio del relleno
Se mide en la planta de azotea la distancia de la B.A.P. al punto másalejado delescurrimiento considerando una pendiente del
2% (Art. 157.RCDF). Secalcula elespesor medio tomando en cuenta queelespesor mínimo esde5.00cm.(Verplano T-7)
eiaK
emax=(Lx 2%)=11.00*0.02=0.22 =22cm
22
£%aed\o
"med
= 11.00cm.
««/fe», =«„„., +*mea =5 - 0 0 + ! ! 'O0=1 6 0 0 «"
daax-5c m .
L/2
->-«-
L/2
11.00
87
\mm/
19 00
2 00
¡p
bOO
4 00
'*,
p l a n t a cl<
ESCUELA
R>NO
IIVolllUlO L t N U C K I l
1 90
T-07
ACO AC ON
MfclROb
FE.CHA
~
4 OSTC 0iJ
Casa-Habitación
JLIA UH T K l M IÜN
AbtSOH
ING ALFlNSüD ABdWRIT PAN!OJA
Vicente Villada No 7 7 Col Ahuizotla M u n N a u c a l p a n de Juarez
llABORO
VICrORi-NHUUt J L L U H / TOR! LS
HD^e)
TESIS PROFESIONAL
. 3 . 2 . Losa de entrepiso
SISTEMA: LOSA DE CONCRETO ARMADO COLADA EN ELLUGAR CONDIFERENTES RECUBRIMIENTOS.
Cargas muertas.
L O S A
D
E
E
N
LOSETA CERÁMICA
MORTERO
ESPESOR
(mts.)
0.01
0.015
LOSA DECONCRETO
YESO
0.10
0.015
MATERIAL
CARGAMUERTAADICIONAL
(ART. 197RCDF)
T
R E
1s o
P
w
PESOVOL.
(kg/m 3 )
1800
2100
(kg/m 8 )
18
32
240
2400
1500
POR CONCRETO
POR MORTERO
23
20
20
353
Wm«
Cargas vivas.
Tabla decargas vivas unitarias (kg/m2)
Destino de piso o cubierta
a).
g).
Habitación
(casa-habitación,
departamentos, viviendas, dormitorios,
cuartos de hotel, internados de
escuelas,
cuarteles,
cárceles,
correccionales, hospitales y similares.).
Cubiertas y azoteas con pendiente no
mayor de5%.
W
(media)
Wa
(instantánea)
Wm
(maxima)
70
90
170
18
70
100
C a r g a de diseño.
Cargas Verticales =Wv=CM +CV =353+170=523
kg.
89
TESIS PROFESIONAL
I.-
D e t e r m i n a c i ó n d e c a r g a p o r c o n c e p t o d e l a s z o n a s d e b a ñ o e n t a b l e r o I y II
A
Cargas muertas.
B A
MATERIAL
AZULEJO
MORTERO
IMPERMEABILIZANTE
FIRME DE CONCRETO POBRE
RELLENO (TEPETATE)
LOSA DECONCRETO
YESO
CARGA MUERTA ADICIONAL
(ART. 197RCDF)
Ñ
O
W
(kg/m 2 )
18
32
5
110
104
240
23
20
20
PESOVOL,
ESPESOR
(kg/m 3 )
(mts.)
1800
0.01
2100
0.015
2200
0.05
1300
0.08
2400
0.10
1500
0.015
POR CONCRETO
POR MORTERO
Wm «
B72
Nota: Porloanterior se considerará un incremento de 200 kg/m2 en lostableros Iy IIIpor concepto de carga adicional para
baños
B
Carga de diseño.
CargasVerticales=Wv=525+200=723-~|
m
II.-
Determinación d e c a r g a por concepto d e muros divisorios sobre losa d e entrepiso.
Información
Cargas lineales: "Los efectos de cargas lineales debidas a muros que apoyan sobre una losa pueden tomarse en
cuenta con cargas uniformemente repartidas
equivalentes.
En particular, el dimensionar una losa perimetralmente apoyada, la carga uniforme equivale en un tablero que soporta
un muro paralelo a uno de sus lados, se obtiene dividiendo el peso del muro entre el área del tablero y multiplicando el
resultado por el factor correspondiente de la tabla 6.1. La carga equivalente así obtenida se sumará a la propiamente
uniforme que actúa en este tablero
90
TESIS PROFESIONAL
Relación de lados m» a i / a a
0.5
0.8
1.0
Muro paralelo al lado corto.
1.3
1.5
1.6
Muro paralelo al lado largo.
1.8
1.7
1.6
Estos valores pueden usarse en relaciones de carga lineal a carga total no mayores
entre los valores tabulados.
(4.3.4. N.T.C.Concreto)."
de 0.5. Se interpolará
linealmente
Tablero I
S i s t e m a : Muro de tabique macizo hecho a m a n o con diferentes recubrimientos.
A
Cargas muertas.
Y
MATERIAL
E
YESO
8
O
A Z
TABIQUE
MORTERO
U
L
J
E
w
AZULEJO
ESPESOR
0.015
0.12
0.015
0.01
PESO VOL.
W
(kg/m 2 )
1500
1500
2100
1800
23
180
32
18
O
W
(KQ/m2 \
(kg/mL)
253
633
/. - Calculo del peso de muro
Wtotai = (WHhHcii) =(253 k9. )f2.50 m) f4.00 m) = 2530 kg
m
TABI
II. - Re lación de lados
ai=4.00
Q
4 0 0
«A, «0.7m
m =—¿i =
=0.67
o , 6.00
iff. - Factor muro paralelo a lado corto = 1.3
a¿=6.00
IV. - Calculo peso de la losa
W,losa
kg
2530 kg
Peso del muro
x Fact. =
x 1.3 = 1 3 7 - ^
l
Area losa
24 m
m'
91
TESIS PROFESIONAL
T a b l e r o II
Sistema: Muro de tabique macizo hecho a mano con diferentes recubrimientos.
A
Cargas muertas.
Y
E
S
A
O
Z
U
L
E
MATERIAL
YESO
TABIQUE
MORTERO
AZULEJO
ESPESOR
PESOVOL.
W
(kg/m 2 )
0.015
1500
0.12
1500
0.015
2100
0.01
1800
23
180
32
18
2.00
•4
J
O
w
(kg/m 2 )
W
(kg/mL)
253
633
II. - Relación
•
m =-
TABII
ai=4.00
III.-
1
a.
de
lados
4.00
= 0.67 * 0.7
6.00
Factores
Factor muro paralelo a lado corto = 1.3
Factor muro paralelo a lado largo = 1.5
IV.- Calculo peso de la losa
•*
a2=6.00
_ ^ 1898 kg , . ,n_ kg
x Fact. =
- x 1.3 = 103- ,Area losa
24 m
m~
„ , 1265 kg , ^ „ rt
Peso del muro
kg
W,losa
xFact.=
- .m~¿ x l . 5 = 79 m2"
Area losa
24
kg
W/osa =103 +79 = 182
m~
W,losa
/. - Cálculo de peso de muro
Wx = Whax = (253)(2.5Q)Ci.QQ) = 1898 kg
W2=Wha2=
^253^2.50^2.00; = 1265 kg
Peso del muro
92
TESIS PROFESIONAL
III.- Peso de la e s c a l e r a
Sistema: Escalera de r a m p a de concreto a r m a d o y escalones de manipostería.
Datos:
Peralte mínimo= 10 cm.
Peralte máximo= 18 cm.
h= 2.60 mts.
Ancho de huella mínima= 25 cm.
I.- Cálculo del número de e s c a l o n e s .
No. escalones =260/18 = 14.44 ¡*15 escalones
II.- Diseño.
P= 18
Condición:
2P + H =6\-65
2(18)+ 28=64=> SE ACEPTA
í r^v>
H=28
•*
•
III.- Analizando tramo unitario.
No.huellas =- 1 '°°- =3.57 » 4 escalones/
0.28
/1.00/w
IV. Cálculo de p e s o
^« u /, r a = ^ « *7 * No. esc.=( - ^ ° - 2 8 ) ( l 500X4) =152 M,
2
m~
93
TESIS PROFESIONAL
A
Cargas muertas.
• s
C A L
E
R A
W
(kg/m 2 )
36
32
152
32
240
PESOVOL
ESPESOR
Kkg/rri3)
(mts.)
0.04
2400
0.015
2100
0.01S
2100
2400
0.10
POR CONCRETO
MATERIAL
CONCRETOARMADO
MORTERO
ESCALÓN (TABIQUE ROJO)
MORTERO
LOSADECONCRETO
CARGA MUERTA ADICIONAL
(ART. 197RCDF)
20
20
POR MORTERO
Wm»
592
Cargas vivas.
Tabla de cargas vivas unitarias (kg/m 2 )
a).
Destino depiso o cubierta
W
(media)
Wa
(instantánea)
Wm
(maxima)
Habitación
(casa-habitación,
departamentos, viviendas, dormitorios,
cuartos de hotel, internados de
escuelas,
cuarteles,
cárceles,
correccionales, hospitales y similares.).
70
90
170
Nota: En áreas de comunicación de casas habitación y edificios de departamentos se considerará la misma carga viva que en el
inciso "a"de la tabla de cargas vivas unitarias. (Art. 199. Fracc. V.Inc. 3)
C a r g a d e diseño.
Carga Verticales =Wv=CM +CV =592+170=762 kg/m2
Carga por proyección.
Carg a Verticales = Wv = 762Cos 32° =641 kg/ m2
C a r g a lineal.
Area =3.00x2.00 =6.00/2 =3.00m2
.-. W¡=/'641j/3.00// =1923/2 =962 kg/ml
94
TESIS PROFESIONAL
5 . 2 . 4 . Transmisión y bajada de c a r g a s
5 . 2 . 4 . 1 . Transmisión de cargas a perímetro de tableros de losa de azotea
Tablero I.
TableroII.
ai=4.00
ai=4.00
a2=6.00
I.- Cálculo de áreas
I.- Cálculo de áreas
A=
4=
, 2 .
bxh
h=
r
6.00 + 2.00
2.00 =8.00m
B +b~\, ("6.00+2.00^
2.00 =8.00 m¿
h=
v 'l
2 ;
4.00x2.00
=4.00ml
A = 'bxh
,2
4=
J
4.00*2.00
4.00m-
II.- Análisis tramo corto
W,
a 2 =6.00
8 2 1 ^ 1 ( 4 . 0 0 ^ )=^ ! ^ =821 A g
'
A 4.00
í\r\ . „ml
;
ml
V m2 v
II.- Análisis tramo corto
W,= 7 4 1 .2 ^ ( 4 . 0 0 W 2 ) = 2 % 4 ^ = 7 4 . ^
{
m
4.00 ml
ml
III.- Análisis tramo largo
III.- Análisis tramo largo
2
6 5 6
* , = Í 8 2 . f2c 1(8.00
^ =714 kg
W; ) =
V
' t
6.00 m/
ml
W J
W,=\1A\
¿g
1(8.00W 2 )2=L .
2
592
Mg_98gj*g
m/
6.00 m/
95
TESIS PROFESIONAL
Tablero III.
T a b l e r o IV.
ai=4.00
ai=4.00
•*
a 2 =5.00
4= K 2 ,
A, =
bxh
h=
500
—•
I.- Cálculo d e áreas
I.- Cálculo de áreas
B +b
ai=4.00
+ 100
4.00x2.00 i
2.00 =6.00rr?
4=
bxh] f 4.00x2.00
=4.00 m¿
. „ 2
= 4.00w
II.- Análisis t r a m o c o r t o
k8
2964k
kS
^14l
IV, = 74l 2)(4.00m^
2 iV
' 4.00 w/
V w
II.- Análisis tramo corto
mi
2964
^=741>
W,= Í74,A?1(
4 .00^)=
2 |V
;
4.00 ml
mi
\
m
III.- A n á l i s i s t r a m o largo
(V,= 741 kg\6.00m2)=
V m
4446Jg = 8 9 Q kg
5.00 m/
w7
96
TESIS PROFESIONAL
T a b l e r o V.
Voladizo No. 1
Wv=741KGIW
ai=0.80
A,
<
a2=4.00
a2= 11.00
I.- Cálculo de área
I.- Cálculo de áreas
B+b
(bxh\
A,=\V2
h=
At =(bxh)=(0.80x11.00)=8.80 m2
4.00+2.00
f2.00xl.00
1.00= 3.00w ¿
1.00 m¿
II.- Análisis tramo largo
IV, = 741
11.00 ml
=5 9 3 ^
mi
Voladizo No. 2
II.- Análisis tramo corto
W,= 741^1(l.00* 2 )=? 4 1 - t e =371 t e
2.00mi
mi
V m
Wv=741 KG/M2
ai=0.80
A,
III.- Análisis tramo largo
•<
2
^ = Í 7 4 1 ^2 ] ( 3 . 0 0 W ) = ^ ü = 5 5 6 ^
y
mT
4.00 ml
a2=4.00
g
mi
I.- Cálculo de área
At =(bxh)=(0.80x4.00)=3.20m2
II.- Análisis tramo largo
W,= 7 4 , ^ ] ( 3 . 2 0 ^ ) = 2 3 Z L ? 1 ^ = 5 9 3 ^
m2
4.00
ml
mi
TESIS PROFESIONAL
CUADRO DETRANSMISIÓN DE CARGAS LINEALES EN TABLEROS DEAZOTEA.
TABLERO
LADOCORTO LADOLARGO
ai
«a
1mu.)
(mt*.)
I
4.00
II
CARGAEN
LOSA
CARGAEN
CARGAEN
LADOCORTO LADOLARGO
W14
Wu
(ta/nü.)
(k*/mL)
6.00
(kE/ma.)
821
821
1095
4.00
6.00
741
741
988
III
4.00
5.00
741
741
890
IV
4.00
4.00
741
741
741
V
2.00
4.00
741
371
556
VOLADIZOI
-
-
741
-
593
VOLADIZOII
-
-
741
-
593
17 00
4 00
i
TAB I
2 00
2:2:272722222222:22:11222:22222222"
1095 kg/rn!
i TAB I
CM
CV=
TINACO
W
4 00
5 00
6 00
641 kg/m'
100 kg/m'
80 kg/m'
821 kg/m'
CM
CV
-f
252222:22122::
890 kg,ml
TABIII
988 kg/ml
641 kg/m'
100 kg/m
W - 741 kg/m
CM
\v
q> eft
641 Kg m
100 kg/m
W - 741 kg/m'
E
eft
E
CO
en
1095 kg/ml
8 00 s
a^L_L;
TAB IV
988 kg/ml
890 kg/ml
593 kg/ml
593 kg,ml
'-777?77- r~"7-
ZZZZ3Z1
?*—
371 kg/ml ,
741 kg/ml
fTABV
, '
W-741 kg/mCMCV-
4 00
641Kg/nv
>00kg,m'
w * /4-Ug/m'
741 kg/ml
Akzz 2^2222222222222222'
' 3/1kg/ml"V7V777^77777?7.Z7rVA
li
—
ESCUELA
IN , i ! i t n o i ( i N t l l l U i O D I 1 AI I N . I h l l
I 9Ú
T-08
Casa- Habitación
MtlHUb
.SISOlT
ING AI 11 n
)L I'
AtJhVihl Í 1AMIUA
UBlCACON
V i c ente VilUda N o
77
Col Ahuizotla
&ABORC
M u n Naucatpan do Juarez
. .,,,.-
V k U h IN -1 Jl r
M U J K A J'HhFS
(ION
TESIS PROFESIONAL
5 . 2 . 4 . 2 . Transmisión de cargas a perímetro de tableros de losa de entrepiso
T a b l e r o I.
Tablero II.
a 2 =6.00
a 2 =6.00
I.- Cálculo de áreas
I.- Cálculo de áreas
AH^W^i^WsW
,^i- , - ' ± - * » .
fbxh^
4.00x2.00
: 4.00 ml
A=\-
( 6.00 + 2.00
4.00x2.00^1
bxh
2.00 = 8.00 m~
•• 4.00 m
v ¿ J
II.- Análisis tramo corto
II.- Análisis tramo corto
k
W,=\8 6 0 ^l1 1(4.00« 2 )=^LÍ8=860
m P
'
4.00 mi
k
I
mi
W, =I 905
] ( 4 . 0 0 m 2 ) = ^ ¿ M ? =905-1*
4.00 ml
ml
m
Ag
III.- Análisis tramo largo
2
^ = 8 6 0 *2 vfe.OO* )- £ § ° * = 1 1 4 7
l
w J
' 6.00 w/
m/
kg
III.- Análisis tramo largo
W, =I 905
INCLUYE :
Wv =CM +CV +Peso baño +Peso muro divisorio
kg
Wv =353+170+200+137=860•
m
kg
Í8.00/w 2 )=
7
- 2 i ? ^ =1207-1
6.00 ml
ml
INCLUYE:
Wv= CM+CV+Peso baño+Peso muro divisorio
Wv= 353+170+200+182= 905 kg/m2
100
TESIS PROFESIONAL
T a b l e r o IV.
Tablero III.
ai=4.00
ai=4.00
ai=4.00
a2=5.00
I.- Cálculo de áreas
I.- Cálculo de áreas
A=
4=
ÍB + b^
\
*
h=
5.00+1.00
f
2.00 =6.00 m1
J
bxh\
("4.00x2.00
bxh\
4= v 2 j
( 4.00X2.00A
•- 4.00 m
=4.00m2
II.-Análisis tramo corto
2 2
^ =Í523^1(4.00^)=^ ^ =523_^
2
' l
II.- Análisis tramo corto
m
4.00 ml
mi
^ , = ( 5 2 3 ^ (V4 . 0 0 W 2 ) = 2 0 9 2 ^ = 5 2 3 ^
' 4.00 ml
mi
V m
III.- Análisis tramo largo
3 3
W, 5 2 3 ^ 1 ( 6 . 0 0 ^ ) = J i ^ = 6 2 8 ^
V
m'
5.00 mi
mi
101
TESIS PROFESIONAL
Tablero V.
Voladizo No. 1
Wv=523KG/M 2
ai=0.80
Ai
ai=1.00
a 2 =4.00
a 2 =2.00
I.- Cálculo de área
I.- Cálculo de áreas
A=
( B +b
\h=
bxh
4=
Ax = (bxh) = (0.80x4.00) = 3.20m2
2.00+1.00
1.00x0.50
-0.50 =0.75m2
II.- Análisis tramo largo
,674
Js=4,9*
W , = | 5 2 3 ^ 1(3.20m2)=
2
{
my
' 4.00 ml
mi
=0.25»?
g
Voladizo No. 2 .
II.- Análisis tramo corto
2
3,
^=Í523^]Í0.25
W )=Í ^=131^
2 y
{
m)
100 ml
mi
Wv= 523 KG/M2
ai=0.80
A,
III.- Análisis tramo largo
•*
3
a2=1.20
g
^ = Í 5 2 3 ^ X] ( 0 . 7 5 ^ ) = ^ i ? = « 9 7 l
' V m)
' 2.00 ml
mi mi
I.- Cálculo de área
Ax = (bxh) = (0.80x1.20) = 0.96m2
II.- Análisis tramo largo
^ 1= Í 5 2 3 ^2 ] ( 0 . 9 6 W 2 ) = 5 0 3 ^ = 4 1 9 ^
{
mP
' \.20 ml
mi
TESIS PROFESIONAL
CUADRO DE TRANSMISIÓN DE CARGAS LINEALES ENTABLEROS DE ENTREPISO.
at
(tuts.)
aa
Imt». |
CARGAEN
LOSA
Wv
(kfL/m*.)
I
4.00
6.00
860
860
1147
II
4.00
6.00
905
905
1207
III
4.00
5.00
523
523
628
IV
4.00
4.00
523
523
523
V
1.00
2.00
523
131
197
VOLADIZOI
-
-
523
-
419
VOLADIZOII
-
-
523
-
419
TABLERO
LADOCORTO LADOLARGO
CARGAEN
CARGAEN
LADOCORTO LADOLARGO
Wu
(ka/ml.1
(kE/ml. |
103
17.00
4.00
mrs
I
2.00
1207kg-'ml
TAB II
1147 kg/ml
¡2'
8.00
ÍE3SZZS
r
i
TAB IV
353kg/m2
170kg/m?
CMCV-
CM=
641kg/m2
"CV=
170kg/m2
TINACO- 80kg/nf
W= 860kg/m2
4.00
>BAÑO- 200kg/m2
MURO=182 kg/m2
W-905 kg/m2
J A Rw
TAB I
E E
628kg/ml
cisr
CM353kg/m-'
CV170 kg/m2
,'" W-523kg/nr
en ¡LO
628 kg/ml
1207 kg/ml
HL
-&-
"197kg/ml"
523kg/ml
5.00
•-•
~77'/?7??7/77~^^7/"r,''.77777?,'
mzzssz^3^z
1147 kg/ml
TAB I
6.00
419 kg/ml
;
f'v5N523kg/m .7*
962 kg/ml
CMCV---
400
2
a>;-:
353%m
-T/OKct'm'
W-523kg/fii 2
ZONA
DE
ESCALERA
W-641 kg/m2
962 kg/ml
22222222mZ:.TL]
523kg/ml
~ZZ2ZZZZZZ22ZZ^Z:7¿ZZ/2.
ESCALA
-
~
-
-
-
-
-
-
-
-
-
-
-
•
-
-
-
•
1 90
T-09
ACOTACIÓN
METROS
" TECHA
AGOSTO 2003
-
-
-
INS¡'IIUTO !tCNUl.OüICO DELA 0ONSTRUC0ION
Casa- Habitación
!Nl¡ ALFONSO D AütiWRTT PANIOJA
Vicente Villada N o . 7 7 , Col. Ahuizotla. M u n . Naucalpan do Juárez
VICTOR [NRiQUL oLÜURA lüRntS
UOB^)
TESIS PROFESIONAL
5 . 2 . 4 . 3 . Calculo de reacciones de trabes
EJE
TRAMO
CARGAS SOBRETRABE
CARGA
TOTAL
íta/wi)
REACCIÓN
CLARO
(mt».)
9^^f^^m^^S^^^^mmmKmm^
RXA-RX»
(kai
NIVEL DE AZOTEA
B
D
E
F
B
D
2
2
2
1-2
1-2
1-2
1-2
2-3
2-3
C-D
D-E
E-F-
W- WL + WPOPO- 821+168821+741+1 6 8 741+741+168741+593+168741+168 -
989
1 730
1650
4.00
4.00
4.00
4.00
4.00
556+168 1095+371+168 -
1 502
909
724
1 634
988+593+168 890+593+168 -
1 749
1 651
6.00
5.00
1 028
2571
2204
1100
691
299
1 512
1 375
1 215
1 327
4.00
4.00
4.00
2.00
R-WL/2 «(989 x 4.00 )/2*
R- (1730 x4.00 )/2 R- (1650 x4.00 )/2*
R- (1502 x4 . 0 0 ) / 2 R- ( 909 x4.00 )/2 R- (724 x 4.00 )/2 R- (1634 x 2.00 )/2 R- (1749 x6.00 )/2 R- (1651 x5.00 )/2 -
1978
3460
3300
3004
1818
1448
1634
R- (1028 x4.00 )/2 R- (2571 x4 . 0 0 ) / 2 *
R- (2204 x4.00 )/2 -
2056
5142
4408
R-( 1 1 0 0 x 4 . 0 0 ) / 2 R- ( 6 9 1 x 4 . 0 0 1 / 2 R- ( 299 x4.00 )/2 R-(1512x2.00 1/2R- (1375 x6.00 )/2 R=( 1215 x 5.00 )/2 R» (1 3 2 7 x 2 . 0 0 ) / 2 =
2200
1382
598
1512
4125
3038
1327
5247
4128
NIVEL DE E N T R E P I S O
B
D
E
F
B
D
2
2
2
T
1-2
860+168 -
1-2
1-2
1-2
2-3
2-3
C-D
D-E
E-F
C-D
860+905+608+168905+523+608+168 523+419+168 523+168131+1681147+197+1681207+168 628+419+168»
197+962+168 -
4.00
4.00
4.00
4.00
2.00
6.00
5.00
2.00
Nota:
1.- Seconsidero u n a sección de 0.20x0.30 m t s . e n trabes, porloq u ese tiene u n peso propio:
Wp0Po= 0.20x0.30x2400 = 168k g / ml
2. Laescalera tiene u n peso lineal de 9 6 2 k g / m l .
3 . - Seconsidero a las t r a b e s como t r a m o s simplemente apoyados.
4.- Peso lineal del m u r o =W m = (253 kg/m 2 )(2.40 m)=6 0 8 k g / m l
105
17 00
4 00
6 00
2 00
SOU
ZZSSZ
TX
TAB I
11I TAB III
TAB I
1978 KG
3ÜU4 KG
3300 KG|
3460KG
I
4 0Ü
1978 KG
. < - 1634 K G - f
i 00
Kit
TAB IV
3004KG
3300 KG1
3460KG
ffi3
5247KG
5247 KG •
4128 KG
4 1 2 8 KG
V\TAB V
1818KG
1448 KG
H818 KG
1448 KG I
4 00
l
magnituddeconcentraciones en azotea
~
PLANO
l '. til l UN
1 JU
T-10
Casa-Habitación
ACOTACIÓN
MURO
At
I ! /I
UBCACION
Vicente Viiluda No 17Gol Ahuizulla Mun Njucdlpan de JLKHÍV
Si n i l
NOftfe]
17 00
4 00
TABI
*>00
6 00
2TO
*rI TAB III
TABU
205oKG
5142 KG
4408KG!
2056KG
5142 KG
4408 KG I
2200KG
4 00
2
800
¿—1 illKi-r?^.
inz^r
TAB IV
4125 KG
4125KG-
!
2200KG
3038 KG
3038Ku
\ TAB V
-ft—1327 KG—»
1382 KG
1
598 KG
4 00
1382KG
598KG l
£ =
magnitud de concentraciones en entrepiso
s;;;r~ - " —
ESCALA
""""•"-"•*"—*
" ' • "•
1M
ACOTACIÓN
-
MMRO
fio.
1,
, <'i i O H
Casa-Habitación
i
i
i
M.
Vicente Villad.i No // Gul Aliuizulla Mun M.iui dlpun ile Ju,mv
_*
mm^m^^^^^^^am^^mmaam^mmmmmmmmm^mmmmi^m^^m^m^mmmmm^^m^m
sasassBsassBi
TESIS
5 . 2 . 4 . 4 . bajada de cargas transmitidas por muros de carga y concentraciones en
ejes
EJE
TRAMO
PESO
PESO
SOBRE
TERRENO
PESOLOSA
DEAZOTEA
PESOMURO
PLANTA
ALTA
PESO
CONCENTRA
CIONESPOR
TRABE
PESOLOSA
DE
ENTREPISO
PESOMURO
PLANTA
BAJA
CONCEISITRACI
ONESPOR
TRABE
(KG/ML)
(KG/ML)
(KG/ML)
(KG/ML)
(KG/ML)
(KG/ML)
(KG/ML)
(KG/ML)
(KG/ML)
PESOSOBRE
CIMIENTO
CARGAS
ULTJM¡A§
(VV)
1
B-D
1095
681
1545
1147
681
1928
7077
7785
10899
1
D-E
988
681
1409
1207
681
1990
6956
7652
10713
1
E-F
890
681
1939
628
681
1835
6654
7320
10248
2
B-C
1836
681
2263
1670
681
2063
9194
10114
14159
PUNTO
D-2
C O N C E N T R A C I Ó N DE CARGA Ci
23166KG
2 5 4 8 3 1KÍ 3 5 6 7 6 KG
PUNTO
E-2
C O N C E N T R A C I Ó N DE CARGA C2
24238KG
2 6 6 6 2 KG 37327 KG
PUNTO
F-2
C O N C E N T R A C I Ó N D E C A R G A Ca
12370 KG
13607 KG 19050 KG
3
B-C
741
681
758
523
681
576
3960
4356
6099
3
C-D
371
681
604
962
681
250
3549
3904
5466
C
2*-3
1297
681
-
962
681
553
4174
4592
6428
Nota:
l.-Se consideró un 10%de peso propio de cimentación (Ws/C) para calcular el peso sobre el terreno (W.,/,).
2.- Las cargas últimas se obtuvieron multiplicando por el factor de carga F.C.= 1.4
108
B
D
E
6 ÜÜ
6 00
19/8 kg
f
1
\
\\
\\
\\
\x
109Uynl
W 681 kg mi
\\\
/
y
/
1141 kg itik
\\
\\
\
' 50
W
\\
\\
\
/
y
x
/
//
// /
'kg
EJE
Sotoiibiduü un 10°o (It ptso piopii
leutitntduon iW )pifaciltular el ptso
obit Itrienu iW )
' L t t caig ib ultinids ^e obtuvieion
tiulliplirandü poi fl l i i t o i d( t irga
0 14
TRAMO
X
y\
y
W
(3300) ( )[¿4tí)
440 i ky
x
/
x
x
x
x
y
x
PESOLOSA
ENTREPISO
/
X
/
x
y
W b81 kg i il
/
\V
/
681 k í . n ü "
X
/
/
X
/
/
X
/
/
X /
/
•X
y
/
W
/
X
/
X
X
/
X
X
/
X
X
y
X
x
/
X
iKG M I )
\
(140b) \h l \ty{\ 220lW 40) Itíw5 kg nil
\
PESOMURO
FLANEA BAJA
y
/
/
x
/
IRARt
<( Mi
/
X
/
X
•
(K&riL)
x
y
x
/
/
\
y
W i 142 i4 4 0 ^ ^ ( 2 40) 19°0 ky n 1
( ("Mí 1 N H A 1 l\if P O R
w> l í i L i i r\M i IÍÍ [ u n
/
y
y
y
2 01 ky
X
\
\Xx
/
x
x
PESOMURO
PLANTA AL TA
\
W f ? 8 k jml
X
/
/
y
/
\ x
IM0yk(jiti
X
/
/
x
/
A)
/
X
x
x
i l¡t\
/•
X
PESOLOSA
AZOTEA
(KG Mi)
/
\ X //
X
PF (.
/
/
x
\
68H > *
X
\
y
JOTA
\W
X
\ XX
y
/
X
/
y
x
X
/
/
y
x
^ 10) 1409 ky m!
/
x
/
x
/
(3460 t-¿300)^
/
//
/
/
/
X
/ W 1?07k|mt\
/
/
X
y
x
W
/
x
y
xx
/
/
x
y
W 681 kg ml
/
/
x
//
/
x
( ¿ 0 J O 2 4 + i b 1 4 ^ ) ( 2 4Ü) 192d kq mi
/
y
y
\
//
//
/"
x
/
x
W b81kgml
\
xx
\
/
\\
y
X
/
x
b14
y
x
/
x
\x
N
\\N
x
/
/
/ W
x
/
/
/
y
/
(1978 2 4) \ (34f)Q^ÍÍ?H¿ 4U> 1b45 kg ml
20b ¡kq
VV 890 kg nil
\Xx
/
//
/ \\
3104 kg
988 kg ml
X
/
\\
\
/
/
/
X
\
/
//
//
/
//
/
y
\
W
3300 kg
W
^ X
\X\
2 50
J UU
"- 00
3460 kg
W
F
14SO
(.N tNI íAÜK NI f CR
RABE
<\( ML
X
CIMIENTO W\ ¡
(KG ML)
PESOSOBRE
PESOSOBRE
HRREN0(W
¡KG ML)
GARGAo
Ul 1 Mho (W )
(KG MI |
10
1
BD
1095
681
1s45
114/
601
1928
/077
8
1
DE
988
681
1409
120?
681
1990
69J6
/bJ
1
E\
890
681
193'!
628
6b1
1835
6654
10 1 >
s>(
1018
Transmisión de cargas verticales Eje 1;Tino. (B-F)
SCULLA
II,
Casa - Habitación
\
|
tóESOH
í
UHCACON
V i c e n t e Villada No / / C u lAhutzotl i M u n N a u c a l p a n ilc J u m ¿
LABORO
V
(
t
j
i
2 50
5 00
2 50
NOTA
1 Se consideiu un 10% de peso piopio
de umentai ion (W jpaia calt ular elpeso
sobie terreno (W )
2 Las caigas ultimas se obtuvieion
multiplicando por elfactor decatya
FC 14
Transmisión de cargas verticales Eje 2;Tmo.CB-F)
ESCAL*
PLANO
ESCUUA
INSmu J i I . I U
1 90
T-13
Casa- Habitación
mx
Mt rhus
l ^ h Uf»!HIJLLIIN
A5ES0A
NI H 1 N ) ( / 1 1
ÍHII
[III A
UBCACON
ec-w
«l us o¿003
Vicente Villddrf No 7f Col Ahuizotla M u n Naut alpan ele Juarez
\ i
fit i SK
i rm
B
C
|
4 00
2 00
^
I
1448 kg
W
\\
\\
s
1
1
\\
741 ky ml
W 371 kg mi
//
\
\\
W
\ .
(1818 2 40)-75$ kg ml
(1446 240) b04<qml
V
\\
13Í 2 kg
^\
598 <g
W-523 kgml
\\
//
/
\\
2 50
/
/
//
\\
\\
\
\
//
\\
W
NOTA
EJE TRAMO
1 beconsideio un 10% de peso piopio
de cimentación (W (para calcular elpeso
/
y
^
\\
/
\ .
VENTANA
\ .
VENTANA
/
^ v
/
\ .
/
/
//
//
//
\\
/ S
Wi- 9b2 kg ml
W -5Q1 kg mi
2 50
VENTANA
/ W -b81 kg,mi
W -6Q1 kg ml
5 00 v
5 00
bOO
1818 kg
1
F
E
D
^"v
VENTANA
y /
/
- 6 8 1kg,ml
N
i1382 240)-b76lKLml
•- (598 2 10) 250 kg
W
\\
\\
ni
/
/
\ .
\\
PESO
PESOLOSA
PLSO MORO
TRABE
ENTREPISO
PLANTA BAJA
(KG ML)
Í Kü M I ,
(KG ML)
(KG ML)
PESOLOSA
PESOMURO
AZOTEA
PLANTA AL FA
(KG ML)
UJNUMRAÍIONFSPOR
PISO
PESOSOBRE
CARGAS
TERhLNOiW )
UthMAS (W)
l>G M i ,
PLSO SOBRE
CIMIENTO (W )
(KGML)
iKG ML]
iKG MI)
CONi N M A Í IONE ,POR
RAM
sobre terreno (W )
3
BC
741
681
758
523
681
576
3960
435r
6099
2 1 ascaigas ultimas seobtuvieron
3
CD
371
681
604
962
681
250
3549
3904
5466
multiplicando porelfactoi de caiga
EC ~ 1 4
-CB-D)
Transmisión de cargas verticales Eje 3;Tmo
ESCUUA
PLANO
ESCALA
III J i l i i ' ] 11' 1
' ,0
T-14
Casa-Habitación
ACOTACIÓN
MfRUS
U(, l
i ON I M I
ASfSOf)
IN,f I H H )
'EiBAh
L'JI ^
,
r
u ¡\
UflCACON
rtcm
. b JM <
Vicrntc Villacld No 7 7 GolAhuizolla M u n N a u i alpun d i Jun</
[IAMRO
J
i
i m
ir
1
2 2
4 00
3
1 00
3 10
c
\
VACIO
W
U s i ky mi
i/V
btsl kg nil
/
2 50
PUERTA
/
1
^ 'kg
W
5 00
\\
\\
\
\
VACIO
/
W
PUVRTA
2 50
W
NOTA
EJE TRAMO
1 Seconsiduo un10 odt, pts,o piopiü
decimentación (W jpaia calcular elpisu
sobie terreno (W )
C
2 3
PESOLOSA
PESOMURO
AZOTEA
PLAÑÍA AtTA
(KG MI l
(KG ML)
129/
681
%2 kg mi
\\
\N
681kg,<nl
\\
\\
\\
( 1 3 2 / 2 40) 553kg,ní1-
prsi
I Ü N L F N KA IM sPOR
11 ABE
<( MI I
N
PESC SOBRE
PESOSOBRE
' ARGAS
CIMIFN10(W )
iKG ML)
IERRLN0(W i
iKG M i l
ULTIMAS iV\ i
(KG Ml)
PI )
tNt INTRACIONE I OR
RAlit
i\G MI
681
5o3
4174
4 'X
o428
PESOLUSA
PLSO MURO
ENTREPISO
PLANTA BAJA
(KG ML)
962
(KG Ml)
2 Las cargtsultimas be obtuvieion
multiplicando poieltaitoi de cargí
1 G 14
Transmisión de cargas verticales
Eje O;Tmo - Ci -3)
ESCALA
l%
T-15
Casa-Habitación
ACOTACIÓN
Mfclrií)
N
UBCACON
TECHA
„
Vict uto VilladuNo
// C ül Ahui/otla Mu(i Naui alpan <le Juirt/
N
i
i r
TESIS PROFESIONAL
5.2.5. D i s e ñ o d e c i m e n t a c i ó n
5 . 2 . 5 . 1 . Diseño de zapata corrida de concreto reforzado
I. - Datos
VIH.- Area de acero
* Casaubicadaenzona detransición(Zona II).
*Capacidad dec&rgaadmisible deterreno(qa) = 7.00tonIm2
II.- Constantes
y
As= pbd
IX. - Area de acero
mínimo
especificaciones
Asma=035d
fe =200kg /cm2
f'y =2800 kg/cm2
F.S.= IA
Fr=0.9
f*c = 0.&f'c=\60kg/cm2
X. - Separación
ó
As
Xí. - Acero
max ^ 3 / ?
transversal
XII. - Esfuerzo cortante
hmn =15 cm
que resiste el
concreto
Vcr=bd Ve :. Ve= Fr 0.5 Jf* c
cimiento
Cargasobrecimiento
_ tonIm
Cap.carga del suelo - Peso propio cimentación tonIm2
V.- Recubrimiento
S
Asi =0.002M
mínimo
IV.- Base de
(longitudinal)
a, xb
f"c = 0.S5f*c = \36kg/cm
III.- Peralte
de acero principal
XIII.- Esfuerzo cortante
exterior
Vu = Vsx F.S. :. Vs = Wnx L
libre
': r, =3.00cm
VI.- Peralte
total
h, =r +d +0lar
VIL- Porcentaje
mínimo de acero
Pm¡n=0J^C^y™
fy
2800
=0.0035
113
TESIS PROFESIONAL
Diseño de zapata corrida de concreto reforzado
T r a m o 1( B - D )
W= 7077 KG/ML
K
1
d
>.
S.C. Momento
S.C. Cortante
A
B; Base
d; Peralte efectivo
h; Peralte total.
S.C,: Sección critica
A
1
d
v
<
C
>
B
v
I. - REVISIÓN DE ESFUERZOS
® Peralte
mínimo
q=-
hmm = 15 cm
Se propone :
h = 25 cm
© Calculo de peso propio de zapata
WPoPo = (yc)(A)(h)
WPoPo = 600 kg/m2
© Calculo de presión
para 1 m
= (2400 kg/m')(l.00
* 0.600 ton/m2
m2 )(0.25 m) =
© Calculo de base
„
W
B =- - =
Wn
7.07
6.40
ton/m , ,„
—- = 1.10 m
ton/m2
ton
= -A
ml
Sí; B = 1.10m
C = 0.20 m
h = 0.25 m
H = 0.75 m (Profundidad
/suelo = 1.6 í o n / m 1 .'.
de
desplante)
fj = (Area del
suelo)(ysuei0)(Ancho)
P2 = (Area de
columna)(ycr)(Ancho)
P3 = (Area de la base )(yCT)( Ancho)
neta
Wn = q a - WpoPo = 7.00 í o n / m 2 -0.480 ton/m2
P
= 6.40
ton/m2
P = (0.90x0.50x1.0x1.6) +(0.2x0.5x1.0x2.4j +f0.25x1.10x1.0x2.4)
P = 0.72 +0.24 +0.66 = 1.62 ton :.
(1.62+7.07J „ „ „ ,
. 2
-=1.90
ton/m1
fl.IOxl.00;
qa = 7.00 ton/m2 <q =7.90 ton/m2
£7 = '
=> No se acepta "B"
114
TESIS PROFESIONAL
Se propone ampliar la base a 1.30 m
® Cálculo de momento flexionante
P = (1.10x0.50x1.00x1.6) +(0.20x0.50x1.00x2.4,/ +(0.25x1.3x1.00x2.4;=
P =0.88+0.24+0.78 = 1.90 ton/ m2
(1.90+7.07;
S.C. = (B-C) = (1.30-0.20; =L = 1.10 m
W para 1 m de ancho = --— =5.30ton / m
1.30
n"
2
2
2
= WnL = (5.30ton/m )(l.\0m)
M
cant
2
¿
l
~ =6.90 ton /m
(i.30xi.oo;
Condición :
M
cant =(3-2°)(lA) = AM ton-m*
2
qa =7.00 ton/m
máximo
2
>q = 6.90 ton/m
Se acepta
= 3 2Q tQn
m
448910kg - cm
Calculo de peralte efectivo "d"
Solución :
II.-REVISIÓN POR MOMENTO FLEXIONANTE
1/ a. opción :proponer un porcentaje bajoacero y obtener el
peralte efectivo.
Nota :El momento flexionante se analiza como un empotramiento en 2/a. opción :proponer un peralte efectivo y obtener un
"cantiliver"
porcentaje de acero "p"
Se tomará la l/a. opción :Se propondrá un porcentaje
bajo de acero.
C
<
>
Se propone P =0.005
Sí; Pmín =0.003
min
Obtención de "q"mediante la utilización de la gráfica de
"Momentos Resistentes de Secciones Rec tan guiares".
i
Wn
!
q =p
fK = fo.005;í28—1 =0.1029 => Q=0.10
fe
V 136 )
Formula :
<
C
X
(
S.C.=B-C
Q=
¿
Frbd
d
d=
fe
M,
FrbfcQ
r
448910
= 19.15 cm
^(o.9;(ioo;(i36;(o.io;
Calculo de peralte
total
hT =r + d + <j>var = 3 + 19.15+1.27 = 23.42 «25.00 cm
115
TESIS PROFESIONAL
©
Cálculo de área de acero principal,
porcentaje de acero
propuesto
conforme
al
III.- REVISIÓN DE FUERZA CORTANTE
® Esfuerzo cortante que resiste la sección de concreto
(Vcr) al cortante enuna "zapata corrida" para un"b"
y "d" dados.
P
mín=0003
Se propuso =0.005
^0.005^100^19.15j =9.57cm2
As=pbd=
© Calculo de acero
Asm{n
ggggggggn^^^gg^
Vc = Fr 0.5(f*c = (Q.9)(Q.5)( vTóO^=5.69 kg /cm2
mínimo
Vc =5.69 kg /cm2
=> Esfuerzo que resiste el concreto.
2
=0.35 d= (03S)(\9.\ 5)=6.70cm
Para un "b" y "d" dados
Condición:
As =9.57cm2 >Asmín
Vcr =bdVc = ^5.69^100^19.15;=
=6.70cm2 => Se acepta
Vcr =10896.35kg* 10.89ton.
© Calculo de separación
de acero principal
(longitudinal)
© Cálculo de fuerza
a„xb
cortante
:. Sepropone; Var. 1/2" .-. a_ =1.27cm
Vu=VsxF.S.
1.27x100 , , „ . , - Se = — — - — =13.27* 13.00cm
ultima
=>
Vs=WnxL
Vs =(5.30)(l.l0) =5.&3ton.
Vu =(5.&3)(\.4) = &.\6ton.
Condición:
S
max
=3h=
® Calculo de acero
3 25
1S cm
( )=
Vcr =10.89ton >VU =8.16 fon
=>Se acepta
transversal
AsT =0.002bh =fO.002^100^25^ =5.00cm2
® Calculo de separación
de acero
D I S E Ñ O
A
transversal
a„xb
S =~ * — .'. Se propone; Var. 1/2" .-. a = 1.27cmL
A
2Var<|>l/2"
T
0.50 m
/\Srp
sJ^/^>=
exteriora
2
25.40,25.00 cm
Nota: En virtud de que los ejes 3(C-D presenta carga similar sobre el
cimiento a la calculada en eje 3(BCD), y además por facilidad de
construcción, se considerarán las jnismas dimensiones de diseño en
todo eleje.
0.75 m
-Var<t>l/2"@25
•
•
Var<|)l/2°(4 25
0.25 m
0.20m
<
X -
1.10 m
1.30 m
Var(t>l/2"«i13
116
TESIS PROFESIONAL
Diseño d e z a p a t a c o r r i d a d e c o n c r e t o r e f o r z a d o
Tramo 2 ( B - C )
W=9194 KG/ML
S.C. Momento
1
S.C. Cortante
d
v
M
<
1
C
>
B
V
I. - REVISIÓN DE ESFUERZOS
© Peralte
mínimo
P
q
hmm = 15 cm
Se propone :
h = 25 cm
® Calculo de peso propio de zapata
MM = (yc)(A){h) = (2400 kg/m")(l.00
2
W
POPO = 600 kg/m
* 0.600 ton/m2
© Calculo d e presión
para 1 m2
m 2 j(0.25 m) =
n =Qa -WpoPo = 7 - 0 0 ton/m2
-0.480 ton/m2
© Calculo de b a s e
W
B=W„
9.19 í o n / m
6.40
ton/m'
ton
^m2
Sí; B = 1.50 m
C = 0.20 m
h = 0.25 m
H =0.75 m (Profundidad
/suelo = 1.6 i o n / m 3 .-.
de
desplante)
P, = (Area <3eZsuelojf/^^jf
Ancho)
P2 =(Area de columna )(ycr)(Ancho)
P3 =(Area de la
base)(y„)(Ancho)
neta
w
-A
= 6.40 í o n / m 2
P = (0.65x0.50x1.0x1.6^2 +(0.2x0.5x1.0x2.4^ + (0.25x1.50x1.0x2.4j
P = 1.04 +0.24 +0.90 = 2.18 ton .\
(2.18 +9.19) „ C I W
. 2
i. = 7.58 ton/m
(1.50x1.00;
qa = 7.00 ton/m2 <q =7.58 ton/m2
q =-'
1.43 m « 1.50 m
=> No se acepta "B"
117
TESISPROFESIONAL
Se propone ampliar la base a 1.70 m
® Cálculo de momento flexionante
M I ^ H
máximo
P=f0.75x0.50xl .00x1.b)2 + ^0.20x0.50x1.00x2.4j +(0.25x1.7x1.00x2.4;=
P= 1.20+0.24+1.02= 2.46ton/ m2
S.C. = (B-C)/2
(2.46+ 9.19J
<?=n.70xi.oo;
W„ para 1 m de ancho =—'— =4.02 ton/m
n
1.70
W
I?
(4.02
ton/m2)(0J5m)2 =2.26 ton -m
n
M,cant
2
2
= fl.70-0.20^/2 =L =0.75m
£ QC
2
; 6.85ton/ m
Condición:
qa =7.00 t o n / m 2 > q = 6.85 ton/m2
Se acepta
_
M
cant = (2-26)(]-4) = 3.16ton-m*
316575 kg - cm
Calculo de peralte efectivo "d"
II.-REVISIÓN POR MOMENTO FLEXIONANTE
Solución :
Nota :El momento flexionante se analiza como un empotramiento en 1 / a " opcion : Pr°P°nerf «£ Porcentaje bajo acero y obtener el
peralte efectivo.
"cantiliver"
2/ a. opción :proponer un peralte efectivo y obtener un
porcentaje de acero "p".
Se tomará la \/a. opción :Se propondrá un porcentaje
bajo de acero.
Sí; Pmfn =0.003 .'. Se propone
Uuyuáoacad
Wn
\
Obtención de "q"mediante la utilización de la gráfica de
"Momentos Resistentes de Secciones Rectan guiares".
q =P fJ = ¿0.005,1
S.C.=(B-C)/2
<
>
B
P =0.005
2800
= 0.1029
136
Q = 0.10
Formula :
M,
Mu
z
Frbd
\Frbf"cQ
f"c
316575
d = /—-70.9^1oo^i36^o.io;
© Calculo de peralte
= 16.08 cm
total
r + d + <f>var = 3+ 16.08+ 1.27 = 20.35 ~ 20.00 cm
118
TESIS PROFESIONAL
© Cálculo de área de acero principal, conforme al
porcentaje de acero propuesto
III.- REVISIÓN DE FUERZA CORTANTE
© Esfuerzo cortante que resiste la sección de concreto
(Vcr) al cortante en una "zapata corrida" para un "b"
y "d" dados.
P
mín=0m3
Se propuso =0.005
As =pbd =(0.005)(\00^16.08;=8.04 cm2
Vc =Fr0.5 ff* c = (0.9)(0.5)(^¡f60)=5.69 kg /cm2
© Calculo de acero mínimo
Vc =5.69 kg/cm2
=> Esfuerzo queresiste el concreto.
2
Asmín =0.35d=(0.35^16.08;=5.62 cm
Para un "b"y "d" dados
Condición:
Vcr=bdVc=
As =8.04cm2 > Asm>n - 5.62cm2 =>Se acepta
© Calculo de separación de acero principal
acxb
S__i
• s e pr0p0ne;
yar_\/2" .-. a „ =1.27 cm¿
V„ =9148.52kg «9.14 ton.
© Cálculo de fuerza cortante exteriora
VU=VS x F.S. => Vs=Wn xL
Vs = (4.02)(0.75)= 3.01 ton.
Vu = (3.0\)(l.4} = 4.22 ton.
= \SJ9i»\S.O0cm
Vcr =9.14 ton > Vu = 4.22ton =>Se acepta
Condición:
S
max
© Calculo de acero
=3h = 3 20 = 6 0 c m
( )
D I S E Ñ O
transversal
2 Vartyl/2"
AsT =0.002bh =(0.002#100;(20;=4.00cm2
A
® Calculo de separación de acero transversal
a„xb
S=—f— /. Se propone; Var.1/2' .-. a s =1.27 cm ¿
SJ^UJP-
ultima
*,
s
As
S =-~~^
(longitudinal)
(5.69^100^16.08; =
31.75,30.00cm
A
Var«))l/2"fe!30
-y
Var <|>l/2'>)30
0.50 m
0.70 m
0.20 m
<
0.75 m
0.20m 0.75
><
*
1.70 m
>
Va! <t>l/2"(«;15
119
TESIS PROFESIONAL
Diseño d e z a p a t a c o r r i d a d e c o n c r e t o r e f o r z a d o
Tramo 3( B - C )
W= 3960 KG/ML
* - * - *
1
S.C. Momento
S.C. Cortante
A
B; Base
d; Peralte efectivo
h; Peralte total.
S.C,; Sección critica
d
v
<
C
>
B
I. - REVISIÓN DE ESFUERZOS
® Peralte
mínimo
P
h
ton
m,n =15 Cm
Se propone :
h = 20 cm
0
Calculo de peso propio de zapata
WPoPo =(yc)(A)(h)
WpoPo = 480 kg/m2
© Calculo de presión
=f2400 kg/m')(\.00
* 0.480 ton/m2
m2)(0.20 m) =
P] =(Area del
P2 =(Area de
P3 = (Area de la
neta
Wn = qa -WPoPo = 7.00 ton/m2
®
para 1 m2
-0.480 ton/m2
Calculo de base
3.96
ton/m
6.52
ton/m'
Sí; B = 0.60 m
C = 0.20 m
h = 0.20 m
H =0.70 m (Profundidad
Tsueh = 1.6 ton/m3 .-.
= 0.60 m
= 6.52
ton/m2
de
desplante)
suelo)(ysuelo)(Ancho)
columna)(ycr)(Ancho)
base)(ycr)(Ancho)
P =f0.40x0.50x1.0x1.6) + /U2x0.5xl .0x2.4J +f0.20x0.6xl .0x2.4J
P = 0.32 +0.24 +0.28 = 0.84 ton :.
fO.84 +3.96; Qna4
2
q =-•
= 8.00 ton/m
f0.60xl .00,/
qa =7.00 ton/m2 <q =8.00 ton/m2
=> No se acepta "B"
120
TESIS PROFESIONAL
® Cálculo de momento
Se propone ampliar la base a 0.80 m
P =(0.60x0.50x1.00x1.6) +f0.20x0.50xl .00x2.4,/+fO.20xO.70xl .00x2.4,/
P =0.48 +0.24 +0.38 =1.10 ton/m2
Condición :
>q =6.32
máximo
S.C. =(B-C) =(0.80- 0.20,/ =L =0.60m
W para 1 m de ancho =TT7 =7.90 ton/m
0.80
WnI? _ ( 7 . 9 0 J q n / m 2 j(0.60 m)2
1.42ton - m
M,cant
M
cant = (l A2)(X A) = l 9 8 ton-m*
198800 kg - cm
(1.10+3.96; r ^ ^
, 2
q = <—
í =6.32 ton/m1
(0.80x1.00^
qa =7.00ton/m2
flexionante
ton/m2
Se acepta
Calculo de peralte
efectivo "d"
Solución :
II.-REVISIÓN POR MOMENTO FLEXIONANTE
Nota: El momento flexionante
' cantiliver"
se analiza como un empotramiento
1/ a. opción : proponer un porcentaje bajo acero y obtener el
peralte efectivo.
en 2/a. opción :proponer un peralte efectivo y obtener un
porcentaje de acero "p".
Se tomará la \/a. opción :Se propondrá un
bajo de acero.
a
I V
' ' Pmín = °- 003
Se propone
porcentaje
P =0.005
Obtención de "q"mediante la utilización de la gráfica de
"Momentos Resistentes de Secciones Rectangulares".
Wn
q = pfy=
f0.OO5A—I =0.1029 => 0 = 0.10
fe
y 136;
Formula :
S.C.=B-C
^x-
B
d=
Q =Frbd*- fe
d=
198800
\¡(o.9y(ioo;(i36;(o.10;
© Calculo de peralte
M,
\¡Frbf"cQ
=12.74 cm
total
hT =r + d +0var =3+12.74+1.27 = 17.01* 20.00cm
121
TESIS PROFESIONAL
©
Cálculo de área de acero principal,
porcentaje de acero
propuesto
conforme
al
III.- REVISIÓN DE FUERZA CORTANTE
© Esfuerzo cortante que resiste la sección de concreto
(Vcr) al cortante en una "zapata corrida" para un"b"
y "d" dados.
P
mm=0003
Se propuso = 0.005
As =pbd =(0J00S)(10Q)(\2J4) =6.37 cm2
© Calculo de acero
As
mín
=
Vc =Fr0.5¡f* c =(0.9K0.5)( JÍ60; =5.69
mínimo
Vc =5.69kg /cm2
kg/cm2
=> Esfuerzo que resiste el concreto.
2
0-35d = (035^12.74;=4.45 cm
Para un "b"y "d" dados
Condición:
z
9
z
As - 6.37c m >Asjn^n =4.45cm
© Calculo de separación
Vcr =bdVc = (5.69^100^12.74; =
9
=> Se acepta
de acero principal
Vcr =7249.06 kg * 7.24 ton.
(longitudinal)
© Cálculo de fuerza
a„xb
z
S __ ¿ . — • se propone; Var.1/2" .-. a „ =1.27
s cm
As
cortante
Vu=VsxF.S.
=>
Vs =(7.90#0.60; =4.74 ton.
Condición:
Vu =(4.74)(\.4) =6.63 ton.
max
=3h
© Calculo de acero
= 3 20 =
( )
6 0 cm
Vcr =7.24ton >Vu =6.63 ton
transversal
acxb
S =-~
de acero
M
M
2Var*l/2"
transversal
.'. Se propone; Var.1/2" .-. a =1.27 cmz
J\.Srr\
Se acepta
D I S E Ñ O
AsT = 0.002bh =f0.002^100^(20; =4.00 cm2
® Calculo de separación
ultima
Vs=WnxL
S = ~7*l00- =19.93*20.00 cm
6.37
S
exteriora
->
-,
^
s=<}*m)=3X75m30Man
4.00
Nota: En virtud de que el eje 3(C-D) presenta carga similar sobre el
cimiento a la calculada en eje 3(B-C), y además por facilidad de
construcción, se considerarán ¡as mismas dimensiones de diseño en el
eje.
0.50m
0.70m
-Var4>l/2*@30
•
•
0.20m
V V
0.20
< mX
0.60m
0.80 m
Var<(>l/2"@30
z¡
Var<|)l/2"(«)20
122
TESIS PROFESIONAL
Diseño dezapata corrida deconcreto reforzado
Tramo C(2"- 3 )
W=4174KG/ML
1
*-*-*
S.C. Momento
S.C. Cortante
•
•
A
d
v
A
C
B
<
>
B
© Peralte
mínimo
I.- REVISIÓN DE ESFUERZOS
Km =15cm
p
Se propone :
Q=
A
h =20cm
® Calculo de peso propio de zapata
© Calculo de presión
m2)(0.20 m)=
-0.480 ton/m2
W
Wn
=6.52
ton/m2
de
desplante)
P, =(Area deí
suelo)(ysuelo)(Ancho)
P2 =(Area d e columna)('ycr)(Ancho)
P¡=(Area d e la base)(ycr)( Ancho)
P =(0.25x0.50x1.0x1.6)2 + (0.2x0.5x1.0x2.4,/ + (0.20x0.70x1.0x2A)
P =0.40 +0.24 +0.33 =0.97 ton :.
® Calculo de base
B
0.70 m
C= 0.20 m
h= 0.20m
H = = 0.70 m (Profundidad
7suelo =1-6ton/m
:.
neta
Wn =qa -WPoPo =7.00 ton/m2
~ m2
Sí ; B=
para 1 m2
WPoPo =(yc)(A)(h) =(2400 kg/m2)(\.00
48
2
W
POPO = ° kg/m
* 0.480 ton/m2
ton
4.17
ton/m
6.52
ton/m2
0.63 m « 0.70m
(0.97 +4.17;
= 7.34 ton/m~
(0.70x1.00,1
qa =7.00ton/m2 <q =7.34 ton/m2
=> Nose acepta "B"
123
l^^HBHBBi^^^^^HI
Se propone ampliar la base a 0.80 m
TESISPROFESIONAL
® Cálculo de momento flexionante
• • ^ ^ ^ • • • • • • • H
máximo
P= (0.30x0.50x1.00x1.6^2 +(0.20x0.50x1.00x2.4;+(0.20x0.80x1.00x2.4;=
P=0.48+0.24+0.38=1.10ton/ m2
S.C. = (B- C)/2 = (0.80- 0.20;/2 =L =0.30 m
0.10 +4.17;
q =-!
=6.58ton/ m
(0.80x1.00;
Condición:
W„
n para 1 m de ancho =-—- =8.22 ton/m
0.80
2
W
L
(8.22
ton
/m2)(0.30m)2
n
M
cant=2~ =
2
= 0.36 ton-m
2
M
qa =7.00ton/m
> q = 6.58 ton/m"
Se acepta
cant = (0.36)(IA) =0.51ton-m*
51786 kg-cm
© Cálculo de peralte efectivo "d"
II.-REVISIÓN POR MOMENTO FLEXIONANTE
Nota :El momento flexionante se analiza como un empotramiento en
"cantiliver"
1
S.C.=(B-C)/2
<
>
Solución :
l/a. opción :proponer un porcentaje bajo acero y obtener el
peralte efectivo.
2/ a. opción :proponer un peralte efectivo y obtener un
porcentaje de acero "p".
Se tomará la \/a. opción :Se propondrá un porcentaje
bajo de acero.
Wn
Se propone P = 0.005
Sí; Pmf„ = 0.003
rnin
Obtención de "q"mediante la utilización de la gráfica de
"Momentos Resistentes de Secciones Rectan guiares".
q=
f"c
= (0.005;'
^ U 0.1029
0 = 0.10
136 )
Formula :
B
M
u
Q--...
Frbd2 f"c
,
d=
M,
^Frbf'cQ
51786
= 6.50 cm
(o.9;(ioo;(i36;(o.io;
® Calculo de peralte
total
hT = r + d + <pvar = 3+6.50 +1.27 = 10.77 * 15.00 cm :. d = 10.73 cm
124
TESISPROFESIONAL
© Cálculo de área de acero principal, conforme al
porcentaje de acero propuesto
III.- REVISIÓN DE FUERZA CORTANTE
0) Esfuerzo cortante que resiste la sección de concreto
(Vcr) al cortante en una "zapata corrida" para un "b"
y "d" dados.
P
mín=0003
Se propuso =0.005
(0.005^100^10.73;=5.36 cm2
As=pbd=
mín
=
=(0.9)(0.S)(^6O) =5.69 kg/cm2
Vc =Fr0.5¡f*c
© Calculo de acero mínimo
As
HHMBHHBHMBBi
Vc =5.69 kg/cm2
=> Esfuerzo que resiste el concreto.
2
03Sd=(03S)(l0.73) =3.75 cm
Para un "b"y "d" dados
Condición:
As =5.36cm2 > Asmin =3.75cm2 => Se acepta
© Calculo de separación de acero principal
(longitudinal)
a„xb
S = - ^ ¡ — .-. Se propone; Var. 3/8" .\ a 0 =0.71 cm2
As
*
Vcr=bdVc=
(5.69^100^10.73;=
Vcr =6105.37 kg * 6.10 ton.
© Cálculo de fuerza cortante exteriora
Vu =Vs x F.S. => Vs =Wn xL
0.71x100 , - . . . . „ „
Sc = - „——= 13.24«15.00 cm
5.36
Vs =(8.22^0.30;=2.46 ton.
Condición:
Vu =(2A6)(\.4) = 3A5ton.
Smax=
® Calculo de acero
ultima
->
3h=3(\5)=45cm
Vcr =6.10 ton >VU = 3.45 ton => Se acepta
transversal
D I S E Ñ O
AsT =0.002bh=(0.00(2)(l00^15) =3.00 cm2
2Var<|>3/8"
® Calculo de separación de acero
a„xb
S= _ s
.
Se pr0p0ne;
transversal
¿
Var <t>3/8"@ 2 5
->
var. 3/8" .-. a =0.71 cm
J\Srp
Var<t>3/8"foj25
sJ~°^p)=23.66»25.00cm
0.65 m
<
0.30 m
><
0.20 m
0.30
3*0.80 m
>
Var<t)3/8"(í/!l5
125
TESIS PROFESIONAL
5 . 2 . 5 . 2 . Diseño dezapata aislada deconcreto reforzado
/.- Datos
VIII.- Revisión de esfuerzo
* Casa ubicada enzona de transición (Zona II).
* Capacidad de carga admisible de terreno (qa) =7.00
II.- Constantes
y
Vu =
IX. - Revisión
por
X. - Area de acero
¿s =
VQa -
V.- Recubrimiento
^smin
=m
W
PoPo
WnL
necesario
As
Frfy(d-~2) a
XI. - Acero de acero
cimiento
s/c
w.
(WnxaxB)F.S.:.
flexión
M„
= 15cm
B
trabe
Bd
mínimo
IV.- Base de
como
i/u=3'- <Vcr=O.s/7*c
especificaciones
fe =250 kg/cm2
f y =3500 kg/cm2
F.S. = 1.4
Fr = 0.9
f*c =0.8/'c =200 kg/cm2
f"c =0 . 8 5 / *c =170 kg /cm
III.- Peralte
ton/m2
cortante
a=
ÍJL
Bf'c
mínimo
~"
0-7/7'
* J ° Bd
f'y
libre
i rL =3.00 cm
VI.- Peralte
efectivo
d =h+r+0Var
VIL- Revisión de peralte
por esfuerzo
cortante
Vu=(Wn(A~(c
+ d)2)F.S..:
v = u <V cr
" bnd'
=Frlf*c
1J
126
TESIS PROFESIONAL
Diseño d e z a p a t a a i s l a d a d e c o n c r e t o r e f o r z a d o
Punto C E - 2 )
W= 24238 KG
/. - REVISIÓN DE ESFUERZOS
1
q=
ton
^n7
Sí; fí = 2.00 m
C = 0.20 m
h = 0.25 m
H =0.75 m (Profundidad
Ysuelo = 1.6 i o n / m 3 .-.
de
desplante)
M
1
P, = (Area deZ suelo )(y^^^
Ancho)
P2 =(Area de
columna)(y„)(Ancho)
P¡ = (Area de la base Xy^ff Ancho)
V
B
® Peralte
mínimo
P =(0.90x0.50x2.0x1.6;2 +(0.2x0.5x2.0x2.4;+ (0.25x2.0x2.0x2.4;
P = 0.28+0.48+2.40 = 3.16 ton :.
Km =15 cm
Se propone :
(3.16+24.23;
2
— í _ 684 ton/m
C2.00x2.00j
g a = 7.00 ton/m2 <q = 6.84 í o n / m 2 =>Se acepta "B"
h = 25 cm
© Calculo de peralte
o _!
efectivo
d = hj- - rL - <¡>var = 25- 3- 1.27 = 20.73 cm
® Calculo de peso propio de zapata
II.- REVISIÓN DE PERALTE POR ESFUERZO CORTANTE
COMO LOSA.
para 1 m2
WPoPo =(rc)(A)(h) = (2400 fcg-/m3;(1.00 m 2 ;f0.25 m) =
WPoPo = 600 kg/m2 * 0.600 ton/m2
© Calculo de presión
neta
Wn =qa -WPoPo = 7.00 ton/m2
-0.600 ton/m2
= 6.40
I d/2
ton/m2
© Calculo de base
24.23 ton
6.40
ton/m2
1.94 m * 2.00 m .. A = 4.00 m"
B
127
TESIS PROFESIONAt
® Cálculo de esfuerzo cortante
Vu=(Wn(A-(c
última
+ d)z)F.S
Vu = (6.84^4.00 - /0.20+0.20^1 .4=36.77ton. *36771.84 kg
Vu
v'=- :.bn=4(c +d) =4^20+20.73J = 162.92«163cm
u
bd
°
v-
u
.ÜZZL8i_= 10 . 88k
063^20.73^
/cm2
Cálculo de esfuerzo cortante
última
Vu=(WnxaxB)F.S
Vu = f6.84#0.70#2.00;i .4=13.40ton. * 13406.40 kg
v
13406.40
v =-lLu =
—
u
Bd (2Q0H20.TS)
„ „„ , . 2 z
=3.23kg/cm
® Calculo de esfuerzo cortante que resiste el concreto
y
v„ =0.sjf*c
=0.5Í200 =7.07kg/ cm2
Calculo de esfuerzo cortante que resiste el concreto
Condición:
Vcr =Fr j p
c =0.8y/200=11.31kg / cm2
Ve,. =7.07kg /cm2 > v'u= 3.23kg /cm2 => Se acepta
Condición,
vcr =11.31 kg/cm
> v'u= 10.88kg/ cm2 => Se acepta
III.•REVISIÓN DE ESFUERZO CORTANTE COMO TRABE
<4^
S.C. de cortante
- ^ como trabe
® Cálculo de "a"
a =„
B-C
2
, 2.00- 020
d=—
2
0.20=0.70 m
IV.-REVISIÓN POR FLEXIÓN
^
S.C. a la flexión
TESISPROFESIONAL
<5) Cálculo de acero mínimo
Asmim n = ° Í Í & .B.d- ^
f'y
Wn
° (200,(20.73,= 13.11cm
3500
2
Se tomará As - =13.11cm
Se propone utilizar :
*var =1/2"= 1.27cfrT •'•
S.C.=(B-C)/2
<
>
JVo.farií/as = ~ ^ ü =10.32 « 11.00 Vari/las
B
(D Cálculo de momento flexionante
S.C. =(B-C)/2
1.27
máximo
D I S E Ñ O
=(2.00- 0.20;/2 =L=0.90rn
__ WnL2 _ ( 6 ^ 8 4 t o n / m 2 ^ 0 . 9 0 m j 2 _
M cant
=2.77ion- m
2
2
M c a n t =(2.70)(\A) =3.87ion- m«387828kg - cm
© Calculo de acero
A
A
principal
Var4>l/2"@20
Ambos sentidos
0.50m
M„B
(387828#2.00;
A. *>/ ' y(d- a/ 2) (0.9^3500J(20.73-a/2;
0.75m
r j . ^ j - j i , ' i , i . '
X
Se propone a - 1.25
775656 , „ „ , 2 2
(387828^2.00;
- =-•--•— =12.24cm
As=
(0.9^(3500j(20.73- 1.25/2> 63330.75
• - - r - ~ _
. .
^
0.25m
v
«1
»
0.90 m
-••
<
0.20m 0.90m
>
<
* =
>
2.00 m
Comprobando valor dea = \.25
a _ A O > = (]2.24jf3S00j = , 2 6
" BjT"c
(200j(170j
a p r o p =1.25% a„„»caí=1.26
Nota: En virtud de que se tiene una carga similar en elpunto (D-2), se
propone el mismo diseño para lamencionada concentración.
Se acepta
129
TESIS PROFESIONAL
Diseño de zapata aislada de concreto reforzado
Punto C F - 2 )
W= 12370 KG
/. - REVISIÓN DE ESFUERZOS
1
P
ton
Sí; B = 1.40m
C = 0.20 m
h = 0.25 m
H = 0.75 m (Profundidad
7suelo =1-6
3
ton/m
de
desplante)
.-.
P, = (Area de/
suelo)(ysuelo)(Ancho)
P2 = f^rea d e
columna)(ycr)(Ancho)
P3 = ("yirea d e /a
base)(ycr)(Ancho)
® Peralte
mínimo
P =(\.20x0.50x1.40x1.6) +(0.2x0.5x1.40x2.4;+(0.25x1.40x1.40x2.4;
P = 1.34 +0.33 +1.17 = 2.84 ton :.
Kn,n =15 Cm
Se propone :
(2.84+12.37; „ „ ^
. 2
.—/_ _ 7 76 ton/m¿
0-40x1.40;
qa = 7.00 ton/m2 <q = 7.76 ton/m2 => No se acepta "B"
Se propone ampliar la base a 1.50 m
h = 25 cm
© Calculo de peralte
d =hT-rL-
q=s
efectivo
0W =25- 3- 1.27 = 20.73 cm
© Calculo de peso propio de zapata
P = (1.30x0.50x1.50x1.6; +(0.2x0.50x1.50x2.4;+ ("0.25x1.50x1.50x2.4;
P =1.56 +0.36 +1.35 = 3.27 ton
para 1 m2
Wpop0=(yc)(A)(h) = (2400 kg/m3)() .00 m2)(0.25 m) =
Wp0po =600 kg/m2 * 0.600 ton/m2
® Calculo de presión
¿3.27+ 12.37;
2
g_L
— = 6.95 í o n / m
0-50x1.50;
Condición :
neta
Wn = qa -WPoPo = 7.00 ton/m2
-0.600 ton/m2
= 6.40
ton/m2
® Calculo de base
qa =7.00 ton/m2
>q = 6.95
ton/m2
Se acepta "B" :.
B = 1.50 m => A = 2.25 m
4
Í2.37 ton
s= '«r = 6.40
ton/m
2
= 1.39 m « 1.40 m .-.A = 1.96 m"
130
TESIS PROFESIONAL
n. - REVISIÓN DE PERALTE POR ESFUERZO CORTANTE
COMO LOSA.
IU.~REVISIÓN DE PERALTE POR ESFUERZO CORTANTE
COMO TRABE.
m.
Id/2
S.C. de cortante
^ como trabe
B
® Cálculo de esfuerzo cortante
Vu=(Wn(A-(c
+
B
última.
® Cálculo de "a"
a = B - C = 1.50 - 0.20 = 1.30 m
d)')F.S
Vu =(6.95^2.25 - (0.20+0.20;2>1.4 =20.33ton. « 20335.70 fcg
V
J/ u = — .-.fa0=4fc +d; =4^20+20.73;= 162.92* 163cm
bd
°
20335.70
2
=6.01 fcg/cm
v _
" 063^20.73;
Cálculo de esfuerzo cortante
última
Vu=(WnxaxB)F.S
VU=(6.95)(13Q)(1.50)\ A = 18.97 ton.* 18973.50kg
v .."=- Bd
18973.50
, 2
i n 1
— =r6.\0
kg/cm
(\50)(2Q.TS)
CaZcuZode esfuerzo cortante que resiste el concreto
Calculo de esfuerzo cortante que resiste el concreto
vCr=FrjT*c
=0.8^00=11.31 kg / cm2
vcr =0.5Jf *c =O.5/2OO =7.07kg /cm2
Condición:
vcr =11.31kg/cm2
> v'u =6.01kg/cm2
=> Se acepta
Condición:
vcr = 7.07 kg /cm2 > v'u= 6.10 kg /cm2 => Se acepta
131
TESIS PROFESIONAL
O) Cálculo de acero
JQJ.- REVISIÓN POR FLEXIÓN.
^
mínimo
S.C. a la flexión
7
C S d
**ndn
= ° - 7 3500
^ 5 0 ' " 0 * 2 0 . 7 3 ; = 9.83 cm2
mm = ° ' ^
fy
¡IIP
Se tomará As = 20.22 cm¿
Se propone utilizar :
Kar =1/2"= 1.27 cm 2 .•
No. Varillas =
B
© Cálculo de momento flexionante
máximo
S.C. = (B-C) = (\.50- 0.20;=L =1.30 m
Wnl?
(6.95ton/m2)(\.30 m)2
B_+
=
cant =—J- =
j
M
cant = í 5 - 8 7 ^ 1A) =8 - 2 2 í o r l - m * 822185 kg-cm
M
@ Calculo de acero
MUB
s
~ Frf'y(d-a/2)~
D I S E Ñ O
~m
A
A
principal
_
(S22AS5)(\.50¿_
Var<j>l/2"@ 10
Ambossentidos
0.50ir
0.75m
(0.9)pÍ5Q0J(20.n-a/2)
Se propone a =2.75
=
2022
= 15.92 * 16.00 Varillas
1.27
Var<t>5/8"@ 15
Ambossentidos
A
.. . . 1 8 ^ 8 2 ^ _
= 1233277J50 =
(0.9*3500*20.73- 2.15/2)
60968.25
0.25m
cm2
1.50 m
Comprobando valor dea= 2.75
a = ^ s / ' y _ (20.22*3500; = 2 ? ?
Bf'c
(150*170;
.
aprop =2.75*acal =2.77 => Se acepta
132
uoo
2 00
•>(iO
^
4 00
2 8oo
4 00
planta de cimentación
PLANO
fbll
T-16
II 1 í
\
Casa- Habitación
I IC »
l\M
t I M I AHÍ
VI I
IHh 1
I ti
UBCW.ÜN
VK ente Villdda No 71Gol Ahui/utld Mun Naucdlpan di. Juaixz
1!
NO"16
CORTES DE ZAPATAS CORRIDAS
Var01/2@ 1 3
2Var01,2
r. 2 Vai 0 1 / 2 "
2Var01/2
_ Var 0 1 / 2 (g? 20
Var 0 1 / 2 @ 1 5
Var 01/2'<a 13
0 50
0 50
-Var 0 1 , 2 (<¿ 25
>
Var 0 1 / 2 (a) 20
Vai 01/2 (g) 15
0 50
_Var01/2 (o)30
c<
' c<
0 25
0 20
_Q
a
Q
n- ^
_o
o
Ü
-O.
d
O
Q.
_o
O.-
Vai 01,2"( S ) 30
3
c(
0 20
O V1 O . o
JO
n
" ^
n
i
30
1 70
0 80
corte a-a'
corte b-b'
corte c-c
Var 01/2' (ó) 20
Var 0 1 2"@15
2 Var 0 1 / 2
,_ 2 Var 01,2"
^ Var 0 1 / 2 (a)15
Var 0 1 / 2 (g> 25
0 50
0 15
D
C<
-i
H
n%^
Var 0 1 / 2 <ú) 20
015
J3
Var 0 1 2 @ 30
0 50
b
d
o
o-
.3
0 80
corteg-g'
corted-d
PLANO
iNsnruTj rrtNOioci oni LACUNÍTRIXU ¡U
Casa- Habitación
T-17
M h FIN JIJ AUi/KIl HW)JA
UBICACIÓN
AGObrU?003
V i c e n t e Villada N o
77
Col
Ahui¿otla
M u n N a u c a l p a n d e Juarez
Vid 1H ENhlJUtbfC. KAI0IHo
no^ e )
CORTESDEZAPATASAISLADAS
Var01/2"@19
ambos sentidos
0 50
Var01/2"@1O
ambos sentidos
o
Var05/8"@15
ambos sentidos
0 50
*
025
025
n
n
Q Q o
Q-NI/-0
o
Q
ü
1 50
200
corte f-f
corte e-e
PLANO
INS111UTO 1tCNULOGICO DELACONbTRUCCION
T-18
METROS
Casa-Habitación
Vicente Villada No 11 Col Ahuizotla Mun Naucalpan deJuarez
—
.
ING ALHJNSOD ARtívVRIl IANT0IA
VICTOR FNRIÜUE SI U J h A l O R R t )
^J
TESIS PROFESIONAL
5.2.6. R e v i s i ó n de m u r o s
5.2.6.1. Verificación de murosa cargas verticales
Observando ladistribución dem u r o s y según latabla de
t r a n s m i s i ó n d e cargas, vemos q u eel m u r o localizado e n el eje
2(B-C) tiene la mayor carga sobre él,porloq u e u n criterioq u e
podemos tomar p a r a e s t a revisión, e selegir eld emayor carga y
verificarlo, y si éste p a s a , sería obvio el n o revisar los d e m á s
muros.
Cálculo de peso resistente (PR)
At =14x400 =5600 cm 2
pR =(Q.6)(0.1)(\9)(560Q) =44688kg
Condición :
Carga sobre muro 2(B-C)
Se emplea el criterio
=9194
kg/mi
PR =44688kg < Pv =12872 kg =>El muro pasa
reglamentario
PR 2Pv :. Pv =(Carga sobre
muro)(F.C)
Pv =(9\94)(\A) =12872 kg/m
P
R =FRFEÍ
*m A •'•
FR =Factor de resistencia =0.6
f*m =Re sistencia de diseño en compresión de la manipostería
de tabiques de barro recocido =15kg /cm2. Se debe tomar
en cuenta que el valor de f *m se aumenta en 4 kg/cm2
por ser muro confinado.
FE =Factor de reducción por excentricidad
int eriores.
=0.7 para
muros
FC =Factor de corg a = 1.4
At - Area del muro en planta
136
^•^•••M^HBHB^H^^BBH^HMI^HHH^MHMIÍ^HHHHHHHHMHHI^^B^MHMI^^H
TESISPROFESIONAL
5.2.6.2. Verificación de murosa cargas horizontales (sismo)
La revisión se h a r á de a c u e r d o con el método
simplificado d eanálisis sísmico estático, aplicable a e s t r u c t u r a s
que n or e b a s e n los 13m.de altura.
E s t i m a c i ó n del p e s o delaplanta alta
En azotea lacarga viva empleada e sde7 0k g /cm 2 p a r a
c u b i e r t a s con pendiente m e n o r al 5 % .
E s t i m a c i ó n del p e s o delaplanta baja
® P e s o losa de e n t r e p i s o
P a r a este efecto seemplea lacarga viva i n s t a n t á n e a ,q u e
p a r a elcaso delentrepiso e sde9 0 k g / c m 2 .
O Peso losa de e n t r e p i s o
PLOSA= 7 8 6 0 1 kg
P e s o muros
Longitud d emuros= 4 2 m .
Peso del muro= 6 8 1 k g / m 2 .
P L O S A = 6 1 2 9 0 kg
Peso muros
PMUROS=(42X681)= 2 8 6 0 2 kg
Longitud demuros= 4 6 m.
Peso delmuro= 6 8 1 k g / m 2 .
© Peso ventanas
Longitud deventanas= 2 7 m .
Peso ventana= 100 k g / m
PMUROS=(46X681)= 3 1 3 2 6 k g
Peso v e n t a n a s
PVENTANAS=(27X100)= 2 7 0 0k g
Longitud deventanas= 19 m.
Peso v e n t a n a = 100 k g / m
© P e s o total
PTOTAL-=78601+28602+2700=
PVENTANAS=(27X100)= 1900 kg
© Peso total
PTOTAL== 1 0 9 9 0 3 k g
PTOTAL-=6 1290+31326+1900=
Nota: Verplano T-20
PTOTAL== 9 4 5 1 6 kg
Nota: VerplanoT-19
137
^
17 00
4 00
(1/
YY7777r^777777777777m77Z-7r77T777777777^777777777^777777777777777^
77777777777777777777777^7/
WZZL
iTABI
I TABU
CM- 353kg/m2
CV
90kg/nV
BANO= 200kg/m2
MURO=137kg/m2
780kg/m2
4 00
5 00
6 00
©
Muro ®
TAB III
oi,
2
C M - 353 kg/m
CV90kg/m2
BANO 200kg/m2
MURO-182kg/m2
825kg/m2
AREA=4 00X600-24 00m
CM=
CV=
AREA=400X500=20 00m?
AREA-4 00X600-24 00m2
©
353 kg/m"
J)0Jg/ny_
443kg/m2
AREA 400X08 0 - 3 20m2
W™ =886x20 00=8860kg
Wu» =825x24 00-19800 kg
W * =780x24 00=18720kg
CMCV
353 kg/m
90kg/m2
443kg/m2
W
443x3 20 1418kg
©I
Muro ©
^
¡00 <>
77777777777}
W7Z&77T'
©
TAB IV
CM=
CV-
W « =443x2 00
353kg/m2
90kq/m2
443 kg/m
Ww
AREA-4 00X400-16 00m
C M - 592 kg/m
CV- ^jMkg/mJ_
682 kg/m
WIBV= 4 4 3 X 16 00-7088kg
AREA=2 00X300=6 00m2
S
4 00
2
©
§1
WEo=682x6 00-4092 kg
-443x0 96=426 kg
Peso losadeentrepiso= 61 290kg
Peso muros
=31326kg
Pesoventanas
= 1900kg
Muro G)
3
7777777777.77777^7}
PesototaldeP B
94516kg
estimación del peso de la planta baja
PLANO
INST TUTÜ I tCNOLOC ICODELA CONSTRUCCIÓN
T-19
Casa-Habitación
METROS
ING AlhJNSOU ABBWR1TFANTOJA
UBCACON
AGOSTO ¿003
Vicente Villadd No 11 Col Ahuizotla Mun Naucalpan de Juarez
VICTOR CNRIOUT SEiURA TOl HEo
lAOBlt]
(F,
17 00
4 00
^ N
( 1 I
<f
<?
6 00
2 00
7
•77777777777,7777777777777777777^^7777777777777777777. 7,
127Í7ZZ7ZZZ777Z2Z
Í
TsM^'
I E 2177777777777777777/7777Z-T777777Z
ITABI
4 00
©
©
©
Pt-;
TAB III
CM= 641kg/m2
C V - _ 70 kg/m
711 kg/m2
CMCV=
AREA=4 00X6 00=24 00m2
WM =791x2400=18984 kg
W1M = 7 1 1 x 2 4 00=19800 kg
TABIV
CM=
CV=
641kg/m2
70kq/rjf_
711 kg/m2
CM=
CV=
AREA=4 00X0 80=3 20m2
W I * I = 7 1 1 x 2 0 00=14220kc
W , -711x320-2276kg
X
2
641kg/m
70kg/m2
711kg/m2
AREA=2 00X4 00=8 00m2
W,ABV=71 1 x 1 6 00-11376 kg b ¿
W « = 7 1 1 x 8 00=5688 kg
i
AREA=4 00X5 00=20 00m2
Wvou=711x8 80=6257 kg
AREA=4 00X4 00=16 00 m ©7
(3, i
CM= 641kg/m2
CV- _70_kg/rrf
7Í1 kg/m2
TABV
4 00
i
641kg/m2
70kg/m_
711 kg/m2
AREA=4 00X6 00=24 00m2
Muro©
2 } 800
<j>
¥ZZ22Z22ZZZZ2ZZ¿ll¿Z2ZZZ2i2ZZZl
Mwo®
TABI
CM=
641kg/m2
CV=
70kg/m2
TINACO- 80 kg/m
791 kg/m2
5 00
Peso losa de entrepiso= 78 601 kg
Peso muros
= 28 602 kg
Peso ventanas
= 2700 kg _
Muro©
(W77777/7Z<W77?77797/77ZV7777777V/y77ZrÁ
7
ZZ/ZZ3ZZZZLZ7ZZ222m
Peso total de PA
=109 903 kg
estimación del peso de la planta alta
INST TUTO IttNOLCUCO DELACONbTFUL,CION
T-20
METROS
Casa-Habitación
Vicente Villada N o 7 7 Col Ahuizotla M u n N a u c a l p a n de Juarez
INC AirUNSOD ABBWRTT I-ANTOJA
VCIOR TNRIQUf StGURATCRRtS
TESIS PROFESIONAL
I.- Cálculo de las fuerzas sísmicas en cada nivel de la
estructura.
© Cálculo de fuerzas en cada nivel
p
F,=
A . V s ...
1
ipfa
Fj = .
•Va
F,
3 5 9 ? = 2 5 1 5 ton
Pl
_ _ , , ,
F| =
•V,
® Esfuerzo cortante resistente
© Cálculo de fuerzas
de
. 35.97 = 10.81 ton.
© Coeficiente sísmico reducido para el método
correspondiente a estructuras del grupo B.
Zona II •=> cs =0.16
construcción
Peso nivel 2 =P2 =109903 kg
Peso nivel 1 =P¡=94516 kg
Peso total =PT = (204419xF.C.) =(204419x1.1;=
PT =224861 kg * 224.86 ton.
© Cálculo de fuerza sísmica (Vs) en la base
=(0.16x224.86^ = 35.97 ton.
cortantes
V2 =F2 =25.15 ton.
Vx =F¡+F2 =25.15 +10.81 =35.97 ton.
II.- Cálculo de fuerzas
resistentes
Manipostería
v* =3kg/cm2
® Peso total de la
J ? l ^ í L Ü ^ _
(109.90x1.1x4.8;+f94.5lxl.1x2.4;
•Vs
Vs =csxPT
. QW.Mxü^
H09.90xl.1x4.8^+(94.5lxl.1x2.4;
smplificado,
Se procederá a determinar la resistencia de los muros,
iniciando con los de la planta baja, según el método simplificado
establecido por el RCDF.
Por loanterior emplearemos la siguiente expresión :
VR =FR(0.5vAt
+ 0.3P)
<\.5FRvAt
Para la aplicación de la expresión anterior se simplificará en la
determinación del esfuerzo vertical que actúa en los muros respectivos
por loque consideraremos que el esfuerzo vertical es el mismo en todo:
los muros de la planta respectiva, por lotanto, el valor de éste losera :
PT
224.86
o-p= ' = '
=
ti
0.14mx46m
224861
—=3.49kg/cm
14x4600
2
:.
vR =(Q.Sv + 0.3o>; = (0.5x3; +(0.3x3.49; =2.54 kg/'cm2
Ahora se procederá a calcular la resistencia de los muros
mediante la expresión simplificada y, además, tomando en cuenta la
esbeltez del muro.
VR =FRvR AT
:. FR = 0 . 7 ; Por ser muros
confinados
140
TESIS PROFESIONAL
Revisión de la resistencia de los muros de la planta baja en la dirección X-X".
USURO
1
2
3
LONGITUD
17.00
4.00
6.00
h/1
0.14
0.60
0.40
COEF. RED.
(1,33 L/hp
ÁREADE MUROS
1
1
1
23 800
5 600
8 400
SUMA=
Vfl =67.21 ton > Vg =35.97 ton =>Los muros en esta dirección resisten
VR«FRV»AT
(kg)
42 317
9 957
14 936
67 210
adecuadamente
Revisión de la resistencia de los muros de la planta baja en la dirección Y-Y'.
MURO
4
"4
5
6
7
8
9
"9
10
'10
LONGITUD
|mti)
1.00
1.00
3.00
3.00
4.00
3.00
1.00
1.00
1.00
1.00
h/1
COEF. RED,
(1.33 L/hp
ÁREADEMUROS
2.40
2.40
0.80
0.80
0.60
0.80
2.40
2.40
2.40
2.40
0.30
0.30
1
1
1
1
0.30
0.30
0.30
0.30
1400
1400
4 200
4 200
5 600
4 200
1 400
1400
1 400
1 400
SUMA=
VR =36.84 ton > Vs =35.97 ton =>Los muros en esta dirección resisten
VR*FRV*AT
(kg)
747
747
7 468
7 468
9 957
7 468
747
747
747
747
36 843
adecuadamente
La revisión de los muros de la planta alta se puede obviar dado que la cantidad de muros y su distribución es más
favorable a la de la planta baja, lo que nos lleva a concluir que esos muros resisten adecuadamente.
141
TESIS PROFESIONAL
5.2.7.
Diseño de
trabes
5 . 2 . 7 . 1 . Diseño d e t r a b e s d e a z o t e a
Diseño d e t r a b e s d e a z o t e a
B(1 •2) y B ( 2 - 3 )
I. - DATOS DE DISEÑO
IV. - DISEÑO POR FLEXIÓN
W¡ = 989 kg /ml
W2 =909 kg /ml
fc =200 kg /cm2
f'y = 4200 kg / cm2 (Armado
longitudinal)
f'y - 2530 kg / cm2 (Re fuerzo
transversal)
2
/ * c = 0 . 8 / ' c = 160 fcg/cm
f"c = 0 . 8 5 / * c = 136 kg/ cm2
Se propone una sección con las siguientes
b = 20 cm
h = 30 cm
r =3 cm
d = 30- 3 = 27 cm
II.- CORTANTES
Formulas
TRAMO B(l - 2)
Porcentaje balanceado
.•
TRAMO B(2 - 3)
3 / 8 WL =3/8(909;(4.00; = (1363.50;i.4 = 1910 kg
5 / 8 WL = 5/8(909J(4.00; = (2272.50;i.4 = 3182 kg
in. - MOMENTOS
de
acero.
© Cálculo de acero
FLEXIONANTES
2
Mol =9/mWL
= 9/128 (989;(4; = (11\2.62)\A = 1558
Mo2 = 9/128 WL2 = 9/128 (9Q9)(A)2 = (1022.62;i.4 = 1432
Moi =1/8 WL2 = 1/8 (989;(4; 2 = (1978;i.4 = -2769
kg-m
kg-m
kg-m
=Pb =-•
-•
f'y
f'y +6000
0J jf'c
-
Porcentaje mínimo = Pmín = - — - —
f'y
= 0.75
136
As^
© Cálculo de acero
p
máximo
4800
0.0114
4200 4200+ 6000
=P^bd =(0.0114;(20;(27; = 6.17 cm
' max
2
de porcentajes
Porcentaje máximo - Pmax = 0.75 Pb
i?, = V, = 3 / 8 WL = 3/8(989^4.00; = 0483.50;!.4 = 2077 kg
R2=V2=5/8WL
=5/8(989;(4.00; = (2472.50;i.4 = 3462 kg
R2=V2=
Ri=V3=
dimensiones
2
mínimo
0.7 Jf'c
0.7J2OO
¡7 =0.0023
<"_- = . . y —
20
f'y
4200
= Pmínbd = (0.0023;(20;(27; = 1.27 cm<
= .
Asmin
142
TESISPROFESIONAL
CD Cálculo de acero necesario para un Mu =1558 kg - m
As=~
Mu
— =
FRf ' y j d
155800
, „, 2
=1.71 cm
Vu <2.0FRbd J/ *c
ro.9;r42oo;co.89x27;
2
2
Asmin = 1.27 cm <As =1.71 cm <As,^ =6.17 cm
=> Se acepta
© Cálculo de acero necesario para un M(-)u =2769 kg - m
,45=
Mu
Ü
= _
_
276900
_ _
V. - DISEÑOPORCORTANTE
Condición :
Condición :
2
• • • • • M ^ H i
„ „„ 2
=3.04 cm2
Se tomará la cortan te más desfavorable del diagrama de
cortan tes.
3462 kg <(2.Q)(0.Z)(2Q)(21)( J\6Q)
3462 kg <10929kg =>Se requiere refuerzo transversal
VI.- SEPARACIÓN DE REFUERZO TRANSVERSAL
Según N.T.C. para concreto
** f'y j d (Q.9)(42W)(0.%9x21)
S < ZBALDL
3.5b
Condición :
Asmin =1.27 cm2 < As =3.04 cm2 <i4smd;<. =6.17 cm2 => Se acepta
© Cálculo de acero necesario para un Mu =1432 kg - m
Mu
>\s =
143200
í' — =
FRf'y j d
Condición :
, en
Se propone utilizar estribos de Var.</> 1/4"
Av =2x0.32 =0.64 cm2
:.
2
= 1.57 cm
S J0WMX2S3O) _1 8 J 0 c m
(0.9#4200#0.89x27)
3.5^20;
Tampoco la separación debe exceder de :
Asmín =1.27 cm2 <As =1.57 cm2 <Asmáx =6.17 cm2 =>
Se acepta
S2 =0.5d Sí Vu
© Armado para zona donde M(-)u =2769 kg - m
Se propone utilizar Var. 1/2"
As =3Var.1/2"= 3x1.27 =3.81cm2
<\.5FRbdJf*c
3462 kg < (i.5)(0.S)(20)(27)(J\60)
3462 kg <8197 kg .:
S2 =0.5(27;=13.50*14.00 cm
TVoía :Para las zonas con momentos últimos positivos, se propone
utilizar
2 Var. 1/2". (Ver plano
T-2\)
143
TESIS PROFESIONAL
VIL- CALCULO DE FUERZA CORTANTE
DEL CONCRETO (Vcr)
RESISTENTE
Por lo anterior la Separación por fuerza cor tan te que toman
los estribos, es :
Para un Vu = 3462 kg
S = F * A , / j / f » . (0.8^0-64^2530^27; = ^ ^
3
V'u
1221
Condiciones:
S 3 = 29 cm
Sí h <70 cm
ó h/ b < 6
Sí no cumple, entonces el valor de Vcr se reducirá un 30%.
La fuerza resistente del concreto (Vcr) se calculará con el criterio
siguiente :
Sí;
cm
Conclusión :
La sección será de 0.20x0.30 m.
La separación de estribos será de :
S =14.00 cm
Nota :Ver plano T - 2 1
Porcentaje p <0.01 .-. Vcr = FR bd(0.2 + 30p)¡f*c
Porcentaje p >0.01 .-. Vcr =0.5FRbdjf *c
El porcentaje de acero utilizado será :
= __»
bd
p
= _iü_
As = 3 War.1/2"= 3.81 cm2
.
= 0.007
(20)(21)
pu =0.007 < 0.01 .-.
Vcr =FR bd(0.2 + 30p)Jf *c
Vcr =(0.*)(20)(nj¡p.2 + 30^0.007;y/¡60 = 2241 kg
Por lo tan to la fuerza cor tan te que toman los estribos (V'u ) es :
V'u= Vu - Vcr = 3462- 2241 = 1221 kg
V'u= 1221 kg
144
TESIS PROFESIONAL
Diseño d e t r a b e s d e a z o t e a
D(1-2) y D(2-3)
I. - DATOS DE DISEÑO
IV.- DISEÑO POR FLEXIÓN
Wj =1730 kg/ml
W2 = 724 kg /ml
fe = 200 kg /cm2
f'y = 4200 kg/cm2 (Armado
f'y = 2530 kg/cm2 (Refuerzo
f*c =0 . 8 / ' c = 160 kg/cm2
f"c = 0 . 8 5 / *c = 136 kg/ cm2
Se propone una sección con las siguientes
longitudinal)
transversal)
b = 25 cm
h =35 cm
r = 3 cm
d = 35- 3 = 32 cm
II. - CORTANTES
Formulas
TRAMO D(l - 2)
Rx =V{ =3 / 8 WL = 3/8(1730/(4.00/ = (2595/1.4 = 3633 kg
R2=V2 ^5/SWL =5 / 8 ( 1730/(4.00/ = (4325/1.4 = 6055 kg
TRAMO D(2 - 3)
R2=V2= 3 / 8 WL = 3/8(724/(4.00/ = (1086/1.4 = 1521 kg
R3=V3=5/&WL
=5/8(724/(4.00/ = (1810/1.4 = 2534 kg
III.- MOMENTOS
dimensiones
de porcentajes
de
acero.
Porcentaje máximo = Pmax = 0.75 Pb
Porcentaje balanceado = Pb =
fe
4800
/'J/
/']y +6000
o.y'fc
Porcentaje mínimo = Pmírl = f'y
® Cálculo de acero
FLEXIONANTES
máximo
4800
= 0.0114
4200 4200+6000
= Pmaxbd = (0.0114/(25/(32/ = 9.12 cm2
Pmax =0-75
136
MO\= 9/128 WL2 = 9/128 (1730/(4/2 = (1947/1.4 = 2725 fcg-rn
Mo2 =9/mWL2
= 9/128 (724/(4/ 2 = (815/1.4 = 1141kg - m
Asmax
Mo3 = 1/8 WL2 = 1/8 (1730/(4/ = (3460/1.4 = -4844 /eg- m
© Cálculo de acero
mínimo
Pmin ^ l l f l
= 0.0023
= ^Im
fy
4200
Asmfn =pmínbd = (0.0023/(25/(32/ = 1.84 cm2
145
TESIS PROFESIONAL
<3) Cálculo de acero necesario para un Mu =2725
kg-m
Mu
272500
„c , 2
As = — =
=2.53 cm1
FRf'y j d f0.9^4200^0.89x32;
Condición:
As = .
Mu
«__. =
FRf'y j d
114100
V.- DISEÑO POR CORTANTE
Condición :
Vu
ASjrfn = 1- 89c m 2 ^As = 2.53cm 2 <As m á x =9.12 cm2 =>Se acepta
® Cálculo de acero necesario para un M(-)u=1141
gg^gggggggggggggggg
kg-m
„, 2
=1.05 cm 2
<2.0FRbdJf*c
Se tomará la cortan te más desfavorable
cor tan tes.
del diagrama de
6055 kg < (2.0)(Q.%)(25)CÍ2)(J\6Q)
6055 kg <16191kg =>Se requiere refuerzo
VI.- SEPARACIÓN DE REFUERZO
^0.9^4200^0.89x32;
Según N.T.C. para
transversal
TRANSVERSAL
concreto
s<íRj^jy
Condición:
ASfnín =1.89cm2 > As = 1.05cm2 < Asmáx =9.12 cm2 =>Nose acepta
© Cálculo de acero necesario para un Mu =4 8 4 4
Mu
484400
,^
— =
=4.49cm
F
R f'y Jd
(0.9^4200^0.89x32;
Condición:
kg-m
2
As =
Asmln =1.89cm2 <As = 4.49cm 2 <As^
Se propone utilizar estribos de Var. <j> 1/4"
Av = 2x0.32 =0.64cm2
:.
S]jm(0:e4)(2530)
=
UMxl5Mcm
3.5(25;
=9.12cm 2 =>Se acepta
Armado para zona donde M(-)u=4844
3.5b
kg-m
Se propone utilizar Var. 1/ 2"
As =4Var.1/ 2"=4x1.27=5.08cm 2
Armado para zona donde M(-)u=2725 kg-m
Tampoco la separación debe exceder de :
S 2 =0.5<¿
Sí
Vu <
\.5FRbdJf*c
6055kg < (\.5)(Q.&)(25)CS2)(JÜ0)
6055kg <12144kg
S2 =0.5(32;=16.00cm
Se propone utilizar Var. I/ 2"
As = 2Var.I/2"=2x1.27=2.54cm2
146
TESIS PROFESIONAL
VU.- CALCULO DE FUERZA CORTANTE
DEL CONCRETO (V„)
RESISTENTE
S = F *4,,/_>,<* = (0.8^0.64^2530^32j = ] 3 9 J
3
V'u
2978
Para un Vu = 6055 kg
Condiciones :
Sí h <70 cm
Por lo anterior la Separación por fuerza cor tan te que toman
los estribos, es :
ó
h/b<6
Sí no cumple, entonces el valor de VCT se reducirá un 30%.
La fuerza resistente del concreto (Vcr) se calculará con el criterio
siguiente :
^
S-j = 14.00 cm
Conclusión :
La sección sera de 0.25x0.35
La separación de estribos será de :
S = 14.00 cm
Sí;
Porcentaje p <0.01 .-. Vcr =FRbd (0.2 + 30p) Jf *c
Porcentaje p >0.01 .-. Vcr = 0.5F#
bdjf*c
Nota :Ver plano T - 21
El porcentaje de acero utilizado será :
pu=—
As
bd
p
l^L
:. As =4 Var.1/2"= 5.08 cm2
= o.006
pu =0.006 < 0.01 .-.
Vcr =FR bd(0.2 + 30p)Jf *c
Vcr = CO.8^25^32^0.2 +30^0.006^/1(50 = 3077 kg
Por lo tan to la fuerza cor tan te que toman los estribos (V'u) es :
Vu= Vu - Vcr = 6055- 3077 = 2978 kg
V'u= 2978 kg
147
TESIS PROFESIONAL
Diseño d e t r a b e d e
EC1-2)
azotea
/. - DATOS DE DISEÑO
® CáZcuIo d e a c e r o
W = 1650 kg /ml
fe = 200 kg /cm2
fy = 4200 kg/cm2 (Armado
fy = 2530 kg /cm2 (Refuerzo
f*c = 0 . 8 / ' c = 160 kg/cm2
fc = 0 . 8 5 / * c = 136 kg /cm2
P m a x = 0.75
longitudinal)
transversal)
H650^4;
2
2
III. MOMENTOS
M„
4200 4200+6000
Cálculo de acero
WL
1-2
4800
p
= (3300,11.4 = 4620/eg
mínimo
0-Vrc = 0^200 =0 _ 0023
4200
/'í/
^s m í „ = ^mm&<¿ = (0-0023^25^32; = 1.84 cm¿
FLEXIONANTES
® Cálculo de acero necesario
WL2
(1650^4/
8
8
= (3300,/1.4 = 4620
kg-m
As =
IV.- DISEÑO POR FLEXIÓN
Se propone una sección con las siguientes dimensiones
0.0114 .'.
= P m a x b d = í-0.0114^25^327 = 9.12 cm2
As^
II. - CORTANTES
R, =R, = V,
136
máximo
:
para un Mu = 4620
M„
462000
pRÍ'yJd
(0.9^4200^0.89x32j
= 4.29 c m '
Condición :
Asmin = 1.84 cm 2 < As = 4.29 cm2 <Asmáx =9.12 cm 2
b = 25 cm
h = 35 cm
r = 3 cm
d = 30- 3 = 32 cm
kg
©
=>Se ac
Armado
Se propone utilizar Var. 1/ 2"
Formulas
de porcentajes
Porcentaje máximo =Pmax =
Porcentaje balanceado = Pb
Porcentaje mínimo =Pmín =•
de
acero.
0.75 Pb
fc
4800
fy
fy +6000
A s = 4 Var.1/2" =4x1.27 = 5.08 cm2
Ver plano T - 21
o.i ffe
fy
148
TESIS PROFESIONAL
VIL- CALCULO DE FUERZA CORTANTE
DEL CONCRETO (Vcr)
V.- DISEÑO POR CORTANTE
RESISTENTE
Condición :
Para un Vu = 4620 kg
Vu<2.0FRbdff*c
Se tomará la cor tan te más desfavorable
cor tan tes.
del diagrama
Sí;
4620 kg < (2.0)(0.%)(25)Ci2)(j\60)
4620 kg <16191kg =>Se requiere refuerzo
VI.- SEPARACIÓN DE REFUERZO
Según N.T.C. para
de
La fuerza resistente del concreto (Vcr) se calculará con el crite
siguiente :
transversal
TRANSVERSAL
concreto
Porcentaje p <0.01 .-. Vcr = FRbd(0.2 + 30p} (f * c
Porcentaje p >0.01 .-. Vcr =
0.5FRbdJf*c
El porcentaje de acero utilizado será :
pyuu=~~
3.5b
p
As
bd
••• As =4 Var.1/2" =5.08 cm2 •
5
^L- = 0.006
f25#32;
= __
Se propone utilizar estribos de Var. <¡> 1/4"
pu = 0.009 < 0.01 .-.
Av =2x0.32 = 0.64 cm2
:.
S i , Í O - M 0 ^ 4 i ^ 3 0 ^ ,4.80.15.00 cm
1
3.5f25;
Tampoco la separación debe exceder de :
S2=0.5d
Sí
Vu<l.SFRbdJf*c
4620kg < (\.5)(0.%)(25)(32)(J\60)
4620kg <12144 kg :.
S2 =0.5f32;=16.00 cm
i
Vcr = FR bd(0.2 +30p)Jf~* c
Vcr = / , 0.8^25;p2;[0.2 +30/'0.006;](,>/l60 = 3077 kg
Por lo tanto la fuerza cortante
que toman los estribos (V'u) e:
Vu= Vu - Vcr =4620-3077 = 1543 kg
V'u= 1543 kg
Por lo anterior la Separación por fuerza cor tan te que toman
los estribos, es :
= FR A, fyd
V'u
= (o.tj(OMH2S30H32)
= 26 86
cm
1543
ST,=27.00 cm
NOTA: En virtud de que la trabe F(l-2) e s de dimensiones y
carga similares a la trabe E(l-2), se considerará el mismo
diseño que esta última.
Conclusión :
La sección será de 0.25x.35 m
La separación de estribos será de :
S =15.00 cm
149
TESIS PROFESIONAL
Diseño d e t r a b e s d e a z o t e a
2 ( D - E ) y 2 ( E-F)
I. - DATOS DE DISEÑO
IV.- DISEÑO POR FLEXIÓN
W{ =1749 kg/mi
W2 =1651 kg/nú
fe = 200 kg/ cm2
f'y =4200 kg /cm2 (Armado
f'y = 2530 kg /cm2 (Refuerzo
f*c =0 . 8 / ' c = 160 kg /cm2
f'c = 0 . 8 5 / * c = 136 kg /cm2
II.-
Se propone una sección con las siguientes
longitudinal)
transversal)
b = 25 cm
h = 40 cm
r = 3 cm
d = 40- 3= 37 cm
CORTANTES
Formulas
TRAMO B(l - 2)
/ ? , = V ¡ = 3 / 8 W L = 3/8(1749;(6.00; = (3926;i.4 = 5496fcg
R2 =V2 = 5 / 8 WL = 5/8(1749;(6.00; = (6559;i.4 = 9183 fcgr
2
de
Porcentaje máximo =Pmax = 0.75 Pb
• , ,
,
f'c
Porcentaje balanceado =Pb = - - •f'y
0.7j/'c
acero.
4800
f'y +6000
f'y
R2=V2= 3 / 8 WL = 3/8(165i;(5.00; = (3096;i.4 = 4334 kg
R} = y, = 5 / 8 WL = 5/8(1651^5.00; = (5160;i.4 = 7224/egr
I//. - MOMENTOS
de porcentajes
Porcentaje mínimo =Pmin =
TRAMO B(2 - 3)
dimensiones
FLEXIONANTES
® Cálculo d e acero
P™«
= 0.75
' max
2
136
4800
Asmax
itfo, = 1 / 8 W L 2 =1/8(1749;(6; 2 = (787i;i.4 = -11019 kg - m
© Cálculo de acero
1
0.0114 .-.
4200 4200+6000
= P m a , b d = (0.0114;(25;(37; = 10.54 cm
Mo¡ = 9 / 1 2 8 WL = 9/128 (1749;(6; = (4428;i.4 = 6199 kg -m
Mo2 =9/128 WL2 = 9/128 (1654;(5; 2 = (2903;i.4 = 4063 kg-m
ojjfc
n
máximo
2
mínimo
o.7j2"oq=0_0023
nun
fy
4200
Asmín = Pmlnbd = (0.0023;(25;(37; = 2.12 cm 2
150
TESIS PROFESIONAL
© Cálculo de acero necesario para un Mu =6199 kg- m
M
u
619900
Ano
2
-=— = =4.98 cm
FR f'y Jd (0.9;(4200# 0.89x37;
Condición :
Condición :
As=-
ASnjn =2.12cm2 <As- 4.98cm2 <Asmáx =10.54cm2
Vu <2.0FRbd
=>Se acepta
© Cálculo de acero necesario para un M(-)u =4063 kg -m
Mu
_ _u— =
AS=
^j?/ ' i /j d
406300
V.- DISEÑO POR CORTANTE
„„, 2
=3.26 cm 2
^0.9^4200^0.89x37;
Se tomará la cor tan te más desfavorable
cor tan tes.
del diagrama
9183 kg < (2.0)(0.S)(2S)(37)(y}\oQ)
9183 kg <18721 kg => Se requiere refuerzo
VI.- SEPARACIÓN DE REFUERZO
Según N.T.C. para
Condición :
jf~*c
de
transversal
TRANSVERSAL
concreto
s<fñAÍ'M
ASmfo =2.12cm 2 <As =3.26cm2 <As,^ =10.54cm 2 =>Se acepta
3.5b
© Cálculo de acero necesario para un Mu =11019 kg - m
As = -
Mu
. H_. - FRf'yJd
1101900
ooc
_ - 8.85cm
2
Se propone utilizar estribos de Var. <f> 5/16"
Av = 2x0.49 = 0.98 cm1 :.
„
/0.8#0.98#2530;
S <A "
/±
1 = 22.66 * 23.00 cm
C0.9;C4200;C0.89x37;
Condición:
3.5^25;
2
2
2
Asm-n =2.12cm <As =8.85cm <Asm4)C= 10.54cm =>Se acepta
© Armado para zona donde Mf-)u=11019 kg - m
Se propone utilizar Var. 5/ 8"
As =5Var.5/S"= 5x1.98=9.90 cm 2
Tampoco la separación debe exceder de :
S2=0.5d
Sí Vu
<\.5FRbdJf*c
9183 kg < (\.5)(Q.%)(25)(31)(-¡\6Q)
9183fcgr< 14041 fcgr ..
S 2 =0.5(21) =18.50 cm
© Armado para zona donde M(-)u- 6199kg - m
Se propone utilizar Var. 5/ 8"
As =3Var.5/ 8"=3x1.98=5.94 cm2
151
TESIS PROFESIONAL
VU.- CALCULO DE FUERZA CORTANTE
DEL CONCRETO (Vcr)
RESISTENTE
Para un VU=9\S3 kg
S, =f*±£V*
Vu
Condiciones :
Sí h <70 cm ó
Por lo anterior laSeparación porfuerza cor tan te que toman
los estribos, es:
h/b<6
Sí no cumple, entonces elvalor de V^. se reducirá un30%.
La fuerza resistente delconcreto (Vcr) se calculará con el criterio
siguiente :
=£0.8^0.9M?530CT = 1 6 . 3 0 cm
4502
S 3 =15.00cm
Conclusión :
La sección sera de 0.25x0.40
La separación de estribos será de :
S =15.00 cm
Sí;
Porcentaje p < 0.01 .-. V„ =FR bd(0.2 +30p)Jf *c
Porcentaje p >0.01 .-. Vcr =
0.5FRbd{f*c
Nota :Ver plano T-22
El porcentaje deacero utilizado será :
As
pu =— .-. As =5 Var.5/8"= 9.90 cm2
bd
9.90
p =_ - _ =0.010
(25MW)
pu =0.01 =0.01 .-.
Vcr=0.5FRbdjf*c
Vcr =(Q.5)(QÜ)(25)(?>1)(^\(>0) = 4681 kg
Por lo tan to lafuerza cor tan te quetoman los estribos (V'u )es:
V'u= Vu - Vcr = 9183- 4681 = 4502kg
V'u= 4502kg
152
DISEÑO DE TRABE DE AZOTEA
B(1-2) YB(2-3)
DISEÑO DE TRABE DE AZOTEA
D(1-2) Y D(2-3)
DISEÑO DE TRABE DE AZOTEA
E(1 -2)
1
FU»0
-
1
tscutm
INS i
T-21
Casa-Habitación
MtlhüS
""
Vicente Villacici No 77 Col Alnnzotla M u n NaLn.jl|j.iii de J u d r c
Ill
It H
ni
N
i Mjí(
)i
•SES„
n
i
\
i
f
lABÜHO
V
.
1 1 1 i\ (i
iJ
N
DISEÑODETRABEDEAZOTEA
2(D-E)Y2(E-F)
DISEÑODETRABEDEAZOTEA
F(1-2)
f;
(*>
2+i.
39 b K9
Sl<¡6 kg
Hffl
PLANO
•
ESCUELA
_-
INSTITUTO K L N O I I G L OUt U U N o l R U U I C N
T-22
Casa- Habitación
METROS
—
ASESOR
NG ALEONAD A B B W R T T P A N I O A
uacAcoN
AGOSTO 200)
Vicente Villada No 7 7 Col Ahuizotla M u n N a u t a l p a n de Juarez
ELABORO
V i U f U N h l U E SE
URAT R R I S
TESIS PROFESIONAL
5 . 2 . 7 . 2 . Diseño de trabes de entrepiso
Diseño de trabes de entrepiso
B(l-2)y
-3)
I. - DATOS DE DISEÑO
IV. - DISEÑO POR FLEXIÓN
W¡ =1028 kg /ml
W2 = 691 kg/ml
fe = 200 kg /cm2
f'y = 4200 kg/cm2 (Armado
f'y = 2530 kg/cm2 (Refuerzo
/ * c = 0 . 8 / ' c = 160 fcg/cm2
f"c = 0 . 8 5 / *c = 136 kg /cm2
Se propone una sección con las siguientes
dimensiones
b =20 cm
h = 30 cm
r =3 cm
d = 30- 3 = 27 cm
longitudinal)
transversal)
Formulas
de porcentajes
de
acero.
II. - CORTANTES
Porcentaje máximo =Pmax = 0.75 Pb
TRAMO B(l - 2)
* • U t
i?, = V, = 3 / 8 WL =3/8(1028^4.00; = (1542^1.4 = 2159 kg
R2=V2= 5 / 8 WL =5/80028#4.00; = (2570^1.4 = 3598 kg
J
Porcentaje mínimo = Pmín =
TRAMO B(2 - 3)
R2=V2=
Ri=Vi=
3 / 8 WL =3/8(69i;f4.00; = (1037J1.4 = 1451 kg
5 / 8 WL = 5/8^691^4.00; = (1728J1.4 = 2419 kg
III.- MOMENTOS
f"c
© Cálculo de acero
4 8 0 0
ry + 6000
OJ-Jf'c
"fy
máximo
136 „ _ 4 8 0 0 _ _
0.0114
4200'4200 + 6000
= Pmaxbd = (0.01\4)(20)(2V = 6-17 cm2
Pmax = 0-75
FLEXIONANTES
Mo] = 9 / 1 2 8 WL2 = 9/128 (1028^4^ =(US7)\ A =\620 kg-m
Mo2 =9/mWL2
=9/128 (691^4^ =(m)\.4 =1088kg - m
Asmax
® Cálculo de acero
M o , = l / 8 l W , 2 = ! / 8 (1028,/(4J2 = f2056^1.4 = -2878
DU
Porcentaje balanceado =Pb =~—•
f'\L
mínimo
kg-m
0.7Jf'c
O.7/2OO
"J - = - y - - =0.0023
f'y
4200
=Pminbd =(OSmWWl)
='-27 cm2
Pmín =Asmin
155
TESISPROFESIONAL
® Cálculo de acero necesario
para un Mu = 1620 kg -m
Mu
162000
, ^0
,
" _=
= 1.78 cmFR f'y j d f0.9^4200^0.89x27;
Condición :
MMHHMBMMM
V.- DISEÑO POR CORTANTE
Condición :
As =
2
2
2
Asmin = 1.27 cm <As = 1.78 cm <Asmáx =6.17 cm
© Cálculo de acero necesario
AS =
Mu
u—
=> Se acepta
para un M(-)u = 1088 kg -m
108800
, in
2
= 1.19 cm 2
=
FRf'yJd
Vu<2.0FRbd(f*c
Se tomará la cor tan te más desfavorable
cor tan tes.
del diagrama
3598 kg <(2.Q)(G.%)(20)(21)( J]60)
3598 kg <10929 kg => Se requiere refuerzo
VI.- SEPARACIÓN DE REFUERZO
de
transversal
TRANSVERSAL
Según N.T.C. para concreto
^0.9^4200^0.89x27;
s<I«A»f'y
Condición :
JJb
As
mín =l- 2 7 c™2 S As = 1.19 cm2 <Asmáx =6.17 cm2 => No se acepta
© Cálculo de acero necesario
Mu
As = --M—
para un Mu = ¿878 kg -m
287800
=
FR fy j d
Se propone utilizar estribos de Var. <¡> 1/4"
Av = 2x0.32 = 0.64 cm2 :.
^,,
2
=3.16 cm2
io.8;ío:641253o;==1850cm
(0 . 9 ; Í 4 2 0 0 #0.89x27;
1
3.5(20;
Condición :
Tampoco la separación debe exceder de :
Asmin = 1.27 cm2 <As = 3.16 cm2 <Asmáx =6.17 cm2
=>Se acepta
S2 = 0.5d
©
Armado
para zona donde M(-)u = 2878 kg -m
Se propone utilizar Var. 1/2"
As =3Var.]/2"= 3x1.27 = 3.81 cm2
Sí
Vu < 1 . 5 F R b d j f * c
3462 kg < (].5)(Q.%)(2Q)(21)lJ]60)
3598 kg <8197 kg :.
S2 = 0.5^27; = 13.50 * 14.00 cm
Nota :Para las zonas con momentos últimos positivos, se propone
utilizar
2 Var. 1/2". (Ver plano T - 23;
156
TESIS PROFESIONAL
VIL- CALCULO DE FUERZA CORTANTE
DEL CONCRETO (V„)
RESISTENTE
Por lo anterior la Separación por fuerza cortan te que toman
los estribos, es :
S =F*A£M
3
V'u
Para un Vu =3598 kg
Condiciones :
Sí h < 70cm ó
= (0-i)(0-M)(2S30)(27)
= 257?
cm
' 1357
S 3 =26.00 cm
h/b<6
Sí no cumple, entonces el valor de Vcr se reducirá un 30%.
Conclusión :
La sección será de 0.20x0.30 m.
La separación de estribos será de :
La fuerza resistente del concreto (Vcr) se calculará con el criterio
siguiente :
S = 14.00 cm
Sí;
Porcentaje p <0.01 .-. Vcr =FR bd(0.2 +30p)//
Porcentaje p >0.01 .-. Vcr =0.5FRbd ^f *c
*c
Nota :Ver plano T - 23
El porcentaje de acero utilizado será :
pu=—
As
bd
.-. As =3Var.\/T=
3.81 cm2
p „ = - ^ - = 0.007
(2QH21)
pu = 0.007 <0.01 .-.
V„ = FR bd(0.2 +30p)Jf* c
Vcr =(0.8#20#27j[0.2 +30^0.007;]fil60 = 2241 kg
Por lo tan to la fuerza cortan te que toman los estribos (V'u ) es :
Vu =VU- Vcr = 3598- 2241= 1357 kg
Vu=\351 kg
157
TESIS PROFESIONAL
Diseño d e t r a b e s d e
D { 1- 2 ) y D ( 2 -
entrepiso
3)
I. - DATOS DE DISEÑO
TV.- DISEÑO POR FLEXIÓN
W¡ =2571 kg/mi
W2 = 299 kg /ml
fe = 200 kg/ cm1
f'y = 4200 kg/cm2 (Armado
f'y = 2530 kg / cm2 (Re fuerzo
f*c =0 . 8 / ' c = 160 kg/cm2
f"c =0 . 8 5 / * c = 136 kg/cm2
Se propone una sección con las siguientes
dimensiones
b = 25 cm
h = 35 cm
r -3 cm
d = 35- 3 = 32 cm
longitudinal)
transversal)
Formulas
de porcentajes
de
acero.
II.-CORTANTES
TRAMO D(l - 2)
Rl=Vl =3 / 8 WL = 3/8(257i;(4.00; = (3857;i.4 = 5400 kg
R2=V2=5/BWL
=5/8(2571^4.00; = (6428;!.4 = 8999 kg
Porcentaje máximo =P m a x = 0.75 Pb
• , ,
,
f"c
Porcentaje balanceado =Pb =-*—f'y •
0.7¿fe
Porcentaje mínimo = Pm
fy
TRAMO D(2 - 3)
R2=V2=3/&WL
R3=V3=5/&WL
=3/8(299^4.00; = (449;i.4 = 628 kg
=5/8(299^4.00; = (748;i.4 = 1047 kg
® Cálculo de acero
M0l = 9/128 WL2 = 9/128 (251\)(^)2 = (2893;i.4 = 4050 kg-m
Mo2 = 9 / 1 2 8 WL2 = 9/128 (299)(A)2 =(337)1.4 =M\ kg-m
136
4800 __
= 0.0114
4200' 4200+ 6000
¿ * W = Pmaxbd = (0.0114tf25;(32; = 9.12 cm1
Cálculo de acero
= l / 8 ( 2 5 7 i ; C 4 ; 2 =(5\42)\.4 =-7199
máximo
= 0.75
III.- MOMENTOS FLEXJONANTES
Mo3 =\/SWL2
4800
f'y +6000
mínimo
kg-m
0 •7jf'c
0.7J: 200
= 0.0023
f'y
4200
ASmín =Pmínbd = (0.0023;(25;(32; = 1.84 cm2
158
TESIS PROFESIONAL
<3) Cálculo de acero necesario para unMu =4050 kg -m
V.- DISEÑO POR CORTANTE
Mu
405000
,,ní 2
— =—
=3.76cm1
FRf'y jd ^0.9^4200^0.89x32;
Condición:
Condición :
As =-
Vu <
As
mín ='- 89cm2 ^As= 3.76cm2 < Asmáx =9.12cm2 =>Se acepta
® Cálculo de acero necesario para unM(-)u=471 kg-m
M
u
« _ =__
AS =
FRf'y jd
47100
__
AA.
¿
2
2.0FRbdJ~*c
Se tomará la cor tante más desfavorable
cor tan tes.
8999kg<(2.Q)(0.%)(25)(?>2)(^160)
8999kg<16191kg =>Serequiere refuerzo
VI.- SEPARACIÓN DE REFUERZO
=o.43cm
^0.9^4200^0.89x32;
Según N.T.C. para
Condición:
del diagrama de
transversal
TRANSVERSAL
concreto
S< IEAJJL
AsmSn =1.89cm2 >As =0.43cm2 < Asmáx =9.12cm2 => No se acepta
3.5b
® Cálculo de acero necesario para unMu =7199 kg -m
M
4c
^ s _
F
"
— __
R f'y jd
7 I 9 9 0 0
Se propone utilizar estribos deVar.<f> 1/4"
Av =2x0.49 =0.98 cm2 :.
AM¡™2
=6.68cm
(0.9^4200^0.89x32)
S,J™J°^™1=
Condición:
As^n =1.89cm2 <As = 6.68cm2 < Asmáx =9.12cm2 =>Se acepta
© Armado para zona donde M(-)u =7 1 9 9 kg -m
Se propone utilizar Var.5/8"
2
As =4Var.5/8"= 4x1.98=7.92cm
© Armado para zona donde M(-)u=4050 kg-m
3.5(25;
22.66 «23.00cm
Tampoco la separación debe exceder de :
S2 =0.5d Sí Vu<1.5F R bdJf *c
8999 kg <
(\.5)(0.Í)(2S)(32HJ\60)
8999kg<12144 kg
S2 =0.5(32; = 16.00 cm
Se propone utilizar Var.5/8"
As = 2Var.5/8"= 2x1.98=3.76cm2
159
TESIS PROFESIONAL
VII.- CALCULO DE FUERZA CORTANTE
DEL CONCRETO (Vcr)
RESISTENTE
Por lo anterior la Separación por fuerza cor tan te que toman
los estribos, es :
s =fR^ryd
Para un Vu = 8999 kg
= (om.9vi252o)(3v
V'u
Condiciones :
Sí h< 70 cm
ó
=
]222cm
5194
S3 =13.00 cm
h/b<6
Sí no cumple, entonces el valor de Vcr se reducirá un 30%.
La fuerza resistente del concreto (Vcr) se calculará con el criterio
siguiente :
Conclusión :
La sección sera de 0.25x0.35
La separación de estribos será de :
S =13.00 cm
Sí;
Porcentaje p <0.01 .-. Vcr =FRbd (0.2 +30p)
Porcentaje p >0.01 .-. V„ =Q.5FR bd(f*c
[f*c
Nota : Ver plano T - 23
El porcentaje de acero utilizado será :
As
pu = — /. As =4 Var.5/S"= 7.92 cm2
bd
7.92
pu =~
u
=0.009
(25)(yi)
pu =0.009 < 0.01 .-.
Vcr =FRbd (0.2+ 30p) Jf* c
Vcr =fO.8^25^3240.2 +30^0.009^160 = 3805 kg
Por lo tan to la fuerza cor tan te que toman los estribos (V'u ) es :
Vu= Vu - Vcr = 8999- 3805 = 5194 kg
V'u=5\94 kg
160
TESIS PROFESIONAL
Diseño d e t r a b e d e
EC1-2)
entrepiso
® Cálculo de acero
/. - DATOS DE DISEÑO
W = 2204 kg /ml
fe = 200 kg/ cm2
f'y = 4200 kg/cm2 (Armado
f'y = 2530 kg/cm2 (Refuerzo
f*c =0 . 8 / ' c = 160 kg/cm2
f"c = 0 . 8 5 / * c = 136 kg /cm2
P m „, = 0.75
longitudinal)
transversal)
136
máximo
4800
4200 4200+6000_
0.0114
Asma* = W " * = (0.0114^25^32; = 9.12 cm2
© Cálculo de acero
mínimo
II. - CORTANTES
WL _ (2204^4;
# , _ R2 _ V,_2
2
HI.- MOMENTOS
M„
P m / „=°^Z£ = ^2^00.=0.0023
= ^4408^1.4 = 6171 kg
2
FLEXIONANTES
WL2
f2204;f4j2
8
8
f'y
CD Cálculo de acero necesario
(4408;i.4 = 6171
kg-m
AS=~Í-.
FRf'yJd
IV.- DISEÑO POR FLEXIÓN
Se propone una sección con las siguientes
dimensiones
para un Mu = 6171 kg -1
«i™°— = 5 . w
(0.9^4200^0.89x32;
Condición :
Asmin = 1.84 cm 2 < As = 5.73 cm 2 < As m d x = 9.12 cm2
b = 25 cm
h = 35 cm
r = 3 cm
d = 35- 3 = 32 cm
Formulas
4200
^ s m i n = Pmínbd = (0.0023tf25^32; = 1.84 cm¿
©
=> Se ac
Armado
Se propone utilizar Var. 1/2"
de porcentajes
de
Porcentaje máximo = P, . m a , = 0 . 7 5 P b
Porcentaje balanceado = Pb =
Porcentaje mínimo = PmiVl =
As = 5 Var.I/ 2"= 5x1.27 = 6.35 cm2
acero.
Ver plano T - 23
4800
/ ' # fy +6000
0.7/Tc
/"y
161
TESIS PROFESIONAL
V.- DISEÑO POR CORTANTE
VIL- CALCULO DE FUERZA CORTANTE
DEL CONCRETO (V„)
Condición :
Para un Vu =6171 kg
Vu
La fuerza resistente del concreto (Vcr) se calculará con el crite
siguiente :
<2.QFRbd^f*c
Se tomará la cortan te más desfavorable
cor tan tes.
del diagrama de
6171 kg < (2.Q)(0.%)(25)(32)(.j\60)
6171kg < 16191kg => Se requiere refuerzo
VI.- SEPARACIÓN DE REFUERZO
^ F R A V
transversal
El porcentaje de acero utilizado será :
As
yu
.-. As = 5Var.\/2" =6.35 cm2
bd
6.35
p =
.—_ = 0.007
"
3.5b
Se propone utilizar estribos de Var. <¡> 1/4"
:.
Si JSMOMM^O) =1
^25^32;
pu =0.007 <0.01 .-. Vcr =FR bd(0.2 + 30p)Jf*c
Vcr =(r0.8^25;p2J/[0.2 +30f0.007;]fv/Í60 = 3320 kg
Por lo tan to la fuerza cortan te que toman los estribos (V'u) et
SM cm
Tampoco la separación debe exceder de :
S2 = 0.5d Sí Vu<\.5 FRbd.¡f* c
6171 kg <(\.5)(0.%)(25)(32)( \6Q)
6171 kg <12144 kg
S2 =0.5/32; = 16.00cm
Porcentaje p <0.01 /. Vcr =FR bd(0.2 +30p) Jf*c
Porcentaje p >0.01 .\ Vcr =0.5FR
bdjf*c
p =
f'y
Av =2x0.32 =0.64cm2
Sí;
TRANSVERSAL
Según N.T.C. para concreto
S
RESISTENTE
Vu=Vu-Vcr
=6171-3320 =2851 kg
Vu= 1543 kg
Por lo anterior la Separación por fuerza cortan te que toman
los estribos, es :
= FRAvfM
= (MJ0MK2S3QXW = R „
V'u
^
2851
S, = 15.00 cm
Conclusión :
La sección será de 0.25x.35 m
La separación de estribos será de :
S = 15.00 crn
162
TESIS PROFESIONAL
Diseño d e t r a b e s d e entrepiso
2 ( D - E ) y 2 ( E - •O
/. - DATOS DE DISEÑO
JV.- DISEÑO POR FLEXIÓN
W{ =
M5kg/ml
W2 =1215 kg/mi
fe = 200 kg /cm2
fy = 4200 kg /cm2 (Armado
fy = 2530 kg /cm2 (Refuerzo
f*c =0.8fe = 160 kg /cm2
fe = 0 . 8 5 / * c = 136 kg/ cm2
Se propone una sección con las siguientes
longitudinal)
transversal)
b = 25 cm
ft = 40 cm
r = 3 cm
d = 40- 3= 37 cm
Formulas
U.-
dimensiones
de porcentajes
de
acero.
CORTANTES
Porcentaje máximo =P m a x = 0.75 Pb
TRAMO B(l - 2)
/?, = V ¡ = 3 / 8 W L = 3/8(1375^6.00J = f3094^1.4 = 4332 kg
R2=V2= 5 / 8 WL = 5/8^375^6.00^ = ^5157^1.4 = 7219 kg
Porcentaje balanceado = PbPorcentaje mínimo = Pm
TRAMO B(2 - 3)
R2=V2= 3 / 8 WL = 3 / 8 ^ 2 1 5 ^ 5 . 0 0 ; = (2219)\A = 3190 kg
R3 = V3 = 5 / 8 WL = 5/8(1215Jf5.00J = (3797)\A = 5316 kg
® Cálculo de acero
III.- MOMENTOS
Pmax = 0.75
FLEXIONANTES
Moy = 9/128 WÚ = 9/128 (\315)(6)2 = (3481^1.4 = 4873fcg- m
Mo2 = 9 / 1 2 8 WL2 = 9/128 (\2\S)(S)2 = (2136^1.4 = 2991 kg-m
Asmax
fy
f y +6000
o.y fe
fy
máximo
136
4800 _
0.0114
4200'4200 +6000
=Pmaxbd = (0.01U)(25)(31) = 10.54 cm2
Cálculo de acero
mínimo
Moy = 1/8 WL2 = 1/8 (\375)((>)2 = /6188J1.4 = -8663 fcg-m
0.7^-0^200^^3
fy
4200
ASmín = Pmínbd = (QM23)(25)(31) = 2.12 cm2
163
TESIS PROFESIONAL
CD Cálculo de acero necesario para un Mu =4873
kg-m
M
u
487300
„ „, 2
*~ =~
=3.91 cm2
FR f'y Jd ^0.9^4200^0.89x37J
Condición :
V.- DISEÑO POR CORTANTE
Condición :
As=~
Vu <2.QFRbd
ASmtn = 2.12cm2 <As =3.91cm2 < A s , ^ =10.54cm2
=> Se acepta
© Cálculo de acero necesario para un M(-)u=2991 kg - m
Mu
299100
„ ín
2
-— =
—•—
=2.40 cm2
FR f'y Jd (0.9#4200#0.89x37J
Condición:
[f*c
Se tomará la cor tan te más desfavorable
cor tan tes.
7219 kg <f2.0;(0.8#25;(37# \iT60;
7219fcgr< 18721 kg => Se requiere refuerzo
VI.- SEPARACIÓN DE REFUERZO
As=-
Según N.T.C. para
ASmin =2.12cm2 <As = 2.40cm2 < A s ^ ^ =10.54cm2
del diagrama de
transversal
TRANSVERSAL
concreto
s<?«Ml
=> Se acepta
3.5b
® Cálculo de acero necesario para un Mu =8663
kg-m
Mu
866300
£n<
2
— =
=6.95 cm
F
RÍ'yJd
^0.9^4200^0.89x37;
Condición:
Av = 2x0.49 = 0.98 cm2
As=
As
min =2.12cm2 < As =6.95cm2 < A s ^ ^ =10.54cm2
Armado para zona donde M(-)u=8 6 6 3
:.
S]¿(0^0M)(2530)=2266x2300cm
1
=> Se acepta
kg-m
Se propone utilizar Var. 5/8"
3.5(25;
Tampoco la separación debe exceder de :
S2 = 0.5d
Sí
Vu < 1 . 5 F R b d J f * c
7219kg < (\.5)(Q.?,)(2S)(n)(J\60)
7219kg<14041 kg :.
As = 4Var.5/«'= 4x1.98=7.92 cm2
Armado para zona donde M(-)u~4873
Se propone utilizar estribos de Var. ^ 5/16"
S2 =0.5(37;=18.50 cm
kg-m
Se propone utilizar Var. 5/ 8"
As = 2Var.5/8" =2x1.98=3.96 cm2
164
TESIS PROFESIONAL
VIL - CALCULO DE FUERZA CORTANTE
DEL CONCRETO (V„.)
RESISTENTE
Para un Vu = 7219 kg
Por lo anterior la Separación por fuerza cor tan te que toman
los estribos, es :
s
3
Condiciones :
Síh<70cm
ó
h/b<6
Sí no cumple, entonces el valor de Vcr se reducirá un 30%.
La fuerza resistente del concreto (Vcr) se calculará con el criterio
siguiente :
_ FzAdJLd = (0.i)(0.9S)(2S20jy7)
Vu
3100
= ^
^
cm
S 3 = 23.00 cm
Conclusión :
La sección sera de 0.25x0.40
La separación de estribos será de :
S = 18.00 cm
Sí;
Porcentaje p <0.01 .-. Vcr = FR bd(0.2 +30p) ¡f* c
Porcentaje p >0.01 .-. Vcr =
0.5FRbdff*c
Nota :Ver plano T - 24
El porcentaje de acero utilizado será :
pu=—
As
bd
:. As =4 Var.5/S"= 7.92 cm2
7.92
pu =— - — =0.008
" (25^37;
pu =0.008 < 0.01 .-.
Vcr = FR bd(0.2 +30p) ff* c
Vcr =(0.%)(25)(21)(0.2 +3<Y0.008#y/l60> = 4119 kg
Por lo tan to la fuerza cor tan te que toman los estribos (V'u) es :
VU=VU -Vcr = 7219-4119 = 3100 kg
V'u= 3100 kg
165
TESIS PROFESIONAL
Diseño d e t r a b e d e
F(l-2)
entrepiso
O CáZcuZo cíe a c e r o m á x i m o
/. - DATOS DE DISEÑO
W = 1100 kg /ml
fe = 200 kg /cm2
f'y = 4200 kg/cm2 (Armado
f'y =2530 kg /cm2 (Refuerzo
f*c =O.Sfc = 160 kg/cm2
/ " c = 0 . 8 5 / * c = 136 kg /cm2
Pmax= 0-75
longitudinal)
transversal)
136 __ 4 8 0 0 _
4200'4200 +6000
= 0.0114 .-.
Asmax = P m a v h d = (0.01\4H20X21) = 6.15 cm 2
Cálculo de acero
mínimo
II. - CORTANTES
R] = R2 =V¡_2 -
WL
f1100^4;
2
2
III. MOMENTOS
M„
~8
p = ° - 7 i ^ = ^ Z l ^ =0.0023
4200
f'y
(2200,/1.4 = 3080/cg
Asmin = Pminbd = (0.0023^20^27; = 1.24 cmL
FLEXIONANTES
0100^4/
~8
® Cálculo de acero necesario
(2200;i.4 = 3080fcgr-m
As=~
TV.- DISEÑO POR FLEXIÓN
308000
= 3.39 cm¿
(0.9^4200^0.89x27;
Condición :
Se propone una sección con las siguientes dimensiones
b = 20 cm
h = 30 cm
r = 3 cm
d = 3 0 - 3 = 27 cm
Formulas
M„
FRfyjd
para un Mu = 3080 kg - i
:
Asmin =1.24 cm2 <As = 3.39 cm 2 < ^ s m á x =6.15 cm2
©
=> Se ac
Armado
Se propone utilizar Var. 1/2"
de porcentajes
Porcentaje máximo - Pm
Porcentaje balanceado =Pb Porcentaje mínimo =Pmín =-•
de
Ver plano T - 24
0.75 Pb
f"c
/'y
/ l s = 3 Var.1/2"= 3x1.27 =3.81 cm2
acero.
4800
/ ' i / + 6000
0.7/7'c
166
TESIS PROFESIONAL
V.- DISEÑO POR CORTANTE
VII.- CALCULO DE FUERZA CORTANTE
DEL CONCRETO (V„)
Condición :
Para un Vu =3080 kg
La fuerza resistente del concreto (Vcr) se calculará con el crite
siguiente :
Vu<2.0FRbd¡J*c
Se tomará la cortan te más desfavorable
cor tan tes.
del diagrama de
3080 kg < (2.0)(0.Z)(20)(21)(j[(>0)
3080 kg < 10929 kg => Se requiere refuerzo
VI.- SEPARACIÓN DE REFUERZO
Sí;
Porcentaje p <0.01 .-. Vcr = FRbd(0.2 + 30p)/f
Porcentaje p >0.01 .-. Vcr =0.5FRbdjf~* c
transversal
As
p
u
.
T
• ^ s = 3 var.1/2"= 3.81 cm2
bd
iBJ^LÍ'y
3.5b
p =__ J - 0 , _ =0.007
Se propone utilizar estribos de Var. <¡> 1/4"
pu =0.007 <0.01 .'.
Av = 2x0.32 =0.64cm2
:.
S 1 , ^ ° W - Í Í ^ ^ = 5 18.50-18.00 cm
3.5(20;
Tampoco la separación debe exceder de :
S2=0.5d
Sí
Vu<\.5FRbdJf*c
*c
El porcentaje de acero utilizado será :
TRANSVERSAL
Según N.T.C. para concreto
S<
RESISTENTE
Vcr = FR bd(0.2 +30p)J~f* c
Vcr =(0.%)(20)(21)\0.2+ 30f0.007J/]f4t60 = 2241 kg
Por lo tan to la fuerza cortan te que toman los estribos (V'u) ei
V'u= Vu - Vcr =3080- 2241=839kg
U- u =839/ca
Por lo anterior la Separación por fuerza cortan te que toman
los estribos, es :
3080kg < i\.5)(Q.%)(2QH21)(Í:í(,0)
3080kg <8197kg :.
S = 3 MJÉ
S2 = 0.5(27) =\3.50 cm
S 3 =40.00 cm
3
= /0;W0-frW2530#27J = ^ fig ^
Vu
839
Conclusión :
La sección será de 0.20x.30 m
La separación de estribos será de :
S =15.00cm
167
DISEÑODETRABEDEENTREPISO
B(1-2)YB(2-3)
DISEÑODETRABEDEENTREPISO DISEÑODETRABEDEENTREPISO
D(1-2)YD(2-3)
E(1-2)
IN II I I
Casa-Habitación
T-23
AC(Jo C AJO
V i c e n t e Villddti No 7 7 Col A h u i z o t l a M u n Nduc a l p d n d t ) u a r e /
J
INf II- No
t A f N F IHN
Ji
ÍNl !
no^ef
DISEÑODETRABEDEENTREPISO
F(1-2)
DISEÑODETRABED EENTREPISO
2(D-E)Y2(E-F)
v2'
#
2+^
Zp>
iNoi ru ü rt NIL oí Ü J I I A C U » muaiON
T-24
METROS
Casa-Habitación
N nil N (J ALBrtHH FAN ü f
Vicente VillacU No / / " Cot Ahuizotla M u n Naucalpctn de Juárez
Vil l i [NI ij [ SI jJR l JH -([ s
*0&*}
TESIS PROFESIONAL
5.2.8.
Diseño de losas
5 . 2 . 8 . 1 . Diseño de losas de azotea
Diseño de losa de azotea
Tablero I
2.- El peralte efectivo se deberá afectar por:
1.- Diseño de tablero I de losa de azotea, elcuál se colará
monolíticamente con sus apoyos.
0.034t/y; ws .-. fa= 0.6f'y
A
TAB.I
Sí no cumple con:
fs < 2000 kg/cm2 y
Ws=821 kg/m 2
Wu=(821)(1.4)=1150 kg/m 2
4.00 m
Ws<3SOkg/m2
Condición:
fs = 0.6f'y = f0.6#3000,/ = 1800kg /cm2
?mmmmmMMmmmmm?,
V
fs =1800kg/cm2 < 2000 kg/cm2
Ws = 821kg/m2 > Ws = 380 kg/m2
® Cálculo de peralte
<-
6.00m
->
/.- DATOS DE DISEÑO
fe =250kg/cm2 (Concreto claseI)
f'y =3000 kg/cm2
f*c = 0.8/'c =200kg /cm2
fe =0.85/*c = 170kg /cm2
II.- CALCULO DE PERALTEEFECTIVO
Se afectará el peralte
efectivo
dm(n =P6rí^° X0.034f7ws
dmin =/ 6 0 °+^Ml^Ltmi^í x «¡MM$\mx*2\))
dmm =(7.50)(\.l8) =8.89 cm * 9.00 cm
© Cálculo de peralte
total
h r = d +r =9+2= 11.00 cm
Consideraciones :
1.- La longitud de lados discontinuos se incrementará
50%; sí no es monolítico.
25%; sí es monolítico.
170
TESIS PROFESIONAL
III.- REVISIÓN DE PERALTE POR FUERZA CORTANTE
IV. - DISEÑO POR FLEXION
La fuerza cor tan te esta dada por la siguiente exp resión :
1.- El diseño de la losa se lievar á a cabo por el método de los
"Coeficientes de momentos para tableros
rectangulares."
1.4 a,i - d \W,
2. - Para el armado se propone utilizar Var. 3/8".
(„ A
1+
Var. 3/8"= 0.71 cm2 = as
Va2 7
3. - La separación entre varillas esta dada por :
Cuando exis tan bordes continuos y bordes discontinuos,
se incrementará en un 15%.
1.4
V„ = —
4.00,
1+
0.09 1150
4.00 \M
6.00
Vu
s
cortante
a b
s f'yd
Mu
3.5h >Smax <50 cm
3075
= 2847 kg
1.08
V.- ARMADO DE LA LOSA
"Ver tabla de cálculo y plano T - 25"
Vu =2847x1.15 = 3274 kg
Vu = 3274 kg
® Cálculo de fuerza
_
b a s t o n e s ® 40 cm
que resiste
la losa de
b a s t o n e s ® 40 cm
concreto
La fuerza cor tan te que resiste la losa esta dada por la
siguiente
expresión
VR = 0.5
Fgbdjpc
VR = (Q.5)(Q.&)(\W)(9)(j2ñ0) = 5091 kg
Condición :
Vu = 3274 kg <VR = 5091 kg => Se acepta
3/8"@20cm
3/8"@ 20 cm
171
TESIS PROFESIONAL
Coeficientes, momentos últimos (Para lasfranjas exrtremas multipliqúense por 0.60)yseparación del armado.
Lado
corto
Tipo de
(«O
largo
(«a)
Relación
dolados
(m^ai/aa)
CLARO CORTO
%
8mu<3.5h
(cm)
Horn» a t o » negatiyo»
• nun 1 4 1 1 1 1 . ^ 1
puf»
F A J A
*WI«
".»I'"J|"M»|II
»tmmmmmmmmm
i I.—I.,NP^1»-.-<¿^c-.yHwi
SH BQRJ5E
«fTERlOR
EN BORDE"'
DESCONTINUO
S|cn)
último*
^W^lHP^*
C E N T R A L
»III3MÍ
t.nW.i^ftiWf...»-..!*»i*.!•&••' i
wii..«•—
itf'pfr"
(
i'
!fll H? Il4ll
500
92 000
20.83
21.00
20.00
299
55 000
34.85
35.00
35,00
51900
F A J A
E X T
36.93
38.00
.^Wft ^'r. y^K>.^P 9&~,T .TT. ..Jff ™* ^^ ff.y.; ',. sí. ~r.
282
EfJCiWTRQ
ytfffjll»»
»»i»t*yo»
EN BORDE
INTERIOR
EN BORDE
DISCONTINUO
S»!»^ ^w ,^|PS¿ . 1 ^ „~rr~ ^* ^ ^
1 150
Doslados
Adyacentes
discontinuos
4.00
6.00
0.65
MF 7^ ^r^ . ^
35.00
—r—T-**
R E M Ü
55 200
34.72
35.00
35.00
33 000
58.09
38.00
35.00
31 100
61.63
38.00
fO
EN CENTRO
35.00
I- iiii»Hi'»iliJln
CLAROLAROO
mmmm
I #f á ,G,mM t,B.4,>
Momo a t o a n e g a t i v o »
EN BORDE
INTERIOR
EN BORDE
DISCONTINUO
442
44 500
43.07
38.00
35.00
242
81 300
23.57
23.00
20.00
26 500
72.33
38.00
35.00
Momentopositiyo
EN CENTRO
144
F A J A
E X T R E M A
Momentos negativo»
EN BORDE
INTERIOR
EN BORDE
DISCONTINUO
Momento
EN CENTRO
26 700
71.79
38.00
35.00
48 800
39.28
38.00
35.00
15900
120.56
38.00
35.00
positivo
N^HÉi^MailIMHMMRMHWullMktfMHlril
172
TESIS PROFESIONAL
Diseño d e losa d e a z o t e a
T a b l e r o II
2.- Diseño de tablero E de losa de azotea, el cuál se colará
monolíticamente con sus apoyos.
2.- El peralte efectivo se deberá afectar por :
0.0344/7; ws
A
TAB. II
.-. fs = 0.6 f-y
Sí no cumple con :
fs < 2000kg/cm2
Ws=741 kg/m 2
Wu=(741)(1.4)=1038 kg/m 2
4.00 m
y Ws< 380 kg/m2
Condición :
fs = 0.6f'y = ^0.6^3000;=1800kg /cm2
Sí
V
fs = 1800kg/cm2 < 2000kg/ cm2
Ws = 741kg/m2 >WS= 380 kg/m2
® Cálculo de peralte
6.00m
<r
->
Perímetro
*~*-mín
I.- DATOS DEDISEÑO
2
f'c =250kg/cm (Concreto clase I)
f'y = 3000 kg/cm2
f*c = 0.8/'c =200kg /cm2
f'c = 0.85/*c =170 kg/cm2
II.- CALCULO DE PERALTEEFECTIVO
300
Se afectará el peralte
efectivo
' xO.034i[f~Ws
dmín J600±6^h^^±^)x
(o.o34)( ilmowi),
dmín =(1.66)(\.\5) = 8.85 cm * 9.00 cm
© Cálculo de peralte
total
hT =d +r =9+2= 11.00 cm
Consideraciones :
I.- La longitud de lados discontinuos se incrementará
50%; sí no es monolítico.
25%;sí es monolítico.
173
TESIS PROFESIONAL
III.- REVISIÓN DE PERALTE POR FUERZA CORTANTE
TV. - DISEÑO POR FLEXION
La fuerza cor tan te esta dada por la siguiente exp resión :
l.- El diseño de la losa se llevará a cabo por el método de los
"Coeficientes de momentos para tableros rec tan guiares."
W„
-d
1.4
V„ = (
1+
a ^
2. - Para el armado se propone utilizar Var. 3/8".
6^
Var. 3/8"= 0.71 cm2 = as
3.- La separación entre varillas esta dada por :
Cuando existan bordes continuos y bordes discontinuos,
se incrementará en un 15%.
1.4
4.00,
S - asbf'yd~
' " Mu
3.5h >Smax <50 cm
-0.09 1038
V„ =
1+
Vu
^4.00
1,6.00
NM
2776
1.08
V.- ARMADO DE LA LOSA
2570 kg
"Ver tabla de cálculo y plano T - 25"
Vu =2570x1.15 = 2956 kg
Vu = 3274 kg
® Cálculo de fuerza
cortante
bastones® 30 cm
que resiste
la losa de
b a s t o n e s ® 4 0 cm
concreto
La fuerza cor tan te que resiste la losa esta dada por la
siguiente exp resión
VR
=0.5FRbdJf*c
VR =( 0 . 5 ^ 0 . 8 ^O O ^ ^ / Í O O ; = 5091 kg
Condición :
Vu = 2956fcg < VR = 5091 kg => Se acepta
3/8"@ 20 cm
3/8"@ 15 cm
174
TESIS PROFESIONAL
Coeficientes, momentos últimos (Para las franjas exrtremas multipliqúense
Lado
corto
Tipo de
Lado
largo
Relación
de lado*
( m*ei/aa)
por 0.60) yseparación del armado.
Momento*
CLARO
últimos
M^CW.a^xlCM
cml
»M""f
Coef»
CORTO
F A J A
EN BORDE
INTERIOR
EN BORDE
DISCONTINUO
500
Mo m e n t o
po»itivo
ENCENTRO
760
Btpecial
EN BORDE
INTERIOR
EN BORDE
DISCONTINUO
Claro corto:
Momento
Aislado
1038
4.00
6.00
0.65
II»
Smax<3.5h
(cm)
1 ™fp#^
«PMprii
C E N T R A L
23.09
23.00
20.00
126 200
15.19
15.00
15.00
—*1 *—-1 " '"i¿ "T"
Home n t o e
^ t fff
f * yi i l l
83 000
F A J A
-rt
S(cm)
w
EXTREMA
negativo»
49 800
38.49
38.00
35.00
75 700
25.32
25.00
25.00
positivo
EN CENTRO
CLARO LARGO
F A J A
"
Claro largo:
Mome ato»
De esquina
EN BORDE
INTERIOR
EN BORDE
DISCONTINUO
M o m e nto
positivo
EN CENTRO
144
* — • * " - • > — —
26.11
26.00
20.00
23 900
80.20
38.00
35.00
E X T R E M A
negativo»
EN BORDE
INTERIOR
EN BORDE
DISCONTINUO
EN CENTRO
-»••>> ••
73 400
F AJ
Momento
*J|..I.HI
negativo»
442
Momento»
C E N T R A L
ii^.i.....i.|»«i.*fri. r i.i.i.«r ...IHÍ.ÉI.1 nmifríi
44 000
43.56
38.00
35.00
14 300
134.05
38.00
35.00
positivo
175
TESIS PROFESIONAL
Diseño d e losa d e a z o t e a
T a b l e r o III
3.- Diseño de tablero HI de losa de azotea, el cuál se colará
monolíticamente con sus apoyos.
2.- El peralte efectivo se deberá afectar
0 . 0 3 4 ( / s ws
A
TAB. I l l
.: fs = 0 . 6 f y
Sí no cumple con :
fs <2000 kg /cm2
4.00 m
W s =741 k g / m 2
W u =(741)(1.4)=1038 k g / m 2
por
y
kg/m2
Ws <380
Condición :
fs = 0.6f'y =^O.ójpOOO; = 1800 kg /cm2
Y
fs = 1800 kg /cm2 <2000 kg/cm2
Ws = 741kg/m2 >WS= 380 kg/m2
® Cálculo de peralte
6.00m
<-
•
Perímetro
>
300
I. - DATOS DE DISEÑO
d„
2
f'c - 250 kg /cm (Concreto clase I)
fy = 3000 kg /cm2
f*c =O.&fc = 200 kg/cm2
fe = 0 . 8 5 / * c = 170kg /cm2
efectivo
-x0.0344[77ws
/600 +400+600^1.25j +400
300
x ^0.034^ */0«00^741;;
d^fa = (%SSñ\{\.\5) = 9.20 cm * 10.00 cm
® Cálculo de peralte
II. - CALCULO DE PERALTE EFECTIVO
Consideraciones
Se afectará el peralte
total
h T = d + r = 10+2 = 12.00 cm
:
1.- La longitud de lados discontinuos
se
incrementará
50%; sí no es monolítico.
25%; sí es monolítico.
176
TESIS PROFESIONAL
III.- REVISIÓN DE PERALTE POR FUERZA CORTANTE
IV.- DISEÑO POR FLEXION
La fuerza cor tan te esta dada por la siguiente exp resión :
i.-El diseño de la losa se lievará a cabo por el método de los
"Coeficientes de momentos para tableros
rectangulares."
V,=
1.41-^! -d
2
1+
W„
'a^
2. - Para el armado se propone utilizar Var. 3/8".
6^
Var. 3/8"= 0.71 cm2 = as
K"2j
3.- La separación entre varillas esta dada por :
Cuando existan bordes continuos y bordes discontinuos,
se incrementará en un 15%.
1.4
4.00
-' -0.10
f4.qo
2761
= 2557 kg
l708
s f'yd
"Ver tabla de cálculo y plano T - 25"
6.00
Cálculo de fuerza
a b
V.- ARMADO DE LA LOSA
Vu =2557x1.15 = 2941 kg
Vu =3274 kg
®
s -
3.5/i > Smax <50 cm
1038
V„ =•
1+
Vu
cortante
b a s t o n e s ® 40 cm
que resiste
la losa de
b a s t o n e s ® 40 cm
concreto
La fuerza cor tan te que resiste la losa esta dada por la
siguiente exp resión
VR=0.5FRbdjf*c
VR =^0.5^0.8^100^10^200; = 5657 kg
Condición :
Vu =2941 kg <VR = 5657 kg =>Se acepta
3/8"@ 20 cm
3/8"@ 20 cm
177
TESIS PROFESIONAL
Coeficientes, momentos últimos (Para lasfranjas exrtremas multipliqúense por0.60)
yseparación del armado.
í
Tipode
tablero
Momento*
últimos
My)0|P{,«i**UM
1
a
(k*7» >
corto
largo
de lado*
( m=ai/aaJ
CLAROCORTO
l
h
"'"
Sícml
S m «<3.5h
(cm)
' " " T" '
i
;'v ""; :'" : r&4>
^JITRAI.
,
^^w, ^ ^flWT F ^ P ™f^ * ^ F t i P * ^ F^ • *ww ^ W ^ í ^ ^
. ,....,,•
•• •••' "V '
i
••
i
„
-
. 1 . . . .
MÉEBKÍR Í
'EfÉOflD» f
OISCOUTINUO
500
83 000
1
'
"
760
f
1
Aislado
^ f f ^ i ^ F 1**?* ^ F • ! * * V ^ F
4.00
6.00
0.65
mft . ^ ^ ^ ^ * " * W ^ r
INTERIOR !
ENB0RP8
Discosniiüb
• S T ^ Í ^ * w * ) ^ TF '9I& e ( W
EtJCpifTRO
. - ...
16.87
16.00
.
25,00
. . .
• - . , > •
. . . . ,i
-.- •
15.00
. L . J . . ^ . . f.... .
42.77
.1,
E^cpfrao'
,,
Momentos
25.00
•
j
•,
75 700
1
Deesquina
*.i •
49800
l
CLARO LARGO
Claro largo:
26.66
'?IJ4 i i n t l i A
-
Discoimmjo
1038
, . , . . .
-
IH^IlJRlOR |4l,
EWPORDE í'""
Clarocorto:
v
126200
^ ^ ^ F * WÉP^Í^p alp- ^ ^ f f ^P t *"ff * F^ • í ^ ^ ^* * " ^ s .ifflr
Ctato
Especial
"
*"
^
,
42.00
35.00
28.00
25.00
,j h
28.13
...i.h
'
w$*- ' F í P *
,T>»
^ P T .,F ^
*
•*% * T I
^ f
negativo* f
73400
442
29.01
29.00
20.00
40 200
52.98
42.00
35.00
242
B r ^ F ^F/ TF T*
144
.
23 900
89.12
F A J A
E X T R E M A
Momento» negativo*
EN BORDE
44000
48.40
INTERIOR
EN BORDE
88.38
24100
DISCONTINUO
Momento positivo
14 300
148.95
ENCENTRO
42.00
• , - , , .
i
35.00
•-'
42.00
35.00
42.00
35.00
42.00
35.00
178
TESIS PROFESIONAL
Diseño de losa de azotea
Tablero IV
4.- Diseño de tablero W de losa de azotea, el cuál se colará
monolíticamente con sus apoyos.
2.- El peralte efectivo se deberá afectar por :
0.034§fs
w/////mmw/////////A
TAB. IV
ws
.:
Sí no cumple con :
A
fs <2000 kg / cm2
W s =741 kg/m2
W U =(741)(1.4)=W
Wu=1038kg/mi
4.00 m
4.00 m
y
Ws <380 kg / m2
Condición :
fs =0.6f y = f0.6#3000; = 1800
kg/cm2
fs =1800 kg /cm2 <2000 kg/cm2
Ws = 741 kg/m2 >Ws =380 kg/m2
V
<
fs=0.6fy
© Cálculo de peralte
>
Perímetro
300
=> Se afectará el peralte
efectivo
x0.034^/ s Ws
I. - DATOS DE DISEÑO
fe = 250 kg / cm2 (Concreto clase I)
fy = 3000 kg/cm2
f * c = 0 . 8 / ' c = 200 kg /cm2
fe =0 . 8 5 / * c = 170kg /cm2
¿mm = (6.00)<\A5) = 6.90 cm » 8.00 cm
II.- CALCULO DE PERALTE EFECTIVO
h r = d +r = 8+2 = 10.00 cm
Consideraciones
© Cálculo de peralte
total
:
I. - La longitud de lados discontinuos
se incrementará
:
50%; sí no es monolítico.
25%; sí es monolítico.
179
TESIS PROFESIONAL
III.- REVISIÓN DE PERALTE POR FUERZA CORTANTE
IV. - DISEÑO POR FLEXION
La fuerza cor tan te esta dada por la siguiente exp resián :
1.- El diseño de la losa se lie var á a cabo por el método de los
"Coeficientes de momentos para tableros
rectangulares."
W„
1.4
V,
2. - Para el armado se propone utilizar Var. 3/8".
6\
Var. 3/8"= 0.71 cm2 = as
1+
3.- La separación entre varillas esta dada por :
Cuando existan bordes continuos y bordes discontinuos,
se incrementará en u n 15%.
1.4
V. =
4.00 1
V
'
-0.08
1038
(4.00^
Vu
¿700
1395 kg
Mu
b a s t o n e s ® 40 cm
que resiste
la losa de
La fuerza cor tan te que resiste la losa esta dada por la
siguiente
expresión
VR = 0.5
'
"Ver tabla de cálculo y plano T - 25"
Vu =1395x1.15 = 1604 kg
Vu =1604 kg
cortante
s f'yd
V.- ARMADO DE LA LOSA
4.00
Cálculo de fuerza
a b
3.5h >Smax <50 cm
2790
1+
®
s -
bastones@ 40 cm
concreto
TAB. IV
FRbdjf*c
VR = f0.5#0.8#l00)(i)(j2b0) = 4525 kg
Condición :
Vu =1604 kg <VR =4525kg=>Se acepta
3/8"@ 20 cm
180
TESISPROFESIONAL
Coeficientes, momentos últimos (Para lasfranjas exrtremas multipliqúense por 0.60) y separación del armado.
p
Tipo de
tablero
W»
íkg/wa)
Lado
corto
(«O
Lado
largo
(*a)
Relaekm
de ladea
(m-ax/aa)
^mmmmmmm^m
I ni V ""
i (opa)
nltbnoa
Momento*
(cm)
*M?1|^a^*|f|-*
mmmmm
&am*<íl.SJtt
,iiiiii)t)i>ij|i||||i!i|i||i|ii
wm
IJI ,,
mmmmm
i.i^TOLffT^7-fT^Vj|-t
i' a%ttrif?' ¿ j L1•' •'¿''TfíWjMBi
»•'•'«[»>>"<•* <&
mtfammn
m••'i'ff-
"ilfiiipiimpl
l
wAw^ii^iewtitowi^pi»!^^
PttlEiatoRr.
inMrnofw*)
324
53 800
53.92
35.00
190
31600
31.67
31.00
35.00
20.00
ii«iaii4i«i¡«ii%i¡w»ii&*iji
1
Sjmp™¡."i¡P,f.ifii i,M Xff.fiIr.' .iB. °
BH^qfGNTRP'r
137
22 800
F A J A
74.73
""Ü;-;I|-"ÍÍ'I'M;'1'
,:..:,Bíl
35.00
35.00
.'''"""* I'" i'jp't'
E X T R E M A
*4*&
ENBORDE
19000
89.68
35.00
35,00
32 300
52.75
35.00
35.00
124.37
35.00
35.00
eww- ^ff iifcejB* "^* wa w ^ ^
gp ^ff (aP ay ^ s w. a #
«••^¡tii . w . i f r w i . M ^ f ^ i . y » ^ » ' . ! * " » ' ' - - ! - •" '
y—«¡.wim
1038
Doslados
Adyacentes
discontinuos
4.00
4.00
1.00
E^CEXTRO
13700
(«WW
CLARO LARGO
i
" :
:
'"•
*t • > „ • ,#„iii>,ff. T„* *i.f,*i» &A
'•',
¡"*¡»>¡y
ENBORDB
INTERIOR
ENBORDE
DISCONTINUO
M°ff«»l«'I,T^M
T»
ENCENTRO
—..{Mtc—H"—•'••"'«•"i"-""1
F A J A
Momento a negativo»
ENBORDE
INTERIOR
ENBORDE
DISCONTINUO
M o m e n t o p o a i t VQ
ENCENTRO
l i l i l í
M mmm
GXT
R E M A
' f
H' i|" " lUl'i'il
<"í
• « mm
181
TESIS PROFESIONAL
Diseño de losa de azotea
TableroV
2.- Elperalte efectivo se deberá afectar por :
5.- Diseño de tablero V de losa de azotea, el cuál se colará
monolíticamente con sus apoyos.
i
TAB.V
0.034*Jf, wa
A
•
Sí no cumple con :
fs <2000 kg / cm2
2.00m
W s =741 k g / m 2
W u =(741)(1.4)= 1038 k g / m 2
I
i
Tmmmmmmmmmmmm?,
y
4.00m
Ws<3%0kg/m2
Condición :
fs = 0.6f y =(0.6^3000,/ =1800 kg /cm2
V
fs =1800 kg/cm2 <2000 kg/cm2
=>Seafectará el peralte
Ws =1038 kg/m2 >WS= 380 kg/m2
® Cálculo de peralte
<r
/s=0.6/'i/
->
Perímetro
d,
300
efectivo
xO.O340sWs
I.- DATOS DE DISEÑO
fe = 250 kg/cm2 (Concreto clase I)
f'y =3000 kg/cm2
f*c =0 . 8 / ' c = 200 kg/cm2
fe = 0 . 8 5 / *c = 170 kg / cm2
dmín =
II. ~ CALCULO DE PERALTE EFECTIVO
hn
Consideraciones
(^.±^m^tí^tmx(Q.o^^imm)
dmin =(4.50)(\A5) = 5.17 cm *8.00cm
© Cálculo de peralte
total
d + r = 8+2== 10.00cm
:
1.- La longitud de lados discontinuos
se incrementará
50%; sínoes monolítico.
25%; síes monolítico.
182
TESIS PROFESIONAL
HI.- REVISIÓN DE PERALTE POR FUERZA CORTANTE
IV. - DISEÑO POR FLEXION
La fuerza cor tan te esta dada por la siguiente exp resión :
1.- El diseño de la losa se lie var á a cabo por el método de los
"Coeficientes de momentos para tableros rec tan guiares."
A
1.4 a,
v2
W„
Vu
2. - Para el armado se propone utilizar Var. 3/8".
6\
1+
Var. 3/8"= 0.71 cm2 = as
Va2 7
3.- La separación entre varillas esta dada por :
Cuando existan bordes continuos y bordes discontinuos,
se incrementará en un 15%.
1.4
M.OO,
1+
Vu
S, =-
asbf'yd
M.,
3.5h >Smax <50 cm
-0.08 1038
2.00^
4.00
1337
= 1324 kg
1.01
V.- ARMADO DE LA LOSA
"Ver tabla de cálculo y plano T - 25"
Vu =1324x1.15 = 1522 kg
Vu =\ 522 kg
© Cálculo de fuerza
cortante
b a s t o n e s ® 4 0 cm
que resiste
la losa de
b a s t o n e s ® 70 cm
concreto
La fuerza cor tan te que resiste la losa esta dada por la
siguiente
expresión
VR=0.5FRbdJf*c
VR =f O ^ O ^ l O O ^ J ^ O J = 4526 kg
Condición :
Vu = 1522 kg <VR = 4526 kg => Se acepta
3/8"@35cm
3/8"® 20 cm
183
TESIS PROFESIONAL
Coeficientes, momentos últimos (Para las franjas exrtremas multipliqúense
Lado
corto
TJjKxIe
Lado
por 0.60) y separación del armado.
j? -
Reboto»
ÉHtimoé
..¡i!
(«i)
8»«<3.5h
>!"!>,'
» !#[ipili>Bif|UiW<»
24800
598
15800
362
'"'""•"'»'"¡"'
'•"•«"
i» M I '
a"«|'
68.70
35.00
107.84
35.00
"»tui¡;i<ijun ii>i''
35.00
i «¡i
l»li|
15000
358
113.60
;
35.00
;
»'wil. ifriliUijijí
35.00
ll l
rf:ii|'- **$?*%> > ' t » . j ' J 1 T I * ' » R E MA !— T". ^ . '"f!,:!fS
¡•w|!"H |i .|1i»ij.Wiyl..t«...i1y|...<'l||'»ij)¡l».nl.,.Mi ,^r,|P..,„;,,p| l ^.A (l i,fT l 4J|S l .,|^g|. i.nT,i.j|)¡,..ltii¡);|l),..i,|.{¡a| WT'"$VrP||||i
l
'5^BÉ^3&'ff''fi*''T|''''! * ' ^ t '
1038
Dos lados
Adyacentes
discontinuos
2.00
4.00
"*'''''"' ' »«''ÜÍ "•«•''•'«Ni \,-i¿ '1w'|.i. i.ni»i>V.)>í'ii..¿|.iiÍ.Vít8Ji(W
35.00
14900
114.36
35.00
0.50
9000
189.33
5TT
"i"
s
di'
8900
QBOSQQCESC:
g>F ii..il|..ii'i¡n»«.iii.
.njj
mimlg
JSli.ftjSjr X B|° "
iI»!
¡A/ i-
EN BORDE
$OONTIHUO
ii-.i. i. ....
' i^íT i i . .
Efi'CElfTRpJ'
35.00
35.00
""IT'
U'
191.46
35.00
.tinlAiOflfi-,?.,!
35.00
•fWgf
|üJil||.i^UK|l r l.| 1 .J¡JI|ili¡|ll,lll
j tJi ! j!i|
'^ffü'^i' 'ifr^iai'wy-'a'-i; "' -'"' ^ s ' w #
ytt o t o l a s J-••1,:Vl:'>l ,
;•i.,:y,*,"•:
W
35.00
475
19 70Q
86.49
258
10700
159.25
35.00
35.00
270.47
35.00
35.00
*; """;<;".yr<p
v "j | " " *. '»I;I
3500
r-jrjp—ij",si"]
152
6300
T f A J A ;;E I f R ' B M A ,;,
•"•#"• t"i"jftl'
ftt'
•iummi IÍIIi.iLtMi*.|l[-S I.Ii-#i.i.n^t"ll"1'"l">"T',"ll^"'* ii*m"JPfc-""—"f tmlH""—•iiii»M«iIEí.ii
EN BORDE
INTERIOR: ,
ENBORDE í'
DISCONTINUO
11800
144.40
35.00
35.00
6 400
266.25
35.00
35.00
.B^CEKTRCI,;,,..^!
3800
I1,-li»
Moma a t o n f l i i t l v o
448.42
3&.00
35.00
— i . : , . - . ; L . - . ) " . . . i : . . . - .jfeii,....
184
bastones @40
4 00
3/8 &¿Q
¡ 0 0 <>
4 00
bastones (g>40
bastones @70
3 8 @35
3/8 @20
Pl>NO
INbTITUTO IEINOIOÜILO DELA COTURUCCION
T-25
Casa- Habitación
METROS
ING ALIONSOD ABBWhTl IANTOJA
U.CXCC
AGOSTO 200J
Vicente Villada No 7 7 Col Ahuizotla M u n IMaucalpan de Juarez
Vil TUR LNRIQUE SH.UHA TuRKEb
I
^O^6
TESIS PROFESIONAL
5 . 2 . 8 . 2 . Diseño de losas de entrepiso
Diseño de losa de entrepiso
Tablero I
1.- Diseño de tablero I de losa de entrepiso, el cuál se colará
monolíticamente con sus apoyos.
2.- El peralte efectivo se deberá afectar por :
0.0344/77ws .: fs= 0.6f'y
A
TAB. I
Sí nocumple con :
fs <2000 kg / cm2
4.00 m
W s =860 k g / m *
W u =(860)(1.4)=1204kg/m ¿
ES
1
%
mmmmmmmmmmmm?,
y Ws <380 kg / m2
Condición :
fs = 0.6f'y = /"0.6/pOOOj =1800
V
fs =1800 kg /cm2 <2000 kg/cm2
Ws = 860 kg/m2 >Ws = 380 kg/m2
(D Cálculo deperalte
6.00 m
<r
•
>
Perímetro
300
I.- DATOS DE DISEÑO
f'c = 250 kg/cm
(Concreto clase I)
f'y = 3000 kg/cm2
f * c = 0.8f'c = 200 kg /cm2
dmin = p.50)(l.\9)
=> Seafectará el peralte
efectivo
xO.034*} fsWt
f600 +400^1.25;+f600 +400;
300
2
x(0.034)(^J(] 800^860;;
= 8.99 cm*9.00cm
/ " c =0.85/*c = 170kg /cm2
® Cálculo deperalte
II.- CALCULO DE PERALTE EFECTIVO
hT = d+ r =9+2 = 11.00cm
Consideraciones
kg/cm2
total
:
1.- Lalongitud de lados discontinuos se
incrementará
50%; sí noes monolítico.
25%; síes monolítico.
186
TESIS PROFESIONAL
IIL- REVISIÓN DE PERALTE POR FUERZA CORTANTE
IV. - DISEÑO POR FLEXION
La fuerza cor tan te esta dada por la siguiente exp resión :
l.- El diseño de la losa se lievará a cabo por el método de los
"Coeficientes de momentos para tableros rec tan guiares."
1.4 a.
W„
2. - Para el armado se propone utilizar Var. 3/8".
V,.=1+
Var. 3/8"= 0.71 cm2 = as
a
3.- La separación entre varillas esta dada por :
Cuando existan bordes continuos y bordes discontinuos,
se incrementará en un 15%.
1.4
Mu
3.5h >Smax <50 cm
f4.00.
1+
Vu
0.09 1204
4.00
6.00
3220
= 2981 kg
1.08
V.- ARMADO DE LA LOSA
"Ver tabla de cálculo y plano T - 26"
bastones@ 4 0 cm
b a s t o n e s ® 40 c m
3/8"@ 20 cm
3/8"@ 20 cm
Vu =2981x1.15 = 3428 kg
Vu = 3428 kg
® Cálculo de fuerza
cortante
que resiste
la losa de
concreto
La fuerza cor tan te que resiste la losa esta dada por la
siguiente
expresión
VR =
0.5FRbdjf*c
VR = (0.5)(0.%)(\00;C9JHr200j = 5091 kg
Condición :
Vu =3428kg <VR=5091kg=>Se acepta
187
^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ • ^ • • ^ ^ • ^ ^ ^ ^ ^ • • • • ^ ^ • • ^ • • • • • • • ¡ ^ ^ • • ^ • • ^ ^ • • M
TESIS
Coeficientes, momentos últimos (Paralasfranjas exrtremas multipliqúense por 0.60)y separación del armado.
mmfm»mfmq**im
Tipo de
tablero
Wu
(fcg/tfta)
Lado
corto
1*1
Relación
largo
(*a)
8(001)
Moreentoa
^•^^^"W*
^^^••w^ ' ^ *a^#p^
WfprWBw f
1
H*
(m*ai/aa)
iV)Afil!ft J?SuljÜiiUJII
11o r e e u t o
mCENTRO
^
**Pifr
^á"iji<,"1ri"A^'t;'.i,,4>
é,^Uif^mkg<j3SSSk
EN BORDE
INTERIOR
EN BORDE
DlSCQWTimJQ
ii
mfmii
ii'Hijiimivn.p, .<|iyjrtw
500
96 300
19.90
20.00
20.00
299
poaltiyo
57 600
33.28
33.00
30.00
282
54 300
35.30
33.00
30.00
35.00
' f A J a
t
^ « R E M A
0
PI,o»,«»,t f,„JEft1,1,11» P» •„>,
1204
4.00
6.00
0.65
í
m&omn
57 800
33.16
33.00
INTERIOR
EN BORDE
34 600
55.40
38.00
35.00
BU CENTRO
32 600
58.80
38.00
35.00
Doslados
CLARO LAROO
Adyacentes
discontinuos
r AJ A
Momento» a e g atlvoe
EN BORDE
INTERIOR
EN BORDE
DESCONTINUO
Momento
. i M . H » , . ^ — ^ » » . « y i i l l > . | . M . f t l . — ^ | i !*••"••>
ENCENTRO
C BW
442
46600
41.13
38.00
35.00
242
85200
22.50
23.00
20.00
poeltivo
27700
144
69.20
38.00
35.00
. m . n < i l l l i l l •tililf.w>-••*•••<••••••-
«.i»
F A J A
Momentos
ENCENTRO
E X T R E M A
negativo»
EN BORDE
INTERIOR
EN BORDE
DISCONTINUO
Momento
T RAL
28000
68.46
3800
35.00
51100
3751
3800
3500
16600
115.48
38.00
35.00
poeltivo
188
TESIS PROFESIONAL
Diseño d e losa d e e n t r e p i s o
T a b l e r o II
2.- Diseño de tablero II de losa de entrepiso, el cuál se colará
monolíticamente con sus apoyos.
2.- El peralte efectivo se deberá afectar por :
0.034*//fu/ s
1
TAB. II
Ws=905 kg/m2
Wu=(905)(1.4)=1267 kg/m 2
<r
6.00m
I
->
A
•-.
Sí no cumple con :
fs < 2000 kg/cm2
4.00 m
fs=0.6fy
y Ws < 380 kg/m2
Condición :
fs =0.6f y = f0.6#3000; =1800kg /cm2
V
fs =1800kg/cm2 < 2000kg/ cm1
Ws =905kg/m1 > Ws = 380 kg/m~
© Cálculo de peralte
Perímetro
300
=> Se afectará el peralte
efectivo
x0.034*J fsWs
/.- DATOS DEDISEÑO
fe = 250kg/cm2 (Concreto clase I)
fy =3000kg /cm1
f*c = 0.8/'c =200 kg /cm2
fe =0.85/ *c = 170kg/ cm2
II.- CALCULO DE PERALTEEFECTIVO
dmm =í 6 ° ° + 6 0 ^ 1 ¿Ibl™±m
x ^0.034^
tf^X^))
dmm =(1M)(\2\) =9.30 cm « 10.00 cm
© Cálculo de peralte
total
h r = d +r =10 + 2= 12.00cm
Consideraciones :
\.~ La longitud de lados discontinuos se incrementará
50%; sí no es monolítico.
25%; sí es monolítico.
189
TESIS PROFESIONAL
III.- REVISIÓN DE PERALTE POR FUERZA CORTANTE
IV.- DISEÑO POR FLEXION
La fuerza cor tan te esta dada por la siguiente exp resión :
1.- El diseño de la losa se lie var á a cabo por el método de los
"Coeficientes de momentos para tableros rec tan guiares.''
W„
1.4 í l -d
V =~ t 2
r
2. - Para el armado se propone utilizar Var. 3/8".
V
Var. 3/8"= 0.71 cm2 = as
KU2j
3.- La separación entre varillas esta dada por :
Cuando existan bordes continuos y bordes discontinuos,
se incrementará en un 15%.
1.4
V„
Vu
s
=asbfyd
Mu
3.5h >Smax <50 cm
4.00 L
— -0.10|1267
2
1+
4.00
J
3370
6\
1.08
V.- ARMADO DE LA LOSA
3121 kg
"Ver tabla de cálculo y plano T - 26"
6.00
Vu =3121x1.15 = 3589 kg
Vu = 3589 kg
® Cálculo de fuerza
cortante
b a s t o n e s ® 26 cm
que resiste
la losa de
b a s t o n e s ® 40 cm
concreto
La fuerza cor tan te que resiste la losa esta dada por la
siguiente
expresión
VR=0.5FRbdjf*c
VR =(0.5X0.8#100#IO#/200; = 5657 kg
Condición :
Vu = 3589 kg <VR =5657 kg =>Se acepta
3/8"@ 20 cm
3/8"@ 13 cm
190
TESIS PROFESIONAL
Coeficientes, momentos últimos (Para las franjas exrtremas multipliqúense
por 0.60)yseparación del armado.
ni i m^imuí njip
t t p o de
tablero
W
Lado
corto
<**)
Lado
burgo
Relaoioa
da lado»
(m*ai/aa)
$nuui'<3>5h
' (cut)
Coef.
Momentos
a^ap§^^^¡i< j^^^Ht^wJs^ ^ p ^ ^ ^ p
ji'iu.at.m—*
CLARO CORTO
imBiiuiitwiji
w
"i iiiiiiiiiiiif
.'uní. .ui giiiiiiii)iiu!iiiiiiiiiii||iiiiiiii¡iiiiii»iiiii«iiiiiB
immmmimi-mmmmm*mmmmmm~mmmmmmmmmmmm
1
(
(
*
W i
r"'1"""!"1"»
^^.
i ^
|>' ....uiinj
.«111 ^
Ti i
r l J A 13» H TR A L
,..«• «di.,m i l .. 3 rmm
S i - i « J i - u rm>m.L mull i|¡Tli iiiiSti n'l'f i i mi'l'n» •"""IL i ' " "
- . M I * • rtW
r ^
ENBpBSpip
INTERIOR
DtSCQÉnNOQ
i'li.ii.'Imni.ji
Elí CENTRO,
'
!
*|j
' I ' T Í
BWfl
<mmmm*m
,u„i
500
101 400
21.00
21.00
20.00
760
154 100
13.82
14.00
1300
i<y¡i f |ii, l n#ii 1 Hi ll! i fli¡i .i, é»1\f '•HMli|i>
X T R EM A
T
T
•*m*.*#tmm.
B i B S i f i i T ij i ° "••I»"
EN BORDE
BORDÉ
EHtSOOtsftlNUp
Mom e a t o a o i | t . i . ^ . . o
Claro corto:
Aislado
^P ^fc^ ^y •fff y^^ y ,.^ff ,. ........
1267
4.00
6.00
0.65
EN CENTRO I
fflftf?^fjflA
Claro largo:
De esquina
»«" •«fH'v
ntumi.i^i.»^— w .—My...ii'.p W "... 1
60 8 0 0
35.03
36.00
35.00
92500
23.02
23.00
20.00
..M..I. ..Hl ..,!»•• .HI...1 !) .L. .
•m
M'""H'|
Mom e a t o a .negativoa
ENBORDE
442
INTERIOR
ENBORDE
DISCOljrriNIK)
Mom e a t i o p o s i t i v o
• • h . . H » i . « . . ^ . f . . p i i . . l . t l .„.,i
EN CENTRO
.-ma.—i,..i,,....iw.
144
89600
23.77
23.00
20.00
29200
72.94
42.00
35.00
42.00
35.00
42.00
35.00
...,,..i.^n——•
F A J A
E X T R E M A
Momento s n e g atlvoa
EN BORDE
53800
39.59
INTERIOR
EN BORDE
DISCONTINUO
Momento
poaitivo
EN CENTRO
17500
121.71
•iÉM«aÉMMMeaMMriHHaÉÉi
191
TESIS PROFESIONAL
Diseño de losa de entrepiso
Tablero III
3 . - Diseño de tablero III de losa de entrepiso, el cuál se colará
monolíticamente con sus apoyos.
2.- El peralte efectivo se deberá afectar por :
0.034$7 S ws
A
TAB. Ill
.-. fs = 0 . 6 f y
Sí no cumple con :
fs <2000 kg /cm2
4.00 m
W s =523 k g / m *
W u =(523)(1.4)=733 k g / m 2
y
Condición :
fs = O.éf'y = CO.óypOOO;= 1800
V
6.00m
kg/cm2
fs =1800 kg /cm2 <2000 kg/cm2
Ws = 523 kg/m2 >Ws =380 kg/m2
O Cálculo de peralte
<r
kg/m2
Ws <380
->
M-mín
=>Se afectará el peralte
efectivo
Perímetro
x0.034*ffs~Ws
300
I. - DATOS DE DISEÑO
f'c = 250 kg /cm2 (Concreto clase I)
f y = 3000 kg / cm2
/ * c = 0 . 8 / c = 200 kg /cm2
f'c = 0 . 8 5 / * c = 170kg /cm2
dmín = ^8.00^1.05; = 8.47 cm * 9.00 cm
II. ~ CALCULO DE PERALTE EFECTIVO
h-r
Consideraciones
© Cálculo de peralte
total
d +r = 9+2 = 11.00 cm
:
I. - La longitud de lados discontinuos
se
incrementará
50%; sí no es monolítico.
25%; sí es monolítico.
192
TESIS PROFESIONAL
III.- REVISIÓN DE PERALTE POR FUERZA CORTANTE
IV. - DISEÑO POR FLEXION
La fuerza cor tan te esta dada por la siguiente exp resión :
l.- El diseño de la losa se lievará a cabo por el método de los
"Coeficientes de momentos para tableros
rectangulares."
1.4 a.
W„
V„
1+
V
2. - Para el armado se propone utilizar Var. 3/8".
<>\
Var. 3/8"= 0.71 cm2 = as
VU2j
3.- La separación entre varillas esta dada por :
Cuando existan bordes continuos y bordes discontinuos,
se incrementará en un 15%.
1.4
f4.00
Vu
asbf'yd
M„
3.5h >Smax <50 cm
0.09 733
V„ =
4.00
1+
6.00
[961
= 1816 /cgf
1.08
V.- ARMADO DE LA LOSA
"Ver tabla de cálculo y plano T - 26"
Vu = 1816x1.15 = 2543 kg
Vu =2543 kg
© Cálculo de fuerza
S, =-
cortante
b a s t o n e s ® 4 0 cm
que resiste
la losa de
bastones® 40 cm
concreto
La fuerza cor tan te que resiste la losa esta dada por la
siguiente
expresión
VR
=Q.5FRbdJf*c
VR =(0.5)(0.&)(\00)f>)(J2to)
= 5 0 9 2 *9
Condición :
Vu = 2543 kg <VR= 5092 kg => Se acepta
3/8"@20cm
3/8"@ 20 cm
193
TESIS PROFESIONAL
Coeficientes, momentos últimos (Para las franjas exrtremas multipliqúense por 0.60) y separación del armado.
Lado
Tipode
corto
"íi
Ralao4o&
de M o t
(m-*i/a a )
"l último»
t?•WP!
EDOIOSEI;
p.111111111 Hjin u n í in ii ni JMIiujiíi mui|iiim ni Mi ii)i M . iii miiiiii ¡iij i ii i mi!
V
,T F A J A •• 1 E N T R A L •
•;'"«•'•""•"';
iSi&yuMN?! ^
ii[i i'iii!U[i'iipiH»'lii'iuii,iiiu|fclliiiiiiMi
.i}.'.»..qi...;ggi. ; ...i»«»ijijlM».iri..¡ii| ! .|¡
MI*l M | , y ; f j i ,'»!,' :,d
~-*y
'éi''»litWf"'*ii:4lg:fí;;!>|?lf
1 ,'•, _i
32.65
58 700
500
«iiif i .11. .T»
30.00
30.00
f—"ntiy
•' T;"|H;."
• P l ^w j^r IPj. P*_
760
ENCENTRO
|ii»«Bfi i ..i.»ujf ) ..l > í. r ...i,<pi.
•>;• I"| "«[;"" 'i 1 ',
¡.y oiiSiiiAi5ii'™.B
Aislado
Clarolargo:
De esquina
733
4.00
6.00
0.65
Momento
ENCEN/TRO
Mo m e a t o i
njHii ;n ¡i t i ¡ M
J±JM
* ' l f , . % l i ' f t i ' h\ ' , : ; ! • — ¿ i — .
54.46
35 200
. j i i . i i " mi l.il.|ii.'.M
20.00
.•i
Mtl I IIÍ! j i ¡ II u l»l|l
l o w » u t o i,o»1ti•'o.
53 500
EfCBíffRQ V
CLA R O L A R G O
ENBORDE
INTERIOR
ENBORDE •
DISCONTINUO
20.00
FA
Jf JR.i iNpii{íll^^.ui,Sl.j|iiS!i,|»B|i. * .
nft.,3.
•nf-
rfscoiriwup .
Clarocorto:
21.49
89 200
I' ' '' - i " « ^ - ü u ; - > " ;
i
¡ ¡ . . S M I Í R ia.«.|gM.,i l ,.„y
38.00
35.00
;.,i. ai
35.83
ff;,t{"
35.00
35.00
'mim
' b
i •'( ..Hírait1:
|i4j...Hf{|jtij[Ll
442
51900
36.93
38.00
35.00
242
28 400
67.50
38.00
35.00
16 900
113.43
38.00
35.00
poaltivo
144
FAJA
negativo»
ENBORDE
INTERIOR
ENBORDE
DISCONTINUO
EXTREMA
•{.-•-»—»-»••»•••)
31 100
61.63
38.00
35.00
17 000
112.76
38.00
35.00
10 100
169.80
38,00
30.00
Momento BO|}tlTO
EN CpfTHQ
194
TESIS PROFESIONAL
Diseño d e losa d e entrepiso
T a b l e r o IV
4.- Diseño de tablero IV de losa de entrepiso, el cuál se colará
monolíticamente consus apoyos.
2.- El peralte efectivo se deberá afectar por :
0.034i¡fTws
W////////////////////W////.
TAB. IV
A
.-. fs= 0.6 fy
Sí no cumple con:
fs <2000 kg/cm2
Ws==523 kg/m ¿
Wu =(523)(1.4)=W
Wu =733 kg/m 2
4.00 m
4.00 m
Condición :
fs =O.bf'y =(0.6^3000) = 1800 kg /cm2
V
<r
kg/m2
y Ws <380
->
fs =1800kg/cm2 <2000 kg/cm2
=>S eafectará el peralte
2
2
Ws =523kg/m
>WS= 380 kg/m
© Cálculo de peralte
Perímetro
300
efectivo
xO.034*jfóws
I.- DATOS DE DISEÑO
dminjm±míl^S!^^
f'c =250 kg/cm2 (Concreto clase I)
f'y =3000 kg/cm2
f*c =0 . 8 / ' c =200 kg /cm2
f'c =0 . 8 5 / * c =170kg/ cm1
dmín =^6.00^1-05^=6.35 cm * 8.00 cm
II.- CALCULO DE PERALTE EFECTIVO
h r = d +r =8+2 =10.00 cm
Consideraciones
® Cálculo de peralte
tf1W523W
x (omAH
total
:
1.-La longitud de lados discontinuos
se
incrementará
50%; sí no es monolítico.
25%; sí es monolítico.
195
TESIS PROFESIONAL
HI.- REVISIÓN DE PERALTE POR FUERZA CORTANTE
TV.- DISEÑO POR FLEXION
La fuerza cor tan te esta dada por la siguiente exp resión :
1.- El diseño de la losa se lievar á a cabo por el método de los
"Coeficientes de momentos para tableros rec tan guiares."
1.4 a. - d
W„
vu=
2. - Para el armado se propone utilizar Var. 3/8".
6\
Var. 3/8"= 0.71 cm2 = as
1 + a,
3.- La separación entre varillas esta dada por :
Cuando existan bordes continuos y bordes discontinuos,
se incrementará en un 15%.
1.4
4.00
,
\
-0.08 733
V„ =
'4.00^
1+
,4.00
Vu
cortante
1970
2.00
f'yd
M.,
V.- ARMADO DE LA LOSA
985fcg
"Ver tabla de cálculo y plano T - 26"
b a s t o n e s ® 40 cm
que resiste
la losa de
La fuerza cor tan te que resiste la losa esta dada por la
siguiente
expresión
VR =0.5FRbd
asb
3.5h >Smax <50 cm
Vu =985x1.15 = 1133 kg
Vu =\133 kg
CD Cálculo de fuerza
S,=
b a s t o n e s ® 40 cm
concreto
TAB. IV
íf*c
VR = (O.S^O.S^lOOp^yiOOJ =4525 kg
Condición :
Vu = 1133 kg <VR = 4525 kg => Se acepta
3/8"@ 20 cm
3/8"@ 20 cm
196
TESIS PROFESIONAL
Coeficientes, momentos últimos (Para las franjas exrtremas multipliqúense por 0.60) y separación del armado.
197
1
17 00
4 00
2 00
6 00
Y
7777Z7777,7777777777?/77777777777777S7?777777S777Z7),Y7^77777777ZW77777?77i7777777777777777777777777/7^77A-\\
\SZZZZ2¿
TAB I
TAB III
TABU
bastones @40
I
1
1
1
V
\
„
/
3,8
(QJ20
^ffl
3/8 @35
ambos sentidos
3,8" @13
bastones @26
A
bastones @40
3/8' @20
?22ZZZZZ%ZZÉZ1
mZZZ22ZZ2ZZZSZZEZSZZZZZZS!ZZW^7ZZZZ&ZZZSZZ2ZZS2ZZZ2Zm
$
bastones@40
3'8'@20
bastones @40
3'8 @20
INSlllUlOlEONOLOGlCOUt LACONSTRUCCIÓN
I 90
T-26
Casa- Habitación
V i c e n t e V i l l a d a No 77 C o l A h u i z o t l a M u n N a u c a l p a n tie J u a r e z
ING ALFONSOD ABBWR11 PAN10JA
VICTORLNRIÜUt SLGURAI0RRES
HD^eJ
800
plant
plant
head
Esc. 1:25
plant
ESCALA
ci
ESC
1:100
NORTE
INSTITUTO TECNOLÓGICO DELA CONSTRUCCIÓN
Proyectoarquitectónico
ACOTACIÓN
METROS
ASESOR
ING,ALFONSO D'AB 8WRIT PANTOJA
UBICACIÓN
AGOSTO 2003
nclpHl
t
KANO
FECHA
H
Vicente Vlllada No.77. Col.Ahuizotla. Mun. Naucalpan de Juárez
ELABORO
VICTOR ENRIQUE SEGURA TORRES
Hcfi&
19.00
t
2.00
VW/WW¿>//M;A
200
4.00
600
— — 6 . 0 0 -
k'\
>/M/»/»M»/J777?.
i
NOTASGENERALES
y////;////////////;/.
*
í
/
y.
A4
zc
zc
zc
',
Al
1 ^ ACOTACIÓNBtl*TROS
Ai
2- TODOSLOS ESGU£fc"$ 00 NGÉ &£ WOIOUCaAfiiMOO
NO ESTA*AESCAIA.
7.
4.00
Clí
I
•.- B6PECIRCACI0NESOELttTERiAiiS
i). CONCRETOCUSE1091 UNf*c=200Kycm2.
b). ACERO0€REFUERZO CON UNf'y «A200lg<aT*
6'
8.00
CZZZZ /¿¿¿//¿/////////¿¿¿¿¿///¿/.////zzzz
CT
//////y//7777
4 - RECUBRIMIENTOUBREOEIAVARIUA,NOSERA
MENOR
OE2.00CM,NlfcCNORQU€SUa*ACTRO.
y//////////////////
CT
5- NO SE TRASLAPARANI SESOLARAMAS Oa50 %DEL
REFUERZO EN UNASECCIÓN
ZA
ZA
\
ZC
ei
',.
i
D'
CT
4.00
i
*
ci!
C'«
ZC
/
/
/
\
'M//////////777.
¿
G'<
zc
\///////////////////.
6- LOS CIMIENTOSSERÁN OECONCRETORBSRZADO
$
í
C'<
íi
'////////////A<vv%g W/M»M/MM//»/MW//M^^^^
Y///////////S/¿¿¿¿¿¿//¿¿¿.
aw/ww,w/¿w^^^^^^
c<
C4
G<
plantade cimentación
UV.0V? @ 13
r
V*.0W@15 -
m 2Vlf.01/2 -
r
_ Va/.0t/?*@13
0¿0
Var.0V?@25
L
í
_£
L 2Var0 V ?
0.50
Var.01/2'<§>30
r
'
0
A Oo """*" *—if
i
1.30
i
Var.01/2-®20. ^ ^ ^ ^ ^ ^ H
S Var.01/5"@15
!
0.25
•
k
i-
*»
**
* * *»
i i
j
a
aso
I
i!
corteb-b
cortea-a
I 2V *01/2" >
r
- Var.01/2-®20 ^ ^ J
^ íVar.01/2-
r
^Vw.01/2^15
.-V«r.01/2"<á)25
030
- Var.0V?© 30
I
HXJ
1.70
r
r V*.01/2"&20
1
i
0.15
« _ : : .
t
0.80
t
I
aao
ais
-VJr.0l/2"^3O
"
:
oIÍ\
i—í
r 4-
4
corted-cT
corte c-c'
_VI»0V2"@2O
0.80
4
corteg-g
z a p a t a s a i s l a d a s d ac o n c r e t o a r m a d o
r
r
i Vw.0V?®19
ambossoiMt
050
Var.01/2-®10
vnbosMfftldOI
0
Var.0V8"@1S
ambossentidos
0.5O
L
i-
0.25
0.25
1 Q•!•O • "
l
2.00
i
;
150
l
cortef-f'
ESCALA
Pl/*0
ESCUELA
1:100
INSTITUTOTECNOLÓGICO DELACONSTRUCCIÓN
Proyectodecimentación
ACOTACIÓN
METROS
ASESOR
ING.ALFONSO D'ABBWRTTPANTOJA
UBICACIÓN
FECHA
AGOSTO2003
Vicente Vttlada No. 7 7 .Gol.Ahulzotla. Mun. Naucalpan deJuárez
ELABORO
VICTOR ENRIQUESEGURATORRES
NOTAS GENERALES
1.- ACOTACIÓHEN METROS.
2.- TODOS LOSESQUEMASOON0ESEINDIQUEELARMADO
NOESTÁNAESCA1A
3.* ESPECIFICACIONES OE MATERIALES:
buten*<•*)
tl«OTM6*>
a) CONCRETOCLASEICONU H Í ' c - 2 5 0 iyfcnfl.
b)ACEBOOE REFUERZOCON UN l'y «4200 l t f c / i £
vr#»
4 * RECUBRIMIENTO UBREOEUVAfflOA NOSERÁ
w®a
MENOR
OE 2.00 CM.. NIMENORQUE SU DIÁMETRO.
5.- NO SE TRASLAPARÁHISESOLDARAMASDEL5Q % DEL
REFUERZOEN UNASECCtóN.
6 - TODOELRERJERZOCORRIDOYLOS BASTONES
EXTREMOSSE ANCLARAl > LONGrTUODE «0CM. COMO
MÍNIMO.
7.- L03 DOBLECESDELAVARILLA SEHARÁNENFRÍO
\
SOBREUN PERNODE DIÁMETROMÍNIMOIGUALA8VECES
ELDEIAVARIÜA
u/ff*t*&?//s/,v//t, yM/t/ff/s/f/ft/'/
WW&'trf'ArwWWrw&Mw.**W/f?%?*efrM*r*'fr*'f'r*
II
L*r©2D —
'///t • / / ,Wfiw?//////M,
h
8 - IASEPARACÚN DE ESTRIBOS EN TRABES EMPEZARÁN
ACONrARAPARTIRD a PUNO DE APOYOCOLOCAHDOSE
a PRMEROALAMfTAOOE 1ASEPARACDN
ESPEOflCAQH
t>Mlonufe>40—
«40
«re» _
*r©ao
9 - LOS CASTILLOSSE ANCLARÁN EN LOSCIMIENTOSAL
MENOS40 CM
doentrepiso
armadodolo
ESPESOR DELOSA DE 12CM
10- a CONCRETOPARACASTUOS YWLAS SERÁ OE
f'C=1WI©t/TíL
ESPESOR DELOSA DE 12 CM.
corto dolosa
castillotipo
c
contratrabetipo
SIMBOLX>QIA
)
77//////////////////,
latón
¥•*«<**•
t
/
w
r
2OHA0EV0UÚO
i/4
3X
E
— 0 20
— 015—i
4Vwv r
i
INDICA MURODIVISORIO.
4V* V?
INDICA TRABEPRIMARIA.
INDICAUMTE DEVOLADO.
Ev i r o 15
E1/4*^ 20
oís
INDICAMURO0E CARGA.
030
INDICA CASTILLO.
fS
/
VBBCP**
IA
DISEÑO D E T R A B E D E ENTREPISO
¿
..
B(1-2)YB(2-3)
. i
DISEÑO D E T R A B E DE ENTREPISO
"* D(1-2)Y D(2-3)
^
DISEÑO D E T R A B E D Eá
B(1 -2) YB(2-3)
DISEÑO D E T R A B E D E ENTREPISO
r>
E(1~2)
• -•?
DISEÑO D E TRABE DE
D(1-2)Y D(2-3)
DISEÑO DET R A B E D E
E(1-2)
>
ÍWfiff
?w
virar
?v»vr
-(e)- »**J
?ww
DISEÑO D E T R A B E DE EISiTREPISO
.R
* 2(D-E)Y
•
jv»
IV»
-^-SL^
?*r
?w*fVI*
2V.W
*S
•
*u*«w
Esnr#vs
DISEÑO DETRABE _
2<D-E)Y2(E-F)
DISEÑO D E TRABE D E ENTREPISO
1
F(1-2)
DISEÑO DE TRABE
FÍ1-2)
tV.
J*r
V*W
b
ev*«o/
IV*
*
Mrt»#»,/
^
I
f«>r**
CLAVE
»
ESCUELA
r*LANO
INSTITUTOTECNOLÓGICODELACONSTRUCCIÓN
Proyectoestructural
ASESOR
ING.ALFONSO D'ABBWRTTPANTOJA
UBICACIÓN
Vicente Villada No.77. Col.Ahuizotla. Mun. Naucalpan de Juárez.
~
^
iv*-**/
iuryr
-<*>-
^
b.
\
W*9*_/
5Vw
v
Vv
ELABORO
VICTOR ENRIQUESEGURATORRES
v
TESIS PROFESIONAL
Conclusiones
A). Elobjetivo deun diseño estructural eseldedeterminar lascaracterísticas físicas dela estructura, quenos permita garantizar la
absorción decargas a lasque vaestar sujeta, sin sufrir daño alguno (Seguridad), y quecumpla con la función adecuada de una
estructura encondiciones deservicio (Funcional): Elcumplimiento delos dos aspectos anteriores, nos llevará a una obra económica
(Costo).
B). Laestructura al estar sometida a acciones estructurales como losonlascargas verticales (Cargas muertas y cargas vivas) y las
cargas horizontales (principalmente por sismo), presenta u n a respuesta de reacción, manifestada en agrietamientos, flechas,
vibraciones, hundimientos y desplazamientos horizontales; Porlo queel diseño de los elementos de la estructura deben ser
diseñados con elfindeevitar estas manifestaciones estructurales, esdecir norebasar sus estados delímite (Estado límite defallay
estado límite de servicio).
Dentro dela seguridad estructural esimportante señalare eluso delos factores decarga (F.C) dentro delos análisis estructurales,
están enfunción de lacombinación de lacombinación de cargas (Cargas muertas, cargas vivasycargas accidentales).
Estos factores decarga seaplican delasiguiente manera: Un valor de 1.4para lacombinación deacciones de cargas muertas más
cargas vivas en estructuras delgrupo "B"y,u n valor de 1.5 para estructuras delgrupo "A". Para combinaciones deaccionesque
incluyan cargas muertas, cargas vivasycargas accidentales, el valor del factor es de1.1.
C). Eneldiseño estructural deunacasa-habitación, es importante conocer lascaracterísticas mecánicas del material a emplear en la
construcción del mismo, yaque estas serán lasque soporten lascargas y proporcionen la resistencia yestabilidad necesaria. Cabe
hacer mención que laresistencia eslapropiedad más importante del material estructural, yaque eslaque define lafuerza que sera
capaz de soportar unelemento estructural antes de que falle (esfuerzo).
D). Las cargas unitarias, eselpeso por metro cuadrado deunelemento, elcuál seobtiene del efecto del peso volumétrico de un material
aplicado enu nvolumen. Las cargas unitarias secalculan con elfindeobtener la carga que será soportada por lacimentación.La
bajada de carga hacia lacimentación serealiza principalmente por muros de carga y por castillos.
E). Eldiseño dela cimentación, esta dada porla condiciones decarga y a lascaracterísticas delsuelo; Por loque elcalculista podrá
contar con lainformación necesaria que le permita proyectar lamejor alternativa, enlo quea tipos de cimentación se refiere.
202
TESIS PROFESIONAL
F). La revisión de muros es una de las etapas más importantes del proyecto, en virtud de que se analizan las fuerzas que actúan sobre
la estructura, tanto verticales como horizontales (Sismo). Así que los resultados del análisis que se realicen determinarán la
seguridad estructural que tiene la estructura para estas fuerzas ortogonales; Por lo que si los resultados son desfavorables será
necesario remplantear el proyecto.
G). La trabe como tal, es una viga que se encuentra apoyada sobre uno, dos ó mas apoyos, según el tipo de trabe, y que soporta una
carga. La trabe por lo tanto tiene una respuesta estructural, siendo estas un valor de fuerza cortante y otro de un momento
flexionante. Esta última será el que determine su diseño por flexión y la fuerza cortante la determine la fuerza a la que estará
sometida.
H). Las losas son elementos estructurales cuyas dimensiones en planta son relativamente grandes comparadas con su espesor. Una losa
no es más que una placa apoyada en un conjunto de trabes, muros o líneas resistentes subdividida en tableros. Los bordes de cada
tablero tendrán diversas condiciones de continuidad, dependiendo de si la losa se prolonga hacia el otro lado del apoyo o termina en
dicho borde. Si la relación geométrica entre el lado corto y el lado largo de cada tablero es mayor que 0.5, entonces el tablero
distribuye su carga en dos direcciones, apoyándose en todo el perímetro y el armado estará dispuesto tanto en lado corto como en el
lado largo, contribuyendo a la resistencia por flexión del sistema.
La solución (análisis) de cada tablero de los que conforman la losa es relativamente compleja, puesto que los desplazamientos en
cada punto son distintos, lo que conduce a un sistema altamente indeterminado. Existen, sin embargo, soluciones aproximadas que
están basadas en la teoría de la elasticidad y que consideran a los bordes de cada tablero con una rigidez infinita; de esta manera,
los tableros se suponen perimetralmente apoyados. Usualmente, estos métodos plantean el empleo de coeficientes que conducen a la
obtención de momentos flexionantes en franjas unitarias (de un metro de ancho) que se cruzan en el centro del tablero. Ejemplo de
estos métodos lo tenemos en el método del Reglamento de Construcciones para el D.F.
203
Bibliografía
Arnal Simón, L. y M. B e t a n c o u r t , Reglamento de
construcciones
para el Distrito Federal, 4 a . e d . ,
T r i l l a s , México, 2 0 0 2 .
A p u n t e s de c l a s e de E s t r u c t u r a s de c o n c r e t o del
Ing. Alfonso D ' a b b w r t t P a n t o j a .
A p u n t e s de c l a s e de M a n i p o s t e r í a y c i m b r a s del
Ing. Alfonso D ' a b b w r t t P a n t o j a .
Gallo Ortiz, G.y L. E s p i n o , Diseño estructural de
casas-habitación,
l a . e d . ,Me. Graw Hill, México,
1997.
Plazola C i s n e r o s , A.Arquitectura
habitacional
I, 5 a .ed., Plazola e d i t o r e s , México, 1992
Vol.
Plazola C i s n e r o s , A.Arquitectura
habitacional
II, 5 a .e d .Plazola e d i t o r e s , México, 1992
Vol.
Sociedad Mexicana de Mecánica de S u e l o s , El
subsuelo y la ingeniería de cimentaciones
en el
área urbana del Valle de México, l a . e d . ,SMMS,
México, 1978.
Memoria de c á l c u l o e s t r u c t u r a l de u n a c a s a h a b i t a c i ó n , u b i c a d a en la calle Golfo deS a n
Lorenzo No. 3 2 .Col. T a c u b a . Del. Miguel Hidalgo.
Ing. E r n e s t o Cabello.
Memoria de c á l c u l o e s t r u c t u r a l de u n a c a s a h a b i t a c i ó n , u b i c a d a en la M a n z a n a No. 10. Lote
26 5 / a . Sección. Condado de S a y a v e d r a . M u n .
Atizapán deZ a r a g o z a . Ing. Pedro Flores Palma.
Murguía Díaz, M. y D. M a t e o s , Detalles
arquitectura,
l a .ed., Árbol, México, 1997.
de
204
Glosario detérminos
DISEÑO: Al c o n j u n t o de a c t i v i d a d e s a d e s a r r o l l a r p a r a d e t e r m i n a r l a s c a r a c t e r í s t i c a s físicas de u n a
e s t r u c t u r a , de t a l m a n e r a q u en o s p e r m i t a g a r a n t i z a r la a b s o r c i ó n de l a s c a r g a s a l a s q u e é s t a va a e s t a r
s u j e t a en l a s d i f e r e n t e s e t a p a s de s u vida ú t i l , sin sufrir d a ñ o a l g u n o ; e s d e c i r , la función a d e c u a d a de u n a
e s t r u c t u r a en c o n d i c i o n e s de s e r v i c i o .
CALCULO: Ala d e t e r m i n a c i ó n de l o s medios m e c á n i c o s de d i s e ñ o , a p l i c a n d o los d i f e r e n t e s p r o c e d i m i e n t o s y
m é t o d o s de c á l c u l o p a r a la o b t e n c i ó n de l a s f u e r z a s i n t e r n a s , o e l e m e n t o s m e c á n i c o s , t a l e s como l a s fuerzas
a x i a l e s , los c o r t a n t e s , los m o m e n t o s f l e x i o n a n t e s y de t o r s i ó n a losq u ev a na e s t a r s o m e t i d o s los d i f e r e n t e s
c o m p o n e n t e s de la e s t r u c t u r a ( m u r o s , v i g a s , c o l u m n a s , e t c . ) .
CASA-HABITACIÓN: Ala m o r a d a o vivienda p r i n c i p a l del h o m b r e de d i f e r e n t e s t i p o s q u ese deriva de v a r i o s
f a c t o r e s p r i n c i p a l e s como son: s i t u a c i ó n geográfica, c l i m a , género de vida social y e c o n ó m i c o , m a t e r i a l e s de
c o n s t r u c c i ó n de q u ese d i s p o n e y h a b i l i d a d e s del h o m b r e , t a n t o m a n u a l e s como m e n t a l e s ; se p u e d e s u m a r a
e s t o s f a c t o r e s el a d e l a n t o a c t u a l en m a t e r i a t é c n i c a .
205