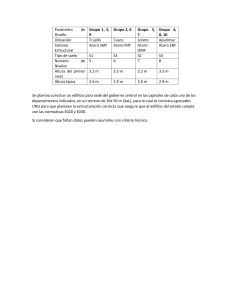
Asignación 1-20% Instrucciones: La asignación en grupos máximo de 3 personas. Grupos que tengan las asignaciones idénticas serán penalizados. En los ejercicios en donde aparece una letra X, deben remplazarlo por los 2 primeros números de su cédula de identidad (uno de los integrantes del grupo). Debe ser los más claro posible, recuerde que es una evaluación y debe justificar bien sus procedimientos. Las gráficas deben ser de elaboración propia a mano, señalando cada detalle dado en clases. No hay consultas en cuanto a los procedimientos, con lo dado en clase y lo que cada quien estudió se puede resolver la asignación. Cada ítem tiene un valor de 5% para sumar un total de 20%. Fecha de entrega Lunes 30-09-24 hasta media noche. 1. Formule y resuelva usando el método grafico cada uno de las siguientes situaciones: a) Una empresa constructora desea construir dos tipos de casas los modelos A y B. El precio de mercado de las casas tipo A es de X millones y el precio de las casas tipo B de 8 millones. El costo de construcción de las casas tipo A es de 9 millones y los costos de construcción de las casas tipo B es de 7 millones. Actualmente, se dispone de un presupuesto de 700 millones de pesos anuales. Se ha determinado que por un tema desarrollo urbanístico, la cantidad de casas tipo A no puede superar el 30% del total de casas y las casas tipo B no pueden superar un total del 80% del total de casas. b) Una tienda desea liquidar 240 botas y 120 zapatos de un modelo pasado de moda. Ofrecen 2 ofertas: 1 y 2. La oferta 1 consta de un conjunto de una bota y un zapato, que se vende a X dólares. La oferta 2 consta de un conjunto de 3 botas y 1 zapato y se vende a 45 dólares. No se desea ofrecer menos de 20 conjuntos de la oferta 1, ni menos de 10 conjuntos de la oferta 2. ¿Cuántos conjuntos de cada tipo se deben vender para maximizar el beneficio de la empresa? c) Una empresa produce tornillos y ramplug, para lo cual requiere de acero y plástico. Las necesidades de acero son siempre menores o iguales que la necesidad de plástico más tres unidades. Por otra parte, el triple de la necesidad de plástico sumado con cuatro veces la necesidad de acero se mantiene siempre menor o igual a X unidades. Hallar el número de unidades de cada materia prima que se deben adquirir para alcanzar un beneficio máximo, sabiendo que, por cada unidad de acero procesada, la cual se compra en 200$, se obtiene un ingreso de $700 y por cada unidad de plástico procesada, la cual se compra en 100$, se obtiene un ingreso de $300. 2. Hasta ahora hemos visto en clase problemas en donde las variables de decisión son no negativas, sin embargo, existen problemas que no cumplen esta condición. Investigue sobre un modelo de programación lineal en donde las variables de decisión puedan tomar cualquier valor real, de un ejemplo de la vida real y formúlelo como un problema de programación lineal. Sugerencia: consulte los libros textos sugeridos pero el ejemplo que va a mostrar no debe ser el mismo dado en el libro, construya uno o realice uno de los propuestos.