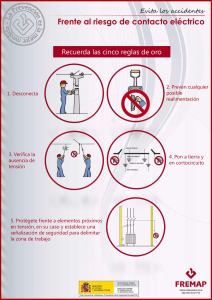
Analisis-de-Cortocircuito-ETAP-11

ETAP®11.0
Análisis de Cortocircuito
en Sistemas Eléctricos de Potencia
Curso de Capacitacion
ETAP
Cortocircuito
1
Diego Moitre, M. Sc.
Ingeniero Mecánico Electricista
Matricula Profesional Nº 10.333 - CIEC
Senior Member, PES – IEEE
RAIEN ARGENTINA S.A. Congreso 2171 – 6º Piso
Código Postal: C1428 BVE
Ciudad Autónoma de Buenos Aires, ARGENTINA
Fijo: (54) 11 4701-9316
Móvil: (54) 358-156000104
[email protected]
[email protected]
Curso de Capacitacion
ETAP
Cortocircuito
2
Análisis de Cortocircuito en Sistemas
Eléctricos de Potencia
Introducción al Análisis de CC.
Nivel de Falla (Potencia de CC).
Métodos Computacionales de análisis de CC equilibrados.
Matriz de Impedancias de Barras Zbarras.
Redes de Secuencia.
Métodos Computacionales de análisis de CC desequilibrados
Técnicas para análisis de CC.
Análisis de Cortocircuito según ANSI/IEEE.
Análisis de Cortocircuito según IEC.
Editor de Estudio de CC ETAP®11
Ejemplos de aplicación utilizando ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
3
Bibliografía
N. Tleis Power Systems Modelling and Fault Analysis:Theory and Practice. Newnes,
Elsevier. 2.008.
P. M. Anderson Analysis of Faulted Power Systems. The Iowa State University Press.
1973.
J. C. Das. Power Systems Analysis: Short-Circuit, Load Flow and Harmonics. CRC
Press, 2002.
J. Arrillaga & C.P. Arnold Computer Analysis of Power Systems. Wiley, 1990.
G. L. Kusic. Computer-Aided Power Systems Analysis. Second Edition. CRC Press,
2008.
A. R. Bergen & V. Vittal Power Systems Analysis. Second Edition. Prentice -Hall, 2000.
O. I. Elgerd. Electric Energy Systems Theory. Second Edition. McGraw-Hill, 1983.
 J. J. Grainger & W. D. Stevenson Power Systems Analysis. McGraw-Hill, 1994.
Curso de Capacitacion
ETAP
Cortocircuito
4
Bibliografía
IEEE Violet Book (IEEE Std 551TM – 2006: Recommended Practice for Calculating
Short-Circuit Currents in Industrial and Commercial Power Systems)
IEEE Brown Book (IEEE Std 399TM – 1997: Recommended Practice for Industrial and
Commercial Power Systems Analysis )
IEEE Red Book (IEEE Std 141TM – 1993: Recommended Practice for Electric Power
Distribution for Industrial Plants)
IEEE C37.5-1979 Guide for Calculation of Fault Currents for Application of AC High Voltage Circuit Breakers Rated on a Total Current Basis.
IEEE C37.04 – 1979 (1988) : Standard Rating Structure for AC High-Voltage Circuit
Breakers Rated on a Symmetrical Current Basis and Supplements.
IEEE C37.04f – 1990: Standard Rating Structure for AC High-Voltage Circuit Breakers
Rated on a Symmetrical Current Basis and Supplements.
IEEE C37.04g – 1986: Standard Rating Structure for AC High-Voltage Circuit Breakers
Rated on a Symmetrical Current Basis and Supplements.
Curso de Capacitacion
ETAP
Cortocircuito
5
Bibliografía
IEEE C37.04h– 1990 : Standard Rating Structure for AC High-Voltage Circuit Breakers
Rated on a Symmetrical Current Basis and Supplements.
IEEE C37.04i – 1991: Standard Rating Structure for AC High-Voltage Circuit Breakers
Rated on a Symmetrical Current Basis and Supplements.
IEEE C37.04 – 1999 : Standard Rating Structure for AC High-Voltage Circuit Breakers
Rated on a Symmetrical Current Basis and Supplements.
IEEE C37.010 – 1979 (1988) : IEEE Application Guide for AC High-Voltage Circuit
Breakers Rated on a Symmetrical Basis and Supplements.
IEEE C37.010b – 1985 : IEEE Application Guide for AC High-Voltage Circuit Breakers
Rated on a Symmetrical Basis and Supplements.
IEEE C37.010e – 1985 : IEEE Application Guide for AC High-Voltage Circuit Breakers
Rated on a Symmetrical Basis and Supplements.
IEEE C37.010 – 1999: IEEE Application Guide for AC High-Voltage Circuit Breakers
Rated on a Symmetrical Basis and Supplements.
Curso de Capacitacion
ETAP
Cortocircuito
6
Bibliografía
IEEE C37.13 – 1990: Standard for Low-Voltage AC Power Circuit Breakers Used in
Enclosures.
IEEE C37.013 – 1997: Standard for AC High-Voltage Generator Circuit Breakers Rated
on a Symmetrical Current Basis.
IEEE C37.20.1 – 2002: Standard for Metal Enclosed Low-Voltage Power Circuit Breakers
Switchgear.
IEC 60909- 0 Ed. 1.0 2001-0. Short-circuit currents in three-phase a.c systems – Part 0:
Calculation of Currents .
IEC 60909- 1 Ed. 2.0 2002-0. Short-circuit currents in three-phase a.c systems – Part 1:
Factors for the calculation of short-circuit currents according to IEC 60909-0.
IEC 60909- 2 Ed. 2.0 2008-11. Short-circuit currents in three-phase a.c systems – Part 2:
Data of Electrical Equipment for short-circuit currents calculations.
IEC 60909- 3 Ed. 3.0 2009-03. Short-circuit currents in three-phase a.c systems – Part 3:
Currents during two separate simultaneous line-to-earth short-circuits and partial shortcircuit currents flowing through earth.
Curso de Capacitacion
ETAP
Cortocircuito
7
Bibliografía
IEC 60909- 4 Ed. 1.0 2000-07. Short-circuit currents in three-phase a.c systems – Part 4:
Examples for the calculation of short-circuit currents.
IEC 61363- 1 Ed. 1.0 1998-02. Electrical installations of ships and mobile and fixed
offshore units – Part 1: Procedures for calculating short-circuit currents in three-phase a.c.
IEC 60947- 1 Ed. 5.0 2007-06. Low-voltage switchgear and controlgear – Part 1: General
Rules.
IEC 60947- 2 Ed. 4.1Consol. With am1 2009-05. Low-voltage switchgear and controlgear
– Part 2: Circuit-Breakers.
IEC 60282- 1 Ed. 7.0 2009-10. High-voltage Fuses – Part 1: Current-limiting Fuses.
IEC 60282- 2 Ed. 3.0 2008-04. High-voltage Fuses – Part 1: Expulsion Fuses
IEC 62271-SER Ed. 1.0 2010-06. High-voltage switchgear and controlgear. ALL PARTS
C. Hartman Understanding Asymmetry. IEEE Trans. On Industry Applications, Vol. IA21, No.4, July/August 1985, pp. 842–848.
Curso de Capacitacion
ETAP
Cortocircuito
8
Bibliografía
A. Berizzi, S. Massucco, A. Silvestri, D. Zaninelli Short-Circuit Current Calculation: A
Comparison between Methods of IEC and ANSI Standards using dynamic simulation as
reference. IEEE Trans. On Industry Applications, Vol. 30, No.4, July/August 1994, pp.
1099–1106.
B. Bridger All Amperes Are Not Created Equal: A Comparison of Current Ratings of HighVoltage Circuit Breakers Rated According to ANSI and IEC Standards. IEEE Trans. On
Industry Applications, Vol. 29, No.1, January-February 1993, pp. 195–201.
J. Dunki-Jacobs, B. Lam, R. Stratford A Comparison of ANSI-Based and Dynamically
Rigorous Short-Circuit Current Calculation Procedures. IEEE Trans. On Industry
Applications, Vol. 24, No.6, November/December 1988, pp. 1180–1194.
G. Knight, H. Sieling Comparison of ANSI and IEC 909 Short-Circuit Current Calculation
Procedures. IEEE Trans. On Industry Applications, Vol. 29, No.3, May/June 1993, pp.
625–630.
A. Rodolakis A Comparison of North American (ANSI) and European (IEC) Fault
Calculation Guidelines. IEEE Trans. On Industry Applications, Vol. 29, No.3, May/June
1993, pp. 515–521.
Curso de Capacitacion
ETAP
Cortocircuito
9
Bibliografía
O. Roennspiess, A. Efthymiadis A Comparison of Static and Dynamic Short-Circuit
Analysis Procedures. IEEE Trans. On Industry Applications, Vol. 26, No.3, May/June
1990, pp. 463–475.
ETAP® 11 User Guide
Curso de Capacitacion
ETAP
Cortocircuito
10
Análisis de Sistemas Eléctricos de
Potencia
 Marco temporal para los fenómenos dinámicos básicos en SEP
Curso de Capacitacion
ETAP
Cortocircuito
11
Análisis de Sistemas Eléctricos de
Potencia
Régimen permanente
Régimen dinámico
Red en condiciones
Red en condiciones
Red en condiciones
Red en condiciones
de operación normal
de operación bajo falla
de operación normal
de operación bajo falla
Equilibrada
Equilibrada
Desquilibrada
Desquilibrada
Equilibrada
Desquilibrada
Equilibrada Desquilibrada
1.
Sistema lineal o no lineal
1.
Sistema lineal o no lineal
2.
Parámetros concentrados
2.
Parámetros concentrados o distribuidos
3.
“Foto” de un instante en el tiempo
3.
Solución en el dominio del tiempo
Sistema de ecuaciones algebraicas
Curso de Capacitacion
ETAP
Sistema de ecuaciones diferenciales
Cortocircuito
12
Introducción al Análisis de Cortocircuito
 Cortocircuito: dos o mas puntos de una red eléctrica que en
condiciones normales de operación se encuentran a distinto
potencial, se ponen accidentalmente en contacto a través de una
impedancia (Zf ≠ 0 o bien Zf = 0).
 Causas:
 Falla de aislamiento por envejecimiento, calentamiento,
contaminación, etc.
 Sobretensiones externas e internas.
 Fallas mecánicas: roturas, deformaciones, desplazamientos, etc.
 Efectos:
 Calentamiento de conductores por efecto Joule.
 Esfuerzos electrodinámicos sobre el equipamiento.
 Variación de la tensión en las distintas fases.
Curso de Capacitacion
ETAP
Cortocircuito
13
Introducción al Análisis de Cortocircuito
 Objetivos del análisis:
 En instalaciones industriales de media y baja tensión: cálculo de la máxima
corriente de cortocircuito para determinar la capacidad de ruptura de
interruptores y los limites térmicos y dinámicos del equipamiento y
conductores de la instalación.
 En redes de alta y media tensión: cálculo de las intensidades de
cortocircuito en cualquier punto de la red y ante cualquier tipo de
cortocircuito para determinar las exigencias de servicio del equipamiento y
el ajuste de las protecciones.
 Clasificación de los CC:
 Equilibrados: las tres fases están involucradas al mismo tiempo y en el
mismo lugar.
 Desequilibrados: no todas las fases están involucradas por igual.
Curso de Capacitacion
ETAP
Cortocircuito
14
Introducción al Análisis de Cortocircuito
 Regímenes de los CC:
 Transitorio: el CC es un proceso electromagnético donde la red en una
situación estacionaria sufre una modificación brusca de su topología. La red
debería modelarse vía EDO.
 Estacionario: Este modelado no es práctico cuando se trata con redes de
cientos de barras y líneas; por ello las normas existentes especifican
aproximaciones al modelado estacionario de la red para el cálculo de CC.
Curso de Capacitacion
ETAP
Cortocircuito
15
Introducción al Análisis de Cortocircuito
R+jωL
e(t)
~
Zc
e( t )  2 E sen t    i( t )  2
i(t)
E

R  R c   L  X c 

2
2
sen t     0 
I0
L  X c
tg 0  
R  Rc
Curso de Capacitacion
ETAP
Cortocircuito
16
Introducción al Análisis de Cortocircuito
R+jωL
e(t)
i(t)
~
di( t )

e( t )  R i( t )  L
dt

i(0)  2 I sen    
0
0

Curso de Capacitacion
ETAP
Cortocircuito
17
Introducción al Análisis de Cortocircuito


 t
i( t )  i(0)  2 I CC sen    exp     2 I CC sen t    







permanente
transitorio
I CC 
tg() 
E
R 2  L 
2
L
R
L
R
t  5  exp( 5)  0,0067  transitorio  0

Curso de Capacitacion
ETAP
Cortocircuito
18
Introducción al Análisis de Cortocircuito
Régimen permanente
Curso de Capacitacion
ETAP
Cortocircuito
19
Introducción al Análisis de Cortocircuito
Régimen transitorio
Curso de Capacitacion
ETAP
Cortocircuito
20
Introducción al Análisis de Cortocircuito


 t
i( t )  i(0)  2 I CC sen    exp     2 I CC sen t    







permanente
Curso de Capacitacion
ETAP
transitorio
Cortocircuito
21
Introducción al Análisis de Cortocircuito
R  jL  Z C  I 0 
E
R  R C   L  X C 
2
2
 I CC 
E
R 2  L 
2
Corriente de prefalla despreciable
frente a la de falla
 t
i( t )   2 I CC sen    exp     2 I CC sen t    








alterna
continua
Curso de Capacitacion
ETAP
Cortocircuito
22
Introducción al Análisis de Cortocircuito

R  0;      ; t  2k  1 k  0,1,2,...  i Max ( t )  i(0)  2 2 I CC
2
si L  R  tg     

 0
2
Para θ=0 la envolvente de las intensidades máximas será:
i
Env
Max

 t
 t 
( t )  i(0) exp     2 I CC sen  1  exp   
 
  


 t 


i Env
(
t
)

2
I
sen

1

exp
  
Max
CC

  

Curso de Capacitacion
ETAP
Cortocircuito
23
Introducción al Análisis de Cortocircuito
i
Curso de Capacitacion
ETAP
Env
Max
Cortocircuito
(t )
24
Introducción al Análisis de Cortocircuito
Su valor eficaz será:
I
Env
Max
( t )  I CC sen 

 t 
1  exp    



De este modo se evalúa la intensidad de corriente
transitoria máxima producida por un cortocircuito a partir
de la intensidad de corriente de cortocircuito en régimen
permanente.
Curso de Capacitacion
ETAP
Cortocircuito
25
Introducción al Análisis de Cortocircuito
Para una red eléctrica general esta expresión adopta la forma:
I
Env
Max
( t )  I CC sen  eq 

 R eq 
t 
1  exp  

X

eq


Donde Req , Xeq y φeq son la resistencia, la reactancia y la fase
equivalentes vistas desde la falla, que se obtienen a partir de la matriz de
impedancias de barras (impedancia de Thevenin vista desde la falla)
Curso de Capacitacion
ETAP
Cortocircuito
26
Introducción al Análisis de Cortocircuito
La intensidad de corriente de pico (de cresta o de choque) es el mayor
valor de la intensidad de corriente máxima en el tiempo:
Ipico
i
Env
Max
(t )
t*
i(t)
Curso de Capacitacion
ETAP
Cortocircuito
27
Introducción al Análisis de Cortocircuito
La intensidad de corriente de pico se obtiene en el tiempo t* cuando:
 
   t   
*
I pico  i t *  i Env
t
Max
*
1
1
s  10 ms 1 2 ciclo 
t 

2 f 100
*
I pico  2 I CC sen 
Curso de Capacitacion
ETAP
Cortocircuito

 R 
1  exp   X  



28
Introducción al Análisis de Cortocircuito
Curso de Capacitacion
ETAP
Cortocircuito
29
Introducción al Análisis de Cortocircuito
Curso de Capacitacion
ETAP
Cortocircuito
30
Introducción al Análisis de Cortocircuito
Curso de Capacitacion
ETAP
Cortocircuito
31
Introducción al Análisis de Cortocircuito
Interruptor en SF6
Curso de Capacitacion
ETAP
Cortocircuito
32
Introducción al Análisis de Cortocircuito
Tiempos de operacion de un Interruptor
Curso de Capacitacion
ETAP
Cortocircuito
33
Comportamiento de la máquina síncrona frente
a un CC equilibrado
Esquema Maquina Síncrona
Curso de Capacitacion
ETAP
Cortocircuito
34
Comportamiento de la máquina síncrona frente
a un CC equilibrado
 Generador Síncrono en vacío
Corriente simétrica en una fase de CC trifásico a
bornes de un GS en vacío
Curso de Capacitacion
ETAP
Envolvente de la corriente simétrica en una fase
de CC trifásico a bornes de un GS en vacío
Cortocircuito
35
Comportamiento de la máquina síncrona frente
a un CC equilibrado
 Generador Síncrono en vacío
Diferencias de corriente simétrica en una fase de CC
trifásico a bornes de un GS en vacío
Corrientes de CC trifásico a bornes de un GS
en vacío
Curso de Capacitacion
ETAP
Cortocircuito
36
Comportamiento de la máquina síncrona frente
a un CC equilibrado
 Generador Síncrono en vacío
Corriente en una fase de CC trifásico a bornes de un GS en vacío (componente transitoria eliminada)
Curso de Capacitacion
ETAP
Cortocircuito
37
Comportamiento de la máquina síncrona frente
a un CC equilibrado
0a :
2 I CC
donde ICC es la corriente de cortocircuito de régimen
permanente
I CC 
Eg
Xd
donde:
Eg : valor eficaz de la tensión fase-neutro en vacío
Xd : reactancia síncrona de eje directo
Curso de Capacitacion
ETAP
Cortocircuito
38
Comportamiento de la máquina síncrona frente
a un CC equilibrado
0b :
2I
'
CC
donde I’CC es la corriente de cortocircuito transitoria
I
'
CC

Eg
X 'd
donde:
Eg : valor eficaz de la tensión fase-neutro en vacío
X’d : reactancia transitoria de eje directo
Curso de Capacitacion
ETAP
Cortocircuito
39
Comportamiento de la máquina síncrona frente
a un CC equilibrado
0c :
2I
''
CC
donde I’’CC es la corriente de cortocircuito subtransitoria
I
''
CC

Eg
X
''
d
donde:
Eg : valor eficaz de la tensión fase-neutro en vacío
X’’d : reactancia subtransitoria de eje directo
Curso de Capacitacion
ETAP
Cortocircuito
40
Comportamiento de la máquina síncrona frente
a un CC equilibrado
i a (t) 
2 Eg
Xd
cos t   0  
 1
1 
 t 


2 Eg  ' 
exp  
'  cos t   0  

Td 

 Xd Xd 
 1
1 


t
2 E g  ''  '  exp  
''  cos t   0 
Td 

 Xd Xd 
Curso de Capacitacion
ETAP
Cortocircuito
41
Comportamiento de la máquina síncrona frente
a un CC equilibrado
Ejemplo: Dos GS están conectados en paralelo al lado de baja tensión de un
transformador trifásico de dos devanados.
50 MVA 13,8 kV X 'd'  25 %
G1
~
G2
~
75 MVA 13,8 / 69 kV X 'd'  10%
25 MVA 13,8 kV X 'd'  25 %
Antes de la falla, la tensión en el lado de alta del trafo es de 66 kV. El trafo
no tiene carga y no circula corriente entre los generadores.
Curso de Capacitacion
ETAP
Cortocircuito
42
Comportamiento de la máquina síncrona frente
a un CC equilibrado
Consideramos los valores de bases siguientes:
AT
Vbase
 69 kV
BT
Vbase
 13,8 kV

S3base
 75 M VA
En valores pu resulta para el Generador 1:
75.000
X G1  0,25 
 0,375
50.000
''
d
E g1 
Curso de Capacitacion
ETAP
66
 0,9565
69
Cortocircuito
43
Comportamiento de la máquina síncrona frente
a un CC equilibrado
En valores pu resulta para el Generador 2:
X 'd' G 2  0,25 
E g2 
75.000
 0,750
25.000
66
 0,9565
69
En valores pu resulta para el trafo: XTR = 0,10.
Curso de Capacitacion
ETAP
Cortocircuito
44
Comportamiento de la máquina síncrona frente
a un CC equilibrado
Diagrama de reactancias antes de la falla
La reactancia subtransitoria en paralelo es:
X 'd' // 
Curso de Capacitacion
ETAP
0,375  0,75
 0,25
0,375  0,75
Cortocircuito
45
Comportamiento de la máquina síncrona frente
a un CC equilibrado
La corriente de cortocircuito subtransitoria del lado de alta tensión del trafo
será:
I TR 
''
CC
Eg
X 'd' //

0,9565
  j 2,7329
j 0,25  j 0,10
y en los generadores:
X 'd' G 2
j 0,75
''
I G1  ''

I
TR

 j 2,7329   j 1,819
CC
''
j 0,375  j 0,75
X d G1  X d G 2
''
CC
X 'd' G1
j 0,375
''
I G 2  ''

I
TR

 j 2,7329   j 0,911
CC
''
j 0,375  j 0,75
X d G1  X d G 2
''
CC
Curso de Capacitacion
ETAP
Cortocircuito
46
Comportamiento de la máquina síncrona frente
a un CC equilibrado
La intensidad de corriente de cortocircuito subtransitoria de los generadores,
expresada en [A]:
I G1  1,819 
''
CC
'
I 'CC
G 2  0,911 
75.000
3 13,8
75.000
3 13,8
 5.707,6 A 
 2.858,5 A 
☺
Aunque las reactancias no son constantes de las máquinas síncronas, ya que
dependen del grado de saturación del circuito magnético, sus valores están
normalmente dentro de ciertos limites para cada tipo de máquina.
Curso de Capacitacion
ETAP
Cortocircuito
47
Comportamiento de la máquina síncrona frente
a un CC equilibrado
 Generador Síncrono en carga
Circuitos de un GS abasteciendo una carga trifásica equilibrada
Curso de Capacitacion
ETAP
Cortocircuito
48
Comportamiento de la máquina síncrona frente
a un CC equilibrado
Impedancia de Thevenin
Z Th

Z  j X  Z

''
d
''
d
ext
L
Z ext  j X  Z L
Corriente de cortocircuito subtransitoria en la falla
I
Curso de Capacitacion
ETAP
''
CC

Vf  Z ext  j X  Z L
Vf


Z Th
Z ext  j X 'd'  Z L

Cortocircuito

''
d

49
Comportamiento de la máquina síncrona frente
a un CC equilibrado
'
I 'CC

Vf
Z Th
Z
E V
''
f
E ''
y
'
I 'CC

''
ext  j X d
  V Z
Z Th

f
E ''  I L  Z ext  j X 'd'  Z L

Z ext  j X 'd'
''
ext  j X d  Z L
ZL
 
  E  IZ  I  j X  I
Z


''
L
ext
Vt
Curso de Capacitacion
ETAP
Cortocircuito
L
''
d
L
L
Vf  0
50
Comportamiento de la máquina síncrona frente
a un CC equilibrado
Tensión (interna) detrás de la reactancia subtransitoria de un GS
E  Vt  I L  j X
''
g
''
d
Tensión (interna) detrás de la reactancia transitoria de un GS
E  Vt  I L  j X
'
g
'
d
Tensión (interna) detrás de la reactancia síncrona de un GS
E g  Vt  I L  j X d
Curso de Capacitacion
ETAP
Cortocircuito
51
Comportamiento de la máquina síncrona frente
a un CC equilibrado
 Motor Síncrono
Tensión (interna) detrás de la reactancia subtransitoria de un MS
E  Vt  I L  j X
''
m
''
d
Tensión (interna) detrás de la reactancia transitoria de un MS
E  Vt  I L  j X
'
m
'
d
Tensión (interna) detrás de la reactancia síncrona de un MS
E m  Vt  I L  j X d
Curso de Capacitacion
ETAP
Cortocircuito
52
Comportamiento de la máquina síncrona frente
a un CC equilibrado
Ejemplo: Un GS abastece a un MS a través de una línea.
30 MVA 13,2 kV X 'd'  20 %
GS
~
30 MVA 13,2 kV X 'd'  20 %
X  10%
~
MS
La reactancia de la línea esta expresada sobre la base de las máquinas. El
motor esta consumiendo 20 MW con un factor de potencia de 0,8 en atraso
(positivo), y una tensión en bornes de 12,8 kV al producirse una falla trifásica
en sus terminales.
Curso de Capacitacion
ETAP
Cortocircuito
53
Comportamiento de la máquina síncrona frente
a un CC equilibrado
Consideramos los valores de bases siguientes:
Vbase  13,2 kV

S3base
 30 MVA
Circuitos equivalentes
Curso de Capacitacion
ETAP
Cortocircuito
54
Comportamiento de la máquina síncrona frente
a un CC equilibrado
12,8
Vf 
 0,9697 0 pu
13,2
30.000 kVA
I base 
 1.312 A 
3  13,2 kV
20.000 kW
IL 
 1.127,6 36,87 A ; pues cos 1 (0,8)  36,87
0,8  3  12,8 kV
1.127,6 36,87 A 
IL 
 0,8594 36,87 pu
1.312 A 
Curso de Capacitacion
ETAP
Cortocircuito
55
Comportamiento de la máquina síncrona frente
a un CC equilibrado
Para el generador:
pu 
 0,9181  j 0,0687 pu  0,92074,28 pu
E 'g'  0,92074,28 pu  0,8594 36,87  j 0,20 pu  0,8407 14,20 pu
Vt  0,9697 0  0,8594 36,87  j 0,10
I 'g' 
0,8407 14,20
pu  2,8023   75,8 pu
j 0,20  j 0,10
I 'g'  2,8023   75,8 pu 1.312 A   3.676,62   75,8 A 
Curso de Capacitacion
ETAP
Cortocircuito
56
Comportamiento de la máquina síncrona frente
a un CC equilibrado
Para el motor:
Vt  Vf  0,9697 0
pu
E 'm'  0,96970 pu  0,8594 36,87  j 0,20 pu  1,0816   7,30 pu
I 'm' 
1,0816   7,30
pu  5,408   97,30 pu
j 0,20
I 'm'  5,408   97,30 pu 1.312 A   7.095,3   97,30 A 
Curso de Capacitacion
ETAP
Cortocircuito
57
Comportamiento de la máquina síncrona frente
a un CC equilibrado
En la falla:
I 'f'  I 'm'  I 'g'  5,408   97,30  2,8023  75,80
pu
pu
I 'f'  8,081   90 pu 1.312 A  10.602,1   90 A 
I 'f'  8,081   90
Contribución del Generador en MVA:
S3g  Vt I 'g'  0,92074,28  2,8023 75,8 pu  2,58 80,08 pu
*
S3g  2,58 80,08 pu 30 [MVA]  77,4 80,08 [MVA]
Curso de Capacitacion
ETAP
Cortocircuito
58
Comportamiento de la máquina síncrona frente
a un CC equilibrado
Contribución del Motor en MVA:
S
3
m
'' *
t m
VI
 0,96970  5,408 97,3 pu  5,2441 97,3 pu
S3m  5,2441 97,3 pu 30 [MVA]  157,32 97,3 [MVA]
Falla total en MVA:
S3f  Vf I 'f'  0,96970  8,081 90 pu  7,8361 90 pu
*
S3f  7,8361 90 pu 30 [MVA]  235,1 90 [MVA]
☺
Curso de Capacitacion
ETAP
Cortocircuito
59
Comportamiento de la máquina síncrona frente
a un CC equilibrado
Ejemplo: resolver el ejemplo anterior utilizando el Teorema de Thevenin
j 0,30  j 0,20
 j 0,12
j 0,30  j 0,20
Vf  0,96970 pu
Z Th 
I 'f' 
Vf
0,96970

 8,081   90
Z Th
j 0,12
pu
☺
Esta corriente es la que sale del circuito en la falla al reducirse a cero la
tensión en el punto. Si esta corriente originada por la falla se divide entre los
circuitos paralelos de las máquinas síncronas inversamente a sus
impedancias, los valores resultantes son las corrientes de cada máquina,
debidas exclusivamente al cambio de la tensión en el punto de falla.
Curso de Capacitacion
ETAP
Cortocircuito
60
Comportamiento de la máquina síncrona frente
a un CC equilibrado
j 0,20
 8,081   90 pu  3,2324   90 pu
j 0,50
j 0,30
''
Im 
 8,081   90 pu  4,8486   90 pu
j 0,50
I 'g'  
A las corrientes de falla de cada máquina se deben sumar las corrientes de
prefalla correspondientes para obtener las corrientes de falla totales.
I 'g'  I L  I 'g' 
I 'g'  0,859436,87  3,2324   90
I 'm'  I L  I 'm' 
I 'm'  0,859436,87  4,8486   90
Curso de Capacitacion
ETAP
Cortocircuito
pu  2,8024  75,8 pu
pu  5,4081  97,3 pu
61
Comportamiento de la máquina síncrona frente
a un CC equilibrado
Teorema de Superposición
Curso de Capacitacion
ETAP
Cortocircuito
62
Comportamiento de la máquina síncrona frente
a un CC equilibrado
Teorema de Superposición
1) Cortocircuitando E’’g, E’’m, Vf , con -Vf en el circuito, se obtienen las
corrientes de falla en las máquinas debidas al cambio de la tensión en el
punto de falla.
2) Cortocircuitando -Vf , con E’’g, E’’m, Vf en el circuito, se obtienen las
corrientes de prefalla en las máquinas.
3) Sumando los dos valores de corriente se obtienen las corrientes de falla
totales en cada una de las máquinas.
Curso de Capacitacion
ETAP
Cortocircuito
63
Nivel de Falla (Potencia de CC )
1
2
Icc
Icc
al resto del sistema
al resto del sistema
3
La potencia de CC (Short-Circuit Capacity) de una barra se define por:
SCC 3  Vprefalla  I falla pu
SCC 3  3  Vprefalla  I falla [MVA]
Curso de Capacitacion
ETAP
Cortocircuito
64
Nivel de Falla (Potencia de CC )
Si consideramos como tensión de prefalla su valor nominal, resulta:
SCC
3
 I falla pu
Si aplicamos el Teorema de Thevenin a la barra 3:
V30
I falla  f
Z  Z Th
V30
I falla 
Z Th
Curso de Capacitacion
ETAP
si Z f  0
si Z f  0 (CC rigido a tierra )
Cortocircuito
65
Nivel de Falla (Potencia de CC )
Si consideramos como tensión de prefalla su valor nominal, resulta:
Z Th 
E=V0
1
SCC
1/SCC3Φ
Sistema
visto desde
la falla
~
Curso de Capacitacion
ETAP
3
Cortocircuito
66
Nivel de Falla (Potencia de CC )
o Para todo propósito práctico, la ZTh es reactiva.
o Para todo propósito práctico, los MVA de CC en el caso de un CC rígido a
tierra es potencia reactiva (inductiva).
o Debido a las variaciones que experimenta la corriente de CC aportada por
las maquinas síncronas, la ZTh no es constante; asume un valor mínimo
inmediatamente después del CC y luego eventualmente aumenta.
o La “firmeza” de una barra es directamente proporcional a su SCC3Φ; esto
es, cuando su SCC3Φ aumenta, la impedancia interna del sistema vista
desde la barra ZTh disminuye. La habilidad de la barra para mantener su
tensión cuando se produce un CC en otras barras en consecuencia
aumenta. Obsérvese, sin embargo, que si el CC ocurre en la barra, un
SCC3Φ elevado implica elevadas corrientes de CC (en la barra). Esto
somete a esfuerzos a los interruptores; esto explica la razón de insertar
reactores en la barra para disminuir artificialmente su SCC3Φ.
Curso de Capacitacion
ETAP
Cortocircuito
67
Nivel de Falla (Potencia de CC )
o Obsérvese que los MVA de CC a los que es sometido un interruptor, esto
es el SCC3Φ de la barra correspondiente, es una mejor medida de la
solicitación del interruptor, más que la corriente de CC que debe interrumpir.
o En ocasiones, a los fines de simplificar el análisis, se supone que una
barra es “infinitamente firme”. Esto significa que suponemos que la barra
tiene un SCC3Φ arbitrariamente elevado. Puesto que esto implicaría una
impedancia interna del sistema ZTh nula, concluimos que una tal barra
mantendrá constante su tensión, excepto para un CC sobre si misma.
o Finalmente, en grandes sistemas de potencia, los SCC3Φ pueden alcanzar
valores del orden de los 50.000 MVA; a 500 kV corresponde a corrientes de
CC del orden de los 60 kA.
Curso de Capacitacion
ETAP
Cortocircuito
68
Ejemplo de Análisis de CC
Ejemplo:
T1
G1
G2
~
~
Δ
Y
Δ
Y
T2
1
2
L1
L2
L3
3
Curso de Capacitacion
ETAP
Cortocircuito
69
Ejemplo de Análisis de CC
Un CC trifásico rígido a tierra se desarrolla en la barra 3. Para determinar
la solicitación de los interruptores y fijar los tiempos de actuación de los
relevadores, se requieren los datos siguientes:
1. Corriente de falla en barra 3, calculadas de tres a cuatro ciclos
posteriores al CC trifásico.
2. SCC3Φ de la barra 3.
3. Corrientes de falla en la red.
4. Tensiones en barras 1 y 2, calculadas de tres a cuatro ciclos posteriores
al CC trifásico.
Curso de Capacitacion
ETAP
Cortocircuito
70
Ejemplo de Análisis de CC

METODOLOGIA DE ANALISIS
1) Conformación del diagrama de red equivalente para la condición de
prefalla.
2) Determinación del estado de prefalla de la red (Flujo de Potencia).
3) Determinación de las variaciones de corrientes y tensiones en la red
causadas por el CC.
4) Superposición de las variaciones de corrientes y tensiones en la red
calculadas en el paso 3 con las corrientes y tensiones de prefalla en la
red calculadas en el paso 2 para obtener las corrientes y tensiones de
falla. (Principio de Superposición)
Curso de Capacitacion
ETAP
Cortocircuito
71
Ejemplo de Análisis de CC
Paso 1: Diagrama de red equivalente para la condición de prefalla.
•
Representación de las líneas de transmisión: impedancias en p.u. referidas a 50
MVA - 120 kV.
•
Representación de generadores y transformadores:
G1: 100 MVA
X’d = 20%
G2: 200 MVA
X’d = 20%
T1: 100 MVA
X= 10%
T2: 200 MVA
X= 10%
Cambiando la base
2
 Vbase1  S base2
 
Z pubase2  Z pubase1  
 Vbase2  S base1
Curso de Capacitacion
ETAP
50.000 kVA
 0,10 [pu]
100.000 kVA
50.000 kVA
X 'd G 2  0,20 
 0,05 [pu]
200.000 kVA
50.000 kVA
XT1  0,10 
 0,05 [pu]
100.000 kVA
50.000 kVA
XT2  0,10 
 0,025 [pu]
200.000 kVA
X 'd G1  0,20 
Cortocircuito
72
Ejemplo de Análisis de CC
•
Representación de las demandas en barras 1 y 3:
SD1=1+ j 0,5 [pu]
SD3=0,5+ j 0 [pu]
Si suponemos que las tensiones de prefalla en ambas barras son los nominales,
entonces de S=|V|2 Y * obtenemos:
1+ j 0,5 [pu] = |1.0|2 YD1 * → YD1= 1 – j 0,5 [pu]
0,5+ j 0 [pu] = |1.0|2 YD3 * → YD2 = 0,5 [pu]
Con el objeto de preservar la linealidad de la red para poder aplicar el
Teorema de Thevenin en el paso 3, suponemos que las admitancias
equivalentes de carga son independientes de la tensión.
Curso de Capacitacion
ETAP
Cortocircuito
73
Ejemplo de Análisis de CC
Curso de Capacitacion
ETAP
Cortocircuito
74
Ejemplo de Análisis de CC
Paso 2. Determinación del estado de
prefalla de la red (Flujo de Potencia)
En nuestro ejemplo supondremos
que:
 Todas las tensiones de prefalla tienen
magnitud 1.0
 Todas las corrientes de prefalla son
nulas.
Estas suposiciones implican que
todas las admitancias en paralelo se
desprecian, por lo tanto el diagrama
de red equivalente se simplifica.
Curso de Capacitacion
ETAP
Cortocircuito
75
Ejemplo de Análisis de CC
Paso 3. Determinación de las
variaciones de corrientes y tensiones
en la red causadas por el CC
El efecto del CC es equivalente a
conectar una impedancia de falla Zf
entre la barra y tierra. Si el CC es
rígido, entonces Zf = 0.
El Teorema de Thevenin afirma que
los cambios en las corrientes y
tensiones de red causados por el
agregado de una impedancia de falla
Zf son equivalentes a aquellos
causados al agregar un fem E=V30 con
todas las otras fuentes de tensión
cortocircuitadas.
Curso de Capacitacion
ETAP
Cortocircuito
76
Ejemplo de Análisis de CC
Para calcular los cambios en las corrientes y tensiones de red en este ejemplo
procedemos a reducirla:
Curso de Capacitacion
ETAP
Cortocircuito
77
Ejemplo de Análisis de CC
Curso de Capacitacion
ETAP
Cortocircuito
78
Ejemplo de Análisis de CC
De la red equivalente e) calculamos la corriente en la falla:
1,0 0º
If 
  j 9,85 pu
º
0,101590
De la red equivalente c) calculamos la corriente de falla se divide entre los
generadores:
j 0,1083
I G1 
I f   j 3,67 pu
j 0,1083  j 0,1883
j 0,1883
IG 2 
I f   j 6,18 pu
j 0,1083  j 0,1883
Curso de Capacitacion
ETAP
Cortocircuito
79
Ejemplo de Análisis de CC
De la red equivalente a) calculamos los cambios en las tensiones de las
barras 1 y 2:
V1  0   j 0,15  j 3,67   0,550 pu
V2  0   j 0,075  j 6,18  0,463 pu
El cambio en las tension de la barra 3 es:
V3  1.0 pu
El vector de tension de barras de Thevenin es:
 0,550
VT   0,463
  1,0 
Curso de Capacitacion
ETAP
Cortocircuito
80
Ejemplo de Análisis de CC
Conocidos los cambios en las tensiones de las barras, finalmente calculamos
los cambios en las corrientes de las líneas:
V2  V1
I 21 
  j 0,87 pu
j 0,1
V1  V3
I13 
  j 4,50 pu
j 0,1
V2  V3
I 23 
  j 5,37 pu
j 0,1
Paso 4. Determinación del estado de falla de la red
V1f  V10  V1  1,0  0,550  0,450 pu
V2f  V20  V2  1,0  0,463  0,537 pu
V3f  0 pu
Curso de Capacitacion
ETAP
Cortocircuito
81
Ejemplo de Análisis de CC
I f  9,85 pu
I1f  I10  I1  0  j 3,67  3,67 pu
I f2  I 02  I 2  0  j 6,18  6,18 pu
I f21  I 021  I 21  ? j 0,87  ? pu
f
0
I13
 I13
 I13  0  j 4,50  4,50 pu
Observemos que para calcular I21f
necesitamos conocer I210
I f23  I 023  I 23  0  j 5,37  5,37 pu
Finalizamos el estudio de CC calculando la Potencia de CC en barra 3
SCC 3
3
Curso de Capacitacion
ETAP
 9,85 pu  9,85  50 MVA  490 MVA
Cortocircuito
☺
82
Ejemplo de Análisis de CC
En los sistemas eléctricos de potencia modernos, existen distintos tipos de
fuentes activas que pueden contribuir a la corriente de cortocircuito en el
momento en que ocurre una falla por cortocircuito en el sistema.
Estas incluyen generadores síncronos y asíncronos, motores síncronos y
asíncronos, y los convertidores electrónicos de potencia conectados a
generadores.
Otros componentes del sistema, tales como las líneas aéreas, cables,
reactores serie, etc, situados entre la localización de la falla por
cortocircuito y las distintas fuentes de corriente afectaran la magnitud de
las corrientes de cortocircuito que alimentan la falla.
En general el efecto consiste en reducir la magnitud y aumentar la tasa de
decaimiento de las corrientes de cortocircuito.
Curso de Capacitacion
ETAP
Cortocircuito
83
Métodos Computacionales para
análisis de CC equilibrados
Por el Teorema de Thevenin:
V
V
V
  T
f
barras
0
barras
n1
n1
n1
Puesto que los cambios en las tensiones de las barras ocurren como resultado
de la corriente de CC If en la barra fallada, o equivalentemente por la inyección
de la corriente -If en la barra fallada, resulta:
V

Z
I
T
barras
  n1
f
n1
Curso de Capacitacion
ETAP
n n
Cortocircuito
84
Métodos Computacionales para
análisis de CC equilibrados
donde:
1
barras
Z barras  Y
 0 
  


I f   I f 


  
 0 
Curso de Capacitacion
ETAP
Conceptualmente es la inversa de la matriz
de admitancias de barras. En la practica no
se invierte Ybarras sino que se construye
Zbarras
q-esima componente; correspondiente a la
falla en barra q.
Cortocircuito
85
Métodos Computacionales para
análisis de CC equilibrados
Entonces:
f
barras
V
V
0
barras
 Z barrasI
f
O, en términos de componentes:
V1f  V10  Z 1qIf
   
Vqf  Vq0  Z qqIf
   
Obsérvese que en
esta etapa If es
desconocida.
Vnf  Vn0  Z nqIf
Curso de Capacitacion
ETAP
Cortocircuito
86
Métodos Computacionales para
análisis de CC equilibrados
Ahora bien, la tensión de falla de la q-esima barra esta relacionada con la
corriente de falla por la ley de Ohm:
Vqf  Z f If
donde Zf es la impedancia de falla. Reemplazando obtenemos la corriente de falla:
Z I  V  Z qq I
f
f
0
q
f
I 
f
Vq0
Z f  Z qq
Reemplazando ahora If en el sistema de ecuaciones obtenemos:
Vi  Vi 
f
Z iq
0
Z  Z qq
f
Vq0
iq
f
Z
Vqf  f
Vq0
Z  Z qq
Curso de Capacitacion
ETAP
Cortocircuito
87
Métodos Computacionales para
análisis de CC equilibrados
Si el CC es rígido:
Vq0
If 
Z qq
Vqf  0
Vif  Vi0 
Z iq
Z qq
Vq0
iq
Finalmente, consideremos la línea de transmisión que conecta la barra α con la barra
β. Si la impedancia de esa línea es Zαβ entonces la corriente de falla Iαβf en la línea
es:
I 
f
Vf  Vf
Z 
Impedancia de la línea,
no de la matriz Z!!
Curso de Capacitacion
ETAP
Cortocircuito
88
Métodos Computacionales para
análisis de CC equilibrados
Ejemplo: Retomamos el
ejemplo anterior y hallamos la
matriz de admitancia de barras.
1
1
1


  j 26,67
j0,15 j0,10 j0,10
1
1
1
y 22 


  j 33,33
j0,075 j0,10 j0,10
1
1
y 33 

  j 20,00
j0,10 j0,10
1
y12  y 21  
 j 10,00
j0,10
1
y13  y 31  
 j 10,00
j0,10
1
y 23  y 32  
 j 10,00
j0,10
y11 
Curso de Capacitacion
ETAP
Cortocircuito
89
Métodos Computacionales para
análisis de CC equilibrados
j10,0
j10,0 
- j 26,67
 j 0,0728
Y   j10,0  j 33,33 j10,0   Z   j 0,0386
 j10,0
 j 0,0557
j10,0
- j 20,0
j 0,0386
j 0,0557
j 0,047
j 0,0557
j 0,047 
j 0,1014
V3f  0
V1f  V10 
Z13 0
j 0,0557
V3  1,0 
 1,0  0,4507 pu
Z 33
j 0,1014
Z 23 0
j 0,047
V V 
V2  1,0 
 1,0  0,5365 pu
Z 33
j 0,1014
f
2
Curso de Capacitacion
ETAP
0
2
Cortocircuito
90
Métodos Computacionales para
análisis de CC equilibrados
V30
1,0
I 

  j 9,8619
Z 33 j 0,1014
f
3
V20
1,0
I 

  j17,9533
Z 22 j 0,0557
f
2
V10
1,0
I 

  j13,7363
Z11 j 0,0728
f
1
V1f  V2f 0,4507  0,5365
I12 

 j 0,8580
Z12
j 0,1
f
V1f  V3f 0,4507  0
I13 

  j 4,507
Z13
j 0,1
f
V2f  V3f 0,5365  0
I23 

  j 5,365
Z 23
j 0,1
f
Curso de Capacitacion
ETAP
Cortocircuito
☺
91
Redes de Secuencia
 Efecto de la TCS sobre los elementos pasivos de la red
Vabc  Z
 Iabc
33
V 0  T -1ZT I  0

Iabc  Y
 Vabc
33
-1
I  0  T
YT

 V 0
Y -0
Z  -0
El mayor valor inherente de la TCS como herramienta de análisis esta
asociado al hecho de que estas matrices tienden a ser diagonales para la
mayoría de los elementos ampliamente usados en SEP. En consecuencia,
no existe acoplamiento entre las redes de secuencia y por lo tanto pueden
tratarse separadamente.
Curso de Capacitacion
ETAP
Cortocircuito
92
Redes de Secuencia
Consideremos el caso de un elemento pasivo de la red en operación
desequilibrada
Línea de transmisión con carga desequilibrada
Curso de Capacitacion
ETAP
Cortocircuito
93
Redes de Secuencia
Va1  Va 2  I a Z L  I a  I b  I c Z n
Vb1  Vb 2  I b Z L  I a  I b  I c Z n
Vc1  Vc 2  I c Z L  I a  I b  I c Z n
Zn
Z n  I a 
Va1  Va 2   Z L  Z n
V   V    Z
 I 
Z

Z
Z
n
L
n
n
 b1   b 2  
  b
 Vc1   Vc 2   Z n
Zn
Z L  Z n   I c 

  
ΔVabc
Curso de Capacitacion
ETAP
Z
Cortocircuito
Iabc
94
Redes de Secuencia
ΔVabc  Z Iabc
-1
ΔV 0  T
ZT

 I  0
Z  -0
Z L  Z n
Z -0  T 1  Z n
 Z n
Curso de Capacitacion
ETAP
Zn
ZL  Zn
Zn
Zn 
Z L
Z n  T   0
 0
Z L  Z n 
Cortocircuito
0
ZL
0
0


0

Z L  3 Z n 
95
Redes de Secuencia
Si definimos:
z   ZL
Impedancia de secuencia positiva
z   ZL
Impedancia de secuencia negativa
z 0  Z L  3 Z n Impedancia de secuencia cero
V1  V 2  z  I 
V1  V 2  z  I 
V01  V02  z 0 I 0
Curso de Capacitacion
ETAP
Cortocircuito
Por ser Z+-0 diagonal,
los componentes de
secuencia están
desacoplados!!
96
Redes de Secuencia
 Efecto de la TCS sobre una maquina síncrona con carga desequilibrada
 Z1
Z   Z 3
 Z 2
Vabc  E abc  Z Iabc
Z2
Z1
Z3
Z3 
Z 2 
Z1 
TV0  E abc  ZT I0
V 0  T E abc  T
ZT

 I  0
-1
-1
Z  -0
Curso de Capacitacion
ETAP
Cortocircuito
97
Redes de Secuencia
1 
1
-1
T E abc  1  2
3
1 1

 z1
Z  0  T -1 z 3
z 2
z2
z1
z3
Curso de Capacitacion
ETAP






 E a 1   3   3  E a 
2   Ea 
 2  1
4
2 
   E a   E a 1        0 
3

 E a 1   2     0 
1    E a 



 z 1   2 z 2  z 3
z3 

z 2  T  
0

z1 
0


Cortocircuito
0
z  z   z 
2
1
2
0
3

0

0

z1  z 2  z 3 
98
Redes de Secuencia
Si definimos:
z   z 1   2 z 2  z 3
Impedancia de secuencia positiva
z   z 1  z 2   2 z 3
Impedancia de secuencia negativa
z 0  z1  z 2  z 3
Impedancia de secuencia cero
V  E a  z  I 
V  0  z  I 
V0  0  z 0 I 0
Curso de Capacitacion
ETAP
Cortocircuito
Por ser Zs diagonal,
los componentes de
secuencia están
desacoplados!!
99
Redes de Secuencia
Ejemplo:
Generador síncrono sujeto a un CC - LT
Curso de Capacitacion
ETAP
Cortocircuito
100
Redes de Secuencia
I a 
I abc   0 
 0 
1 
I  
I   1 1  2
  3
1 1
 I 0 

 Ia 
 
 2  I a   3 
I
I

   0    a   I   I   I 0  a
3
3

1   0   I a 
3
 
Ia
V  E a  z 
3
Ia
V  0  z 
3
Ia
V0  0  z 0
3
Curso de Capacitacion
ETAP
Cortocircuito
101
Redes de Secuencia
Ia
Va  I a Z  V  V  V0  E a  z   z   z 0 
3
f
Ia 
Ea
Zf 
Va  E a
1
z   z   z 0 
3
Zf
1
Z  z   z   z 0 
3
f
Curso de Capacitacion
ETAP
Cortocircuito
102
Redes de Secuencia
Ia 
Ia
Ia

Vb   V  V  V0    E a  z    z   z 0
3
3
3

3 2 Z f  z   2    z 0  2  1
Vb  E a
3Z f  z 0  z   z  
2
2




Ia 
Ia
Ia

2
Vc  V   V  V0   E a  z     z   z 0
3
3
3

3Z f  z     2  z 0   1
Vc  E a
3Z f  z 0  z   z  
2

Curso de Capacitacion
ETAP

Cortocircuito
103
Redes de Secuencia
 Impedancias de secuencia de maquinas síncronas
o
Secuencia positiva
z  j Xd
para régimen permanente
z   j X 'd'
para CC, 1 ciclo
'
z  j Xd
para CC, 3-4 ciclos
o Secuencia negativa
z  j X
o Secuencia cero
z0  j X0
Curso de Capacitacion
ETAP
Cortocircuito
104
Redes de Secuencia
Va
z 
Ia
Medición de impedancias de secuencia negativa
Curso de Capacitacion
ETAP
Cortocircuito
105
Redes de Secuencia
E
z0 
I0
Medición de impedancias de secuencia nula
Curso de Capacitacion
ETAP
Cortocircuito
106
Redes de Secuencia
 Impedancias de secuencia de líneas de transmisión
Las impedancias de secuencia positiva y negativa de componentes de
redes lineales, simétricos y estáticos son idénticas, porque la impedancia
de tales circuitos es independiente del orden de fase, siempre que las
tensiones aplicadas estén equilibradas. La impedancia de secuencia cero
de una línea de transmisión es distinta (normalmente mayor) que la
impedancia a las corrientes de secuencia positiva y negativa.
Curso de Capacitacion
ETAP
Cortocircuito
107
Métodos Computacionales de análisis de
CC desequilibrados
 Construcción de redes de secuencia del SEP
V barras  Z  barras J  barras
  
Secuencia positiva
V barras  Z  barras J  barras
Secuencia negativa
V0 barras  Z 0 barras J 0 barras
Secuencia cero
n 1
Curso de Capacitacion
ETAP
nn
n 1
Cortocircuito
108
Métodos Computacionales de análisis de
CC desequilibrados
0
 v 1   z 11 0
v   0 z
0
11
 1  
 v 01   0
0 z 011
  

   
 v i   z i1 0
0
  
 v i    0 z i1 0
v   0
0 z 0i1
0i
  

   
 v  z
0
0

n

n
1
  
 v  n   0 z  n1 0
  
0 z 0 n1
 v 0n   0
Curso de Capacitacion
ETAP
z 1i 0
0
 0 z 1i 0
0
0 z 01i


z ii 0
0
 0 z ii 0
0
0 z 0ii


z  ni 0
0
 0 z ni 0
0
0 z 0 ni
Cortocircuito
z 1n 0
0   J 1 
 0 z 1n 0   J 1 
0
0 z 01n   J 01 
 


  
z in
0
0   J i 
 
 0 z in
0   J i 
0
0 z 0in   J 0i 
 


  
z  nn 0
0  J  n 
 
 0 z nn 0  J n 
 
0
0 z 0 nn   J 0 n 
109
Métodos Computacionales de análisis de
CC desequilibrados
 V 01  Z  011
    

 
 V 0i    Z  0i1

 
    
 V 0 n  Z  0n1
Vi 
V 0i  Vi 
 V0i 
Curso de Capacitacion
ETAP
 Z  01i


 Z  0ii


 Z  0ni
J i 
J  0i  J i 
 J 0i 
Cortocircuito
 Z  01n   J  01 

    
 Z  0in   J  0i 



   
 Z  0nn  J  0 n 
z ij

Z  0ij   0
 0

0
z ij
0
0 

0 
z 0ij 
110
Métodos Computacionales de análisis de
CC desequilibrados
Matriz de impedancia de barras
Vector de inyecciones de
corrientes de secuencia en
barras
de componentes de secuencia
V 0 barras  Z  0 barras J  0 barras


 




3n1
3n3n
3n1
Vector de tensiones de secuencia
de barras
Curso de Capacitacion
ETAP
Cortocircuito
111
Métodos Computacionales de análisis de
CC desequilibrados
Ejemplo: retomamos el ejemplo del SEP de tres barras.
 j 0,0728
Z  barras   j 0,0386
 j 0,0557
j 0,0386
j 0,0557
j 0,0470
j 0,0557
j 0,0470
j 0,1014
Red de secuencia positiva
Curso de Capacitacion
ETAP
Cortocircuito
112
Métodos Computacionales de análisis de
CC desequilibrados
 j 0,0728
Z barras   j 0,0386
 j 0,0557
j 0,0386
j 0,0557
j 0,0470
j 0,0557
j 0,0470
j 0,1014
Red de secuencia negativa
Curso de Capacitacion
ETAP
Cortocircuito
113
Métodos Computacionales de análisis de
CC desequilibrados
j5
j5 
- j 30
Y0barras   j 5  j 50
j 5 
 j 5
j5
- j10

 j 0,0380
Z 0barras   0,0060
 j 0,0220
j 0,0060
j 0,0220
j 0,0140
j 0,0220
j 0,0140
j 0,1180
Red de secuencia cero
Curso de Capacitacion
ETAP
Cortocircuito
114
Métodos Computacionales de análisis de
CC desequilibrados
0
0
0,0386
0
0
0,0557
0
0 
0,0728
 0

0
,
0728
0
0
0
,
0386
0
0
0
,
0557
0


 0
0
0,0380
0
0
0,0060
0
0
0,0220


0
,
0386
0
0
0
,
0557
0
0
0
,
0470
0
0


Z  0 barras  j  0
0,0386
0
0
0,0557
0
0
0,0470
0 


0
0
0
,
0060
0
0
0
,
0220
0
0
0
,
0140


0,0557
0
0
0,0470
0
0
0,1014
0
0 


0,0557
0
0
0,0470
0
0
0,1014
0 
 0
 0
0
0,0220
0
0
0,0140
0
0
0,1180 

Curso de Capacitacion
ETAP
Cortocircuito
115
Métodos Computacionales de análisis de
CC desequilibrados
 Formulación general para tensiones y corrientes de CC
Corriente de falla en la barra q
 I faq 
 
I fabcq  I fbq 
 I fcq 
 
Tensión de falla en la barra q
 Vaqf 
 f 
f
Vabcq
 Vbq

f
 Vcq 
 
Curso de Capacitacion
ETAP
Cortocircuito
116
Métodos Computacionales de análisis de
CC desequilibrados
V Z
I

 33 
f
f
abcq
f
abcq
31
Matriz impedancia de falla
31
dependen del tipo de CC
f
I fabcq  Y f Vabcq
Matriz admitancia de falla
Vf 0 q  T -1 Z f T I f 0 q



Z f -0
I
f
 0 q
T Y TV



-1
f
f
 0 q
Matriz impedancia de
secuencias de falla
Matriz admitancia de
secuencias de falla
Yf 0
Curso de Capacitacion
ETAP
Cortocircuito
117
Métodos Computacionales de análisis de
CC desequilibrados
Por el Teorema de Thevenin:
V f 0barras  V 00barras  Z  0 barras I f 0barras

 
  
3n1
donde:
Curso de Capacitacion
ETAP
3 n1
3 n3n
3n1
 0 
  


I f 0barras   I f 0 q 


  
 0 
q-esimo elemento
Cortocircuito
118
Métodos Computacionales de análisis de
CC desequilibrados
Reescribiendo la ecuación matricial anterior en forma vectorial:

V f  V 0  Z  01q I f
 01
 01
 0q

 

31
33
31
 31
.....................................
 f
3  n V  0q  V 00q  Z  0 qq I f 0q
  

33
31
31
31

........................................
f
V f  V 0  Z
I
0 nq  0q
 0n
 0n




31
33
31
 31
Curso de Capacitacion
ETAP
Cortocircuito
119
Métodos Computacionales de análisis de
CC desequilibrados
La corriente de falla se obtiene de:
V f 0q  V 00q  Z  0qqI f 0q
y
Vf 0q  Z f-0 If 0q
despejando obtenemos:


V 00q  Z f 0  Z  0qq I f 0q
cuya solución es:

I  0q  Z  0  Z  0qq
f
Curso de Capacitacion
ETAP
f
Cortocircuito
 V
1
0
 0q
120
Métodos Computacionales de análisis de
CC desequilibrados
Sustituyendo la corriente de falla obtenemos:

V  0i  V  0i  Z  0iq Z  0  Z  0qq
f
f
 0q
V
0

f
 Z  0 Z  0  Z  0qq
f
Curso de Capacitacion
ETAP
f
 V
1
Cortocircuito
 V
1
0
 0q
iq
0
 0q
121
Métodos Computacionales de análisis de
CC desequilibrados
Conocidas las tensiones de falla y la corriente de falla, calculamos las
corrientes en las líneas. Si la línea conecta las barras ρ-μ y esta
caracterizada por:
y 
Y 0   0
 0
0
y
0
0
0 
y 0 
La corriente de falla en la línea esta dada por:

If-0   Y-0  Vf -0   Vf -0 
Curso de Capacitacion
ETAP
Cortocircuito

122
Métodos Computacionales de análisis de
CC desequilibrados
0BSERVACIONES:

Las fórmulas son completamente generales y pueden usarse para un
sistema de n barras. La falla ocurre en cualquier barra q.

Una vez que la matriz de impedancia de barras de secuencias de falla Z+0barras ha sido conformada y almacenada en memoria, podemos extender
nuestro análisis fácilmente a cualquier tipo de falla.

Todas las fórmulas involucran vectores de dimensión 3 y matrices de
dimensión 3×3 con valores complejos. Las matrices Z+-0ij son diagonales,
pero las matrices de impedancia de secuencias de falla Z+-0f no lo son.
Curso de Capacitacion
ETAP
Cortocircuito
123
Métodos Computacionales de análisis de
CC desequilibrados

Todas las fórmulas calculan las corrientes y tensiones de falla
expresados en componentes de secuencia. Para convertirlos a valores
por fase se debe aplicar la TCS inversa.

Las tensiones de prefalla son equilibradas, por lo tanto las componentes
de secuencia negativa y de secuencia nula se anulan. O sea, para toda
barra q:
V0q  Vq0 

  
0
V  0q   0    0 
 0  0

  
Curso de Capacitacion
ETAP
Cortocircuito
124
Métodos Computacionales de análisis de
CC desequilibrados
Las ecuaciones anteriores fueron deducidas basadas en la existencia de la
matriz impedancia de secuencia de falla:
Z f -0
Dependiendo del tipo de falla, esta puede no existir, en cuyo caso existe la
matriz admitancia de secuencia de falla:
Yf 0
En tal caso se deduce un nuevo conjunto de ecuaciones basadas en la
matriz admitancia de secuencia de falla. De las ecuaciones:
V f 0q  V 00q  Z  0qqI f 0q
obtenemos:
Curso de Capacitacion
ETAP
y
If 0q  Yf 0 Vf 0q
V f 0q  V 00q  Z  0qq Yf 0 V f 0q
Cortocircuito
125
Métodos Computacionales de análisis de
CC desequilibrados
Y de aquí:

V  0q  Id  Z  0qq Y 0
f
f
V
-1
0
 0q
donde Id es la matriz identidad. De la ecuación:
I
f
 0 q
Y
f
 0
f
 0 q
V
obtenemos reemplazando en:
Y
f
 0
Id  Z
 0 qq Y
0
 0 q
V f 0i  V 00i  Z  0iq I f 0q

V f 0i  V 00i  Z  0iq Yf-0 Id  Z  0qq Yf-0
Curso de Capacitacion
ETAP
V
1
f
 0
Cortocircuito
V
1
0
 -0q
iq
126
Determinación de las matrices de
secuencia de falla
De la anterior discusión, debe quedar claro que la clave del análisis consiste
en disponer de las matrices de impedancia y de admitancia de falla. En este
sentido el análisis de CC desequilibrado es diferente y mas complicado que el
caso equilibrado, donde una impedancia de falla escalar Zf era suficiente para
representar todos los casos. En el caso extremo en que el cortocircuito es
rígido a tierra Zf = 0; en el otro caso extremo donde Zf =  no hay falla.
La situación es completamente diferente en el caso desequilibrado. Siempre
que tengamos un caso extremo de impedancia de falla nula o infinita en una
fase la matriz de impedancia o de admitancia de falla no estará definida. Tales
casos extremos son mas la regla que la excepción y es necesario aprender
como manipularlos en nuestro análisis. Para ello consideramos el caso
general desequilibrado siguiente:
Curso de Capacitacion
ETAP
Cortocircuito
127
Determinación de las matrices de
secuencia de falla
Falla desequilibrada genérica
Curso de Capacitacion
ETAP
Cortocircuito
128
Determinación de las matrices de
secuencia de falla






Vaqf  I faq Z a  I faq  I fbq  I fcq Z g
f
Vbq
 I fbq Z b  I faq  I fbq  I fcq Z g
Vcqf  I fcq Z c  I faq  I fbq  I fcq Z g
 Vaqf   Z a  Z g
Zg
Z g   I faq 
 f  
 f 
Zb  Zg
Z g  I bq 
Vbq    Z g
f 
 Vcqf   Z g


Z
Z

Z
I
g   cq 
  g c
Zf
Curso de Capacitacion
ETAP
Cortocircuito
129
Determinación de las matrices de
secuencia de falla
Aplicando la TCS a la matriz de impedancia de falla Zf obtenemos:
Z
f
 -0
 Za  Zb  Zc
1
Z f-0   Z a  Z b   2 Z c
3
 Z a   2 Z b  Z c

Curso de Capacitacion
ETAP
1
T Z T
f
Z a   2 Z b  Z c
Za  Zb  Zc
Z a  Z b   2 Z c
Cortocircuito
Z a  Z b   2 Z c 

Z a   2 Z b  Z c 
Z a  Z b  Z c  9Z g 
130
Determinación de las matrices de
secuencia de falla
Y Y  Y  Y 
Y Y
1

Y Y
Y Y  Y  Y 

 I faq 
  Vaqf 
 Ya Yc
a
b
c
g
a b
 f 
  f 
I


Y
Y
a b
b
a
c
g
b c
 bq  Y  Y  Y  Y
 Vbq 
a
b
c
g
 I fcq 

  Vcqf 



Y
Y

Y
Y
Y
Y

Y

Y
a
c
b
c
c
a
b
g
  
 
Yf
Yf 0 
1
Ya  Yb  Yc  Yg
 1
 3 Yg Ya  Yb  Yc  

 Ya Yb  Yb Yc  Yc Ya 
1
2
 Yg Ya  Yb   Yc 
3
 Yb Yc   2 Ya Yb  Yc Ya
 1
2
 Yg Ya   Yb  Yc
 3







Curso de Capacitacion
ETAP


1
Yg Ya   2 Yb  Yc 
3
Yb Yc  Ya Yb   2 Yc Ya
1
Yg Ya  Yb  Yc  
3
Ya Yb  Yb Yc  Yc Ya 
1
Yg Ya  Yb   2 Yc
3


Cortocircuito



1
Yg Ya  Yb   2 Yc 

3


1

Yg Ya   2 Yb  Yc 
3


1
Yg Ya  Yb  Yc  
3






131
Determinación de las matrices de
secuencia de falla
Caso 1: CC trifásico equilibrado
Za  Zb  Zc  Z 
1
Y
Z 0
0 


Z f -0   0 Z
0 
 0 0 Z  3Z g 



Y 0

Yf 0   0 Y
0 0


Curso de Capacitacion
ETAP
Cortocircuito


0

0

YYg 
Yg  3Y 
132
Determinación de las matrices de
secuencia de falla
f
Puesto que Z  -0 es diagonal y lo mismo es cierto para la matriz Z  -0qq
se deduce que la matriz
Z
f
 0
 Z  0qq
 también es diagonal.
1
Puesto que el vector de tensiones de prefalla solo tiene componentes de
secuencia positiva resulta que la corriente

I  0q  Z  0  Z  0qq
f
f
 V
1
0
 0q
también contiene solo componentes de secuencia positiva. De hecho, lo mismo
ocurre con tensiones postfalla:
1
f
0
f
V  0i  V  0i  Z  0iq Z  0  Z  0qq V 00q
iq


Vf 0q  Z f 0 Z f 0  Z  0qq

 V
1
0
 0q
Puesto que corrientes de secuencia cero, el potencial del punto N es el de
tierra local y en consecuencia no circula corriente por Zg. ☺
Curso de Capacitacion
ETAP
Cortocircuito
133
Determinación de las matrices de
secuencia de falla
Zb  Zc  
Caso 2: CC monofásico a tierra
Zg  0
Y   
f
Za  Zf 
Z f -0
1
Yf
indefinida
1 1 1
Y 

f
Y 0 
1
1
1

3 
1 1 1
f
☺
Curso de Capacitacion
ETAP
Cortocircuito
134
Determinación de las matrices de
secuencia de falla
Caso 3: CC bifásico sin contacto a tierra
Za  
Zg  
Ya  0
Y  0
g
Yb  Yc  2Yf
Z f -0
indefinida
 1  1 0
Yf 0  Y f  1 1 0
 0 0 0
☺
Curso de Capacitacion
ETAP
Cortocircuito
135
Ejemplo de Análisis de CC desequilibrado
Ejemplo: retomamos
el ejemplo del SEP de
tres barras para el
cual la matriz de
impedancia de barras
de componentes de
secuencia Z+-0barras ya
ha sido calculada.
Supongamos que en
la barra 3 se
desarrolla un CC
monofásico a tierra.
T1
G1
G2
~
~
Δ
Y
Δ
Y
T2
1
2
L1
L2
L3
3
Curso de Capacitacion
ETAP
Cortocircuito
136
Ejemplo de Análisis de CC desequilibrado
0
0
0,0386
0
0
0,0557
0
0 
0,0728
 0

0
,
0728
0
0
0
,
0386
0
0
0
,
0557
0


 0
0
0,0380
0
0
0,0060
0
0
0,0220


0
,
0386
0
0
0
,
0557
0
0
0
,
0470
0
0


Z  0 barras  j  0
0,0386
0
0
0,0557
0
0
0,0470
0 


0
0
0
,
0060
0
0
0
,
0220
0
0
0
,
0140


0,0557
0
0
0,0470
0
0
0,1014
0
0 


0,0557
0
0
0,0470
0
0
0,1014
0 
 0
 0
0
0,0220
0
0
0,0140
0
0
0,1180 

Curso de Capacitacion
ETAP
Cortocircuito
137
Ejemplo de Análisis de CC desequilibrado
Las tensiones en la barra q=3 se obtienen de la ecuación:
f
 -0q
V

 Id  Z  0qq Y
De acuerdo al Caso 2:
V
-1
f
 -0
f
 -0q
1 1 1
Y 

f
Y 0 
1
1
1

3 
1 1 1
f
por lo tanto:
 1 0 0 z  qq


Vf -0q   0 1 0   0
 0 0 1  0
 

Curso de Capacitacion
ETAP
0
z -qq
0
-1
0  f 1 1 1   Vq0 
Y 
  0 
0 
1
1
1
  
3 
1 1 1   0 
z 0qq 

Cortocircuito
138
Ejemplo de Análisis de CC desequilibrado
calculando:
 Yf



1

z

z
- qq
0qq 

3


f
Vq0
Y
f


V -0q 
 z -qq
f


3
Y
f
z qq  z -qq  z 0qq  
1

Y
3
 z 0qq


3


La corriente de CC en la barra q=3 se obtiene de la ecuación:
I
f
 0 q
Y
f
 0
f
 0 q
V
Yf
3
1
1
I f -0q  Vq0

Yf
z qq  z -qq  z 0qq  1
1
3
Curso de Capacitacion
ETAP
Cortocircuito
139
Ejemplo de Análisis de CC desequilibrado
Finalmente, las tensiones postfalla en barras i ≠q se obtienen de la ecuación:
V f 0i  V 00i  Z  0iq I f 0q
 Vi0  z iq
  
Vf -0i   0    0
0  0
  
0
z -iq
0
0 

0  If 0q
z 0iq 
Yf
 Vi0 
z iq 
 


3
Vf -0i   0   Vq0
z

iq


Yf
0
z qq  z -qq  z 0qq  z 0iq 
1
 
3
Curso de Capacitacion
ETAP
Cortocircuito
140
Ejemplo de Análisis de CC desequilibrado
Todas las ecuaciones se simplifican si el CC es rígido a tierra:
z -qq  z 0qq 


Vf -0q 

z
qq

z qq  z -qq  z 0qq    z

0qq


Vq0
1
1
I f -0q 
z qq  z -qq  z 0qq  1

Vq0
 Vi0 
z iq 
0
V
 


q
Vf -0i   0  
z
iq 

z qq  z -qq  z 0qq  
0
 z 0iq 


 
Curso de Capacitacion
ETAP
Cortocircuito
iq
141
Ejemplo de Análisis de CC desequilibrado
A los fines de calcular numéricamente, en este ejemplo Vq0=1:
 j 0,1014
Z -033   0
 0
0
j 0,1014
0
0 
0  p.u.
j 0,1118
 j 0,1014  0,1014  0,685 
1

   0,317 p.u.
Vf -03 

j
0,1014
 

j 0,1014  0,1014  0,1118 

  0,369
 j 0,1118
1
3,12
1
1   j 3,12 p.u.
I f-03 


j 0,1014  0,1014  0,1118  
1
3,12
Curso de Capacitacion
ETAP
Cortocircuito
142
Ejemplo de Análisis de CC desequilibrado
Ahora calculamos las tensiones postfalla en barras 1 y 2:
 j 0,0557
Z  -013   0
 0
0
j 0,0557
0
0 
0 
j 0,0220
 j 0,0472
Z  -023   0
 0
0
j 0,0472
0
0 
0 
j 0,0140
1
 j 0,0557  0,826 
1
 j 0,0557    0,174  p.u.
Vf -01  0 
 

j 0,1014  0,1014  0,1180 
0
 j 0,0220  0,069
1
 j 0,0472  0,853 
1
 j 0,0472    0,147  p.u.
Vf -02  0 
 

j 0,1014  0,1014  0,1180 
0
 j 0,0140  0,044
Curso de Capacitacion
ETAP
Cortocircuito
143
Ejemplo de Análisis de CC desequilibrado
Ahora, por ejemplo, calculamos la corriente en la línea que vincula las barras
1 y 3:

If-013  Y-013 Vf -01  Vf -03
 j 0,10
Z -013   0
 0
0
j 0,10
0
 j 10
If-013   0
 0
Curso de Capacitacion
ETAP

 j 10
Y -013   0
 0
0 
0  p.u.
j 0,20
0
0 
 j 10
0 
0
 j 5
0
0   0,826   0,685  
1,42


 j 10
0    0,174    0,317    j 1,42 p.u.
1,50
0
 j 5  0,069  0,369 
Cortocircuito
144
Ejemplo de Análisis de CC desequilibrado
Los correspondientes valores por fase, por ejemplo para la barra 3 se obtienen
de:
f
abc3
V
TV
f
 03
Vaf3  
1
1
1  0,685  
0
0
 

 f  






f
Vabc3  Vb3    0,5  j0,866  0,5  j0,866 1  0,317   0,553  j0,868  1,0292   122,5 p.u
 Vcf3   0,5  j0,866  0,5  j0,866 1  0,369  0,553  j0,868  1,0292 122,5 
 
I
f
abc3
TI
f
 03
I fa 3  
1
1
1  j 3,12  j 9,36
 
Ifabc3  I fb 3    0,5  j0,866  0,5  j0,866 1  j 3,12   0  p.u.
 I fc3   0,5  j0,866  0,5  j0,866 1  j 3,12  0 
 
☺
Curso de Capacitacion
ETAP
Cortocircuito
145
Técnicas para Análisis de CC
 Simulación de cortocircuitos
CC a través de una impedancia de falla
Curso de Capacitacion
ETAP
Cortocircuito
146
Técnicas para Análisis de CC
 Simulación de cortocircuitos
Red de prefalla
Curso de Capacitacion
ETAP
Cortocircuito
147
Técnicas para Análisis de CC
 Simulación de cortocircuitos
Simulación del CC a través de FF’
Curso de Capacitacion
ETAP
Cortocircuito
148
Técnicas para Análisis de CC
 Simulación de cortocircuitos
Cálculo de los cambios de tensión y corriente debidos al CC usando Thevenin
Curso de Capacitacion
ETAP
Cortocircuito
149
Técnicas para Análisis de CC
 Variación en el tiempo de las componentes ac y dc de la corriente de CC
Curso de Capacitacion
ETAP
Cortocircuito
150
Técnicas para Análisis de CC
 Variación en el tiempo de las componentes ac y dc de la corriente de CC
Curso de Capacitacion
ETAP
Cortocircuito
151
Técnicas para Análisis de CC
 Variación en el tiempo de las componentes ac y dc de la corriente de CC
Curso de Capacitacion
ETAP
Cortocircuito
152
Técnicas para Análisis de CC
 Variación en el tiempo de las componentes ac y dc de la corriente de CC
Curso de Capacitacion
ETAP
Cortocircuito
153
Técnicas para Análisis de CC
 Variación en el tiempo de las componentes ac y dc de la corriente de CC
Curso de Capacitacion
ETAP
Cortocircuito
154
Técnicas para Análisis de CC
 Variación en el tiempo de las componentes ac y dc de la corriente de CC
Curso de Capacitacion
ETAP
Cortocircuito
155
Técnicas para Análisis de CC
 Variación en el tiempo de las componentes ac y dc de la corriente de CC
La observación importante es que el decaimiento de la
componente de alterna de la corriente de CC es muy
pronunciado en el caso de falla cercana al generador pero
despreciable en el caso de falla lejana (eléctricamente) al
generador.
Contrariamente, el decaimiento de la componente de
continua de la corriente de CC es mayor en el caso de falla
lejana que en el caso de falla cercana.
Curso de Capacitacion
ETAP
Cortocircuito
156
Técnicas para Análisis de CC
 Variación en el tiempo de las componentes ac y dc de la corriente de CC
Curso de Capacitacion
ETAP
Cortocircuito
157
Técnicas para Análisis de CC
 Variación en el tiempo de las componentes ac y dc de la corriente de CC
Curso de Capacitacion
ETAP
Cortocircuito
158
Técnicas para Análisis de CC
 Variación en el tiempo de las componentes ac y dc de la corriente de CC
Curso de Capacitacion
ETAP
Cortocircuito
159
Técnicas para Análisis de CC
 Variación en el tiempo de las componentes ac y dc de la corriente de CC
Curso de Capacitacion
ETAP
Cortocircuito
160
Técnicas para Análisis de CC
 Variación en el tiempo de las componentes ac y dc de la corriente de CC
Curso de Capacitacion
ETAP
Cortocircuito
161
Estándares para Análisis de CC
 Revisión Histórica
En 1918 Fortescue presentó en una conferencia del AIEE (American Institute of
Electrical Engineers) una de las más poderosas herramientas para análisis de
cortocircuito en redes polifásicas equilibradas y desequilibradas:
 Fortescue, C. L. Method of Symmetrical Coordinates Applied to the Solution of
Polyphase Networks. Trans. AIEE 37: 1027-1140,1918
El procedimiento era aplicable al cálculo de soluciones analíticas así como también a
los cuadros de cálculo en cc y ca, por lo que fue ampliamente adoptado en Europa y
EEUU durante los primeros años de la industria eléctrica. Sin embargo, la complejidad
de los cálculos de cortocircuito para cualquier sistema de potencia en la práctica
industrial estaba mas allá del alcance de los cálculos manuales, independientemente
de la potencia del método de componentes simétricas. Resultaba claro la necesidad
de aproximar ciertas interacciones eléctricas para complementar el método de
componentes simétricas a través de un estándar.
Curso de Capacitacion
ETAP
Cortocircuito
162
Estándares para Análisis de CC
 Revisión Histórica
La primera metodología estándar para calcular corrientes de cortocircuito fue
introducida en 1929 por la VDE (Verband Deutscher Electrotechniker). En ese mismo
año, el MIT (Massachusetts Institute of Technology) y GE (General Electric Company)
desarrollaron conjuntamente un cuadro de cálculo en ca. Los estudios de cortocircuito
que podían hacerse en un cuadro de cálculo en cc, se podrían hacer a partir de ese
momento en forma mas precisa en un cuadro de cálculo en ca.
Entre 1940 y 1950 en EEUU la ASA (American Standards Association) desarrolló
estándares para calcular corrientes de cortocircuito similares a los de la VDE en el uso
de componentes simétricas pero diferentes en relación a los factores empíricos que
cada estándar usaba para aproximar fenómenos tales como el decaimiento temporal
de la corriente durante un cortocircuito. En 1969, ASA adopta el nombre de ANSI
(American National Standards Institute). En 1987, el estándar VDE 0102 fue
incorporado a un nuevo estándar IEC 909.
Con el paso del tiempo, los factores empíricos de los estándares se tornaron más
críticos debido al hecho de que la capacidad nominal del equipamiento eléctrico era
establecida en consonancia con cada método particular de cálculo.
Curso de Capacitacion
ETAP
Cortocircuito
163
Estándares para Análisis de CC
 Revisión Histórica
Como consecuencia de ello, tanto los estándares ANSI como los IEC para análisis de
cortocircuito han refinado su metodología y factores empíricos.
El estándar IEC 909 fue actualizado en 2001 como IEC 60909. El estándar IEEE
C37.010 (1999) es una actualización del de 1988 y éste del de 1979. Antes de 1964 el
estándar estaba basado en la corriente total en oposición al actual basado en la
corriente simétrica.
A diferencia del IEC 60909, el cual establece solamente los procedimientos de cálculo
de corrientes de cortocircuito, el IEEE C37.010 esta orientado al cálculo de las
solicitaciones de servicio de interruptores. En consecuencia, la metodología de cálculo
de corrientes de cortocircuito esta incluida dentro de la guía de aplicación de
interruptores.
Actualmente, la mayoría de los estudios de cortocircuito basados en estos estándares
se realiza en computadora digital, y los procedimientos empíricos para predecir la
respuesta del equipamiento han sido combinados con técnicas analíticas de reducción
de redes basadas en la manipulación de matrices ralas.
Curso de Capacitacion
ETAP
Cortocircuito
164
Editor de Estudio de CC ETAP®11
Selector de Modos de Estudio
Análisis de CC
Curso de Capacitacion
ETAP
Cortocircuito
165
Editor de Estudio de CC ETAP®11
Barra de Herramientas
Editor de Estudio
de CC
Curso de Capacitacion
ETAP
Cortocircuito
166
Editor de Estudio de CC ETAP®11
Tomas
transformadores
Nombre
del caso
de estudio
Subsistemas
monofásicos
CC a
bornes de
la carga
Impedancia de
cables y
protecciones
Contribución
Motores
Niveles
tensión barras
selección
barras CC
Hasta 120
caracteres
alfanuméricos
Curso de Capacitacion
ETAP
Cortocircuito
167
Análisis de Cortocircuito según
ANSI/IEEE
 AMERICAN NATIONAL STANDARDS INSTITUTE (ANSI)
Curso de Capacitacion
ETAP
Cortocircuito
168
Análisis de Cortocircuito según
ANSI/IEEE
 AMERICAN NATIONAL STANDARDS INSTITUTE (ANSI)
El estándar IEEE C37.010 es aplicable a interruptores de potencia con tensión
nominal mayor a 1 kV para uso en sistemas eléctricos de potencia industriales,
comerciales, así como en la red de transmisión y distribución, operados a
frecuencia nominal de 60 Hz. La metodología de cálculo fue desarrollada para
suministrar resultados conservativos para la determinación de las exigencias de
servicio por cortocircuito (short-circuit duties) y la determinación y selección de las
capacidades nominales de los interruptores de potencia.
La forma de onda de la corriente de cortocircuito asimétrica se supone que tiene la
máxima componente de continua.
El estándar no hace distinción entre los cortocircuitos alimentados por una única
fuente (red radial) o por múltiples fuentes (redes malladas).
El estándar trata solo con el calculo de las máximas corrientes de cortocircuito y
distingue entre cortocircuitos locales (con decaimiento de corriente) o remotos (sin
decaimiento).
Curso de Capacitacion
ETAP
Cortocircuito
169
Análisis de Cortocircuito según
ANSI/IEEE
 Descripción General de la metodología de cálculo
 Se reemplazan todos las fuentes de tensión externas y las fem internas de las maquinas por
una fuente de tensión equivalente en la localización de la falla, igual a la tensión de prefalla.
 Todas las máquinas se representan por sus impedancias internas.
 Las capacitancias de las líneas y las cargas estáticas se desprecian.
 Las fallas trifásicas son sólidas (no se considera resistencia de arco).
 Las impedancias del sistema se suponen equilibradas.
 Se emplea el método de Componentes Simétricas.
 Se conforman tres redes de secuencia para calcular las corrientes de cortocircuito
momentánea, de interrupción, y de régimen permanente; así como las exigencias de servicio
(duties) de los distintos dispositivos de protección. Estas redes son: la red de ½ ciclo (red
subtransitoria), la red de 1,5 - 4 ciclos (red transitoria) y la red de 30 ciclos (red de régimen
permanente).
Se determina una X/R para cada barra individual fallada. Esta relación se usa para determinar
el factor de multiplicación (MF) para cuantificar la componente de continua para la corriente de
cortocircuito.
Curso de Capacitacion
ETAP
Cortocircuito
170
Análisis de Cortocircuito según
ANSI/IEEE
 Red de ½ ciclo
Curso de Capacitacion
ETAP
Cortocircuito
171
Análisis de Cortocircuito según
ANSI/IEEE
 Red de ½ ciclo
Curso de Capacitacion
ETAP
Cortocircuito
172
Análisis de Cortocircuito según
ANSI/IEEE
 Red de 1,5 - 4 ciclos
Curso de Capacitacion
ETAP
Cortocircuito
173
Análisis de Cortocircuito según
ANSI/IEEE
 Red de 1,5 - 4 ciclos
Curso de Capacitacion
ETAP
Cortocircuito
174
Análisis de Cortocircuito según
ANSI/IEEE
 Red de 30 ciclos
Curso de Capacitacion
ETAP
Cortocircuito
175
Análisis de Cortocircuito según
ANSI/IEEE
 Red de 30 ciclos
Curso de Capacitacion
ETAP
Cortocircuito
176
Análisis de Cortocircuito según
ANSI/IEEE
 Factor de Multiplicación (MF)
El factor MF se determina a partir de la relación X/R del sistema equivalente en el
punto de falla.
 Contribuciones locales y remotas
Una contribución local a una corriente de cortocircuito es la porción de la corriente
de cortocircuito suministrada fundamentalmente por generadores que distan no
mas de un nivel de transformación o una reactancia en serie menor que 1,5 veces
la reactancia subtransitoria del generador. Toda otra contribución se considera
remota.
 Relación de no decaimiento de la corriente alterna (NACD)
Curso de Capacitacion
ETAP
Cortocircuito
177
Análisis de Cortocircuito según
ANSI/IEEE
 Cálculo de la corriente de CC momentánea
La corriente de CC momentánea representa el valor máximo de corriente de CC y
se calcula usando la red de ½ ciclo.
 Procedimiento de Cálculo
1) Cálculo del valor eficaz simétrico de la corriente de CC momentánea
donde Zeq es la impedancia equivalente de la red de ½ ciclo vista desde la falla.
2) Cálculo del valor eficaz asimétrico de la corriente de CC momentánea
Donde:
Curso de Capacitacion
ETAP
Cortocircuito
178
Análisis de Cortocircuito según
ANSI/IEEE
 Cálculo de la corriente de CC momentánea
3) Cálculo del valor pico de la corriente de CC momentánea
donde
Estos valores de la corriente de CC momentánea se usan para:
 Capacidad de cierre de interruptores de alta tensión (HVCB).
 Capacidad de interrupción de fusibles e interruptores de baja tensión (LVCB).
 Capacidad de esfuerzos en barras.
 Ajuste instantáneo de relevadores
Curso de Capacitacion
ETAP
Cortocircuito
179
Análisis de Cortocircuito según
ANSI/IEEE
 Cálculo de la corriente de CC de interrupción para HVCB
La corriente de CC de interrupción representa el valor de corriente de CC en el
periodo transitorio (1,5 - 4 ciclos) y se calcula usando la red de 1,5 - 4 ciclos.
Tiempo de partida de los contactos: La magnitud de la componente de
corriente continua en la corriente de CC de interrupción para interruptores de alta
tensión (HVCB) depende del tiempo de partida de los contactos (Contact Parting
Time: CPT)
Factor S: refleja la habilidad de un HVCB (con valores nominales simétricos)
para interrumpir una corriente de CC con componente de continua. Se define
como el cociente entre el valor eficaz asimétrico de la corriente de interrupción
nominal del HVCB y el valor eficaz simétrico de la corriente de interrupción
nominal del HVCB.
Curso de Capacitacion
ETAP
Cortocircuito
180
Análisis de Cortocircuito según
ANSI/IEEE
 Cálculo de la corriente de CC de interrupción para HVCB
 Procedimiento de Cálculo
1) Cálculo del valor eficaz simétrico de la corriente de CC de interrupción:
donde Zeq es la impedancia equivalente de la red de 1,5 - 4 ciclos vista desde la falla.
2) Cálculo de las contribuciones desde las otras barras a la corriente de CC de
interrupción
Curso de Capacitacion
ETAP
Cortocircuito
181
Análisis de Cortocircuito según
ANSI/IEEE
 Cálculo de la corriente de CC de interrupción para HVCB
o Si la contribución es desde una
barra remota, el valor eficaz
simétrico de la corriente de CC de
interrupción es corregido por el factor
de multiplicación para contribuciones
remotas:
donde t= CPT [ciclos].
Curso de Capacitacion
ETAP
Cortocircuito
182
Análisis de Cortocircuito según
ANSI/IEEE
 Cálculo de la corriente de CC de interrupción para HVCB
o Si la contribución es desde un
generador local, el valor eficaz
simétrico de la corriente de CC de
interrupción es corregido por el factor
de multiplicación para contribuciones
locales MFl
Curso de Capacitacion
ETAP
Cortocircuito
183
Análisis de Cortocircuito según
ANSI/IEEE
 Cálculo de la corriente de CC de interrupción para HVCB
3) Cálculo de las contribuciones remotas y locales totales y a partir de ellas del NACD
4) Cálculo del valor eficaz ajustado (asimétrico) de la corriente de CC de interrupción:
donde:
Curso de Capacitacion
ETAP
Cortocircuito
184
Análisis de Cortocircuito según
ANSI/IEEE
 Cálculo de la corriente de CC de interrupción para HVCB
5) Para HVCB con valores nominales simétricos, el valor eficaz ajustado (asimétrico)
de la corriente de CC de interrupción se calcula por:
S=1 para HVCB con valores nominales sobre la base de la corriente total.
Curso de Capacitacion
ETAP
Cortocircuito
185
Análisis de Cortocircuito según
ANSI/IEEE
 Cálculo de la corriente de CC de interrupción para LVCB
Debido a la acción instantánea de los LVCB a los máximos valores de corriente de
CC, la red de ½ ciclo se utiliza para calcular la corriente de CC de interrupción.
 Procedimiento de Cálculo
1) Cálculo del valor eficaz simétrico de la corriente de CC de interrupción:
donde Zeq es la impedancia equivalente de la red de ½ ciclo vista desde la falla.
Curso de Capacitacion
ETAP
Cortocircuito
186
Análisis de Cortocircuito según
ANSI/IEEE
 Cálculo de la corriente de CC de interrupción para LVCB
2) Cálculo del valor eficaz ajustado (asimétrico) de la corriente de CC de interrupción:
donde:
Basado en
corriente de
pico
Basado en
corriente
asimetrica
Curso de Capacitacion
ETAP
Cortocircuito
187
Análisis de Cortocircuito según
ANSI/IEEE
 Comparación de las capacidades nominales con las exigencias de
servicio (duties) de los distintos dispositivos de protección
Curso de Capacitacion
ETAP
Cortocircuito
188
Análisis de Cortocircuito según
ANSI/IEEE
 Interruptores asociados a generadores síncronos (IEEE C37.013 1997)
Curso de Capacitacion
ETAP
Cortocircuito
189
Análisis de Cortocircuito según
ANSI/IEEE
 Interruptores asociados a generadores síncronos (IEEE C37.013 1997)
Curso de Capacitacion
ETAP
Cortocircuito
190
Editor de Estudio de CC ETAP®11
Selección de la
tensión de prefalla
Norma
Capacidad de
interrupción
HVCB
Capacitancia
de secuencia
cero
Capacidad de
interrupción
LVCB
Resistencia de
armadura de
generadores
Factor de
multiplicación de
HVCB
Factor de
multiplicación de
LVCB
Exigencia de
servicio
Curso de Capacitacion
ETAP
Cortocircuito
191
Editor de Estudio de CC ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
192
Editor de Estudio de CC ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
193
Editor de Estudio de CC ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
194
Editor de Estudio de CC ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
195
Editor de Estudio de CC ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
196
Barra de Herramientas ANSI/IEEE
Curso de Capacitacion
ETAP
Cortocircuito
197
Barra de Herramientas ANSI/IEEE
Curso de Capacitacion
ETAP
Cortocircuito
198
Ejemplo de aplicación usando ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
199
Ejemplo de aplicación usando ETAP®11
CC
Curso de Capacitacion
ETAP
Cortocircuito
200
Ejemplo de aplicación usando ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
201
Ejemplo de aplicación usando ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
202
Ejemplo de aplicación usando ETAP®11
Visualización de
resultados
Curso de Capacitacion
ETAP
Cortocircuito
203
Ejemplo de aplicación usando ETAP®11
Visualización de
resultados
Curso de Capacitacion
ETAP
Cortocircuito
204
Ejemplo de aplicación usando ETAP®11
Alertas
Curso de Capacitacion
ETAP
Cortocircuito
205
Ejemplo de aplicación usando ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
206
Ejemplo de aplicación usando ETAP®11
Informe de
resultados
Curso de Capacitacion
ETAP
Cortocircuito
207
Ejemplo de aplicación usando ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
208
Ejemplo de aplicación usando ETAP®11
Informe de
resultados
Curso de Capacitacion
ETAP
Cortocircuito
209
Ejemplo de aplicación usando ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
210
Ejemplo de aplicación usando ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
211
Ejemplo de aplicación usando ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
212
Ejemplo de aplicación usando ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
213
Ejemplo de aplicación usando ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
214
Ejemplo de aplicación usando ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
215
Análisis de Cortocircuito según IEC
 INTERNATIONAL ELECTROTECHNICAL COMMISSION (IEC)
Curso de Capacitacion
ETAP
Cortocircuito
216
Análisis de Cortocircuito según IEC
 INTERNATIONAL ELECTROTECHNICAL COMMISSION (IEC)
La norma IEC 60909 y sus estándares asociados clasifican a las corrientes de CC
según su magnitud (máxima o mínima) y la distancia de la falla al generador (lejana
o cercana). Las corrientes de CC máximas determinan las capacidades del
equipamiento, mientras que la mínimas fijan los valores de ajuste de los
dispositivos de protección. La clasificación de la falla en cercana o lejana al
generador determina si se modela o no el decaimiento de la componente alterna,
respectivamente. El estándar es aplicable a sistemas eléctricos de baja tensión y de
alta tensión hasta 550 kV y de frecuencia nominal 50 Hz o de 60 Hz.
La norma IEC 61363-1 calcula las corrientes de CC en función del tiempo y calcula
su valor instantáneo usando las reactancias subtransitoria y transitoria, así como
las constantes de tiempo subtransitoria, transitoria y de corriente continua.
Curso de Capacitacion
ETAP
Cortocircuito
217
Análisis de Cortocircuito según IEC
 Descripción General de la metodología de cálculo
 Se reemplazan todos las fuentes de tensión externas y las fem internas de las
maquinas por una fuente de tensión equivalente en la localización de la falla. Se
aplica un factor de tensión c para ajustar el valor de la fuente de tensión equivalente
para calcular las corrientes mínimas y máximas de CC.
 Todas las máquinas se representan por sus impedancias internas.
 Las impedancias del sistema se suponen equilibradas.
 Se emplea el método de Componentes Simétricas.
 Se considera la distancia eléctrica desde la falla a los generadores asíncronos.
 Para fallas alejadas del generador se supone que la corriente de CC de régimen
permanente es igual a la corriente de CC inicial simétrica.
 En el cálculo de fallas desequilibradas se consideran las capacitancias de
secuencia cero de líneas de transmisión, cables y admitancias paralelo.
Curso de Capacitacion
ETAP
Cortocircuito
218
Análisis de Cortocircuito según IEC
 Descripción General de la metodología de cálculo
 Solo las componentes de corriente continua decrecen, excepto en el caso de fallas
cercanas al generador donde se considera el decaimiento de ambas componentes
(continua y alterna).
 La relación X/R determina la tasa de decrecimiento de las componentes continua y
alterna de las corrientes de cortocircuito empleándose diferentes valores para
generadores y motores cercanos a la falla.
 Definiciones
 Corriente de CC inicial simétrica (I”k): es el valor eficaz de la componente simétrica
de la corriente alterna de una corriente de CC presunta si la impedancia tuviera un
valor nulo.
 Corriente de CC pico (Ip): es el valor máximo instantáneo de la corriente de CC
presunta.
 Corriente de CC de ruptura simétrica (Ib): es el valor eficaz de la componente
simétrica de la corriente alterna de una corriente de CC presunta en el instante de
separación del contacto del primer polo del dispositivo de corte.
Curso de Capacitacion
ETAP
Cortocircuito
219
Análisis de Cortocircuito según IEC
 Definiciones
 Corriente de CC de régimen permanente (Ik): es el valor eficaz de la corriente
alterna de una corriente de CC presunta que permanece después del decaimiento del
transitorio.
Tensión Subtransitoria de la maquina síncrona (E”): es el valor eficaz de la fem
simétrica de la maquina síncrona la cual esta activa detrás de la reactancia
subtransitoria en el momento del CC.
 Cortocircuito alejado del generador: es la condición de CC durante la cual la
magnitud de la componente simétrica de corriente alterna de la corriente presunta de
CC permanece esencialmente constante.
Cortocircuito cercano al generador: es la condición de CC en la cual al menos una
máquina síncrona contribuye a la corriente presunta inicial de CC con más del doble
de su corriente nominal, o la condición de CC en la cual motores asíncronos y
síncronos contribuyen con más del 5% de la corriente de CC inicial simétrica sin
motores.
Curso de Capacitacion
ETAP
Cortocircuito
220
Análisis de Cortocircuito según IEC
 Definiciones
 Reactancia Subtransitoria de la maquina síncrona (Xd”): es la reactancia (saturada)
en el momento del CC. La impedancia de un motor asíncrono se calcula por
donde kVn y kVr son las tensiones nominales de barras y del motor, respectivamente.
Cmax se determina sobre la base de la tensión nominal del motor, Xd” es la reactancia
subtransitoria de la maquina (p.u) y φr es el ángulo del factor de potencia nominal del
motor síncrono.
Curso de Capacitacion
ETAP
Cortocircuito
221
Análisis de Cortocircuito según IEC
 Definiciones
 Tiempo de retardo mínimo del interruptor (Tmin): es el mínimo tiempo entre el
comienzo de la corriente de CC y la separación del primer contacto de un polo del
dispositivo.
 Factor de Tensión c: es el factor usado para ajustar el valor de la fuente de tensión
equivalente para calcular las corrientes mínimas y máximas de CC.
Curso de Capacitacion
ETAP
Cortocircuito
222
Análisis de Cortocircuito según IEC
 Métodos de cálculo
 Corriente de CC inicial simétrica (I”k):
donde Zk es la impedancia equivalente de la red vista desde la falla.
 Corriente de CC pico (Ip):
donde k es depende de la relación R/X de la red vista desde la falla.
Curso de Capacitacion
ETAP
Cortocircuito
223
Análisis de Cortocircuito según IEC
La norma IEC recomienda tres métodos:
 Método A
Ip 
 R 
" 
2 I k 1,02  0,98  exp  3 
X 
 


k
donde R/X es el menor valor existente de todas las ramas de la red
Curso de Capacitacion
ETAP
Cortocircuito
224
Análisis de Cortocircuito según IEC
 Método B
o
o
Baja Tensión
I p  1,08  2 I "k
Media Tensión

 R 
I p  1,15  2 I "k 1,02  0,98  exp   3 
X 
 


k
o
Alta Tensión
I p  2  2 I "k
donde R/X corresponde a la impedancia de la red vista desde la falla.
Curso de Capacitacion
ETAP
Cortocircuito
225
Análisis de Cortocircuito según IEC
 Método C
Ip 
 R 
" 
2 I k 1,02  0,98  exp  3 
X 
 


k
R /X se establece ahora por:
R R C 20

X X C 50
donde RC y XC corresponden a la impedancia de la red vista desde la falla
definida para una frecuencia estacionaria en la red de 20 Hz, si la
frecuencia nominal de la red es 50 Hz. (Para una frecuencia nominal de 60
Hz la frecuencia de calculo es 24 Hz)
Curso de Capacitacion
ETAP
Cortocircuito
226
Análisis de Cortocircuito según IEC
 Métodos de cálculo
 Corriente de CC de ruptura simétrica (Ib):
Para un CC alejado del generador:
Para un CC cercano al generador:
para maquinas síncronas
para maquinas asíncronas
donde μ y q son factores que tienen en cuenta el decaimiento de la componente
de corriente alterna.
Curso de Capacitacion
ETAP
Cortocircuito
227
Análisis de Cortocircuito según IEC
 Métodos de cálculo
 Componente de continua de la corriente de CC:
donde f es la frecuencia del sistema, tmin es el tiempo mínimo de retardo del dispositivo
de protección y X/R corresponde a la impedancia de la red vista desde la falla.
Corriente de CC de ruptura asimétrica :
Ii 
valor _ eficaz _ componente _ alterna 2  valor _ eficaz _ componente _ continua 2
Curso de Capacitacion
ETAP
Cortocircuito
228
Análisis de Cortocircuito según IEC
 Métodos de cálculo
 Corriente de CC de régimen permanente:
La corriente de CC de régimen permanente Ik es la combinación de las contribuciones de
los aportes de los generadores asíncronos:
donde IrG es la corriente nominal del generador y λ es función de la tensión de excitación
del generador, así como de otros parámetros del generador.
Curso de Capacitacion
ETAP
Cortocircuito
229
Análisis de Cortocircuito según IEC
 Comparación de las capacidades nominales con las exigencias de servicio (duties)
de los distintos dispositivos de protección
Curso de Capacitacion
ETAP
Cortocircuito
230
Análisis de Cortocircuito según IEC
 Comparación de las capacidades nominales con las exigencias de servicio (duties)
de los distintos dispositivos de protección
 Interruptores de Media Tensión:
Curso de Capacitacion
ETAP
Cortocircuito
231
Análisis de Cortocircuito según IEC
 Comparación de las capacidades nominales con las exigencias de servicio (duties)
de los distintos dispositivos de protección
 Interruptores de Baja Tensión:
Curso de Capacitacion
ETAP
Cortocircuito
232
Análisis de Cortocircuito según IEC
 Comparación de las capacidades nominales con las exigencias de servicio (duties)
de los distintos dispositivos de protección
 Fusibles:
Curso de Capacitacion
ETAP
Cortocircuito
233
Análisis de Cortocircuito según IEC
 Comparación de las capacidades nominales con las exigencias de servicio (duties)
de los distintos dispositivos de protección
 Corriente de CC equivalente térmica:
Curso de Capacitacion
ETAP
Cortocircuito
234
Editor de Estudio de CC ETAP®11
Factor de ajuste
de impedancias
de generadores y
transformadores
Norma
Capacitancia
de secuencia
cero
Método de
calculo de la
corriente de CC
de pico
Exigencia de
servicio
Valores nominales
de ruptura del
LVCB
Curso de Capacitacion
ETAP
Cortocircuito
235
Editor de Estudio de CC ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
236
Editor de Estudio de CC ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
237
Editor de Estudio de CC ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
238
Editor de Estudio de CC ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
239
Editor de Estudio de CC ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
240
Barra de Herramientas IEC
Curso de Capacitacion
ETAP
Cortocircuito
241
Barra de Herramientas IEC
Curso de Capacitacion
ETAP
Cortocircuito
242
Barra de Herramientas IEC
Curso de Capacitacion
ETAP
Cortocircuito
243
Ejemplo de aplicación usando ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
244
Ejemplo de aplicación usando ETAP®11
CC
Curso de Capacitacion
ETAP
Cortocircuito
245
Ejemplo de aplicación usando ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
246
Ejemplo de aplicación usando ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
247
Ejemplo de aplicación usando ETAP®11
Visualización de
resultados
Curso de Capacitacion
ETAP
Cortocircuito
248
Ejemplo de aplicación usando ETAP®11
Visualización de
resultados
Curso de Capacitacion
ETAP
Cortocircuito
249
Ejemplo de aplicación usando ETAP®11
Informe de
resultados
Curso de Capacitacion
ETAP
Cortocircuito
250
Ejemplo de aplicación usando ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
251
Ejemplo de aplicación usando ETAP®11
Informe de
resultados
Curso de Capacitacion
ETAP
Cortocircuito
252
Ejemplo de aplicación usando ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
253
Ejemplo de aplicación usando ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
254
Ejemplo de aplicación usando ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
255
Ejemplo de aplicación usando ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
256
Ejemplo de aplicación usando ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
257
Ejemplo de aplicación usando ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
258
Ejemplo de aplicación usando ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
259
Ejemplo de aplicación usando ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
260
Ejemplo de aplicación usando ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
261
Ejemplo de aplicación usando ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
262
Ejemplo de aplicación usando ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
263
Ejemplo de aplicación usando ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
264
Ejemplo de aplicación usando ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
265
Ejemplo de aplicación usando ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
266
Ejemplo de aplicación usando ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
267
Ejemplo de aplicación usando ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
268
Ejemplo de aplicación usando ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
269
Ejemplo de aplicación usando ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
270
Ejemplo de aplicación usando ETAP®11
Curso de Capacitacion
ETAP
Cortocircuito
271