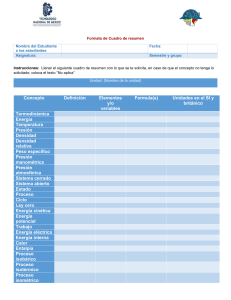
Universidad Nacional de Trujillo Filial Valle de Jequetepeque Curso: Termodinámica Docente: Dr. Ing. José Angel Florián Gutiérrez [email protected] Ingeniería Mecánica Primera ley de la termodinámica ➢ La primera ley de la termodinámica (o principio de la conservación de la energía) estudia la interacción de las diferentes formas de energía presentes en un sistema. alrededores Energía total de entrada Energía total de salida Sistema Cambio total de energía 30 J Sistema Cambio total de energía ¿El sistema gana, pierde, o mantiene su energía? 20 J 50 J Sistema Cambio total de energía 100 J ¿El sistema gana, pierde, o mantiene su energía? 70 J Sistema Cambio total de energía 70 J ¿El sistema gana, pierde, o mantiene su energía? Ecuación general del balance de energía para cualquier sistema (*) Forma de energía: J 𝐸𝑒𝑛𝑡𝑟𝑎𝑑𝑎 − 𝐸𝑠𝑎𝑙𝑖𝑑𝑎 = ∆𝐸𝑠𝑖𝑠𝑡𝑒𝑚𝑎 (1) (2) (3) (1) : Energía total que ingresa a un sistema por medio de calor, trabajo y masa. (2) : Energía total que sale de un sistema por medio de calor, trabajo y masa. (3) : Cambio total de las energías macroscópicas (cinética, potencia y otros) y microscópicas (interna, cinética, potencial, química, entre otros.) en un sistema. 𝐸𝑒𝑛𝑡𝑟𝑎𝑑𝑎 = 𝑄𝑒𝑛𝑡𝑟𝑎𝑑𝑎 + 𝑊𝑒𝑛𝑡𝑟𝑎𝑑𝑎 + 𝐸𝑚𝑎𝑠𝑎,𝑒𝑛𝑡𝑟𝑎𝑑𝑎 𝐸𝑠𝑎𝑙𝑖𝑑𝑎 = 𝑄𝑠𝑎𝑙𝑖𝑑𝑎 + 𝑊𝑠𝑎𝑙𝑖𝑑𝑎 + 𝐸𝑚𝑎𝑠𝑎,𝑠𝑎𝑙𝑖𝑑𝑎 ∆𝐸𝑠𝑖𝑠𝑡𝑒𝑚𝑎 = ∆𝑈 , ∆𝑈 ∶ Cambio de energía interna. Los otros cambios de energía se desprecian. (*) Forma de energía por unidad de tiempo: J/s = W 𝐸ሶ 𝑒𝑛𝑡𝑟𝑎𝑑𝑎 − 𝐸ሶ 𝑠𝑎𝑙𝑖𝑑𝑎 = 𝑑𝐸𝑠𝑖𝑠𝑡𝑒𝑚𝑎 /𝑑𝑡 (1) (2) (3) (1) : Razón de energía total que ingresa a un sistema por medio de calor, trabajo y masa. (2) : Razón de energía total que sale de un sistema por medio de calor, trabajo y masa. (3) : Razón de cambio total de las energías macroscópicas (cinética, potencia y otros) y microscópicas (interna, cinética, potencial, química, entre otros.) en un sistema. 𝐸ሶ 𝑒𝑛𝑡𝑟𝑎𝑑𝑎 = 𝑄ሶ 𝑒𝑛𝑡𝑟𝑎𝑑𝑎 + 𝑊ሶ 𝑒𝑛𝑡𝑟𝑎𝑑𝑎 + 𝐸ሶ 𝑚𝑎𝑠𝑎,𝑒𝑛𝑡𝑟𝑎𝑑𝑎 𝐸ሶ 𝑠𝑎𝑙𝑖𝑑𝑎 = 𝑄ሶ 𝑠𝑎𝑙𝑖𝑑𝑎 + 𝑊ሶ 𝑠𝑎𝑙𝑖𝑑𝑎 + 𝐸ሶ 𝑚𝑎𝑠𝑎,𝑠𝑎𝑙𝑖𝑑𝑎 𝑑𝐸𝑠𝑖𝑠𝑡𝑒𝑚𝑎 /𝑑𝑡 = 𝑑𝑈/𝑑𝑡 , 𝑑𝑈/𝑑𝑡: Razón de cambio de energía interna. Los otros cambios de energía se desprecian. (*) Forma de energía por unidad de masa: J/kg 𝑒𝑒𝑛𝑡𝑟𝑎𝑑𝑎 − 𝑒𝑠𝑎𝑙𝑖𝑑𝑎 = ∆𝑒𝑠𝑖𝑠𝑡𝑒𝑚𝑎 (1) (2) (3) (1) : Energía total por unidad de masa que ingresa a un sistema mediante calor, trabajo y masa. (2) : Energía total por unidad de masa que sale de un sistema mediante calor, trabajo y masa. (3) : Cambio total de las energías macroscópicas (cinética, potencia y otros) y microscópicas (interna, cinética, potencial, química, entre otros.) en un sistema por unidad de masa. 𝑒𝑒𝑛𝑡𝑟𝑎𝑑𝑎 = 𝑞𝑒𝑛𝑡𝑟𝑎𝑑𝑎 + 𝑤𝑒𝑛𝑡𝑟𝑎𝑑𝑎 + 𝑒𝑚𝑎𝑠𝑎,𝑒𝑛𝑡𝑟𝑎𝑑𝑎 𝑒𝑠𝑎𝑙𝑖𝑑𝑎 = 𝑞𝑠𝑎𝑙𝑖𝑑𝑎 + 𝑤𝑠𝑎𝑙𝑖𝑑𝑎 + 𝑒𝑚𝑎𝑠𝑎,𝑠𝑎𝑙𝑖𝑑𝑎 ∆𝑒𝑠𝑖𝑠𝑡𝑒𝑚𝑎 = ∆𝑢 , ∆𝑢 ∶ Cambio de energía interna por unidad de masa (o cambio de energía interna específica). Los otros cambios de energía se desprecian. 1. Balance de energía para sistemas cerrados ➢ En un sistema cerrado, puede existir transferencia de energía por calor y trabajo, pero no por flujo de masa. (*) Forma de energía: J ∆𝑼 = 𝑼𝟐 − 𝑼𝟏 = (𝑸𝒆𝒏𝒕𝒓𝒂𝒅𝒂 +𝑾𝒆𝒏𝒕𝒓𝒂𝒅𝒂 ) − (𝑸𝒔𝒂𝒍𝒊𝒅𝒂 +𝑾𝒔𝒂𝒍𝒊𝒅𝒂 ) , Sin usar convección de signos ∆𝑈: Cambio de energía interna en el sistema. ∆𝑈(+): La energía interna del sistema aumenta. 𝑈1 : Energía interna inicial en el sistema. 𝑈2 : Energía interna final en el sistema. ∆𝑈(−): La energía interna del sistema disminuye. Estado inicial Sistema 𝑼𝟏 Estado final 𝑄𝑒𝑛𝑡𝑟𝑎𝑑𝑎 𝑄𝑠𝑎𝑙𝑖𝑑𝑎 Sistema 𝑊𝑒𝑛𝑡𝑟𝑎𝑑𝑎 𝑊𝑠𝑎𝑙𝑖𝑑𝑎 Sistema 𝑼𝟐 ∆𝑼 = 𝑼𝟐 − 𝑼𝟏 = 𝑸 − 𝑾 , Usando convección de signos 𝑄 = 𝑄𝑒𝑛𝑡𝑟𝑎𝑑𝑎 − 𝑄𝑠𝑎𝑙𝑖𝑑𝑎 𝑊 = 𝑊𝑠𝑎𝑙𝑖𝑑𝑎 − 𝑊𝑒𝑛𝑡𝑟𝑎𝑑𝑎 Convección de signo o nomenclatura del calor y trabajo Interpretación de los signos en la ecuación de la 1° ley de la termodinámica para sistemas cerrados Interpretando la ecuación de la 1° ley de la termodinámica en su sistema cerrado cilindro-pistón (*) Forma de energía por unidad de tiempo: J/s = W 𝒅𝑼/𝒅𝒕 = 𝑼𝟐 (𝒕) − 𝑼𝟏 (𝒕) = (𝑸ሶ 𝒆𝒏𝒕𝒓𝒂𝒅𝒂 +𝑾ሶ 𝒆𝒏𝒕𝒓𝒂𝒅𝒂 ) − (𝑸ሶ 𝒔𝒂𝒍𝒊𝒅𝒂 +𝑾ሶ 𝒔𝒂𝒍𝒊𝒅𝒂 ) , Sin usar convección de signos 𝑑𝑈/𝑑𝑡: Razón de cambio de energía interna en el sistema. 𝑈1 (𝑡): Razón de energía interna inicial en el sistema. 𝑈2 (𝑡): Razón de energía interna final en el sistema. 𝑑𝑈/𝑑𝑡(+): La energía interna del sistema aumenta en el tiempo. 𝑑𝑈/𝑑𝑡(−): La energía interna del sistema disminuye en el tiempo. Estado inicial Sistema 𝑼𝟏 (𝒕) Estado final 𝑄ሶ 𝑒𝑛𝑡𝑟𝑎𝑑𝑎 Sistema 𝑊ሶ 𝑒𝑛𝑡𝑟𝑎𝑑𝑎 𝒅𝑼/𝒅𝒕 = 𝑼𝟐 (𝒕) − 𝑼𝟏 (𝒕) = 𝑸ሶ − 𝑾ሶ 𝑄ሶ = 𝑄ሶ 𝑒𝑛𝑡𝑟𝑎𝑑𝑎 − 𝑄ሶ 𝑠𝑎𝑙𝑖𝑑𝑎 𝑊ሶ = 𝑊ሶ 𝑠𝑎𝑙𝑖𝑑𝑎 − 𝑊ሶ 𝑒𝑛𝑡𝑟𝑎𝑑𝑎 𝑄ሶ 𝑠𝑎𝑙𝑖𝑑𝑎 𝑊ሶ 𝑠𝑎𝑙𝑖𝑑𝑎 , Usando convección de signos Sistema 𝑼𝟐 (𝒕) (*) Forma de energía por unidad de masa: J/kg ∆𝒖 = 𝒖𝟐 − 𝒖𝟏 = (𝒒𝒆𝒏𝒕𝒓𝒂𝒅𝒂 +𝒘𝒆𝒏𝒕𝒓𝒂𝒅𝒂 ) − (𝒒𝒔𝒂𝒍𝒊𝒅𝒂 +𝒘𝒔𝒂𝒍𝒊𝒅𝒂 ) , Sin usar convección de signos ∆𝑢: Cambio de energía interna por unidad de masa en el sistema. ∆𝑢(+): La energía interna del sistema aumenta. 𝑢1 : Energía interna inicial por unidad de masa en el sistema. ∆𝑢(−): La energía interna del sistema disminuye. 𝑢2 : Energía interna final por unidad de masa en el sistema. Estado inicial Sistema 𝒖𝟏 ∆𝒖 = 𝒖𝟐 − 𝒖𝟏 = 𝒒 − 𝒘 𝑞 = 𝑞𝑒𝑛𝑡𝑟𝑎𝑑𝑎 − 𝑞𝑠𝑎𝑙𝑖𝑑𝑎 𝑤 = 𝑤𝑠𝑎𝑙𝑖𝑑𝑎 − 𝑤𝑒𝑛𝑡𝑟𝑎𝑑𝑎 Estado final 𝑞𝑒𝑛𝑡𝑟𝑎𝑑𝑎 𝑞𝑠𝑎𝑙𝑖𝑑𝑎 Sistema 𝑤𝑒𝑛𝑡𝑟𝑎𝑑𝑎 , Usando convección de signos 𝑤𝑠𝑎𝑙𝑖𝑑𝑎 Sistema 𝒖𝟐 Ejemplo: ➢ Para los sistemas mostrados en las siguientes figuras: a) Determinar el cambio de energía interna, en kJ. Ejemplo: ➢ Un recipiente rígido contiene un fluido caliente y se enfría por agitación mediante las aspas de un ventilador. Durante el proceso de enfriamiento el fluido pierde 600 kJ de energía en forma de calor mientras que las aspas del ventilador realizan un trabajo de 200 kJ sobre el fluido. La energía interna inicial del fluido es de 1000 kJ e ignore la energía almacenada en el ventilador. a) Determinar la energía interna final del fluido, en kJ. Ejemplo: ➢ Un dispositivo cilindro-pistón contiene una masa de 4 kg de un gas y este realiza un proceso según la siguiente expresión 𝑃 ∙ 𝑉 1,5 = constante. La presión inicial del gas es de 3 bar, el volumen inicial de 0,1 𝑚3 y el volumen final de 0,2 𝑚3 . La variación de la energía interna del gas en este proceso es de – 4,6 kJ/kg y se desprecian los cambios en las energías cinética y potencial del gas. a) Determinar la transferencia neta de calor durante el proceso, en kJ. Práctica de ejercicios 1. Para los sistemas mostrados en las siguientes figuras: a) Determinar el cambio de energía interna, en kJ. 2. Complete cada renglón de la siguiente tabla, con base en el principio de conservación de energía para un sistema cerrado. 3. Un recipiente rígido contiene 10 L de una mezcla de agua líquida y vapor que está a la temperatura de 100°C y con una calidad de 12,3 %. Luego, la mezcla se calienta hasta la temperatura de 180°C. a) Determinar la transferencia de calor necesaria para este proceso, en kJ/kg. 4. Durante un proceso de un sistema cerrado, la energía total del sistema se incrementa en 60 kJ debido a un trabajo realizado sobre el sistema de 120 kJ. a) Determinar la transferencia neta de calor durante el proceso, en kJ. 5. Un sistema cerrado contiene inicialmente vapor saturado de agua. Este se enfría hasta líquido saturado a la presión constante de 40 kPa. a) Determinar la transferencia de calor durante el proceso, en kJ/kg. b) Dibujar el diagrama P-𝜐. 6. El aire contenido en un cilindro-émbolo vertical sostiene un pistón que tiene una masa de 100 kg y un área de sección transversal de 0,05 𝑚2 . El aire contenido en el cilindro tiene una masa de 10 g y un volumen inicial de 10 L. El aire pierde 2 kJ de energía en forma de calor y su volumen disminuye a 0,005 𝑚3 . La presión atmosférica es de 100 kPa y desprecie la fricción entre el pistón y la pared del cilindro. a) Determinar el cambio de energía interna específica del aire, en kJ/kg. 7. Un sistema cerrado cilindro-émbolo contiene inicialmente vapor saturado de R134a. Este se enfría hasta líquido saturado a 100°F y a presión constante. a) Determinar el trabajo realizado durante este proceso, en BTU/lbm. b) Determinar el calor transferido durante este proceso, en BTU/lbm. c) Dibujar el diagrama P-𝜐. 8. Un dispositivo cilindro-émbolo contiene inicialmente vapor saturado de agua. Este se condensa isotérmicamente hasta líquido saturado a 200°C. a) Determinar el trabajo realizado durante este proceso, en kJ/kg. b) Determinar el calor transferido durante este proceso, en kJ/kg. c) Dibujar el diagrama P-𝜐. 9. Un recipiente rígido y aislado contiene 5 kg de vapor húmedo de agua a 100 kPa. Inicialmente, tres cuartos de la masa está en fase líquida. Una resistencia eléctrica se coloca en el recipiente y se conecta con un suministro de voltaje de 110 V. Al cerrar un interruptor pasa una corriente de 8 A por la resistencia eléctrica. a) Determinar el tiempo necesario para evaporar todo el líquido, en min. b) Dibujar el diagrama T-V. 10. Un dispositivo aislado cilindro-émbolo contiene 5 L de líquido saturado de agua a una presión de 175 kPa. Una rueda de paletas agita el agua y una resistencia eléctrica calienta el agua por donde pasa una corriente de 8 A durante 45 min. Durante el proceso a presión constante, la mitad del líquido se evapora y el trabajo de la rueda de paletas es de 400 kJ. a) Determinar el voltaje de suministro, en V. b) Dibujar el diagrama T-V. 11. Un dispositivo cilindro-émbolo con carga de resorte contiene vapor de agua a 75 kPa de presión, a 2 𝑚3 de volumen y a 8% de calidad como se muestra en la figura. El vapor de agua se calienta hasta alcanzar un volumen de 5 𝑚3 y una presión de 225 kPa. a) Determinar el trabajo realizado durante este proceso, en kJ. b) Determinar el calor transferido, en kJ. c) Dibujar el diagrama P-𝜐.