Suelos

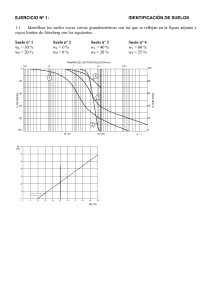
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
Curso de Mecánica de Suelos I.
Profesor Gerardo Silva Chandía.
Ingeniero Civil UC.
I. Objetivos generales de la asignatura.
Al término de la asignatura, el alumno estará en condiciones de:
a) Identificar en los suelos las características y propiedades de un material de ingeniería.
b) Identificar y calcular parámetros de diseño en obras civiles en relación con los suelos.
c) Planificar procesos de compactación en obra.
II. Unidades temáticas.
1. Introducción.
Definición de suelo. Naturaleza y origen. Suelos orgánicos e inorgánicos. Factores de formación. Suelos residuales y
transportados. Agentes de transporte. Alteraciones posteriores a la depositación. Reconocimiento del subsuelo.
2. Propiedades índice.
Propiedades de las partículas. Composición química y mineralógica. Tamaño. Forma. Superficie específica. Grado de
redondez. Textura superficial. Color.
Breve análisis de las partículas de arcilla.
Propiedades de los agregados.
Propiedades cualitativas. Textura. Estructura. Consistencia. Compacidad.
Propiedades cuantitativas. Relaciones de pesos y volúmenes. Consistencia. Compacidad. Ensayo de penetración
standard.
3. Ensayos de clasificación.
Determinación de características intrínsecas. Peso específico de los sólidos. Análisis granulométrico. Límites de
Atterberg.
Determinación de características de estado. Contenido de carbonatos. Humedad. Densidad aparente seca máxima y
mínima en suelos granulares. Angulo de reposo en arenas. Densidad aparente humeda.
4. Sistemas de clasificación.
Sistema USCS.
Características de ingeniería de los suelos según su clasificación USCS.
Sistema AASHTO.
Características de ingeniería de los suelos según su clasificación AASHTO.
Otros sistemas de clasificación de suelos.
5. Propiedades mecánicas e hidráulicas.
Resistencia al corte.
Estado de tensiones en un punto de la masa de suelo. Teorías de falla. Determinación de los parámetros de resistencia al
corte. Sensitividad. Tixotropia.
Características de compresión.
Generalidades. Distribución de presiones aplicadas, en el interior de la masa de suelo. Cálculo del asentamiento
instantáneo. Ensayo de consolidación 1D. Cálculo del asentamiento en el tiempo St.
Características de compactación.
Generalidades. Características de los ensayos mas frecuentes. Resultados de los ensayos de compactación.
Especificaciones de compactación. Control de calidad.
Hidráulica del suelo.
Presión efectiva. Presiones de escurrimiento. Permeabilidad. Capilaridad. Parámetros de presión de poros. Redes de
flujo.
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
MECÁNICA DE SUELOS BASICA
LABORATORIO
I.
Objetivos generales:
Capacitar al alumno para identificar los métodos y características de los ensayos que se utilizan para medir
propiedades en los suelos.
II.
Unidades temáticas:
1. Identificación y descripción de suelos.
2. Determinación de características intrínsecas.
3. Determinación de características de estado.
4. Determinación de propiedades mecánicas.
5. Determinación de propiedades hidráulicas.
6. Ensayos de control de calidad.
Bibliografía:
Foundation analysis and design, Bowles, Ed. Mc GrawHill. Kogakusha.
Soil mechanics and engineering. Scott and Schoustra. Mc GrawHill
Soil mechanics. Lambe and Whitman. Ed. Wiley Int.
Carreteras, calles y aeropistas. Raul Valle Rodas. Ed. El Ateneo.
Mecánica de suelos en la ingeniería vial. Dujisín y Rutllant.
Mecánica de suelos en la ingeniería práctica. Terzaghi y Peck. Ed. El Ateneo.
Theoretical Soil Mechanics. Terzaghi. Ed. Wiley and Sons
Soil testing for engineers. Lambe. Ed. Wiley and Sons.
Normas INN de mecánica de suelos.
Normas ASTM de mecánica de suelos.
Mecánica de suelos. Juarez Badillo (3 volúmenes)
Notas:
Las actividades del Laboratorio de Mecánica de suelos se integran dentro del quehacer propio de la asignatura de
Mecánica de Suelos I, razón por la cual, no se entrega un texto independiente para guiar las distintas prácticas.
En el Capítulo 4 de este texto, se incluye un conjunto de planillas Excel para facilitar la toma de datos y cálculo de
resultados en algunos ensayos, así como los sistemas de clasificación de suelos USCS y AASHTO, junto con tablas de
aplicaciones.
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
CAPITULO 1.
INTRODUCCIÓN.
1.1. Definición de suelo.
En Geología:
Roca → Todo material constituyente de la corteza.
Suelo→ Porción de la corteza que constituye el suelo vegetal.
En Mecánica de Suelos:
Roca: Agregado de minerales unidos por fuerzas cohesivas intensas y permanentes que en estado natural se encuentra en
grandes masas o fragmentos.
Suelo: Agregado natural de particulas minerales separables por medios mecánicos de poca intensidad de energía, como
por ejemplo: agitación en agua.
1.2 Naturaleza y Origen.
Según el origen de sus elementos componentes los suelos se clasifican en:
a) Suelos inorgánicos: resultan de la desintegración física y de la descomposición química de las rocas. Se subdividen
en:
• Suelos residuales: se encuentran en el mismo lugar de formación.
• Suelos transportados: se encuentran alejados de su lugar de formación.
b) Suelos orgánicos: resultan de la descomposición de vegetales (turbas), de la acumulación de fragmentos de
esqueletos o caparazones de crustáceos, moluscos u otros organismos.
En general se encuentran en el mismo lugar de formación.
La transformación de roca en suelo es un proceso que no alcanza nunca un estado de equilibrio permanente.
1.3 Factores de formación de los suelos inorgánicos.
• Material de origen o roca madre.
Pertenecen a los tipos ígneas, sedimentarias o metamórficas. Las ígneas y sedimentarias presentan una variedad de
silicatos. En general las rocas prersentan distintos minerales.
• El agua.
En la desintegración física: todas las rocas tienen un cierto grado de porosidad. Si existe agua en los poros y la
temperatura baja, permitiendo el paso al estado de hielo, el aumento de volumen (~9%) genera tensiones internas que se
renuevan en forma cíclica en los procesos hielo – deshielo. Esto conduce con el tiempo a la fragmentación del macizo
rocoso. Una vez fragmentados, los trozos de roca son arrastrados por los cursos de agua. Los torrentes arrastran los
bloques golpeándolos entre si o contra el lecho del cauce, fraccionándolos y desgastándolos por roce.
En los cursos inferiores de los ríos, la acción erosiva disminuye y la acción es más bien de transporte.
En la descomposición química: al tomar contacto con los elementos químicos y materia orgánica del suelo, el agua
produce reacciones físicoquímicas que originan una permamente transformación del suelo.
Al combinarse con CO2 origina ácido carbónico que ataca al Ca, Fe y Mg de las rocas.
Efecto de hidrólisis: a pesar de su baja concentración, los iones hidrógeno del agua, decomponen los silicatos,
disociándolos, solubilizándolos y transformándolos.
• Topografía o relieve.
Incide a través de las condiciones que presenta para el escurrimiento superficial o la acumulación del agua de las lluvias
y su acción subsecuente.
Los terrenos planos presentarán capas de suelo de espesor mayor que en las colinas y en ellos existirá una mayor
dependencia suelo-clima.
• Clima.
En general a mayor precipitación, mayor contenido de suelos formados por descomposición química.
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
• Temperatura.
Influye junto con el clima en la mayor o menor vegetación y en la existencia de materia orgánica.
En la desintegración física:
Las variaciones de temperatura producen cambios de volumen diferentes en cada uno de los minerales que componen la
roca, y distintos también en la superficie de la roca que en su interior. Esto origina tensiones internas alternativas que
van destruyendo la estructura rocosa.
En la descomposición química:
Las temperaturas altas acentúan el efecto de hidrólisis, por lo cual, los países fríos en general presentan suelos en
espesores de estratos pequeños y de formación por vía física, en tanto que las regiones tropicales, la acción química es
intensa y se generan profundos estratos de suelos arcillosos. En los desiertos, la temperatura es alta, pero al no existir
agua, no se produce hidrólisis, no hay acción química, el suelo es arenoso o pedregoso.
RESUMEN
En la desintegración física, la acción de los factores de formación se traduce en un progresivo y creciente
fraccionamiento de la roca y sus fragmentos sin cambiar su composición química, hasta alcanzar tamaños muy reducidos
de partículas homogéneas y compuestas en general por un solo mineral (bloques, cantos rodados, bolones, gravas, arena,
limo).
En la descomposición química, los factores de formación originan un suelo de composición mineralógica distinta a la de
la roca madre y de una finura muchísimo mayor que la acción física (arcilla).
1.4 Suelos residuales y transportados.
•
•
Suelos residuales: se encuentran en el lugar de su formación. Su espesor depende de las condiciones climáticas
pudiendo alcanzar varias decenas de metros. En las zonas templadas, salvo excepciones, constituyen suelos firmes y
estables.
Suelos transportados: se encuentran alejados de su lugar de formación, constituyendo sedimentos o depósitos.
Pueden ser:
a) Aluviales o aluvionales: transportados por el agua.
b) Aeolianos o eólicos: transportados por el viento (dunas, loess).
c) Glaciales: Originados por movimientos de glaciares.
d) Coluviales o eluviales: movidos por la gravedad (detritos de ladera o escombros de falda).
1.5 Influencia de los agentes de tranporte en los depósitos de suelos transportados.
En general: alteran la forma, textura y tamaño de las partículas, por abrasión, impacto, roce y disolución. Clasifican las
partículas permitiendo su depositación al variar la energía, velocidad o condiciones fisicoquímicas de transporte. A
mayor energía del flujo en el momento de la depositación, más compactos y estables serán los depósitos o sedimentos.
• El agua: torrentes, ríos, lagos, océanos.
Interesa la energía del transporte
Origina depósitos homogéneos en planta, de partículas redondeadas, con heterogeneidad vertical.
Depósito aluvial o fluvial.
Cono o abanico fluvial.
Predominio de grava.
Bolones
Grava
Depósitos de arena
Depósitos
marinos
Finos de origen
Glacial
Finos eventuales
(Depósitos lacustres)
Finos por
Floculación en
ambientes salinos
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
•
Viento:
•
Glaciares: Originan depósitos con gran diversidad de tamaños (desde bloques hasta limos), heterogéneos, de
partículas angulosas y estriadas.
Loess: llanuras de finos y arenas.
Dunas: acumulación de granos uniformes por pérdida de energía del flujo de transporte.
Característica de los depósitos eólicos: gran selectividad de tamaño.
1.6 Alteraciones del suelo después de su formación.
Además de las características adquiridas en el proceso de formación del suelo, se debe considerar los cambios
producidos o por producirse, en forma posterior, debidos a:
• Historia de esfuerzos.
La presión asimilada por la masa de suelo, es proporcional a la profundidad respecto a las últimas capas depositadas. Si
ellas aun permanecen, el suelo se designa como normalmente consolidado (N.C.). Si ellas han sido removidas, el suelo
se designa como preconsolidado o precargado (P.C.).
En general el aumento de los esfuerzos aplicados a la masa de suelo, hará variar sus propiedades de comportamiento.
• Tiempo.
Permite la acción de factores como agua, presión y cambios de contorno.
Influye en las reacciones químicas de la descomposición del suelo.
• Agua.
Disminuye la fuerza de atracción entre partículas de arcilla. En los poros del suelo puede compartir presiones aplicadas
al mismo.
En general reduce la resistencia del suelo.
Puede realizar una acción de erosión.
• Cambios de contorno o ambiente.
Las propiedades del suelo cambian al variar la naturaleza del fluido de los poros y la temperatura.
Ejemplo 1: arenas cementadas del norte de Chile, pierden resistencia al sufrir la acción artificial del agua, motivada por
la presencia humana. EM2001-05-19A.htm Video
Ejemplo 2: Hundimientos (subsidencia) de la superficie de masas de suelo, por descenso de la napa por captación de
agua subterránea.
1.7 Reconocimiento del subsuelo.
Cuando se considera la posibilidad de construir una obra civil en un lugar dado, debe realizarse un reconocimiento del
subsuelo.
Este reconocimiento está conformado por las siguientes etapas:
a)
Recopilación de información.
Se trata de reunir información existente relacionada con el sitio del proyecto.
Se puede obtener en las Direcciones de Obras Municipales, en los Laboratorios de Mecánica de Suelos, en el
Laboratorio Nacional de Vialidad, en el Ministerio de Obras Públicas (MOP), en oficinas de consultores en
Geotecnia, etc.
En algunos casos se puede obtener mapas, cartas o planos con información de zonificaciones sísmicas, tipos de
suelo, etc.
b) Exploración indirecta.
En proyectos de importancia, se estima los principales parámetros geotécnicos en base a exploraciones superficiales
que son rápidas y económicas, tales como los reconocimientos basados en estudios sísmicos de superficie,
gravimetría, resistividad eléctrica, etc.
c)
Exploración directa.
Consiste en definir si el reconocimiento del subsuelo se realizará utilizando calicatas, zanjas, pozos o sondajes.
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
Las calicatas son excavaciones de dimensiones reducidas, en general de forma rectangular y de no mas de 2 a 4 m,
ejecutadas a mano o con retroexcavadora.
Las zanjas se ejecutan con retroexcavadora o bulldozer y en general buscan determinar las características de
posibles empréstitos desde donde extraer material.
Los pozos son excavaciones de planta circular o rectangular, de profundidades del orden de hasta 20 m, ejecutadas
por personal experto, utilizando las medidas de seguridad adecuadas, especialmente entibación (sostenimiento de las
paredes) cuando es necesario, y ventilación forzada.
Los sondajes son exploraciones profundas que pueden alcanzar varias decenas de metros, ejecutadas con maquinas
especiales llamadas “sondas”.
La exploración directa puede o no ser precedida, según el tipo de proyecto, de un reconocimiento preliminar
indirecto, tales como las prospecciones sísmicas de superficie, estudios de resistividad eléctricos, estudios
geológicos, etc.
Siempre debe realizarse la etapa de exploración del subsuelo.
Si existe un conocimiento previo de las características generales del lugar, entonces esta exploración tendrá un
carácter de “verificación”, se realizarán pocas perforaciones y reducida cantidad de ensayos de laboratorio o terreno.
Si el lugar es poco “conocido” de antemano, entonces será necesario una información geológica preliminar y luego
una cantidad de exploraciones y ensayos que dependerán de la importancia del proyecto.
En el CD se puede ver un video que ilustra una perforación del subsuelo pero para obtener agua subterránea.
Si desea verlo haga clic aquí.
d) Muestreo.
En las exploraciones se obtendrán tanto muestras perturbadas como no perturbadas, en lo posible, con el objeto de
realizar los ensayos de laboratorio que permitan clasificar adecuadamente los estratos de suelo comprometidos por
el proyecto, y conocer las propiedades índice necesarias para los cálculos geotécnicos.
e)
Ensayos in situ.
En algunos casos es necesario realizar ensayos en el terreno mismo, lo que en general resulta caro y lento, pero
puede ser indispensable según el tipo de proyecto, ya que hay casos en que los ensayos de laboratorio no resultan
representativos.
1.8 Interpretación de resultados.
Los resultados de las exploraciones y ensayos efectuados, deben ser interpretados por ingenieros de experiencia, para
poder responder preguntas tales como:
- Capacidad de soporte del suelo.
- Asentamientos esperados.
- Empujes de rellenos contra las estructuras.
- Gasto de agua que infiltraría.
- Selección de materiales y procedimientos de colocación en obra.
- Etc.
1.9 Informes de Mecánica de Suelos o Informes Geotécnicos.
Reúnen toda las informaciones anteriores y entregan las recomendaciones necesarias para la construcción del proyecto,
en lo relacionado con el suelo, expresado en términos de Especificaciones Técnicas y planos.
Material complementario en inglés obtenido de Internet:
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
CAPITULO 2.
PROPIEDADES INDICE
Llamamos propiedades índice a aquellas características que permiten diferenciar los distintos tipos de suelos entre si, y
aquellos diferentes aun dentro de una misma categoría.
Como el comportamiento de una masa de suelo depende de propiedades significativas de los granos, y de propiedades
determinadas por el acomodo de las partículas, consideraremos:
• Propiedades de las partículas.
• Propiedades de los agregados.
2.1. Propiedades de las partículas.
2.1.1. Composición química y mineralógica
En las rocas se encuentran en combinación con el oxígeno los siguientes elementos: Al, Fe, Mg, Ca, Na, K (metales + O2
→ óxidos + H2O → Bases)
Si se combinan (Metaloides + O2 → Anhídridos + H2O → ácidos).
Mineral es un elemento o compuesto químico presente en la naturaleza y formado por un proceso geológico.
Principales minerales (según el arreglo o estructura de los átomos), que se encuentran en las rocas:
Cuarzo (Sílice SiO2 o anhidrido silícico)
Feldespato (Silicatos dobles de Al y Na o K o Ca)
Mica (Silicatos hidratado de Al + K o Fe o Mg)
Caolinita (Silicato hidratado de Al)
Serpentina. Talco (Silicatos de Mg)
Calcita (Carbonato de Ca)
Dolomita (Carbonato de Ca y Mg)
Yeso (Sulfato de Ca hidratado)
Los minerales según su composición química (naturaleza de los átomos), se dividen en:
Silicatos, carbonatos, óxidos (magnetita, hematita, limonita) y sulfatos.
Características tales como plasticidad y velocidad de degradación en los suelos finos, dependen de la descomposición
química de las partículas.
2.1.2. Tamaño de las partículas.
Depende del tipo de minerales que componen el suelo.
Es la primera característica que se observa y la menos difícil de “medir”.
No existe una nomenclatura única y uniforme para designar los diferentes tamaños.
Adoptaremos la del sistema unificado de clasificación de suelos (USCS)
• Cantos rodados:
Tamaño mayor de 8”
• Bolones:
Tamaño entre 3” y 8”
• Grava:
Tamaño entre 4.76 mm (Malla N° 4 ASTM) y 3”
• Arena:
Tamaño entre 0.074 mm Malla N° 200 ASTM) y 4.76 mm
• Finos (Limos y arcillas)
Tamaño menor de 0.074 mm
Gravas y arenas constituyen la “Fracción gruesa” del suelo, partículas visibles a simple vista.
Desarrollan una gran estabilidad cuando se encuentran confinadas, no tienen cohesión debido al gran tamaño de sus
partículas.
Limos y arcillas constituyen la “fracción fina” del suelo, partículas prácticamente invisibles a simple vista.
En caso de las arcillas, debido a su extrema finura, las partículas están sujetas a fuerzas de tipo molecular y eléctrico,
cuya atracción mutua les permite desarrollar resistencia al corte, formando el campo de los suelos cohesivos.
Los limos constituyen un campo intermedio, ya que sus partículas son de tamaño insuficiente como para formar un
esqueleto resistente y desarrollar alta estabilidad y muy grandes para adquirir cohesión por fuerzas de tipo eléctrico y
molecular.
El tamaño de las partículas influye en las propiedades de capilaridad y permeabilidad del suelo.
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
2.1.3. Forma de las partículas.
Está relacionada con la composición mineralógica del material.
Influye en la formación de vacíos o espacios (poros o huecos) en la masa del suelo.
En general las partículas de gravas, arenas y limos son aproximadamente equidimensionales a excepción de las
partículas de mica que tienen forma de placas, y los fragmentos conocidos como “lajas”.
Las partículas de arcilla son en su mayoría en forma de placas, y en menor proporción en forma de barras o agujas.
2.1.4. Superficie específica.
Es una característica importante en el comportamiento de las fracciones finas.
Es la relación entre el área superficial o envolvente, y el volumen de las partículas del suelo.
2.1.5. Grado de redondez, textura superficial y color.
El grado de redondez se refiere a la agudeza o filo de los bordes y esquinas de la partícula. Se califica como: angular,
subangular, subredondeada, redondeada, bien redondeada.
La textura de la superficie se califica como: opaca, brillante, suave, áspera, estriada, etc.
El color, si bien tiene poca aplicación directa (excepto la identificación de suelos orgánicos), debe ser usado siempre en
las descripciones de suelo, teniendo presente que puede variar con la humedad o composición química.
Las materias orgánicas en general presentan colores café oscuro-negruzco, negro o verdoso.
Los componentes de hierro originan colores rojizos (alto contenido de Fe 2O3) a gris.
2.2. Breve análisis de las partículas de arcilla.
2.2.1. Generalidades.
Los minerales constituyentes de la roca madre, se pueden diferenciar en términos generales, en fuertes y débiles respecto
a los procesos de desintegración física y descomposición química, que dan origen a las partículas de suelo.
Los minerales o agregados de minerales fuertes, resisten la acción de los factores de formación, en una medida que
permite la obtención de partículas de tamaños cada vez menores, pero los cuales llegados a un cierto límite, ya no se
degradan y en términos de las presiones aplicadas normalmente en los problemas de ingeniería, se consideran
adecuadamente resistentes de modo que en general, un análisis mineralógico de un suelo granular, no tiene
consecuencias prácticas.
Por el contrario, los minerales débiles, durante el proceso de formación del suelo, son removidos químicamente de la
roca madre o sus fragmentos y pasan a formar parte de una solución, la cual posteriormente al darse condiciones
favorable, da origen a una recristalización y recombinación de los minerales primitivos, dando como resultado nuevos
minerales (minerales arcillosos), cuyo rango de tamaños y comportamiento, depende de la forma cristalográfica
alcanzada.
Los minerales arcillosos se agrupan en general, en tres tipos principales: caolinitas, montmorillonitas e illitas.
2.2.2. Composición mineralógica.
Los minerales arcillosos están compuestos por dos tipos de “ladrillos” o unidades estructurales básicas.
Símbolo
Mineral
Fórmula
Estructura
Molecular
Estructura del agregado
molecular
Sílice, dióxido de silicio
SiO2
Tetraedro
Láminas o placas
Gibsita, hidróxido de Al
Al (OH)2
Octaedro
Láminas o placas
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
H
•
Caolinitas:
Nota: escala vertical muy exagerada
B
B
A
D
0.1 a 10
A
D/H : 40/1 a 50/1
Unidades estructurales
Partícula de caolín
La unión de sílice y gibsita para formar la unidad estructural básica, es posible gracias al espaciamiento similar de las
moléculas de los dos “ladrillos” y a su distribución hexagonal en el plano de las láminas, constituyendo un enlace
relativamente fuerte.
De la misma forma es posible la unión de las unidades estructurales según los planos “AA” y “BB” para conformar la
partícula en agrupaciones sucesivas. Este enlace sin embargo, es relativamente más débil que el anterior.
Se obtiene entonces:
Partícula constituída por
varias láminas hexagonales
•
120°
Montmorillonitas:
Nota: escala vertical muy exagerada.
B
A
H
B
A
C
Moléculas de agua (hasta 6 capas)
C
Unidad estructural
D<0.1
D/H: N x 100 : 1
Los enlaces “AA” y “BB” son relativamente fuertes.
Los enlaces “CC” son relativamente débiles. Constituyen planos de clivaje que originan tamaños muy pequeños de
partícula. Presentan tendencia a la absorción de moléculas de agua, lo que hace crecer la razón W W/WS (peso de agua /
peso sólido) a valores elevados.
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
•
Illitas:
Nota: escala vertical muy exagerada.
Estructura relativamente estable originada por la aptitud del potasio para ubicarse en el plano “CC”
Potasio
C
C
1 A 10
Es posible que elementos como Fe y Mg, puedan formar parte de las unidades estructurales básicas, sustituyendo en el
caso de la gibsita algunos átomos de Al, por lo cual, se puede obtener una gran variedad de minerales arcillosos
(sustitución isomórfica).
2.2.3. Actividad de superficie.
En general las partículas arcillosas debido a su forma de placas, presentan una gran superficie respecto a su volumen.
Debido a su estructura molecular se tiene:
•
•
Cargas negativas de cara
Cargas negativas de borde
Partícula de arcilla
_
_
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
Este hecho origina dos tipos principales de interacción con el agua de los poros:
Solución neutra
Características:
Escasos electrolitos
Capa adsorbida fuerte (doble capa)
Mutua repulsión de las partículas
Estructura microscópica de tipo disperso
No hay contacto sólido - sólido
Estructura dispersa
Solución salina
+
+
+
+
+
+
+
+
Características:
Abundantes electrolitos
Capa adsorbida débil
Atracción de las partículas
Estructura microscópica de tipo floculento
Hay contactos cara – borde
(Estructura similar a un castillo de naipes)
Estructura floculenta
2.3. Propiedades de los agregados.
Se aplica el término “agregado”, al suelo mismo, en contra posición a sus elementos constituyentes (partículas).
Los agregados pueden diferir:
•
•
Cualitativamente: textura, estructura, consistencia, compacidad.
Cuantitativamente: valores de relaciones pesos – volúmenes, consistencia y compacidad.
Los datos cualitativos se obtienen en terreno, por inspección visual, y sirven de base para definir los sucesivos estratos
del subsuelo.
Los datos cuantitativos se obtienen por medio de ensayos de laboratorio o ensayos “in situ”, según el caso.
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
2.3.1.
a)
Propiedades cualitativas.
Textura.
Se refiere al grado de fineza y uniformidad del suelo. Se describe en términos como harinoso, suave, arenoso, áspero,
etc., según la sensación que produce al tacto.
b) Estructura.
Se refiere a la forma en que las partículas están dispuestas en el agregado de suelo, identificables a simple vista. Algunas
estructuras posibles son las que se describen a continuación:
•
•
•
•
•
•
•
•
•
c)
Estructura de adobe: grietas de contracción grandes y profundas, que forman bloques aproximadamente
cúbicos. Es típica en suelos con alto contenido de arcillas coloidales.
Estructura de panal: grietas finas que forman figuras regulares de 5 ó 6 lados. Indica una mayor proporción de
limo.
Estructura vesicular: Cavidades redondeadas y suaves. Es típica en suelos de alta compresibilidad.
Estructura de migajón: masa de suelo porosa, formada por partículas de forma irregular. En general
corresponde a suelos de baja consistencia.
Estructura densa: suelos con escasos poros visibles y ausencia de grietas.
Estructura laminar o estratificada: capas de pequeño espesor. Consistencia media a baja.
Estructura toscosa: partículas unidas con un alto grado de cementación, siendo el ligante de tal naturaleza, que
no se altera en presencia de agua.
Estructura simple granular: suelo granular sin cohesión ni arreglo especial de las partículas. En general,
corresponde a fracción gruesa.
Estructura conglomerada: suelo granular con finos cohesivos. En general presenta integradas las fracciones
gruesas y finas.
Consistencia y compacidad.
Dicen relación con la resistencia que opone el suelo a las fuerzas que tienden a deformarlo o romperlo.
En el caso de los suelos sin cohesión, se clasifica la compacidad como muy suelta, suelta, medianamente densa, densa,
muy densa.
En el caso de los suelos cohesivos, se clasifica la consistencia como muy blanda, blanda, media firme, muy firme, dura.
En el caso de los suelos finos es posible estimar en las paredes de una excavación de reconocimiento, su consistencia
intentando diferentes pruebas simples de penetración tales como las de la tabla siguiente:
Prueba de penetración
Consistencia
Se hunde el puño
Muy blanda
Puño deja huella
Blanda
Se hunde el pulgar
Media
Pulgar deja huella
Firme
Se hunde punta de lápiz Muy firme
Punta de lápiz deja huella Dura
Se raya con cuchillo
Muy dura
2.3.2.
•
Propiedades cuantitativas.
Relaciones de pesos y volúmenes.
En la masa de suelo encontramos tres elementos o fases constituyentes: partículas minerales, agua y aire (u otros fluidos
eventualmente). Las relaciones entre los pesos y volúmenes de estos elementos dan origen a los siguientes términos,
explicados en el modelo.
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
Modelo de tres fases del suelo:
Volumen
Suelo
Peso
VA
Aire
WA= 0
Agua
WW
VV
VW
VT
WT
VS
Sólido
WS
Relaciones de fase:
=
WW
 100
WS
S=
VW
V
 100 = W  100
VA + VW
VV
 =
WW + WS WT
=
VT
VT
Humedad (%)
Grado de saturación (%)
Peso unitario húmedo o densidad aparente húmeda (Kg/Lt)
d =
WS
VT
S =
WS
VS
GS =
S
w
Peso unitario seco o densidad aparente seca (Kg/Lt)
Densidad de los sólidos (Kg/Lt)
Peso específico de los sólidos
=
VA + VW
V
 100 = V  100
VT
VT
e=
VA + VW VV
=
VS
VS
Porosidad o porcentaje de huecos (%)
Indice de huecos (valor decimal)
Con estas definiciones básicas, se pueden derivar otras relaciones:
Ejemplo: Hallar n = n(e).
Como e = Vv / VS, si asignamos arbitrariamenmte en el modelo el valor “1” a VS, se obtiene:
Vv = e Vs = e · 1= e ; VT = VV + VS = e + 1 ; n = VV / VT = e / (1 + e)
e
Vv
1
Vs
1+e
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
Ejemplo: Hallar e = e(n).
Como n = Vv / VT, si asignamos arbitrariamente en el modelo el valor “1” a V T, se obtiene:
VV = n · VT = n · 1 = n ; VS = VT - VV = 1 - n ; e = VV / VS = n / (1 - n)
Vv
1
Vs
n
1-n
Ejemplo: Hallar  =  (d,)
 =
WW + WS 0.01WS + WS WS (1 + 0.01 )
=
=
=  d (1 + 0.01 )
VT
VT
VT
; con  en %
Otras relaciones usuales:
d =

1 + 0.01 ; con  en %
GS · = S·e
G
e = S  −1
d
 (G + e·S )
=  S
1+ e
•
Compacidad.
Dado que la forma de los granos y su uniformidad de tamaño, ejercen una gran influencia sobre la porosidad, valores
aislados de “n” o “e”, no proporcionan una indicación de si un suelo es suelto o denso.
El grado de densificación que un suelo no cohesivo presenta en un estado natural (compacidad), se obtiene por
comparación con los estados más denso y más suelto posibles del mismo.
Numéricamente, el grado de compacidad de un suelo sin cohesión se puede expresar por su densidad relativa (DR) o
índice de densidad:
DR(%) =
emax − e
 ( −  dmin)
100 = dmax d
100
emax − emin
 d ( dmax −  dmin)
Con:
emax: índice de huecos del suelo en la condición más suelta
emin: índice de huecos del suelo en la condición más densa
e : índice de huecos del suelo en el terreno
dmax: peso unitario seco del suelo en la condición más densa
dmin: peso unitario seco del suelo en la condición más suelta
d : peso unitario seco del suelo en terreno
Sobre la base del valor de la “DR” los suelos sin cohesión se caracterizan como:
DR(%)
0 – 15
15 – 35
35 – 65
65 – 85
85 – 100
Descripción
Muy suelto
Suelto
Medianamente denso
Denso
Muy denso
Nspt * (arenas)
0 – 4 golpes/pie
4 – 10
10 - 30
30 - 50
> 50
* Nspt: Número de golpes en el ensayo de penetración standard (Standard Penetration Test) que se explica mas adelante.
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
•
Consistencia.
La medida cuantitativa mas directa de la consistencia de los suelos cohesivos se obtiene a través de la determinación de
la resistencia a la compresión simple o no confinada, de muestras prismáticas o cilíndricas de suelo:
Consistencia
Muy blanda
Blanda
Media
Firme
Muy firme
Dura
•
Resistencia a la compresión simple (qu)
< 0.25 Kgf/cm2
0.25 – 0.5
0.5 – 1.00
1.0 – 2.0
2.0 – 4.0
> 4.0
Nspt (arcilla)
< 2 golpes/pie
2-4
4-8
8 - 15
15 - 30
> 30
Determinación de la compacidad y consistencia por ensayos IN SITU.
Se obtienen a través del ensayo de penetración standard, SPT, normalizado en ASTM D1586 – 63T. Los parámetros mas
importantes del ensayo son:
Peso del martinete: 140 libras, altura de caída libre 30 pulgadas, penetración guía: 6 pulgadas (15 cm), penetración
registrada: 12 pulgadas (30 cm). Se cuenta el número de golpes necesario para avanzar un pié (1 foot), con la “cuchara
normal” como herramienta muestreadora.
El ensayo se realiza en el interior de un sondaje de reconocimiento del subsuelo, a las profundidades especificadas por el
Mecánico de Suelos, o bien, a profundidades representativas de los estratos que se van descubriendo.
En el desarrollo del sondaje se distinguen tres etapas:
a) Avance o profundización, para lo cual se usan herramientas adecuadas al material que se está atravesando, y
b) Muestreo, el cual se puede hacer usando la “cuchara normal” u otro muestreador adecuado al material
encontrado. Si se especifica la realización del ensayo SPT, entonces debe usarse la cuchara normal, siempre que
se esté en un suelo arenoso o fino.
c) Término del sondaje. Este se define como la profundidad pre establecida por el Mecánico de Suelos para ese
sondaje, o bien, por la llamada condición de “Rechazo”. Son “Condiciones de rechazo”: N >= 100 golpes/pie ó
avance menor que 1” para 50 golpes. Una correlación empírica entre “Nspt”, o sea, el número de golpes
necesarios para enterrar 30 cm la cuchara normal en las condiciones normalizadas, y la compacidad ó
consistencia según el caso, se señala en los párrafos anteriores.
Detalles del ensayo de penetración standard y de la ejecución de sondajes de reconocimiento del subsuelo, se ilustran en
una sesión de diapositivas presentadas en la clase presencial.
En el CD se puede ver un video que ilustra una perforación del subsuelo pero para obtener agua subterránea.
Si desea verlo haga clic aquí.
Como dato anecdótico conviene señalar que en el caso de las exploraciones del tipo calicatas, zanjas y pozos, se puede
estimar el valor qu (resistencia a la compresión simple o no confinada) del suelo de los estratos cohesivos, utilizando un
“Penetrómetro de bolsillo”, el cual se presiona en las paredes de la exploración, hasta hundirlo hasta una cierta marca
grabada en el cilindro de penetración.
Este proceso requiere de una fuerza que es calibrada por el resorte interno del equipo y permite estimar q u en Kg/cm2.
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
CAPITULO 3.
ENSAYOS DE CLASIFICACIÓN
Llamamos ensayos de clasificación a aquellos que permiten la determinación de propiedades índice, y la subsecuente
ubicación del suelo estudiado, en algún sistema de clasificación adecuado a los fines del proyecto.
3.1 Determinación de características intrínsecas.
3.1.1. Peso específico de los sólidos.
Es la razón entre la densidad de la materia que constituye las partículas de suelo y la densidad del agua destilada a la
misma temperatura. En la práctica se obtiene calculando la razón entre el peso de los sólidos y el volumen de agua que
desalojan a la temperatura ambiente.
El valor obtenido se corrige para expresarlo en base a alguna temperatura de referencia (4°C ó 20°C).
El valor GS (peso específico de los sólidos) interviene en la mayor parte de los cálculos de mecánica de suelos, y
ocasionalmente sirve también para fines de clasificación. Los procedimientos de ensayo varían según el tipo de suelo:
• Suelos no cohesivos
• Suelos cohesivos
• Gravas
Algunos valores típicos:
Cuarzo (2.6 – 2.66), ortoclasa feldespato (2.56), plagioclasa feldespato (2.62 – 2.76), muscovita (mica) (2.8 – 2.9),
biotita (mica)(3.00 – 3.10), caolinita (2.60 – 2.63), illita (2.60), montmorillonita (2.40), bentonita (2.13 – 2.18), limonita
(3.8), hematita (4.9 – 5.2).
Para los granos de arena, el promedio es en general 2.65 (cuarzosas) y para las arcillas varía entre 2.5 y 2.9, con un
promedio estadístico de 2.7.
3.1.2. Análisis granulométrico.
Objetivo: determinar el tamaño de las partículas componentes del suelo, estableciendo en porcentaje del peso seco total,
la cantidad de granos de distintos tamaños presentes.
Medios: harneado, cribado ó tamizado, para la parte de suelo correspondiente a la fracción gruesa, en que se usa suelo
seco, y análisis vía húmeda para la fracción fina, por métodos basados en el fenómeno de sedimentación, en el cual se
aplica la ley de Stokes:
V =
2 S − f D 2
( )
9 n
2
Análisis granulométrico vía seca:
En base al tamaño máximo (Tmáx) de la muestra de suelo que se obtiene en la exploración de reconocimiento,
correspondiente a un estrato a estudiar, se traslada al laboratorio una cantidad adecuada de material.
Si la naturaleza del suelo es inorgánica, se procede a secar al horno a 110ºC  5ºC una porción de la muestra inicial,
seleccionada por un proceso denominado de “cuarteo” porque se basa en subdividir la muestra inicial en 4 partes.
El peso seco total de la muestra a tamizar Ws se determina cuidadosamente.
Si existen finos, estos se separan por un proceso de lavado sobre el tamiz Nº200 (0.074 mm) y el resto del material se
vuelve a secar al horno.
Una vez seco, el suelo restante se hace pasar por una serie de tamices normalizados, vibrando cada tamiz manualmente o
en una máquina.
Se pesa lo retenido en cada tamiz, y en base a cálculos simples, se determina la composición granulométrica del
material, graficándose eventualmente la curva de resultado.
En el tamizado se mide el ancho de la partícula por comparación con la abertura nominal de la sección cuadrada de la
malla que permite el paso del material.
3”
3”
D  3”
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
Análisis granulométrico vía húmeda:
Esta prueba de laboratorio también es conocida como Boyoucus, y se basa en el conocido principio de que si una
muestra de suelo es disgregada en sus elementos componentes, agitándola en agua por ejemplo, se producirá al dejar la
suspensión en reposo, una sedimentación paulatina de los diferentes tamaños de grano, en el orden siguiente:
Gravas, en forma inmediata.
Arenas en menos de un minuto.
Limos en menos de 20 a 30 minutos.
Arcillas hasta en 24 horas.
Coloides, no decantan en condiciones normales.
Esta prueba simple puede hacerse en cualquier recipiente transparente y después de 24 horas, si es que hay arcilla, medir
las proporciones relativas de los estratos formados, respecto del espesor o altura sólida total, estimando las proporciones
de los diferentes tamaños de grano presentes.
Las gravas y arenas, incluyendo sus subdivisiones (gruesa, media, fina) asi como los limos y arcillas, se distinguen
visualmente con facilidad. En el caso del limo y la arcilla además del hecho de que este se ubica debajo de la arcilla si es
que existe, es de color café amarillento.
La existencia de partículas coloidales menores de un micrón se reconoce por la opacidad de la solución después de las
24 horas de observación.
Por sedimentación, la dimensión que se obtiene es el diámetro de la esfera “equivalente”, que se deposita a la misma
velocidad que la partícula.
Este diámetro equivalente puede ser mucho menor que el ancho de la misma.
La prueba se realiza utilizando un matraz de 1 lt de capacidad, en el interior del cual se disgrega una cantidad de suelo
fino por agitación usando una varilla de vidrio.
Eventualmente se puede agregar elementos químicos destinados a asegurar la separación completa de las partículas
componentes del suelo.
Este tipo de elementos químicos se llaman desfloculantes, y se determina experimentalmente cual es el mas adecuado en
cada caso, y en que proporción.
Una vez lograda la suspensión uniforme del suelo en el agua, se deje reposar el matraz en una superficie estable y se
mide a intervalos preestablecidos, la temperatura y la densidad m de la suspensión en ese momento.
El tamaño de las partículas más grandes que aun no sedimentan en el momento de medir la densidad de la suspensión, se
calcula por medio de la ley de Stokes y el peso de las partículas menores que ese tamaño, se determina con el valor de la
densidad de la suspensión a ese nivel, densidad obtenida con la lectura del instrumento llamado hidrómetro.
Para una suspensión de Ws (gr) de suelo en 1000 cc de volumen total (Vt), se tiene:
Volumen
Peso
1-(N Ws/1000Gsw)
Líquido
N Ws /1000Gsw
Sólido
[1-(N Ws/1000Gsw)] w
m
1 cm3
N Ws /1000
N(%), porcentaje que “pasa”
Material complementario en inglés obtenido de Internet:
El ensayo hidrométrico (Presentación en Power Point)
3.1.3. Estados de consistencia. Limites de Atterberg.
La fracción fina de un agregado de suelo, si se hace variar su contenido de agua en forma decreciente, puede alcanzar los
siguientes estados de consistencia:
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
•
•
•
•
•
Estado líquido: propiedades y apariencia de una suspensión.
Estado semilíquido: propiedades de un fluido viscoso.
Estado plástico: el suelo se comporta plásticamente.
Estado semisólido: apariencia del sólido, pero aun disminuye su volumen al ser sometido a un mayor secamiento.
Estado sólido: el volumen alcanzado no varía con un mayor secado.
Se dice que un suelo presenta plasticidad, o es capaz de un comportamiento plástico, cuando es posible que soporte
deformaciones rápidas, sin variación volumétrica apreciable y sin desmigajarse o agrietarse.
Límites de Atterberg:
•
Límites de plasticidad:
Límite líquido (LL): contenido de humedad bajo el cual el suelo alcanza un estado plástico.
Límite plástico (LP): contenido de humedad bajo el cual el suelo alcanza un estado semisólido.
•
Límite de contracción: contenido de humedad bajo el cual el suelo alcanza un estado sólido.
La plasticidad de un suelo fino queda definida por (LL;IP), siendo el índice de plasticidad IP = LL-LP.
En la determinación de LL y LP, la muestra se seca inicialmente al aire, y luego se procede al ensayo.
•
Descripción del ensayo de LL:
En este ensayo se usa un equipo denominado Máquina de Casagrande, compuesto básicamente por un tazón de bronce,
una base resiliente contra la que golpea el tazón, un mecanismo de leva que levanta el tazón una altura normalizada y
luego lo deja caer en caída libre, y una herramienta acanaladora para formar un surco en la pasta de suelo en forma de
“V”.
Se usa suelo fino bajo tamiz Nº200 y se agrega suficiente agua para formar una pasta semilíquida, que se deposita en el
interior de un casquete semiesférico o tazón de bronce.
Se gira la manivela de la leva contando los golpes hasta que el surco se cierra en 1/2 pulgada, se anota el número de
golpes y se coloca una muestra suelo de la zona cerrada en el horno para determinar su humedad.
Se repite el proceso con muestras cada vez mas secas por remoldeo, y finalmente se dibuja una “Curva de fluidez”
R = 54 mm
Humedad w(%)
(Escala aritmética)
11 mm
Límite Líquido %
8 mm
5
10
20
30
N (número de golpes)
(Escala logarítmica)
LL: N = 25 golpes; surco cierra en ~1/2”; S aprox: 25grf/cm 2 (Resistencia al corte aproximada)
If: índice de fluidez: pendiente de la recta de flujo.
40
50
2 mm
•
Descripción del ensayo de LP: se realiza el remoldeo de un cilindrito de suelo plástico de aproximadamente 3 mm
de diámetro hasta lograr su desmigajamiento y agrietamiento. En arcillas muy plásticas se debe aplicar considerable
presión para formar los rollitos.
En algunos suelos finos y arenosos, no es posible hacer el ensayo de LP, lo que indica falta de plasticidad. Se
consigna el resultado como NP (no plástico).
•
Límite de contracción:
a) Método de Terzaghi

1 

LC (%) = 100   −

G
S 
 d
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
Esta expresión supone que el agua llena todos los vacíos de la muestra seca. Se requiere previamente conocer G S.
b) Método de la PRA.
Consiste en formar una pasta fluida con el suelo a ensayar y luego llenar sin dejar burbujas de aire, una cápsula metálica
cilíndrica, enrasándola y pesándola.
Se deja secar al aire gradualmente tratando de evitar su agrietamiento, y luego se seca al horno.
LC (%) =
W1 − WS − (V1 − V2 ) 
WS
V1: volumen de la muestra húmeda = volumen de la cápsula.
W1: peso de muestra húmeda
V2: volumen de la muestra seca
No se requiere GS
El volumen de la muestra seca al horno, se determina por desplazamiento en mercurio (Hg~13.56 T/m3)
3.2 Determinación de características de estado.
3.2.1. Presencia de carbonatos.
Sobre una muestra de suelo seco disgregado, se vierten algunas gotas de HCl, el cual al humedecer la muestra, origina
un fenómeno de efervescencia al reaccionar con los carbonatos presentes.
Esta reacción se clasifica como fuerte, débil o ninguna, indicando cualitativamente la proporción de carbonato presente.
El fenómeno se puede apreciar mejor cuanto más fino sea el grado de desagregación del suelo considerado.
3.2.2. Humedad.
La humedad de un suelo, vale decir, su contenido de agua, se obtiene a través de la expresión =100 WW/WS (%).
WW se determina por diferencia de peso de una muestra de suelo, antes y después de ser sometida a secado en un horno
de temperatura constante e igual a 110°C  5°C.
El tiempo de secado es aquel necesario y suficiente para permitir que la muestra alcance una masa constante, vale decir,
ya no pierda más agua bajo esas condiciones.
Agua que se pierde en el proceso de secado al horno:
En el agregado de suelo, el agua está presente en alguna de las tres formas siguientes:
a) Agua gravitacional o libre: es susceptible de ser movilizada por acción gravitacional o de inercia.
b) Agua capilar: permanece entre los granos, sometida a fuerzas físicas de tensión superficial.
c) Agua de constitución o pelicular: en las partículas más finas se hace parte del sólido uniéndose a través de fuerzas
eléctricas y moleculares.
El agua que se pierde en el secado, es agua gravitacional y capilar.
3.2.3. Densidad aparente seca, máxima y mínima, en suelos granulares.
Resumen de la norma:
Tmax partícula
Peso muestra
3“
1 1/2 “
¾“
3/8 “
4.76 mm (malla N°4)
100 Lb
25 Lb
25 Lb
25 Lb
25 Lb
dmin
Herramienta
Pala o poruña
Poruña
Poruña
Embudo 1” salida
Embudo ½ “ salida
Volumen
Sobrecarga
Vibración
recipiente
FrecuenciaAmpl.
0.5 Ft3
1901 Lb 3600 Entre
0.1 Ft3
570.5 Lb CPM 0.002”
0.1 Ft3
570.5 Lb
y
0.1 Ft3
570.5 Lb
0.025”
0.1 Ft3
570.5 Lb
con 250
(ambas equivalentes a p=2psi) Lb carga
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
3.2.4. Angulo de reposo en arena.
Con arena seca y usando un embudo, se llena un cilindro sin tapa ni fondo, apoyado sobre una superficie lisa y
horizontal.
Una vez lleno el recipiente, se eleva el cilindro suavemente, dejando que la arena forme un cono.
En este cono se mide el diámetro promedio, y al repetir el ensayo se halla una altura promedio.
Embudo
Arena
Hprom

Diámetro “D”
Radio promedio
: ángulo de reposo, se relaciona con un parámetro resistente del suelo llamado ángulo de fricción interna ()
 2H 
;  
 D 
 = ARCTG 
3.2.5. Densidad aparente húmeda.
 = WT/VT
Para hallar VT:
a) Método geométrico.
Se talla o excava una figura geométrica regular, cuyo volumen sea fácil de determinar.
b) Método de inmersión en mercurio de una probeta de suelo.
Se registra la masa del mercurio desplazado por el suelo, y se calcula su volumen, el que se supone igual al de la probeta
de suelo.
c) Método por inmersión en agua de una probeta de suelo, encerada.
Se registra la masa de agua desplazada por el suelo encerado, se calcula su volumen, el que se supone igual al de la
probeta encerada. Conociendo la masa y densidad de la cera que cubre el suelo, se calcula el volumen de cera que
recubre el suelo, valor que descontado al anterior, permite obtener el volumen del suelo.
3.2.6 Otros ensayos.
a)
Estimación del contenido de materia orgánica por el método colorimétrico:
Se prepara una solución de NaOH3 al 3% en agua destilada y se disgrega en ella una porción de suelo hasta formar
una suspensión.
Después de 24 horas se observa el color de la solución.
El color negro corresponde a un elevado contenido de materia orgánica, en tanto que colores mas claros hasta
transparente, indican menores contenidos de materia orgánica, hasta la ausencia de la misma.
b) Determinación del contenido de materia orgánica por secado en mufla.
La mufla es un horno especial que permite temperaturas del orden de 500 a 600 ºC.
La muestra de suelo debe ser secada previamente al aire y pesada.
Después de estar en la mufla 24 horas, se pesa de nuevo y la diferencia representa en porcentaje el contenido de
materia orgánica perdido por incineración.
Bibliografía obligatoria:
Normas INN de mecánica de suelos: (Matías Cousiño 64 piso 5)
Normas del Laboratorio Nacional de Vialidad (LNV)
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
3.3 Planillas Excel.
A continuación se incluye a modo de ejemplo algunas planillas Excel que pueden ser usadas para tomar datos y calcular
los resultados de algunos ensayos de laboratorio.
Una forma de usarlas es imprimirlas y llenarlas a mano, efectuando los cálculos con calculadora!
Otra forma es definir en las celdas adecuadas, las fórmulas descritas en las mismas planillas, con lo cual estas prestarán
una verdadera utilidad.
En este caso no olvide grabar sus planillas modificadas, con otro nombre, y conservar las originales como respaldo.
Planilla Excel de:
Granulometría
Curva granulométrica (Note que tiene datos de ejemplo, no tiene fórmulas de cálculo e incluye un gráfico)
Límites de Plasticidad
Densidad aparente húmeda (Muestra encerada)
Densidad aparente (Por desplazamiento de Mercurio)
Límite de contracción (Método de la P.R.A.)
Límite de contracción (Método de Terzaghi)
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
CAPITULO 4.
Introducción.
Esta parte del curso, se presenta en general utilizando planillas Excel, pero no se han definido fórmulas que permitan
obtener resultados inmediatos, lo que puede ser desarrollado por el usuario, en copias de las planillas originales.
Por ejemplo, en el sistema de clasificación AASHTO, se debe calcular el valor denominado Índice de Grupo (IG).
En la planilla correspondiente, se describe la fórmula de cálculo del IG, pero no se ha definido específicamente celdas
para ser llenadas con los valores dados de un suelo específico, por lo cual, el usuario debe hacer esto adecuadamente y
así obtendrá una excelente ayuda al momento de clasificar.
Lo mismo ocurre con el sistema de clasificación USCS.
SISTEMAS DE CLASIFICACION DE SUELOS
4.1. Sistema USCS (Unified Soil Clasification System)
Planilla USCS
Carta de plasticidad
4.2. Características de los suelos clasificados por el sistema USCS.
Planilla de características de los suelos según USCS
4.3. Sistema de clasificación H.R.B. (AASHTO)
Planilla AASHTO
Descripción de los grupos.
Grupo A-1: mezcla de grava, arena y finos de poca o ninguna plasticidad. Buena graduación. Se incluye además en el
grupo a los suelos gruesos sin finos.
Subgrupo A-1-a: materiales predominantemente formados por grava y, en general, partículas gruesas con o sin finos.
Subgrupo A-1-b: material predominantemente formado por arenas gruesas con o sin finos.
Grupo A-3: arenas finas y uniformes, sin cantidades importantes de limo o arcilla, tipo arenas de playa y arenas de
dunas.
Grupo A-2: incluye a todos los materiales granulares que no quedan clasificados en A-1 y A-3.
Subgrupo A-2-4 y A-2-5: corresponde a suelos tipo gravas y arenas gruesas, con contenido de finos cuyo índice plástico
es mayor que los indicados en A-1. La fracción bajo la malla N° 40 tiene las características de A-4 y A-5,
respectivamente.
Subgrupo A-2-6 y A-2-7: características similares a los A-2-4 y A-2-5. La fracción bajo la malla N° 40 tiene
características de A-6 y A-7, respectivamente.
Grupo A-4: el material característico de este grupo corresponde a un limo de moderada o ninguna plasticidad. En
presencia de agua pierde gran parte de su estabilidad y es erosionable.
Grupo A-5: Suelo similar al A-4, con excepción de tener un carácter micáceo y límite líquido muy alto. Es altamente
elástico. En presencia de agua pierde su estabilidad y es muy erosionable.
Grupo A-6: El material correspondiente a este grupo es una arcilla plástica que puede contener ciertas cantidades de
grava y arena. Tiene una resistencia alta en estado seco, que disminuye significativamente al absorber agua.
Grupo A-7: El material típico de este grupo es similar al A-6, excepto por su alto límite líquido lo que lo hace elástico y
sujeto a altos cambio volumétricos.
Subgrupo A-7-5: incluye a los materiales con moderado índice de plasticidad con relación al límite líquido. Pueden ser
elásticos y expansivos.
Subgrupo A-7-6: incluye a los materiales con alto índice de plasticidad en relación al límite líquido y que están sujetos a
grandes movimientos de contracción y expansión.
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
4.4. Características de los suelos clasificados por el sistema AASHTO.
Según Dujisín y Rutllant, Mecánica de Suelos en la Ingeniería Vial, 1974.
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
CAPITULO 5.
PROPIEDADES MECANICAS E HIDRAULICAS
5.1. Resistencia al corte.
El suelo como material no falla por compresión isotrópica, a menos que las presiones aplicadas sean muy elevadas de
manera de fracturar los contactos intergranulares.
Por otra parte se define que el suelo no puede resistir esfuerzos de tracción, en régimen permanente, por cuanto está
constotuído por partículas fácilmente separables entre sí a nivel de estructura.
Por lo tanto, el único estado de solicitaciones que puede conducir a la falla del suelo, es aquel en que se generan directa
o indirectamente, esfuerzos de cizalle o de corte, en planos bien definidos.
5.1.1. Estado de tensiones en un punto de la masa de suelo.
Z
ZZ
ZY
ZX
XZ
XY
XX
XX
Y
YY
X
1
3
1, 2, 3 esfuerzos principales
2
Si se considera un caso con simetría axial en que 2 = 3:
1



3
Por condiciones de equilibrio se obtiene:
 = (1 + 3) / 2 + (1 - 3) / 2 cos2
 = (1 - 3) / 2 sen2
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
El estado de tensiones en el punto, para cualquier orientación  se representa fácilmente a través del Círculo de Mohr:


2
3


1
A cada punto del Círculo corresponde por consiguiente un par de valores, tensión normal  y tensión tangencial , que
corresponden a una orientación determinada del elemento de suelo en cuestión.
Las intersecciones del círculo con las normales al elemento representan las tensiones principales 1 y 3, que se ejercen
según dos direcciones perpendiculares a la superficie elemental.
Por lo tanto el radio del círculo vale: ½ (3 - 1).
En particular, el valor de (3 - 1) se llama esfuerzo ‘desviador’.
1, 2,3 esfuerzos principales.
1 > 2 > 3
El estado de tensiones en un punto para cualquier orientación , se representa fácilmente a través del círculo de Mohr.
5.1.2. Teorías de falla.
Coulomb (1786) encontró experimentalmente que en las arenas, el problema de la resistencia al corte, era similar al del
deslizamiento de un bloque sobre una superficie, vale decir, la fuerza horizontal necesaria para producir el movimiento,
era proporcional al peso.
Fv
Fv
Fh1
En equilibrio
Fv
Fh2
A punto de desplazar
Fh3
En movimiento
 FH 2 

 FV 
F
tg  =  H 2
FV
 = arctg
FHlim = FV ; en suelos  ~  ; : ángulo de fricción interna.
En términos de tensiones, en estos suelo sería:
lim = (tg  ) = S =  f
S: resistencia al corte del suelo, del inglés Shear.
=F/A
S =  tg 
Coulomb también comprobó que suelos como las arcillas no seguían este comportamiento, ya que resistían cizalle aun
sin existir una fuerza normal al plano de deslizamiento. Esta propiedad la llamó cohesión (c).
S=c
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
En un suelo en que se presenten ambas componentes, la expresión será:
S = c +  tg 
Posteriormente Terzaghi a comienzos del siglo XX, estableció que la resistencia al corte del suelo dependía de la
“presión efectiva” entre los granos de suelo, la cual se puede evaluar como:
 '=  − 
’: presión efectiva o intergranular
 : presión total
 : presión del fluido en los poros del suelo.
En términos de presión efectiva, c y , parámetros de resistencia al corte del suelo, debieran ser evaluados considerando
el efecto del fluido de poros, con lo cual se obtiene c’ y ’, parámetros de resistencia al corte del suelo en términos de
presiones efectivas:
S = c’ + ’tg ’.
, presión del fluido en los poros, se encontró luego que dependía en forma notable de la velocidad de aplicación de la
carga en relación a la permeabilidad del suelo, lo que condujo a distinguir dos tipos de resistencia al corte en el suelo:
• Resistencia al corte lenta o drenada.
• Resistencia al corte rápida o no drenada.
Hvorslev determinó que en las arcillas saturadas c = c(), S = f()+(-)tg.
Esta expresión, aproximadamente válida en arcillas NC con c~0, debe ser modificada para las arcillas PC, en las cuales
la relación no sería lineal.
5.1.3. Determinación de los parámetros de resistencia al corte (c, ).
a) Ensayo de compresión simple o no confinada (qu).
El ensayo de compresión simple o no confinada, sólo se puede aplicar a suelos con cohesión, de manera que a partir de
muestras no perturbadas obtenidas en exploraciones de reconocimiento, y trasladadas a laboratorio, de ellas se puedan
tallar probetas aproximadamente cilíndricas, cuando no vienen ya con esa forma debido al muestreador usado.
En una prensa simple, incluso de acción manual, se registra la carga aplicada y la deformación de acortamiento
observada en la probeta.
Una vez rota la probeta, se mide el ángulo de rotura formado con la horizontal.
Si las probetas se agrietan en sus extremos, o bien, se ensanchan en su diámetro principal, no es posible estimar el
angulo de fricción interna del suelo, y sólo se tendrá una estimación de la cohesión, o en el caso particular de estar el
suelo saturado, se tendrá la resistencia al corte no drenada Su.
v = Fv / Ac; Ac: área corregida
Curvas típicas: (1) Consistencia firme.
(2) Consistencia blanda.
Fv
v
a
v
a
vf
elevación
1
vf
2
Sección
transversal A
corte a-a
f
20%
v
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
Bajo las hipótesis que  = 0 y Volúmen = constante, se calcula el área corregida Ac, y se estima que el valor c = 0.5 qu,
siendo:
qu = vf
con vf = v max si existe un valor máximo en la curva esfuerzo deformación, o bien:
vf = v para v = 20 % si no existe un máximo bien definido.
Si los ensayos aplicados sobre muestras inalteradas se repiten sobre las mismas probetas después de ser amasadas con un
contenido de humedad constante, se obtienen nuevos valores que permiten definir la sensitividad del suelo fino.
Sensitividad = St = qu MNP / qu Mrem
MNP : Muestra no perturbada
Mrem: Muestra remoldeada
Puede observarse que la inclinación de la curva tensión-deformación para una muestra inalterada de arcilla de baja
sensibilidad decrece continuamente con el aumento de la deformación como aquella de la curva 1, mientras que para
arcillas altamente sensitivas la pendiente permanece casi constante hasta que se llega al punto de rotura.
Se concluye que las arcillas altamente sensitivas se comportan en estado inalterado como materiales frágiles, pero que al
ser amasadas adquieren la consistencia de líquidos muy viscosos.
Esta sería la causa de los fenómenos destructivos masivos llamados “quick clays” que pueden afectar grandes
extensiones de suelo y dañar personas y bienes.
b) Ensayo de corte directo.
Fv
h
Fh
El ensayo puede hacerse con las siguientes características:
• Suelo no perturbado, o suelo remoldeado.
• Tensiones controladas o deformaciones controladas.
• Drenado o no drenado.
Para el suelo a ensayar, se recortan o preparan varias probetas.
Para una probeta se fija FV y se hace crecer FH hasta la falla, se obtiene (V,f)1.
Se repite el ensayo en una segunda y tercera probeta, aumentando cada vez F V, con lo cual se obtienen nuevos valores
(V,f)2,3,…
El gráfico para cada probeta ensayada será del tipo:

f
h
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
El gráfico para todas las probetas consideradas sería:


c

c)
Ensayo de compresión triaxial.
Consiste en ensayar a compresión axial, una probeta de suelo, no perturbado, o remoldeado, permitiendo o no, su
drenaje; y confinando la probeta a través de la presión transmitida por un fluido envolvente.
La siguiente figura ilustra una cámara de ensayo triaxial:
ESPITA
PISTON DE CARGA

PARED TRANS.
FLUIDO A PRESIÓN
“O” RINGS
MEMBRANA
V.P.C
FLEXIBLE
V.D.I 
V.D.S
VDS: Válvula de drenaje superior
VDI: Válvula de drenaje inferior
VPC: Válvula de presión de cámara
c.1.) Ensayo UU (ensayo Q) [no consolidado, no drenado].
in situ
muestreo saturación
compresión
isotrópica
3
v
3
h
v0, u0
compresión
axial sin
drenaje
1
v1>v0
uc
v1
u=0
v1
u=3
3
u=3+A(1 - 3)
En la falla, la probeta cambia de forma, pero no de volumen. Como está saturada y no se permite drenaje,
=, por lo cual ’ =  -  = 0. No se moviliza la capacidad de resistencia por fricción.
Curvas típicas:
d
Suelo denso/firme
d: esfuerzo desviador axial.
d = 1-3
Suelo suelto/blando
v
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
Si se ensayan varias probetas del mismo suelo, en que: 3(k+1) > 3(k)

=
Su

qu 
11
c.2.) Ensayo CU (ensayo R) [consolidado, no drenado].
in situ
muestreo
saturación
v1>v0
v1, u=0
consolidación
isotrópica
compresión
isotrópica
compresión
axial sin
drenaje
u=3 (t=0)
Vo; u=A(1 - 3)
v
h
v0, u0
Curvas típicas:
d
u=0, v0
Suelo denso/firme
d: esfuerzo desviador axial.
d = 1-3
Suelo suelto/blando
v
Si se ensayan varias probetas del mismo suelo, en que: 3(k+1) > 3(k)
cu
ccu
c.3.) Ensayo CD (ensayo S) [consolidado, drenado]
in situ
muestreo
saturación
compresión
isotropica
3
consolidación
isotropica
3
compresión
axial con drenaje
1
v
h
v0, u0
3
v1>v0
v1, u=0
u=3 (t=0)
3
v0, u=0
3
v’<v0, u=0
(para todo t)
El esfuerzo desviador d se aplica tan lento, que en todo instante  =  = 0
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
Curvas típicas:
d
Suelo denso/firme
d: esfuerzo desviador axial.
d = 1-3
Suelo suelto/blando
v
Si se ensayan varias probetas del mismo suelo, en que: 3(k+1) > 3(k)
’
c’
c’ y ’ se llaman cohesión y fricción efectivas o verdaderas del suelo ensayado.
Nota: si en el ensayo CU, se efectúa mediciones de presión de poros, el ensayo se simboliza
círculos de Mohr en términos de presiones efectivas, que permiten hallar c’ y ’.
___
CU, y se puede dibujar
Simulación de un ensayo triaxial:
En Internet.
Si no está conectado, en el CD-ROM podrá acceder a parte de la simulación.
Necesitará tener cargado el Plug in “Cosmo Player”. Si no lo tiene, instálelo desde el CD-ROM, desde aquí.
También conectado a Internet, estudie el “Laboratorio Virtual”:
Laboratorio de Suelos Virtual:
Si ya tiene instalado Macromedia Authorware Player, y está conectado a Internet, entonces haga clic AQUÍ
Si NO tiene instalado Macromedia Authorware Player, y está conectado a Internet, entonces haga clic AQUÍ
En el CD-ROM existe otra simulación de triaxial. Al utilizarla retroceda con “Back” o “Atrás” cada vez.
d) Ensayo de la veleta (Vane Test).
En aquellos suelos que sufren variaciones de su resistencia al corte al ser perturbados por el muestreo, o en que se quiere
conocer su resistencia in situ, se utiliza este ensayo.
Existen dos formas de aplicarlo:
• Como parte de la realización de un sondaje en terreno.
• En las paredes de una calicata, zanja o pozo de reconocimiento, utilizando un equipo de bolsillo, similar al
“Penetrómetro de bolsillo” descrito con anterioridad. Este equipo incluye adaptadores para trabajar en suelos finos
con diferente consistencia.
torque T
H
Planta
D
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
1 
1
T = S  D2 H + D3 
6 
2
S : resistencia al corte del suelo
S = Su resistencia al corte no drenada
5.1.4. Sensitividad y tixotropía.
Sensitividad es la pérdida de resistencia al corte que experimenta un suelo fino al ser remoldeado o perturbado. Toda vez
que se construye obras como pilotes, cajones, excavaciones, rellenos o fundaciones, en forma que pueda perturbar estos
suelos, se debe evaluar su sensibilidad a través de:
St = qu(M.N.P.) / qu(M.REM.)
M.N.P. Muestra no perturbada
M.REM. Muestra remoldeada
Grado de sensitividad:
2 – 4 poco sensitivo
4 – 8 sensitivo
8 – 16 extra sensitivo
>16 quick clays.
Se llama tixotropía la ganancia o recuperación de resistencia al corte que con el tiempo, se desarrolla en un suelo fino,
después de haber sido perturbado o remoldeado. Esto en general ocurre si S t < 16.
5.1.5. Valores de “c” y “” típicos.
A falta de valores de ensayos de laboratorio, y sólo como una primera aproximación a la resolución de un problema
geotécnico, se puede estimar la cohesión y fricción de la siguiente tabla:
Arcilla de consistencia
C = 0.5 qu (Si  = 0)
Suelo
Rango 
Muy blanda
<0.12 Kg/cm2
Gravas
35 - 45
Blanda
0.12 - 0.25
Arenas
25 - 35
Media
0.25 - 0.50
Limos
15 - 25
Firme
0.50 - 1.00
Arcillas
0 - 30
Muy firme
1.00 - 2.00
Dura
>2.00
5.2. Características de compresión.
Generalidades.
Ante una solicitación externa, como por ejemplo el traspaso al suelo de fundación de las cargas de una superestructura, a
través de un sistema de fundación, el agregado de suelo modifica su estructura reduciendo su volumen. Este
comportamiento también puede tener su origen en variaciones del nivel de la napa. El desplazamiento de la fundación en
el primer caso, se llama asentamiento (S, , , , etc.) y el descenso de la superficie del terreno en el segundo caso, se
llama hundimiento o subsidencia.
Asentamiento uniforme de una fundación superficial aislada:
Fv
Asentamiento “S”
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
Fenómeno de subsidencia o hundimiento del terreno:
Cota de terreno original
hundimiento
Nivel original de la napa
Nivel de la napa deprimida por agotamiento
Estrato firme o roca
El asentamiento tiene dos componentes:
•
Asentamiento “inmediato o instantáneo” (Si)
•
Asentamiento en función del tiempo (St).
El Si se puede calcular por expresiones empíricas, o bien, por teoría de elasticidad, si el suelo se puede aproximar a un
medio homogéneo, isotrópico y elástico.
St es importante en los suelos finos saturados. Para precisar sus características se efectúan ensayos de consolidación
unidimensional (consolidación 1D o ensayos oedométricos).
5.2.1. Distribución de presiones aplicadas, en el interior de la masa de suelo.
a) Método de Boussinesq (se basa en la teoría de elasticidad).
Hipótesis: el suelo no tiene peso, es elástico, homogéneo, semi infinito, isótropo y cumple con la ley de Hooke. El
cambio de volumen en el suelo es poco significativo, carece de tensiones antes aplicar la carga. Existe continuidad en las
tensiones. La distribución de tensiones es simétrica respecto al eje vertical “Z”.
3Q
cos5 
2
2Z
r
tg =
Z
2
2
R = r + Z2
cos 5  = (Z/R)5
qV =
Q
R Z
3QZ 3
3Q
1
qV =
=
5
5
2
2
2
2R
2Z 
1+ r 
Z 

( )
qh =
(1 − 2 )cos  
Q 
3sen2  cos3  −

2 
2Z 
1 + cos 
qv
r
2
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
En el caso de un área circular con carga uniforme q 0
dQ
dQ = q0 dA
Q =  q0 dA
A
dA = 2rdr
3q0
1
dq =
2rdr
5
2
2
2
2Z 

1+ r
Z 

dr
r
Z
( )
r
3q0
1
2rdr
5
2
2
2
2

Z
0
1 + r

Z 

q=
( )




1
q = q0 1 −
3 
 1 + r 2  2 
 
Z  
( )
P
dqv
Esta última expresión se puede reordenar convenientemente a:
−2
r
=
Z

q 3
1 −  − 1
 q0 
En esta expresión, (r/Z) es el tamaño relativo de un área circular de carga, que da una razón única (q/q 0) en el elemento
de suelo a la profundidad Z.
Si se da valores a la razón (q/q0), se obtienen valores (r/Z) que sirven para dibujar una serie de círculos concéntricos, lo
que constituye una “carta de influencia”.
En la página siguiente se ilustra la “Carta de Newmark”, tomada del libro Foundation Análisis and Design, de J.E.
Bowles.
El uso de estos métodos manuales, en la actualidad, ha sido descartado,
y se utiliza programas computacionales que se pueden encontrar en la pagina
web del curso o en este mismo CD-ROM. Ver Documentación de SIGMA/W.
A la derecha se ilustra una aplicación del programa computacional SIGMA/W,
al cálculo de presiones bajo un estanque:
Aplicaciones de la Carta de Newmark:
Cálculo del incremento de presión sobre un elemento de suelo, bajo una
zapata, un grupo de zapatas, una losa de fundación, zapatas con diferentes
presiones de contacto, cargas en varios otros puntos.
Modo de uso de la carta de Newmark:
Dibujar la planta de fundación, a escala, tal que Z=AB (Z: profundidad del
punto de suelo considerado) y AB, longitud de un trazo de referencia en la
carta.
El punto cuyo incremento de presión se desea conocer, debe ubicarse con su
proyección horizontal coincidiendo con el centro de los círculos.
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
Contabilice las unidades y fracciones de sectores, interceptados por la planta de fundaciones (M).
El incremento de presión viene dado por:
q = q0 M I
I: valor o coeficiente de influencia.
I=1/N; N: número total de sectores considerados al dibujar la carta.
q0: presión de contacto de la fundación.
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
En el caso particular, de puntos del suelo ubicados con su proyección horizontal coincidiendo con una esquina de una
superficie rectangular con carga uniforme, se puede hallar el incremento de presión vertical, usando la figura siguiente
(Figura 8.6 del libro Mecánica de Suelos de Lambe y Whitman).
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
En el caso de zapatas aisladas, circulares, cuadradas o continuas, es más útil el concepto de “bulbo de presiones”.
Ellos se construyen dibujando a diferentes escalas la planta de la zapata, y aplicando la carta de influencia.
A continuación se reproduce algunos bulbos de presión y un gráfico que permite hallar el incremento de presiones bajo
el centro de un terraplén, tomados de los libros Foundation Análisis and Design de J.E. Bowles, Mecánica de Suelos de
Lambe y Whitman, y Mecánica de Suelos en la Ingeniería Vial de Dujisin y Rutllant.
Bulbos de presiones para suelos homogéneos e isótropos:
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
Para calcular los incrementos de presión generados en el suelo, por la acción de un terraplén, se puede usar la expresión
de Carothers:
p =

 
h 
z
1 + 2 + 2 (l −  )

 
h cot  R

p: incremento de presión del suelo en el punto P.
Como se analiza solo la mitad del terraplén, debe superponerse los incrementos generados por la otra mitad.
El caso más simple, del cálculo del incremento de presiones bajo el centro del terraplén, se puede resolver usando la
Figura 5.22. del texto Mecánica de Suelos en la Ingeniería Vial de Dujisin y Rutllant.
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
Sobrepresión vertical debida al terraplén.
, 1, 2, en radianes.
Figura_5.22._Determinación gráfica de los esfuerzos normales bajo el centro de un terraplén.
p = 2·I ·p = 2·I · ·h Terraplén simétrico
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
b) Método de Westergaard.
Para suelos estratificados (capas sucesivas de suelos finos y gruesos), Westergaard propuso la expresión siguiente: (se
considera capas de materiales elásticos, e inelásticos que permiten deformación vertical)
(1 − 2 )(2 − 2 )
Q
3
2
2
2Z 
 2
(
1 − 2 )(2 − 2 ) + r
Z 

si  = 0
qv =
qv =
( )
Q
1
3
2
2
Z 
 2
1+ 2 r
Z 

( )
Para una presión de contacto q0, con:
a=
1 − 2
2 − 2
Q =  q0 dA
A
dA = 2rdr
( )
−3
2
2
q a
q = 0 2  a + r  2rdr
Z 

2Z
lo que permite obtener:
r
=
Z
a
1 − q 

q0 

2
−a
Esta expresión permite construir una carta de influencia de la misma manera que Newmark, y también bulbos de
presión, como se ilustra en las páginas siguientes.
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
Carta de influencia de Westergaard:
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
Bulbo de presiones para zapatas cuadradas y corridas, basado en Westergaard:
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
c)
Método 2:1.
Es una aproximación simple de cálculo sencillo, que permite estimar el incremento de presión vertical en un plano dado,
a una profundidad Z bajo el sello de fundación.
Se asume que la carga superficial se distribuye en planos horizontales cuya extensión queda definida por una proyección
trapezoidal de la planta de fundación en una relación 2:1 (Vertical : Horizontal)
Fv

z
q

Z
otros criterios :
2:1
30
0
45
0
Para una zapata rectangular (B x L)
B: ancho
L: largo
q=
Fv
(B + Z )(L + Z )
Si es cuadrada:
q=
Fv
(B + Z )2
5.2.2. Cálculo del asentamiento “inmediato” o “instantáneo”.
En el caso de suelos (c,), arcillas y limos no saturados, suelos granulares, y el asentamiento inmediato de suelos
cohesivos saturados; se puede usar la expresión siguiente, basada en la teoría de elasticidad:
(
)
Si = q0 B 1 −  2 I / ES
q0: incremento de presión aplicado al suelo, a través de la fundación.
B: Ancho de fundación (“D” en zapatas circulares)
I: factor de forma (ver tabla mas abajo).
ES: módulo esfuerzo-deformación del suelo.
: módulo de Poisson del suelo (ver tabla mas abajo)
En el caso de cargas excéntricas, el giro de zapatas rígidas, se puede calcular por:
tg  =
e=
FV e 1 −  2
IM
BL2 ES
M
FV
tg  =
M 1−2
IM
BL2 ES

Fv
L
e: excentricidad
M: momento solicitante
FV: carga actuante
: giro de fundación
Fv
Valores típicos de :
0.30 – 0.35 arenas
0.40 – 0.50 arcillas
~ 0.5 arcilla saturada
e
IM: factor de forma (ver tabla mas abajo)
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
Valores del módulo de Poisson para diferentes suelos, según Bowles:
Suelo
Arcilla saturada
Arcilla no saturada
Arcilla arenosa
Limo
Arena densa
Gruesa (e = 0.4-0.7)
Fina (e = 0.4-0.7)
Roca
Módulo de Poisson
0.4-0.5
0.1-0.3
0.2-0.3
0.3-0.35
0.2-0.4
0.15
0.25
0.1-0.4 (dependiendo del tipo de roca)
Valores de los coeficientes Iw e Im según Bowles:
Fundación
Circular
Cuadrada
Rectangular:
L/B = 1.5
2
5
10
100
-------------- Flexible ----------------Centro Esquina
Promedio
1.00
0.64 (borde)
0.85
1.12
0.56
0.95
Rígida
Iw
Im
0.88
0.82
3.7
1.36
1.53
2.10
2.52
3.38
1.06
1.20
1.70
2.10
3.40
0.68
0.77
1.05
1.26
1.69
1.20
1.31
1.83
2.25
2.96
4.12
4.38
4.82
4.93
5.06
El módulo esfuerzo-deformación ES del suelo, se puede obtener a partir de ensayos triaxiales, o de pruebas de carga en
terreno.
Es en suelos granulares:
“ES” en suelos granulares depende notablemente de: profundidad (confinamiento), índice de huecos “e” y de
d = 1 - 3.
Si Es se desea estimar a través de una prueba de carga:
Placa de carga
Fundación proyectada
ancho
ancho Bf = N · Bp
Bp
Sp
Sf
Bulbo de presión
de la placa
D
Bulbo de presión de la
Fundación
N·D
S P BP
D
=
=
S F BF ND
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
Terzaghi propuso la relación empírica:
S F  2 BF 

=
S P  BF + BP 
2
Con la cual se deduce:
B  B + BP 

EF = EP F  F
BP  2 BF 
2
Para un mismo incremento de presión aplicado “q 0”:
SP =
FV L q0 D
=
A E
EP
SF =
q0 ND
EP
Es en suelos cohesivos:
“ES” en suelos cohesivos, es relativamente independiente de la profundidad, pero depende en forma importante del
contenido de humedad, y el índice de huecos. Una expresión para estimar esta variación sería:
 2 
E = E0 1 − 2 
 0 
E: módulo a la humedad 
E0: módulo a la humedad =0
0: humedad cuando E=0
En base a la experiencia de proyectos y estudios realizados en áreas urbanas, se establece algunas veces expresiones que
permiten estimar ES en algunos lugares.
Ejemplo:
Estudios realizados en el ripio típico de Santiago permiten estimar:
E(Z) ~ 600(Z)0.45 con Z en (m) y ES en (Kgf/cm2).
Como la expresión planteada para hallar Si, basada en la teoría de elasticidad, implica el cumplimiento por parte del
suelo, de una serie de hipótesis (ver hipótesis de Boussinesq), de difícil verificación real; se ha planteado otros métodos
de cálculo de Si:
Método de Janbu:
El método de Janbu es aplicable a dos estratos de rigidez relativa muy diferentes (blando sobre firme, firme sobre roca).
Ver figura en la página siguiente:
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
Método de Lambe:
n
Si =  H j j
1
Procedimiento:
•
•
•
Subdividir el suelo comprometido en profundidad, en base a características constitutivas o de comportamiento, en
estratos o capas (1,2,3, …j,…n-1, n)
Realizar ensayos de compresión triaxiales, sobre muestras obtenidas a diferentes profundidades, representativas de
cada capa.
Construir los gráficos d vs. v para cada caso. (d = 1 - 3).
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
•
•
•
•
•
Calcular 1 para los puntos considerados representativos de cada capa de suelo (usar Boussinesq, Westergaard, 2:1,
etc.)
Calcular 3 en función de 1.
Calcular (1 - 3) para cada punto de análisis, y en el gráfico correspondiente obtener j.
Calcular Sj para cada estrato de espesor Hj, como Sj = Hjj.
Calcular el asentamiento como la suma de las deformaciones de los estratos comprometidos.
Nota: a falta de valores experimentales, se puede estimar algunos valores de características del suelo, a partir de los
siguientes datos:
Valores “”:
Suelo
Arena Seca suelta
Saturada suelta
Seca densa
Saturada densa
Limo o arena limosa:
Arcilla
suelta
Densa
Tipo de ensayo triaxial
UU
CU
28.5°-34°
28.5°-34°
35°-46°
1° a 2° menos
que seca densa
20°-22°
25°-30°
0° (saturada)
14°-20°
CD
43°-50°
43°-50°
27°-30°
30°-35°
28°-30°
Valores “” también
pueden estimarse en
suelos granulares, a
partir de la densidad
relativa (compacidad),
o a través del número
“Nspt” del ensayo de
penetración standard.
(ver figura inferior)
Gráfico Nspt vs. Angulo de fricción interna:
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
Valores “c”:
Si es válida la hipótesis  ~ 0°; c~1/2 qu y qu se correlaciona desde la consistencia estimada in situ en base a pruebas de
penetración sencillas (hundir pulgar, etc.)
También puede estimarse ‘c’ a partir de la expresión:
qu = 2c N

qu = 2c tg( 45 + )
2
con:

N = tg 2 (45 + )
2
Rangos para “ES”:
Suelo
Arcilla muy blanda
Arcilla blanda
Arcilla media
Arcilla dura
Arcilla arenosa
Arena limosa
Arena suelta
Arena densa
Arena densa y grava
Loess
ES (Kgf/cm2)
4-30
20-40
40-80
70-180
280-420
70-210
100-250
490-840
980-2000
980-1300
5.2.3. Ensayo de consolidación 1D.
Alternativas de ensayo:
Piedras porosas
Fv
Fv
Anillo flotante
Anillo fijo
Ho
Anillo
Anillo
La disposición de anillo fijo se debe usar si se requiere conocer U(%)=U(t), grado de consolidación o de disipación del
exceso de presión de poros en función del tiempo.
Se registra V(t)=vt y el tiempo.
Hay dos procedimientos:
Para cada aplicación de carga vertical, se obtiene un gráfico como el siguiente (v vs. Log(t)):
v
vo
v100
Cons. primaria
tp
Cons. secundaria
Log (t)
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
Para estimar vo, se asume una parábola tomando como incremento en las abscisas desde t a 4t en las mediciones
iniciales, y duplicando hacia arriba el valor v encontrado.
El registro de la deformación en el tiempo, también se puede dibujar en un gráfico v vs. √t como el siguiente:
v
√t
Del gráfico v vs. log t, se obtiene:
Cv = T H2 / t : Coeficiente de consolidación
Siendo T: factor tiempo.
T es función del grado de consolidación U(%) y de la distribución u(z) a lo alto de la probeta.
Ver tabla u = u (z) mas abajo.
H: camino más largo posible de drenaje.
t: tiempo necesario para alcanzar un grado U(%) de consolidación.
Es frecuente usar:
Cv = 0.197 H2 / t50
Como =p(FV) se aplica en incrementos (en general i+1=2i), Cv depende del rango de presión aplicada.
Para cada aplicación , se mide vt y se calcula e = e(), con lo cual se obtiene:
Valores del factor T para diferentes distribuciones de presión de poros u = u (z) en profundidad:
U(%)
0
10
20
30
40
50
60
70
80
90
100
Caso I
0.000
0.008
0.031
0.071
0.126
0.197
0.287
0.403
0.567
0.848

Caso II
0.000
0.048
0.090
0.115
0.207
0.281
0.371
0.488
0.652
0.933

Caso I
u0
Caso Ia
u0
Caso II
ui
ui
ui
H
H
ui = u0
H
ui = u0 - u1 (z/H)
ui = u0 sen (·z/H)
Método de Casagrande para hallar la presión de preconsolidación (pc’, pc, ’VM o VM).
e
horizontal
Punto de máx.
curvatura
bisectriz
tg en el punto de máxima curvatura
tg a curva virgen
pc (v máx)
Log(p)
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
Si ’VM>’V in situ: arcilla P.C.
Si ’VM>’V in situ: arcilla N.C.
Si en el ensayo de consolidación 1D se aplican descargas y recargas sucesivas, se tiene:
e
Curva virgen
C. de recompresión
C. de descarga
Log (p)
Hipótesis de la teoría de la consolidación unidimensional:
•
•
•
•
•
•
Estrato de suelo homogéneo.
Suelo saturado (S=100%)
vt se debe a la disminución de “e” y puede ocurrir sólo si el agua libre es expulsada de los poros del suelo.
vt es en la dirección de la carga aplicada (vertical).
El flujo del agua expulsada es en la dirección de la carga aplicada (vertical).
CV es constante durante el ensayo.
Del gráfico e-p, (e-p’), (e-) o (e-’), se obtiene:
Coeficiente de compresibilidad:
av =
e
p '
Otras relaciones:
Coeficiente de compresibilidad volumétrica:
mv =
av
1 + e0
S
e
=
H 1 + e0
S: Asentamiento por consolidación (vt)
H: Altura de la muestra, espesor compresible.
S = mvp’H
cv =
k (1 + e)
  av
k: coeficiente de permeabilidad.
De la curva virgen en el gráfico e - log(p’)
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
cc =
e
log( p'2 / p'1 )
cc: índice de compresión
e = e0-e
De donde:
e = e0 - cc log(p’2/p’1) permite calcular e = e(z)
Como p2 = p1+p y S = (eH)/(1+e0) y e = e0-e = cc log(p’2/p’1) , entonces se tiene:
S=
cc H
p' +p'
log 0
1 + e0
p'0
Expresión válida en arcillas N.C.
En ellas se tiene que, aproximadamente:
CC~0.009 (LL-10)
En arcillas limosas y arcillas inorgánicas CC~0.30(e0-0.27).
e
e0
ec
1
Cr
1
Si el suelo es preconsolidado, la expresión más general sería:
S=
Cc
pf '
cc H
p'
cH
log c + c log
1 + e0
p'0 1 + ec
p'c
ef
p0
pc
pf log(p)
5.3. Características de compactación.
5.3.1. Generalidades.
Compactación es el proceso mecánico mediante el cual se disminuye la cantidad de huecos de una masa de suelo,
obligando a las partículas sólidas a ponerse en un contacto más íntimo entre sí.
La compactación de un suelo, aumenta su densidad, resistencia al corte y características de esponjamiento; disminuye la
permeabilidad y compresibilidad.
Con el objeto de establecer valores de referencia para la ejecución de rellenos compactados, se han desarrollado varios
métodos de preparar suelos compactados en laboratorio.
Ellos son: Proctor normal o standard, Proctor modificado, Harvard miniatura, Iowa, Proctor - Hilf, etc.
Estos métodos son aplicables a todos aquellos suelos en que al efectuarse el ensayo, se obtiene como resultado una curva
humedad - densidad bien definida, con un solo valor máximo. Ello ocurre en general a aquellos suelos con mas de 12%
de finos limosos o arcillosos.
Si el agregado tiene menos de 12% de finos, o bien, al hacer el ensayo no se obtiene una curva humedad - densidad bien
definida, entonces se debe expresar su grado de compactación por el valor de la Densidad Relativa (D.R.), que requiere
conocer previamente los valores de Densidad Seca Máxima y Densidad Seca Mínima.
Cada método de compactación de laboratorio se caracteriza por entregar al suelo una cantidad de energía por unidad de
volumen dada, y diferente de un método a otro.
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
En general, estos ensayos de laboratorio se utilizan como referencia para controlar el grado de compactación con que se
ejecutan obras de tierra tales como mejoramiento de subrasantes, construcción de bases y sub bases, rellenos
compactados, terraplenes, tranques, etc.
En el proceso de compactación se busca alcanzar la máxima densidad.
Los principales factores que influyen son: contenido de agua, forma y magnitud de la energía de compactación aplicada,
y el tipo de suelo.
Características de los ensayos más frecuentes:
Ver normas INN correspondientes: NCh1534/I, 1534/II.
5.3.2.Resultados de los ensayos de compactación:
Para un ensayo dado, vale decir, una energía de compactación por unidad de volumen de suelo, específica, se obtiene:
Curva de compactación, o curva humedad - densidad:
Suelo con finos plásticos, no válida en granulares limpios o con finos no plásticos.
Cada punto experimental de la curva, se obtiene aplicando una misma energía al suelo, por unidad de volumen; variando
la humedad del mismo, para obtener los puntos necesarios.
d
B
DMCS
Curva de saturación del suelo ensayado
Ton/m3
d = Gs·w / (1 + Gs · ) con  en valor decimal
A
C
Rama seca
Rama húmeda
 op
Antes de “A”: hidratación
Entre “A” y “B”: lubricación
Entre “B” y “C”: expansión
Después de “C”: saturación
 (%)
Aire libre
aire ocluido
aire entra en dilución
Si la misma energía del ensayo descrito, se aplica a otros suelos, se tiene:
Suelo B
d Ton/m3
Suelo A
Suelo C
 (%)
dmax depende de: Gs, granulometría, forma de las partículas, plasticidad de los finos, etc.
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
Cada suelo se caracteriza por un solo valor (dmax, wopt ) para una energía dada de compactación.
Por el contrario si a un suelo dado, lo sometemos a ensayos que le transmiten diferentes energías de compactación, se
aprecia que:
dmax aumenta al aumentar “E”.
 op Disminuye al aumentar “E”.
d Ton/m3
Curva de saturación del suelo ensayado
E3
E2
E3 > E2 > E1
E1
 (%)
5.3.3. Especificaciones de compactación.
Las especificaciones de compactación de un proyecto, debieran reflejar los requerimientos de compresibilidad,
resistencia al corte y permeabilidad, con que la obra debe operar, y no como ocurre en general, en que no se indica sino
un grado de compactación mínimo a cumplir.
En el caso de proyectos que se desarrollan con frecuencia, las instituciones supervisoras han establecido
“especificaciones típicas” que fijan para los materiales: bandas granulométricas, características de plasticidad de los
finos, grados mínimos de compactación y otras características como tamaño máximo de partícula, resistencia al
desgaste, capacidad de soporte, etc.
Como todo diseño, el grado de extensión en la precisión de los aspectos especificados debe ser consecuente con la
importancia económica y social de la obra, con las hipótesis de los métodos de cálculo y con las características reales de
la ejecución de la obra.
Si se considera la variabilidad de los parámetros del suelo y la de las correlaciones entre propiedades mecánicas e
hidráulicas con el grado de compactación, se concluye que el diseño y control de ejecución de obras de suelo debería
incluir metodologías estadísticas que reflejan en mejor forma las condiciones de riesgo e incertidumbre envueltas.
Todo relleno constructivo debe ser controlado, por lo menos en su composición y grado de compactación. De lo
contrario, es probable que en algún plazo variable, manifieste un mal comportamiento.
Cuando se debe ejecutar obras en suelos constituidos por rellenos no controlados, el problema reside en que no se puede
estimar parámetros representativos del suelo.
5.3.4. Compactación en obra.
Fijado por las condiciones de obra, o por las especificaciones del proyecto, el suelo a compactar, se debe tener claro el
equipo más adecuado a usar según la forma de transmitir la energía de compactación:
• Por presión: rodillos lisos, neumáticos, pata de cabra, equipo pesado de construcción.
• Por impacto: pisones neumáticos.
• Por (presión + vibración): rodillos vibradores y planchas vibradoras.
Equipo de compactación recomendado según tipo de suelo:
A1
A1a
A1b
R. Liso
1
2
R. Neumático
2
2
R. Pata de cabra 5
5
Pisón impacto 2
2
R. Vibratorio
1
1
A3
2
2
5
1
1
Clasificación AASHTO
A2
A24
A25
A26
A27
1
1
1
2
1
1
1
1
4
4
3
2
2
2
2
4
1
1
3
4
A4
A5
A6
A7
2
2
2
4
3
3
2
1
4
3
3
2
1
4
5
4
3
1
4
5
Clasificación: 1 (excelente), 2 (bueno), 3 (regular), 4 (deficiente), 5 (inadecuado).
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
Recomendaciones generales sobre el proceso de compactación.
a)
Equipo: rodillos lisos, en gravas y arenas mecánicamente estables. Rodillos neumáticos, en arenas uniformes, y
suelos cohesivos con humedades próximas al límite plástico. Rodillos pata de cabra, en suelos finos con humedades
en el rango (LP-7%) a (LP-12%). Equipos vibratorios, en suelos granulares.
b) Espesor de capa: debe ser proporcional a la magnitud del equipo en uso y considerar el tipo de suelo. En equipos
medianos ~ 20cm. El espesor de capa debe ser al menos de tres a 5 veces el valor del Tmáx (Tamaño máximo de
partícula) del material usado.
c) Número de pasadas: no más de seis pasadas por punto. Si no se ha obtenido antes el valor deseado de compactación,
se debe revisar los otros parámetros.
d) Velocidad de pasada: en general ~ 6Km/hr, salvo Rodillos Vibratorios ~ 3 Km/hr y planchas vibradoras ~ 1.5
Km/hr.
e) Humedad: en general conviene compactar con una humedad levemente inferior a la óptima. En suelos granulares
limpios, conviene una humedad intermedia entre seco y saturado.
Control de compactación.
a) Por medición de la densidad de terreno.
Se determina d IN SITU y se expresa como porcentaje respecto a dmax obtenido en el ensayo de referencia,
generalmente el Proctor Modificado, cuyo valor dmax es conocido como DMCS (Densidad Máxima Compactada Seca);
o a través de su valor de densidad relativa. En general se hace una determinación cada 50 a 100 m 3 de suelo
compactado.
La determinación de la densidad puede ser directa, midiendo la masa del suelo y el volumen que ocupa (métodos: cono y
arena, volume tester, otros métodos para hallar el volumen), o bien, indirecta, como en el caso de usar dispositivos
nucleares.
b) Especificación de tipos de equipo de compactación y modo de empleo.
En canchas de prueba se encuentra la combinación óptima: tipo de equipo, espesor de capa, velocidad y número de
pasadas, humedad; la cual luego se controla en su riguroso cumplimiento.
c) Otros métodos:
Medición de penetración, rodillo especial de prueba, etc.
Material tomado de Internet:
Road Design - Earthwork.htm
máquinas.htm
minimáquinas.htm
Máquinas y equipos.htm
5.4 HIDRAULICA DEL SUELO
5.4.1. Presión Efectiva (`):
Se llama presión efectiva a aquella que ejercen recíprocamente las partículas individuales del agregado de suelo.
Piezómetro
S < 100%
hc
Z
S ~ 100%
Napa
u=0
S = 100%
Zw
1
h1
Zona de aireación
2
h2
Zona capilar
3
h3
Zona de agua libre
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
El agua en la zona capilar contribuye al peso del suelo, ya que por estar sujeta a las fuerzas de tensión superficial, no es
libre para movilizarse entre los poros.
Para la zona de aireación: =1=d (1 + ); : valor decimal.
Para un punto P(z) tal que 0  Z  h1 : v = z;  = 0; ’v = v -  = z
Para la zona capilar: 2 = sat = d (1 + sat)
Para un punto P(z) tal que h1 < Z < ( h1 + h2): v =  h1, + sat (Z– h1);
 = w Z w con Zw < 0 y zw hc; ’v = v - 
Para la zona de agua libre: 3 = sat = d (1 + sat)
Para un punto P(z) tal que (h1 + h2)  Z : v =h1 + sat h2 + sat (z – h1 – h2)

Zw
v = h1 + sat ( z – h1)
 = w Zw con zw  0;
’v= v -  = h1 + sat h2 + satZw - wZw
’v = h1 + sath2 + (sat - w)Zw
Al término (sat - w) se le llama peso unitario sumergido o buoyante (’), con lo cual:
’v = h1 + sath2 + ’Zw
5.4.2 Presiones de escurrimiento.
Si en la ecuación propuesta por Terzaghi ( `=  -  ), se considera que la presión de poros puede aumentar como
resultado de una acción externa, esta variación se podría incluir como `=  - ( + ).
Si se genera un  suficientemente elevado, es posible obtener en el suelo, `= 0 (licuación de suelos granulares).
Una forma experimental de generar esta condición, es la siguiente:
Válvula
Sección transversal al flujo
Rebalse
Área 
h
h2
sat
Rebalse
Wl
L
Wl : sobrecarga permeable (T/m2)
 = sat
En el punto A:
Fv = [ (h2 – L)w + L + Wl]
Fv = (h + h2)w (fuerza de escurrimiento)
En el equilibrio límite : Fv = Fv; FS = 1 al desplazamiento vertical de “A”
(h + h2)w = h2w - wL + L + Wl
hw = ( - w)L +Wl = ’L +Wl
h/L = ’/w + Wl/(Lw)
Al término h/l se le llama gradiente hidráulico “i”
En este caso se tendría un gradiente hidráulico crítico “ic”.
Si i > ic el suelo del punto “A” se desplazaría hacia arriba.
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
Este fenómeno de migración de partículas de suelo a través de los huecos de las restantes, se llama erosión interna o
erosión retrógrada, y en inglés se conoce como “piping”.
ic = ’/w + Wl/ Lw
Si consideramos que no hay sobrecarga permeable, Wl = 0
ic = ’/w = (Gs – 1)/ (1+e)
Como para las arenas Gs ~ 2.65 y el rango para el índice de huecos e varía entre 0.25 a 1.00; se tendría que en general
el valor del gradiente hidráulico crítico estaría cercano a 1 ( ic ~ 1), dentro se un rango de 0.8 a 1.3
5.4.3 Permeabilidad.
El flujo del agua en el suelo, en condiciones no turbulentas, ha sido expresado por Darcy, a través de la relación:
v=k·i
i: gradiente hidráulico (h / l)
k: coeficiente de permeabilidad o índice de conductividad hidráulica, con unidades (longitud / tiempo)
v: velocidad ficticia de escurrimiento (longitud / tiempo).
La magnitud del flujo se cuantifica por el gasto “q”:
q = v · A = k · i · A (volumen/tiempo)
Valores típicos del coeficiente “k” (cm/seg)
Grava limpia, GW, GP
Grava limpia y mezclas de arena, GW, GP, SW, SP, GM
Mezclas arena – limo, SM, SC
Arcillas
102 a 100
100 a 10-3
10-3 a 10-7
10-7 a 10-9
El valor del coeficiente “k” se puede determinar por ensayos de laboratorio y por ensayos in situ.
Los ensayos de laboratorio más frecuentes son:
Rebalse
•
Permeámetro de carga constante
Se deduce que:
h
k = Q·L / (A·h·t)
Sección transversal al flujo
L
Área “A”
Probeta graduada, recoge Q(t) en un
tiempo “t”
•
Permeámetro de carga variable
Tubo de área interna “a”
Sección transversal al flujo
h1 se mide en t = t1
h2 se mide en t = t2
t = t2 - t1
Nivel del agua descendiendo
h1
Área “A”
h2
L
Se recoge Q para hallar la sección “a”
2.3 · a · L
Se deduce que: k = ----------- log (h1/h2)
A·t
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
Los ensayos de terreno mas frecuentes son:
Ensayo Lugeon en roca. Presentación1. Presentación2. (Seleccione Ejecutar desde Internet, Aceptar. En Advertencia de
Seguridad, marque “Si”)
Ensayo Le Franc en suelo.
Determinación práctica in situ:
2r
Se estima el valor “k” como:
2r
k ~ q / (5.5·r·H)
H
con:
Tubo metálico
 10r
H
q: gasto infiltrado (vol/tiempo)
r: radio interior del tubo
H: diferencia de carga hidráulica
(constante durante el ensayo)
Estrato permeable
 10r
Prueba de agotamiento:
“q”
En este caso existe un flujo radial
2r
Se puede demostrar que:
R
radio de acción del pozo
“k” = q·ln(R/r) / [ (ho2 - h12)]
(Hipótesis de Dupuit)
ho
h1
Estrato impermeable.
Factores que influyen en el valor de “k”.
Para un mismo suelo dado, el valor del coeficiente de permeabilidad depende de la temperatura del agua (la viscosidad
del agua varía inversamente con la temperatura) y del grado de saturación del suelo en el cual se desarrolla el flujo.
Como la velocidad de escurrimiento del fluido es inversamente proporcional al grado de viscosidad, se tiene:
k20°C · 20°C = kt°C · t°C  k20°C = kt°C · t°C / 20°C
: coeficiente de viscosidad del agua.
5.4.4. Agua capilar.
d
El ascenso capilar del agua en el suelo puede estimarse como:
Fv = dTcos
Fv = WW = d2hcW/4
Fv = 0
hc = 4Tcos/(Wd)
hc: altura de ascenso capilar
d: diámetro de los poros (se puede estimar d ~ 1/5D10)
T

hc
Ww
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm
Universidad de Santiago de Chile. Facultad de Ingeniería. Departamento de Ingeniería en Obras Civiles.
Curso de Mecánica de Suelos Básica. Profesor Gerardo Silva Chandía. Ingeniero Civil UC.
T: tensión superficial del agua (~ 0.075grf/cm)
: ángulo de intersección de la superficie de la película y el tubo capilar (~ 0)
Debido a que el sistema de poros del suelo no es regular, esta expresión sobreestima el ascenso capilar.
En general hc < 1.2 a 1.5 m, pero se desarrolla en todas direcciones en el espacio.
5.4.5. Parámetros de presión de poros.
Para evaluar los incrementos de presión de poros inducidos por un cambio en los esfuerzos aplicados a un suelo, parcial
o completamente saturado, Skempton ha propuesto la expresión:
= B[3 + A(1 - 3)]
: cambio en la presión de poros.
A, B: parámetros de presión de poros.
1, 3: cambio en los esfuerzos principales debido a la aplicación de una carga al suelo.
B varía de 0.0 a 1.0 al variar el grado de saturación de 0 a 100% (no es una variación lineal).
B se obtiene en el ensayo triaxial, midiendo  al variar sólo 3.
A: depende del tipo de suelo y de su historia de esfuerzos.
Valores típicos de “A” (en la falla):
Material
Arcilla altamente sensitiva
Arcilla normalmente consolidada
Arcilla arenosa compactada
Arcilla ligeramente preconsolidada
Arcilla muy preconsolidada
Arena fina muy suelta
Rango
1.2 a 2.5
0.7 a 1.3
0.75 a 0.25
0.3 a 0.7
-0.5 a 0.0
2a3
Proyecto de Desarrollo Docente financiado por la Vicerrectoría de Docencia y el Departamento de Ingeniería
Civil en Obras Civiles. Mayo de 2001. Actualizaciones en http://lauca.usach.cl/doocc/mdidacti/ms2.htm