plan de apoyo mat 10°

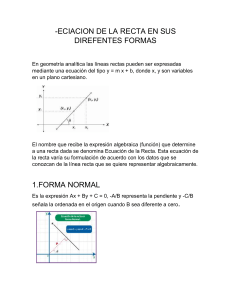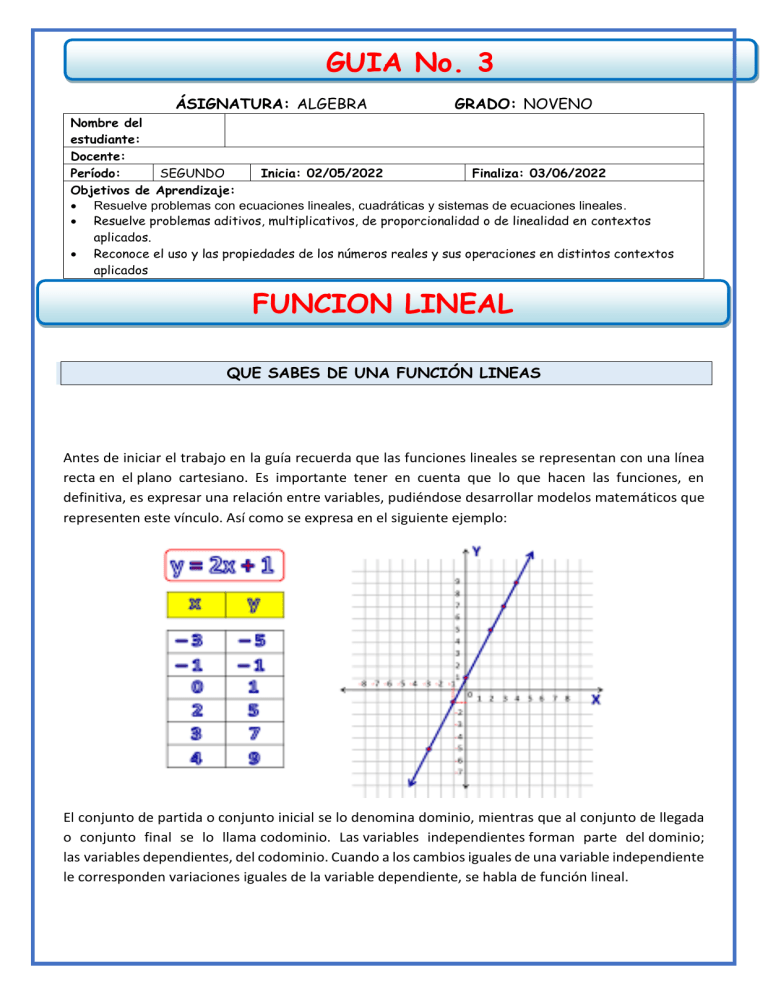
GUIA No. 3
ÁSIGNATURA: ALGEBRA
GRADO: NOVENO
Nombre del
estudiante:
Docente:
Período:
SEGUNDO
Inicia: 02/05/2022
Finaliza: 03/06/2022
Objetivos de Aprendizaje:
• Resuelve problemas con ecuaciones lineales, cuadráticas y sistemas de ecuaciones lineales.
• Resuelve problemas aditivos, multiplicativos, de proporcionalidad o de linealidad en contextos
aplicados.
• Reconoce el uso y las propiedades de los números reales y sus operaciones en distintos contextos
aplicados
FUNCION LINEAL
QUE SABES DE UNA FUNCIÓN LINEAS
Antes de iniciar el trabajo en la guía recuerda que las funciones lineales se representan con una línea
recta en el plano cartesiano. Es importante tener en cuenta que lo que hacen las funciones, en
definitiva, es expresar una relación entre variables, pudiéndose desarrollar modelos matemáticos que
representen este vínculo. Así como se expresa en el siguiente ejemplo:
El conjunto de partida o conjunto inicial se lo denomina dominio, mientras que al conjunto de llegada
o conjunto final se lo llama codominio. Las variables independientes forman parte del dominio;
las variables dependientes, del codominio. Cuando a los cambios iguales de una variable independiente
le corresponden variaciones iguales de la variable dependiente, se habla de función lineal.
Y = X + 2 es un ejemplo de función lineal.
Supongamos que en el dominio tenemos los valores de -3 hasta 3. Si la función señala que Y es igual
a X + 2, en el codominio encontraremos los valores siguientes valores:
Y=X+2
Entonces al reemplazar los valores de X se obtienen:
• X = -3
Y = -3 +2
Y=1
•
Y = -1
• X=0
Y=0+2
• X= -2
Y= -2 + 2
Y=2
Y=0
• X= 1
Y=1+2
• X= -1
Y= -1 + 2
X= 2
Y= 2 + 2
Y=4
• X= 3
Y=3+2
Y=5
Y=3
Quedando así la siguiente tabla de valores con los pares ordenados (x,y)
X
-3
-2
-1
0 1
2
3
Y
-1
0
1
2 3
4
5
Al llevar esta función lineal a un gráfico en coordenadas cartesianas, nos encontraremos con una línea
recta creciente: a medida que crecen los valores de X, crecen proporcionalmente los valores de Y.
Ahora en la siguiente actividad No 1 realiza la aplicación de los conceptos mencionados
Actividad No 1: Tabular y graficar las siguientes funciones lineales. NOTA: esta actividad se debe
desarrollar y hace parte del paquete de evidencias que se debe enviar al finalizar la guía
1) Y = x + 5
2) Y = 3x – 2
3) Y = -x + 1
Observa los siguientes ejemplos para que observes la aplicación de la fórmula de la pendiente
ACTIVIDADES DE APLICACIÓN Y DEMOSTRACIÓN NÚMEROS ENTEROS
Calcular la pendiente que pasa por cada par de puntos y mencionar si es ascendente (creciente),
descendente (decreciente), horizontal o una recta vertical.
a. (6,8) y (2, 3)
b. (-2, 7) y (3, -3)
c. (-1,2) y (5, 2)
d. (5, 3) y (2, 8)
e. (4, -4) y (-8, 8)
1
f. (0, -5) y (4, 2 )
5
g. (2 , 2 ) 𝑦 (0 , 0)
h. (-1, -2) y (-3, -4)
i. (-4, -2) y (-1, 0)
QUE SABES DE LA ECUACION DE UNA RECTA
Los ejemplos abordados en el transcurso de la guia son claros pero una dinamica que se puede realizar
para estudiar es retomarlos uno por uno y desarrollarlos para despues compararlos nuevamente con
los resultados de la guia, asi puedes ir dinamizando y fortaleciendo tu disciplina de estudio.
ACTIVIDADES DE APLICACIÓN Y DEMOSTRACIÓN ECUACION DE UNA RECTA
QUE SABES DE PENDIENTE DE LAS RECTAS PARALELAS Y PERPENDICULARES
Ahora observemos los siguientes ejemplos donde aplicamos los conceptos aquí abordados, primero
las rectas paralelas
Rectas Paralelas
Dos rectas no verticales en un plano son paralelas si tienen:
• la misma pendiente
• distintas intersecciones en y
Cualquier par de rectas verticales en un plano son paralelas.
Observemos el desarrollo de los siguientes ejemplos:
Ejemplo 1
Problema
Encontrar la pendiente de una recta que es paralela a la recta y = −3x+ 4.
La recta dada se escribe como y = mx + b, con m =
−3 y b = 4. La pendiente es −3.
Respuesta
La pendiente de la recta paralela es −3.
Identifica la pendiente de la
recta dada.
Una recta paralela a la recta
dada tiene la misma pendiente.
Ejemplo 2
Problema Determina si las rectas y = 6x + 5 y y = 6x – 1 son paralelas.
La recta dada se escribe como y = mx + b con m= 6 para Identifica la pendiente de la
la primera recta y m = 6 para la segunda recta. La
recta dada.
pendiente de ambas rectas es 6.
La primera recta tiene una intersección en <i>y</i> en
(0, 5), y la segunda recta tiene una intersección en
<i>y</i> en (0, −1). No son la misma recta.
Observa b, el valor de y de la
intersección en <i>y</i>, para
ver si las rectas son la misma,
en cuyo caso no decimos que
son paralelas.
Respuesta
Las rectas son paralelas.
Las pendientes de las rectas
son las mismas y tienen
diferentes intersecciones en y,
entonces no son la misma recta
y son paralelas.
Ahora trabajemos las características de las rectas perpendiculares
Rectas Perpendiculares
Dos rectas no verticales son perpendiculares si la pendiente de una es el recíproco negativo de la
pendiente de la otra. Si la pendiente de la primera ecuación es 4, entonces la pendiente de la
segunda ecuación será
porque las rectas son perpendiculares.
También puedes probar las pendientes para ver si las rectas son perpendiculares multiplicando las
dos pendientes. Si son perpendiculares, el producto de las pendientes será −1. Por
ejemplo,
.
Ejemplo 1
Problema
Encontrar la pendiente de la recta perpendicular a la recta y = 2x – 6.
La recta dada se escribe como y = mx + b, con m =
2 y b = -6. La pendiente es 2.
Respuesta
Identifica la pendiente de la
recta dada.
Para encontrar la pendiente de
la recta perpendicular,
La pendiente de la recta perpendicular es
.
encuentra el recíproco, , y
luego encuentra el opuesto del
recíproco
Observa que el producto
perpendiculares.
.
, lo que significa que las pendientes son
En el caso donde una de las rectas es vertical, la pendiente de esa recta no está definida y no es
posible calcular el producto de un número indefinido. Cuando una recta es vertical, la recta
perpendicular a ella será horizontal, teniendo una pendiente de cero (m = 0).
Ejemplo 2
Problema
Determinar si las rectas y = −8x + 5 y
o ninguna.
son paralelas, perpendiculares,
Las rectas dadas están escritas en la
Identifica las pendientes de las
forma y = mx + b, con m = −8 para la primera recta rectas dadas.
ym=
−8 ≠
para la segunda recta.
, entonces las rectas no so paralelas.
El recíproco opuesto de −8 es
rectas son perpendiculares.
Respuesta
Determina si las pendientes
son la misma o si son
recíprocas opuestas.
, entonces las
Las rectas son perpendiculares.
Las pendientes de las rectas
son recíprocas opuestas, por lo
que las rectas son
perpendiculares.
Aplica lo aprendido en la siguiente pregunta:
¿Cuáles de las siguientes rectas son perpendiculares a la recta
?
I.E SEMILLA DE LA ESPERANZA
Resolución de aprobación No. 1796 de septiembre 4 de 2002
Código DANE 276520005248
A)
B)
NIT. 815004247-7
Código: GAC-DC-O220
Versión: 01
Fecha: mayo-2020
y
y
C)
D) Todas las rectas son perpendiculares.
Escribiendo Rectas Paralelas y Perpendiculares
Las relaciones entre pendientes de rectas paralelas y perpendiculares pueden usarse para escribir ecuaciones
de rectas paralelas y perpendiculares.
Empecemos con un ejemplo de rectas paralelas
Ejemplo 1
Problema
Escribir la ecuación de una recta que sea paralela a la recta x – y = 5 y pase por el
punto (−2, 1).
x–y=5
−y = −x + 5
y=x–5
Reescribe, si es necesario, la
recta que quieres que sea
paralela de la forma
y = mx + b.
98
I.E SEMILLA DE LA ESPERANZA
Resolución de aprobación No. 1796 de septiembre 4 de 2002
Código DANE 276520005248
NIT. 815004247-7
En la ecuación anterior, m = 1 y b = −5.
Como m = 1, la pendiente es 1.
La pendiente de la recta paralela es 1.
Código: GAC-DC-O220
Versión: 01
Fecha: mayo-2020
Identifica la pendiente de la
recta dada.
Para encontrar la pendiente de
una recta paralela, usa la
misma pendiente.
y = mx + b
Usa el método para escribir
una ecuación a partir de la
pendiente y un punto en la
recta. Sustituye 1 por m, y el
punto (−2, 1) por x y y.
1 = 1(−2) + b
1 = −2 + b
Resuelve b.
3=b
Respuesta
y=x+3
Escribe la ecuación usando la
nueva pendiente para m y
la b que acabas de encontrar.
Cuando trabajas con rectas perpendiculares, normalmente tendrás una de las rectas y un punto adicional.
Ejemplo 2
Problema
Escribir la ecuación de una recta que contenga el punto(1, 5) y sea perpendicular
a la recta y = 2x – 6.
La recta dada se escribe en la forma y = mx+ b,
como m = 2 y b = -6. La pendiente es 2.
La pendiente de la recta paralela es
.
Identifica la pendiente de la
recta con la que tu recta debe
ser perpendicular.
Para encontrar la pendiente de
una recta perpendicular,
99
I.E SEMILLA DE LA ESPERANZA
Resolución de aprobación No. 1796 de septiembre 4 de 2002
Código DANE 276520005248
NIT. 815004247-7
Código: GAC-DC-O220
Versión: 01
Fecha: mayo-2020
encuentra el recíproco,
luego su opuesto,
,y
.
Usando el método de escribir
una ecuación a partir de su
pendiente y un punto en la
recta. Sustituye
por m, y
el punto (1, 5) por xy y.
Resuelve b.
Respuesta
Escribe la ecuación usando la
nueva pendiente para m y
la b que acabas de encontrar.
Resuelve la pregunta opción múltiple realizando el proceso.
¿Cuál de la siguientes es la ecuación de una recta paralela a y = −2x – 14 y pasa por el punto (−3, 1)?
A) y = −2x + 1
B)
100
I.E SEMILLA DE LA ESPERANZA
Resolución de aprobación No. 1796 de septiembre 4 de 2002
Código DANE 276520005248
NIT. 815004247-7
Código: GAC-DC-O220
Versión: 01
Fecha: mayo-2020
C)
D) y = −2x – 5
Ejemplo 3
Problema
Escribir la ecuación de una recta que sea paralela a y = 4.
y=4
y = 0x + 4
Reescribe, si es necesario, la recta en la
forma
y = mx + b.
Podrás haber notado sin hacerlo que y = 4
es una recta horizontal 4 unidades sobre el
eje-x. Porque es horizontal, y sabes que la
pendiente es cero.
En la ecuación anterior, m = 0 y b = 4.
Identifica la pendiente de la recta dada.
Como m = 0, la pendiente es 0. Esta es
una recta horizontal.
La pendiente de la recta paralela
también es 0.
y = 10
Para encontrar la pendiente de una recta
paralela, usa la misma pendiente.
Como la recta paralela será una recta
horizontal, su forma es
y = una constante.
Escoge una constante para crear la recta
paralela.
Respuesta
y = 10
Esta recta es paralela a y = 4 e intersecta el
eje-y en (0, 10).
101
I.E SEMILLA DE LA ESPERANZA
Resolución de aprobación No. 1796 de septiembre 4 de 2002
Código DANE 276520005248
NIT. 815004247-7
Código: GAC-DC-O220
Versión: 01
Fecha: mayo-2020
Sumario
Cuando rectas en un plano so paralelas (es decir, nunca se cruzan), tienen la misma pendiente. Cuando rectas
son perpendiculares (es decir, se cruzan formando un ángulo de 90°), sus pendientes son recíprocas opuestas
una de la otra. El producto de sus pendientes siempre será -1, excepto en el caso donde una de las rectas es
vertical, porque su pendiente no está definida. Puedes usar estas relaciones para encontrar la ecuación de una
recta que pase por un punto en particular y que sea paralela o perpendicular a otra recta.
ACTIVIDADES DE APLICACIÓN Y DEMOSTRACIÓN RECTAS PARALELAS Y
PERPENDICULARES
1) Determinar si las siguientes rectas son o no paralelas o perpendiculares:
2) Determinar si las siguientes rectas son o no paralelas o perpendiculares:
102
I.E SEMILLA DE LA ESPERANZA
Resolución de aprobación No. 1796 de septiembre 4 de 2002
Código DANE 276520005248
NIT. 815004247-7
Código: GAC-DC-O220
Versión: 01
Fecha: mayo-2020
3) Hallar la recta paralela a la recta y=2x−3 y que pasa por el punto (−3,1)
4) Hallar la recta perpendicular a la recta y=2x−3 y que pasa por el punto (−2,2)
5) Determinar si las siguientes rectas son perpendiculares a la recta y=3x+3:
EVALÚO MI PROCESO
a. ¿Aprendiste el tema?
____________________________________________________________________
b. ¿Comprendiste las explicaciones y conceptos?
____________________________________________________________________
c. ¿Las actividades fueron fáciles de resolver?
____________________________________________________________________
d. ¿Qué se puede mejorar para la siguiente guía?
____________________________________________________________________
103