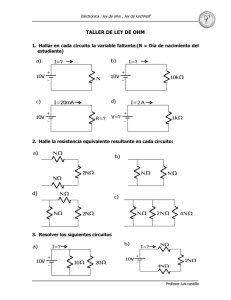
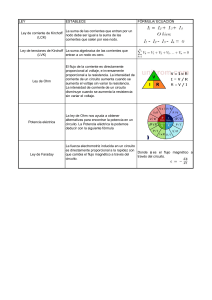
Electricidad y magnetismo Unidad 1 (Electrostática) • 1.5 Ley de Coulomb La ley de Coulomb establece que la fuerza entre dos cargas eléctricas es directamente proporcional al producto de sus magnitudes e inversamente proporcional al cuadrado de la distancia entre ellas. Matemáticamente, se expresa como: F = k * (q1 * q2) / r^2 Donde F es la fuerza, q1 y q2 son las magnitudes de las cargas, r es la distancia entre ellas, y k es la constante de proporcionalidad La ley de Coulomb señala que la fuerza F (newton, N) con que dos carga eléctricas Q y q (culombio, C) se atraen o repelen es proporcional al producto de las mismas e inversamente proporcional al cuadrado de la distancia r (metro, m) que las separa. Ley de Coulomb En muchos casos es útil el concepto de campo eléctrico, que se puede definir como la fuerza por unidad de carga. Así para una carga Q, el módulo del campo eléctrico producido a una distancia r es: E=K*Q/R r^2 y que apunta alejándose de Q si la carga es positiva y en dirección a Q si es negativa. Una carga q en el seno del campo eléctrico sentirá una fuerza que viene dada por: F=qE Ley de Coulomb La existencia de más de una carga produce en cada punto un conjunto de fuerzas individuales cuya resultante es la suma vectorial. Cuando esta resultante vale cero el campo eléctrico en ese punto también es cero. Podemos estudiar el campo eléctrico utilizando una carga Qp que pende de un hilo, el péndulo eléctrico. Únicamente el péndulo estará vertical en aquellos puntos en los que el campo valga cero. Ley de Coulomb En nuestra experiencia tenemos dos cargas Q1 y Q2, y vamos a sondear la recta delimitada por ellas. El campo eléctrico se hará cero en algunos puntos sobre la línea: en los tramos izquierdo, central o derecho (dependiendo de los signos de las cargas y sus valores). Todos los puntos fuera de la recta presentan un campo distinto de cero. Una vez localizado un punto de campo cero, se miden las distancias a cada carga d1 y d2. Las fuerzas deben ser iguales en módulo y sentido contrario:: Ley de Coulomb Se quiere localizar los puntos de campo eléctrico nulo de un sistema formado por dos cargas eléctricas mediante un péndulo eléctrico. La aplicación de la ley de Coulomb en dichos puntos, una vez medidas las distancias a cada una, comprueba la bondad de la ley. Ley de Coulomb Se presentan en cada oportunidad que se pulsa el botón Otro caso dos cargas positivas Q1 y Q2 diferentes y separadas por 1 m. En todo caso el péndulo eléctrico se carga con una carga Qp= +1’00 C. Para encontrar el punto de campo nulo situado a la distancia x de la carga izquierda, desliza la posición del cursor de la parte inferior y pulsa el botón Soltar. El sentido del desplazamiento indicará hacia donde mover el deslizador. Considera el punto encontrado cuando leves movimientos del cursor provoquen desplazamientos del péndulo opuestos. Calcula las fuerzas debidas a cada carga. Ley de Coulomb Ley de Gauss y sus aplicaciones • 1.6 Ley de Gauss y sus aplicaciones La ley de Gauss establece que el flujo eléctrico a través de una superficie cerrada es proporcional a la carga total encerrada por dicha superficie. Esta ley se puede utilizar para determinar el campo eléctrico en algunos casos simétricos. El número de líneas de campo que atraviesan una determinada superficie depende de laorientación de esta última con respecto a las líneas de campo. dS~ es un vector de módulo el elementode área infinitesimal de la superficie, dirección perpendicular a la misma ysentido hacia afuera de la curvatura. Ley de Gauss El flujo del vector campo eléctrico a través de una superficie cerrada es igual a la carga encerrada ensu interior dividida por la permitividad del medio. La superficie gaussiana no es una superficie real ( es matemática). La ley de Gauss simplifica los cálculos de campo eléctrico en casos de gran simetría. Ley de Gauss Ley de Gauss El flujo neto del campo eléctrico estático a través de cualquier superficie cerrada es igual a 4π*k veces el valor de la carga neta encerrada por dicha superficie. Ley de Gauss Reformulación de la ley de Gauss en términos de la permitividad del vacío ∈0 Ley de Gauss El flujo eléctrico neto a través de cualquier superficie gaussiana cerrada es igual a la carga neta que se encuentre dentro de ella, dividida por la permitividad del vacío. Esta ley sólo puede aplicarse a problemas con gran simetría. Ley de Gauss Ley de Gauss Receta para la ley de Gauss: Escoger superficie de Gauss de acuerdo a la simetría. Que pase por P. Que sea cerrada. Que E sea constante (por lo menos en parte) de la superficie. Que E sea paralela a la superficie en las partes donde no es constante. El integral sale directo a una expresión algebráica que contiene E. Calcular qN Es lo que distingue cada situación y cada región. Es diferente en cada región. A veces hay que calcular la densidad de carga. qN es el producto de densidad por el volumen de carga dentro de la superficie. Resolver por E algebráicamente Ley de Gauss La ley de Gauss tiene varias aplicaciones en la física y la ingeniería, algunas de las cuales incluyen: 1.- Cálculo del campo eléctrico: La ley de Gauss se utiliza para calcular el campo eléctrico generado por una distribución de carga conocida. Al elegir una superficie cerrada adecuada y aplicar la ley de Gauss, podemos determinar el campo eléctrico en puntos específicos del espacio. 2.- Cálculo de la densidad de carga: Si conocemos el campo eléctrico en un punto, podemos utilizar la ley de Gauss para determinar la densidad de carga en ese punto. Esto es especialmente útil cuando se trabaja con cargas distribuidas en objetos o sistemas complejos. Ley de Gauss y sus aplicaciones 3.- Cálculo del flujo eléctrico: La ley de Gauss permite calcular el flujo eléctrico a través de una superficie cerrada, lo cual es útil para determinar la cantidad de carga que pasa a través de una región determinada. 4.- Ley de Gauss en el magnetismo: La ley de Gauss también se aplica al campo magnético. En este caso, la ley de Gauss magnética establece que el flujo magnético a través de una superficie cerrada es igual a cero, lo que implica que no existen monopolos magnéticos. Unidad 1 (Electrostática) • 1.7 Definición de potencial eléctrico El potencial eléctrico se define como el trabajo necesario para llevar una carga de prueba positiva desde el infinito hasta un punto determinado en el campo eléctrico. Potencial Eléctrico: Es el trabajo desarrollado por la Fuerza Externa por unidad de carga puntual Definición de potencial eléctrico Caso particular de un Campo Uniforme Unidades del Potencial: Voltio (V) Unidades del Campo Eléctrico: V/m o N/C Definición de potencial eléctrico Caso general: Campo Eléctrico no uniforme y trayectoria no rectilínea Debemos dividir la trayectoria en pequeños desplazamientos infinitesimales, de forma que El Potencial en este caso será Definición de potencial eléctrico Para un desplazamiento curvilíneo ds= dx i + dy j + dz k la variación de Potencial es dV = −E ds = −Exdx −Eydy −Ezdz Con esta expresión, podemos, conocido el Potencial Eléctrico, calcular el Campo Eléctrico asociado Definición de potencial eléctrico Si dejamos en libertad una carga de prueba en el seno de un campo eléctrico, se acelerará en el sentido de dicho campo a lo largo de las líneas de fuerza. El hecho de que se acelere hace que aumente su energía cinética, con lo cual, su energía potencial debe disminuir. Esto quiere decir que las Líneas de Campo señalan en la dirección en la que disminuye el Potencial Eléctrico. Visto en términos del gradiente, ya que su significado físico es la dirección de máxima variación de la función, el signo menos indica sentido decreciente del Potencial. Definición de potencial eléctrico Se puede calcular el Potencial de una carga puntual a partir del Campo Eléctrico que produce. I.- Calculemos el Trabajo realizado por el Campo para desplazar la carga desde el punto A al punto B Definición de potencial eléctrico II.- Un método alternativo es calcular el Trabajo que debe realizar una Fuerza Exterior para traer una carga desde el infinito hasta un punto r. En este caso el punto A coincide con el infinito. Definición de potencial eléctrico La Energía Potencial de una carga qo, situada a una distancia r de q, será: La Energía Potencial de un sistema de cargas puntuales será el trabajo necesario para llevar cada una de ellas desde el infinito hasta su posición final. Cálculo de potencial eléctrico • 1.8 Calculo de potencial eléctrico Matemáticamente, se expresa como: V = k * q / r Donde V es el potencial eléctrico, q es la carga, r es la distancia desde la carga hasta el punto donde se quiere calcular el potencial, y k es la constante de proporcionalidad. Existen dos métodos para calcular el Potencial Eléctrico asociado a una distribución continua de cargas: 1.- Conocido el Campo Eléctrico creado por la distribución En este caso debemos tomar como origen de potenciales un punto de referencia arbitrario. Cálculo de potencial eléctrico 2.- Para el caso de distribuciones finitas de carga, para las cuales podemos suponer que V( ) = 0. En este caso podemos suponer conocido el V para la carga puntual y aplicar superposición Cálculo de potencial eléctrico Ejemplo 1.- Potencial Eléctrico sobre el eje de un anillo cargado. Cálculo de potencial eléctrico Ejemplo 2.- Potencial Eléctrico sobre el eje de un disco uniformemente cargado. Cálculo de potencial eléctrico Ejemplo 3.- Potencial Eléctrico en el interior y el exterior de un Cascarón (corteza) Esférico de carga. Cálculo de potencial eléctrico EJEMPLO 7.10 ¿Qué voltaje produce una pequeña carga en una esfera de metal? Las cargas de la electricidad estática suelen estar en el rango de los nanoculombios (nC) y microculombios (μC) . ¿Cuál es el voltaje a 5,00 cm del centro de una esfera de metal sólida de 1 cm de diámetro que tiene una carga estática de –3,00 nC? Estrategia Como ya comentamos en Cargas y campos eléctricos, la carga en una esfera de metal se propaga uniformemente y produce un campo como el de una carga puntual situada en su centro. Por lo tanto, podemos calcular el voltaje utilizando la ecuación V=kqr. Solución Al introducir los valores conocidos en la expresión del potencial de una carga puntual, obtenemos Unidad 3 (Electrodinámica) • 3.4 La ley de Ohm La ley de Ohm establece que la corriente que fluye a través de un conductor es directamente proporcional al voltaje aplicado e inversamente proporcional a la resistencia del conductor. Matemáticamente, se expresa como: I = V / R Donde I es la corriente, V es el voltaje y R es la resistencia. La ley de Ohm, postulada por el físico y matemático alemán Georg Simón Ohm, es una ley de la electricidad; en la cual se establece que la diferencia de potencial V que aparece entre los extremos de un conductor determinado es proporcional a la intensidad de la corriente I que circula por el citado conductor. Ohm completó la ley introduciendo la noción de resistencia eléctrica ; que es el factor de proporcionalidad que aparece en la relación entre V e I: Ley de Ohm Tensión o diferencia de potencial “voltaje”: Es una magnitud física que cuantifica la diferencia de potencial eléctrico entre dos puntos; su unidad en el Sistema Internacional de Unidades es el Volt [V]. Calculando la tensión mediante la ley de Ohm: 𝑉[𝑉] = 𝐼[𝐴] ∗ 𝑅[Ω] La corriente eléctrica: Es el flujo de cargas eléctricas o flujo de electrones en forma ordena a través de un conductor eléctrico. La unidad en el Sistema Internacional de Unidades es ampere [A]. Ley de Ohm Resistencia Eléctrica: Es la propiedad física de un elemento o dispositivo de impedir el flujo de corriente. La unidad en el Sistema Internacional de Unidades Ohm [Ω]. Calculando la resistencia mediante la ley de Ohm: 𝑅[Ω] = 𝑉[𝑉] 𝐼[𝐴] Ley de Ohm Potencia eléctrica3 : Es el periodo de absorción o de entrega de energía; este tema se desarrollara en el apartado de potencia. La unidad en el Sistema Internacional de Unidades es Watt [W] Un circuito eléctrico o red eléctrica es una interconexión de elementos eléctricos unidos entre sí en una vía cerrada, de modo que una corriente eléctrica pueda fluir constantemente. Ley de Ohm Ley de Ohm Sentido de la corriente eléctrica La corriente eléctrica es la circulación de electrones a través de un material conductor que se mueven siempre del polo negativo (-) al polo positivo (+) de la fuente de suministro. Ley de Ohm Aunque el sentido convencional de circulación de la corriente eléctrica es a la inversa, del polo positivo (+) al polo negativo (-). Ley de Ohm Ejemplos de la aplicación de la Ley de Ohm en diferentes circuitos eléctricos a) ¿Calcule la corriente total I que circula por el siguiente circuito? Ley de Ohm b) ¿Calcule la tensión que se genera en la resistencia, si fluye en el circuito una corriente de 2?5 A? Ley de Ohm c) ¿Calcule el valor de la resistencia, se conecta a una fuente de 14V y fluye en el circuito una corriente de 2.5 m[𝐴]? Ley de Ohm Fórmulas de acuerdo a la Ley de Ohm Ley de Ohm Formulas de ley Ohm Ley de Ohm Formulas de ley de Ohm Ley de Ohm Formulas de ley de Ohm Leyes de Kirchhoff • 3.5 Las leyes de Kirchhoff Las leyes de Kirchhoff son dos principios que se utilizan para analizar circuitos eléctricos. La ley de corrientes de Kirchhoff establece que la suma de las corrientes que entran a un nodo es igual a la suma de las corrientes que salen del mismo nodo. La ley de voltajes de Kirchhoff establece que la suma de las caídas de voltaje alrededor de cualquier lazo o circuito cerrado es i Leyes de Kirchhoff Las leyes (o Lemas) de Kirchhoff fueron formuladas por Gustav Kirchhoff en 1845. Son muy utilizadas en ingeniería eléctrica para obtener los valores de intensidad de corriente en ramas de un circuito eléctrico y potencial eléctrico en cada punto del circuito. Dichas leyes surgen de la aplicación de la ley de conservación de la carga (ley de los nudos) y de la conservación de la energía (ley de las mallas). En circuitos complejos, estas leyes se pueden aplicar utilizando un algoritmo sistemático, programable en sistemas de cálculo informatizado mediante matricesgual a cero. Ley de Kirchhoff Definiciones Para su enunciado es necesario previamente definir los conceptos de nudo o nodo, rama, malla y celda en un circuito eléctrico Nudo o nodo: es el punto donde concurren varias ramas de un circuito (más de 2 ramas). El sentido de las corrientes es arbitrario y debe asignarse previamente al planteo del problema. Rama: es el fragmento de circuito eléctrico comprendido entre dos nodos consecutivos. Malla: es un recorrido cerrado del circuito que resulta de recorrer el esquema eléctrico en un mismo sentido regresando al punto de partida, pero sin pasar dos veces por la misma rama Celda: es aquella malla cuyo recorrido define una superficie que no contiene en su interior ninguna otra rama. Ley de Kirchhoff En la figura se observa un circuito resistivo que tiene las siguientes características: 5 resistencias 3 fuentes de fuerza electromotriz 4 nudos 6 ramas 6 corrientes en rama 7 mallas 3 celda Ley de Kirchhoff Enunciado de las Leyes Ley de los nudos o ley de corrientes de Kirchhoff (1a. Ley de circuito de Kirchhoff): En todo nudo, la suma de corrientes entrantes es igual a la suma de corrientes salientes. Ley de Kirchhoff Ley de las "mallas" o ley de tensiones de Kirchhoff (2a. Ley de circuito de Kirchhoff): En toda malla la suma de todas las caídas de tensión (voltajes en las resistencias) es igual a la suma de todas las fuerzas electromotrices. Un enunciado alternativo es: en toda malla la suma algebraica de las diferencias de potencial eléctrico debe ser cero Ley de Kirchhoff Ley de Ohm Cuando en los extremos de un conductor de resistencia R se mantiene una diferencia de potencial V, por dicha resistencia circulará una corriente i. Se dice que el material conductor de resistencia R es óhmico si la relación entre V e i es proporcional (Ley de Ohm). La ley de Ohm, es una propiedad específica de ciertos materiales. Un conductor cumple con la ley de Ohm sólo si su curva V-i es lineal; esto es si R es independiente de V y de i: V=Ri En donde, empleando unidades del Sistema internacional: Ley de Kirchhoff ANALISIS DE UN CIRCUITO RESISTIVO MEDIANTE LAS LEYES DEKIRCHHOFF CONCEPTO: electricidad básica EQUIPOS Y COMPONENTES ELECTRÓNICAS 1 fuentes de poder 1 Tester o multímetro. Tablero de conexiones. Conectores Resistencias piroliticas de : 100 Ω 150Ω 200Ω 270Ω PROPÓSITO El propósito de esta actividad de laboratorio es: Investigar sobre el voltaje y la corriente, en circuitos resistivos Demostrar experimentalmente las leyes de Kirchhoff. Medir una resistencia en forma precisa con el Puente de Wheatstone. Ley de Kirchhoff PROCEDIMIENTO a.- Análisis de un circuito, mediante las Leyes de Kirchhoff 1. Medir cada resistencia y anote en la tabla su valor 2. En el tablero de conexiones, armar el circuito de resistivo de la figura, mida la resistencia total RT , anote su valor 3. Utilizando las leyes de Kirchhoff, calcular la corriente y el voltaje en cada resistencia, anotar en la tabla. 4. Conectar la fuente de voltaje, medir los voltajes en cada resistencia y en la fuente de energía. Calcule la corriente en cada resistencia, anotar en la tabla 5. Verificar que se cumple la ley de los nudos y la ley de las mallas, anote en la tabla 6. Calculo de la resistencia RAD del circuito Calcule la resistencia equivalente entre los puntos A y D. (conexión mixta) Con el voltaje de la fuente y la corriente iT, calcular la resistencia entre los puntos A y D. Desconecte la fuente y mida la resistencia con entre los puntos A y D Divisor de corriente y voltaje • 3.6 Divisor de corriente y de voltaje El divisor de corriente se utiliza para calcular la corriente que fluye a través de cada rama de un circuito en paralelo. El divisor de voltaje se utiliza para calcular el voltaje en cada elemento de un circuito en serie. Divisor de corriente y voltaje El voltaje Vs(t) se divide en los voltajes que caen en las resistencias R1 y R2. Esta fórmula sólo es válida si la salida v2(t) está en circuito abierto (no circula corriente por los terminales donde se mide v2(t)). Divisor de corriente y voltaje Análogamente, la corriente Is(t) se divide en las corrientes que atraviesan las dos conductancias. Unidad 3 (Electrodinámica) • 3.7 Energía eléctrica y potencia La energía eléctrica se define como el trabajo realizado por una corriente eléctrica en un tiempo determinado. La unidad de medida es el kilovatio-hora (kWh). La potencia eléctrica es la tasa a la que se consume energía eléctrica. Se mide en vatios (W) y se calcula como el producto de la corriente y el voltaje. Unidad 3 (Electrodinámica) • 3.7.1 Ley de Joule La ley de Joule establece que la energía térmica producida por la resistencia eléctrica es proporcional al cuadrado de la corriente que fluye a través de ella, a la resistencia y al tiempo durante el cual fluye la corriente. Matemáticamente, se expresa como: Q = I^2 * R * t Donde Q es la energía térmica producida, I es la corriente, R es la resistencia y t es el tiempo. • 3.7.2 Potencia eléctrica La potencia eléctrica se calcula como el producto de la corriente y el voltaje. Matemáticamente, se expresa como: P = I * V Donde P es la potencia, I es la corriente y V es el voltaje. Unidad 4 (Campo magnético) • 4.4 Fuerza magnética sobre una carga La fuerza magnética sobre una carga se puede calcular utilizando la ley de Lorentz. Esta ley establece que la fuerza magnética sobre una carga es proporcional a la velocidad de la carga, al campo magnético y al seno del ángulo entre la velocidad y el campo magnético. Matemáticamente, se expresa como: Fm = q * v * B * sen(θ)Donde Fm es la fuerza magnética, q es la carga, v es la velocidad, B es el campo magnético y θ es el ángulo entre la velocidad y el campo magnético. • 4.5 Fuerza magnética y par sobre un conductor que conduce corriente La fuerza magnética y el par sobre un conductor que conduce corriente se pueden calcular utilizando la ley de Laplace. Esta ley establece que la fuerza magnética sobre un conductor es proporcional a la corriente que fluye por él, a la longitud del conductor y al campo magnético. Matemáticamente, se expresa como: Fm = I * L * B * sen(θ)Donde Fm es la fuerza magnética, I es la corriente, L es la longitud del conductor, B es el campo magnético y θ es el ángulo entre la dirección de la corriente y el campo magnético. Unidad 4 (Campo magnético) • 4.6 Fuerza magnética entre conductores paralelos La fuerza magnética entre dos conductores paralelos puede calcularse utilizando la ley de Ampère. Esta ley establece que la fuerza magnética entre dos conductores paralelos es proporcional al producto de las corrientes que fluyen por los conductores, a la longitud de los conductores y al inverso de la distancia entre ellos. Matemáticamente, se expresa como: Fm = (μ0 * I1 * I2 * L) / (2 * π * d) Donde Fm es la fuerza magnética, μ0 es la permeabilidad magnética del vacío (valor aproximado de 4π × 10^-7 T·m/A), I1 e I2 son las corrientes que fluyen por los conductores, L es la longitud de los conductores y d es la distancia entre ellos. • 4.7 Ley de Faraday La ley de Faraday establece que un cambio en el flujo magnético a través de una superficie cerrada induce una corriente eléctrica en un circuito. Matemáticamente, se expresa como:ε = -dΦ/dt Donde ε es la fem (fuerza electromotriz) inducida en el circuito, Φ es el flujo magnético y t es el tiempo. El signo negativo indica que la fem inducida es opuesta a la dirección del cambio del flujo magnético. Unidad 4 (Campo magnético) • 4.8 Ley de Lenz La ley de Lenz establece que la fem inducida en un circuito es tal que se opone al cambio que la produce. Es decir, la corriente inducida fluye en una dirección tal que su campo magnético se opone al cambio en el campo magnético que la produce. Esta ley se utiliza para determinar la dirección de la corriente inducida en un circuito. Unidad 5 (Inducción electromagnética ) • 5.1 Definición de inductancia La inductancia es una propiedad de un circuito que mide su capacidad para generar una fuerza electromotriz (fem) inducida cuando la corriente que lo atraviesa cambia. Se representa por la letra L y se mide en henrios (H). La inductancia depende de la geometría del circuito y de los materiales utilizados en su construcción. • 5.3 Energía asociada al campo magnético La energía asociada al campo magnético se refiere a la energía almacenada en un inductor debido a la corriente que fluye a través de él. Cuando la corriente cambia, se genera un campo magnético que acumula energía. La energía almacenada en el campo magnético de un inductor se calcula mediante la siguiente fórmula:E = (1/2) * L * I^2Donde E es la energía almacenada, L es la inductancia y I es la corriente que fluye a través del inductor. Unidad 5 (Inducción electromagnética ) • 5.4 Inductancia mutua La inductancia mutua se refiere a la capacidad de un circuito para influir en la inductancia de otro circuito cercano. Cuando hay dos circuitos cercanos, la corriente que fluye en uno de ellos puede generar un campo magnético que induce una fem en el otro circuito. La inductancia mutua se representa por la letra M y se mide en henrios (H). La inductancia mutua depende de la geometría y la posición relativa de los circuitos, así como de los materiales utilizados.