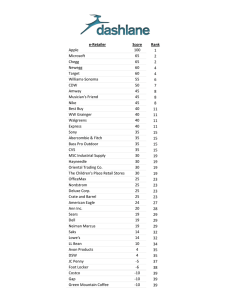
Delivery arrangement in online distribution channels under different power structures

Omega 126 (2024) 103070
Contents lists available at ScienceDirect
Omega
journal homepage: www.elsevier.com/locate/omega
Delivery arrangement in online distribution channels under different
power structures✰
Xiongwei Zhou a, Chaoqun Zhu a, Dan Cai b, *
a
b
School of Business, Central South University, Changsha, 410083, PR China
School of Economics and Management, Chongqing University of Posts and Telecommunications, Chongqing, 400065, PR China
A R T I C L E I N F O
A B S T R A C T
Keywords:
Supply chain management
Delivery arrangement
Online distribution channel
Nonlinear delivery cost
Power structure
Logistics delivery is a critical but costly operation in e-commerce. The e-retailer who sells products online may
ask the supplier to ship products to customers, and the supplier responds by accepting or rejecting such a delivery
proposal. Motivated by these observations, we consider an online distribution channel with two competing
suppliers and one common e-retailer and analytically characterize the equilibrium delivery arrangement based
on the nonlinear delivery cost in the E-retailer-Stackelberg, Supplier-Stackelberg, and Vertical-Nash games. Our
analysis reveals that the market follower might be more willing to deliver products than the market leader in
each Stackelberg game. Counterintuitively, the e-retailer prefers undertaking the delivery when there is a large
delivery diseconomy under each power structure but prefers asking both suppliers to deliver products when there
is a delivery economy (a small delivery diseconomy) in the E-retailer-Stackelberg and Vertical-Nash games
(Supplier-Stackelberg game). The suppliers agree to ship products only when the delivery economy is apparent in
the E-retailer-Stackelberg game but reject to do so in the Vertical-Nash game; in the Supplier-Stackelberg game,
they accept the delivery proposal even though there is a significant delivery diseconomy. Although both suppliers
can benefit from refusing to undertake the delivery when there is fierce competition in each Stackelberg game,
interestingly, they still agree to do so and trap themselves in a prisoner’s dilemma. In each Stackelberg game,
only shifting the delivery responsibility to the suppliers might achieve a triple-win situation for the channel
members, consumers, and society; in the Vertical-Nash game, however, this situation never occurs, and the
consumer surplus and social welfare are invariant to the delivery arrangement.
1. Introduction
Developments in payment and internet technologies have stimulated
the rapid growth of e-commerce worldwide in the past decades. One
salient feature of online retailing is that firms must deliver products to
consumers once the payment is completed. It is well established that
delivering products is a costly operation in online retailing (X. [1–6]). As
per a recent report by the Council of Supply Chain Management Pro­
fessionals, logistics costs for businesses in the United States rose by 22.4
% to $1.85 trillion, accounting for 8 % of the country’s GDP in 2021.1
Similarly, the China Federation of Logistics and Purchasing reported
that China spent approximately 335.2 trillion RMB on logistics in 2021,
an increase of 9.2 % from the previous year.2 Given the significance of
logistics delivery in online transactions, delivery arrangement, i.e., who
is responsible for delivering products to consumers, has always been
among the most critical issues for online distribution channel members.
It is evident from practical observations that e-retailers who sell
products online often take up the responsibility of product delivery.
However, for some product categories, e-retailers may ask the suppliers
to ship products to consumers directly. In response, the suppliers accept
or reject this delivery proposal. For instance, JD.com, one of the largest
e-retail giants in China, delivers substitutable products when selling
✰
Area - Supply Chain Management This manuscript was processed by Associate Editor Shen.
* Corresponding author at: School of Economics and Management, Chongqing University of Posts and Telecommunications, Chongqing, 400065, PR China.
E-mail address: [email protected] (D. Cai).
1
https://cscmp.org/ (accessed July 10, 2023).
2
http://www.chinawuliu.com.cn/ (accessed July 10, 2023).
https://doi.org/10.1016/j.omega.2024.103070
Received 16 July 2023; Accepted 27 February 2024
Available online 8 March 2024
0305-0483/© 2024 Elsevier Ltd. All rights reserved.
X. Zhou et al.
Omega 126 (2024) 103070
products for competing suppliers such as Haier3 and Midea.4 Conversely,
for suppliers like Li-Ning5 and ANTA,6 JD.com may ask them to deliver
products, and both agree. The same commercial phenomenon also oc­
curs with other e-retailers such as Gome,7 Suning,8 Amazon (Direct
Fulfillment Program) ,9 and Walmart (Dropship Vendor Program) .10
Another typical example is that, on the wholesale website 1688 in China,
some suppliers accept the e-retailer’s delivery proposal while others
reject it.11 The above anecdotal evidence implies that the attitudes of
channel members towards undertaking the delivery are sometimes
inconsistent, which, thus, also stimulates our interest in exploring the
underlying mechanism that drives the delivery arrangement in online
distribution channels.
As mentioned above, product shipping is expensive for firms because
it involves associated operations such as warehouse building or renting,
package handling, and product transporting. Particularly when
encountering scale diseconomies of delivery (G. [7]), channel members
might be reluctant to undertake the delivery due to the increased costs.
Suppliers usually consider these operational costs when deciding
whether to accept the e-retailer’s delivery proposal. However, as is well
documented in the literature, the delivery of products may also exhibit
economies of scale ([8]; B. [9]). In this regard, JD.com12 and Haier13
have also publicly reported that delivering online orders may exhibit
economies of scale. These two types of delivery scale effects are opposite
and thus can profoundly affect the channel members’ preferences over
undertaking the delivery. Despite these delivery scale effects, little is
understood about their implications for the delivery arrangement in
online distribution channels. Therefore, further investigation is neces­
sary to comprehend how and why these different scale effects shape
firms’ delivery arrangement preferences.
In addition to the delivery scale effect, power structure also mate­
rially matters because a dominant market power can ensure sufficient
profits to cover the delivery cost (Y. [10]) and is essential in influencing
channel members’ delivery willingness. When the e-retailer plays a
dominant role in online distribution channels, she could claim retail
markup at first, which narrows the wholesale price the supplier demands
later and thus might reduce his willingness to be responsible for deliv­
ering products to customers. In contrast, a powerful supplier can sub­
stantially extract the wholesale price, leaving the e-retailer with
inadequate retail markup to compensate for the associated costs when
she undertakes the delivery. In recent years, with the expansion of on­
line sales scale and the continuous integration of related businesses,
many e-retailers are becoming more formidable than their suppliers;
e-retail giants such as Amazon, Walmart, and JD.com often exploit
power to push their suppliers towards the situation where they have less
bargaining power ([11]; Yujie [12,13]). In the vertical competition be­
tween channel members, well-known and influential suppliers such as
Huawei, Siemens, Xiaomi, Nike, and Adidas may play a leading role
when distributing products through downstream smaller e-retailers
([14]; G. [15]; T.-Y. [16]). In many cases, however, channel members
may be involved in the vertical Nash competition (S. [17,18]). Although
the existing literature has emphasized the critical role of the power
structure in the supply chain’s operation behaviors ([19–23]; X. [24]),
there is no existing theory that thoroughly explains how the power
structure affects the delivery arrangement in online distribution
channels.
Both forces discussed above make the problem of delivery arrange­
ment more complex, and the equilibrium arrangement cannot be readily
observed. To fill the research gap, we consider the nonlinear delivery
cost reflecting delivery economy or diseconomy and develop a gametheoretic model to fully characterize the equilibrium delivery arrange­
ment under three power structures: E-retailer-Stackelberg, SupplierStackelberg, and Vertical-Nash games. In particular, we attempt in this
paper to pursue the following research questions: (1) How would the
power structure and nonlinear delivery cost shape firms’ delivery
arrangement preferences? (2) Which delivery arrangement can be sus­
tained as an equilibrium outcome under different power structures? If
so, under what conditions? (3) Is there a particular delivery arrangement
that benefits the channel members involved and generates the highest
consumer surplus and social welfare concurrently? To address these is­
sues, we consider an online distribution channel consisting of one
common e-retailer and two competing suppliers. The e-retailer and
suppliers are assumed to have the ability and funds to undertake the
delivery. Initially, the e-retailer decides to ask none, one, or both of the
suppliers to ship products to customers. After that, the supplier, condi­
tional upon receipt of a delivery proposal from the e-retailer, determines
whether to undertake the delivery. Based on the interactions between
the supplies and the e-retailer, we study three delivery arrangements:
EE, SE/ES, and SS. The delivery arrangement EE means that the eretailer undertakes the delivery of two substitutable products, the hybrid
delivery arrangement SE/ES denotes that only one of the suppliers de­
livers products to customers, and the delivery arrangement SS represents
that both suppliers are responsible for shipping products to consumers.
Our analysis reveals several noteworthy findings. (1) The market
follower is more willing to undertake the delivery than the market
leader when the delivery is economy in each Stackelberg game. (2)
Channel members prefer undertaking the delivery when the delivery
diseconomy is significant but may avoid it when there is a delivery
economy. (3) The delivery arrangement EE might emerge in equilibrium
under each power structure, irrespective of the delivery scale effect;
however, the delivery arrangement SS emerges in equilibrium only
when the delivery economy is large (the delivery diseconomy is not so
small and the competition intensity is not too large) in the E-retailerStackelberg (Supplier-Stackelberg) game; even in a symmetric setting,
the hybrid delivery arrangement SE/ES can emerge in equilibrium in the
Supplier-Stackelberg game. (4) Interestingly, even if both suppliers can
earn higher profits by rejecting the e-retailer’s delivery proposal when
there is fierce competition in each Stackelberg game, they still accept it
and eventually fall into a prisoner’s dilemma. (5) In each Stackelberg
game, only shifting the delivery responsibility to the suppliers might
benefit channel members and generate the highest consumer surplus
and social welfare concurrently (i.e., a triple-win situation). In the
Vertical-Nash game, however, such a situation never occurs, and the
consumers and society are indifferent to who ships products.
Our contribution is threefold. First, to the best of our knowledge, we
are among the first to examine the delivery arrangement in an online
distribution channel under different power structures and show that the
equilibrium delivery arrangements under the three power structures are
dramatically different. Moreover, the market follower who possesses
less negotiation power might be more willing than the market leader to
be responsible for delivering products. Therefore, our research provides
novel insights into how power structure impacts the delivery arrange­
ment. Second, our analysis provides surprising insights that channel
members might benefit from delivering the product with a significant
delivery diseconomy but suffer from shipping the product with the
apparent delivery economy. Third, our research sheds light on the
implication of an e-retailer’s delivery proposal for the competing sup­
pliers and suggests that such a delivery proposal might lead to a
3
https://item.jd.com/100037217877.html (accessed July 10, 2023).
https://item.jd.com/100022748756.html (accessed July 10, 2023).
5
https://item.jd.com/100033049869.html (accessed July 10, 2023).
6
https://item.jd.com/100044484654.html (accessed July 10, 2023).
7
https://item.gome.com.cn/9140420462-1131249887.html (accessed July
10, 2023).
8
https://product.suning.com/0000000000/12183309510.html? (accessed
July 10, 2023).
9
https://vendorcentral.amazon.com/ (accessed July 10, 2023).
10
https://supplierhelp.walmart.com/s/ (accessed July 10, 2023).
11
https://www.1688.com (accessed July 10, 2023).
12
https://finance.sina.com.cn/stock/relnews/hk/2023-08-29/docimziwkqa1409310.shtml (accessed October 10, 2023).
13
https://www.sohu.com/a/16607610_115469 (accessed October 10, 2023).
4
2
X. Zhou et al.
Omega 126 (2024) 103070
prisoner’s dilemma in each Stackelberg game. Overall, our findings
uncover the underlying mechanism behind the delivery arrangement
and provide concrete and valuable guidelines for channel members on
who and when to undertake the delivery.
We also consider three alternative extended scenarios in the Online
Appendix, namely asymmetric suppliers with different market poten­
tials, differentiated delivery scale effects between channel members, and
a lower linear delivery cost for the e-retailer, to verify the robustness of
our main results. The remainder of the article proceeds as follows. We
review the relevant literature in Section 2 and introduce the model in
Section 3. Section 4 conducts the comparative analysis, and Section 5
derives the equilibrium delivery arrangement. Section 6 presents the
welfare implications, and Section 7 concludes this study. All equilibrium
outcomes and proofs are relegated to the Online Appendix.
a proposal and ultimately fall into the prisoner’s dilemma. Therefore, on
this point, our research sheds light on the dark side of the e-retailer’s
delivery proposal.
Our work also contributes to the growing literature investigating the
impact of power structure on supply chain performance. Power structure
usually refers to different timing rules involving demanding profit
margins. For instance, S. C. Choi [36] investigates the implications of
power structure for manufacturers’ decisions when distributing prod­
ucts through a retailer in a two-echelon supply chain. Nagarajan and
Sošić [37] investigate the role of the power structure in supplier alli­
ances in a decentralized assembly system with the consideration of
Supplier-Stackelberg, Vertical-Nash, and Assembler-Stackelberg game
models. Pan, Lai, Leung, &Xiao [38] focus on a supply chain consisting
of two competing manufacturers and a shared retailer or a single
manufacturer and two competing retailers to demonstrate that the
power structure influences the selection of two types of contracts. Using
a game-theory-based framework, Shi, Zhang, &Ru [39] examine the
impacts of the power structure and demand model on supply chain
performance. Luo, Chen, Chen, &Wang [18] explore how the power
structure affects pricing policies for differentiated brands by considering
horizontal and vertical competition. Liao, Yano, &Trivedi [23] discuss
how the power structure influences producer choice and store-brand
quality optimization. With a dual-channel supply chain, Yujie Xiao,
Niu, Zhang, &Xue [13] analyze how quality differentiation and power
structure affect the retailer’s store-brand introduction incentive and
profitability.
Overall, these studies have discussed the impacts of power structure
on the supply chain’s marketing strategy or operational behavior but
neglect the implications of power structure for the delivery arrange­
ment. However, one exception is a study reported by Geng, Krishnan,
&Queyranne [40], which explores the focal retailer’s internalization
decision in logistics under different power structures. Specifically,
considering the three power structures, Geng, Krishnan, &Queyranne
[40] examine the conditions under which the focal retailer would
benefit from internalizing the inbound logistics that raise its costs.
Nevertheless, our work differs from theirs in the following ways. First,
we allow two competing suppliers to respond by accepting or rejecting
the e-retailer’s delivery proposal. In contrast, they allow only one focal
retailer to decide whether or not to undertake the inbound logistics
delivery. Importantly, our findings suggest that the competing suppliers
might fall into the prisoner’s dilemma by accepting the e-retailer’s de­
livery proposal. Second, in their study, the delivery cost structure would
differ due to the internalization decision, whereas, in our study, the
delivery cost structure is consistent regardless of who undertakes the
delivery. Under this assumption, each supplier might be willing to un­
dertake the delivery. Third, their work reveals that one retailer can
benefit from undertaking the inbound logistics delivery because such a
decision can negatively affect its rival profit; however, our analysis
shows that the suppliers can benefit from accepting the e-retailer’s de­
livery proposal because of the higher demands they can obtain.
2. Literature review
Our paper is related to the vast literature on logistics delivery-related
operational problems in online distribution channels. As one of the
critical operations for online sellers, logistics delivery has attracted
much research interest (Y. [25,26]). One stream of the literature ex­
amines the logistics delivery-related operational problems from the
perspective of demand-enhancing service. For example, X. Li, Li, Cai,
&Shan [2] explore the service channel choice for supply chain players by
considering four different service formats. By comparing three coordi­
nation models, W. Liu et al. [27] reveal the implications of demand
disruption for logistics service supply chain (LSSC) coordination. Qin,
Liu, &Tian [4] investigate the strategic and economic impacts of logis­
tics service sharing in a hybrid platform. Considering a retailer-led
supply chain, Lou et al. [28] investigate logistics outsourcing choices
and find that the retailer does not necessarily benefit from offering lo­
gistics services. Some recent works also examine firms’ logistics delivery
strategies with other considerations including selling mode choice [29],
service channel integration (Y. [10]), direct channel opening (L. [30]),
channel structure selection (H. [31]), competition at the e-commerce
platform [1] and platform-based co-opetition supply chain structure (P.
[32]). Another stream of the literature investigates those problems by
focusing on the delivery cost. Among them, Tian, Vakharia, Tan, &Xu
[33] study the optimal selling mode for an e-commerce platform and
reveal that the fulfillment (i.e., delivering physical goods to customers)
costs and upstream competition intensity jointly play a critical role in
the choice of selling mode. Niu et al. [34] consider the delivery cost gap
between the fast-food restaurant and the online food-delivery platform
and derive the optimal delivery arrangement for the fast-food restau­
rant. Likewise, B. He, Gupta, &Mirchandani [9] discuss the optimal
selling and delivery strategy for a local Brick-and-Mortar store in the
context of emerging online-to-offline (O2O) third-party platforms. Based
on the linear logistics delivery cost, P. He et al. [35] explore the impacts
of manufacturer encroachment and the e-commerce platform’s logistics
integration strategy.
Although the above papers have identified the significant role of
logistics delivery in online distribution channels, one missing feature
among all existing research is the delivery economy or diseconomy
prevalent in real-life business settings. Our aim, however, is to under­
stand how and why these different scale effects shape firms’ delivery
preferences. Counterintuitively, our analysis shows that the channel
members prefer undertaking the delivery when there is a large delivery
diseconomy but might prefer to refrain from undertaking the delivery
when there is a delivery economy. Hence, this unexpected result chal­
lenges the conventional presumption that the channel members might
be less willing to undertake the delivery when the delivery of products is
more expensive. Furthermore, departing from the existing literature, we
examine the equilibrium delivery arrangement in an online distribution
channel with supplier competition. Interestingly, when there is fierce
competition, the competing suppliers can achieve higher profits by
rejecting the e-retailer’s delivery proposal but cannot help rejecting such
3. Model setup
Consider an online distribution channel with two identical suppliers
(indexed by 1 and 2) selling substitutable products through a nonex­
clusive e-retailer (indexed by e). The suppliers produce goods with a
symmetric and constant marginal cost, which we normalize to zero
without losing generality. We refer to either supplier as he and the eretailer as she. Table 1 summarizes all notations used in this study.
In line with the extant literature [41,42], the consumer demand for
each product is given by14
14
These demand functions are derived by maximizing the representative
∑
consumer utility U =
(aqi − qi 2 /2 − pi qi ) − kq1 q2 .
i=1,2
3
X. Zhou et al.
Omega 126 (2024) 103070
Table 1
Notation.
Notation
Description
∧
∼
−
pi
qi
wsi
mei
a
k
cqi
bq2i
Δei
Δsi
Πe
Πsi
EE
SE
SS
CS
SW
Superscript used to denote the E-retailer-Stackelberg game
Superscript used to denote the Supplier-Stackelberg game
Superscript used to denote the Vertical-Nash game
Retail price of product i
Demand of product i
Supplier i’s wholesale price
E-retailer’s retail markup for product i
Market Potential
Intensity of competition (degree of product differentiation)
Linear part of delivery cost
Nonlinear part of delivery cost
E-retailer’s unit profit for product i
Supplier i’s unit profit
E-retailer’s payoff
Supplier i’s payoff
The delivery arrangement where the e-retailer undertakes the delivery of two substitutable products
The hybrid delivery arrangement where supplier 1 undertakes the delivery of his product while the e-retailer undertakes the delivery of supplier 2′s product
The delivery arrangement where both suppliers undertake the delivery of their products
Consumer surplus
Social welfare
Fig. 1. Delivery arrangements: EE, SE, and SS.
(
)
a
p1
kp2
1−
+
1+k
1− k 1− k
(
)
⎪
a
p2
kp1
⎪
⎪
⎩ q2 =
1−
+
1+k
1− k 1− k
⎧
⎪
⎪
⎪
⎨ q1 =
fulfill online orders for the products (e.g., sofa, bed, air conditioner,
refrigerator, fresh food, and television) with characteristics such as large
volume, heavy weight, perishable, or fragile because the increased sales
quantities of these products need more expensive capacity or profes­
sional operation, and result in a lower delivery efficiency (G. [7]).
However, when channel members fulfill online orders for products (e.g.,
electronic products, digital accessories, clothes, hats, and shoes) that are
easy to handle, the delivery might be economy due to economies of
scope ([8]; B. [9]). Therefore, to capture the essential feature of the
delivery economy or diseconomy, we consider a nonlinear delivery cost
cq + bq2 . Specifically, c represents the unit delivery cost, determined by
delivery distance, product weight, volume, and other factors; b > 0 in­
dicates that the firms face the delivery diseconomy, while b < 0 implies
that the firms encounter the delivery economy.15 This cost structure has
been widely used in operations management literature to characterize
the diseconomy or economy of scale [43–46]. Note that channel mem­
bers are indifferent to who undertakes the delivery in the case of linear
delivery cost; thus, we omit the analysis of this trivial case. The delivery
cost is assumed to be identical when the e-retailer or the supplier
(1)
The parameter k ∈ [0, 1) characterizes the degree of product differ­
entiation; a larger k implies more intense competition between the
substitutable products. Here, p1 (p2 ) represents the retail price of prod­
uct 1 (2), which is the sum of the wholesale price ws1 (ws2 ) that supplier 1
(2) demands and the retail markup me1 (me2 ) that the e-retailer claims for
product 1 (2). q1 (q2 ) is the quantity of product 1 (2). Suppliers are
assumed to possess equal market potential, a, normalized to 1 without
losing generality. We relax this assumption in the Online Appendix D
and show that our main results hold qualitatively.
In practice, product delivery can often be undertaken by different
parties of the online distribution channel (X. [2,29]). In this study, we
assume that both the supplier and the e-retailer have sufficient capital
and capability to undertake the delivery. As highlighted previously, the
delivery of online orders generally exhibits different scale effects. When
the marginal delivery cost increases with the online order volume, we
refer to it as the delivery diseconomy; conversely, when the marginal
delivery cost decreases with the online order volume, we refer to it as the
delivery economy. Delivery diseconomy might occur when merchants
15
When b < 0, we focus on −2bc > q so that the delivery is economy. A similar
assumption was adopted by Shang, Ha, &Tong (35) and Zhao and Li (47).
4
X. Zhou et al.
Omega 126 (2024) 103070
Fig. 2. Sequence of events.
undertakes the delivery to clarify the implications of the power structure
for the delivery arrangement. We relax this assumption in the Online
Appendix E and F to check the robustness of our core model.
Following industry practice, we consider three possible delivery ar­
rangements, depicted in Fig. 1. Under the delivery arrangement EE, the
e-retailer undertakes the delivery of two substitutable products and in­
curs associated costs. Such an arrangement arises if the e-retailer asks
neither of the suppliers to undertake the delivery or if the e-retailer asks
at least one supplier to undertake the delivery and no suppliers agree to
do it. Hence, the channel parties’ payoffs under this arrangement are ΠEE
s1
EE
EE
EE
EE EE
EE EE
EE EE
EE EE
= wEE
s1 q1 , Πs2 = ws2 q2 , and Πe = me1 q1 − (c + bq1 )q1 + me2 q2 −
EE
(c + bqEE
2 )q2 . Under the hybrid delivery arrangement SE, product 1 is
delivered by supplier 1, while product 2 is by the e-retailer; this
arrangement occurs when the e-retailer asks at least one supplier to
deliver products to customers, but only one supplier does. Thus, the
channel parties’ payoffs under the delivery arrangement SE are ΠSE
s1 =
SE
SE
SE
SE SE
SE SE
SE SE
SE SE
wSE
s1 q1 − (c + bq1 )q1 , Πs2 = ws2 q2 , and Πe = me1 q1 + me2 q2 −
SE
(c + bqSE
2 )q2 . Since the two suppliers are symmetric, we omit the
analysis of the hybrid delivery arrangement ES in the remainder of our
study. Under the delivery arrangement SS, both suppliers undertake the
delivery of their products and incur corresponding costs. This arrange­
ment happens when the e-retailer asks two suppliers to deliver products
to consumers, and both agree. Accordingly, the channel parties’ payoffs
SS
SS SS
SS SS
under such an arrangement are ΠSS
s1 = ws1 q1 − (c + bq1 )q1 , Πs2 =
SS
SS SS
SS SS
SS SS
SS SS
ws2 q2 − (c + bq2 )q2 , and Πe = me1 q1 + me2 q2 .
We consider three different power structures: E-retailer-Stackelberg
game (denoted by superscript “∧”), Supplier-Stackelberg game (denoted
by superscript “∼”), and Vertical-Nash game (denoted by superscript “ −
”). In the E-retailer-Stackelberg game, the e-retailer initially claims her
retail markups for two products, and then the suppliers set their
wholesale prices. On the contrary, in the Supplier-Stackelberg game, the
suppliers demand wholesale prices, followed by the e-retailer claiming
her retail markups. In the Vertical-Nash game, the suppliers and the eretailer make decisions simultaneously. The sequence of events under
each power structure is illustrated in Fig. 2. In the first stage, the eretailer decides to ask none, one, or both of the suppliers to deliver
products to consumers.16 Then, the supplier, conditional on receiving
the e-retailer’s delivery proposal, determines whether to accept this
delivery proposal. After the product delivery arrangement, the suppliers
and the e-retailer set their wholesale prices and retail markups in the
second stage under different power structures, respectively. Notably, it
is not the channel member with greater pricing power that can deter­
mine the delivery arrangement, but the e-retailer who acts as the
product owner may ask the supplier to be responsible for delivering
products (Yongbo [29,47]) and the supplier can respond by agreeing or
rejecting to do so. For example, JD.com, Gome, Walmart, and Amazon
have greater pricing power and ask the suppliers to be responsible for
delivering products to customers, but some suppliers refuse to undertake
the delivery. Another example is that numerous e-retailers working as
market followers on the wholesale website 1688 in China ask the sup­
plier to deliver products, and the suppliers decide whether to undertake
it. To ensure that the equilibrium outcomes are positive and unique and
there exists the delivery economy, we assume that b > (k − 1)(k +2)/2
and max{̂c 1 (b, k), 0} < c < 1 (b > k − 1 and max{̃c1 (b, k), ̃c2 (b, k),
0} < c < 1) in the E-retailer-Stackelberg (Supplier-Stackelberg) game.
Similarly, we assume that b > k2 − 1 and max{c1 (b, k), 0} < c < 1 in the
Vertical-Nash game. More details about the expressions of ̂c 1 (b, k), ̃c1 (b,
k), ̃c2 (b, k), and c1 (b, k) are presented in the Online Appendix A.
4. Comparison and analysis
In this section, we compare the equilibrium outcomes to investigate
the performance of the three arrangements and reveal how and why
these comparative results vary with the power structure. All equilibrium
outcomes and proofs appear in the Online Appendix A.
4.1. Retail markups and wholesale prices
This subsection examines e-retailer’s retail markups and suppliers’
wholesale prices across the three delivery arrangements. The compara­
tive results of e-retailer’s retail markups are summarized in the
following lemma.
Lemma 1 (E-retailer’s Retail Markups).
̂ SS
̂ SE
̂ EE
(1) For the E-retailer-Stackelberg game, max{ m
ei , m
e1 } < min{ m
ei ,
̂ SE
m
e2 }.
SS
SE
EE
SE
̃ ei , m
̃ e1 } < min{m
̃ e2 }.
̃ ei , m
(2) For the Supplier-Stackelberg game, max{m
SE
max{mSS
ei , me1 }
SE
min{mEE
ei , me2 }.
(3) For the Vertical-Nash game,
<
Lemma 1 (1) and (3) show that, compared with when the supplier
undertakes the delivery, the e-retailer always claims a higher retail
markup for the product when she undertakes the delivery in the Eretailer-Stackelberg and Vertica-Nash games. The intuition is that the eretailer incurs associated costs when delivering products to customers,
which we call the cost-increasing effect, and she prefers to keep the retail
markup high to compensate for these costs. Lemma 1 (2) replicates the
results of Lemma 1 (1) and (3). However, the key rationale behind this is
twofold: on the one hand, when the e-retailer undertakes the delivery,
she prefers to keep the retail markup high owing to the cost-increasing
effect; on the other hand, when the supplier (i.e., the market leader)
undertakes the delivery, he might claim a higher wholesale price and
thus leaves the e-retailer (i.e., the market follower) a lower retail
markup, which we call the margin-squeezing effect.
16
Logistics delivery requires upfront operations, such as picking arrange­
ments, warehousing layout, and route planning. These operations stay mostly
the same, while the price decision often changes. Therefore, we assume that the
delivery arrangement occurs before the price decision.
5
X. Zhou et al.
Omega 126 (2024) 103070
Lemma 2 presents the comparison results of the suppliers’ wholesale
prices.
Lemma 2 (Suppliers’ Wholesale Prices).
derstand the above results, note that the demand for a product is
negatively affected by its price but positively impacted by the substitute
product price, and the retail prices across the three delivery arrange­
ments are equal when there is no delivery scale effect.17 When the eretailer (i.e., the market leader) undertakes the delivery, compared with
without the delivery scale effect, the delivery economy directly moti­
vates her to reduce retail markup, which, however, indirectly forces the
supplier (i.e., the market follower) to raise his wholesale price because
the supplier’s wholesale price is negatively affected by the retail markup
̂ EE
̂ SS
̂ SE
(1) For the E-retailer-Stackelberg game, max{ w
si , w
s2 } < min{ w
si ,
̂ SE
w
s1 }.
SS
SE
EE
SE
̃ s2 } < min{w
̃ s1 }
̃ si , w
̃ si , w
(2) For the Supplier-Stackelberg game, max{w
√̅̅̅
if ( 5 − 1)/2 < k < 1, 0 < b < k2 + k − 1 and 0 < c < ̃c3 (b, k); and
̃ EE
̃ SE
̃ SE
̃ SS
max{w
si , w
s2 } < min{w
si , w
s1 } otherwise.
SE
SS
SE
(3) For the Vertical-Nash game, max{wEE
si , ws2 } < min{wsi , ws1 }.
The expression of ̃c3 (b, k) is provided in the Online Appendix A.
Lemma 2 (1) indicates that, compared with when the e-retailer un­
dertakes the delivery, the supplier always claims a higher wholesale
price when delivering products in the E-retailer-Stackelberg game. The
supplier prefers to keep the wholesale price high due to the costincreasing effect when undertaking the delivery while earning a lower
wholesale price because of the margin-squeezing effect when shifting
the delivery to the market leader (i.e., the e-retailer). Because of the
cost-increasing effect, the supplier in the Vertical-Nash game claims a
higher wholesale price when he undertakes the delivery, as shown by
Lemma 2 (3).
Similar to Lemma 2 (1) and (3), Lemma 2 (2) suggests that, in the
Supplier-Stackelberg game, compared with when the e-retailer un­
dertakes the delivery, the supplier always claims a higher wholesale
price when undertaking the delivery in the case of delivery economy.
However, somewhat surprisingly, Lemma 2 (2) reveals that when there
is a delivery diseconomy, compared with under the delivery arrange­
ment EE, the supplier might even demand a lower wholesale price under
the delivery arrangement SS. When the delivery is economy, compared
with the delivery arrangement EE, the delivery arrangement SS not only
motivates the supplier to demand a higher wholesale price due to the
cost-increasing effect but also prevents the supplier from drastically
̃ EE
reducing his wholesale price as competition becomes fierce (i.e., ∂w
si
̂ EE
̂ EE
̂ SE
̂ SE
the e-retailer demands (i.e., ∂ w
si /∂ m
ei < 0 and ∂ w
s2 /∂ m
e2 < 0) in such
a case. However, when the product is delivered by the supplier,
compared with without the delivery scale effect, such a delivery econ­
omy only directly motivates the supplier to reduce his wholesale price.
Therefore, with the delivery economy, the double marginalization effect
is alleviated when the supplier undertakes the delivery while aggravated
when the e-retailer does it. Consequently, because of the dominant role
the price of a product itself plays, shifting the delivery to the supplier
generates a lower retail price (see Lemma A1 (1) in the Online Appendix
A) and a higher demand for the product. On the contrary, when the
delivery is diseconomy, shifting the delivery to the e-retailer can alle­
viate the double marginalization effect and thus generate a lower retail
price (see Lemma A1 (1) in the Online Appendix A) and a higher
demand.
The results of Lemma 3 (2) are in stark contrast to those of Lemma 3
(1). That is because shifting the delivery responsibility to the market
leader (follower) can alleviate the double marginalization effect in on­
line distribution channels when there is a delivery diseconomy (econ­
omy), and the price leadership in the Supplier-Stackelberg game is
opposite to that in the E-retailer-Stackelberg game. However, different
from parts (1) and (2), part (3) reveals that, in the Vertical-Nash game,
the product demands are invariant to the delivery arrangement. When
all channel members make decisions simultaneously, although the de­
livery arrangement makes the e-retailer (the supplier) claim different
retail markups (wholesale prices), it does not change the sum of retail
markup and wholesale price for a product. Consequently, the retail
prices and product demands do not vary with the delivery arrangement
(see Lemma A1 (3) in the Online Appendix A and Lemma 3 (3)).
SS
̃ si /∂k < 0). As a consequence, compared with when not un­
/∂k < ∂w
dertaking the delivery, the supplier always claims a higher wholesale
price when undertaking the delivery in the case of a delivery economy.
Differently, when the delivery is diseconomy, compared with the de­
livery arrangement EE, although the delivery arrangement SS motivates
the supplier to demand a higher wholesale price due to the costincreasing effect, it forces the supplier to reduce his wholesale price
̃ SS
̃ EE
more drastically as competition becomes intense (i.e., ∂w
si /∂k < ∂w
si
/∂k < 0). Ultimately, compared to under the delivery arrangement EE,
the supplier even demands a lower wholesale price under the delivery
√̅̅̅
arrangement SS as competition becomes fierce (i.e., ( 5 − 1)/2 < k
< 1), and the cost-increasing effect gets small (i.e., 0 < b < k2 +k − 1 and
0 < c < ̃c3 (b, k)).
4.3. Unit profits
We compare firms’ unit profits across the three delivery arrange­
ments. The primary distinction between the unit profit and the retail
markup (wholesale price) is that when the firm incurs the delivery cost,
the former incorporates that cost while the latter does not. Let
Δxei = mxei − Zxei (c +bqxi ) be the e-retailer’s unit profit for the product i and
Δxsi = wxsi − Zxsi (c +bqxi ) be the supplier i’s unit profit under the delivery
arrangement x ∈ {EE, SE, SS}, where Zeix , Zxsi ∈ {0,1}, and Zxsi = 1 − Zxei .
The parameters Zxei and Zxsi assign the delivery cost to the e-retailer and
the supplier, respectively. Zxei = 1 (i.e., Zxsi = 1 − Zxei = 0) implies that the
e-retailer undertakes the delivery for the product i and Zsix = 1 (i.e., Zxei =
1 − Zxsi = 0) indicates that the supplier i undertakes the delivery under
the delivery arrangement x. We first consider the e-retailer’s unit profits.
Lemma 4 (E-retailer’s Unit Profits).
4.2. Product demands
We now proceed to examine the product demands across the three
delivery arrangements.
Lemma 3 (Product Demands).
EE
SE
SS
SE
(1) For the E-retailer-Stackelberg game, max{̂
qi , ̂
q 2 } < min{ ̂
qi , ̂
q1 }
SS
SE
max{̂
qi , ̂
q1 }
EE
SE
if (k − 1)(k +2)/2 < b < 0 and
q 2 } if b > 0.
qi , ̂
< min{ ̂
SS SE
EE SE
(2) For the Supplier-Stackelberg game, max{̃
qi , ̃
q1 } < min{̃
q2 }
qi , ̃
EE SE
SS SE
q2 } < min{̃
qi , ̃
q1 } if b > 0.
k − 1 < b < 0 and max{̃
qi , ̃
SE
SS
(3) For the Vertical-Nash game, qEE
= qSE
i
2 = q1 = qi .
̂ EE = Δ
̂ SE = Δ
̂ SE = Δ
̂ SS if
(1) For the E-retailer-Stackelberg game, Δ
ei
e1
e2
ei
(k − 1)(k +2)/2 < b < 0 or b > 0.
̃ SE < Δ
̃ EE < Δ
̃ SS < Δ
̃ SE if
(2) For the Supplier-Stackelberg game, Δ
e2
ei
ei
e1
√̅̅̅
̃ SE < Δ
̃ SS < Δ
̃ EE < Δ
̃ SE if
0 < k < ( 5 − 1)/2 and k2 + k − 1 < b < 0; Δ
e2
ei
ei
e1
if
Part (1) of Lemma 3 indicates that, in the E-retailer-Stackelberg
game, the demands of products delivered by the suppliers (both products
under the delivery arrangement SS and product 1 under the delivery
arrangement SE) are higher than those of products shipped by the eretailer (both products under the delivery arrangement EE and product 2
under the delivery arrangement SE) when the delivery is economy;
however, the reverse is true when the delivery is diseconomy. To un­
̃ SE < Δ
̃ SS < Δ
̃ EE < Δ
̃ SE if b > max{k2 +
k − 1 < b < min{k2 +k − 1, 0}; Δ
e1
ei
ei
e2
√
̅̅̅
̃ SE < Δ
̃ EE < Δ
̃ SS < Δ
̃ SE if ( 5 − 1)/2 < k < 1 and 0 < b <
k − 1, 0}; and Δ
e1
ei
ei
e2
k2 + k − 1.
17
6
This result can be verified with a simple algebraic operation.
X. Zhou et al.
Omega 126 (2024) 103070
SE
EE
SS
compared with not undertaking delivery, the supplier will obtain a
lower unit profit by undertaking the delivery for products with delivery
diseconomy. Counterintuitively, Lemma 5 (1) illustrates that, in the Eretailer-Stackelberg game, both suppliers can achieve the highest unit
profits via shifting the delivery to the e-retailer (i.e., the delivery
arrangement EE) when the delivery is economy but can earn the highest
unit profits through undertaking the delivery (i.e., the delivery
arrangement SS) when the delivery is diseconomy. Before explaining
this result, it is necessary to understand what factors and how they affect
the suppliers’ unit profits under different delivery arrangements. On the
downside, undertaking the delivery generates a cost-increasing effect
that negatively affects the suppliers’ unit profits; on the upside, it also
enables both suppliers to raise their wholesale prices, which alleviates
the competition between them and thus generates the competitionmitigating effect, positively affecting the suppliers’ unit profits. Be­
sides, we learn from Lemma 2 (1) that when shifting the delivery re­
sponsibility to the e-retailer, the suppliers will suffer from the marginsqueezing effect that negatively affects their unit profits. When there
is a delivery economy, undertaking the delivery generates a costincreasing effect, which dominates the competition-mitigating and
margin-squeezing effects; thus, the suppliers earn the highest unit profits
under the delivery arrangement EE in such a situation. Whereas in the
case of the delivery diseconomy, both the competition-mitigating and
margin-squeezing effects become more prominent. Therefore, the sup­
pliers earn the highest unit profits under the delivery arrangement SS
even though the delivery is diseconomy.
Different from Lemma 5 (1), Lemma 5 (2) demonstrates that, in the
Supplier-Stackelberg game, both suppliers can achieve the highest unit
profits through undertaking the delivery (i.e., the delivery arrangement
SS) when the delivery is economy but can earn the highest unit profits
via shifting the delivery to the e-retailer (i.e., the delivery arrangement
EE) if the delivery is diseconomy. When the suppliers possess dominant
market power, their unit profits will no longer be negatively affected by
the margin-squeezing effect if they shift the delivery to the e-retailer.
Therefore, which delivery arrangement can bring about the maximum
unit profits hinges on the tradeoff between the cost-increasing effect and
the competition-mitigating effect. Specifically, when there is a delivery
economy, the delivery arrangement SS generates the most apparent
EE
̃ SE
̃ SE
̃ SS
wsi , w
competition-mitigating effect (i.e., w
si > max{̃
s1 , w
s2 }) that
overweighs the cost-increasing effect, thereby resulting the highest unit
profits for them. Conversely, when the delivery is diseconomy, under­
taking the delivery might generate the competition-mitigating effect
(shown by Lemma 2 (2)), but this effect is immaterial compared with the
cost-increasing effect the suppliers can avoid by shifting the delivery to
the e-retailer. Hence, the delivery arrangement EE eventually generates
the highest unit profits for the suppliers in such a case.
Lemma 5 (3) indicates that, in the Vertical-Nash game, the suppliers
obtain the same and highest unit profits for products delivered by the eretailer (both products under the delivery arrangement EE and product 2
under the delivery arrangement SE) when there is a delivery economy;
the reverse is true when there is a delivery diseconomy. The reason is
that the cost-increasing effect avoided by shifting the delivery to the eretailer dominates (is dominated by) the competition-mitigating effect
resulting from undertaking the delivery when the delivery is economy
(diseconomy), and the suppliers obtain the same wholesale prices and
the same demands for products delivered by the e-retailer (or
themselves).
To sum up, the differences in the comparison results of firms’ unit
profits under the three power structures are driven by the fact that the
power structure changes the number of driving forces affecting the unit
profit and the relative magnitude of these driving forces. When the eretailer (supplier) does not undertake the delivery, the marginsqueezing effect does not influence her (his) unit profit in the Eretailer-Stackelberg and Vertical-Nash games (Supplier-Stackelberg and
Vertical-Nash games) but by that effect when she (he) works as the
SE
(3) For the Vertical-Nash game,Δe2 = Δei < Δei = Δe1 if k2 − 1 < b <
SS
Δei
SE
Δe1
SE
Δe2
EE
Δei
0 and
=
<
=
if b > 0.
Lemma 4 (1) shows that the e-retailer earns the same unit profits
across the three delivery arrangements in the E-retailer-Stackelberg
game. When the e-retailer acts as the market leader, she never suffers
from the margin-squeezing effect when shifting the delivery to the
market follower (i.e., the supplier), which implies that the dominant
position enables her to obtain a reasonable retail markup when not
undertaking the delivery. Such a dominant position, however, also en­
dows the e-retailer with the power to demand a sufficiently high retail
markup to cover associated costs when undertaking the delivery. As a
result, she achieves the same unit profits under the three delivery
arrangements.
However, in the Supplier-Stackelberg game, Lemma 4 (2) suggests
that when there is a delivery economy, the e-retailer earns the highest
unit profit for the product the supplier delivers under the hybrid
arrangement SE. When shifting the delivery of products to both sup­
pliers, the e-retailer can avoid the cost-increasing effect but suffers from
̃ SS
̃ SE
the margin-squeezing effect severely (i.e., m
ei < m
e1 ), and when un­
̃ SE
dertaking the delivery, the e-retailer can avoid that effect (i.e., m
e1 <
̃ SE
̃ EE
min{m
ei , m
e2 }) but it is overshadowed by the cost-increasing effect. As a
result, when the delivery is economy, the e-retailer earns the highest
unit profit for the product delivered by the supplier under the hybrid
arrangement SE. Unlike when the delivery is economy, the e-retailer
earns the highest unit profit for the product she delivers under the
hybrid arrangement SE when the delivery is diseconomy, which arises
because the e-retailer can avoid the margin-squeezing effect and de­
̃ SE
̃ EE
̃ SE
̃ SS
mands the highest retail markup (i.e.,m
e2 > max{m
ei , m
e1 , m
ei }) to
compensate for the increased operational costs. Lemma 4 (2) further
shows that, compared with the delivery arrangement SS, whether the
delivery arrangement EE can bring about a higher unit profit for the eretailer depends on the competition intensity (k) and delivery scale ef­
fect (b). These results still hinge on the trade-off between the marginsqueezing effect caused by the delivery arrangement SS and the costincreasing effect arising under the delivery arrangement EE.
Lemma 4 (3) indicates that, in the Vertical-Nash game, the e-retailer
obtains the same and highest unit profits for products delivered by the
suppliers (both products under the delivery arrangement SS and product
1 under the delivery arrangement SE) when there is a delivery economy;
the opposite holds when there is a delivery diseconomy. Recall from
Lemma 1 (3) that the cost-increasing effect stemming from undertaking
the delivery stimulates the e-retailer to demand higher retail markups.
Compared with such a positive impact, its negative impact on the unit
profits is more (less) apparent when the delivery is economy
(diseconomy). In addition, Lemma 1 (3) and Lemma 3 (3) show that the
e-retailer obtains the same retail markups and the same demands for
products delivered by suppliers (or herself). As such, the e-retailer ob­
tains the same and highest unit profits for products shipped by suppliers
(herself) in the case of a delivery economy (diseconomy).
The following lemma presents the comparison results of the sup­
plier’s unit profits.
Lemma 5 (Supplier’s Unit Profits).
̂ SE < Δ
̂ SS < Δ
̂ SE < Δ
̂ EE if
(1) For the E-retailer-Stackelberg game, Δ
s2
si
s1
si
√
̅̅̅̅̅̅̅̅̅̅̅̅̅
̅
SS
SE
SE
̂ <Δ
̂ <Δ
̂ <Δ
̂ EE if
(k − 1)(k +2)/2 < b < (k2 − 4 +k 8 + k2 )/4; Δ
si
s2
s1
si
√̅̅̅̅̅̅̅̅̅̅̅̅̅̅
̂ SS < Δ
̂ SE < Δ
̂ SE < Δ
̂ EE if k − 1 < b
(k2 − 4 +k 8 + k2 )/4 < b < k − 1; Δ
si
s1
s2
si
̂ EE < Δ
̂ SE < Δ
̂ SE < Δ
̂ SS if b > 0.
< 0; and Δ
si
s2
s1
si
̃ EE < Δ
̃ SE < Δ
̃ SE < Δ
̃ SS if k − 1
(2) For the Supplier-Stackelberg game, Δ
si
s1
s2
si
̃ SS < Δ
̃ SE < Δ
̃ SE < Δ
̃ EE if b > 0.
< b < 0 and Δ
si
s2
s1
si
SS
SE
SE
EE
(3) For the Vertical-Nash game, Δsi = Δs1 < Δs2 = Δsi if k2 − 1 < b <
SE
EE
SS
SE
0 and Δs2 = Δsi < Δsi = Δs1 if b > 0.
Because of weak pricing power, one might intuitively believe that,
7
X. Zhou et al.
Omega 126 (2024) 103070
market follower in the Supplier-Stackelberg (E-retailer-Stackelberg)
game.
(2) indicates that the e-retailer can obtain higher demands by asking the
suppliers to deliver products; however, Lemma 4 (2) shows that she
achieves much lower unit profits. Ultimately, when the delivery be­
comes more diseconomy, the decreased unit profits are higher than the
increased demands as the e-retailer shifts the delivery to the suppliers.
Hence, the e-retailer prefers to undertake the delivery in such a situa­
tion. However, it is worth mentioning that when there is a large delivery
diseconomy, the force that drives the e-retailer to prefer undertaking the
delivery in the E-retailer-Stackelberg game is the higher demand, but the
one in the Supplier-Stackelberg or Vertical-Nash game is the higher unit
profit.
The suppliers’ delivery arrangement preferences are shown in the
following proposition.
Proposition 2 (Suppliers’ Delivery Arrangement Preferences).
(1)
For
the
E-retailer-Stackelberg
game,
when
̂
(k − 1)(k +2)/2 < b < b 1 (k), the suppliers prefer being the only supplier to
5. Equilibrium delivery arrangement
In this section, we first investigate channel members’ delivery
arrangement preferences and then derive the equilibrium delivery
arrangement. All proofs are provided in the Online Appendix B.
5.1. Firms’ preferences of delivery arrangement
The following proposition summarizes the e-retailer’s preference for
delivery arrangement.
Proposition 1 (E-retailer’s Delivery Arrangement Preference).
(1) For the E-retailer-Stackelberg game, when (k − 1)(k +2)/2 < b < 0,
̂ SS
the e-retailer prefers both suppliers to deliver products, i.e., Π
e
EE
̂ SE > max{ Π
̂ EE , Π
̂ SE , Π
̂ SS }; when
undertake the delivery, i.e., Π
s1
si
s2
si
̂
b 1 (k) < b < 0, the suppliers prefer the e-retailer to deliver products, i.e.,
SE
̂ ,Π
̂ }; when b > 0, the e-retailer prefers undertaking the de­
> max{ Π
e
e
̂ EE > max{ Π
̂ SE , Π
̂ SS }.
livery by herself, i.e., Π
e
e
e
̂ EE > max{ Π
̂ SE , Π
̂ SE , Π
̂ SS }; when b > 0, the suppliers prefer both of them to
Π
si
s1
s2
si
(2) For the Supplier-Stackelberg game, when b > ̃
b1 (k) or k − 1 < b < 0,
̃ EE
the e-retailer prefers undertaking the delivery by herself, i.e., Π
̂ SS > max{ Π
̂ EE , Π
̂ SE , Π
̂ SE }.
undertake the delivery, i.e., Π
si
si
s1
s2
̃ SS > max{Π
̃ EE , Π
̃ SE }.
to deliver products, i.e., Π
e
e
e
(3) For the Vertical-Nash game, when k2 − 1 < b < 0, the e-retailer
̃ SE > max{Π
̃ EE , Π
̃ SE , Π
̃ SS }; when ̃
undertake the delivery, i.e., Π
k2 < k < 1
s2
si
s1
si
and k − 1 < b < min{0, ̃
b2 (k)}, the suppliers prefer both of them to under­
̃ SS > max{Π
̃ EE , Π
̃ SE , Π
̃ SE }; when b > max{0, ̃
take the delivery, i.e., Π
b3 (k)},
(2) For the Supplier-Stackelberg game, when 0 < k < ̃
k1 and
max{k − 1, ̃
b2 (k)} < b < 0, the suppliers prefer being the only supplier not to
e
̃ SE , Π
̃ SS }; when 0 < b < ̃
> max{Π
b1 (k), the e-retailer prefers both suppliers
e
e
SS
EE
SE
prefers both suppliers to deliver products, i.e., Πe > max{Πe , Πe }; when b
EE
si
> 0, the e-retailer prefers undertaking the delivery by herself, i.e., Πe >
SE
si
s1
s2
the suppliers prefer being the only supplier to undertake the delivery, i.e.,
̃ SE > max{Π
̃ EE , Π
̃ SE , Π
̃ SS }; when ̃
Π
k1 < k < 1 and 0 < b < ̃
b3 (k), the sup­
s1
si
s2
si
SS
max{Πe , Πe }.
The expression of ̃
b1 (k) is provided in the Online Appendix B.
Proposition 1 (1) presents the e-retailer’s delivery arrangement
preference in the E-retailer-Stackelberg game. Compared with when the
delivery is economy, the delivery of products is more expensive when
there is a delivery diseconomy. Hence, one may expect that the e-retailer
will prefer the suppliers to deliver products when there is a delivery
diseconomy but prefer to undertake the delivery when there is a delivery
economy. Counterintuitively, as illustrated in Fig. 3(a), when the de­
livery is economy, the e-retailer prefers both suppliers to be responsible
for delivery; however, when the delivery is diseconomy, she prefers
undertaking the delivery for two substitutable products. These results
happen because, as shown by Lemma 3 (1) and Lemma 4 (1), the eretailer achieves the highest demands by asking both suppliers to deliver
products (undertaking the delivery for two substitutable products) when
there is a delivery economy (diseconomy) and earns the same unit
profits across the three delivery arrangements. Proposition 1 (3) repli­
cates the result of Proposition 1 (1). However, it is notable that the eretailer prefers both suppliers (herself) to deliver products only because
of the highest unit profits in the Vertical-Nash game when there is a
delivery economy (diseconomy).
Nevertheless, Proposition 1 (2) reveals that, in the SupplierStackelberg game, the e-retailer prefers undertaking the delivery
either when the delivery is economy or when the delivery diseconomy is
apparent; however, she wants both suppliers to undertake the delivery if
the delivery diseconomy is small (see Fig. 3(b)). The key driver is the
tradeoff between the demands and the unit profits the e-retailer can
obtain under different delivery arrangements. When there is a delivery
economy, although Lemma 4 (2) tells us that the e-retailer might earn
higher unit profits by asking the suppliers to deliver products, Lemma 3
(2) demonstrates that she achieves higher demands under the delivery
arrangement EE. Consequently, the increases in product demands are
overwhelmingly beneficial, and the e-retailer prefers to deliver products
in such a case. By contrast, when there is a small delivery diseconomy,
the e-retailer prefers asking both suppliers to undertake the delivery
because the higher demands gained in this arrangement are appealing.
Furthermore, as the delivery diseconomy becomes significant, Lemma 3
̃ EE > max{Π
̃ SE , Π
̃ SE , Π
̃ SS }.
pliers prefer the e-retailer to deliver products, i.e., Π
si
s1
s2
si
(3) For the Vertical-Nash game, when k2 − 1 < b < 0, the suppliers
EE
SE
SE
SS
prefer not to undertake the delivery, i.e., Πsi = Πs2 > max{Πs1 , Πsi }; when
SE
SE
b > 0, the suppliers prefer to undertake the delivery, i.e., Πs1 = Πs2 >
EE
SS
max{Πsi , Πsi }.
The expressions of ̃
k1 , ̃
k2 , ̂
b 1 (k), ̃
b2 (k), and ̃
b3 (k) are provided in the
Online Appendix B.
Proposition 2 (1) describes the suppliers’ delivery arrangement
preferences in the E-retailer-Stackelberg game. As illustrated in Fig. 4
(a), when the delivery economy is large, the suppliers prefer being the
only supplier to undertake the delivery. However, with a small delivery
economy, they are better off when the e-retailer delivers products. The
intuition behind these results still hinges on the impact of delivery
arrangement on the product demands and the unit profits the suppliers
can obtain. Specifically, when the delivery economy is apparent, Lemma
3 (1) and Lemma 5 (1) jointly demonstrate that the suppliers can achieve
a higher demand and a relatively higher unit profit by becoming the only
supplier to deliver the product. Therefore, the suppliers prefer being the
unique supplier to undertake the delivery. As the delivery economy
becomes small, although Lemma 3 (1) indicates that the suppliers can
achieve a higher demand by undertaking the delivery, Lemma 5 (1)
suggests that the suppliers obtain a much lower unit profit. Conse­
quently, the higher demand gained from undertaking the delivery
cannot offset the loss of the unit profit in such a case; thus, the suppliers
prefer the e-retailer to undertake the delivery. Surprisingly, Proposition
2 (1) further shows that when there is a delivery diseconomy, the sup­
pliers always prefer to undertake the delivery. In such a situation, un­
dertaking the delivery can make the suppliers avoid the salient marginsqueezing effect arising from the e-retailer’s delivering products and
earn a higher unit profit because of the competition-mitigating effect. As
a result, the increase in unit profit makes up for the decrease in demand
when both suppliers switch from not undertaking the delivery to doing
it.
Proposition 2 (2) characterizes the suppliers’ delivery arrangement
8
X. Zhou et al.
Omega 126 (2024) 103070
Fig. 3. E-retailer’s delivery arrangement preference.
preferences in the Supplier-Stackelberg game. As shown in Fig. 4(b),
when competition is weak, the suppliers prefer being the only supplier
not to undertake the delivery if there is a delivery economy but prefer
being the only supplier to undertake the delivery in the case of delivery
diseconomy. These results can also be attributed to the trade-off be­
tween the demands and the unit profits under different delivery ar­
rangements. More specifically, compared with other delivery
arrangements, Lemma 5 (2) and Lemma 3 (2) suggest that when
competition is weak, the supplier who undertakes (does not undertake)
the delivery under the hybrid delivery arrangement SE can obtain not
only a relatively large unit profit but also a relatively high product de­
mand if the delivery is diseconomy (economy). Thus, the suppliers
prefer being the only supplier to (not to) undertake the delivery when
there is a diseconomy (economy). However, as competition becomes
fierce, the suppliers prefer to undertake the delivery when there is a
delivery economy but prefer the e-retailer to undertake the delivery
when there is a delivery diseconomy (see Fig. 4(b)). The rationale lies in
the fact that when there is a delivery economy (diseconomy), the
increased unit profits are so high as to offset the loss of demands as the
suppliers switch from other delivery arrangements to the delivery
arrangement SS (EE). Lastly, Proposition 2 (3) reveals that, in the
Vertical-Nash game, the suppliers prefer not to undertake the delivery
when there is a delivery economy but prefer to undertake the delivery
when there is a diseconomy. It is intuitive because, as indicated by
Lemma 5 (3) and Lemma 3 (3), the suppliers obtain the highest unit
profits through undertaking the delivery (shifting the delivery to the eretailer) when the delivery is diseconomy (economy) and achieve the
same demands across the three arrangements.
Therefore, we can learn from Proposition 2 that the suppliers’ de­
livery arrangement preferences vary with the power structure. Specif­
ically, when there is a small delivery economy (a small delivery
diseconomy), the suppliers might prefer the e-retailer (both of them) to
deliver products in the E-retailer-Stackelberg and Vertical-Nash games;
however, the results reverse in the Supplier-Stackelberg game. The
reason for these different outcomes is that the delivery arrangement
yielding the highest unit profit varies with the power structure.
Furthermore, when there is a large delivery economy, the suppliers
might prefer being the only supplier to deliver the product in the Eretailer-Stackelberg game; conversely, in the Supplier-Stackelberg and
Vertical-Nash games, they might like being the unique supplier not to
ship products. The suppliers prefer to do so in the E-retailer-Stackelberg
or Supplier-Stackelberg game because of the relatively higher unit
profits and product demands. However, the suppliers prefer to do so in
the Vertical-Nash game because of only the highest unit profits. It is also
worth mentioning that when there is a large delivery diseconomy, the
suppliers prefer undertaking the delivery due to the higher unit profits in
the E-retailer-Stackelberg and Vertical-Nash games but do so owing to
the higher demands in the Supplier-Stackelberg game.
9
Omega 126 (2024) 103070
X. Zhou et al.
Fig. 4. Suppliers’ delivery arrangement preferences.
We obtain three remarkable observations based on the firms’ de­
livery arrangement preferences. First, compared with the market leader,
the market follower endowed with weaker pricing power might be more
willing to deliver the product when the delivery is economy in each
Stackelberg game. The main reason is that it can bring a higher product
demand to the market follower. Second, channel members might benefit
from undertaking the delivery when the delivery is diseconomy while
suffering from undertaking the delivery when the delivery is economy.
Specifically, in the E-retailer-Stackelberg and Vertical-Nash games, the
e-retailer benefits from undertaking the delivery when the delivery is
diseconomy but benefits from not undertaking the delivery when the
delivery is economy. In the Supplier-Stackelberg and Vertical-Nash
games, the suppliers might benefit from being the only supplier to
(not to) undertake the delivery when the delivery is diseconomy
(economy). Third, our work shows the non-negligible impact of power
structure on channel members’ preferences regarding the delivery
arrangement and also reveals that the drivers may change with the
power structure.
We next characterize the equilibrium delivery arrangement under
each power structure.
b 2 (k), and EE is
(2) EE and SS are two possible equilibria if ̂
b 1 (k) < b < ̂
Pareto optimal;
(3) EE is the unique equilibrium if ̂
b 2 (k) < b < 0, or b > 0.
The expression of ̂
b 2 (k) is provided in the Online Appendix B.
Part (1) of Proposition 3 indicates that when the delivery economy is
large, the delivery arrangement SS emerges in equilibrium, as shown in
the region I in Fig. 5(a). When there is a large delivery economy, given
that the competitor rejects to undertake the delivery, the supplier ben­
efits from undertaking the delivery because he can obtain a higher de­
mand. However, when the competitor agrees to undertake the delivery,
the supplier has no incentive to deviate from agreeing to undertake the
delivery because of the higher demand loss. Therefore, the delivery
arrangement SS emerges in equilibrium in such a case. However, in the
region I in Fig. 5(a), a surprising result manifests: when competition
becomes intense and the delivery economy gets small,18 the delivery
arrangement SS remains a pure-strategy equilibrium even though it
̂ SS < Π
̂ EE ). Put differently, two sup­
hurts the suppliers’ profits (i.e., Π
si
si
pliers are better off rejecting to undertake the delivery when there is
fierce competition, yet they cannot help refusing to do so and eventually
get involved in the prisoner’s dilemma. When the delivery economy is
moderate, Proposition 3 (2) suggests that the delivery arrangements SS
and EE are two possible equilibria (see the region II in Fig. 5(a)). It is
natural to pick EE as the equilibrium outcome because both suppliers
benefit more from this arrangement. As the delivery economy becomes
5.2. Equilibrium delivery arrangement
The following proposition characterizes the equilibrium delivery
arrangement in the E-retailer-Stackelberg game.
Proposition 3 (Equilibrium Delivery Arrangement in the Eretailer-Stackelberg Game).
(1) SS is the unique equilibrium if (k − 1)(k + 2)/2 < b < ̂
b 1 (k);
18
10
The expressions of ̂
b 3 (k) and ̂
b 4 (k) are provided in the Online Appendix B.
X. Zhou et al.
Omega 126 (2024) 103070
Fig. 5. Equilibrium delivery arrangement.
small, Proposition 3 (3) reveals that the delivery arrangement EE
emerges in equilibrium, shown by the region III in Fig. 5(a). The intui­
tion behind this result is that the increase in unit profit justifies the
demand reduction when both suppliers switch from agreeing with the
delivery proposal to rejecting it. Finally, because the e-retailer prefers
delivering products when the delivery is diseconomy, Proposition 3 (3)
indicates that the delivery arrangement EE emerges in equilibrium
naturally (see the region IV in Fig. 5(a)).
The following proposition shows the equilibrium delivery arrange­
ment in the Supplier-Stackelberg game.
Proposition 4 (Equilibrium Delivery Arrangement in the
Supplier-Stackelberg Game).
(1) EE is the unique equilibrium if b > ̃
b1 (k), k − 1 < b < 0, or ̃
k1 < k <
loss of unit profits because the small delivery diseconomy limits the
competition-mitigating effect when there is fierce competition (shown
by Lemma 5 (2)). Ultimately, the higher demands gained through un­
dertaking the delivery cannot make up for the higher loss of unit profits.
Hence, both suppliers refuse to undertake the delivery, and delivery
arrangement EE emerges in equilibrium. Furthermore, when the de­
livery diseconomy is not too small, whereas the competition is intense
(see the region III in Fig. 5(b)), Proposition 4 (2) reveals that the hybrid
delivery arrangement SE or ES emerges in equilibrium even if two
competing suppliers are identical. It is worth noting that, compared with
the delivery arrangement EE, the hybrid delivery arrangement benefits
the supplier who agrees to undertake the delivery while harming the
supplier who refuses to do it. Lastly, as the competitive intensity and
delivery diseconomy fall into the region IV in Fig. 5(b), SS emerges in
equilibrium because the increased demand gained by undertaking the
delivery in such a case is so appealing that it enables the supplier to
agree to deliver products regardless of which strategy the competitor
adopts. Interestingly, there also exists a prisoner’s dilemma: when
competition intensifies, and the delivery diseconomy gets small (i.e.,
̃
k3 < k < 1 and max{0, ̃
b2 (k)} < b < ̃
b4 (k), see the region IV in Fig. 5(b))
1 and 0 < b < ̃
b3 (k);
(2) SE or ES is the unique equilibrium if ̃
k1 < k < 1 and ̃
b3 (k) < b
̃
< b2 (k);
(3) SS is the unique equilibrium if max{0, ̃
b2 (k)} < b < ̃
b1 (k).
From Proposition 1 (2), we know that the e-retailer prefers to un­
dertake the delivery either when there is a large delivery diseconomy or
when the delivery is economy in the Supplier-Stackelberg game.
Therefore, Proposition 4 (1) shows that the delivery arrangement EE
emerges in equilibrium naturally in these two cases (see the regions I
and V in Fig. 5(b)). Alternatively, Proposition 4 (1) demonstrates that
the delivery arrangement EE can also be sustained as an equilibrium
outcome when there is fierce competition and a relatively small delivery
diseconomy (see the region II in Fig. 5(b)). Note that both suppliers can
obtain higher product demands by undertaking the delivery in such a
case (shown by Lemma 3 (2)); however, they suffer from a significant
,19 both suppliers agree to undertake the delivery but obtain lower
profits compared with the case of rejecting to do it.
The equilibrium delivery arrangement in the Vertical-Nash game is
presented in the following proposition.
Proposition 5 (Equilibrium Delivery Arrangement in the
Vertical-Nash Game). EE is the unique equilibrium.
19
11
The expressions of ̃
k3 and ̃
b4 (k) are provided in the Online Appendix B.
X. Zhou et al.
Omega 126 (2024) 103070
Fig. 6. Consumer surplus-maximizing arrangements.
may make the two suppliers unable to escape from this undesirable
result in the E-retailer-Stackelberg game; nevertheless, in the SupplierStackelberg game, the decrease of delivery diseconomy (i.e., the de­
livery is less expensive) might make them unable to avoid this unfor­
tunate outcome.
Our results might also provide a plausible explanation for the busi­
ness practices: some products are shipped by the e-retailer and others by
the suppliers. In the E-retailer-Stackelberg game, online retail giants
might prefer asking the competing suppliers to deliver products to
consumers when the delivery is economy. A canonical example is that
when selling home appliances for competing suppliers Haier and Midea,
JD.com chooses to undertake the delivery because of the delivery
diseconomy of these products. However, when selling products with a
significant delivery economy (e.g., clothing and hats) online, JD.com
may propose to let the competing suppliers Li-Ning and ANTA deliver
products, and both agree to do it. By contrast, in the SupplierStackelberg game, numerous e-retailers might prefer asking the up­
stream suppliers to deliver products to customers when there is a de­
livery diseconomy and undertaking the delivery when the delivery is
economy. For example, when selling home appliances for competing
suppliers such as GREE and Hisense, the downstream e-retailers prefer
asking them to ship products to customers because of the delivery
diseconomy of these products, whereas, in the case of selling digital
products for suppliers such as Xiaomi and OPPO, the downstream eretailers undertake the delivery due to the delivery economy of those
items.
Proposition 5 shows that the delivery arrangement EE constitutes the
only equilibrium outcome in the Vertical-Nash game, which is entirely
different from the equilibrium delivery arrangements in the other two
games. Recall from Proposition 1 (3) that the e-retailer prefers deliv­
ering products when the delivery is diseconomy while prefers asking
both suppliers to undertake the delivery when the delivery is economy.
Thus, the delivery arrangement EE emerges in equilibrium naturally in
the context of delivery diseconomy. When the delivery is economy,
because of the lower unit profits the suppliers obtain by undertaking the
delivery and the same demands the suppliers get among the three
different delivery arrangements, both suppliers reject the e-retailer’s
delivery proposal; thus, the delivery arrangement EE emerges in equi­
librium again (see Fig. 5(c)).
Based on the above analysis, our research underscores the substantial
implications of power structure for the delivery arrangement in online
distribution channels. The delivery arrangement EE might emerge in
equilibrium under certain conditions in each Stackelberg game. How­
ever, it is the unique equilibrium arrangement in the Vertical-Nash
game. The delivery arrangement SS might emerge in equilibrium
when there is a large delivery economy in the E-retailer-Stackelberg
game, but only when the competition intensity is not too strong and the
delivery diseconomy is not so small in the Supplier-Stackelberg game.
That is because the power structure alters the conditions under which
the e-retailer asks the suppliers to undertake the delivery and changes
the conditions under which the suppliers can benefit from agreeing to
undertake the delivery. Besides, our analysis shows that the hybrid de­
livery arrangement SE can emerge in equilibrium only in the SupplierStackelberg game. Moreover, a prisoner’s dilemma might arise in each
Stackelberg game when competition becomes fierce. Notably, the
decrease in the delivery economy (i.e., the delivery is more expensive)
6. Welfare implications
In this section, we explore the impacts of delivery arrangements on
12
X. Zhou et al.
Omega 126 (2024) 103070
Fig. 7. Social welfare-maximizing arrangements.
consumer surplus and social welfare. The consumer surplus and social
∑
welfare are respectively given by CS =
(aqi − qi 2 /2 − pi qi ) − kq1 q2
and thus bring about the highest consumer surplus. In contrast, when the
delivery is diseconomy, Lemma A1 (1) in the Online Appendix A and
Lemma 3 (1) reveal that, compared with the other delivery arrange­
ments, the delivery arrangement EE can mitigate the double marginal­
ization effect the most greatly and thus results in the highest consumer
surplus. Following similar reasoning, in the Supplier-Stackelberg game,
Proposition 6 (2) indicates that the delivery arrangement EE (SS) leads
to the highest consumer surplus when there is a delivery economy
(diseconomy), as shown in Fig. 6(b). Whereas in the Vertical-Nash game,
because of the equal prices and the equal demands across the three
different delivery arrangements (see Lemma A1 (3) in the Online Ap­
pendix A and Lemma 3 (3)), the consumer surplus is equal under the
three delivery arrangements.
Note that the mitigation of the double marginalization effect not only
generates lower prices and higher demands but also leads to higher
profits for the whole supply chain. Thus, Proposition 7 and Fig. 7 indi­
cate that the changing trend of the delivery arrangement that generates
the highest social welfare is very similar to that of the delivery
arrangement that leads to the highest consumer surplus.
Proposition 7 (Social Welfare).
i=1,2
and SW = CS + Πe + Πs1 + Πs2 . All proofs are provided in the Online
Appendix C. The following proposition summarizes the consumer
surplus.
Proposition 6 (Consumer Surplus).
SE
EE
SS
̂ > max{ CS
̂ , CS
̂ } if
(1) For the E-retailer-Stackelberg game, CS
SS
EE
SE
̂
̂
̂
̂
̂
(k − 1)(k +2)/2 < b < b 5 (k); CS > max{ CS , CS } if b 5 (k) < b < 0;
̂ EE > max{ CS
̂ SE , CS
̂ SS } if b > 0.
and CS
̃ EE > max{CS
̃ SE , CS
̃ SS } if k − 1
(2) For the Supplier-Stackelberg game, CS
̃ SS > max{CS
̃ EE , CS
̃ SE } if b > 0.
< b < 0 and CS
EE
SE
SS
(3) For the Vertical-Nash game, CS = CS = CS .
The expression of ̂
b 5 (k) is provided in the Online Appendix C.
As illustrated in Fig. 6(a), Proposition 6 (1) shows that, in the Eretailer-Stackelberg game, the hybrid delivery arrangement SE gener­
ates the highest consumer surplus when the delivery economy is large,
and the delivery arrangement SS generates the highest consumer surplus
when the delivery economy becomes small; nevertheless, when the de­
livery is diseconomy, only the delivery arrangement EE can benefit the
consumers at most. Mitigating the double marginalization effect gen­
erates lower prices and higher demands, thus benefiting consumers.
Along this line, the intuition behind the above results mainly hinges on
the degree to which the delivery arrangement mitigates the double
marginalization effect. Specifically, as shown in Lemma A1 (1) in the
Online Appendix A and Lemma 3 (1), when the delivery economy is
small (large), the delivery arrangement SS (SE) can alleviate the double
marginalization effect compared with the other delivery arrangements
̂ SE > max{ SW
̂ EE , SW
̂ SS } if
(1) For the E-retailer-Stackelberg game, SW
̂ SS > max{ SW
̂ EE , SW
̂ SE }
(k − 1)(k +2)/2 < b < ̂
b 6 (k);
SW
if
EE
SE
SS
̂
̂
̂
̂
b 6 (k) < b < 0; and SW > max{ SW , SW } if b > 0.
̃
(2) For the Supplier-Stackelberg game, SW
EE
SE
̃SS > max{SW
̃EE , SW
̃SE } if b > 0.
1 < b < 0 and SW
EE
SS
̃ , SW
̃ } if k −
> max{SW
SE
SS
(3) For the Vertical-Nash game, SW = SW = SW .
The expression of ̂
b 6 (k) is provided in the Online Appendix C.
To conclude, the delivery arrangements from which the consumer
13
X. Zhou et al.
Omega 126 (2024) 103070
and society can benefit under the three power structures are funda­
mentally different. When there is a delivery economy (diseconomy),
shifting the delivery to the suppliers (the e-retailer) generates the
highest consumer surplus and social welfare in the E-retailer-Stackel­
berg game but hurts the consumers and society in the SupplierStackelberg game. The above results are different in that the delivery
arrangement that can alleviate the double marginalization effect in the
E-retailer-Stackelberg game is opposite to that in the SupplierStackelberg game. However, in the Vertical-Nash game, the consumers
and society are indifferent to who delivers products. Moreover, in each
Stackelberg game, when the delivery arrangement EE maximizes the
consumer surplus and social welfare, it benefits the e-retailer only; in
contrast, the delivery arrangement SS might benefit each channel
member and generate the highest consumer surplus and social welfare
simultaneously (i.e., a triple-win situation). However, this triple-win
situation never happens in the Vertical-Nash game. Based on
Figs. 5–7, we can see that such a triple-win situation might occur only
when there is a delivery economy (i.e., max{(k − 1)(k + 2) /2, ̂
b 4 (k)} <
outcome. Finally, although the delivery arrangement SS might maximize
the profits of the entire supply chain, such an arrangement cannot be an
equilibrium outcome under certain conditions. One key takeaway is that
channel members can increase their profits and achieve a Pareto
improvement through compensation. Concretely, when there is a small
delivery economy in the E-retailer-Stackelberg game, it should be up to
the e-retailer to compensate the suppliers to make them accept her de­
livery proposal. However, when there is a large delivery diseconomy in
the Supplier-Stackelberg game, the supplier should make up for the eretailer so that she will shift the delivery to them.
There are several limitations to this study. First, we focus on an
online distribution channel with two suppliers and one e-retailer. It
would be interesting to examine the delivery arrangement under
different channel structures. Second, our study only considers the sym­
metric information. Therefore, it would be worth exploring how the
information communication interacts with the delivery arrangement.
Finally, we only consider the wholesale price contract prevalent in
business practice. However, e-retailers like JD.com, Amazon, and Sun­
ing also offer logistics delivery services to suppliers under agency
selling. Thus, examining the delivery arrangement under different
selling modes would also be a promising research topic.
b<̂
b 3 (k), see Fig. 5(a)) in the E-retailer-Stackelberg game but only
when there is a delivery diseconomy (i.e., max{0, ̃
b4 (k)} < b < ̃
b1 (k), see
Fig. 5(b)) in the Supplier-Stackelberg game. With Figs. 5–7, we also
observe that the increased competition intensity shrinks the triple-win
region in the E-retailer-Stackelberg game but generates a nonmonotonic effect on that region in the Supplier-Stackelberg game.
CRediT authorship contribution statement
Xiongwei Zhou: Conceptualization, Supervision, Validation,
Writing – review & editing. Chaoqun Zhu: Conceptualization, Meth­
odology, Formal analysis, Writing – original draft. Dan Cai: Conceptu­
alization, Supervision, Resources, Writing – review & editing.
7. Concluding remarks
This paper explores the delivery arrangement in an online distribu­
tion channel with two competing suppliers selling substitutable products
through a common e-retailer. Our analysis highlights the substantial
implications of power structure for the delivery arrangement. The eretailer’s delivering products (i.e., EE) might emerge in equilibrium in
each Stackelberg game but constitutes the only equilibrium delivery
arrangement in the Vertical-Nash game. The suppliers’ undertaking the
delivery (i.e., SS) is the equilibrium outcome only if the delivery econ­
omy is significant (the competition is not too fierce and the delivery
diseconomy is not too small) in the E-retailer-Stackelber (SupplierStackelberg) game. Only the Supplier-Stackelberg game can induce a
hybrid delivery arrangement. Although both suppliers can achieve
higher profits by refusing to undertake the delivery in each Stackelberg
game, they might still agree to do so and fall into the prisoner’s dilemma.
The rationale behind the above results is that the power structure alters
the impacts of delivery arrangement on the unit profits and the demands
the channel members obtain. These results might help us understand the
business observations that some products are delivered by e-retailers
while others by suppliers. Furthermore, we show that only shifting the
delivery responsibility to the suppliers in each Stackelberg game might
benefit channel members and generate the highest consumer surplus
and social welfare simultaneously; in the Vertical-Nash game, however,
this triple-win situation never occurs, and the consumer surplus and
social welfare are invariant to the delivery arrangement.
Our work also offers some valuable insights for online distribution
channel members. First, compared with the market leader, the market
follower might benefit more from undertaking the delivery when there is
a delivery economy in each Stackelberg game. Second, counterintui­
tively, the supply chain players might benefit from delivering products
with a significant delivery diseconomy but dislike undertaking the de­
livery of products with an apparent delivery economy. Hence, firms
should distinguish types of products with different delivery scale effects
when making delivery decisions. Furthermore, as competition becomes
fierce in each Stackelberg game, the suppliers might trap themselves in a
prisoner’s dilemma by accepting the e-retailer’s delivery proposal. Thus,
our work uncovers the dark side of the e-retailer’s delivery proposal and
suggests that the suppliers can reduce the intensity of competition by
enhancing their product design differentiation to escape this undesirable
Declaration of competing interest
The authors declare that they have no known competing financial
interests or personal relationships that could have appeared to influence
the work reported in this paper.
Data availability
No data was used for the research described in the article.
Acknowledgments
The authors thank the editor and all reviewers for their valuable
comments, which greatly improved the paper. This work was supported
by the National Social Science Foundation of China [Grant No.
21AZD117] and the National Natural Science Foundation of China
[Grant No. 71991463].
Supplementary materials
Supplementary material associated with this article can be found, in
the online version, at doi:10.1016/j.omega.2024.103070.
References
[1] Lai G, Liu H, Xiao W, Zhao X. “Fulfilled by Amazon”: a strategic perspective of
competition at the e-commerce platform. Manufactur Serv Oper Manag 2022.
https://doi.org/10.1287/msom.2022.1078.
[2] Li X, Li Y, Cai X, Shan J. Service channel choice for supply chain: who is better off
by undertaking the service? Product Oper Manag 2016;25(3):516–34. https://doi.
org/10.1111/poms.12392.
[3] Niu B, Xie F, Chen L, Xu X. Join logistics sharing alliance or not? Incentive analysis
of competing E-commerce firms with promised-delivery-time. Int J Product Econ
2020;224:107553. https://doi.org/10.1016/j.ijpe.2019.107553.
[4] Qin X, Liu Z, Tian L. The strategic analysis of logistics service sharing in an ecommerce platform. Omega (Westport) 2020;92:102153. https://doi.org/
10.1016/j.omega.2019.102153.
14
X. Zhou et al.
Omega 126 (2024) 103070
[26] Wang Y, Wallace SW, Shen B, Choi T-M. Service supply chain management: a
review of operational models. Eur J Oper Res 2015;247(3):685–98. https://doi.
org/10.1016/j.ejor.2015.05.053.
[27] Liu W, Liu Y, Zhu D, Wang Y, Liang Z. The influences of demand disruption on
logistics service supply chain coordination: a comparison of three coordination
modes. Int J Product Econ 2016;179:59–76. https://doi.org/10.1016/j.
ijpe.2016.05.022.
[28] Lou Y, Feng L, He S, He Z, Zhao X. Logistics service outsourcing choices in a
retailer-led supply chain. Transport Res Part E: Logist Transport Rev 2020;141:
101944. https://doi.org/10.1016/j.tre.2020.101944.
[29] Qin X, Liu Z, Tian L. The optimal combination between selling mode and logistics
service strategy in an e-commerce market. Eur J Oper Res 2021;289(2):639–51.
https://doi.org/10.1016/j.ejor.2020.07.029.
[30] Wang L, Chen J, Lu Y. Manufacturer’s channel and logistics strategy in a supply
chain. Int J Product Econ 2022;246:108415. https://doi.org/10.1016/j.
ijpe.2022.108415.
[31] Liu H, Xu T, Jing S, Liu Z, Wang S. The interplay between logistics strategy and
platform’s channel structure design in B2C platform market. Eur J Oper Res 2023.
https://doi.org/10.1016/j.ejor.2023.02.043.
[32] Wang P, Du S, Hu L, Tang W. Logistics choices in a platform supply chain: a coopetitive perspective. J Oper Res Soc 2023;74(1):93–111. https://doi.org/
10.1080/01605682.2021.2023675.
[33] Tian L, Vakharia AJ, Tan Y, Xu Y. Marketplace, reseller, or hybrid: strategic
analysis of an emerging e-commerce model. Product Oper Manag 2018;27(8):
1595–610. https://doi.org/10.1111/poms.12885.
[34] Niu B, Li Q, Mu Z, Chen L, Ji P. Platform logistics or self-logistics? Restaurants’
cooperation with online food-delivery platform considering profitability and
sustainability. Int J Product Econ 2021;234:108064. https://doi.org/10.1016/j.
ijpe.2021.108064.
[35] He P, He Y, Tang X, Ma S, Xu H. Channel encroachment and logistics integration
strategies in an e-commerce platform service supply chain. Int J Product Econ
2022;244:108368. https://doi.org/10.1016/j.ijpe.2021.108368.
[36] Choi SC. Price competition in a channel structure with a common retailer. Market
Sci 1991;10(4):271–96. https://doi.org/10.1287/mksc.10.4.271.
[37] Nagarajan M, Sošić G. Coalition stability in assembly models. Oper Res 2008;57(1):
131–45. https://doi.org/10.1287/opre.1080.0536.
[38] Pan K, Lai KK, Leung SCH, Xiao D. Revenue-sharing versus wholesale price
mechanisms under different channel power structures. Eur J Oper Res 2010;203
(2):532–8. https://doi.org/10.1016/j.ejor.2009.08.010.
[39] Shi R, Zhang J, Ru J. Impacts of power structure on supply chains with uncertain
demand. Product Oper Manag 2013;22(5):1232–49. https://doi.org/10.1111/
poms.12002.
[40] Geng X, Krishnan H, Queyranne M. Cost-raising internalization in supply chain
design. Nav Res Logist (NRL) 2021;68(3):295–311. https://doi.org/10.1002/
nav.21951.
[41] Abhishek V, Jerath K, Zhang ZJ. Agency selling or reselling? Channel structures in
electronic retailing. Manage Sci 2015;62(8):2259–80. https://doi.org/10.1287/
mnsc.2015.2230.
[42] Ha AY, Luo H, Shang W. Supplier Encroachment, Information Sharing, and
Channel Structure in Online Retail Platforms. Product Oper Manag 2022;31(3):
1235–51. https://doi.org/10.1111/poms.13607.
[43] Anand KS, Mendelson H. Information and organization for horizontal multimarket
coordination. Manage Sci 1997;43(12):1609–27. https://doi.org/10.1287/
mnsc.43.12.1609.
[44] Ha AY, Tong S, Zhang H. Sharing demand information in competing supply chains
with production diseconomies. Manage Sci 2011;57(3):566–81. https://doi.org/
10.1287/mnsc.1100.1295.
[45] Shang W, Ha AY, Tong S. Information sharing in a supply chain with a common
retailer. Manage Sci 2015;62(1):245–63. https://doi.org/10.1287/
mnsc.2014.2127.
[46] Zhao D, Li Z. The impact of manufacturer’s encroachment and nonlinear
production cost on retailer’s information sharing decisions. Ann Oper Res 2018;
264(1):499–539. https://doi.org/10.1007/s10479-017-2717-7.
[47] Xiao Y, Chen FY, Chen J. Optimal inventory and dynamic admission policies for a
retailer of seasonal products with affiliate programs and drop-shipping. Nav Res
Logist (NRL) 2009;56(4):300–17. https://doi.org/10.1002/nav.20346.
[5] Raghavan S, Zhang R. The driver-aide problem: coordinated logistics for last-mile
delivery. Manufact Serv Opera Manag 2023. https://doi.org/10.1287/
msom.2022.0211.
[6] Sun G, Cavusoglu H, Raghunathan S. Strategic implications of online retail
platforms’ membership-based free shipping programs. Inform Syst Res 2023.
https://doi.org/10.1287/isre.2022.0208.
[7] Li G, Zhang X, Chiu S-M, Liu M, Sethi SP. Online market entry and channel sharing
strategy with direct selling diseconomies in the sharing economy era. Int J Product
Econ 2019;218:135–47. https://doi.org/10.1016/j.ijpe.2019.05.006.
[8] Geng X, Krishnan H, Sohoni MG. Operational collaboration between rivals: the
impact of cost reduction. Product Opera Manag 2021. https://doi.org/10.1111/
poms.13651. n/a(n/a).
[9] He B, Gupta V, Mirchandani P. Online selling through O2O platform or on your
own? Strategic implications for local Brick-and-Mortar stores. Omega (Westport)
2021;103:102424. https://doi.org/10.1016/j.omega.2021.102424.
[10] Hu Y, Qu S, Li G, Sethi SP. Power structure and channel integration strategy for
online retailers. Eur J Oper Res 2021;294(3):951–64. https://doi.org/10.1016/j.
ejor.2019.10.050.
[11] Xu P, Xiao T. Analysis of online rebates and commission formats in a retailerStackelberg supply chain with cashback website. Decisi Sci 2022. https://doi.org/
10.1111/deci.12586. n/a(n/a).
[12] Tong Y, Xiao T. Sourcing strategy of a dominant platform: signaling game’s
perspective. Omega (Westport) 2024;124:103016. https://doi.org/10.1016/j.
omega.2023.103016.
[13] Xiao Y, Niu W, Zhang L, Xue W. Store brand introduction in a dual-channel supply
chain: the roles of quality differentiation and power structure. Omega (Westport)
2023;116:102802. https://doi.org/10.1016/j.omega.2022.102802.
[14] Fang F, Gurnani H, Natarajan HP. Leadership, dominance, and preeminence in a
channel structure with a common retailer. Decisi Sci 2018;49(1):65–120. https://
doi.org/10.1111/deci.12266.
[15] Li G, Tian L, Zheng H. Information sharing in an online marketplace with coopetitive sellers. Product Oper Manag 2021;30(10):3713–34. https://doi.org/
10.1111/poms.13460.
[16] Wang T-Y, Chen Z-S, He P, Govindan K, Skibniewski MJ. Alliance strategy in an
online retailing supply chain: motivation, choice, and equilibrium. Omega
(Westport) 2023;115:102791. https://doi.org/10.1016/j.omega.2022.102791.
[17] Choi S, Fredj K. Price competition and store competition: store brands vs. national
brand. Eur J Oper Res 2013;225(1):166–78. https://doi.org/10.1016/j.
ejor.2012.07.016.
[18] Luo Z, Chen X, Chen J, Wang X. Optimal pricing policies for differentiated brands
under different supply chain power structures. Eur J Oper Res 2017;259(2):
437–51. https://doi.org/10.1016/j.ejor.2016.10.046.
[19] Chen X, Wang X. Free or bundled: channel selection decisions under different
power structures. Omega (Westport) 2015;53:11–20. https://doi.org/10.1016/j.
omega.2014.11.008.
[20] Chen X, Wang X, Zhou M. Firms’ green R&D cooperation behaviour in a supply
chain: technological spillover, power and coordination. Int J Product Econ 2019;
218:118–34. https://doi.org/10.1016/j.ijpe.2019.04.033.
[21] Chung H, Lee E. Asymmetric relationships with symmetric suppliers: strategic
choice of supply chain price leadership in a competitive market. Eur J Oper Res
2017;259(2):564–75. https://doi.org/10.1016/j.ejor.2016.11.013.
[22] Lau AHL, Lau H-S. Some two-echelon supply-chain games: improving from
deterministic-symmetric-information to stochastic-asymmetric-information
models. Eur J Oper Res 2005;161(1):203–23. https://doi.org/10.1016/j.
ejor.2003.08.040.
[23] Liao B, Yano CA, Trivedi M. Optimizing store-brand quality: impact of choice of
producer and channel price leadership. Product Oper Manag 2020;29(1):118–37.
https://doi.org/10.1111/poms.13084.
[24] Hu X, Cai J, Yue X. Power structure preferences in a dual-channel supply chain:
demand information symmetry vs. asymmetry. Eur J Oper Res 2023. https://doi.
org/10.1016/j.ejor.2023.10.041.
[25] Niu B, Liu J, Zhang J, Chen K. Promised-delivery-time-driven reselling facing
global platform’s private label competition: game analysis and data validation.
Omega (Westport) 2024;123:102990. https://doi.org/10.1016/j.
omega.2023.102990.
15