I.E. FAUSTINO MALDONADO
I. Datos informativos:
DESCUBRIMOS PATRONES NUMÉRICOS
Título de la
actividad
Eda
“Iniciamos el año escolar en una convivencia armoniosa, demostrando nuestras
habilidades deportivas con fe y reflexión”
Grado y Sección
Quinto Grado “C”
Fecha
de marzo del 2024
área
MATEMÁTICA
Docente
II.
Duración
90 minutos
EFRAIN CHECYA ALATA
Propósitos de aprendizaje: jugamos descubriendo patrones
Área
MAT
Enfoques
Transversales
Evidencia
Competencia
Desempeño
Resuelve problemas de
regularidad, equivalencia
y cambio.
– Traduce
datos
y
condiciones a expresiones
algebraicas.
– Comunica su comprensión
sobre las relaciones
algebraicas.
Usa
estrategias
y
procedimientos
para
encontrar equivalencias y
reglas generales.
Argumenta afirmaciones
sobre relaciones de cambio y
equivalencia
DE DERECHOS
Expresa, con lenguaje
algebraico y diversas
representaciones, su
comprensión de la regla de
formación de un patrón de
segundo orden, así como
de los símbolos o letras en
la ecuación y de la
proporcionalidad como un
cambio constante.
Criterio De
Instrumento
Evaluación
Identifica
la Escala de
regularidad y expresa valoración
en un patrón aditivo o
multiplicativo.
Representa la regla
de
formación
numérica de un
patrón.
Explica la regla de
formación de un
patrón aditivo o
multiplicativo
Establece y expresa el patrón de formación aditiva o multiplicativa
III .- PROCESO DIDÁCTICO
SECUENCIA DIDÁCTICA
INICIO
El propósito del día de hoy se logrará con los criterios:
¿Qué tomaré
en cuenta?
Identificar la regularidad que expresa en un patrón
aditivo o multiplicativo.
Representar la regla de formación numérica de un
patrón.
Explicar la regla de formación de un patrón aditivo o
multiplicativo.
Nos divertimos con las tarjetas de casinos:
o Se entrega casinos Y se indica que formaran el siguiente patrón.
¿?
o Se pide que continúen el patrón para ello se pregunta ¿Qué continuará?
o Forman otros patrones numéricos con dos criterios
Responden:
¿Cómo hallaron el casino que continúa?
¿Qué tipo de patrón es?
¿Qué otros materiales del aula nos pueden ayudar a formar patrones que aumenten?
El reto a lograr el día de hoy es:
Reto:
HALLAMOS PATRONES NUMÉRICOS PARA ORGANIZAR
LAS ACTIVIDADES ESCOLARES
Recordamos las siguientes recomendaciones:
Tener sus materiales educativos
Seguir las indicaciones de la maestra(o)
Respetar la opinión de los demás
DESARROLLO
Comprensión del problema
Se plantea el siguiente problema:
Susy y Paco organizaron grupos para limpiar el aula y el patio de la escuela. El grupo
que limpia menos días del mes el aula, limpiará el patio. ¿A qué grupo le toca limpiar
el patio?
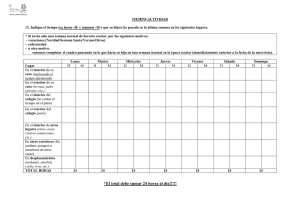
Ellos marcaron las actividades en el siguiente calendario:
Responden las siguientes preguntas:
¿Qué actividades realizaran los grupos de Susy y Paco?
Según el calendario ¿Qué días limpiará el grupo de Susy?
Según el calendario ¿Qué días limpiará el grupo de Paco?
¿Qué nos pide el problema?
Búsqueda de estrategias
Responden las preguntas:
¿Cómo podemos qué grupo limpiara el patio?
Identifica el patrón numérico de cada cuantos días realizan las actividades de acuerdo a las fechas que
marcaron en el calendario
• El grupo de Susy limpia cada
días. En total, limpian
días en el mes de marzo.
• El grupo de Paco limpia cada
días. En total, limpian
días en el mes de marzo.
• ¿Coincidirán en algún día?
¿Por qué?
Representación
Util izan un tabla para hallar el patrón de cada grupo para limpiar el salón o el patio; por ejemplo, la siguiente:
Día del mes que limpian el salón de clases
Grupo de
Susy
2
6
10
Grupo de
Paco
1
3
5
14
Re sponden las preguntas: ¿Cada cuántos días limpia cada grupo?; ¿Qué tipo de patrón es creciente o
d ecreciente?, ¿por qué?
Vol untariamente explican cuál es la regla de formación del patrón aditivo creciente y qué procedimiento s
re alizaron para encontrar la fecha y los días trascurridos.
Exp resan que grupo limpiara el patio:
R espuesta. Al grupo de
le toca limpiar el patio porque limpia solo
días en el mes de marzo.
Formalización
Se explica sobre los patrones numéricos:
Se plantea otro problema:
Re suelve otras actividades de extensión de patrones numéricos
Reflexión
Refl exionan sobre los procesos y estrategias para hallar la respuesta de que grupo limpiara el patio: ¿qué
debemos tener en cuenta para que un grupo de números forme un patrón aditivo?, ¿en todos los patrones
aditivos se suma la misma cantidad a un número?, ¿Los patrones aditivos solo aumentan? ¿O también
di sminuye?
CIERRE
Comparte con sus compañeros como hallaron el patrón numérico de formación.
Reflexionan respondiendo las preguntas:
¿Qué aprendiste del patrón de formación?
¿Cómo lo aprendiste?
¿Para qué te servirá lo aprendido?
Reflexiono sobre mis aprendizajes
Ahora te invitamos a reflexionar sobre lo aprendido. Para hacerlo completa la siguiente tabla:
Lo logré
Mis aprendizajes
Identifique la regularidad y expresa en un
patrón aditivo o multiplicativo.
Represente la regla de
numérica de un patrón.
formación
Explique la regla de formación de un
patrón aditivo o multiplicativo.
Lo estoy
intentando
¿Qué necesito mejorar?
ANEXOS
JUGAMOS CON LOS PATRONES NUMÉRICOS
Comprensión del problema
Se plantea el siguiente problema:
Susy y Paco organizaron grupos para limpiar el aula y el patio de la escuela. El grupo que
Ellos marcaron las actividades en el siguiente calendario:
Responden las siguientes preguntas:
¿Qué actividades realizaran los grupos de Susy y Paco?
Según el calendario ¿Qué días limpiará el grupo de Susy?
Según el calendario ¿Qué días limpiará el grupo de Paco?
¿Qué nos pide el problema?
Búsqueda de estrategias
Responden las preguntas:
¿Cómo podemos qué grupo limpiara el patio?
Identifica el patrón numérico de cada cuantos días realizan las actividades de acuerdo a las fechas que
marcaron en el calendario
• El grupo de Susy limpia cada
días. En total, limpian
días en el mes de marzo.
• El grupo de Paco limpia cada
días. En total, limpian
días en el mes de marzo.
• ¿Coincidirán en algún día?
¿Por qué?
Representación
Util izan untabla para hallar el patrón de cada grupo para limpiar el salón o el patio; por ejemplo, la siguiente:
Día del mes que limpian el salón de clases
Grupo de
Susy
2
6
10
Grupo de
Paco
1
3
5
14
Re sponden las preguntas: ¿Cada cuántos días limpia cada grupo?; ¿Qué tipo de patrón es creciente o
d ecreciente?, ¿por qué?
Vol untariamente explican cuál es la regla de formación del patrón aditivo creciente y qué procedimiento s
re alizaron para encontrar la fecha y los días trascurridos.
Exp resan que grupo limpiara el patio:
R espuesta. Al grupo de
le toca limpiar el patio porque limpia solo
días en el mes de marzo.
Formalización
Se explica sobre los patrones numéricos:
Los patrones aditivos y multiplicativos
Patrones
Un patrón es una sucesión de signos orales, fenómenos naturales, gráficos, sucesiones
numéricas, entre otros, que se construyen siguiendo una regla, ya sea de repetición o
de recurrencia. Los patrones se observan en la vida real y pueden responderá un
modelo matemático.
Patrones de repetición
Patrones de recurrencia
Cuando los patrones se construyen siguiendo
una regla de repetición, los elementos que lo
componen se presentan de forma periódica.
Cuando los patrones se construyen siguiendo
una regla de recurrencia, la regularidad con
que se presentan los elementos cambia y a
partir de ellos tiene que inferirse su ley de
Ejemplos:
Alexander está haciendo una torre con cubos. ¿Cuántos cubos necesitará para construir los siguientes
pisos?
Rpta.: Necesitará 6, 9 y 12 cubos.
Pedro puso 6 vasos de plástico en una bandeja, 18 en la segunda bandeja y 54 en la tercera bandeja,
¿cuántos vasos de plástico pondrá Pedro en la cuarta bandeja?
Rpta.: En la cuarta bandeja pondrá 162 vasos.
Cuaderno de trabajo
1. Suma las fechas pintadas. ¿Cuál es la regla de formación?
• Completa la tabla.
Respuesta. La regla de formación de la suma de las fechas pintadas es:
.
2. Dibuja lo que sigue en el patrón. ¿Cuántas tapitas hay en la figura 7?
N.° de figura
1
2
Cantidad de tapitas
1
4
3
4
5
6
7
8
a. Completa las tablas con la expresión matemática para cada caso.
N.° de
figura
Expresion
matematica
Cantidad
de tapitas
N.° de
figura
1
1x3-2
1
7
2
2x3–2
4
8
3
3x3–2
7
10
4
4x3-2
10
20
5
b. Exp lica cómo calcular la cantidad de tapitas en la figura 50.
3. Lol a
encon tró
varias
relaci ones
numé ricas en
el tablero 100.
¿Cuáles son?
a. Co
mpleta
las cruces y
las relaciones
numé ricas.
• ¿Se cumple la misma relación en otras cruces? Explica.
50
Expresion
matematica
Cantidad
de tapitas
b. Completa la tabla según las flechas
en el tablero 100.
Número de
inicio
Operación
matemática
Número
final
Número de
inicio
7
7 + 23
30
45
62 + 23
77
c. Completa estas figuras que fueron extraídas del tablero 100.
d. Describe la regla de formación de los números de la siguiente figura.
. Describe la regla de formación de los números de la siguiente figura.
e. Encuentra otra regularidad en el tablero 100.
Operación
matemática
Número
final