r.
l'
" ,....
Curso
de Difracción
de Rayos
•
-<,
X
Contenido
página
Cristalografía
1
Básica
1.1 Introducción
1.2 Redes y sistemas
cristalinos
1.3 Simetría
1.4 Estructuras
1.5 Planos
Tema 11
cris~alinas
y direcciones
Propiedades
cristalográficas
de los Rayos X
15
2.1 introducción
2.2 Espectro
continuo
2.3 Absorción
de rayos
2.4 Producción
X
de rayos
2.5 Detección
Te.a III Difracción
y caracteristfco
de rayos
de Rayos
X
X
X
25
3.1 Introducción
3.2 Ley de Bra"
3.3 Métodos
de difracción
del haz difractado
3.4 Intensidad
3.5 Factor
Tema IV
de e s t ru e t u.r a
36
Difractómetro
4.1 Introducción
4.2 Características
generales
4.3 Optica
X
4.4 Sistema
de rayos
de registro
,
~
\,
Tema V
IJ~\
Referencias
Aplicaciones
del Diftactóllletro
5.1 Medición
del parámetro
5.2 Medición
del tamal"io de partícula
5.3 Kedición
de esfuerzos
5.4 Análisis
cualitativo
5.5 Análisis
cuantitativo
5.6 Análisis
cuantitativo
44
reticular
I
residuales
58
,1
I
I
I
I
Tema
1 Cristalografía
Básica
1.1 Introducción
Un cristal
en un patrón
periódico
cristalino~
tienen
sino
está
presente.
peque~o
atómico
simétricas
definidas.
importante
saber
mediante
Para
y
sistemas
vectores
a su vez pueden
y
direcciones
y
COlO
como constantes
comola
describirse
1, donde
y
o parámetros
La figura 2 muestra
como un arreglo
idéntico
en un número
posee
en diferentes
características
de los
cristales
es
cristalográficas
a,
b
y
e,
qu~
se
son
Estos
de sus longitudes
r , Estas longitudes
y
a, b
ángulos
se
reticulares.
defin en no s Ó loa
un ejemplo
de puntos
del cristal
de la celda.
en términos
a, {3
que cada punto posee un alrededor
alrededor
que
del lisIO y en forma general
que al total de puntos en· la red cristalina
define
química
parte .ás peque"a
ejes cristalográficos
Los veetores a, b y e
vectores.
o unión
o
como los índices de Miller.
en la figura
el ángulo entre ellos
conocen
las propiedades
y simetría
como se muestra
conocidos
c,
puro
a su vez se dividen
planos
se define
vectores
y
La estructura
se agrupan
uno de los cuales
universal
las propiedades
representa
~nlace
no
cristalinos
Una celda unitaria
conserva
que
definir
los
de
son
los cuales
un elemento
cristalinas
cada
denotar
presente
arreglades
los sólidos
amorfos
en su interior.
por el tipo
de átocos
No todos
materiales
que
cristalinos
una simbología
1.2 Redes
existen
at6mico
espaciale~
compuesto
dimensiones.
Las estructuras
o grupos
un sólido
regular
determinado
de sistemas
redes
en tres
o el arreglo
compuesto
como
que también
un arreglo
cristalina
este
es definido
1a ee1da u nita r
por la translación
de una red espacial,
en el espacio,
idéntico.
que lo que se observa
-1-
arreglados
Entendiéndose
í
al
sin o
de los
la cual se
de tal forla
por un
en la red desde una dirección
Figura
1
Celda
unitaria.
·~~----~~~------~~------~~I
I
~'------'+-'-:",__---+--+---, ......
i
~~------~~~------~~------_."
Figura
2 Red
espacial
-2-
,.
o puntual.
I
////
.
"
debe ser igual a lo observado
La taba 1 presenta
se muestran
de Bravais
y
de los ejes
las catorce
los símbolos
N
= Ni
reticulares
+ (Nf/Z)
puntos en las caras
Como se mencionó
la red espacial
cristalográficos.
conocidas
denotado
como redes
por PoR
está dado ?or:
(1)
+ (Nc/8)
de puntos
puede definirse
en el interior,
de puntos
anterior.ente
en el
redes de Bravais.
por celda unitaria
Nc el número
y
clasificados
en las caras) e ¡(centrado
las catorce
Ni es el número
donde
ángulos
y
de cada red espacial,
La figura 3 muestra
El número de puntos
cristalinos
redes espaciales
P (centrado
(simple o primitiva),
cuerpo).
otra dirección.
a los siete sistemas
en base a las longitudes
Asimismo
en cualquier
Nf el número de
en las esquinas.
la posición
de cualquier
punto en
en base a los ejes cristalográficos,
así
por ejemp1o, 1a red es pae ia 1 cúb i ca c entrada en el cuerpo ti e n e 2 pun t os
(átomos)
por celda unitaria
(esquinas
de la celda)
y
los cristales
operaciones
sobre
el cuerpo
simetría.
operaciones
rotación,
inversión
cubo tiene un eje de rotación
sobre la diagonal
y
y
es ~métrico
Algunos
en la figura 4, donde
las clases de simetría
(1,
2,3,
tal forla que al efectuar
operaciones
macroscópicas
formado
de simetría:
Por ejemplo
un
por la unión de los centros
el cuadrado,
-3-
de
en cada cara, un eje ternario
de estos elementos
4 06).
con el
o elementos
rotación-inversión.
cuaternaria
uno binario
de dos bordes opuestos.
muestran
o estructura
se produce coincidencias
se denominan
reflexión,
diferentes
se arreglande
mismo. Estas operaciones
Existen cuatro
0,0,0
reales exhiben
Se dice que un cuerpo
cuando sus partes componentes
ciertas
en las posiciones
l/Z, 1/2, 1/2 (centro de la celda).
y
1.3 Siaetría
Las redes de Bravais
clases de simetría.
localizados
de si.etría
triángulo
y
elipse
se
designan
Tabla
Sistemas
Cristalinos
Sy¡!em
y
Redes de Bravais
Bravail
lattic:e
Axials leng!;'1 and onglel
I
lottic:e ¡
symbol I
I
I
I
Tlvea equal a"el al rig;'1 ongles
" - " - r, az~=y=9(f
Cubic:
Thrae a"es al rig;'1 anglel, Iwo equal
" .. c , a = t' a " :: 9rf'
Tetragonol
ti -
!
I
¡
I
Simple
Body-cenlered
Foca-cenlare<!
Ii
p
I
F
I Simple
Body-cenlered
p
I
p
Three unequal a"es al rig;'1 angles
a"'~·Y=9ao
u "'''!Ór.
Simple
Body-cenlered
Bas.-canlered
Faca-canlered
Rhombohedral
Tlvee equal axel, aqually inclined
ll.-b-r,
0-11-",.900
Simple
R
Hexagonal
T...,oequal caplanar a"eI al 12lf',
Ihird axis al rig;'1 angles
a-b.~,
a"II=9oD,
y e 12(f
Simple
p
MonacJinic
Three unequal axes,
one poir nol al righl angla
a"b .. ~, a-,,_9QO"1I
Simple
Bas.-cenlered
e
Thr.. unequal axa, unequally inclined
and none al rillhl angles
a"b,,~,
a '" 11 " )' ,,9QO
S~J.
,
Orthorhombic
.
TricJinic
• Also called trigona].
-4-
-
I
C
F
-
p
I
I
~DIPI.E
(TBIC fI')
BOO\' -CEXTER EO F.H'E-<'EXTERED
(TBJ(' (1,
(TRI(' (f')
BOD\' ..('E:!\'TERED
TETRAGONAL
SI:\IPLE
TETRAGONAL
SD.lPLE
ORTHORBO:\IBIC
(P)
(1)
(P)
B,\:"E-<'EXTERED
ORTHOIlHO:\IHIC
BODY-CENTERED
ORTHORHO~lB((.'
F.\C'E-<:ENTEREO
ORTHORHO:\tBl<'
(/)
RHO:\IHOHEDRAL
HEXAGONAL
:PI
,p"
Ir)
\
-:1 \1 PI.E
\JO:'\\H '1.1:'\1\'
Figura
3
.t-,
IU":F-( 'J-:YfEHEI)
\W\ ...("L1\1I" .t >,
Las catorce
redes
,.
-;:¡-
'fHlCLI.\"
u ,/'1
de Bravais.
I
I
I
I~,
(1, 1
i?
"',
o~ ,
0·1;.0
I
1"1
hl,
I
Pigura 4 Elelentos de sioetrl. ~e un cubo. la) Plano de rotación.
lb) Eje de rotación'. (c) Centro de inversión. (d) Eje de
rotaci5n-inversi6n.
I
I
-6-
I
El número mínimo
de elementos
en la tabla 2. Algunos
presenta
el mínimo del sistema
1.4 Estructuras
de cada sistema cristalino
se
pueden tener más elementos
que
pero no menos.
cristalinas
de la cristalografía
nada acerca de los cristales
los componen.
colocar
cristales
a que pertenece,
Hasta aquí se ha tratado
tratado
de simetría
Los cristales
los átomos
reales
más simples
en los mismos
y
matemática
no se ha
de los átomos los cuales
que uno, son aquellos
puntos
y
formados
de las redes de Bravais.
al
NQ
pero afortunadamente
muchos de los
todos estos cristales existen,
metales cristalizan en la estructura cúbica centrada en el el cuerpo
(bcc o ce)
y
cúbica centrada
en las caras
ellas posee 2 átomos por celda unitaria
en la figura
hexagonal
y
compacta
se obtiene
interior
5. Otra estructura
y
esta estructura es 1.633.
El número de átomos vecinos
si.ple
volumen
colocando
lás cercanos
tres átomos
teórica
a cualquier
es la
en el
de e/a para
átolo en la red
se denota por z. El número de
y
de un átomo en fcc o hc es 12, en bcc 8
y
en dia.ante
4. Entre más peque~o sea el número
de la celda unitaria
aproximadamente
ocupada
de
no es una Red de Bravais
6. La relación
se define como el número de coordinación
cúbico
co.ún entre los .etales
(hcp o hc). Esta estructura
a partir de la hexagonal
La primera
la otra 4 como se muestra
cristalina
COlO se muestra en la ficura
coordinaci6n
(fcc o cee).
relacionada
y
de las celdas unitarias
fce
58 % para la bce. La forma del cristal
con la Ley de los Indices
las caras desarrolladas
corresponden
ocupado
un 74 % del volumen
por los ~tomos
de coordinación menor es el
,
por los atomos, de tal forma que
Racionales
por los cristales
sie.pre son las que
a planos con índices de "iller
-7-
la cual expresa
peque~oS~
y
hcp es
est3
que
Tab 1 a 2
Elementos
Sistema
de Simetría
",ínimos
El e sen t c s de simetría
Cúbico
4 ejes de rotación ternarios
Tetra,onal
1 eje
Ortorró.bico
3 ejes perpendiculares
de rotación cuaternario
r.~aci6n
de
binaria
ternario
Roaboedral
1 eje de rotaci6n
Hela,onal
1 eje de rotación hela,onal
Monoclíco
1 eje de rotación binario
Triclínico
nj.llgu
no
-8-
I
I
I
I
I
I
I
I
I
I
I
I
I
sn'
Fi , ur a 5 Es t r u e tu r a s b e e ( Pe,
F('('
er ,
" o , V)
y
f e e ( e u,
I
I
I
I
I
I
Figura
6
estructura
hcp
-9-
(Ti, Zn, "g).
Al,
A u) .
1.7 Planos
direcciones
y
Las direcciones
describirse
indica
de cualquier
mediante
celda unitaria
pudiendo
punto
ser negativos
la figura 7 se ejemplifica
diferente
son empleados
u, v y w son siempre
de direcciones
se representa
de direcciones
En
en cualquier
y se definen
para designar
como el valor recíproco
del plano con los ejes cristalográficos.
Por ejeapIo
son (hkl), entonces
1/1 con los ejes
a, b
en la figura 8. La faailia de planos
y
en este caso por {hkl} e indica
todas las coabiDaciones
los índices de ailler incluyendo
los números negativos.
diferentes
índices
En el caso de .ateriales
índices relacionados
para una dirección
de direcciones
a los cuatro
y
(hki1)
=
-t
se denota
posibles
de
En la figara
9
de Miller de planos cristalinos.
con una estructura
los índices de Miller tanto
si
el plano
fraccionales
c como se muestra
l/h, llk
los
de las
tiene las intercepciones
se presentan
del
como Cuvw>.
universalmente
los indices del plano cristalográficos
y
[uv.]
al hexagonal.
cristalográficos
intercepciones
y
de una
uvw. Entonces
[uvw]. Al conjunto
la localización
Los índices de Miller
planos
Los valores
como familia
puede
a trlvés del origen
de coordenadas
de la línea.
mismo tipo se le designa
sistema
línea en la red cristalina
el trazo de la línea
y cualquier
la dirección
enteros,
cristalográficas
cristalina
coao planos
hexagoaal,
incluyen
ejes cristalográficos.
cuatro
Esto es, [uvtw]
para un plano con la característica
de que
siempre:
u + v
En la figura 10 se muestra
una celda unitaria
Los diferentes
tienen
diferentes
distancia
o
la localización
hexagonal.
juegos de planos,
espaciaaientos
interplanar
(2)
h + k = -i
de planos
direcciones
en
como se auestra en la figura
11,
y
entre planos lo que es conocido
(d). Por ejemplo
dado por:
-10-
para el sistema
cúbico
como
d está
I
I
I
I
I
I
I
I
I
I
I
I
I
Figura 7 Indices de direcciones.
I
I
1.\
I
I
1.\
Designación
JA
(hl
lal
Figura 8
:.lA
de planos
-11-
por índices de miller.
~..a~,.~_
!--d¡tll---;
,
.
-
.,.
-...,'
~:"
-
,
~
'."
,
.
",
.
"'"
',-
( 1101
(2001
( IIMI,I
,
.
'
, ',::': . < ~:
"
:1,.'
-,
~i~:''::',- _
""':~r
. ';-;.~(;
,x
~
"
,
(íw;
Figura
9
(llf2 )
(llí)
Indices
de Miller
de planos
¡0011
Figura
10 Indices
de planos
y
direcciones
-1l-
en una celda
hexagonal.
I
I
I
I
I
I
------
11(1)
(1) )
(13)
Figura
11
Red espacial
en dos dimensiones
de distancia
interplanar.
I
-13-
.ostrando
el concepto
d
= a / V h¿ '+ k.? + l.?
h k I
J~s fórmulas
En la tabla 3 se presentan
interplanar
(3 )
para los diferentes
sistemas
para calcular
la distancia
cristalinos.
Tabla 3
Fórmulas
le Distancia
Interplanar.
Cubic:
Tetraqona}:
Hexagonal:
Rlro",ho¡'edrol:
J
ú2
=
(/¡! + k~ -+- ,1, sin!"Z + ).(¡'k + kl + "' )(cos!2 - COS ::r)
--------~~D'l(~I--~3~c~o~s~2-::r-+~2~co-s~J~::r~,------~~
1
Orthorhomhic:
MOllodinic :
¡,2
kl
12
-;=,+-;+,
d'
a: hr:
2.. =
ell
_1_ (.'.h2 + k2 sin2fi + ,2
sin1, , ,al
,,2
('2
Tndinir:
-14-
_
2'"cos
0('
fJ)
Tela
2.1
de los Rayos
X
Introducción
Los rayos
y
11 Propiedades
X fueron
descubiertos
fueron llamados así debido
rayos son invisibles,
en 1895 por el físico
a su origen
pero viajan
incierto
en ese tiempo.
en línea recta y afectan
fotográfica
en la lisma forma que la lúz. Po otro lado,
penetrantes
que la lúz y pueden
humano,
metales
y
materiales
Los rayos X se aplican
de absorción
alemán
pasar fácilmente
son mucho más
a través
del cuerpo
opacos.
en la radiografía
en base al diferente
de los rayos X para cada material
la cual tiene una resolución
nos permite estudiar
la estructura
tanto se aplica a auchos problemas
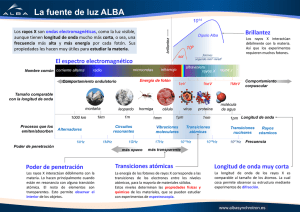
En la figura 12 se auestra
espectro
electroaagnético
Estos
una placa
en la
del orden de 10-s cm; es decir,
interna de los cristales
y
por lo
X
en el
metalúrgicos.
la localización
y éstos
grado
y tiene una resolución
del orden de 10-1 cm. Por otro lado, los rayos X se aplican
difracción,
Roetgen
se enc~entran
de los rayos
en el rango d~ 0.5 a
2.5 A.
1.2 Espectro ~ontinuo y característico
Los rayos X son producidos cuando
una energía cinética
usados cOlúnmente
alta se desacelera
para este propósito,
tubo de rayos X, el cual contiene
electrodos
de metal. Se aplica
.il volts, y rápidamente
anticátodo,
las direcciones.
partícula
rápidamente.
la radiación
eléctrica
con
Los electrones
son
es producida
una fuente de electrones
un alto voltaje,
los electrones
en el cual los electrones
Los rayos X se producen
consisten
cualquier
del orden de unos diez
con alta velocidad
y
se impactan.
se radian en todas
Cuando los rayos X son analizados
-15-
y dos
se atraen hacia el inodo o
en el punto de impacto
de una mezcla de radiaciones
en un
de diferente
se encuentra
longitud
que
de onda
Figura
12 Espectro
de radiaciones
-16-
electromanégtico.
y diferente
intensidad
li figura
13.
dependientes
conocida
como
Aquí se observa
del voltaje
y la intensidad
por las curvas
heUrocromática
por muchas
se conoce
El espectro
rápida desaceleraciónde
todos los electrones
de máxima
onda (recordando
E = energía,
onda).
e
de onda son
de onda
corta. La radiación
como radiación
como también
blanca,
se le conoce,
los electrones
continua
y otros
energía;
=
o
cl ¡ h
de onda del límite
dada por la siguiente
(algunos
en un solo impacto
radiaciones
de la Iúz , '"
velocidad
La longitud
,,=
no
se emiten radiaciones
es frenado
es decir,
por la
y ya que
en la misma forma
parcialmente)
h " y
se origina
en el anticátodo
son desacelerados
que E
=
y longitud
X de
a la lúz blanca que está constituída
diferente longitud de onda.
El caso cuando un electrón
fotones
rayos
de onda.
continuo,
totalmente
de los
es cero en una londitud
de onda
ya que es similar
longitudes
en el espectro
lue la intensidad
como límite de longitud
representada
frenados
se muestra
=
=
son
con
se producen
de baja longitud
de
cte. de Planck,
frecuencia
= longitud de
y 1
de onda corta en angstroms
está
ecuación:
=
1SWL
(4)
12 400/V
donde V es el voltaje del tubo en volts.
Por otro lado, la intensidad
de los rayos X en el espectro
continuo
está dado por:
=
le.c.
donde A es una constante
valor aproximado
del anticátodo.
intensidad
rayos X rebasa
anticátodo
de 2. i la corriente
Cabe hacer
notar
característico
un valor crítico
produciendo
(5 )
vm
de proporcionalidad,
pero no la longitud
El espectro
A i Z
una contante
con un
del tubo y Z el número
atómico
I
que el material
del espectro
cuando
aplicado
del aaterial
de picos de intensidad
-17-
afecta
la
continuo.
el voltaje
característico
la aparición
anticátodo
al tubo de
del
máxima
I
I
I
I
I
..
I
l· .
;;I---_y
....
,_1..:..
I
""ar:II'lrri~, i"
racliatiutl
; 4~-
-.__~~~~
~
~
ron Iinuflu...
l'lulÍ31 ion
i/
;....31----'--
I
."
."
~
Z
2
;..
--<
."
Figura
13
Espectro de rayos
voltaje aplicado.
X del molibdeno
como una funci6n
del
I
I
I
I
-18-
I
sobre-
puestos
longitudes
en el espectro
continuo.
de onda son caracteristicas
com~ lineas caracter isticas.
suficiente
considerar
electrones
en varias
bombardea
de alta energía.
exteriores
y
Si es cubierta
radiación
y
energia
normal.
una longitud
K. La vacancia
por un electrón
de onda definida
d os eompon entes a
1
onda muy cercanas
ya que los ele~trones
capa K provienen
de la capa L, ~ero de
ejemplo el molibdeno
2
(
eon oc ido
presenta
excitado
en el ":
y
en la
se le
co.,.,o
coao
capas
las líneas K son las .ás
K a puede presentar
e1 do b1ete la)
eon Ion, itudes de
que cubren la vacancia
d¡~~n~
las siguientes
orbital.
en la
Así por
radiaciones
caracteristicas:
K el
\
O • 709 26 A
K el
2
0.71354
A
0.63225
A
Kf3
La intensidad
de cualquier
i.
=
donde B es una constante,
línea característica
B i (Y-Vdn
de excitación
K, n una constante
con un valor de aproximadamente
corriente
y
del tubo
K está dada por:
(6)
VK es el voltaje
V el voltaje aplicado.
-19-
por
como radiaci¿n
para las diferentes
de rayos X. La radiación
a
éste puede
de la capa M se le conoce
L, M, etc. Sin embargo,
Y
que
de la capa K puede ser cubierta
K ~ • Esto mismo se pued e aplicar
útiles en difracción
de
La energía emitida
en este caso se le denomina
y
sus
de las capas inmediatas
su estado
posee
tener la radiación
cinética,
de la capa K, e s i t Le ndo energía
el átomo recupera
de la capa L
rodeado
al átoBo en un estado
Uno de los electrones
cubre la vacancia
un electrón
y
(figora 14). Si uno de los electrones
de la capa K, dejando
conoce como radiación
y
el origen de estas lineas es
por un n~cleo
tiene saficiente
forma de una radiación
K a.
Para entender
capas
son angostos
del material usado se les conoce
a un átom~ formado
el anticátodo
sacar un electrón
proceso
Ya que éstos
de la línea
de 1.5, i la
,.
Figura
14
Transiciones
electrónicas
-20-
en un ito.o.